The Impacts of International Political and Economic Events on Japanese Financial Markets
Abstract
1. Introduction
2. Methodology
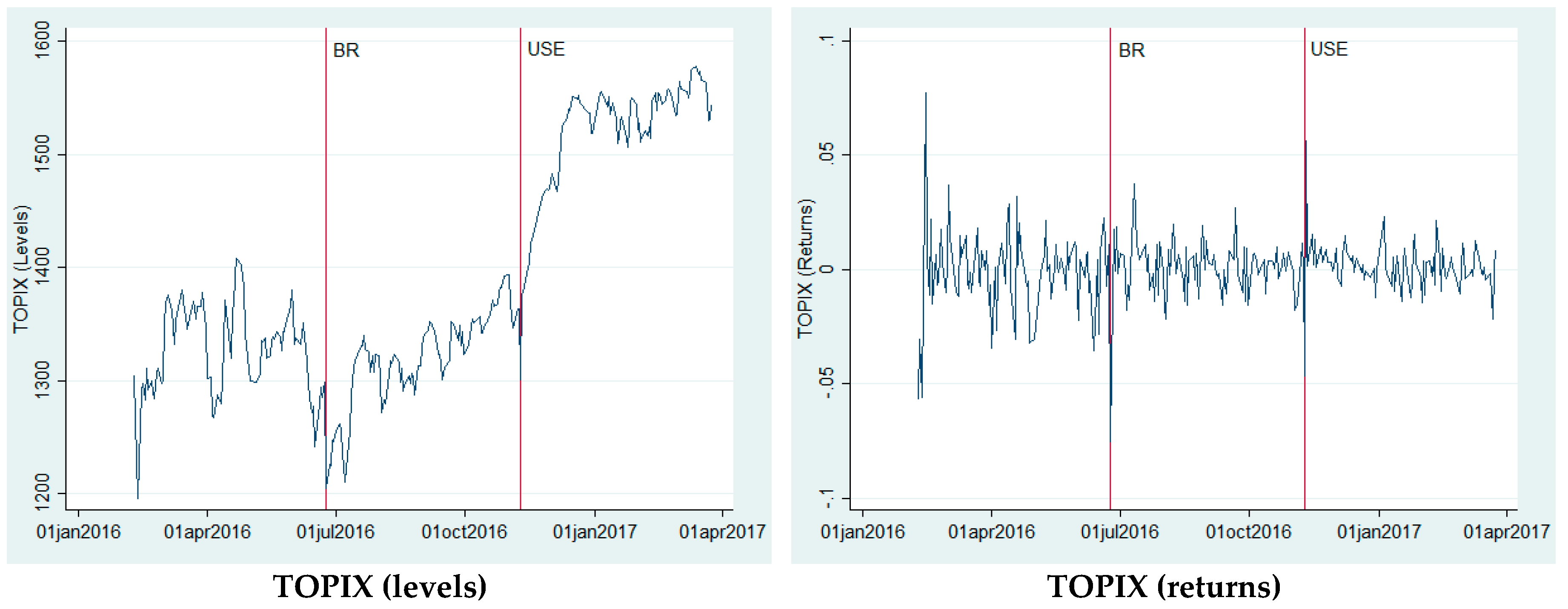
3. Data Description
4. Empirical Results
4.1. Model Estimations
4.2. Changes in Causality Relationship
5. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Agren, Martin. 2006. Does Oil Price Uncertainty Transmit to Stock Markets? Working Paper Series 2006: 23; Uppsala: Uppsala University, Department of Economics. [Google Scholar]
- Bashir, Usman, Gilney Figueira Zebende, Yugang Yu, Muntazir Hussain, Ahmed Ali, and Ghulam Abbas. 2019. Differential market reactions to pre and post Brexit referendum. Physica A: Statistical Mechanics and its Applications 515: 151–58. [Google Scholar] [CrossRef]
- Belke, Ansgar, Irina Dubova, and Thomas Osowski. 2018. Policy uncertainty and international financial markets: the case of Brexit. Applied Economics 50: 3752–70. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalised autoregressive conditional hetroscedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Ray Chou, and Kenneth Kroner. 1992. ARCH modeling in finance: A review of the theory and empirical evidence. Journal of Econometrics 52: 5–59. [Google Scholar] [CrossRef]
- Box, George, and David Pierce. 1970. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. Journal of the American Statistical Association 65: 1509–26. [Google Scholar] [CrossRef]
- Chung, Chae-Shik, and Youngmin Jang. 2000. Analysis of changes in the relationship between the KRW/USD exchange rate and JPY/USD exchange rate before and after the economic crisis. East Asian Economic Review 4: 65–93. [Google Scholar] [CrossRef]
- Dickey, Alan, and Arthur Wayne Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dickey, Alan, and Arthur Wayne Fuller. 1981. Likelihood ration statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Engle, Robert. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional hetroscedasticity models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert, and Kevin Sheppard. 2001. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate GARCH. NBER Working Paper No. 8554. Available online: https://ssrn.com/abstract=1296441 (accessed on 30 March 2020).
- Glosten, Lawrence, Ravi Jagannathan, and David Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hamori, Shigeyuki. 2003. An Empirical Investigation of Stock Markets: The CCF Approach. New York: Kluwer Academic Publisher. [Google Scholar]
- Hanabusa, Kunihiro. 2010. Effects of foreign disasters on the petroleum industry in Japan: A financial market perspective. Energy 35: 5455–63. [Google Scholar] [CrossRef]
- Hong, Yongmiao. 2001. A test for volatility spillover with application to exchange rates. Journal of Econometrics 103: 183–224. [Google Scholar] [CrossRef]
- Jarque, Carlos, and Anil Bera. 1987. A test for normality of observations and regression residuals. International Statistical Review 55: 163–72. [Google Scholar] [CrossRef]
- Kadiric, Samir, and Arthur Korus. 2019. The effects of Brexit on credit spreads: Evidence from UK and Eurozone corporate bond markets. International Economics and Economic Policy 16: 65–102. [Google Scholar] [CrossRef]
- Karfakis, Costas, and Theodore Panagiotidis. 2015. The effects of global monetary policy and Greek debt crisis on the dynamic conditional correlations of currency markets. Empirica (Journal of European Economics) 42: 795–811. [Google Scholar] [CrossRef]
- Lin, Chin-Tsai, and Yi-Hsien Wang. 2005. An analysis of political changes on Nikkei 225 stock returns and volatilities. Annals of Economics and Finance 6: 169–83. [Google Scholar]
- Ljung, Greta, and George Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Nelson, Daniel. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Ross, Stephen. 1989. Information and volatility: The no-arbitrage Martingale approach to timing and resolution irrelevancy. Journal of Finance 44: 1–17. [Google Scholar] [CrossRef]
- Schwert, William. 1989. Why does stock market volatility change over time? Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Shaikh, Imlak. 2017. The 2016 U.S. presidential election and the stock, FX and VIX markets. The North American Journal of Economics and Finance 42: 546–63. [Google Scholar] [CrossRef]
- Sultonov, Mirzosaid, and Shahzadah Jehan. 2018. Dynamic linkages between Japan’s foreign exchange and stock markets: Response to the Brexit referendum and the 2016 U.S. presidential election. Journal of Risk and Financial Management 11: 34. [Google Scholar] [CrossRef]
- Taylor, Stephen. 1986. Modelling Financial Time Series. Chichester and New York: Wiley. [Google Scholar]
- Wang, Lin, and Ali Kutan. 2013. The impact of natural disasters on stock markets: Evidence from Japan and the US. Comparative Economic Studies 55: 672–86. [Google Scholar] [CrossRef]
| 1 |

| Variables | Obs. | Mean | Std. Dev. | Skewness | Kurtosis | Jarque–Bera | ADF |
|---|---|---|---|---|---|---|---|
| Whole period: 9 February 2016 to 24 March 2017 | |||||||
| JPY | 276 | −0.00019 | 0.00840 | −0.54315 | 8.59034 | 373.00 *** | −3.633 *** |
| Nikkei | 276 | 0.00045 | 0.01514 | −0.45002 | 9.52024 | 498.20 *** | −5.304 *** |
| TOPIX | 276 | 0.00041 | 0.01458 | −0.36411 | 9.87909 | 550.30 *** | −5.303 *** |
| Before BR: 9 February 2016 to 23 June 2016 | |||||||
| JPY | 92 | −0.00123 | 0.00865 | −1.95794 | 11.7919 | 355.10 *** | −3.468 ** |
| Nikkei | 92 | −0.00050 | 0.01856 | 0.05303 | 5.24109 | 19.300 *** | −3.264 ** |
| TOPIX | 92 | −0.00066 | 0.01866 | 0.14395 | 6.35728 | 43.520 *** | −3.068 *** |
| After BR and before USE: 24 June 2016 to 8 November 2016 | |||||||
| JPY | 92 | −0.00002 | 0.00793 | −0.61696 | 5.09002 | 22.580 *** | −3.467 ** |
| Nikkei | 92 | 0.00061 | 0.01402 | −2.01021 | 15.1419 | 627.10 *** | −3.381 *** |
| TOPIX | 92 | 0.00053 | 0.01324 | −1.82225 | 13.5368 | 476.50 *** | −3.347 *** |
| After USE: 9 November 2016 to 24 March 2017 | |||||||
| JPY | 92 | 0.00069 | 0.00857 | 0.96898 | 6.62240 | 64.700 *** | −2.959 ** |
| Nikkei | 92 | 0.00125 | 0.01224 | 0.54557 | 13.9792 | 466.60 *** | −2.951 ** |
| TOPIX | 92 | 0.00135 | 0.01081 | 0.46879 | 12.6791 | 362.50 *** | −2.657 * |
| JPY | JPY | JPY | Nikkei | Nikkei | Nikkei | TOPIX | TOPIX | TOPIX | |
|---|---|---|---|---|---|---|---|---|---|
| Mean | |||||||||
| C | 0.0000 (0.0005) | −0.0001 (0.0029) | −0.0003 *** (0.0001) | 0.0000 (0.0002) | 0.0004 ** (0.0002) | 0.0001 *** (0.0000) | 0.0004 *** (0.0001) | 0.0002 (0.0009) | 0.0004 (0.0008) |
| −0.0205 (0.0869) | −0.0430 (0.3057) | −0.0940 *** (0.0022) | 0.0265 *** (0.0028) | 0.0373 (0.1296) | 0.0086 ** (0.0038) | 0.0297 ** (0.0137) | 0.1099 (0.1164) | 0.0247 (0.0782) | |
| Brexit 1 week | 0.0035 (0.0043) | −0.0017 (0.0430) | −0.0333 (0.0373) | ||||||
| Brexit 2 weeks | −0.0004 *** (0.0000) | −0.0062 (0.0081) | −0.0048 *** (0.0009) | ||||||
| USE 1 week | 0.0084 (0.0107) | −0.0013 (0.0062) | −0.0066 (0.0180) | ||||||
| USE 2 weeks | 0.0084 *** (0.0002) | 0.0030 *** (0.0010) | 0.0028 (0.0029) | ||||||
| Variance | |||||||||
| ω | −17.037 *** (2.8158) | −17.744 *** (1.1457) | −19.152 *** (1.2575) | −0.4111 ** (0.1937) | −6.7280 (7.6965) | −0.5606 (0.3791) | −0.4377 * (0.2253) | −0.8037 (0.5124) | −0.4830 (0.9977) |
| −0. 1143 (0.0727) | −0.1253 (0.0792) | −0.0470 (0.0829) | −0.3005 *** (0.0746) | −0.3462 * (0.1861) | −0.3002 *** (0.0794) | −0.2934 *** (0.0710) | −0.3987 *** (0.1260) | −0.2919 *** (0.1085) | |
| α1 | 0.0289 (0.1806) | −0.0197 (0.1490) | −0.0127 (0.1146) | 0.0303 (0.0550) | 0.3277 (0.3088) | 0.0912 (0.1093) | 0.0653 (0.0662) | 0.1312 (0.1272) | 0.0950 (0.3392) |
| β1 | −0.7649 *** (0.2939) | −0.8206 *** (0.1229) | −0.9651 *** (0.1084) | 0.9532 *** (0.0221) | 0.2360 (0.8813) | 0.9350 *** (0.0442) | 0.9517 *** (0.0251) | 0.9111 *** (0.0575) | 0.9458 *** (0.1149) |
| Brexit 1 week | 2.1566 * (1.2185) | 2.0436 (1.4497) | 0.5064 (0.8815) | ||||||
| Brexit 2 weeks | 1.3502 (1.1926) | 0.0598 (0.1573) | 0.0160 (0.0819) | ||||||
| USE 1 week | 1.0209 (1.2260) | 1.5501 (1.9073) | 0.0544 (0.6265) | ||||||
| USE 2 weeks | 0.9928 (0.9905) | −0.2012 (0.1998) | −0.1171 (0.5512) | ||||||
| GED parameter | 0. 1204 (0.1291) | 0.1668 (0.1543) | 0.1608 (0.1334) | 0.1253 (0.1215) | 0.1980 (0.3048) | 0.1400 (0.1178) | 0.1928 (0.1280) | 0.4538 * (0.2597) | 0.1943 (0.1466) |
| Diagnostic | |||||||||
| Q(5) | 5.0193 (0.4135) | 3.8026 (0.5782) | 3.5284 (0.6191) | 2.5675 (0.7663) | 6.7945 (0.2364) | 1.7072 (0.8880) | 3.0440 (0.6932) | 3.5301 (0.6188) | 2.7364 (0.7405) |
| Q2(5) | 1.0372 (0.9595) | 1.2148 (0.9434) | 0.9833 (0.9639) | 1.4679 (0.9167) | 6.2153 (0.2858) | 1.2978 (0.9352) | 1.6036 (0.9008) | 3.9060 (0.5630) | 2.0401 (0.8436) |
| Pair | Before BR | After BR (Before USE) | After USE |
|---|---|---|---|
| JPY to Nikkei | −0.0387 | 0.0190 | 0.0337 |
| Nikkei to JPY | 0.2852 *** | 0.0581 | 0.0749 * |
| JPY to TOPIX | −0.0871 | −0.0219 | 0.0547 |
| TOPIX to JPY | 0.2625 *** | −0.0669 | 0.0000 |
| Nikkei to TOPIX | −0.0029 | 0.1284 | −0.0423 |
| TOPIX to Nikkei | 0.0285 | −0.1518 | −0.0304 ** |
| Pair | Before BR | After BR (Before USE) | After USE |
|---|---|---|---|
| JPY to Nikkei | −0.0562 * | 0.0132 ** | −0.0032 ** |
| Nikkei to JPY | 0.4434 *** | −0.0478 ** | 0.6210 *** |
| JPY to TOPIX | −0.0629 * | −0.0114 ** | 0.0184 ** |
| TOPIX to JPY | 0.3480 *** | −0.0413 ** | 0.5774 *** |
| Nikkei to TOPIX | −0.0562 | −0.0072 ** | 0.0123 * |
| TOPIX to Nikkei | 0.1631 | −0.0141 ** | 0.0023 * |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultonov, M. The Impacts of International Political and Economic Events on Japanese Financial Markets. Int. J. Financial Stud. 2020, 8, 43. https://doi.org/10.3390/ijfs8030043
Sultonov M. The Impacts of International Political and Economic Events on Japanese Financial Markets. International Journal of Financial Studies. 2020; 8(3):43. https://doi.org/10.3390/ijfs8030043
Chicago/Turabian StyleSultonov, Mirzosaid. 2020. "The Impacts of International Political and Economic Events on Japanese Financial Markets" International Journal of Financial Studies 8, no. 3: 43. https://doi.org/10.3390/ijfs8030043
APA StyleSultonov, M. (2020). The Impacts of International Political and Economic Events on Japanese Financial Markets. International Journal of Financial Studies, 8(3), 43. https://doi.org/10.3390/ijfs8030043





