Currency Market Efficiency Revisited: Evidence from Korea
Abstract
:1. Introduction
2. Analytical Framework and a Review of the Relevant Literature
3. Data and Methodology
4. Empirical Analysis and Results
4.1. Runs Test for Detecting Randomness
4.2. Test for the Forward Rate Unbiasedness Hypothesis (FRUH)
4.2.1. Price Discrepancy (Forecast Error) Test
4.2.2. Johansen Cointegration Test and Error Correction Model (ECM) Approach
4.2.3. Fama’s Regression Approach
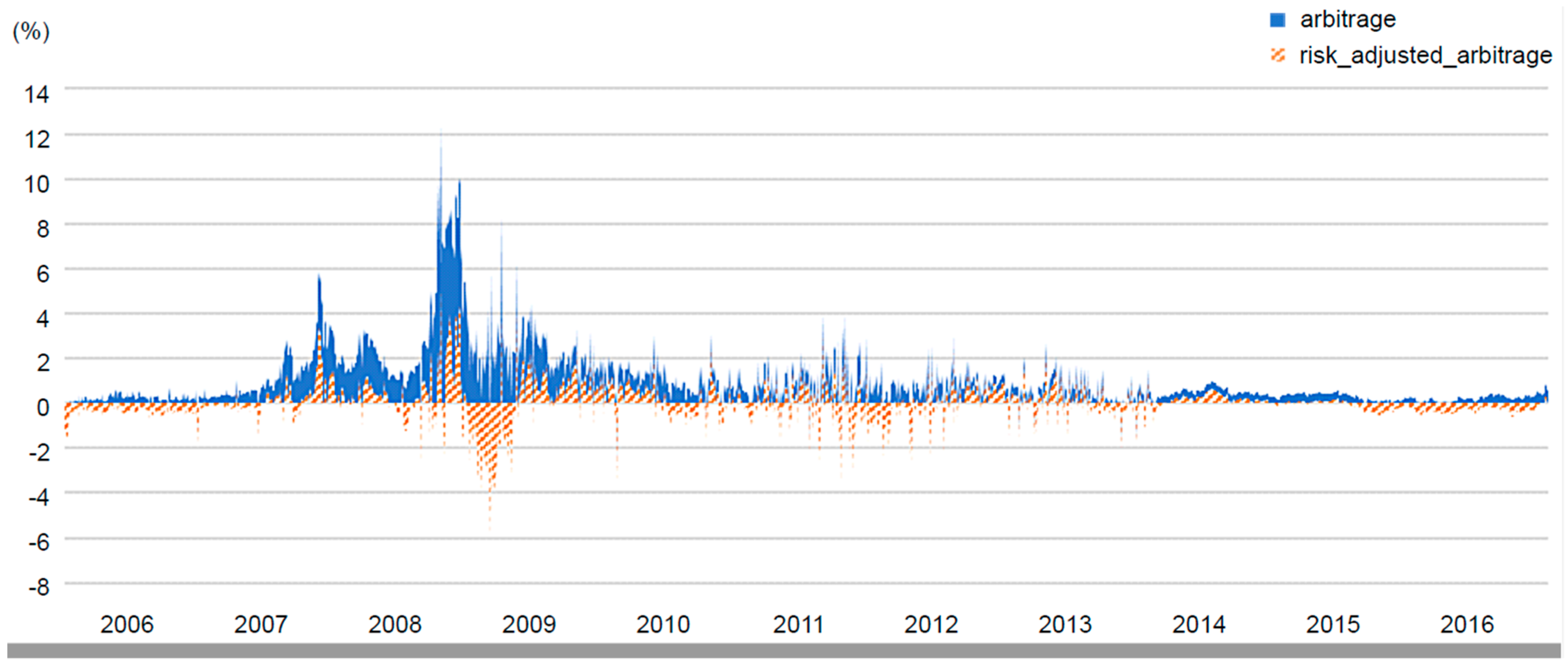
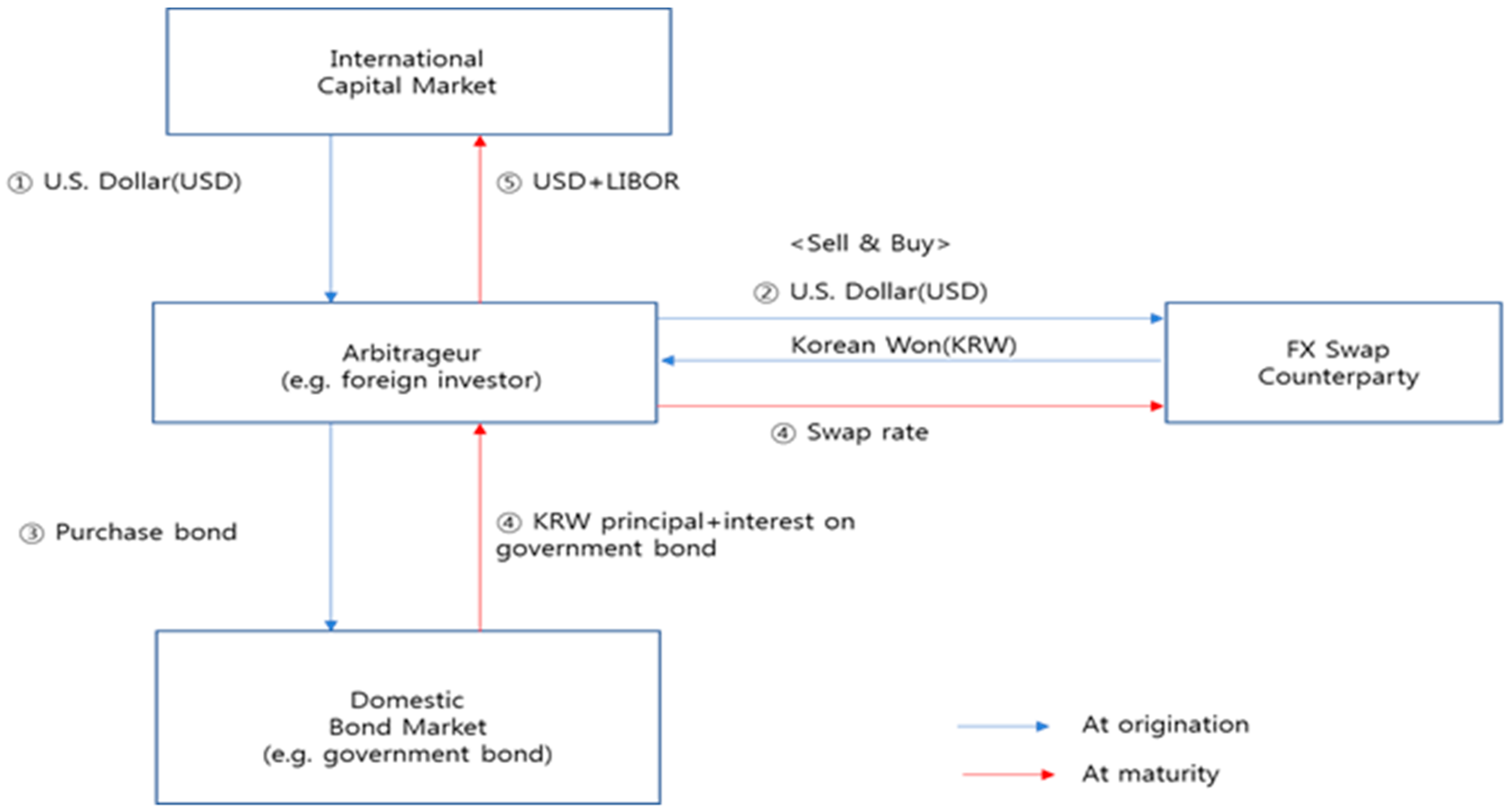
4.3. Puzzling Deviation from Covered Interest Rate Parity (CIP)
5. Concluding Remarks
Funding
Conflicts of Interest
Appendix A
| (A) Entire sample period | |||
| Spot Intervention (s) | Forward Intervention (f) | Risk Factor (r) | |
| spot intervention (s) | 1 | ||
| forward intervention (f) | 0.164759 | 1 | |
| risk factor (r) | −0.321210 | −0.053677 | 1 |
| (B) post-crisis period | |||
| Spot Intervention (s) | Forward Intervention (f) | Risk Factor (r) | |
| spot intervention (s) | 1 | ||
| forward intervention (f) | 0.304054 | 1 | |
| risk factor (r) | −0.008382 | −0.148939 | 1 |
Appendix B

References
- Ahmad, Rubi, S. Ghon Rhee, and Yuen Meng Wong. 2012. Foreign exchange market efficiency under recent crises: Asia-Pacific focus. Journal of International Money and Finance 31: 1574–92. [Google Scholar] [CrossRef]
- Baba, Naohiko, and Frank Packer. 2009. Interpreting deviations from covered interest parity during the financial market turmoil of 2007–08. Journal of Banking and Finance 33: 1953–62. [Google Scholar] [CrossRef]
- Baba, Naohiko, and Ilhyock Shim. 2014. Dislocations in the won-dollar swap markets during the crisis of 2007–2009. International Journal of Finance and Economics 19: 279–302. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Tim Bollerslev. 1989. Common stochastic trends in a system of exchange rates. The Journal of Finance 44: 167–81. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Tim Bollerslev. 2000. The forward premium anomaly is not as bad as you think. Journal of International Money and Finance 19: 471–88. [Google Scholar] [CrossRef]
- Bank of International Settlement. 2016. The triennial central bank survey of FX and over-the-counter (OTC) derivatives markets in 2016. Press Release, December 11. [Google Scholar]
- Bank of Korea. 2017. Foreign exchange market trends during 2016. Press Release, January 19. [Google Scholar]
- Bhar, Ramprasad, Suk-Joong Kim, and Toan M. Pham. 2004. Exchange rate volatility and its impact on the transaction costs of covered interest rate parity. Japan and the World Economy 16: 503–25. [Google Scholar] [CrossRef]
- Burt, John, Fred R. Kaen, and G. Geoffrey Booth. 1977. Foreign exchange market efficiency under flexible exchange rates. The Journal of Finance 32: 1325–30. [Google Scholar] [CrossRef]
- Chang, Eui Tae. 2008. Determinants of deviations from covered interest parity in Korea during 1999~2007. Journal of Money and Finance 22: 185–215. [Google Scholar]
- Chung, Heechun. 2010. The Bank of Korea’s Policy Response to the Global Financial Crisis. BIS Papers, No. 54. Basel: Bank for International Settlements. [Google Scholar]
- Coffey, Niall, Warren B. Hrung, and Asani Sarkar. 2009. Capital Constraints, Counterparty Risk, and Deviations from Covered Interest Rate Parity. Federal Reserve Bank of New York Staff Reports, No. 393. New York: Federal Reserve Bank of New York. [Google Scholar]
- Cornell, Bradford. 1977. Spot rates, forward rates and exchange market efficiency. Journal of Financial Economics 5: 55–65. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Engel, Robert F., and Clive W. J. Granger. 1987. Co-integration and error correction: Representation, estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Evans, Martin D. D., and Karen K. Lewis. 1993. Trends in excess returns in currency and bond markets. European Economic Review 37: 1005–19. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1984. Forward and spot exchange rates. Journal of Monetary Economics 14: 319–38. [Google Scholar] [CrossRef]
- Finch, Gavin. 2017. World’s Biggest Banks Fined $321 Billion Since Financial Crisis. Bloomberg. Available online: https://www.bloomberg.com/news/articles/2017-03-02/world-s-biggest-banks-fined-321-billion-since-financial-crisis (accessed on 4 November 2017).
- Frankel, Jeffrey A. 1980. Test of rational expectations in the forward exchange market. Southern Economic Journal 46: 1083–101. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A., and Jumana Poonawala. 2010. The forward market in emerging currencies: Less biased than in major currencies. Journal of International Money and Finance 29: 585–98. [Google Scholar] [CrossRef]
- Frenkel, Jacob A., and Richard M. Levich. 1975. Covered interest arbitrage: Unexploited profits? Journal of Political Economy 83: 325–38. [Google Scholar] [CrossRef]
- Frenkel, Jacob A., and Richard M. Levich. 1977. Transaction costs and interest arbitrage: Tranquil versus turbulent periods. Journal of Political Economy 85: 1209–26. [Google Scholar] [CrossRef]
- Froot, Kenneth A., and Richard H. Thaler. 1990. Anomalies: Foreign exchange. Journal of Economic Perspectives 4: 179–92. [Google Scholar] [CrossRef]
- Gilmore, Stephen, and Fumio Hayashi. 2011. Emerging market currency excess returns. American Economic Journal: Macroeconomics 3: 85–111. [Google Scholar] [CrossRef]
- Grauer, Frederick L. A., Robert H. Litzenberger, and Richard E. Stehle. 1976. Sharing rules and equilibrium in an international capital market under uncertainty. Journal of Financial Economics 3: 233–56. [Google Scholar] [CrossRef]
- Griffoli, Tommaso M., and Angelo Ranaldo. 2012. Limits to Arbitrage during the Crisis: Funding Liquidity Constraints and Covered Interest Parity. Working Papers on Finance, Swiss Institute of Banking and Finance, No. 2012/12. St. Gallen: Swiss Institute of Banking and Finance. [Google Scholar]
- Hakkio, Craig S., and Mark Rush. 1989. Market efficiency and cointegration: An application to the sterling and deutschemark exchange markets. Journal of International Money and Finance 8: 75–88. [Google Scholar] [CrossRef]
- Jensen, Michael C. 1978. Some anomalous evidence regarding market efficiency. Journal of Financial Economics 6: 95–101. [Google Scholar] [CrossRef]
- Johansen, Søren. 1988. Statistical analysis of cointegrating vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Johansen, Søren. 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59: 1551–80. [Google Scholar] [CrossRef]
- Levich, Richard M. 1989. Is the foreign exchange market efficient? Oxford Review of Economic Policy 5: 40–60. [Google Scholar] [CrossRef]
- Muth, John F. 1961. Rational expectations and the theory of price movements. Econometrica 29: 315–35. [Google Scholar] [CrossRef]
- Park, Dae Keun. 2000. The non-deliverable forward exchange market and the Korean currency crisis. Kukje Kyungje Yongu 6: 1–22. [Google Scholar]
- Park, Hae Sik. 2010. Persistent factor of interest rate arbitrage in the Korean economy. Weekly Finance Brief, Korea Institute for Finance 19: 12–13. [Google Scholar]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Ryoo, Sangdai, Taeyong Kwon, and Hyejin Lee. 2013. Foreign Exchange Market Developments and Intervention in Korea. BIS Paper, No. 73. Basel: Bank for International Settlements. [Google Scholar]
- Sarno, Lucio. 2005. Viewpoint: Towards a solution to the puzzles in exchange rate economics: Where do we stand? The Canadian Journal of Economic/Revue Canadienne d’Economique 38: 673–708. [Google Scholar] [CrossRef]
- Song, Chi Young, and Kyung Soo Kim. 2008. What lies behind persistent failure of covered interest parity in the won/dollar exchange market: An empirical investigation. Korea Review of Applied Economics 10: 5–32. [Google Scholar]
- Taylor, Mark P. 1987. Covered interest parity: A high-frequency, high-quality data study. Economica 54: 429–38. [Google Scholar] [CrossRef]
| Articles | Data | Estimation Techniques | Results | |
|---|---|---|---|---|
| FRUH (or Forward bias puzzle) testing | Frankel (1980) | GBP, DEM, FRF, ITL July 1974 to April 1978 | OLS estimation |
|
| Fama (1984) | Nine major currencies August 1973 to December 1982 | OLS estimation |
| |
| Hakkio and Rush (1989) | GBP, DEM July 1975 to October 1986 | Cointegration test Error correction model |
| |
| Evans and Lewis (1993) | GBP, DEM, JPY January 1975 to December 1989 | Johansen test |
| |
| Baillie and Bollerslev (2000) | DEM January 1974 to December 1991 | OLS estimation |
| |
| Frankel and Poonawala (2010) | 14 emerging market (EM) currencies December 1996 to April 2004 | OLS estimation |
| |
| Gilmore and Hayashi (2011) | 20 EM currencies plus 9 major currencies June 1996 to December 2010 | OLS estimation |
| |
| Ahmad et al. (2012) | 12 Asia-Pacific currencies January 1997 toJune 2010 | Johansen test OLS estimation |
| |
| Persistent CIP deviations puzzle | Baba and Packer (2009) | FX swap implied rate (EUR), dollar Libor, CDS spreads September 2006 to September 2008 | EGARCH (1,1) |
|
| Griffoli and Ranaldo (2012) | EUR, CHF, JPY, GBP, CDS, VIX, TED, Libor-OIS March 2006 to April 2009 | Time-series, panel regression |
| |
| Song and Kim (2008) | KRW January 2000 to April 2007 | OLS estimation |
| |
| Chang (2008) | KRW April 1999 to December 2007 | OLS estimation |
|
| Type of Risk | Property of Risk | Relevant Data | |
|---|---|---|---|
| Credit risk | Counterparty risk | Perceived credit or default risk in the economy from the perspective of a lender | Credit default swap (CDS) premium on the Korean government bond with a maturity of one year † |
| Liquidity risk | Funding liquidity risk ‡ | Difficulty of borrowing in the international financial market | TED spread, which is the difference between the Libor and U.S. T-bills |
| Market liquidity risk | Transaction costs incurred when a trade is executed | Bid-ask spread in the Korean foreign exchange market | |
| Entire Period (1 January 2006~31 December 2016) | Post-Crisis Period (1 January 2010~31 December 2016) | |||||
|---|---|---|---|---|---|---|
| + | - | 0 | + | - | 0 | |
| Runs in days | 1321 | 1379 | 38 | 838 | 882 | 20 |
| Total observed Runs | 1296 | 823 | ||||
| Total expected runs | 1350.38 | 860.44 | ||||
| Standard error | 25.96 | 20.72 | ||||
| Z statistic † | 2.09 | 1.81 | ||||
| Result | Reject the null hypothesis of random process | Do not reject the null hypothesis | ||||
| Mean | Standard Error | t-Statistic | Autocorrelation | Partial Correlation | ||||
|---|---|---|---|---|---|---|---|---|
| Lag 1 | Lag 2 | Lag 3 | Lag 1 | Lag 2 | Lag 3 | |||
| −0.000689 | 0.001096 | −0.628633 | 0.980 | 0.963 | 0.947 | 0.980 | 0.063 | 0.037 |
| ADF | PP | ||||
|---|---|---|---|---|---|
| t-Statistic | Probability | t-Statistic | Probability | ||
| Spot rates | Level | 0.472731 | 0.8169 | 0.491109 | 0.8213 |
| First difference | −59.54119 | 0.0001 | −59.54119 | 0.0001 | |
| Forward rates | Level | 0.100381 | 0.7144 | 0.092737 | 0.7121 |
| Fist difference | −56.70606 | 0.0001 | −56.70606 | 0.0001 | |
| (A) Unrestricted cointegration rank test (Trace) | |||
| Hypothesized No. of Cointegrating Equation(s) | Trace Statistic | 0.05 Critical Value | Probability |
| None * | 37.11482 | 20.26184 | 0.0001 |
| At most 1 | 4.640844 | 9.164546 | 0.3251 |
| (B) Unrestricted cointegration rank test (maximum eigenvalue) | |||
| Hypothesized No. of Cointegrating Equation(s) | Max. Eigen-Statistic | 0.05 Critical Value | Probability |
| None * | 32.47398 | 15.89210 | 0.0001 |
| At most 1 | 4.640844 | 9.164546 | 0.3251 |
| t-Statistic | Probability | ||
|---|---|---|---|
| Augmented Dickey-Fuller test statistic | −4.659592 | 0.0000 | |
| 7.16 × 10−5 | 0.018271 | −0.005835 * | 0.465808 | 0.981871 | −2.112434 |
| Wald Statistic | F-Probability | |||||
|---|---|---|---|---|---|---|
| Entire sample period (1 January 2006~31 December 2016) | 0.001155 | 0.761797 | 1.041198 | 8.454262 | 3.692133 | 0.0250 |
| Post-crisis period (1 January 2010~31 December 2016) | −0.003093 | 0.667737 | −3.004856 | 5.946705 | 15.79272 | 0.0000 |
| (A) Risk-adjusted arbitrage | ||||
| Entire Sample Period | Post-Crisis Period | |||
| Coefficient | t-Statistic | Coefficient | t-Statistic | |
|---|---|---|---|---|
| Constant (α) | 0.022979 | 0.437559 | 0.008062 | 0.207459 |
| Spot intervention (s) | −0.010874 | −0.969072 | −0.002904 | −0.260960 |
| Forward intervention (f) | 0.059555 *** | 3.754809 | 0.024829 ** | 2.179205 |
| Adj. R2 | 0.085954 | 0.034060 | ||
| (B) Original arbitrage | ||||
| Entire Sample Period | Post-Crisis Period | |||
| Coefficient | t-Statistic | Coefficient | t-Statistic | |
| Constant (α) | 0.084393 | 1.127275 | 0.222637 *** | 2.716893 |
| Spot intervention (s) | −0.015182 | −1.284817 | −0.001679 | −0.157680 |
| Forward intervention (f) | 0.059540 *** | 3.758595 | 0.019852 * | 1.801014 |
| Risk factor (r) | 0.943651 *** | 19.25290 | 0.635225 *** | 5.115877 |
| Adj. R2 | 0.769758 | 0.226943 | ||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.-w. Currency Market Efficiency Revisited: Evidence from Korea. Int. J. Financial Stud. 2019, 7, 52. https://doi.org/10.3390/ijfs7030052
Kang M-w. Currency Market Efficiency Revisited: Evidence from Korea. International Journal of Financial Studies. 2019; 7(3):52. https://doi.org/10.3390/ijfs7030052
Chicago/Turabian StyleKang, Min-woo. 2019. "Currency Market Efficiency Revisited: Evidence from Korea" International Journal of Financial Studies 7, no. 3: 52. https://doi.org/10.3390/ijfs7030052
APA StyleKang, M.-w. (2019). Currency Market Efficiency Revisited: Evidence from Korea. International Journal of Financial Studies, 7(3), 52. https://doi.org/10.3390/ijfs7030052





