Forecasting Term Structure of Interest Rates in Japan
Abstract
1. Introduction
Literature Review
2. Theoretical Model
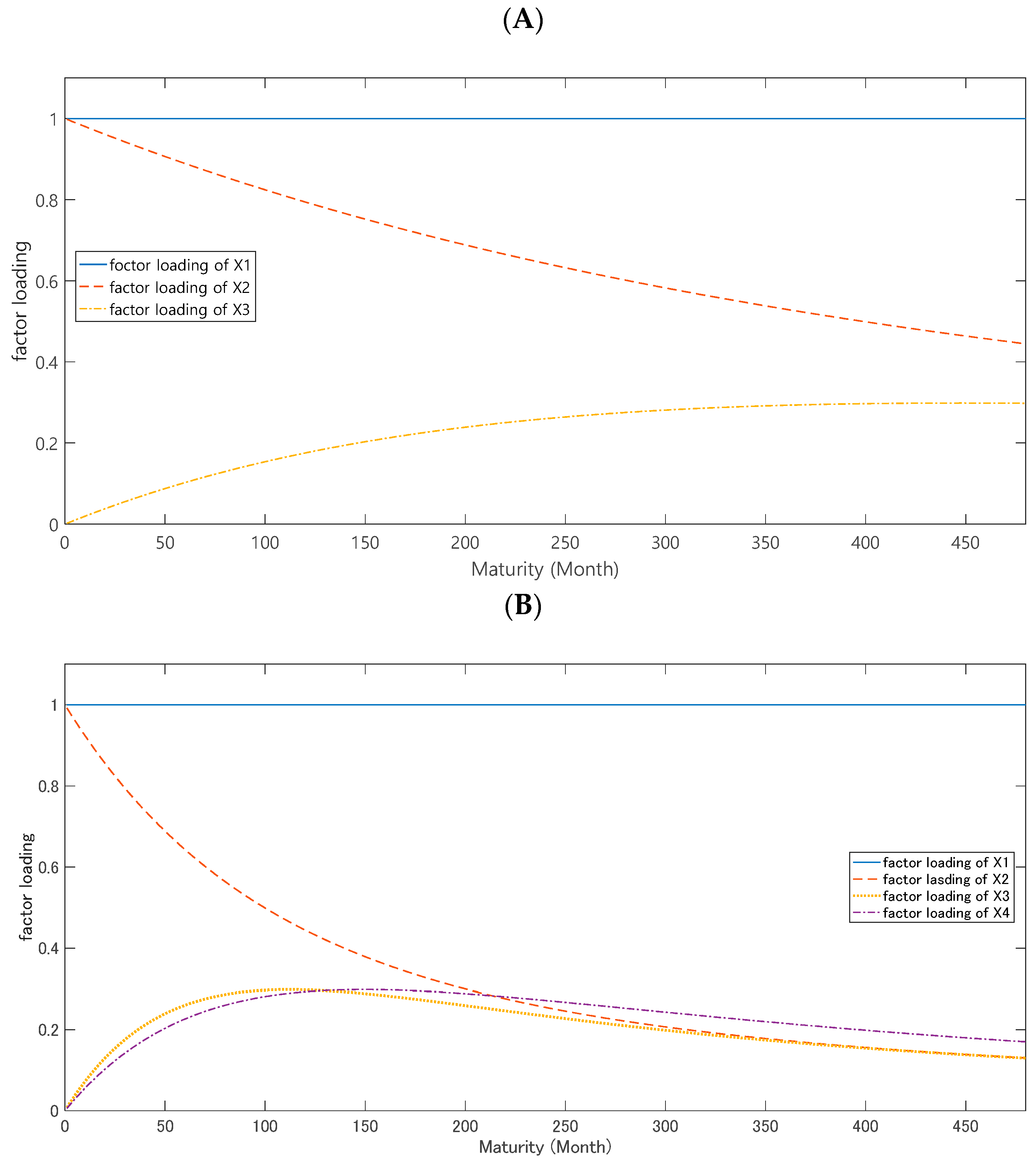
2.1. The Framework of the DNS and the DNSS Model
2.2. Affine Term Structure Model
2.3. Continuous-Time AFNS Framework
2.4. Discrete-Time AFNS
3. Empirical Models
4. Estimation
4.1. Estimation of the Values of
4.2. Estimation of Latent State Variables
4.3. Estimation of the Transition Matrix
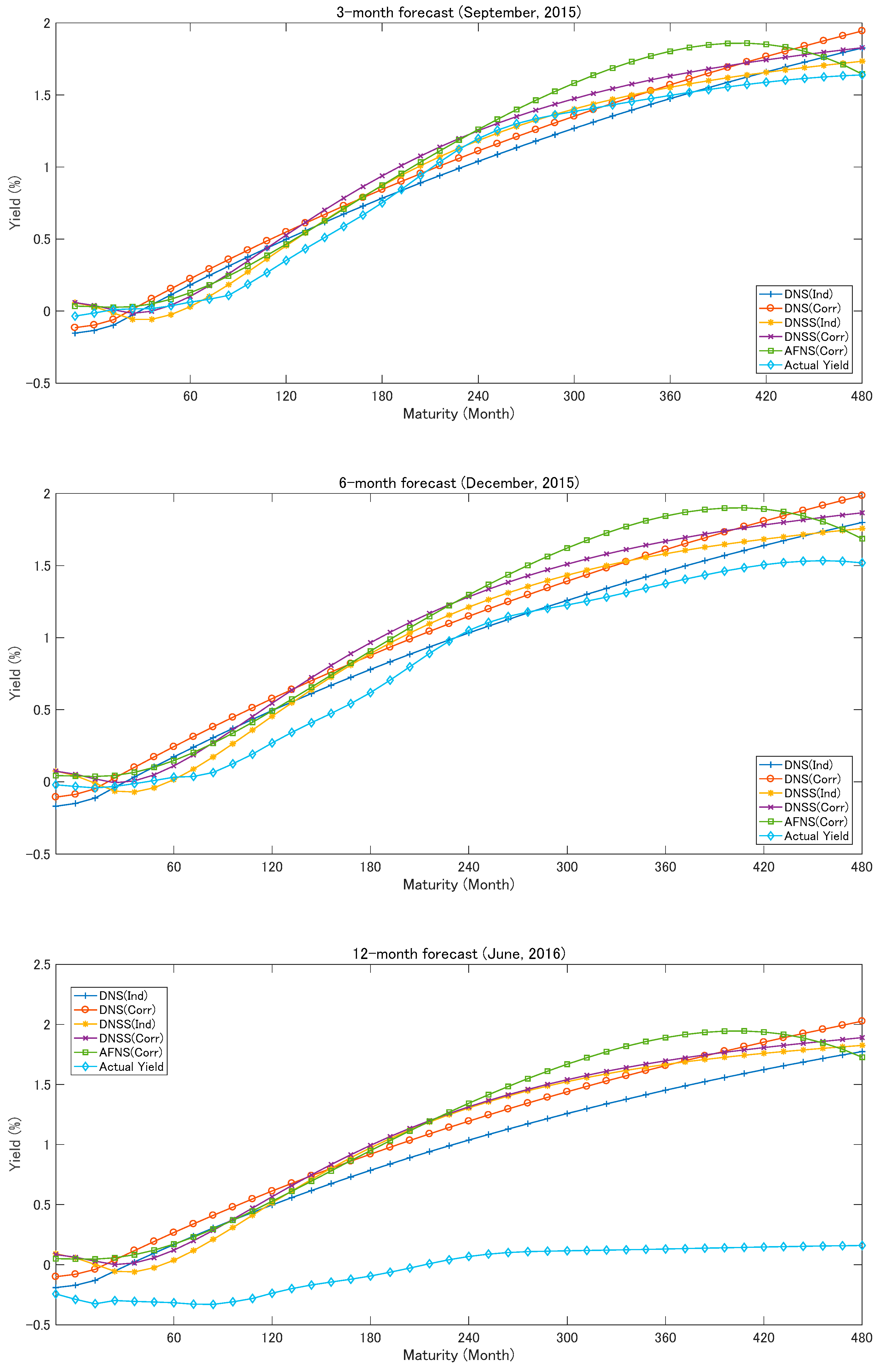
5. Results: Forecasting Performances of the Three Models
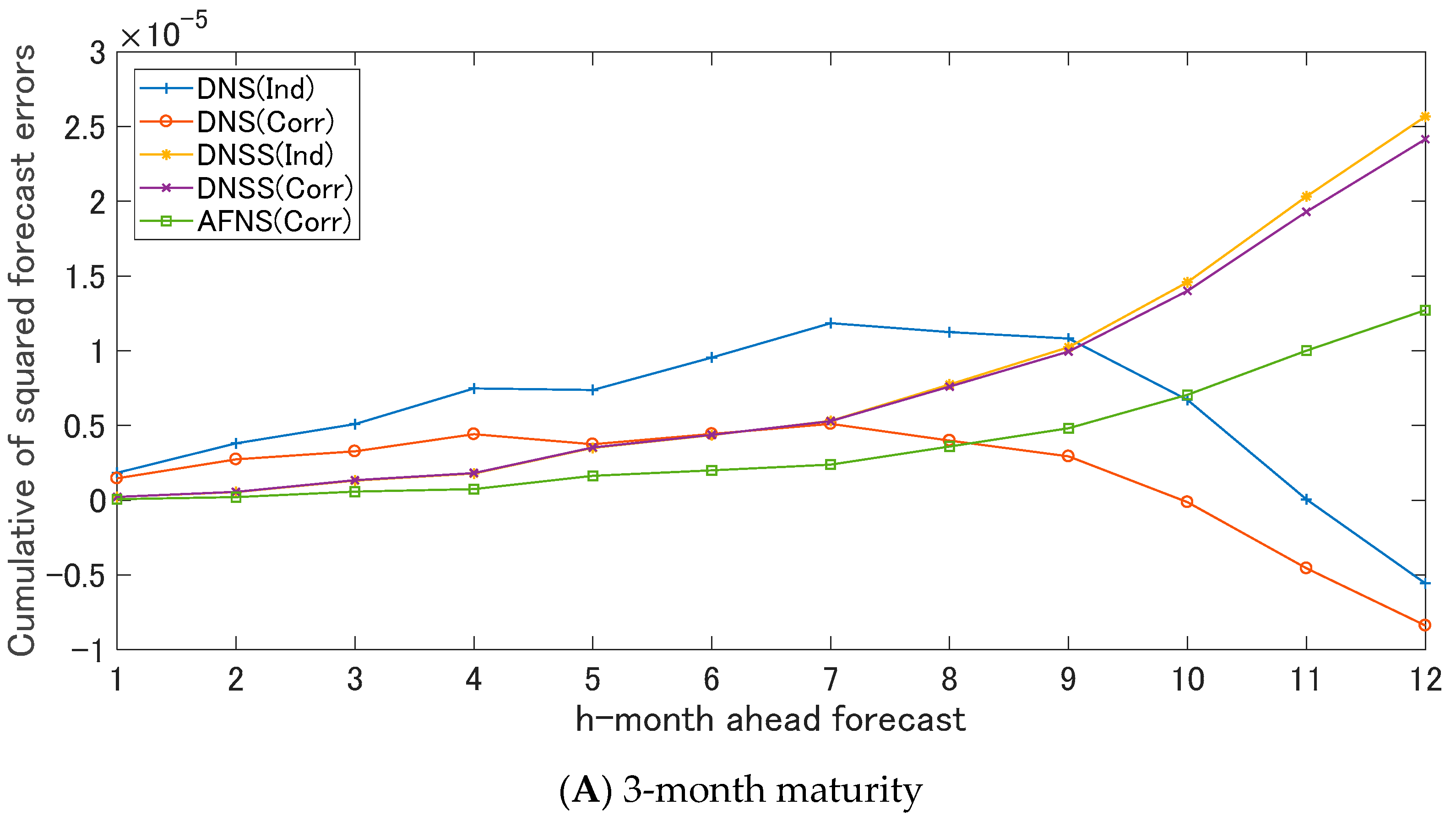
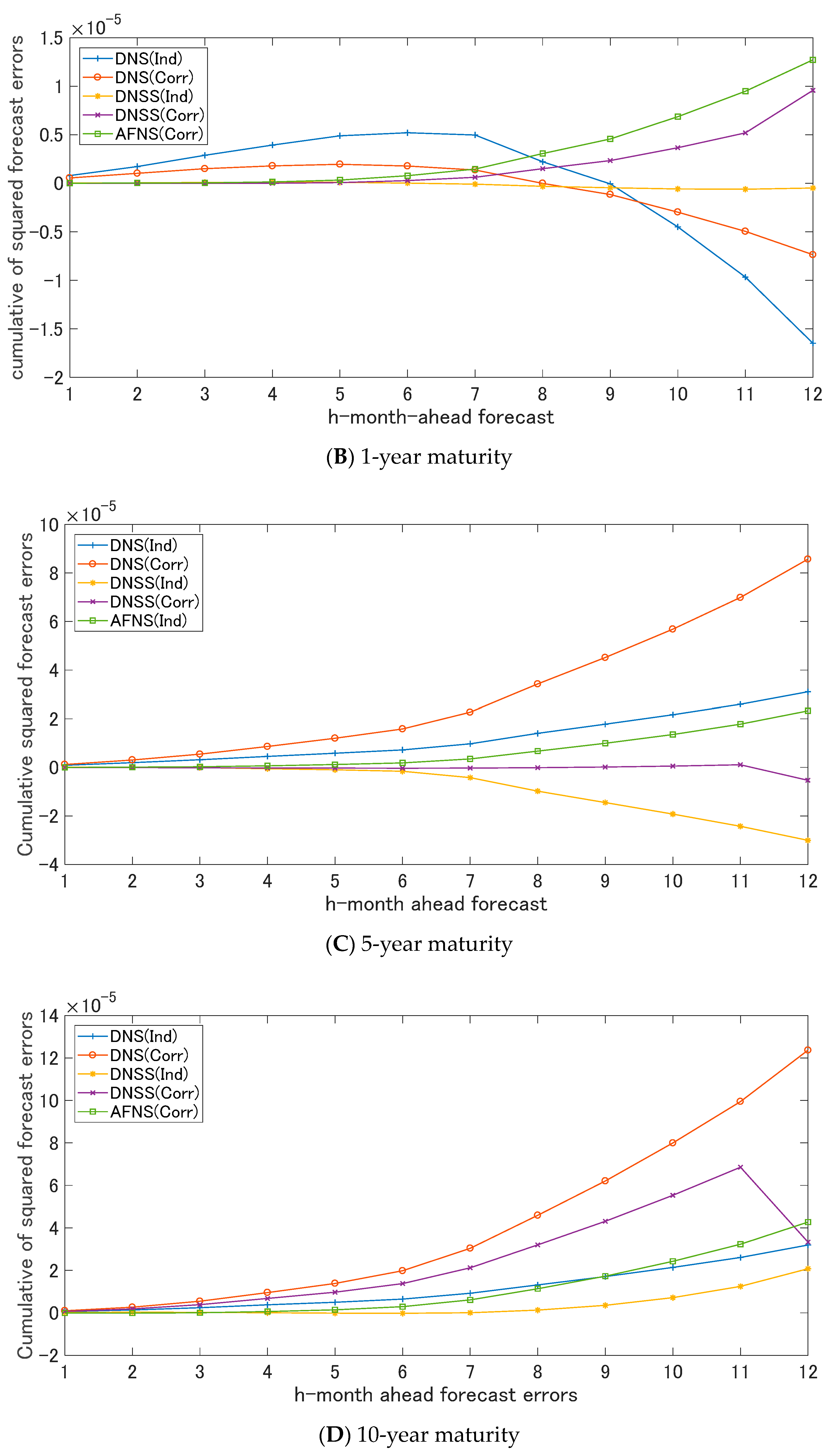
5.1. Out-of-Sample Forecasting: Comparison of Forecasting Performances
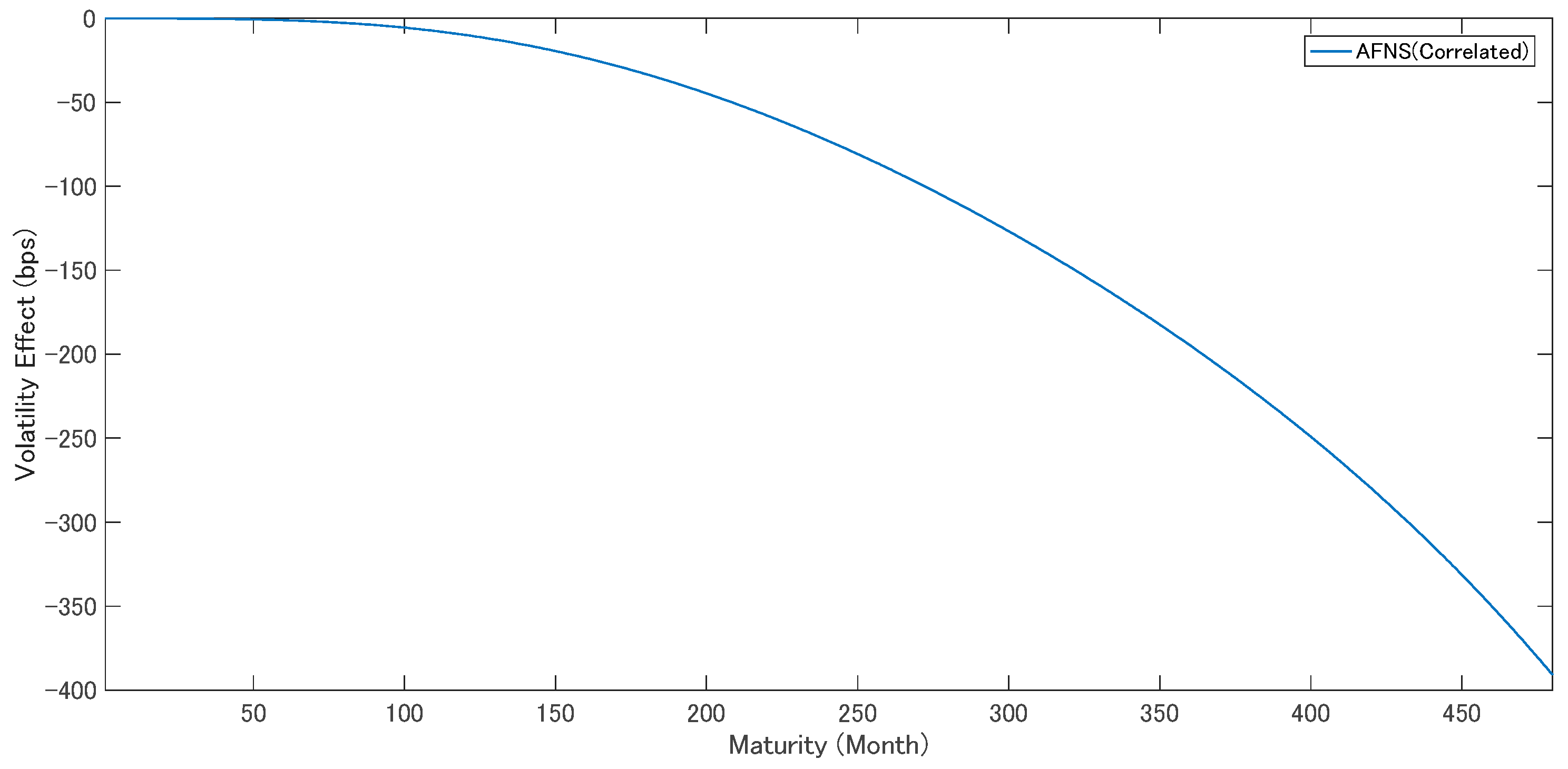
5.2. Volatility Effect
6. Conclusions
Funding
Conflicts of Interest
Appendix A. Derivation of the Theoretical Models
Appendix A.1. Yield of the Nelson–Siegel Model
Appendix A.2. Yield of the Nelson–Siegel–Svensson Model
Appendix A.3. Affine Term Structure Model of Duffie and Kan
Appendix A.4. Arbitrage-Free Nelson–Siegel Model
Appendix A.5. Yield Adjustment Term of Arbitrage-Free Nelson–Siegel Model
References
- Alfaro, Rodrigo A. 2011. Affine Nelson-Siegel model. Economics Letters 110: 1–3. [Google Scholar] [CrossRef]
- Al-Zoubi, Haitham A. 2009. Short-term spot rate models with nonparametric deterministic drift. Quarterly Review of Economics and Finance 49: 731–47. [Google Scholar] [CrossRef]
- Ang, Andrew, and Monika Piazzesi. 2003. A no-arbitrage vector autoregression of term structure dynamics with macroeconomi and latent variables. Journal of Monetary Economics 50: 745–87. [Google Scholar] [CrossRef]
- Bjork, Tomas, and Bent Jesper Christensen. 1999. Interest rate dynamics and consistent forward rate curves. Mathematical Finance 9: 323–48. [Google Scholar] [CrossRef]
- Chan, Ka-keung Ceajer, Andrew Karolyi, Francis A. Longstaff, and Anthony B. Sanders. 1992. An empirical comparison of alternative models of the short-term interest rate. Journal of Finance 47: 1209–27. [Google Scholar] [CrossRef]
- Chen, Yu-chin, and Kwok Ping Tsang. 2013. What does the yield curve tell us about exchange rate predictability? Review of Economics and Statistics 95: 185–205. [Google Scholar] [CrossRef]
- Christensen, Jens H. E., Francis X. Diebold, and Glenn D. Rudebusch. 2009. An arbitrage-free generalized Nelson-Siegel term structure model. Econometrics Journal 12: C33–C64. [Google Scholar] [CrossRef]
- Christensen, Jens H.E., Francis X. Diebold, and Glenn D. Rudebusch. 2011. The affine arbitrage-free class of Nelson-Siegel term structure models. Journal of Econometrics 164: 4–20. [Google Scholar] [CrossRef]
- Coroneo, Laura, Ken Nyholm, and Rositsa Vidova-Koleva. 2011. How arbitrage-free is the Nelson-Siegel model? Journal of Empirical Finance 18: 393–407. [Google Scholar] [CrossRef]
- Cox, John, Jonathan E. Ingersol, and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica 53: 385–407. [Google Scholar] [CrossRef]
- De Rezende, Rafael B., and Mauro S. Ferreira. 2013. Modeling and forecasting the yield curve by an extended Nelson-Siegel class of models: A quantile autoregression approach. Journal of Forecasting 32: 111–23. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Robert S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 134–44. [Google Scholar]
- Diebold, Francis X., and Glenn D. Rudebusch. 2013. Yield Curve Modeling and Forecasting. Princeton: Princeton University Press. [Google Scholar]
- Duffee, Gregory R. 2002. Term premia and interest rate forecasts in affine models. Journal of Finance 57: 405–43. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Rui Kan. 1996. A yield-factor model of interest rates. Mathematical Finance 6: 379–406. [Google Scholar] [CrossRef]
- Fama, Eugene F. 2006. The behavior of interest rates. Review of Financial Studies 19: 359–79. [Google Scholar] [CrossRef]
- Fujii, Mariko, and Makoto Takaoka. 2007. Kinri no Kikannkozo to Macrokeizai: Nelson—Siegel Moderu wo Motiita Approach [Term Structure of Interest Rates and Macroeconomy: Nelson—Siegel Model Approach]. FSA Research Review. Tokyo: Financial Services Agency, pp. 219–48. [Google Scholar]
- Gasha, Giancarlo, Ying He, Carlos Medeiros, Marco Rodriguez, Jean Salvati, and Jiangbo Yi. 2010. On the Estimation of Term Structure Models and an Application to the United State. IMF Working Paper WP/10/258. Washington: International Monetary Fund. [Google Scholar]
- Gurkaynak, Refet S., Brian Sack, and Jonathan H. Wright. 2007. The U.S. treasury yield curve: 1961 to the present. Journal of Monetary Economics 54: 2291–304. [Google Scholar] [CrossRef]
- Gurkaynak, Refet S., and Jonathan H. Wright. 2012. Macroeconomics and the term structure. Journal of Economic Literature 50: 331–67. [Google Scholar] [CrossRef]
- Hamilton, James D., and Jing Cynthia Wu. 2012. Identification and estimation of Gaussian affine term structure models. Journal of Econometrics 168: 315–31. [Google Scholar] [CrossRef]
- Hördahl, Peter, Oreste Tristani, and David Vestin. 2005. A joint econometric model of macroeconomic and term-structure dynamics. Journal of Econometrics 131: 405–44. [Google Scholar] [CrossRef]
- Hull, John, and Alan White. 1990. Pricing interest rate derivative securities. Review of Financial Studies 3: 573–92. [Google Scholar] [CrossRef]
- Ishii, Hokuto. 2018. Modeling and predictability of exchange rate changes by the extended relative Nelson–Siegel class of models. International Journal of Financial Studies 6: 68. [Google Scholar] [CrossRef]
- Krippner, Leo. 2015. Zero Lower Bound Term Structure Modeling. New York: Palgrave Macmillan. [Google Scholar]
- Litterman, Robert, and Jose Scheinkman. 1991. Common factors affecting bond returns. Journal of Fixed Income 1: 54–61. [Google Scholar] [CrossRef]
- 2008. Moench, Emanuel 2008. Forecasting the yield curve in a data-rich environment: a no-arbitrage factor augmented VAR approach. Journal of Econometrics 146: 26–43. [CrossRef]
- Niu, Linlin and Gengming Zeng. 2012. The discrete-time framework of the arbitrage-free Nelson-Siegel class of term structure models. SSRN 2015858: 1–68. [Google Scholar] [CrossRef][Green Version]
- Nelson, Charles, and Andrew Siegel. 1987. Parsimonious modeling of yield curves. Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Piazzesi, Monika 2010. Affine term structure models. In Handbook of Financial Econometrics. Amsterdam, New York and Oxford: Elsevier, pp. 691–766.
- Rudebusch, Glenn D., and Tao Wu. 2008. A macro-finance model of the term-structure, monetary policy, and the economy. Economic Journal 118: 906–26. [Google Scholar] [CrossRef]
- Svensson, Lars E. O. 1994. Estimating and Interpreting Forward Interest Rates: Sweden 1992–1994. NBER Working Paper #4871. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Vasicek, Oldrich. 1977. An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Wu, Tao. 2006. Macro Factors and the Affine Term Structure of Interest Rates. Journal of Money, Credit and Banking 38: 1847–75. [Google Scholar] [CrossRef]
| 1 | Svensson (1994) extended the three-factor model of Nelson and Siegel (1987) to the four-factor model. |
| 2 | Gurkaynak et al. (2007) showed that Nelson–Siegel–Svensson model captured U.S. yields well. Chan et al. (1992) compared a variety of affine term structure models. |
| 3 | |
| 4 | In real world, investors and market participations behave with risk-aversion, so that we need to consider the risk premium to ensure the model is risk-neutral. |
| 5 | |
| 6 | There are the nine volatility parameters, but they are not separately identified. Only the six terms , , , , , and can be identified. Following Christensen et al. (2011), we specify the matrix as the triangular volatility matrix, . Krippner (2015) suggested using the Cholesky decomposition representation. |
| 7 | The elements of the column vector are a difference between the continuous version and the discrete version. However, it is . |
| 8 | We used the MATLAB financial and financial instruments toolboxes to translate the par-yield (the treasury discount bill and the prevailing interest rates) into the zero-coupon yield. |
| 9 | |
| 10 | |
| 11 | |
| 12 | Christensen et al. (2011) estimated each λ of the DNS and the AFNS model separately; however, the values were almost the same. |
| 13 | Coroneo et al. (2011) showed that the constant term bias was negligibly small for U.S. data; so, they used the state variables of DNS for AFNS. |
| 14 | In the first step, was estimated; however, it is possible that the value of β is a locally convergent value as we used non-linear least-squares in the first step. For this reason, we estimated the value of βi again, using OLS in the second step. The OLS estimator had more consistency. |
| 15 | Christensen et al. (2011) reported that the variance-covariance matrix was using U.S. bond data. |
| 16 | This paper employed the monthly frequency. The number of the observations is 82. |
| 17 | The RMSFE is the forecast error using the estimated value from Equation (72). We calculate the RMSFE as . |
| 18 | DNSS is a four-factor model, so it might be unfair to compare DNNS with AFNS directly. Therefore, it may be more appropriate to compare the forecast performance of DNS with that of AFNS. |
| 19 | Bank of Japan employed the unconventional monetary policy and the negative interest rate policy after 2000s, so the term structure of interest rates is very sensitive to the changes of the policy stance. Especially, the long-term forecast is affected by the changes of the policy stance. |
| 20 | The volatility effect is identical to the yield adjustment term. |

| Mean | Std. Dev. | |||
|---|---|---|---|---|
| DNS | ||||
| 0.028 | 0.016 | 0.936 | 0.564 | |
| −0.029 | 0.016 | 0.939 | 0.582 | |
| 0.025 | 0.033 | 0.961 | 0.746 | |
| DNSS | ||||
| 0.022 | 0.003 | 0.783 | −0.043 | |
| −0.021 | 0.003 | 0.815 | 0.008 | |
| −0.090 | 0.027 | 0.895 | 0.219 | |
| 0.080 | 0.038 | 0.932 | 0.531 | |
| AFNS (Ind) | ||||
| 0.345 | 0.016 | 0.936 | 0.564 | |
| −0.342 | 0.016 | 0.939 | 0.582 | |
| −0.364 | 0.033 | 0.961 | 0.746 | |
| AFNS (Corr) | ||||
| 0.210 | 0.016 | 0.936 | 0.564 | |
| −0.210 | 0.016 | 0.939 | 0.582 | |
| −0.195 | 0.033 | 0.961 | 0.746 |
| DNS (Independent) | DNS (Correlated) | |||||||
| 0.936 | 0 | 0 | - | −0.389 | −1.151 | −0.071 | - | |
| (0.041) | (0.570) | (0.529) | (0.084) | |||||
| 0 | 0.939 | 0 | - | 1.203 | 1.977 | 0.070 | - | |
| (0.040) | (0.571) | (0.530) | (0.084) | |||||
| 0 | 0 | 0.962 | - | 2.036 | 1.952 | 0.984 | - | |
| (0.034) | (0.976) | (0.906) | (0.144) | |||||
| DNSS (Independent) | DNSS (Correlated) | |||||||
| 0.782 | 0 | 0 | 0 | 0.419 | −0.291 | −0.024 | −0.025 | |
| (0.063) | (0.194) | (0.202) | (0.034) | (0.027) | ||||
| 0 | 0.815 | 0 | 0 | 0.379 | 1.060 | 0.034 | 0.034 | |
| (0.064) | (0.204) | (0.212) | (0.035) | (0.028) | ||||
| 0 | 0 | 0.895 | 0 | −1.075 | −0.497 | 0.174 | −0.603 | |
| (0.049) | (1.134) | (1.184) | (0.201) | (0.155) | ||||
| 0 | 0 | 0 | 0.932 | 2.316 | 0.412 | −0.840 | 1.608 | |
| (0.041) | (1.372) | (1.431) | (0.243) | (0.188) | ||||
| AFNS (Independent) | AFNS (Correlated) | |||||||
| 0.936 | 0 | 0 | - | −0.389 | −1.151 | −0.071 | - | |
| (0.041) | (0.570) | (0.529) | (0.084) | |||||
| 0 | 0.939 | 0 | - | 1.203 | 1.977 | 0.070 | - | |
| (0.040) | (0.571) | (0.530) | (0.084) | |||||
| 0 | 0 | 0.962 | - | 2.036 | 1.952 | 0.984 | - | |
| (0.034) | (0.976) | (0.906) | (0.144) | |||||
| DNS (Independent) | DNS (Correlated) | |||||||
| 3.429 × | 0 | 0 | - | 3.213 × | −3.212 × | −5.147 × | - | |
| 0 | 3.394 × | 0 | - | −3.212 × | 3.216 × | 5.141 × | - | |
| 0 | 0 | 0.941 × | - | −5.147 × | 5.141 × | 9.406 × | - | |
| DNSS (Independent) | DNSS (Correlated) | |||||||
| 3.409 × | 0 | 0 | 0 | 3.183 × | −3.276 × | 8.170 × | −1.363 × | |
| 0 | 3.777 × | 0 | 0 | −3.276 × | 3.511 × | −1.091 × | 1.625 × | |
| 0 | 0 | 1.332 × | 0 | 8.170 × | −1.091 × | 1.093 × | −1.260 × | |
| 0 | 0 | 0 | 1.963× | −1.363 × | 1.625 × | −1.260 × | 1.597 × | |
| RW | DNS | DNSS | AFNS | |||
|---|---|---|---|---|---|---|
| Maturity | Ind | Corr | Ind | Corr | Corr | |
| 3-month | 0.20 | 13.56 | 12.10 | 4.71 | 4.77 | 2.84 |
| 6-month | 0.05 | 12.19 | 10.73 | 2.03 | 2.40 | 1.97 |
| 1-year | 0.50 | 8.98 | 7.51 | 1.73 | 0.80 | 1.09 |
| 2-year | 0.80 | 1.91 | 0.40 | 4.74 | 2.94 | 1.33 |
| 3-year | 0.20 | 3.73 | 5.28 | 5.14 | 2.73 | 1.80 |
| 4-year | 0.20 | 6.73 | 8.33 | 5.19 | 2.37 | 1.12 |
| 5-year | 1.51 | 9.40 | 11.05 | 3.42 | 0.33 | 1.40 |
| 6-year | 3.02 | 13.44 | 15.14 | 1.24 | 4.49 | 4.16 |
| 7-year | 3.73 | 14.53 | 16.29 | 3.97 | 7.30 | 4.92 |
| 8-year | 4.46 | 11.72 | 13.55 | 3.43 | 6.80 | 2.55 |
| 9-year | 4.16 | 10.17 | 12.07 | 4.50 | 7.86 | 2.08 |
| 10-year | 3.76 | 8.65 | 10.62 | 5.74 | 9.08 | 2.14 |
| 15-year | 3.62 | 1.90 | 0.47 | 6.87 | 10.09 | 3.41 |
| 20-year | 2.79 | 19.25 | 16.42 | 5.84 | 2.58 | 1.50 |
| 25-year | 3.07 | 13.21 | 9.92 | 1.64 | 1.84 | 13.07 |
| 3-year | 1.39 | 4.35 | 0.57 | 1.21 | 5.00 | 22.73 |
| 40-year | 2.31 | 17.987 | 22.69 | 5.96 | 10.39 | 7.28 |
| RW | DNS | DNSS | AFNS | |||
|---|---|---|---|---|---|---|
| Maturity | Ind | Corr | Ind | Corr | Corr | |
| 3-month | 1.96 | 13.18 | 10.63 | 6.90 | 6.97 | 4.79 |
| 6-month | 0.83 | 12.34 | 9.72 | 3.22 | 3.87 | 3.21 |
| 1-year | 0.71 | 9.85 | 7.12 | 1.94 | 0.47 | 1.50 |
| 2-year | 1.28 | 3.05 | 0.25 | 5.99 | 2.85 | 1.59 |
| 3-year | 0.33 | 3.46 | 6.28 | 6.23 | 2.12 | 2.85 |
| 4-year | 1.60 | 7.42 | 10.42 | 5.55 | 1.39 | 3.43 |
| 5-year | 3.63 | 10.83 | 13.94 | 3.22 | 2.66 | 4.64 |
| 6-year | 5.01 | 14.81 | 18.01 | 1.40 | 7.05 | 7.26 |
| 7-year | 7.23 | 17.28 | 20.63 | 5.56 | 11.35 | 9.61 |
| 8-year | 8.52 | 15.05 | 18.55 | 5.79 | 11.57 | 8.21 |
| 9-year | 8.20 | 13.53 | 17.16 | 6.90 | 12.68 | 7.82 |
| 10-year | 7.29 | 11.56 | 15.32 | 7.75 | 13.46 | 7.39 |
| 15-year | 6.44 | 2.22 | 5.67 | 9.01 | 14.34 | 8.14 |
| 20-year | 4.83 | 18.14 | 13.39 | 4.63 | 3.46 | 3.77 |
| 25-year | 4.20 | 12.95 | 7.53 | 1.62 | 5.80 | 16.21 |
| 3-year | 3.29 | 3.85 | 4.44 | 3.50 | 9.59 | 26.54 |
| 40-year | 3.84 | 17.97 | 26.54 | 7.51 | 14.84 | 4.85 |
| RW | DNS | DNSS | AFNS | |||
|---|---|---|---|---|---|---|
| Maturity | Ind | Corr | Ind | Corr | Corr | |
| 3-month | 3.83 | 13.18 | 9.42 | 9.35 | 9.37 | 6.93 |
| 6-month | 2.50 | 12.12 | 8.28 | 5.41 | 6.22 | 5.32 |
| 1-year | 1.87 | 9.50 | 5.77 | 1.98 | 2.86 | 4.07 |
| 2-year | 1.55 | 2.78 | 2.80 | 5.63 | 2.34 | 4.08 |
| 3-year | 1.40 | 3.62 | 8.16 | 6.54 | 1.76 | 4.86 |
| 4-year | 3.23 | 8.30 | 13.01 | 5.46 | 2.39 | 6.14 |
| 5-year | 5.84 | 12.41 | 17.26 | 2.67 | 5.33 | 8.05 |
| 6-year | 7.88 | 17.02 | 22.03 | 2.91 | 10.53 | 11.44 |
| 7-year | 10.73 | 20.28 | 25.46 | 7.81 | 15.58 | 14.53 |
| 8-year | 13.05 | 19.12 | 24.53 | 9.29 | 16.96 | 14.22 |
| 9-year | 13.10 | 17.96 | 23.58 | 10.99 | 18.54 | 14.31 |
| 10-year | 12.32 | 16.12 | 21.95 | 12.17 | 19.54 | 14.13 |
| 15-year | 13.27 | 8.15 | 14.62 | 16.28 | 22.69 | 17.08 |
| 20-year | 11.99 | 14.29 | 10.31 | 7.98 | 12.28 | 13.09 |
| 25-year | 11.05 | 10.33 | 8.79 | 9.52 | 15.13 | 24.89 |
| 3-year | 8.91 | 4.60 | 12.52 | 10.57 | 17.54 | 33.92 |
| 40-year | 8.87 | 20.42 | 33.47 | 13.26 | 22.14 | 8.17 |
| RW | DNS | DNSS | AFNS | |||
|---|---|---|---|---|---|---|
| Maturity | Ind | Corr | Ind | Corr | Corr | |
| 3-month | 13.07 | 11.15 | 10.05 | 19.61 | 19.29 | 16.64 |
| 6-month | 14.32 | 10.48 | 11.09 | 17.96 | 18.55 | 17.51 |
| 1-year | 15.64 | 10.36 | 13.54 | 15.51 | 17.44 | 18.73 |
| 2-year | 16.05 | 13.04 | 18.75 | 12.80 | 16.21 | 20.04 |
| 3-year | 17.91 | 18.68 | 25.12 | 13.25 | 17.64 | 22.33 |
| 4-year | 20.00 | 23.34 | 30.16 | 14.24 | 19.67 | 24.14 |
| 5-year | 23.56 | 28.53 | 35.63 | 17.44 | 23.90 | 27.36 |
| 6-year | 26.92 | 34.47 | 41.82 | 23.09 | 30.24 | 32.19 |
| 7-year | 30.90 | 39.10 | 46.69 | 29.14 | 36.42 | 36.61 |
| 8-year | 35.61 | 40.82 | 48.63 | 33.57 | 40.50 | 39.08 |
| 9-year | 37.73 | 41.92 | 49.95 | 37.67 | 44.19 | 41.38 |
| 10-year | 39.02 | 42.29 | 50.53 | 41.18 | 47.23 | 43.34 |
| 15-year | 51.59 | 46.73 | 55.91 | 58.44 | 62.41 | 58.24 |
| 20-year | 62.88 | 47.83 | 56.93 | 62.85 | 65.42 | 67.12 |
| 25-year | 69.03 | 56.74 | 67.71 | 72.27 | 75.30 | 84.70 |
| 3-year | 73.22 | 66.78 | 79.86 | 79.36 | 83.34 | 98.00 |
| 40-year | 78.08 | 84.73 | 102.04 | 85.58 | 91.80 | 79.54 |
| 6-Month | 3-Month | 6-Month | 1-Year | 2-Year | 3-Year | 3-Year | 5-Year | 6-Year | 7-Year | 8-Year |
|---|---|---|---|---|---|---|---|---|---|---|
| DM | −3.61 | −3.13 | −0.26 | −4.81 | −7.43 | −4.32 | 2.59 | 3.87 | 3.61 | 4.04 |
| -value | 0.000 | 0.001 | 0.791 | 0.000 | 0.000 | 0.000 | 0.010 | 0.000 | 0.000 | 0.000 |
| 9-year | 10-year | 15-year | 20-year | 25-year | 30-year | 40-year | ||||
| DM | 3.57 | 0.69 | −3.44 | 2.26 | 3.98 | −1.73 | −3.03 | |||
| -value | 0.000 | 0.488 | 0.000 | 0.023 | 0.000 | 0.082 | 0.002 | |||
| 12-Month | 3-month | 6-month | 1-year | 2-year | 3-year | 3-year | 5-year | 6-year | 7-year | 8-year |
| DM | −3.91 | −3.35 | 1.494 | 2.42 | 2.47 | 2.92 | 3.68 | 4.59 | 4.49 | 4.74 |
| -value | 0.000 | 0.001 | 0.134 | 0.015 | 0.013 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 |
| 9y | 10y | 15y | 20y | 25y | 30y | 40y | ||||
| DM | 3.45 | −2.30 | −3.17 | 0.04 | −2.19 | −2.73 | −2.94 | |||
| -value | 0.001 | 0.021 | 0.002 | 0.965 | 0.030 | 0.001 | 0.003 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishii, H. Forecasting Term Structure of Interest Rates in Japan. Int. J. Financial Stud. 2019, 7, 39. https://doi.org/10.3390/ijfs7030039
Ishii H. Forecasting Term Structure of Interest Rates in Japan. International Journal of Financial Studies. 2019; 7(3):39. https://doi.org/10.3390/ijfs7030039
Chicago/Turabian StyleIshii, Hokuto. 2019. "Forecasting Term Structure of Interest Rates in Japan" International Journal of Financial Studies 7, no. 3: 39. https://doi.org/10.3390/ijfs7030039
APA StyleIshii, H. (2019). Forecasting Term Structure of Interest Rates in Japan. International Journal of Financial Studies, 7(3), 39. https://doi.org/10.3390/ijfs7030039




