Heavy Metals: Might as Well Jump

Abstract

Financial times series, and commodity prices in particular, are known to exhibit fat tails in the distribution of prices. As with many natural resources price series, the arrival of new information can lead to unexpectedly rapid changes—or jump—in prices. This suggests that natural resource commodity prices should follow a more complex process than geometric Brownian motion (GBM), which is linked to the Gaussian distribution. The presence of jumps (discontinuities) in several heavy metal price series is investigated, as well as time-varying volatility. The results demonstrate that allowing for jumps and time-varying volatility provides statistically important improvements in the modelling or prices, relative to GBM. These complex processes contributed to the fatness of the tails in the distribution of heavy metal price returns.

1. Introduction

A central characteristic of many commodity prices is the stochastic element driving the pricing process. This is evident from the large fluctuations experienced by commodity prices over the past 20 years. In particular, the price of gold, between 2009 and 2011, more than doubled, and Guzmán and Silv (2018) note that copper prices tripled between 2003 and 2008. Such price movements can be seen across a range of nonrenewable commodities. While the current range of prices is below the (nominal) highs observed in the pre-2009 period, significant fluctuations continue to occur, which has lead researchers to investigate a wide array of models to explain such phenomenon. As such changes in metals prices continue to catch both experts and consumers by surprise, understanding the underlying stochastic process is of clear importance. Furthermore, metal price dynamics are of importance for derivative pricing, hedging and forecasting activities.

While commodity markets have experienced their fair share of booms and busts, the most recent cycle has received a significant amount of attention. The explanations for recent fluctuations of metal prices can be organized into several categories. The first relates to the underlying fundamentals (physical supply and demand) for the commodity. Within this realm, the recent price increases have been linked to a strong increase in demand for commodities, particularly from China (Humphreys 2010), without an offsetting increase in supply, due in part to capacity constraints and insufficient foresight. Secondly, the recent financialization of commodities markets—the use of commodities as financial instruments—has led to an increase in the demand for metals related securities and an increase in financial speculation related to commodities (Guzmán and Silv 2018). It should be noted that the two explanations are not mutually exclusive.

Underlying much of the literature on modelling the data-generating process of metal prices is the assumption that the market price follows a continuous stochastic process Brennan and Schwartz (1985); Schwartz (1997); Schwartz and Smith (2000). This assumption has conveniently provided researchers with tractable models that typically facilitate closed form solutions. But such continuous time models fail to reproduce the relatively fat-tails observed in a distribution of returns—a common feature of financial data. In this study, the daily price path for several heavy metals is investigated utilizing techniques that allow for the potential presence of jumps. To this end, the pricing process for five heavy metals price series is modeled, alternatively, as continuous and discontinuous processes. The discontinuous process is assumed to follow the mixed jump-diffusion process, similar to that of Merton (1976). Since fat-tails may result from the volatility clustering associated with time-varying volatility in commodity price (Pindyck 2004), the models can also be supplemented with a generalized autoregressive conditional heteroscedasticity (GARCH)component. Allowing for this potential interaction of the GARCH with both the continuous and discontinuous process means four potential processes are investigated. The nested feature of the maximum likelihood framework allows for direct tests among the model. Overall, the results indicate that allowing for jumps yields a statistically important improvement in explanatory power, as does allowing for time varying volatility.

2. Literature Review

The empirical importance of jumps has been documented in other commodity markets, including oil (Askari and Krichene 2008; Postali and Picchetti 2006; Wilmot and Mason 2013), natural gas markets (Mason and Wilmot 2016), carbon markets (Chevallier and Ielpo 2014) and electricity markets (Huisman and Mahieu 2003). Much of the existing work analyzing metals markets focuses on time-varying volatility (Batten and Lucey 2010; Tully and Lucey 2007), forecasting (Aye et al. 2006; Pierdzioch et al. 2016), and nonstationarity (Lee et al. 2006).

Early work in the area of commodity price analysis was conducted by Pindyck and Rotemberg (1990). The authors study the comovement of a broad spectrum of commodities that are as unrelated as possible, which include both gold and crude oil. The results suggest that the prices of these largely unrelated, raw commodities have a persistent tendency to move together. Following this line of research, Ciner (2001) observes a separation between gold and silver prices during the 1990s. There is reason to believe that comovement among certain commodities should persist, though as discussed in Hammoudeh et al. (2009), the comovement in price among the commodities could be nebulous. While some commodities can be seen as substitutes (i.e., gold and silver in jewlery), others may be complements (oil and metals), and certainly a distinct subset have idiosyncratic forces acting on the market (i.e., gold held by central banks). To that end, Hammoudeh et al. (2009) examines the comovements in price among four commodities—gold, silver, copper and oil. Utilizing daily prices, to improve the information content and processing mechanism relative to lower frequency data, the authors report two cointegrating vectors among the four commodity prices. They also report a separation between gold and silver prices, which aligns with the research of Ciner (2001). However, it is suggested by the authors that asset managers should consider gold and silver as a hedge in a portfolio that includes copper.

Fernandez (2015), building on the excess co-movement hypothesis of Pindyck and Rotemberg (1990), examines several classes of commodities, including an industrial metal class. Based on a century of annual data, Fernandez (2015) finds excess co-movement between industrial metals and oil. As an explanation of the results, the author cites both the increasingly energy dependent mining production process and the financialization of commodities. Guzmán and Silv (2018) examines the copper market using a vector autoregressive (VAR) model, which includes 16 variables. The authors conclude that the impact of financial speculation has become significant during the mid 2000s (prior to great Recession, 2003–2008), but represented a small component of price. Arezki et al. (2014) provide an overview of recent work on the financialization of commmodity markets.

To better account for the thick tails, in the distribution of returns, several authors have modelled price returns using GARCH models. Tully and Lucey (2007) apply an asymmetric power GARCH model to investigate gold prices over the 1983–2003 period. The authors reports a stable relationship between gold and silver, though within sub periods this relationship may have weakened. Using intra-day trading data, over the decade beginning in 1999, Khalifa et al. (2011) examine the process governing price variability in gold, silver and copper. The authors find that the distribution of daily futures returns is not described by a normal distribution, even when standardized by various integrated volatility measures. In the conclusion, the authors suggest that future research into the response of price movements to new information, or the arrival of unexpected “news”, and its link to (identified) jumps would be valuable.

The goal in this paper is to provide a deeper understanding of the stochastic process driving heavy metal prices. To this end, the familiar model of a stochastic pricing process is extended to allow for unexpected changes, or jumps. The more general model, can be combined with time-varying volatility, a main stay of the asset pricing literature. A GARCH framework is utilized. A likelihood function, which incorporates all these elements in the data generating process is formulated, which leads directly to an estimation procedure and hypothesis tests regarding the appropriate specification of the stochastic process.

The econometric methodology is applied to five important heavy metal futures time series; gold, silver, copper, platinum and zinc. We compare four ‘competing’ data-generating processes: GBM (refereed to as PD), GBM allowing for GARCH (referred to as GPD), GBM allowing for a jump diffusion process (referred to as JD) and GBM allowing for both GARCH and a jump diffusion process (referred to as GJD).

As both GARCH and jumps will induce fat tails, the empirical results herein may have implications for the decision to undertake large-scale investments; a particularly acute example given the costs involved in large-scale mining of industrial metals. The decision to open a mine, or to close a mine has been modelled as a real option (Brennan and Schwartz 1985), which involves the application of (financial) options concepts to value real assets. As demonstrated in Mason and Wilmot (2016) incorporating GARCH and jumps into a real options model tends to increase the value at which it becomes optimal for the firm to ‘exercise’ the option, and invest in large scale projects. The results of the analysis, could support a delay between the observed rise in prices and the firms’ decision to invest in large-scale mining projects.

3. Econometric Framework

In order to develop the maximum likelihood framework used to estimate the parameters of the four models, a brief examination of the stochastic processes under investigation is presented. Let $P_t$ denote price at time t; its time path is said to follow a geometric Brownian motion (GBM) process with trend $\alpha$ and variance parameter $\sigma$ if

$$d{P}_t=\alpha P_{t}dt+\sigma P_{t}dz.$$

(1)

In Equation (1), $dz$ represents an increment of a Wiener process $dz={\xi }_t\sqrt{dt},$ where ${\xi }_t$ has zero mean and a standard deviation equal to 1 (Dixit and Pindyck 1994). Denote the log returns, i.e., the natural logarithm of the ratio of price in period t to the price in period $t-1$, by $x_t=ln(P_t/P_{t-1})$. If $P_t$ follows a GBM process then $x_t$ is normally distributed with variance ${\sigma }^2$ and mean $\mu =\alpha -{\sigma }^2/2$. This gives the pure diffusion (PD) model

$$x_t=\mu +\sigma z_t.$$

(2)

The term $z_t$ in Equation (2) is an identically and independently distributed (i.i.d.) random variable with mean zero and variance one.

Jumps are introduced into the model in the style of Merton (1976), by assuming that two types of changes affect the log returns. The first type are ‘normal’ fluctuations, represented through the geometric Brownian motion process. The second type, ‘abnormal’ shocks, are modeled through a discontinuous process. These abnormal shocks can be thought of as occurring via the arrival of new information (Elder et al. 2013). We view these shocks as transitory, as opposed to quasi-permanent changes in the fundamental underlying structure of the market. This assumption makes it more natural to include a jump process, as opposed to a regime shifting framework. We assume the discontinuities are described by a Poisson distribution governing the number of discrete-valued events, $n_t\in \left\{0,1,2,\dots \right\}$, that occur over the interval $\left(t-1,t\right)$; accordingly, the probability that j jumps are observed during this interval equals

$$P\left(N_t=j\right)=\frac{exp\left(-\lambda \right){\lambda }^j}{j!}.$$

(3)

A key element in Equation (3) is $\lambda$, which can be interpreted as the probability of observing a jump in any brief time interval of length $dt$. The choice of the Poisson process—along with a GARCH process—is motivated not only by the ability of contrast with the basic pure diffusion model, but also through it symbiosis with the analytics associated with evaluating optimal investment, or real options literature. Dixit and Pindyck (1994, p. 171) show that including a Poisson process into a conventional Brownian motion framework adds only one (non-linear) term to the key equation that defines the optimal value function associated with investing. While alternative specifications of the jump process have been adopted in the literature (Bernouilli, Levy, etc), the current specification is restricted to the Poisson process for the reasons previously stated. Thus, the arrival of jumps is a Poisson distribution from which we can describe the change in the number of jumps observed by

$$d{n}_t=\left\{\begin{array}{cc}0& \mathrm{with}\mathrm{probability}1-\lambda dt\\ 1& \mathrm{with}\mathrm{probability}\lambda dt\end{array}\right.$$

(4)

As in Askari and Krichene (2008), when abnormal information arrives at time t, prices jump from $P_{t-}$ (the limit as the time index tends towards t from left) to $P_t=exp\left(J_t\right)P_{t-}$; accordingly, $J_t$ measures the percentage change in price. The resultant stochastic process for the random variable $P_t$ may then be written as

$$\frac{d{P}_t}{P_t}=\alpha dt+\sigma d{z}_t+\left(exp\left(J_t\right)-1\right)d{n}_t,$$

(5)

where $d{z}_t$ has the same properties assumed in Equation (1) and $d{n}_t$ is the independent Poisson process described in Equation (4). Together the terms $d{z}_t$ and $d{n}_t$ make up the instantaneous component of the unanticipated return. It is natural to assume these terms are independent, since the first component reflects ordinary movements in price while the second component reflects unusual changes in price. The size of the jump, $Y_{t,k}$, is itself a random variable; we assume it is normally distributed with mean $\theta$ and variance ${\delta }^2$, and that it is independent of the distribution for the arrival of a jump. The jump component affecting returns between time t and time t+1 is then

$$J_t=\sum _{k=0}^{n_t}{Y}_{t,k}.$$

(6)

Thus, the mixed jump-diffusion (JD) process for the log-price returns can be described by

$$x_t=\mu +\sigma z_t+J_t.$$

(7)

The probability density function governing $x_t$ can be derived by applying Bayes’ law (Chan and Maheu 2002; Maheu and McCurdy 2004). To this end let $f\left(x_t\right|n_t=j,{\mathsf{\Omega }}_{t-1})$ denote the conditional density of returns if j jumps have occurred and given the available information ${\mathsf{\Omega }}_{t-1}$. Based on Bayes rule, when $x_t$ is observed, the posterior probability that j jumps will occur at time t is

$$P(n_t=j|{\mathsf{\Omega }}_{t-1})=\frac{f\left(x_t\right|n_t=j,{\mathsf{\Omega }}_{t-1})P(n_t=j|{\mathsf{\Omega }}_{t-1})}{P\left(x_t\right|{\mathsf{\Omega }}_{t-1})}.$$

(8)

Then, assuming that the conditional density of $x_t$ is normally distributed, and using Equation (3) to describe the probability that j jumps occur, we obtain:

$$f\left(x_t\right|n_t=j,{\mathsf{\Omega }}_{t-1})=\frac{1}{\sqrt{2\pi ({\sigma }^2+j{\delta }^2)}}exp(-\frac{{(x_t-\mu -\theta j+\theta \lambda )}^2}{2({\sigma }^2+j{\delta }^2)}).$$

(9)

Finally, integrating out the discrete valued number of jumps yields an expression for the conditional density in terms of observable variables:

$${\displaystyle P\left(x_t\right|{\mathsf{\Omega }}_{t-1})=\sum _{j=0}^{\infty }f\left(x_t\right|n_t=j,{\mathsf{\Omega }}_{t-1})P(n_t=j|{\mathsf{\Omega }}_{t-1}).}$$

(10)

An alternative explanation for the “fat tails” that are often observed in commodity price data is that $P_t$ is subject to time-varying volatility. An example of such a phenomenon is the GARCH framework. Adapting the pure diffusion model to allow for this form of time-varying volatility gives the GARCH-diffusion (GPD) process:

$$x_t=\mu +\sqrt{h_t}{z}_t,$$

(11)

where the conditional variance, $h_t$ is described by the process

$$h_t=\kappa +{\alpha }_1{\left(x_{t-1}-\mu \right)}^2+{\beta }_1{h}_{t-1}^{}.$$

(12)

Note that when $h_t={\sigma }^2$ the GARCH diffusion model reduces to pure diffusion model. On the other hand, when $\kappa >0$ and ${\alpha }_1+{\beta }_1<1$, the unconditional variance of the volatility of the process exists and equals $\frac{\kappa }{1-{\alpha }_1-{\beta }_1}$. The process described in Equations (11) and (12) is characterized by four parameters, $\mu ,\kappa ,{\alpha }_1$ and ${\beta }_1$. There is a general consensus in the literature is that a GARCH model with a limited number of terms performs reasonably well (Akgiray 1989; Hansen and Lunde 2005; Sadorsky 2006), and so the focus of the analysis is restricted to this more parsimonious representation.

Allowing for jump discontinuities would result in the GARCH(1,1) jump-diffusion (GJD) process:

$$x_t=\mu +\sqrt{h_t}{z}_t+J_t,$$

(13)

where $h_t$ is described by Equation (12). Duan (1997) shows that the diffusion limit of a large class of GARCH(1,1) models contain many diffusion processes allowing the approximation of stochastic volatility models by the GARCH process.

We evaluate the four models using maximum likelihood estimation methods. To this end, we note that the parameters of our four candidate models—PD, JD, GPD, GJD—may be nested into the general log-likelihood function

$$L\left(\varphi ,x_t\right)=-T\lambda -\frac{T}{2}ln\left(2\pi \right)+\sum _{t=1}^{T}ln\left[\sum _{n=0}^{\infty }\frac{{\lambda }^n}{n!}\frac{1}{\sqrt{h_t+n{\delta }^2}}exp\left(\frac{-{\left(x_t-\mu -n\theta \right)}^{}}{2\left(h_t+n{\delta }^2\right)}\right)\right],$$

(14)

where n indexes the number of jumps, combined with the description of $h_t$ given in Equation (12).1 In this framework, the $GPD$ model corresponds to the parameter restriction $\lambda =\theta =\delta =0$; the $JD$ model corresponds to the restriction ${\alpha }_1={\beta }_1=0$; and the $PD$ model corresponds to the restriction ${\alpha }_1={\beta }_1=\lambda =\theta =\delta =0$. Comparing any pair of potential models can thus be framed as a test of an appropriate parameter restriction. For example, the comparison of the $PD$ and $GPD$ models is conducted by testing the parameter restriction ${\alpha }_1={\beta }_1=0$; the comparison of the $PD$ and $JD$ models is conducted by testing the parameter restriction $\lambda =\theta =\delta =0$. The empirical validity of the parameter restriction of interest can be evaluated by use of the likelihood ratio test (Johnston and DiNardo 1997). This approach compares the likelihood function under a particular restriction, L(${\varphi }^R$;x), to that of the unrestricted or less restricted likelihood function, $L(\widehat{\varphi };x)$. Under the null hypothesis that the restriction is empirically valid, the decrease in the likelihood function associated with the restriction will be small. Such an approach can be used to make pairwise-comparisons between a more general model and a more restricted model. The test statistic is the log-likelihood ratio

$$LR=2[L(\widehat{\varphi };x)-L({\varphi }^R;x)];$$

under the null hypothesis this statistic will be distributed as a Chi-square random variable with m degrees of freedom, where m is the number of parameter restrictions.

4. Data and Data Properties

The data for this study consist of daily closing Front Month futures prices for five heavy metals commodity series. The data, obtained from Bloomberg (2018), cover the period from 5 January 2000 through the end of 2018. This time frame includes a number of events with, a priori, would be good candidates for arrivals of ‘unusual’ information: the global recession (late summer 2008), the “Arab Spring” (early 2011), and various regional geopolitical events local to the commodity producing country, such as the 2005 gold miners strike in South Africa. Gold, silver, copper and platinum represent the four most active metals futures contracts traded on the CME exchange in the third quarter of 2018 (CME Group 2018). In the real options literature, the firm holds the right to invest in the development of a ‘mine’, which is likely to take time to build. The value of this option should depend on the information available in the spot and futures markets. The focus of this analysis is on the futures market, as prices in the two markets are expected to be highly, positively correlated. As evidence, Silvapulle and Moosa (1999) observe nonlinear bidirectional causality among futures prices and spot prices, and conclude that both markets react simultaneously to new information. Additionally, well developed futures markets exist for each of the heavy metals examined.

For each of the five heavy metal time series, the price returns are calculated as

$$r_{j,t}=100\left[ln(P_{j,t}/P_{j,t-1})\right],$$

(15)

where $P_{j,t}$ is the futures closing price on day t, of the commodity j. A variety of summary statistics for the relative price returns of each of the time series are presented in

Table 1. Summary statistics of (log) front month future price returns.

Commodity	Gold	Silver	Copper	Zinc	Platinum
Average	0.032	0.022	0.024	0.015	0.013
Variance	1.246	3.743	3.017	4.518	2.293
Std. Dev.	1.116	1.935	1.737	2.126	1.514
Coefficient of
Variation	35.33	86.95	73.19	139.55	117.19
Skewness	−0.226	−0.913	−0.250	−0.977	−1.506
Kurtosis	5.752	7.842	4.614	22.378	25.494
Kolmogorov
-Smirnov	0.072	0.089	0.063	0.076	0.062
p-value	<0.010	<0.010	<0.010	<0.010	<0.010
Count	4771	4771	4771	4691	4770
Unit Root Test
ERS	−10.718	−4.074	12.02	−5.15	−4.35
Lags	16	19	12	22	12
p-value	<0.010	<0.010	<0.010	<0.010	<0.010

At the 1% level, the critical value for the ERS test is −3.480. The value of Kurtosis presented is often referred to as excess kurtosis.

. As evidenced by the the first four moments (mean, variance, skewness and kurtosis), heavy metal commodity returns display a substantial amount of variation, with zinc displaying the highest level of variance. The values of skewness provide evidence of asymmetry in the distribution of returns, particularity evident with the platinum series. Each of the series also displays leptokurtosis or “fat-tails” through the large value for (excess) kurtosis. Also reported, is the Kolmogorov–Smirnov (KS) test, which measures the departure from the normal distribution. In each case, under the null hypothesis that the sample data come from a normal distribution, we can reject the null with the implication being that each series is not normally distributed. The results of the normality test for the first three metal series accord with those reported in Khalifa et al. (2011). Lastly, Table 1 contains the results of the modified ADF test (Elliott et al. 1996) of nonstationarity. In each of the series, the log returns rejects the null hypothesis of a unit root, in favor of a stationarity. 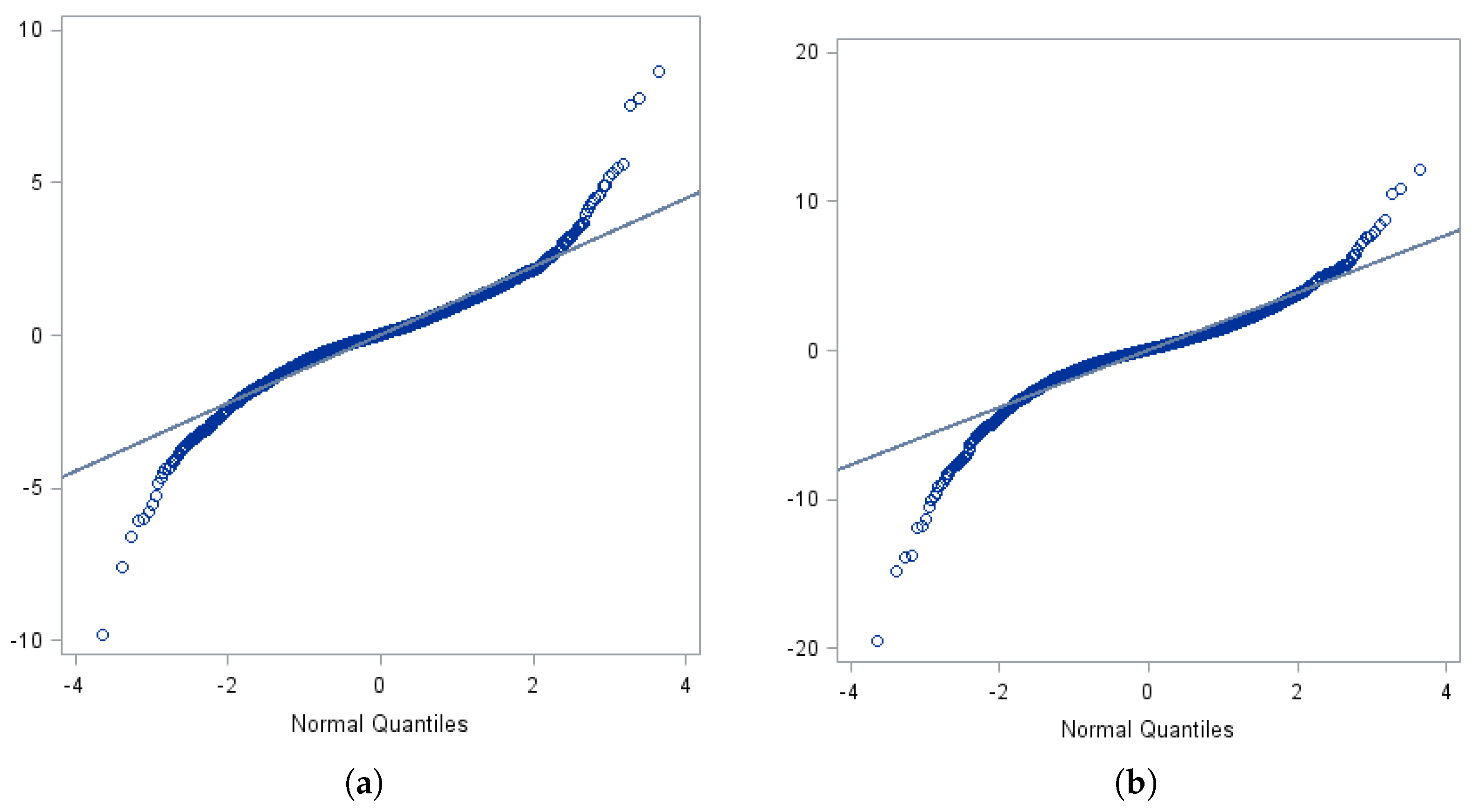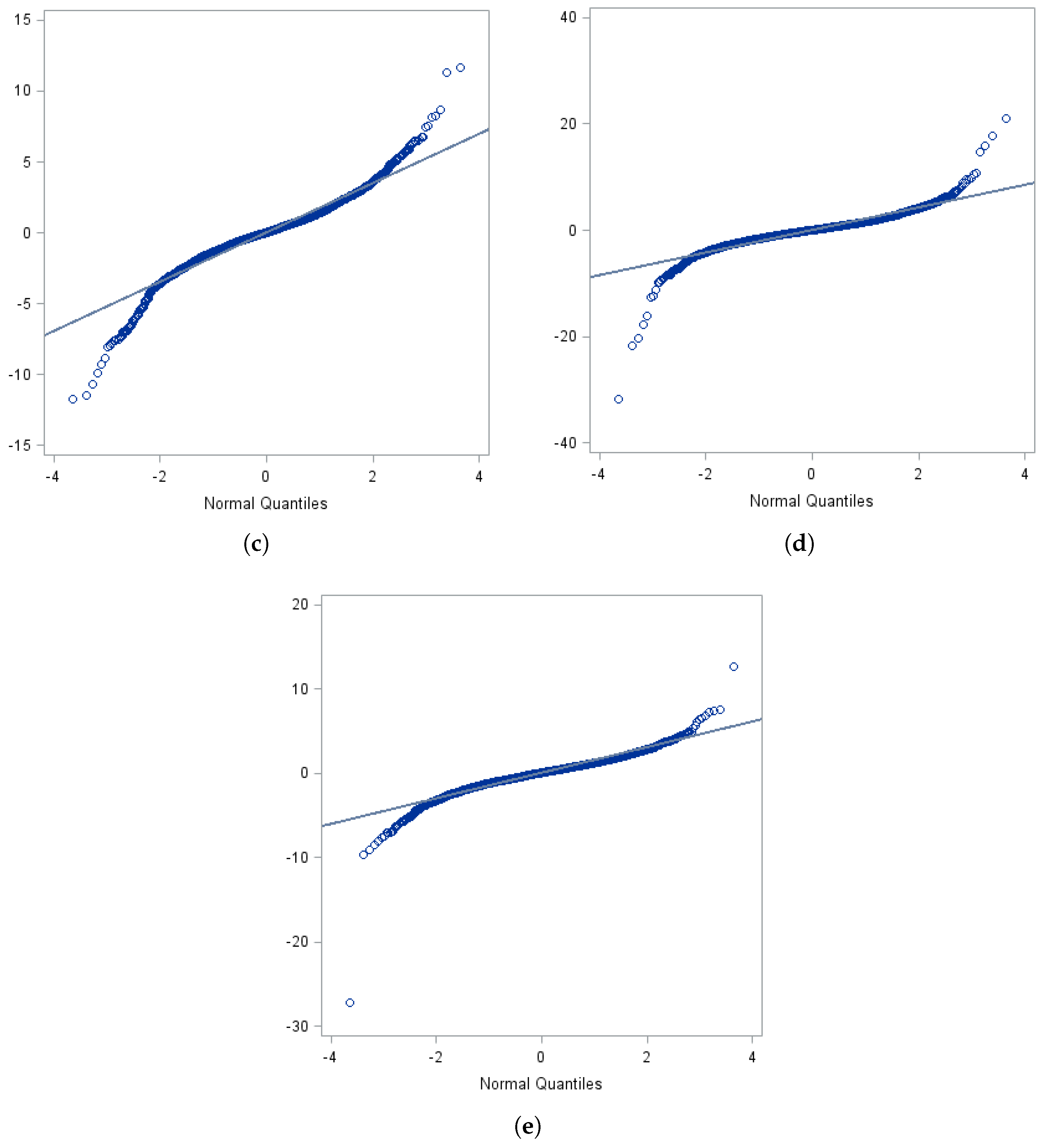2

The results are corroborated by Figure 1, which display “quantile–quantile” (QQ) plots, for the natural log of metal price returns. If the log returns of the metal prices follow geometric Brownian motion (GBM), then the commodity prices would be log-normally distributed; that is the natural log of the commodity prices would be normally distributed, and hence “normal-tailed”. The QQ plots compare the values observed in the empirical distribution (measured on the y-axis) against the value from the inverse of a theoretical normal distribution whose mean and standard deviation corresponds to the value associated with the empirical distribution (measured on the x-axis). If the empirical distribution of the natural log of the price return series is close to the normal distribution, the QQ plot will be well described by a straight line. Alternatively, if there are significant departures from a linear relationship, then the return series is not well-described by a normal distribution. Based on the Figure 1a–e, we see consistent departures from a linear relation, particularly in the tails, which indicate significance lepotkurtosis and cast doubt on the assumption of an underlying GBM process.

5. Results

5.1. Maximum Likelihood Estimation

Using maximum likelihood methods, the four stochastic processes (PD, JD, GPD, GJD) are estimated using the daily futures date for the five metal price return series.3 Results for the metal series are reported in

Table 2. Estimation of the model parameters for daily price returns.

	$\mathit{\mu }$	$\mathit{\sigma }$	$\mathit{\kappa }$	${\mathit{\alpha }}_1$	${\mathit{\beta }}_1$	$\mathit{\lambda }$	$\mathit{\theta }$	$\mathit{\delta }$	L
	A. Gold
PD	0.0316 **	1.1163 ***							−1.529
	(0.016)	(0.011)
JD	0.0755 ***	0.5949 ***				0.1901 ***	−0.2632 ***	1.8221 ***	−1.455
	(0.021)	(0.074)				(0.197)	(0.051)	(0.132)
GPD	0.0282 **		0.0114 ***	0.0337 ***	0.9563 ***				−1.452
	(0.014)		(0.001)	(0.003)	(0.004)
GJD	0.0520		0.0017 ***	0.0269 ***	0.9559 ***	0.2197 ***	−0.1250	1.3502 ***	−1.410
	(0.015)		(0.002)	(0.003)	(0.005)	(0.074)	(0.082)	(0.173)
	B. Silver
PD	0.0022	1.934 ***							−2.079
	(0.021)	(0.019)
JD	0.1659 ***	1.0182 ***				0.4357 ***	−0.3298 ***	2.3932 ***	−1.964
	(0.025)	(0.043)				(0.055)	(0.078)	(0.129)
GPD	−0.0047		0.0304 ***	0.0489 ***	0.9410 ***				−1.951
	(0.021)		(0.003)	(0.005)	(0.005)
GJD	0.0793 ***		0.0079 ***	0.0252 ***	0.9574 ***	0.1235 ***	−0.7823	2.9383 ***	−1.906
	(0.022)		(0.003)	(0.003)	(0.005)	(0.023)	(0.208)	(0.237)
	C. Copper
PD	−0.0238 ***	1.7366 ***							−1.971
	(0.025)	(0.018)
JD	0.0405 **	1.0140 ***				0.4435 ***	−0.0375	2.8321 ***	−1.895
	(0.021)	(0.081)				(0.120)	(0.070)	(0.212)
GPD	0.009		0.0266 ***	0.0454 ***	0.9445 ***				−1.854
	(0.020)		(0.002)	(0.005)	(0.005)
GJD	0.0373		0.0001	0.0317 ***	0.9554 ***	0.2143 *	−0.1559	1.8081 ***	−1.831
	(0.023)		(0.005)	(0.004)	(0.006)	(0.105)	(0.131)	(0.322)
	D. Zinc
PD	0.0154 ***	2.1251 ***							−2.173
	(0.015)	(0.021)
JD	0.0313 ***	1.3741 ***				0.1844 ***	−0.0861 ***	3.5276 ***	−2.037
	(0.029)	(0.042)				(0.032)	(0.122)	(0.266)
GPD	−0.0072		0.0277 ***	0.0476 ***	0.9423 ***				−1.970
	(0.022)		(0.003)	(0.005)	(0.005)
GJD	0.0329		0.0104 ***	0.0316 ***	0.9583 ***	0.0300 ***	−1.3607 **	4.3655 ***	−1.941
	(0.021)		(0.002)	(0.003)	(0.0031)	(0.009)	(0.636)	(0.675)
	E. Platinum
PD	−0.2139 ***	1.5147 ***							−1.834
	(0.022)	(0.015)
JD	0.1014 ***	1.0701 ***				0.1834 ***	−0.4824 ***	2.3213 ***	−1.742
	(0.021)	(0.029)				(0.034)	(0.121)	(0.173)
GPD	0.0140		0.0344 ***	0.0714 ***	0.9137 ***				−1.718
	(0.018)		(0.008)	(0.007)	(0.009)
GJD	0.0790 ***		0.0128 ***	0.0401 ***	0.9372 ***	0.1199 ***	−0.6243 ***	1.9723 ***	−1.697
	(0.021)		(0.004)	(0.006)	(0.008)	(0.032)	(0.171)	(0.216)

Note: The estimates are obtained using GAUSS. The standard errors are given in parentheses and the * represents statistical significance at the 10% level, ** at the 5% level and *** at the 1% level. L is the mean log-likelihood value.

, while test statistics for the pairwise comparisons of the four models follow in

Table 3. Likelihood ratio test statistics.

	${\mathit{LR}}_{\mathit{PD},\mathit{JD}}$	${\mathit{LR}}_{\mathit{PD},\mathit{GPD}}$	${\mathit{LR}}_{\mathit{JD},\mathit{GJD}}$	${\mathit{LR}}_{\mathit{GPD},\mathit{GJD}}$
Gold Price Returns	702.6	731.7	1135.0	403.3
	<0.001	<0.001	<0.001	<0.001
Silver Price Returns	1091.5	1219.8	556.5	428.1
	<0.001	<0.001	<0.001	<0.001
Copper Price Returns	728.0	1118.3	606.5	216.2
	<0.001	<0.001	<0.001	<0.001
Zinc Price Returns	1276.1	1900.7	901.0	276,4
	<0.001	<0.001	<0.001	<0.001
Platinum Price Returns	876.8	1108.8	423.1	2191.1
	<0.001	<0.001	<0.001	<0.001

Note: p-values presented below test statistics.

. The discussion of the results begins with the pure diffusion model, and progress across the remaining three (JD, GPD, GJD) models.

Examining the pure diffusion (PD) model, we note the estimated drift parameter, $\mu$, was statistically significant in four of five metal return series. Only platinum returns have a significantly negative drift parameter, while the drift for silver returns was not statistically different from zero. The estimated instantaneous rate of variance, $\sigma$, was statistically significant across all five returns series, with zinc displaying the largest variance. A comparison between the PD and JD models demonstrates the importance of including jumps, as the jump intensity $\lambda$ is statistically significant across the five series. Furthermore, the instantaneous rate of variance in the JD model is notably reduced, relative to values observed in the PD model, in each series. Also, the average jump appears to be negative, as $\delta$, was less than 0 for each series, and statistically significant in four of the five.

Comparing the results of the PD and GPD models, we see that allowing for GARCH also improved the models predictive power—the log-likelihood function has increased. In addition, all of the parameters associated with the volatility process were strongly statistically significant. The GARCH(1,1) model GPD provided variance parameter estimates ($\widehat{{\alpha }_1},\widehat{{\beta }_1}$) that were less than one in magnitude, and we note that $\kappa$ tends to be be relatively small, when compared with these estimates. The jump intensity parameter $\lambda$ in the GJD model remains significant across the models, yet has notably decreased relative to the JD estimates. This result indicates that metal returns experienced less frequent jumps when time-varying volatility is accounted for in the model. For example, the results of the JD model suggest silver prices experience a jump approximately every 2.3 days, while the GJD model suggest a jump occurs approximately every 8.1 days.

5.2. Likelihood Ratio Test Results

We now turn out attention to an analysis of pairwise comparisons of the models, which are conducted using likelihood ratio (LR) tests. Results for these hypothesis tests are presented in Table 3. Each entry in the table is a test statistic of the form $L{R}_{x,y}$, where the null hypothesis is that the appropriate stochastic process describing the data is x and the alternative hypothesis is that the appropriate stochastic process describing the data is y. The value in parentheses, below each test statistic, gives the probability that the null hypothesis is preferred to the alternative. In the case of gold price returns, the first $LR$ test indicates that the JD model is preferred to the PD process, at the 1% level. The results indicate that in every case the null hypothesis is rejected at the 1% level of significance. As such, the test results point to a statistically important gain in predictive power associated with adopting the added complexity associated with moving to specification y from x. Based on these results, the preferred model allows for both jumps and time-varying volatility (GJD), in every case.

5.3. Implied Probabilities

The results from the empirical analysis can be used to assess the tendency for jumps to occur in the five metals markets. The probability that at least one jump occurred is then 1 minus the probability of observing no jumps. Recall, the probability that no jumps occur at any time t can be obtained from Equation (9). The predicted probabilities, that at least one jump occurred in each day of the sample, was calculated. The resultant predicted probabilities during 2018, for gold and copper, which are representative of the remaining series, are plotted in Figure 2. the jagged nature of the figures indicates the high frequency of jumps that occur within a year. Finally, the pairwise correlation among the jump probabilities was examined, with the result that very little correlation was observed between the implied jump probabilities. The highest correlation was observed between the probability of at least one jump in the gold market and the silver market (0.345). The remaining correlations varied between 0.04 and 0.245. Given the literature on co-movement among commodities Pindyck and Rotemberg (1990); Hammoudeh et al. (2009) the correlation observed is considered rather low. However, the pairwise correlations levels are higher within metallurgical categories (e.g., precious metals) than across categories.

6. Conclusions

The goal in this paper is to re-examine the assumption that the relative price returns of important heavy metal prices, such as gold and copper, can be modeled using a continuous time process, with an eye towards developing a more accurate understanding of the stochastic forces driving these futures prices. Several important conclusions derive from the results of the analysis. For the five metal price series, the data strongly suggest that allowing for jumps or time-varying volatility in price returns generates improved fit, relative to the pure diffusion model. Moreover, combining a process that allows for jumps with a GARCH process (GJD) outperforms all alternative stochastic processes. Thus, the results indicate that incorporating both time-varying volatility and jumps into empirical models of metals futures prices improves predictive power. Such an improvement should be of clear benefit to market traders, which is important given the financialization of commodity markets. Furthermore, events in the market for a dominant resources, within an economy, can be important for policymakers, since price shocks could be followed by economic downturns.

There are many reasons why a better understanding of the stochastic process driving price of heavy metals would be useful. Such commodity resources can have important microeconomic effects; certainly commodity price risk would have an impact on the profits of extraction-based firms. A better understanding of the underlying stochastic process could aid in forecasting futures prices, increasing the hedging ability of the firm. Furthermore, the added benefits accrue from the ability to better frame the underlying stochastic model in an investment under uncertainty framework, which we believe has real potential for evaluating important large-scale infrastructure investments such as a mine’s operation or closure decision. The potential for substantial (societal) welfare implications of these investments underscores the importance of developing a better understanding of the stochastic process underlying heavy metals prices, which in turn highlights the value of developing a more accurate empirical model to describe these prices.

Future work could extend the analysis is several noteworthy areas. The literature contains many extensions of the GARCH process, and research has taken note of the asymmetries in positive and negative shocks. Moreover, the inclusion of a stochastic process driving the volatility, which also allows for jumps to occur could be incorporated (see Rockinger and Semenova (2005)). Finally, herein the jump events were not specified ex ante, but rather the econometric results were allowed to pick out the key parameters. An alternative would be to use some criterion to decide when a jump has occurred, as in Chevallier and Ielpo (2014).