The Effects of Quantitative Easing Announcements on the Mortgage Market: An Event Study Approach
Abstract
:1. Introduction
2. Literature Review
2.1. Quantitative Easing (QE) Announcement Effects on Interest Rates and Asset Prices
2.2. QE Announcement Effects Analysis Using Event Studies
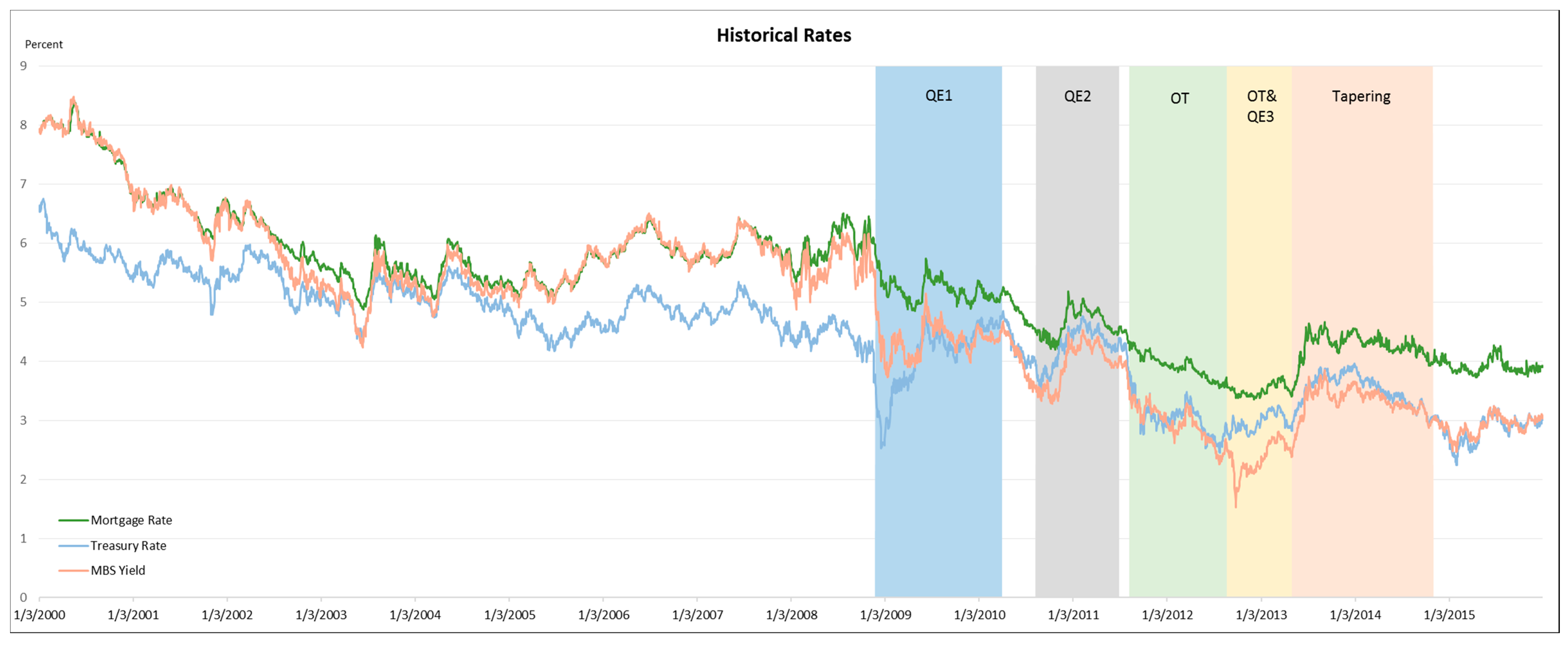
3. Data
4. Methodology
4.1. QE Announcement Dates for Event Study
4.2. Event Window, Issues and GARCH
5. Results
5.1. Individual Events
5.2. Delayed Effects
5.3. Comparing the Results with Literature
6. Events Grouped by Announcement Type and QE Round
6.1. Regressions with Grouped Event Dummies
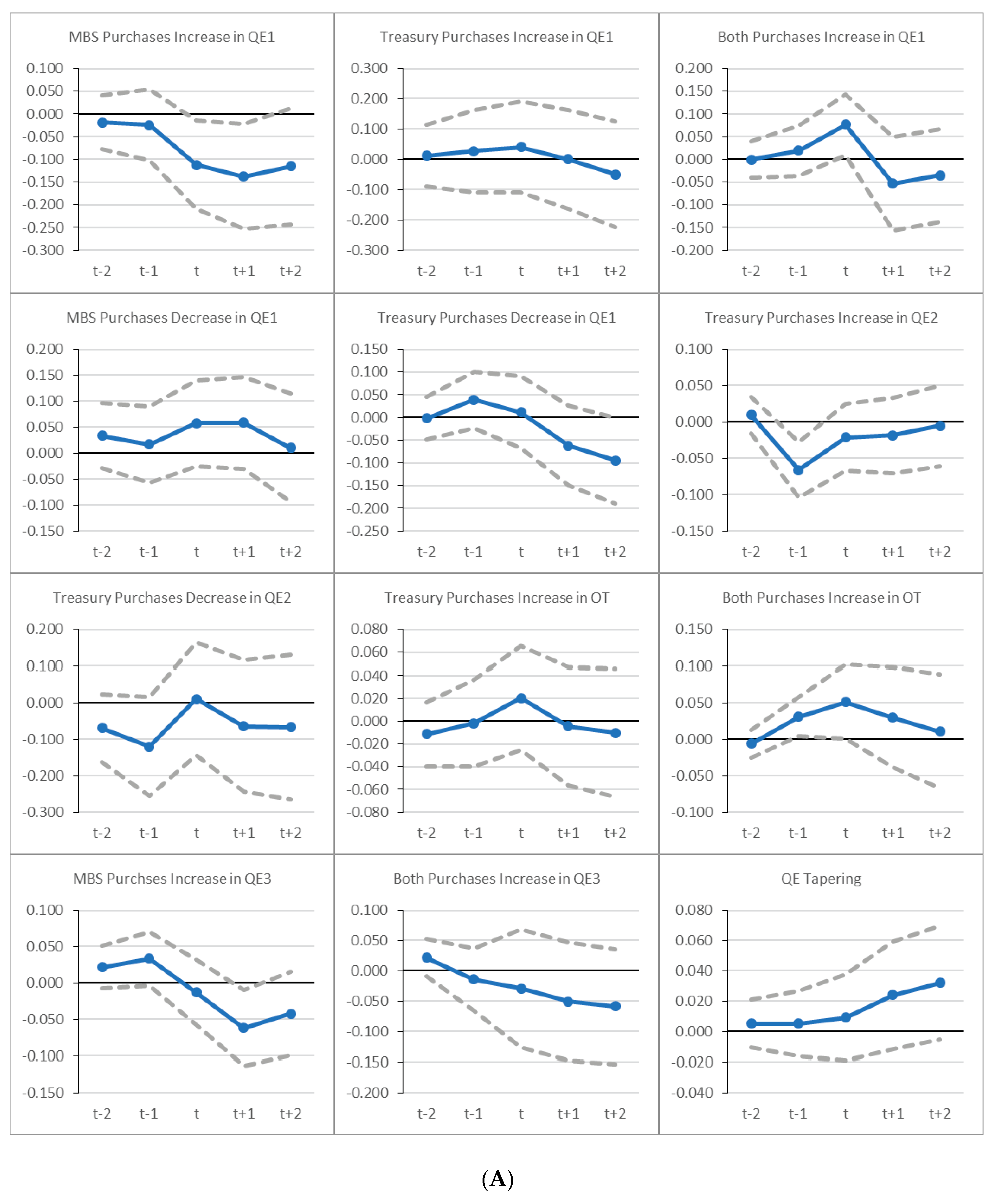
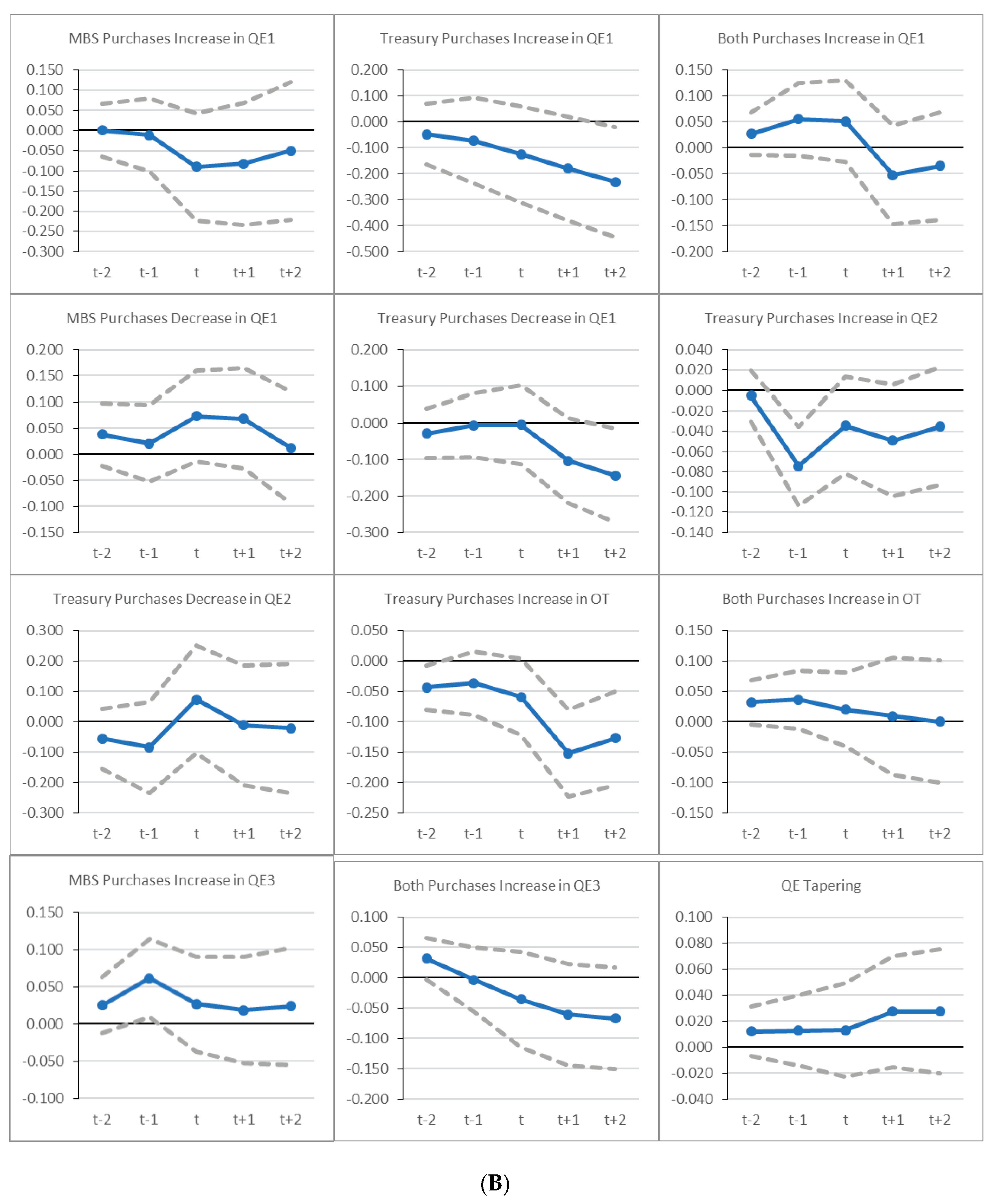
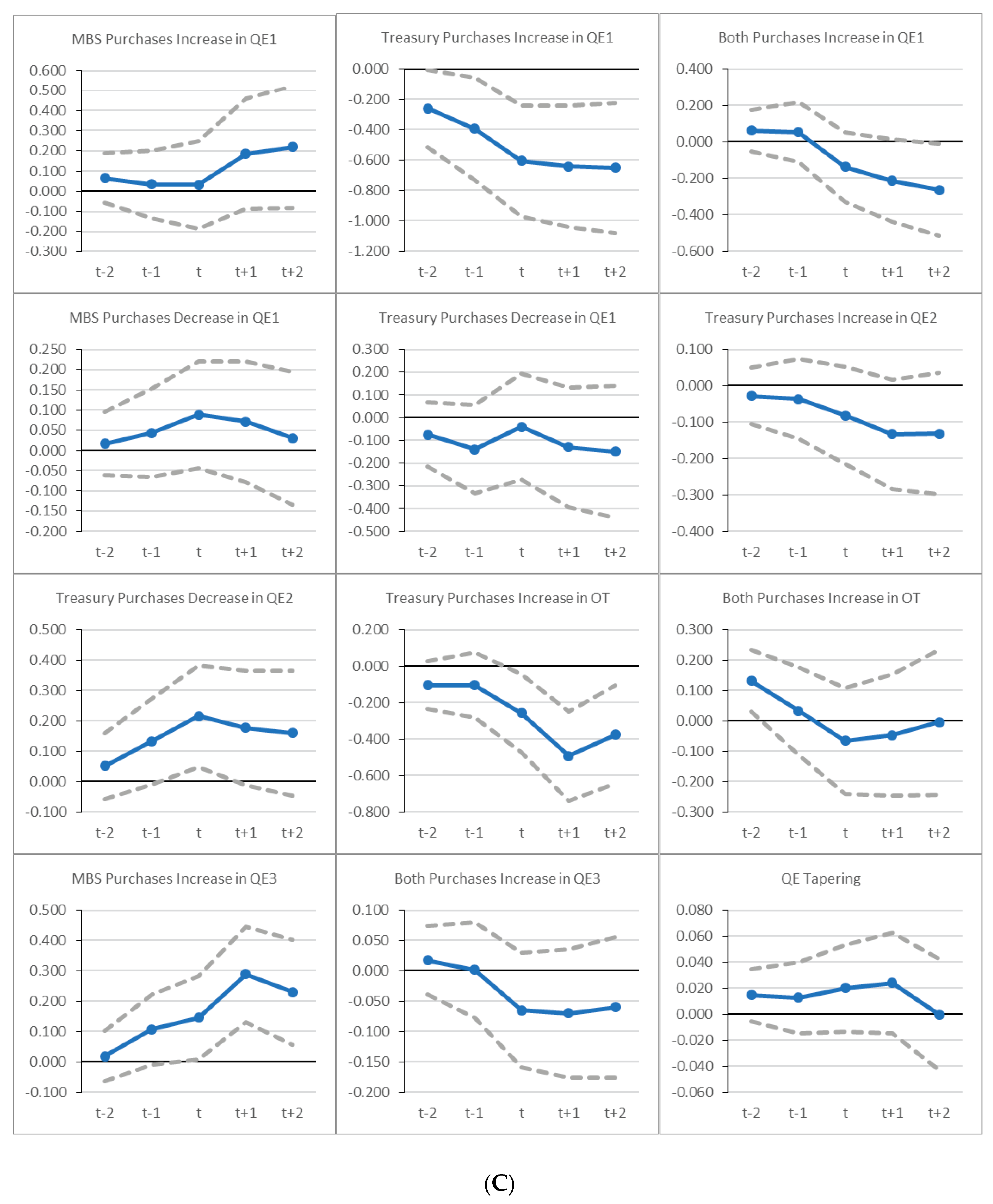
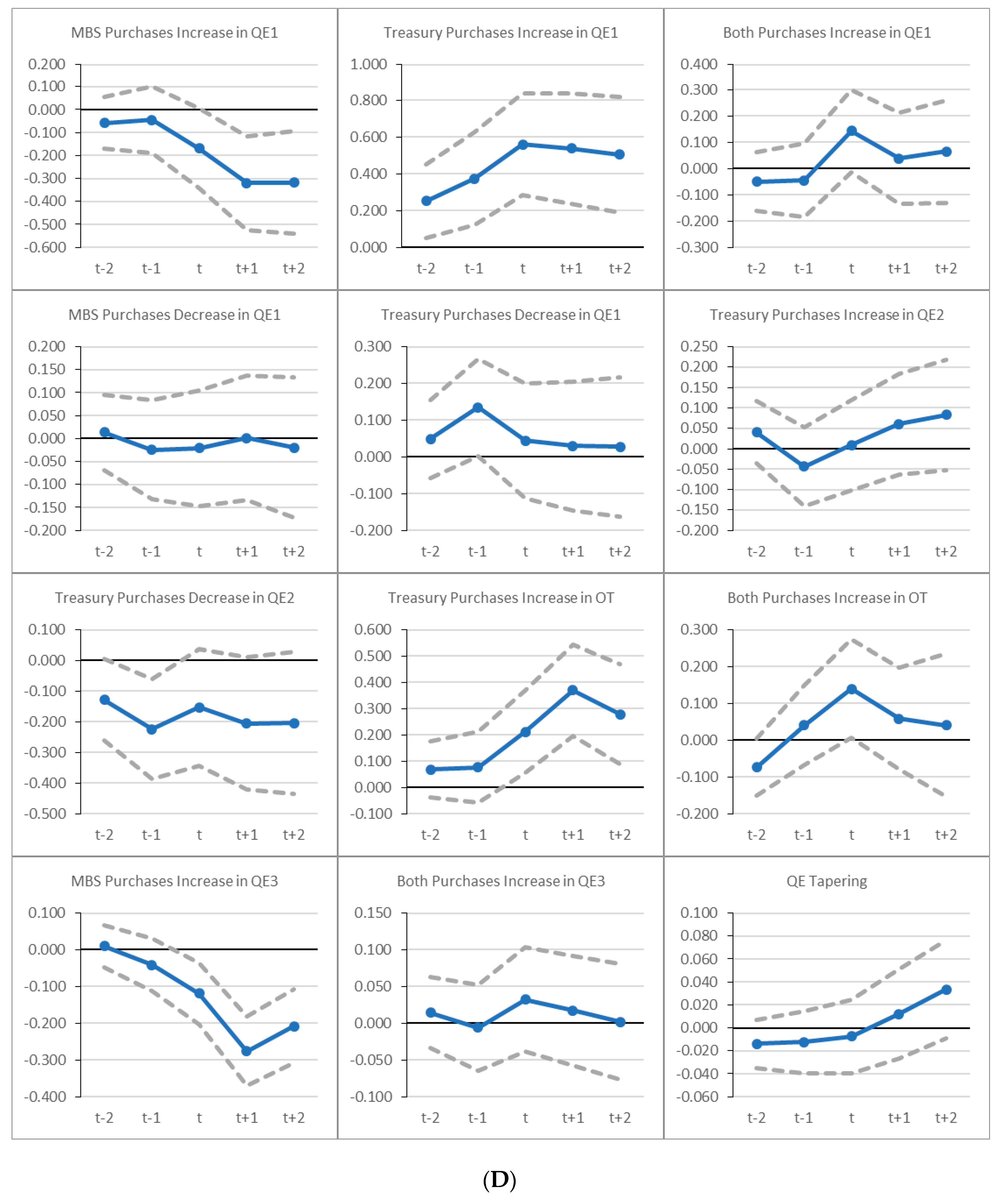
6.2. Evolution of Cumulative Abnormal Returns (CARs) for Grouped QE Events
7. Robustness Checks
7.1. Adding More Controls into the Model
7.2. Using 10-Year instead of 30-Year Treasury Rate
8. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
Appendix A
| Obs. | Frequency | Mean | Median | SD | Min | Max | Skewness | Kurtosis | |
|---|---|---|---|---|---|---|---|---|---|
| 30-year Mortgage Rate | 1998 | Daily | 4.52 | 4.34 | 0.75 | 3.36 | 6.51 | 0.65 | −0.38 |
| 30-year Treasury Rate | 1998 | Daily | 3.63 | 3.61 | 0.67 | 2.25 | 4.85 | 0.08 | −1.34 |
| 10-year Treasury Rate | 1998 | Daily | 2.72 | 2.63 | 0.71 | 1.43 | 4.27 | 0.24 | −1.14 |
| Freddie Mac 30-year MBS Current Coupon | 1998 | Daily | 3.674 | 3.438 | 0.959 | 1.522 | 6.177 | 0.680 | −0.121 |
| Consumer Price Index | 96 | Monthly | 225.859 | 227.196 | 8.892 | 211.398 | 238.302 | −0.131 | −1.497 |
| Case-Shiller House Price Index | 96 | Monthly | 155.62 | 148.02 | 14.85 | 137.08 | 184.03 | 0.45 | −1.34 |
| Unemployment Rate | 96 | Monthly | 7.57 | 7.75 | 1.63 | 4.90 | 10.00 | −0.15 | −1.35 |
| Date | Program | Event | Announcement | Group |
|---|---|---|---|---|
| 11/25/2008 | QE1 | FOMC Meeting | The FOMC “will purchase $100 billion in GSE debt and $500 billion in GSE MBS.” | MBS_Increase |
| 12/1/2008 | QE1 | Bernanke Speech | He stated Fed “could purchase longer-term Treasury or agency securities.” | T_Increase |
| 12/16/2008 | QE1 | FOMC Meeting | The Fed cut federal funds rate target from 1 percent to 0–0.25 percent, was “ready to expand its purchases of agency debt and MBSs as conditions warrant”, and suggested of extending QE to Treasury purchases. | Both_Increase |
| 1/28/2009 | QE1 | FOMC Meeting | The Fed was ready to expand the quantity and duration of MBS purchases. | MBS_Increase, |
| 3/18/2009 | QE1 | FOMC Meeting | The FOMC “will purchase up to an additional $750 billion of agency MBSs with a total of $1.25 trillion, up to $100 billion agency debt this year with a total of $200 billion and up to $300 billion longer-term Treasury securities over the next six months.” | Both_Increase |
| 8/12/2009 | QE1 | FOMC Meeting | The FOMC “decided to gradually slow the pace” of Treasury purchases. | T_Decrease |
| 9/23/2009 | QE1 | FOMC Meeting | The FOMC “will gradually slow the pace” of MBS purchases. | MBS_Decrease |
| 11/4/2009 | QE1 | FOMC Meeting | The FOMC “will purchase a total of $175 billion of agency debt” instead of $200 billion. It also “will gradually slow the pace of its purchases of agency debt and MBSs and these transactions will executed by the end of first quarter of 2010.” | MBS_Decrease |
| 8/10/2010 | QE2 | FOMC Meeting | The FOMC “will keep constant the Fed’s holdings of securities … by reinvesting principal payments from agency debt, agency MBSs in longer-term Treasury securities.” It also “will continue roll over Treasury securities holdings.” | T_Increase |
| 8/27/2010 | QE2 | Bernanke Speech | He suggested additional QE “should further action prove necessary.” | T_Increase |
| 9/21/2010 | QE2 | FOMC Meeting | The FOMC “is prepared to provide additional accommodation if needed.” | T_Increase |
| 10/15/2010 | QE2 | Bernanke Speech | Bernanke commented the drawbacks of large scale asset purchases. | T_Decrease |
| 11/3/2010 | QE2 | FOMC Meeting | The FOMC “intends to purchase a further $600 billion of longer term Treasury securities by the end of second quarter of 2011, at a pace of about $75 billion per month.” | T_Increase |
| 8/9/2011 | OT | FOMC Meeting | The FOMC “is prepared adjust those (securities) holdings as appropriate.” | Both_Increase |
| 8/26/2011 | OT | Bernanke Speech | He announced “employ its tools … to promote a stronger economic recovery.” | Both_Increase |
| 9/21/2011 | OT | FOMC Meeting | The FOMC “intends to purchase, by the end of June 2012, $400 billion of Treasury securities with remaining maturities of 6 years to 30 years and sell an equal amount of Treasury securities with remaining maturities of 3 years or less”. | T_Increase |
| 6/20/2012 | OT | FOMC Meeting | The FOMC decided to “continue through the end of the year its program to extend average maturity of its holdings of securities.” | T_Increase |
| 8/22/2012 | OT/QE3 | FOMC Minutes Released | FOMC members “judged that additional monetary accommodation would likely be warranted fairly soon.” | Both_Increase |
| 8/31/2012 | OT/QE3 | Bernanke Speech | He remarked about unconventional monetary policy tools. | Both_Increase |
| 9/13/2012 | OT/QE3 | FOMC Meeting | The FOMC “will purchase additional agency MBSs at a pace of $40 billion per month”, along with OT will together increase “holdings of longer-term securities by about $85 billion each month through the end of the year.” | MBS_Increase |
| 12/12/2012 | OT/QE3 | FOMC Meeting | The FOMC “will purchase longer—term Treasury securities after OT is completed at the end of the year, initially at a pace of $45 billion per month.” | T_Increase |
| 5/1/2013 | Tapering | FOMC Meeting | The FOMC “is prepared to increase or reduce the pace of its purchase.” | Tapering |
| 5/22/2013 | Tapering | Bernanke Speech and testimony | He remarked about a potential “step down” in the pace of asset purchases. | Tapering |
| 6/19/2013 | Tapering | Bernanke’s Press Conference | He said “If the incoming data are broadly consistent with this forecast, … be appropriate to moderate the monthly pace of purchases later this year.” | Tapering |
| 12/18/2013 | Tapering | FOMC Meeting | The FOMC “Beginning in January … will add to its holdings of agency MBSs … $35 billion rather than $40 billion per month, long-term Treasury securities … $40 billion rather than $45 billion per month.” | Tapering |
| 1/29/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in February … will add to its holdings of agency MBSs … $30 billion rather than $35 billion per month, long-term Treasury securities … $35 billion rather than $40 billion per month.” | Tapering |
| 3/19/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in April … will add to its holdings of agency MBSs … $25 billion rather than $30 billion per month, long-term Treasury securities … $30 billion rather than $35 billion per month.” | Tapering |
| 4/30/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in May … will add to its holdings of agency MBSs … $20 billion rather than $25 billion per month, long-term Treasury securities … $25 billion rather than $30 billion per month.” | Tapering |
| 5/7/2014 | Tapering | Yellen Testimony | She said “further measured reductions in asset purchases were appropriate.” | Tapering |
| 6/18/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in July … will add to its holdings of agency MBSs … $15 billion rather than $20 billion per month, long-term Treasury securities … $20 billion rather than $25 billion per month.” | Tapering |
| 7/15/2014 | Tapering | Yellen Testimony | She said “will make further measured reductions in the pace of asset purchases at upcoming meetings.” | Tapering |
| 7/30/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in August … will add to its holdings of agency MBSs … $10 billion rather than $15 billion per month, long-term Treasury securities … $15 billion rather than $20 billion per month.” | Tapering |
| 8/22/2014 | Tapering | Yellen Speech | She said “we have reduced our pace of asset purchases and expect to complete this program in October.” | Tapering |
| 9/17/2014 | Tapering | FOMC Meeting | The FOMC “Beginning in October … will add to its holdings of agency MBSs … $5 billion rather than $10 billion per month, long-term Treasury securities … $10 billion rather than $15 billion per month.” | Tapering |
| 10/29/2014 | Tapering | FOMC Meeting | The FOMC “decided to conclude its asset purchase program this month.” It is also “maintaining its existing policy of reinvesting principal payments from its holdings of agency debt and agency MBSs in agency MBSs and of rolling over maturing Treasury securities at auction.” | Tapering |
| Dependent Variable | ||||||||
|---|---|---|---|---|---|---|---|---|
| Control Variables | Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE |
| −0.008 | 0.014 | −0.012 | 0.015 | 0.013 | 0.026 | −0.021 | 0.021 | |
| 0.013 | 0.012 | 0.019 | 0.014 | 0.026 | 0.024 | 0.033 | 0.021 | |
| −0.003 | 0.012 | 0.006 | 0.014 | 0.014 | 0.022 | 0.011 | 0.022 | |
| −0.009 | 0.011 | −0.012 | 0.012 | −0.018 | 0.018 | 0.005 | 0.018 | |
| −0.016 | 0.011 | −0.022 | 0.014 | 0.013 | 0.021 | −0.050 ** | 0.020 | |
| 0.010 | 0.012 | 0.006 | 0.012 | 0.006 | 0.018 | 0.021 | 0.017 | |
| −0.028 | 0.020 | −0.020 | 0.027 | 0.026 | 0.032 | −0.010 | 0.032 | |
| 0.009 | 0.018 | 0.024 | 0.020 | −0.019 | 0.031 | 0.022 | 0.030 | |
| 0.031* | 0.018 | 0.026 | 0.021 | 0.019 | 0.031 | 0.016 | 0.030 | |
| Mortgage Rate (Controlling for 10-year Treasury Rate) | Mortgage Rate (Controlling for 30-year Treasury Rate) | |||
|---|---|---|---|---|
| CAR | SE | CAR | SE | |
| QE1_MBS_Increase | −0.124 ** | 0.061 | −0.115 * | 0.065 |
| QE1_T_Increase | −0.024 | 0.082 | −0.049 | 0.089 |
| QE1_Both_Increase | −0.038 | 0.051 | −0.035 | 0.052 |
| QE1_MBS_Decrease | 0.010 | 0.047 | 0.010 | 0.053 |
| QE1_T_Decrease | −0.044 | 0.042 | −0.095 * | 0.048 |
| QE2_T_Increase | 0.032 | 0.026 | −0.005 | 0.028 |
| QE2_T_Decrease | −0.059 | 0.094 | −0.066 | 0.101 |
| OT_T_Increase | −0.063 ** | 0.027 | −0.010 | 0.029 |
| OT_Both_Increase | −0.011 | 0.040 | 0.011 | 0.040 |
| QE3_MBS_Increase | −0.046 * | 0.027 | −0.042 | 0.029 |
| QE3_Both_Increase | −0.048 | 0.035 | −0.059 | 0.048 |
| Tapering | 0.022 | 0.017 | 0.032 * | 0.019 |
References
- Adalid, Ramón, and Matteo Falagiarda. 2018. How Repayments Manipulate Our Perceptions about Loan Dynamics after a Boom. Working Paper Series No. 2211; Frankfurt, Germany: European Central Bank. [Google Scholar]
- Altavilla, Carlo, and Domenico Giannone. 2017. The Effectiveness of Nonstandard Monetary Policy Measures: Evidence from Survey Data. Journal of Applied Econometrics 32: 952–64. [Google Scholar] [CrossRef]
- Altavilla, Carlo, Giacomo Carboni, and Roberto Motto. 2015. Asset Purchase Programmes and Financial Markets: Lessons from the Euro Area. Working Paper Series No. 1864; Frankfurt, Germany: European Central Bank. [Google Scholar]
- Altavilla, Carlo, Domenico Giannone, and Michele Lenza. 2016. The financial and macroeconomic effects of the OMT announcements. International Journal of Central Banking 12: 29–57. [Google Scholar]
- Borrallo, Fructuoso, Ignacio Hernando, and Javier Valles. 2016. The Effects of US Unconventional Monetary Policies in Latin America. Working Papers, No. 1606. Madrid, Spain: Banco de España. [Google Scholar]
- Bowman, David, Juan Londono, and Horacio Sapriza. 2015. U.S. Unconventional Monetary Policy and Transmission to Emerging Market Economies. Journal of International Money and Finance 55: 27–59. [Google Scholar] [CrossRef]
- Christensen, Jens, and Glenn Rudebusch. 2012. The response of interest rates to US and UK quantitative easing. The Economic Journal 122: F385–414. [Google Scholar]
- Degryse, Hans, Moshe Kim, and Steven Ongena. 2009. Microeconometrics of Banking. Oxford: Oxford University Press. [Google Scholar]
- Di Maggio, Marco, Christopher Palmer, and Amir Kermani. 2016. How Quantitative Easing Works: Evidence on the Refinancing Channel. NBER Working Paper 22638. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Eser, Fabian, and Bernd Schwaab. 2016. Evaluating the impact of unconventional monetary policy measures: Empirical evidence from the ECB’s Securities Markets Programme. Journal of Financial Economics 119: 147–67. [Google Scholar] [CrossRef]
- Falagiarda, Matteo, and Stefan Reitz. 2015. Announcements of ECB unconventional programs: Implications for the sovereign spreads of stressed euro area countries. Journal of International Money and Finance 53: 276–95. [Google Scholar] [CrossRef]
- Gagnon, Joseph, Matthew Raskin, Julie Remache, and Brian Sack. 2011. The Financial Market Effects of the Federal Reserve’s Large-Scale Asset Purchases. International Journal of Central Banking 7: 3–43. [Google Scholar]
- Glick, Reuven, and Sylvain Leduc. 2012. Central bank announcements of asset purchases and the impact on global financial and commodity markets. Journal of International Money and Finance 31: 2078–101. [Google Scholar] [CrossRef]
- Glick, Reuven, and Sylvain Leduc. 2015. Unconventional Monetary Policy and the Dollar: Conventional Signs, Unconventional Magnitudes. International Journal of Central Banking 14: 103–52. [Google Scholar] [CrossRef]
- Hancock, Diana, and Wayne Passmore. 2011. Did the Federal Reserve’s MBS Purchase Program Lower Mortgage Rates? Journal of Monetary Economics 58: 498–514. [Google Scholar] [CrossRef]
- Hancock, Diana, and Wayne Passmore. 2012. The Federal Reserve’s Portfolio and Its Effects on Mortgage Markets (March 6, 2012); FEDS Working Paper No. 2012-22. Washington, DC, USA: Board of Governors of the Federal Reserve System.
- Hancock, Diana, and Wayne Passmore. 2015. How Does the Federal Reserve’s Large-Scale Asset Purchase (LSAPs) Influence Mortgage-Backed Securities (MBS) Yields and U.S. Mortgage Rates? Real Estate Economics 43: 855–90. [Google Scholar] [CrossRef]
- Hattori, Masazumi, Andreas Schrimpf, and Vladyslav Sushko. 2016. The Response of Tail Risk Perceptions to Unconventional Monetary Policy. American Economic Journal: Macroeconomics 8: 111–36. [Google Scholar] [CrossRef]
- Hollifield, Burton. 2011. Comments on ‘Did the Federal Reserve’s MBS Purchase Program Lower Mortgage Rates?’. Journal of Monetary Economics 58: 515–17. [Google Scholar] [CrossRef]
- Jarrow, Robert, and Hao Li. 2014. The Impact of Quantitative Easing on the U.S. Term Structure of Interest Rates. Review of Derivatives Research 17: 287–321. [Google Scholar] [CrossRef]
- Kozicki, Sharon, Eric Santor, and Lena Suchanek. 2015. Large-Scale Asset Purchases: Impact on Commodity Prices and International Spillover Effects. Bank of Canada Working Paper, No. 2015-21. Ottawa, ON, Canada: Bank of Canada. [Google Scholar]
- Krishnamurthy, Arvind, and Annette Vissing-Jorgensen. 2011. The Effects of Quantitative Easing on Interest Rates: Channels and Implications for Policy. Brookings Paper on Economic Activity, NBER Working Paper No. 17555. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Li, Canlin, and Min Wei. 2012. Term Structure Modelling with Supply Factors and the Federal Reserve’s Large Scale Asset Purchase Programs; FEDS Working Paper, No. 2012-37. Washington, DC, USA: Board of Governors of the Federal Reserve System.
- Makenzie, Andrew M., Michael R. Thomsen, and Bruce L. Dixon. 2004. The Performance of Event Study Approaches Using Daily Commodity Futures Returns. Journal of Futures Markets 24: 533–55. [Google Scholar] [CrossRef]
- Neely, Christopher. 2015. Unconventional monetary policy had large international effects. Journal of Banking and Finance 52: 101–11. [Google Scholar]
- Patrabansh, Saty, William Doerner, and Samuel Asin. 2014. The Effects of Monetary Policy on Mortgage Rates; FHFA Working Papers 14-2. Washington, DC, USA: The Federal Housing Finance Agency.
- Sirmans, Stace, Stanley Smith, and Stacy Sirmans. 2015. Determinants of Mortgage Interest Rates: Treasuries versus Swaps. Journal of Real Estate and Financial Economics 50: 34–51. [Google Scholar] [CrossRef]
- Swanson, Eric, Lucrezia Reichlin, and Jonathan Wright. 2011. Let’s Twist Again: A High-Frequency Event-Study Analysis of Operation Twist and Its Implications for QE2. Brookings Papers on Economic Activity 2011: 151–207. [Google Scholar] [CrossRef]
- Szczerbowicz, Urszula. 2015. The ECB Unconventional Monetary Policies: Have They Lowered Market Borrowing Costs for Banks and Governments? International Journal of Central Banking 11: 91–127. [Google Scholar]
- Thornton, Daniel. 2017. Effectiveness of QE: An Assessment of Event-Study Evidence. Journal of Macroeconomics 52: 56–74. [Google Scholar] [CrossRef]
- Woodford, Michael. 2012. Methods of Policy Accommodation at the Interest-Rate Lower Bound. Presented at the Jackson Hole Symposium “The Changing Policy Landscape”, Jackson, WY, USA, August 31–September 1. [Google Scholar]
- Wright, Jonathan. 2012. What Does Monetary Policy Do to Long-Term Interest Rates at the Zero Lower Bound? The Economic Journal 122: F447–66. [Google Scholar] [CrossRef]
| 1 | ZLB period started at the end of 2008 when the Fed reduced the federal funds rate to be in the range of 0 to 0.25 percent, and concluded at late 2015 when the Fed decided to increase the federal funds rate to be in the range of 0.25 to 0.5 percent. |
| 2 | Also known as maturity extension program (or MEP). |
| 3 | The stock effect means the effect of increases in the Fed’s asset holdings, while the flow effect means the effect of QE announcements. |
| 4 | Event study literature and methodology are discussed in the Supplemental Materials, Part 1. |
| 5 | Specifically, the mortgage rate is the daily overnight 30-year US home mortgage national average from the bank rate. We only estimate the 30-year mortgage rate here since 60–70 percent mortgages originated during ZLB period were 30-year FRMs. The 30-year mortgage rate is a good reflection of the general borrowing cost of mortgages. |
| 6 | It is known as the effect of traditional monetary policy. |
| 7 | The announcement on 20 March 2013 is considered irrelevant to QE since it only remarked on the improved economic and labor market conditions. It was treated as an unconventional monetary policy announcement (i.e., forward guidance) in Bowman et al. (2015), but should not be regarded as a QE announcement here. |
| 8 | Event windows larger than five days are not considered in my study to avoid the effects of other news. |
| 9 | The test results can be found in Table S1 in the Supplementary Materials. |
| 10 | From the data, the windows for event on 11/25/2008 and the one on 12/1/2008 overlapped. |
| 11 | Usually return means the percentage change of a variable, here I name change of rate as return since mortgage and Treasury rates are already in percent. Also, since “abnormal return” is widely used by researchers doing event studies, it is used in this paper instead of “abnormal change” to avoid confusions. |
| 12 | The name “market model regression” can be found in Degryse et al. (2009). |
| 13 | A constant mean return regression is preferred to a market model regression for estimating the Treasury rate because there is no single reference series (market rate) that simulates or determines the Treasury rate. |
| 14 | The identification of issues, ARMA and GARCH selections, and the skewed t distribution analysis are discussed in the Supplementary Materials, Part 2. |
| 15 | The trivial impacts are mentioned by Altavilla and Giannone (2017), we found similar results in robustness check part. |
| 16 | The ARs for calculating CARs can be found in the Supplementary Materials, Tables S3 and S4. |
| 17 | Events on 1/28/2009 and 3/18/2009. Events on 12/1/2008 and 12/16/2008 are not counted since they both focused on Treasury bond purchases. |
| 18 | Events on 6/19/2013 and 12/18/2013. |
| 19 | They are 8/27/2010 for QE2, 8/9/2011 for OT, 8/22/2012 for QE3. |
| 20 | Department of Commerce reported real GDP growth of 1.6 percent in second quarter of 2010, which was higher than the consensus value of 1.3 percent. From Bloomberg, no other significant macroeconomic news was announced on the same dates as the QE announcement dates. |
| 21 | See Bloomberg article 9/13/2012. |
| 22 | An exception is the first QE announcement on 11/25/2008 which announced only the MBS purchase, but both mortgage rate and Treasury rate had significantly large and negative ARs and CARs. |
| 23 | The Delta method estimates the standard errors of 1st order Taylor expansion of , which can be expressed as . In the equation, is a transformation of regression parameter vector and is the gradient of . Here, is TAR or TCAR. |
| 24 | The cumulative effects are graphed in the Supplementary Materials, Figure S4. |
| 25 | The cumulative abnormal returns of the mortgage rate and the Treasury rate for the 1-day window in my study were −23 and −54 basis points, while those in other studies were all around −100 basis points. |
| 26 | A total of 31 events are in the sample at this part. As we discuss in Part 5, the event on 8/27/2010 is excluded since it is contaminated by the better economy report on the same day. Event on 11/3/2010, 6/20/2012 and 12/12/2012 are excluded given that these 3 events were well expected by the market. In fact, plenty of other researchers exclude those four events in their studies as well. After the deletion, my sample of events is consistent with Krishnamurthy and Vissing-Jorgensen (2011), Bowman et al. (2015) and Borrallo et al. (2016). |
| 27 | ARs and CARs of mortgage rate here are from market model regressions. |
| 28 | Events of only increasing Treasury purchases happened in QE2 and OT periods too. |
| 29 | They claim that since only important events are considered, the effect of which were tremendous and take over macroeconomic news within the event window. |
| 30 | An unexpected change of GDP growth is another indicator of macroeconomic surprises. However, it is hard to estimate since quarterly GDP growth rate would be revised several times in a long time span by the Bureau of Economic Analysis (or U.S. Department of Commerce). |
| 31 | Dickey–Fuller unit root test results are found in the Supplementary Materials, Table S1. |
| 32 | All three ARMA models are sufficient. From the Supplementary Materials, Figures S5 and S6, we can see that the autocorrelation function (ACF) and the partial autocorrelation function (PACF) of residuals in three models for all lags are insignificant. |
| 33 | Similar studies using 1-day and 3-day window sizes are done and result in the similar outcomes as the ones without including these 3 determinants in the models, and we don’t report the results in this paper. |
| Panel A | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| AR | SE | AR | SE | AR | SE | AR | SE | |
| Mean Model | ||||||||
| 11/25/2008 | −0.121 ** | 0.048 | −0.165 *** | 0.052 | −0.166 * | 0.095 | 0.002 | 0.079 |
| 12/1/2008 | 0.011 | 0.046 | −0.053 | 0.044 | −0.220 ** | 0.093 | 0.205 *** | 0.076 |
| 12/16/2008 | 0.039 | 0.043 | 0.008 | 0.040 | −0.127 | 0.091 | 0.129* | 0.077 |
| 1/28/2009 | −0.066 | 0.043 | −0.012 | 0.043 | 0.214 *** | 0.078 | −0.225 *** | 0.078 |
| 3/18/2009 | 0.064 ** | 0.028 | −0.005 | 0.026 | −0.239 *** | 0.072 | 0.202 *** | 0.076 |
| 8/12/2009 | −0.027 | 0.031 | −0.001 | 0.038 | 0.085 | 0.073 | −0.068 | 0.054 |
| 9/23/2009 | 0.051 * | 0.030 | 0.055 | 0.034 | 0.006 | 0.064 | 0.054 | 0.052 |
| 11/4/2009 | 0.026 | 0.035 | 0.047 | 0.037 | 0.083 | 0.054 | −0.050 | 0.055 |
| 8/10/2010 | 0.043 ** | 0.018 | 0.044 * | 0.022 | −0.013 | 0.062 | 0.052 | 0.047 |
| 8/27/2010 | −0.175 *** | 0.017 | −0.134 *** | 0.019 | 0.165 *** | 0.053 | −0.266 *** | 0.050 |
| 9/21/2010 | 0.000 | 0.059 | −0.002 | 0.057 | −0.079 | 0.060 | 0.036 | 0.069 |
| 10/15/2010 | 0.117 ** | 0.055 | 0.156 *** | 0.051 | 0.088 * | 0.051 | 0.028 | 0.069 |
| 11/3/2010 | −0.055 | 0.044 | −0.014 | 0.047 | 0.171 *** | 0.050 | −0.152 ** | 0.060 |
| 8/9/2011 | 0.040 *** | 0.015 | 0.002 | 0.019 | −0.122* | 0.072 | 0.151 ** | 0.060 |
| 8/26/2011 | −0.017 | 0.023 | −0.032 | 0.029 | −0.054 | 0.090 | 0.039 | 0.062 |
| 9/21/2011 | 0.020 | 0.018 | −0.024 | 0.020 | −0.161 ** | 0.075 | 0.161 *** | 0.057 |
| 6/20/2012 | 0.016 | 0.016 | 0.014 | 0.017 | −0.004 | 0.051 | 0.016 | 0.037 |
| 8/22/2012 | −0.048 ** | 0.020 | −0.061 *** | 0.023 | −0.071 | 0.046 | 0.001 | 0.031 |
| 8/31/2012 | 0.022 | 0.017 | 0.007 | 0.019 | −0.061 | 0.039 | 0.061 * | 0.033 |
| 9/13/2012 | −0.046 *** | 0.016 | −0.034* | 0.020 | 0.047 | 0.040 | −0.104 *** | 0.034 |
| 12/12/2012 | −0.026 *** | 0.010 | −0.003 | 0.013 | 0.080 ** | 0.032 | −0.084 *** | 0.023 |
| 5/1/2013 | −0.010 | 0.016 | −0.024 | 0.019 | −0.040 | 0.035 | 0.020 | 0.026 |
| 5/22/2013 | 0.068 *** | 0.017 | 0.091 *** | 0.024 | 0.074 * | 0.040 | 0.025 | 0.026 |
| 6/19/2013 | 0.036 | 0.037 | 0.055 | 0.044 | 0.084 ** | 0.041 | −0.002 | 0.045 |
| 12/18/2013 | 0.012 | 0.023 | 0.019 | 0.027 | 0.030 | 0.034 | −0.001 | 0.028 |
| 1/29/2014 | −0.003 | 0.020 | −0.022 | 0.025 | −0.055* | 0.032 | 0.029 | 0.027 |
| 3/19/2014 | 0.045 *** | 0.017 | 0.053 ** | 0.023 | 0.037 | 0.036 | 0.030 | 0.031 |
| 4/30/2014 | −0.024 | 0.037 | −0.037 | 0.042 | −0.020 | 0.035 | −0.003 | 0.048 |
| 5/7/2014 | −0.026 | 0.046 | −0.002 | 0.044 | 0.020 | 0.035 | −0.063 | 0.053 |
| 6/18/2014 | 0.009 | 0.031 | 0.005 | 0.033 | −0.009 | 0.035 | 0.010 | 0.040 |
| 7/15/2014 | 0.016 | 0.027 | 0.023 | 0.024 | 0.006 | 0.035 | 0.005 | 0.037 |
| 7/30/2014 | −0.106 ** | 0.042 | −0.091 ** | 0.044 | 0.093 ** | 0.035 | −0.148 ** | 0.059 |
| 8/22/2014 | 0.009 | 0.050 | −0.007 | 0.058 | −0.028 | 0.036 | 0.046 | 0.058 |
| 9/17/2014 | 0.008 | 0.041 | 0.015 | 0.046 | 0.017 | 0.039 | −0.013 | 0.049 |
| 10/29/2014 | 0.013 | 0.038 | 0.020 | 0.034 | 0.009 | 0.032 | 0.004 | 0.049 |
| Panel B | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE | |
| Mean Model | ||||||||
| Intercept | −0.001 *** | 0.001 | −0.002 *** | 0.001 | −0.001 | 0.001 | 0.000 | 0.001 |
| 0.280 *** | 0.013 | |||||||
| −0.094 *** | 0.023 | −0.004 | 0.023 | |||||
| −0.032 | 0.020 | −0.033 | 0.021 | |||||
| −0.031 | 0.021 | −0.052 ** | 0.021 | |||||
| −0.018 | 0.021 | −0.044 ** | 0.020 | |||||
| −0.041* | 0.021 | −0.024 | 0.022 | |||||
| −0.009 | 0.021 | 0.014 | 0.021 | |||||
| −0.037* | 0.020 | −0.048 ** | 0.021 | |||||
| −0.044 * | 0.023 | |||||||
| −0.041 * | 0.023 | |||||||
| −0.028 | 0.023 | |||||||
| −0.050 ** | 0.023 | |||||||
| −0.048 ** | 0.023 | |||||||
| −0.234 *** | 0.023 | |||||||
| −0.056 ** | 0.023 | |||||||
| −0.033 | 0.023 | |||||||
| −0.060 ** | 0.023 | |||||||
| −0.082 *** | 0.023 | |||||||
| −0.062 *** | 0.022 | |||||||
| Variance Model | ||||||||
| 0.084 *** | 0.016 | 0.103 *** | 0.015 | 0.039 *** | 0.006 | 0.047 *** | 0.000 | |
| 0.403 * | 0.211 | 0.249 * | 0.128 | 0.961 *** | NA | 0.953 *** | NA | |
| 0.513 *** | 0.649 *** | |||||||
| Quality of Model | ||||||||
| Log Likelihood | 3720.612 | 3484.149 | 2939.588 | 2950.285 | ||||
| AIC | −3.678 | −3.442 | −2.900 | −2.910 | ||||
| BIC | −3.544 | −3.311 | −2.777 | −2.784 | ||||
| Panel A | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| CAR | SE | CAR | SE | CAR | SE | CAR | SE | |
| Mean Model | ||||||||
| 11/25/2008 | −0.149 ** | 0.065 | −0.202 *** | 0.077 | −0.199 | 0.140 | 0.006 | 0.108 |
| 12/1/2008 | 0.005 | 0.063 | −0.098 | 0.076 | −0.342 ** | 0.132 | 0.274 ** | 0.106 |
| 12/16/2008 | −0.146 *** | 0.053 | −0.270 *** | 0.063 | −0.387 *** | 0.121 | 0.150 | 0.097 |
| 1/28/2009 | −0.084 | 0.056 | −0.020 | 0.062 | 0.265 ** | 0.116 | −0.284 *** | 0.097 |
| 3/18/2009 | −0.006 | 0.036 | −0.037 | 0.036 | −0.094 | 0.118 | 0.040 | 0.095 |
| 8/12/2009 | −0.065 | 0.043 | −0.079 | 0.054 | −0.070 | 0.115 | −0.003 | 0.076 |
| 9/23/2009 | 0.036 | 0.047 | 0.011 | 0.057 | −0.060 | 0.101 | 0.090 | 0.073 |
| 11/4/2009 | 0.029 | 0.057 | 0.076 | 0.066 | 0.164* | 0.090 | −0.105 | 0.079 |
| 8/10/2010 | −0.017 | 0.020 | −0.035 | 0.022 | −0.069 | 0.093 | 0.057 | 0.060 |
| 8/27/2010 | −0.127 *** | 0.023 | −0.121 *** | 0.030 | 0.030 | 0.080 | −0.134 ** | 0.064 |
| 9/21/2010 | −0.140 ** | 0.063 | −0.177 ** | 0.078 | −0.138 | 0.091 | −0.015 | 0.090 |
| 10/15/2010 | −0.007 | 0.075 | 0.037 | 0.085 | 0.128 | 0.079 | −0.109 | 0.090 |
| 11/3/2010 | −0.014 | 0.065 | 0.010 | 0.078 | 0.070 | 0.074 | −0.088 | 0.082 |
| 8/9/2011 | −0.057 *** | 0.017 | −0.135 *** | 0.029 | −0.282 ** | 0.112 | 0.176 *** | 0.064 |
| 8/26/2011 | 0.017 | 0.028 | 0.020 | 0.044 | 0.015 | 0.136 | 0.031 | 0.080 |
| 9/21/2011 | 0.002 | 0.021 | −0.111 *** | 0.031 | −0.392 *** | 0.113 | 0.300 *** | 0.081 |
| 6/20/2012 | −0.001 | 0.022 | 0.003 | 0.028 | 0.022 | 0.078 | −0.010 | 0.053 |
| 8/22/2012 | −0.118 *** | 0.023 | −0.151 *** | 0.032 | −0.112 | 0.071 | −0.029 | 0.043 |
| 8/31/2012 | 0.003 | 0.023 | −0.014 | 0.029 | −0.053 | 0.061 | 0.037 | 0.044 |
| 9/13/2012 | −0.080 *** | 0.020 | −0.007 | 0.030 | 0.265 *** | 0.069 | −0.272 *** | 0.041 |
| 12/12/2012 | −0.008 | 0.014 | 0.027 | 0.020 | 0.124 ** | 0.050 | −0.089 *** | 0.033 |
| 5/1/2013 | 0.016 | 0.024 | 0.004 | 0.030 | −0.034 | 0.055 | 0.029 | 0.039 |
| 5/22/2013 | 0.114 *** | 0.025 | 0.131 *** | 0.037 | 0.046 | 0.062 | 0.088 *** | 0.034 |
| 6/19/2013 | 0.246 *** | 0.051 | 0.290 *** | 0.065 | 0.165 *** | 0.063 | 0.129 ** | 0.056 |
| 12/18/2013 | 0.053 | 0.037 | 0.065 | 0.046 | 0.034 | 0.055 | 0.037 | 0.040 |
| 1/29/2014 | −0.016 | 0.031 | −0.025 | 0.038 | −0.016 | 0.054 | −0.012 | 0.036 |
| 3/19/2014 | 0.118 *** | 0.028 | 0.127 *** | 0.038 | 0.030 | 0.057 | 0.097 ** | 0.040 |
| 4/30/2014 | 0.020 | 0.054 | 0.000 | 0.066 | −0.049 | 0.047 | 0.066 | 0.067 |
| 5/7/2014 | −0.127 ** | 0.056 | −0.092 | 0.063 | 0.046 | 0.051 | −0.170 * | 0.067 |
| 6/18/2014 | 0.019 | 0.039 | 0.037 | 0.046 | 0.065 | 0.053 | −0.024 | 0.051 |
| 7/15/2014 | 0.002 | 0.038 | 0.002 | 0.043 | 0.004 | 0.053 | 0.011 | 0.050 |
| 7/30/2014 | 0.008 | 0.061 | 0.032 | 0.070 | 0.068 | 0.053 | −0.042 | 0.079 |
| 8/22/2014 | 0.042 | 0.074 | 0.014 | 0.089 | −0.075 | 0.052 | 0.069 | 0.080 |
| 9/17/2014 | 0.005 | 0.057 | 0.008 | 0.074 | 0.037 | 0.060 | −0.035 | 0.072 |
| 10/29/2014 | −0.009 | 0.053 | 0.002 | 0.059 | 0.026 | 0.052 | −0.029 | 0.070 |
| Panel B | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE | |
| Mean Model | ||||||||
| Intercept | −0.001 *** | 0.001 | −0.002 *** | 0.001 | −0.001 | 0.001 | 0.000 | 0.001 |
| 0.280 *** | 0.013 | |||||||
| −0.098 *** | 0.023 | 0.000 | 0.023 | |||||
| −0.031 | 0.020 | −0.034 | 0.021 | |||||
| −0.026 | 0.021 | −0.054 ** | 0.022 | |||||
| −0.007 | 0.021 | −0.039 * | 0.021 | |||||
| −0.052 ** | 0.021 | −0.029 | 0.022 | |||||
| −0.011 | 0.021 | 0.013 | 0.021 | |||||
| −0.044 ** | 0.020 | −0.055 ** | 0.021 | |||||
| −0.040 * | 0.023 | |||||||
| −0.045 * | 0.024 | |||||||
| −0.030 | 0.024 | |||||||
| −0.054 ** | 0.024 | |||||||
| −0.047 * | 0.024 | |||||||
| −0.233 *** | 0.023 | |||||||
| −0.042 * | 0.023 | |||||||
| −0.032 | 0.024 | |||||||
| −0.069 *** | 0.023 | |||||||
| −0.090 *** | 0.023 | |||||||
| −0.074 *** | 0.023 | |||||||
| Variance Model | ||||||||
| 0.087 *** | 0.016 | 0.105 *** | 0.016 | 0.036 *** | 0.006 | 0.039 *** | 0.008 | |
| 0.268 | 0.170 | 0.176 * | 0.095 | 0.964 *** | 0.961 *** | |||
| 0.645 *** | 0.718 *** | |||||||
| Quality of Model | ||||||||
| Log Likelihood | 3795.506 | 3550.227 | 2982.218 | 3005.344 | ||||
| AIC | −3.683 | −3.438 | −2.873 | −2.895 | ||||
| BIC | −3.352 | −3.110 | −2.553 | −2.572 | ||||
| Panel A. | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| CAR | SE | CAR | SE | CAR | SE | CAR | SE | |
| Mean Model | ||||||||
| 11/25/2008 | N/A | N/A | N/A | N/A | N/A | NA | N/A | N/A |
| 12/1/2008 | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| 12/16/2008 | −0.090 | 0.067 | −0.232 *** | 0.073 | −0.484 *** | 0.137 | 0.253 ** | 0.115 |
| 1/28/2009 | −0.082 | 0.067 | 0.020 | 0.079 | 0.367 ** | 0.145 | −0.358 *** | 0.109 |
| 3/18/2009 | −0.005 | 0.046 | 0.002 | 0.047 | 0.043 | 0.146 | −0.051 | 0.107 |
| 8/12/2009 | −0.095 ** | 0.047 | −0.142 ** | 0.062 | −0.152 | 0.139 | 0.029 | 0.091 |
| 9/23/2009 | 0.087* | 0.050 | 0.050 | 0.059 | −0.115 | 0.121 | 0.165* | 0.086 |
| 11/4/2009 | −0.053 | 0.064 | −0.003 | 0.071 | 0.185* | 0.109 | −0.179 ** | 0.090 |
| 8/10/2010 | 0.002 | 0.025 | −0.028 | 0.026 | −0.101 | 0.110 | 0.109 | 0.072 |
| 8/27/2010 | −0.133 *** | 0.029 | −0.142 *** | 0.033 | −0.018 | 0.095 | −0.093 | 0.076 |
| 9/21/2010 | −0.104 | 0.079 | −0.149* | 0.090 | −0.147 | 0.106 | 0.010 | 0.108 |
| 10/15/2010 | −0.073 | 0.086 | −0.026 | 0.097 | 0.154* | 0.090 | −0.204 ** | 0.104 |
| 11/3/2010 | −0.029 | 0.077 | 0.021 | 0.089 | 0.176 ** | 0.086 | −0.154 | 0.097 |
| 8/9/2011 | −0.108 *** | 0.019 | −0.086 ** | 0.035 | 0.067 | 0.143 | −0.073 | 0.079 |
| 8/26/2011 | 0.023 | 0.032 | 0.042 | 0.044 | 0.081 | 0.131 | −0.005 | 0.085 |
| 9/21/2011 | −0.013 | 0.023 | −0.130 *** | 0.032 | −0.381 *** | 0.118 | 0.279 *** | 0.084 |
| 6/20/2012 | −0.008 | 0.026 | 0.010 | 0.033 | 0.066 | 0.097 | −0.033 | 0.061 |
| 8/22/2012 | −0.067 *** | 0.024 | −0.088 ** | 0.036 | −0.102 | 0.085 | 0.015 | 0.050 |
| 8/31/2012 | −0.010 | 0.021 | −0.016 | 0.030 | −0.015 | 0.072 | −0.002 | 0.051 |
| 9/13/2012 | −0.045 ** | 0.022 | 0.021 | 0.032 | 0.230 *** | 0.081 | −0.208 *** | 0.046 |
| 12/12/2012 | 0.009 | 0.018 | 0.035 | 0.025 | 0.100* | 0.060 | −0.063 | 0.039 |
| 5/1/2013 | 0.039 | 0.030 | 0.074 ** | 0.037 | 0.120* | 0.063 | −0.048 | 0.041 |
| 5/22/2013 | 0.120 *** | 0.030 | 0.133 *** | 0.043 | 0.052 | 0.067 | 0.086 ** | 0.037 |
| 6/19/2013 | 0.361 *** | 0.064 | 0.448 *** | 0.078 | 0.296 *** | 0.075 | 0.152 ** | 0.066 |
| 12/18/2013 | 0.041 | 0.043 | 0.038 | 0.051 | −0.021 | 0.064 | 0.056 | 0.047 |
| 1/29/2014 | −0.047 | 0.034 | −0.049 | 0.041 | −0.022 | 0.063 | −0.028 | 0.041 |
| 3/19/2014 | 0.121 *** | 0.031 | 0.127 *** | 0.041 | 0.015 | 0.064 | 0.110 ** | 0.047 |
| 4/30/2014 | 0.204 *** | 0.066 | 0.190 *** | 0.072 | −0.066 | 0.053 | 0.232 *** | 0.076 |
| 5/7/2014 | −0.181 *** | 0.058 | −0.149 ** | 0.064 | 0.110 ** | 0.055 | −0.262 *** | 0.070 |
| 6/18/2014 | 0.017 | 0.044 | 0.028 | 0.050 | 0.035 | 0.058 | −0.003 | 0.055 |
| 7/15/2014 | 0.296 *** | 0.040 | 0.270 *** | 0.045 | −0.096* | 0.052 | 0.352 *** | 0.054 |
| 7/30/2014 | −0.010 | 0.049 | 0.006 | 0.054 | 0.062 | 0.054 | −0.047 | 0.066 |
| 8/22/2014 | 0.011 | 0.075 | 0.015 | 0.092 | −0.043 | 0.058 | 0.003 | 0.080 |
| 9/17/2014 | 0.071 | 0.069 | 0.065 | 0.080 | −0.022 | 0.067 | 0.062 | 0.075 |
| 10/29/2014 | 0.023 | 0.063 | 0.041 | 0.072 | 0.057 | 0.061 | −0.020 | 0.078 |
| Panel B | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Estimate | SE | Estimate | SE | Estimate | SE | Estimate | SE | |
| Mean Model | ||||||||
| Intercept | −0.002 *** | 0.001 | −0.002 *** | 0.001 | −0.001 | 0.001 | 0.000 | 0.001 |
| 0.280 *** | 0.013 | |||||||
| −0.085 *** | 0.022 | 0.007 | 0.022 | |||||
| −0.035 * | 0.020 | −0.043 ** | 0.021 | |||||
| −0.023 | 0.021 | −0.052 ** | 0.022 | |||||
| −0.005 | 0.020 | −0.030 | 0.021 | |||||
| −0.073 *** | 0.022 | −0.046 ** | 0.022 | |||||
| −0.004 | 0.022 | 0.020 | 0.022 | |||||
| −0.048 ** | 0.021 | −0.065 *** | 0.021 | |||||
| −0.029 | 0.023 | |||||||
| −0.046 * | 0.024 | |||||||
| −0.031 | 0.024 | |||||||
| −0.054 ** | 0.025 | |||||||
| −0.038 | 0.025 | |||||||
| −0.220 *** | 0.023 | |||||||
| −0.043 * | 0.023 | |||||||
| −0.027 | 0.023 | |||||||
| −0.060 ** | 0.024 | |||||||
| −0.099 *** | 0.024 | |||||||
| −0.075 *** | 0.024 | |||||||
| Variance Model | ||||||||
| 0.080 *** | 0.017 | 0.099 *** | 0.018 | 0.036 *** | 0.007 | 0.039 *** | 0.009 | |
| 0.309 * | 0.161 | 0.203* | 0.106 | 0.964 *** | 0.961 *** | |||
| 0.611 *** | 0.699 *** | |||||||
| Quality of Model | ||||||||
| Log Likelihood | 3853.002 | 3608.316 | 3031.920 | 3062.150 | ||||
| AIC | −3.673 | −3.429 | −2.854 | −2.884 | ||||
| BIC | −3.151 | −2.910 | −2.344 | −2.370 | ||||
| (5) | (6) | (7) | (8) | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||||||||||||||||||
| 1-day | 3-day | 5-day | 1-day | 3-day | 5-day | 1-day | 3-day | 5-day | 1-day | 3-day | 5-day | |||||||||||||
| Date | TAR | SE | TCAR | SE | TCAR | SE | TAR | SE | TCAR | SE | TCAR | SE | TAR | SE | TCAR | SE | TCAR | SE | TAR | SE | TCAR | SE | TCAR | SE |
| 11/25/2008 | −0.096 ** | 0.038 | −0.118 * | 0.062 | N/A | N/A | −0.139 ** | 0.044 | −0.169 ** | 0.073 | N/A | N/A | −0.137 * | 0.078 | −0.163 | 0.132 | N/A | N/A | 0.001 | 0.051 | 0.004 | 0.097 | N/A | N/A |
| 12/1/2008 | 0.008 | 0.036 | 0.004 | 0.058 | N/A | N/A | −0.044 | 0.037 | −0.082 | 0.073 | N/A | N/A | −0.181 ** | 0.077 | −0.281 ** | 0.125 | N/A | N/A | 0.134 *** | 0.050 | 0.178* | 0.094 | N/A | N/A |
| 12/16/2008 | 0.031 | 0.034 | −0.115 * | 0.050 | −0.071 | 0.065 | 0.007 | 0.034 | −0.225 *** | 0.061 | −0.192 *** | 0.071 | −0.105 | 0.075 | −0.318 *** | 0.115 | −0.404 *** | 0.133 | 0.084* | 0.050 | 0.097 | 0.088 | 0.166 | 0.109 |
| 1/28/2009 | −0.052 | 0.034 | −0.066 | 0.053 | −0.064 | 0.065 | −0.010 | 0.036 | −0.017 | 0.059 | 0.016 | 0.076 | 0.177 *** | 0.064 | 0.218 ** | 0.109 | 0.306 ** | 0.142 | −0.147 *** | 0.051 | −0.184 ** | 0.087 | −0.235 ** | 0.103 |
| 3/18/2009 | 0.050 ** | 0.023 | −0.005 | 0.033 | −0.004 | 0.044 | −0.004 | 0.022 | −0.031 | 0.034 | 0.002 | 0.045 | −0.197 *** | 0.061 | −0.077 | 0.113 | 0.035 | 0.141 | 0.132 *** | 0.050 | 0.026 | 0.085 | −0.033 | 0.100 |
| 8/12/2009 | −0.022 | 0.025 | −0.051 | 0.040 | −0.074 | 0.046 | −0.001 | 0.032 | −0.066 | 0.052 | −0.117* | 0.060 | 0.070 | 0.061 | −0.057 | 0.108 | −0.126 | 0.135 | −0.044 | 0.036 | −0.002 | 0.068 | 0.019 | 0.085 |
| 9/23/2009 | 0.041* | 0.024 | 0.028 | 0.044 | 0.069 | 0.048 | 0.046 | 0.028 | 0.009 | 0.054 | 0.042 | 0.057 | 0.005 | 0.052 | −0.050 | 0.095 | −0.096 | 0.117 | 0.035 | 0.034 | 0.058 | 0.065 | 0.108 | 0.082 |
| 11/4/2009 | 0.021 | 0.028 | 0.023 | 0.053 | −0.041 | 0.062 | 0.039 | 0.032 | 0.063 | 0.063 | −0.003 | 0.069 | 0.069 | 0.045 | 0.135 | 0.085 | 0.154 | 0.105 | −0.033 | 0.036 | −0.068 | 0.071 | −0.117 | 0.086 |
| 8/10/2010 | 0.034 ** | 0.014 | −0.013 | 0.019 | 0.001 | 0.024 | 0.037 ** | 0.019 | −0.029 | 0.021 | −0.023 | 0.026 | −0.010 | 0.051 | −0.057 | 0.088 | −0.084 | 0.107 | 0.034 | 0.031 | 0.037 | 0.054 | 0.071 | 0.067 |
| 8/27/2010 | −0.139 *** | 0.015 | −0.100 *** | 0.021 | −0.104 *** | 0.028 | −0.112 ** | 0.017 | −0.101 *** | 0.028 | −0.118 *** | 0.032 | 0.136 *** | 0.044 | 0.024 | 0.076 | −0.015 | 0.092 | −0.174 *** | 0.034 | −0.087 | 0.058 | −0.061 | 0.070 |
| 9/21/2010 | 0.000 | 0.046 | −0.110* | 0.059 | −0.081 | 0.077 | −0.002 | 0.048 | −0.148 ** | 0.073 | −0.123 | 0.087 | −0.065 | 0.050 | −0.114 | 0.086 | −0.123 | 0.103 | 0.024 | 0.045 | −0.010 | 0.081 | 0.007 | 0.101 |
| 10/15/2010 | 0.092 ** | 0.044 | −0.006 | 0.070 | −0.057 | 0.083 | 0.131 ** | 0.043 | 0.031 | 0.081 | −0.020 | 0.095 | 0.073* | 0.042 | 0.106 | 0.074 | 0.128 | 0.087 | 0.018 | 0.045 | −0.071 | 0.081 | −0.134 | 0.098 |
| 11/3/2010 | −0.044 | 0.035 | −0.011 | 0.061 | −0.023 | 0.074 | −0.012 | 0.040 | 0.008 | 0.074 | 0.017 | 0.087 | 0.141 *** | 0.042 | 0.057 | 0.070 | 0.146 * | 0.084 | −0.099 ** | 0.040 | −0.057 | 0.074 | −0.101 | 0.091 |
| 8/9/2011 | 0.032 *** | 0.012 | −0.045 *** | 0.016 | −0.085 *** | 0.018 | 0.002 | 0.016 | −0.112 *** | 0.027 | −0.071 ** | 0.034 | −0.101* | 0.059 | −0.232 ** | 0.104 | 0.056 | 0.141 | 0.099 ** | 0.040 | 0.114 ** | 0.058 | −0.048 | 0.075 |
| 8/26/2011 | −0.013 | 0.018 | 0.014 | 0.026 | 0.018 | 0.031 | −0.027 | 0.024 | 0.017 | 0.042 | 0.035 | 0.042 | −0.045 | 0.075 | 0.012 | 0.129 | 0.068 | 0.126 | 0.026 | 0.041 | 0.020 | 0.072 | −0.003 | 0.079 |
| 9/21/2011 | 0.016 | 0.014 | 0.002 | 0.019 | −0.010 | 0.022 | −0.020 | 0.017 | −0.093 *** | 0.030 | −0.107 *** | 0.032 | −0.133 ** | 0.062 | −0.322 *** | 0.107 | −0.318 *** | 0.115 | 0.105 *** | 0.038 | 0.195 *** | 0.073 | 0.183 ** | 0.078 |
| 6/20/2012 | 0.012 | 0.013 | −0.001 | 0.020 | −0.006 | 0.025 | 0.012 | 0.014 | 0.002 | 0.026 | 0.008 | 0.032 | −0.003 | 0.042 | 0.018 | 0.073 | 0.055 | 0.094 | 0.011 | 0.024 | −0.006 | 0.047 | −0.022 | 0.057 |
| 8/22/2012 | −0.038 ** | 0.016 | −0.093 *** | 0.022 | −0.052 ** | 0.023 | −0.051 *** | 0.019 | −0.126 *** | 0.031 | −0.073 ** | 0.035 | −0.059 | 0.038 | −0.092 | 0.067 | −0.085 | 0.083 | 0.001 | 0.020 | −0.019 | 0.039 | 0.010 | 0.047 |
| 8/31/2012 | 0.017 | 0.014 | 0.002 | 0.021 | −0.008 | 0.021 | 0.006 | 0.016 | −0.012 | 0.028 | −0.013 | 0.029 | −0.050 | 0.032 | −0.043 | 0.057 | −0.012 | 0.070 | 0.040 * | 0.022 | 0.024 | 0.040 | −0.001 | 0.048 |
| 9/13/2012 | −0.036 *** | 0.013 | −0.063 *** | 0.019 | −0.035* | 0.021 | −0.029 * | 0.017 | −0.005 | 0.028 | 0.017 | 0.031 | 0.039 | 0.033 | 0.218 *** | 0.065 | 0.191 ** | 0.079 | −0.068 *** | 0.022 | −0.177 *** | 0.037 | −0.136 *** | 0.044 |
| 12/12/2012 | −0.020 *** | 0.008 | −0.006 | 0.013 | 0.007 | 0.017 | −0.003 | 0.011 | 0.022 | 0.019 | 0.029 | 0.024 | 0.066 ** | 0.026 | 0.102 ** | 0.047 | 0.084 | 0.058 | −0.055 *** | 0.015 | −0.057 * | 0.030 | −0.041 | 0.036 |
| 5/1/2013 | −0.008 | 0.013 | 0.013 | 0.022 | 0.031 | 0.029 | −0.020 | 0.016 | 0.004 | 0.029 | 0.061* | 0.037 | −0.033 | 0.029 | −0.028 | 0.052 | 0.100 | 0.062 | 0.013 | 0.017 | 0.019 | 0.034 | −0.032 | 0.039 |
| 5/22/2013 | 0.054 *** | 0.013 | 0.090 *** | 0.023 | 0.094 *** | 0.029 | 0.076 *** | 0.021 | 0.109 *** | 0.035 | 0.110 *** | 0.042 | 0.061* | 0.033 | 0.038 | 0.059 | 0.043 | 0.065 | 0.017 | 0.017 | 0.057 * | 0.030 | 0.056 | 0.035 |
| 6/19/2013 | 0.028 | 0.029 | 0.194 *** | 0.048 | 0.284 *** | 0.062 | 0.046 | 0.037 | 0.242 *** | 0.062 | 0.371 *** | 0.076 | 0.069 ** | 0.033 | 0.136 ** | 0.060 | 0.247 *** | 0.073 | −0.001 | 0.030 | 0.084 * | 0.050 | 0.100 | 0.063 |
| 12/18/2013 | 0.009 | 0.018 | 0.042 | 0.034 | 0.032 | 0.042 | 0.016 | 0.023 | 0.055 | 0.044 | 0.032 | 0.050 | 0.025 | 0.028 | 0.028 | 0.052 | −0.018 | 0.063 | 0.000 | 0.018 | 0.024 | 0.036 | 0.037 | 0.044 |
| 1/29/2014 | −0.002 | 0.016 | −0.013 | 0.029 | −0.037 | 0.033 | −0.018 | 0.021 | −0.021 | 0.037 | −0.040 | 0.040 | −0.045 * | 0.027 | −0.013 | 0.052 | −0.019 | 0.061 | 0.019 | 0.018 | −0.008 | 0.032 | −0.019 | 0.038 |
| 3/19/2014 | 0.036 *** | 0.014 | 0.093 *** | 0.027 | 0.095 *** | 0.030 | 0.044 ** | 0.020 | 0.106 *** | 0.036 | 0.105 *** | 0.040 | 0.030 | 0.030 | 0.025 | 0.053 | 0.013 | 0.062 | 0.020 | 0.021 | 0.063 * | 0.036 | 0.072 | 0.044 |
| 4/30/2014 | −0.019 | 0.029 | 0.016 | 0.051 | 0.160 ** | 0.064 | −0.031 | 0.036 | 0.000 | 0.062 | 0.157 ** | 0.071 | −0.017 | 0.029 | −0.041 | 0.045 | −0.055 | 0.052 | −0.002 | 0.031 | 0.043 | 0.060 | 0.152 ** | 0.072 |
| 5/7/2014 | −0.021 | 0.036 | −0.100 * | 0.053 | −0.142 ** | 0.056 | −0.001 | 0.037 | −0.076 | 0.060 | −0.123 * | 0.061 | 0.016 | 0.029 | 0.038 | 0.048 | 0.092 * | 0.053 | −0.041 | 0.034 | −0.110 * | 0.060 | −0.172 ** | 0.067 |
| 6/18/2014 | 0.007 | 0.024 | 0.015 | 0.037 | 0.013 | 0.042 | 0.004 | 0.028 | 0.031 | 0.044 | 0.023 | 0.049 | −0.007 | 0.029 | 0.053 | 0.050 | 0.029 | 0.056 | 0.007 | 0.026 | −0.016 | 0.046 | −0.002 | 0.052 |
| 7/15/2014 | 0.013 | 0.021 | 0.002 | 0.036 | 0.232 *** | 0.040 | 0.019 | 0.021 | 0.001 | 0.041 | 0.223 *** | 0.045 | 0.005 | 0.029 | 0.003 | 0.050 | −0.080 | 0.050 | 0.003 | 0.024 | 0.007 | 0.045 | 0.231 *** | 0.051 |
| 7/30/2014 | −0.084 ** | 0.034 | 0.006 | 0.057 | −0.008 | 0.047 | −0.076 ** | 0.037 | 0.027 | 0.066 | 0.006 | 0.052 | 0.077 *** | 0.029 | 0.056 | 0.050 | 0.052 | 0.052 | −0.097 ** | 0.039 | −0.027 | 0.070 | −0.031 | 0.061 |
| 8/22/2014 | 0.007 | 0.040 | 0.033 | 0.069 | 0.009 | 0.071 | −0.006 | 0.048 | 0.012 | 0.085 | 0.012 | 0.092 | −0.023 | 0.030 | −0.062 | 0.050 | −0.036 | 0.057 | 0.030 | 0.038 | 0.045 | 0.072 | 0.002 | 0.074 |
| 9/17/2014 | 0.006 | 0.033 | 0.004 | 0.054 | 0.056 | 0.067 | 0.012 | 0.039 | 0.007 | 0.070 | 0.054 | 0.078 | 0.014 | 0.032 | 0.031 | 0.057 | −0.018 | 0.065 | −0.008 | 0.032 | −0.023 | 0.065 | 0.041 | 0.071 |
| 10/29/2014 | 0.011 | 0.030 | −0.007 | 0.050 | 0.018 | 0.061 | 0.017 | 0.029 | 0.002 | 0.056 | 0.034 | 0.070 | 0.007 | 0.027 | 0.021 | 0.049 | 0.047 | 0.059 | 0.003 | 0.032 | −0.019 | 0.062 | -0.013 | 0.073 |
| Study | Event Window Size | Round of QE | Mortgage Rate (Market Model) | Mortgage Rate (Constant Mean Return Model) | Treasury Rate | Spread |
|---|---|---|---|---|---|---|
| My Estimation in this paper | 1-day, 3-day, 5-day | QE1 | −7, −38, −37 | −23, −63, −56 | −54, −76, −58 | 31, 19, 10 |
| QE2 | 4, −16, −10 | 4, −21, −18 | −9, −21, −25 | 9, 4, 12 | ||
| OT | 4, −4, −10 | −5, −23, −17 | −34, −66, −23 | 35, 51, 20 | ||
| QE3 | −7, −20, −12 | −9, −17, −8 | −9, 10, 11 | −4, −26, −19 | ||
| Tapering | 5, 49, 107 | 10, 60, 124 | 22, 35, 48 | −6, 21, 64 | ||
| Gagnon et al. (2011) | 1-day, 2-day | QE1 | −113, −115 | −91, −105 | ||
| Krishnamurthy and Vissing-Jorgensen (2011) | 2-day for QE1, 1-day and 2-day for QE2 | QE1 | −107 | −73 | ||
| QE2 | −9, −8 | −9, −21 | ||||
| Christensen and Rudebusch (2012) | 1-day | QE1 | −100 | |||
| Neely (2015) | 1-day | QE1 | −100 | |||
| Altavilla and Giannone (2017) | 2-day | QE1 | −104 | |||
| QE2 | −29 | |||||
| OT | −43 | |||||
| QE3 | −4 | |||||
| Tapering | 40 | |||||
| Bowman et al. (2015) | 2-day | QE1 | −99 | |||
| QE2 | −28 | |||||
| OT | −41 | |||||
| QE3 | −9 | |||||
| Tapering | 37 | |||||
| Borrallo et al. (2016) | 2-day | QE1 | −104 | |||
| QE2 | −29 | |||||
| OT | −37 | |||||
| QE3 | −10 | |||||
| Tapering | 42 | |||||
| Di Maggio et al. (2016) | 3-month, 6-month | QE1 | −117, −140 | |||
| QE2 | −37, −47 | |||||
| OT | −46, −63 | |||||
| QE3 | −18, −32 | |||||
| Tapering | 26, −53 |
| Panel A. 1-day window | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| AR | SE | AR | SE | AR | SE | AR | SE | |
| QE1_MBS_Increase | −0.095 *** | 0.033 | −0.086 | 0.052 | 0.004 | 0.079 | −0.130 ** | 0.066 |
| QE1_T_Increase | 0.010 | 0.046 | −0.056 | 0.045 | −0.223 ** | 0.100 | 0.210 *** | 0.079 |
| QE1_Both_Increase | 0.055 ** | 0.024 | −0.001 | 0.024 | −0.198 *** | 0.060 | 0.164 *** | 0.057 |
| QE1_MBS_Decrease | 0.038* | 0.023 | 0.051 ** | 0.025 | 0.045 | 0.041 | 0.000 | 0.041 |
| QE1_T_Decrease | −0.027 | 0.032 | −0.001 | 0.039 | 0.085 | 0.075 | −0.069 | 0.054 |
| QE2_T_Increase | 0.038 * | 0.021 | 0.038 * | 0.023 | −0.050 | 0.044 | 0.047 | 0.040 |
| QE2_T_Decrease | 0.117 ** | 0.058 | 0.157 *** | 0.053 | 0.087 | 0.057 | 0.029 | 0.073 |
| OT_T_Increase | 0.020 | 0.018 | −0.023 | 0.021 | −0.162 ** | 0.077 | 0.161 *** | 0.058 |
| OT_Both_Increase | 0.013 | 0.030 | −0.014 | 0.021 | −0.094 | 0.059 | 0.092 * | 0.054 |
| QE3_MBS_Increase | −0.046 *** | 0.018 | −0.034 * | 0.020 | 0.047 | 0.040 | −0.104 *** | 0.035 |
| QE3_Both_Increase | −0.019 | 0.031 | −0.025 | 0.025 | −0.066 ** | 0.031 | 0.027 | 0.027 |
| Tapering | 0.006 | 0.010 | 0.001 | 0.012 | 0.008 | 0.011 | 0.009 | 0.011 |
| Panel B. 3-day window | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| CAR | SE | CAR | SE | CAR | SE | CAR | SE | |
| QE1_MBS_Increase | −0.116 ** | 0.049 | −0.101 | 0.072 | −0.018 | 0.120 | −0.178 * | 0.103 |
| QE1_T_Increase | 0.004 | 0.067 | −0.107 | 0.081 | −0.358 ** | 0.154 | 0.311 *** | 0.118 |
| QE1_Both_Increase | −0.048 | 0.045 | −0.082 * | 0.048 | −0.268 ** | 0.104 | 0.082 | 0.078 |
| QE1_MBS_Decrease | 0.024 | 0.037 | 0.031 | 0.045 | 0.052 | 0.068 | −0.013 | 0.061 |
| QE1_T_Decrease | −0.064 | 0.042 | −0.079 | 0.056 | −0.068 | 0.120 | −0.006 | 0.079 |
| QE2_T_Increase | −0.025 | 0.023 | −0.044 * | 0.026 | −0.109 | 0.069 | 0.036 | 0.056 |
| QE2_T_Decrease | −0.006 | 0.084 | 0.038 | 0.092 | 0.128 | 0.087 | −0.108 | 0.101 |
| OT_T_Increase | 0.004 | 0.025 | −0.109 *** | 0.036 | −0.393 *** | 0.119 | 0.299 *** | 0.086 |
| OT_Both_Increase | 0.034 | 0.034 | −0.021 | 0.051 | −0.161 * | 0.095 | 0.114 * | 0.066 |
| QE3_MBS_Increase | −0.079 *** | 0.023 | −0.004 | 0.033 | 0.264 *** | 0.072 | −0.271 *** | 0.044 |
| QE3_Both_Increase | −0.066 | 0.046 | −0.087 ** | 0.039 | −0.085 * | 0.049 | 0.004 | 0.035 |
| Tapering | 0.021 | 0.017 | 0.016 | 0.020 | 0.009 | 0.017 | 0.028 | 0.018 |
| Panel C. 5-day window | ||||||||
| (5) | (6) | (7) | (8) | |||||
| Mortgage Rate | Mortgage Rate | Treasury Rate | Spread | |||||
| CAR | SE | CAR | SE | CAR | SE | CAR | SE | |
| QE1_MBS_Increase | −0.115 * | 0.065 | −0.050 | 0.087 | 0.220 | 0.154 | −0.318 *** | 0.114 |
| QE1_T_Increase | −0.049 | 0.089 | −0.231 ** | 0.108 | −0.651 *** | 0.220 | 0.505 *** | 0.161 |
| QE1_Both_Increase | −0.035 | 0.052 | −0.035 | 0.053 | −0.263 ** | 0.130 | 0.066 | 0.100 |
| QE1_MBS_Decrease | 0.010 | 0.053 | 0.012 | 0.054 | 0.031 | 0.084 | −0.020 | 0.078 |
| QE1_T_Decrease | −0.095 * | 0.048 | −0.144 ** | 0.066 | −0.149 | 0.148 | 0.027 | 0.096 |
| QE2_T_Increase | −0.005 | 0.028 | −0.035 | 0.029 | −0.132 | 0.085 | 0.083 | 0.069 |
| QE2_T_Decrease | −0.066 | 0.101 | −0.022 | 0.109 | 0.160 | 0.105 | −0.203 * | 0.118 |
| OT_T_Increase | −0.010 | 0.029 | −0.127 *** | 0.039 | −0.375 *** | 0.137 | 0.279 *** | 0.096 |
| OT_Both_Increase | 0.011 | 0.040 | 0.000 | 0.052 | −0.005 | 0.122 | 0.041 | 0.099 |
| QE3_MBS_Increase | −0.042 | 0.029 | 0.024 | 0.040 | 0.230 *** | 0.088 | −0.208 *** | 0.051 |
| QE3_Both_Increase | −0.059 | 0.048 | −0.067 | 0.043 | −0.060 | 0.059 | 0.002 | 0.040 |
| Tapering | 0.032 * | 0.019 | 0.028 | 0.024 | 0.000 | 0.022 | 0.034 | 0.022 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G. The Effects of Quantitative Easing Announcements on the Mortgage Market: An Event Study Approach. Int. J. Financial Stud. 2019, 7, 9. https://doi.org/10.3390/ijfs7010009
Wang G. The Effects of Quantitative Easing Announcements on the Mortgage Market: An Event Study Approach. International Journal of Financial Studies. 2019; 7(1):9. https://doi.org/10.3390/ijfs7010009
Chicago/Turabian StyleWang, Gang. 2019. "The Effects of Quantitative Easing Announcements on the Mortgage Market: An Event Study Approach" International Journal of Financial Studies 7, no. 1: 9. https://doi.org/10.3390/ijfs7010009
APA StyleWang, G. (2019). The Effects of Quantitative Easing Announcements on the Mortgage Market: An Event Study Approach. International Journal of Financial Studies, 7(1), 9. https://doi.org/10.3390/ijfs7010009





