Abstract
In an economy with a sovereign wealth fund (SWF), the government may draw on the fund to supplement other government revenues. If the fund is invested in risky assets, this introduces a new stochastic element into the government’s budget. We analyze the interaction between the draw from and risk taking in the SWF. Using non-expected utility preferences, we distinguish between intended changes and stochastic changes in the SWF draws over time. We show that the desire for smoothness in taxes and public services translates into smoothing of SWF draws and lower risk taking. It can even lead to procyclical rebalancing of the SWF portfolio. Future interest rates are associated with interest-rate risk. We show that this risk may lead to a higher optimal equity share in the SWF portfolio. Policy makers can use the draws from the SWF to smooth over time variation in risk-free rates.
JEL Classification:
G11; G23
1. Introduction
For a country with a large enough sovereign wealth fund (SWF), its financial returns can fund substantial parts of government spending. Blissful as this situation may seem, it raises a fundamental dilemma in that the financial returns are procyclical whereas the fiscal needs are fairly stable over time or even countercyclical. This dilemma carries important implications for the fund’s desired risk profile.
Whereas some of today’s SWFs date back to the 1970s (Kunzel et al. 2011; Baldwin 2012; Paltrinieri and Pichler 2013), the number of such funds grew significantly in the 1990s and especially after the Asian financial crisis towards the end of that decade. Whereas some such funds remain relatively small, others have grown to become very large, such as those owned by the United Arab Emirates, Saudi Arabia, China, and Norway. Decisions regarding fund management and draws on the fund naturally grow in importance as the fund grows in magnitude. The authors’ interest in SWFs has been inspired by the policy debate surrounding the Norwegian Government Pension Fund Global (GPFG), whose market value at the time of writing is reported to be $940 billion.1 However, as other SWFs grow as well, we believe the issues we study could be of equal interest to many other countries.
SWFs have been funded from a variety of sources. In some cases, especially after the Asian financial crisis, large trade surpluses have been added to the foreign-exchange reserves of some countries, notably China, so as to substantially exceed the normal needs for foreign-exchange stabilization. In other cases, such as Singapore, government pension systems have accumulated substantial reserve funds. The currently most typical, however, are SWFs funded by revenues from harvesting non-renewable natural resources, such as oil and gas.
The asset composition of the SWFs’ investment portfolios affects portfolio risk and may also restrict draws from the funds. The funds have been established for a variety of purposes, as documented by Bernstein et al. (2013), Dreassi et al. (2017), as well as the references listed above and the literature surveyed by Alhashel (2015). Some, such as the Canada Pension Plan Investment Board, have been established as pure pension funds tied to future pension obligations.2 They are typically managed more or less like private pension funds, sometimes with sizeable positions in non-listed assets. Others, such as the China Investment Corporation, have been established more or less as instruments of the government’s foreign policy and thus take risk profiles that serve these purposes (Johan et al. 2013). The emergence of such funds has been the source of some apprehension about reversed colonialism, as discussed by Baldwin (2012). A third group consists of stabilization funds, exemplified by Chile’s Economic and Social Stabilization Fund. This fund is maintained as a buffer against copper price fluctuations, allowing the government to draw on the fund to cover budget deficits when copper prices are low, subsequently to be refilled when copper prices recover. The fourth group, which interests us the most, consists of the funds accumulated by petroleum exporting countries. The first big wave of such funds came in the 1970s as leading oil exporting countries, mainly in the Middle East, accumulated revenues faster than they were able to spend meaningfully or invest domestically. Later there followed similar funds in Azerbaijan, Kazakhstan, Norway, and Russia.
These oil funds, in short, were established as a way to convert the financially concentrated wealth of below-ground natural resources into a balanced portfolio of liquid financial assets in support of future fiscal obligations. The channeling of extraordinary revenues into SWFs, furthermore, serves as protection against the so-called Dutch disease, analyzed by Van Wijnbergen (1984), Corden (1984), Krugman (1987), and many others. That is, they are supposed to shield the economy from a temporary expansion of domestic spending that risks depleting the stock of human capital in traditional export industries and thus leave the economy worse off when the non-renewable resources are depleted than before they were discovered. At the same time—and more or less by the same token—these funds are also intended as saving funds to allow the financial benefits of the finite resource stock to be shared by future generations.
The challenge raised by this strategy is that the string of future generations starts with the current one. Thus, it is arguably desirable to allow part of the resource revenue to fund current government spending while saving the lion’s share for future use. This challenge is easily managed as long as the fund is small. However, the Norwegian GPFG has, as one example, grown from 80% of the country’s annual GDP in 2006 to two and a half times that currently. During the same period, the share of public spending funded by draws on the GPFG increased from 8% to no less than 19% in 2018.
The challenges facing a government with a SWF of this magnitude are similar to those of many university endowment funds: on the one hand, one will want the fund to take considerable risk so as to generate large average yields to fund government services. But on the other hand, one will want the same services to be as smooth as possible over time, as argued, for example, Barro (1979). In addition—and in contrast to university endowments—variations in public spending or taxation may have considerable adverse macroeconomic consequences. In fact, it is easy to make a macroeconomic argument that the government deficit—apart from the SWF—should be countercyclical. This is hard to reconcile with high SWF risk taking, which tends to make the SWF budget contribution procyclical. The nature and possible handling of this dilemma is the focus of the present paper.
This dilemma appears to have been ignored by the SWF literature so far. Chambers et al. (2012) argue that “The Norway Model” makes the GPFG especially able to harvest risk premia because its investment horizon is effectively infinite. However, a fiscal rule, adopted in 2001, allows an annual draw on the fund as a regular source of fiscal revenue corresponding to the expected real financial return, initially estimated as 4%, from 2018 on lowered to 3%. Although Chambers et al. note this rule, they do not pursue its consequences for the SWF to take on risky positions.
The Norwegian fiscal rule has been motivated by the permanent-income theory in macroeconomics (e.g., Hall 1978). Its great weakness is that it ignores risk. Simple extensions to the risky case can be found in the classical analyses by Phelps (1962), Samuelson (1969), and Merton (1969) of an individual’s optimal spending and portfolio allocation. However, these studies ignore the fiscal need for smooth tax rates and government services, which we refer to as backward smoothing. Thus, we believe that SWF investing should be analyzed in the broader framework of asset liability management, as in Choudhry (2007). As yet another complication, the substantial movements in risk-free interest rates in recent decades raise the question of how such movements should influence the rules for drawing from an SWF, such as the lowering of the Norwegian rule from 4% to 3%. Our paper addresses all of these concerns.
These considerations contrast starkly with the challenge of sovereign debt management for countries with net debt positions. Although a net asset position may seem obviously preferable, we show in this paper that the simultaneous tasks of investing the fund and using it as a source of fiscal revenue is far from trivial. The normative literature on SWF management has mainly focused on emerging economies, where the majority of SWFs are located. Thus, van der Ploeg and Venables (2011) focus on the cases where limited access to global financial markets may present an argument for investing a disproportionate part of the fund domestically. Carroll and Jeanne (2009) and Sá and Viani (2013) follow the same vein by focusing on the effects on global balances and exchange rates of SWF development in emerging economies. Guerra-Salas (2014) compares the effects of fiscal responses, including SWF investing as well as domestic public investment to oil price changes in Mexico and Norway. In a slightly different context, Collier and Gunning (2005) argue for using an oil windfall primarily to reduce domestic debt.
In a somewhat different vein, van den Bremer et al. (2016) focus on the interaction between the financial portfolio and the value of the natural resources that fund that portfolio. Although we find this issue important, we bypass it in our study, which then can best be interpreted as an analysis of SWF management and spending once the natural resource has been depleted.
Once an SWF of the type we study has been established, policy makers have to decide on at least three important issues: first, how much risk to assume in the asset portfolio, and second, how much to draw from the fund to support current spending. A third decision will be equally important, namely, how to distribute the draws from the fund over time. The goal of this paper is to address all three of these issues and how they fit into the overall fiscal policy framework. The issues are related and we address them simultaneously. Although risk premia may motivate high risk taking, our observations suggest that policy makers have low tolerance for non-stochastic, or planned, variation over time in tax rates and public services as well as a strong desire to preserve value for future generations. This combination of attitudes cannot be reconciled within the standard expected utility framework. To encompass the stylized facts, we use non-expected utility preferences as proposed by Epstein and Zin (1991). These preferences allow us to distinguish between risk aversion and willingness to undertake intertemporal substitution. Furthermore, we borrow the tools of habit formation (see e.g., Constantinides 1990; Campbell and Cochrane 1999) to include preferences for smooth changes in public services. We derive closed-form solutions for the portfolio selection problem. Interestingly, the preferences for planned variation over time do not affect the portfolio choice, i.e., the distribution between risky and non-risky assets. Although this insight has already been established in the literature going back to Svensson (1989) for the basic case of a constant riskless rate and no habit formation, we show that it holds also when these assumptions are relaxed.
Ideally, we would have carried out a complete modeling of policy makers’ desire for smooth tax rates as well as government services. Unfortunately, such a complete analysis does not generally lend itself to informative, closed-form solutions. As an introduction of the issue in the paper, we choose instead to approximate policy makers’ preference as a case of habit formation regarding SWF draws. Under this assumption, we derive closed form solutions for how the preferences for maintaining the spending habit affect the spending rate. Because, in contrast, risk taking feeds volatility, we find habit-influenced preferences to have a profound effect on the portfolio selection problem. They reduce short-term risk taking because a larger part of the investment portfolio must be used to safeguard the habit level of consumption.
A side effect of this smoothing of public spending and taxes is that the portfolio risk for the long run increases. We find that this increased portfolio risk spills over into public spending and can increase the long-run spending risk considerably. For short-horizon portfolio-selection problems, treasury STRIPS or other zero-coupon bonds can be good substitutes for risk-free investments. For portfolio-selection problems with long horizons, like the infinite horizons for many SWFs, “risk-free investments” are risky because interest rates fluctuate randomly. We address the effect of interest rate uncertainty on the optimal draw from the fund and on the portfolio-selection problem.
Our analysis is partial in the sense that it treats policy makers as a representative investor and consumer, but does not present a model for the underlying macro economy. Carroll and Jeanne (2009) and Sá and Viani (2013) analyze related topics to what we analyze. While they include a model for the macro economy, their asset-price dynamics and preference specification are simpler than ours. Parts of our analysis follows from results in the existing literature, but the generalization to the case of non-expected utility is, to the best of our knowledge, novel for the cases of habit formation and time-varying risk-free rates. This generalization is particularly important for decisions regarding portfolio allocation for SWFs and the use of such funds as budget revenues. Yang (2015) includes habit formation and long-run risks in a non-expected utility framework. While his analysis is methodologically related to our analysis, his focus is not on portfolio choice and spending, but rather to analyze asset market phenomena from the macro-finance literature.
There have been several studies of Norway’s GPFG, but they all have a different focus than ours. Two of the studies that have received the most attention (Ang et al. 2009; and Dahlquist and Ødegaard 2018), analyze empirically the performance of the fund’s investment portfolio. Only a small fraction of the fund is actively managed, and the choice of benchmark index has, therefore, been most important for the fund’s (absolute) performance.
Our paper is organized as follows: Section 2 uses Svensson’s (1989) generalization to Epstein-Zin preferences of the Merton model with a constant risk-free rate and no backward smoothing to gain some preliminary insights into the respective roles of risk aversion and intertemporal substitution for decisions about portfolio allocation and use of the proceeds of a SWF. Section 3 studies the implications of backward smoothing of tax rates and public services based on a generalization of the model of Constantinides (1990). Such smoothing turns out to have implications for the normal rebalancing of the fund as well as its long-term performance, which we consider in Section 4. Section 5 extends the analysis to the case of time variation in the risk-free rate. Section 6 presents our conclusions and some plans for further research.
2. Risk Aversion vs. Intertemporal Substitution
We start by considering the different roles of risk aversion and intertemporal substitution for the owner of an SWF. For this purpose, we use the Epstein–Zin formulation of non-expected utility, which in discrete time can be expressed by the following value function:
Here, is the subjective discount rate, is the standard measure of relative risk aversion, and , where is the elasticity of intertemporal substitution. Thus, can be interpreted as a measure of aversion against non-stochastic or planned time variations of consumption , which we interpret as the annual draw on the fund. denotes wealth, i.e., the total value of the SWF portfolio. A fraction of the fund’s assets is invested in a risky asset (equity) and a fraction in a safe asset. As is well known, this formulation simplifies to standard power expected utility if . However, we will not make this assumption because these two parameters serve rather substantially different functions in our present context, and we believe policy makers’ attitudes towards risk and non-stochastic time variation can be quite different.
Although decision making with non-expected utility is more easily analyzed in discrete time, continuous-time analysis yields more informative solutions. For this reason, we carry out our analysis in continuous time, but leave most of the mathematical derivations to Appendix A.
As shown in Appendix A.1, after transformation, taking the limit as the discrete time intervals approach zero, the value function (1) is equivalent to the Bellman equation:
where .
Equation (2) needs to be supplemented by a dynamic budget constraint. In this section, we assume that the risk-free return is constant over time. In continuous-time notation, the flow budget constraint is given by:
where is a Wiener process. The risky asset has return , where is the time-invariant equity premium. Then, is the expected portfolio return and its variance. This formulation ignores the possibility of stock-price mean reversion (e.g., Fama and French 1988), as well as uncertainty about long-term trends (Bansal and Yaron 2004; and Yang 2015). We offer some informal comments on these issues below.
Proposition 1.
Under the assumptions given in (2) and (3), the optimal equity share α is constant and the optimal consumption is a constant share η of wealth, where,
and,
This proposition was originally proved by Svensson (1989). Our proof, which is somewhat different than his in order to facilitate our subsequent analysis, is provided in Appendix A.1 and Appendix A.2.
The solution for the equity share is identical to that derived by Merton (1969) for the expected-utility case. Although known from previous research such as Svensson’s, it may be worth noting that this part of Merton’s results is not influenced by the double duty served by the risk-aversion parameter as the reciprocal of the elasticity of substitution in the expected-utility case.3
Our main interest concerns the optimal draw on the fund. The draw rate in our case differs from the draw rate derived by Merton. Thus, while we have the same equity share as in the Merton model, going forward, the different draw rate makes the value of the investment portfolio, and thereby the amount invested in equity, different from the corresponding investments by the Merton investor. The draw rate is expressed as a linear combination—if as a weighted average—of what Giovannini and Weil (1989) and Campbell and Viceira (2002) refer to as a myopic and an annuity component, respectively. The myopic component may be large if the investor is impatient, so that is large. For policy makers, we believe this would be roughly equivalent to a desire to favor current generations over future ones. However, policy makers would then also need to be willing to plan for draws on the fund to vary non-stochastically over time, so that .
In his seminal empirical study, Hall (1988) concludes that the intertemporal elasticity of substitution is likely to be small. This observation indicates that the income effect is more important than the substitution effect. Later studies, like Bansal and Yaron (2004) and Thimme (2016) have found larger values of , indicating that the substitution effect of reactions to changes in rates of return is important. However, our casual observations of policy-maker behavior in advanced-economy countries with sovereign wealth funds suggest that their overriding concern is about preserving the fund for future generations. We believe that, if anything, this attitude reveals lower elasticities of intertemporal substitution than those estimated for households. Acknowledging that is likely to be close to zero, we thus read SWF decision-makers as focusing mainly on the annuity component. This attitude would also be consistent with a desire for smoothness in the time-series behavior of public services and tax rates, as argued by Barro (1979) and many others. In Section 3 we return to further implications of this literature.
A near-zero elasticity of intertemporal substitution does not imply high risk aversion, however. Rational decision makers can be highly averse to planned variations in consumption over time and yet be highly tolerant of variations that result from stochastic movements in stock prices. On the other hand, we note that the annuity component in (4b) contains a risk adjustment. The permanent-income theory in its simplest form ignores uncertainty and recommends consumption of the entire expected return. When risk is considered, this would naturally be optimal only with risk neutrality, i.e., . In general, the greater the risk aversion, the smaller the draw rate should be. More specifically, the safety buffer should correspond to half the expected return of the optimally chosen risky portion of the portfolio. For example, if the equity premium is 4% and the equity share has been optimally chosen as 60%, we can conclude that the annuity component of the optimal draw is 1.2 percentage points higher than the risk-free rate or, equivalently, 1.2 percentage points lower than the expected return on the entire portfolio. This difference is far from trivial.
Mean reversion in stock returns would make this correction smaller. Mean reversion has been noted by Fama and French (1988) and Poterba and Summers (1988) and discussed further in Campbell and Viceira (2002). However, Bansal and Yaron (2004) argue, convincingly, in our view, that a proper explanation of observed risk premia requires recognition of uncertainty, not only about current returns, but also about their long-term trend. Swanson (2016) implements Bansal and Yaron’s specification in a complete macro model with apparent success and concludes similarly. Trend uncertainty would naturally add to the optimal risk correction of the annual draw. Thus, we do not believe that our derivation overstates it.
As we shall see in the following sections, the results in Formula (4a) and (4b) will have to be modified if taxes and public spending are smoothed or if the risk-free rate varies over time. However, the desirability of a safety buffer is a general finding, which we summarize as:
Observation 1.
As a provision against risk, the annuity part of the optimal draw rate should be lower than the expected return on the portfolio.
3. Backward Smoothing
As the owner of a SWF, the government will want to use it to enhance government services and/or keep a lid on taxes. Barro (1979) and others have presented convincing arguments that both the tax system and the stream of government services ought to be smooth. This smoothness should work backward as well as forward. That is, policy makers should not only plan for smoothness in future services and tax rates, they should also avoid sudden changes from past patterns in response to unexpected shocks. In practice, policy makers often have only limited leeway when it comes to changing government services from one period to the next.
In our framework, forward smoothing is ensured by a low value of the elasticity of intertemporal substitution . Backward smoothing is provided to some extent by risk aversion because low risk taking limits the effects of negative random shocks. However, in the model as specified so far, the degree of (relative) risk aversion is independent of the level of consumption and wealth. A more natural assumption would be that this aversion becomes stronger the more strained the government’s finances are compared to recent experience. This assumption can be approximated by introducing habit formation in the model. We naturally do not mean that policy decisions are governed by habits in a literal sense, but that models of habit formation offer a suitable technique for modelling variations in risk aversion and hence backward smoothing.
The consumption literature distinguishes between external and internal habits. External habits refer to people’s valuation of their own consumption relative to that of others: “catching up with the Jones’,” cf. Abel (1990) or Campbell and Cochrane (1999). Internal habits refer instead to how people tend to get used to their standard of living and derive utility only from consumption over and above that standard. We believe the latter formulation of habit formation is the most relevant for our purpose because our decision maker is the government deciding for the entire nation.
Constantinides (1990) has introduced habit formation in a model of portfolio investment in continuous time with expected-utility preferences. We extend his analysis to Epstein–Zin preferences by letting the consumption variable in the Bellman Equation (2) be replaced by consumption over and above a habit level , so that . The habit level is assumed to start from an exogenously given initial level and to develop over time according to:
Appendix A.3 extends Constantinides’ results for this specification to the case of Epstein–Zin non-expected utility. We show there that, in this case, the SWF can be thought of as consisting of two portfolios, one part with value , providing safe financing for the minimum consumption level defined by the habit and a remaining part with value financing the rest. The portfolio with value needs to be risk free because otherwise a bad random draw could make consumption fall below , which would make utility drop to negative infinity. Safe funding of this minimum level of consumption turns out to require
Relative risk aversion in this setup is defined by the transformed value function defined after Formula (2) above. Without habit formation, it is simply:
For the analysis of behavior under habit formation, this transformed value function is replaced by . Thus, relative risk aversion is then defined as:
For , this measure is unambiguously larger than for the case without habit formation. It is larger the smaller the difference between total wealth and the wealth needed to maintain safe funding for the minimum habit level of consumption. The more “squeezed” public finances are, the more risk averse policy makers will be. This is the property that we wanted our preference specification to have.
Under these conditions, the optimal equity share is no longer constant, and the optimal draw on the fund is no longer proportional to wealth. Instead, they follow the same rules that Constantinides shows for expected utility and which Appendix A.3 shows hold also with the more general Epstein–Zin preferences. We summarize them as:
Proposition 2.
With Epstein–Zin preferences and Constantinides habit formation as defined in (5), the optimal equity share and the optimal SWF draw are given by the following formulae:
and,
where is defined as in (4b).
Risk taking now clearly is limited by the need to be able to maintain the habit level of consumption without risk. The equity share is proportional to the ratio of “free” wealth to total wealth . An adverse development in the equity market should be followed by a reduction of the equity share. Put differently, the amount of wealth invested in the risky asset is a fixed proportion of the free wealth:
Draws from the fund must be large enough to permit consumption to at least equal the habit level of consumption. However, it also needs to be limited by the need to retain sufficient wealth to fund the habit level of consumption without risk. First, the “free” level of consumption (over and above the habit level) is a fixed proportion of only the “free” wealth. Second, this proportion is a little lower than the one in Section 2 because of the need continuously to set aside some money to ensure the continued safe funding of the habit level of consumption. This is the price to be paid for the opportunity to maintain at least the habit level of consumption no matter what happens to the return on risky assets.
For optimization with habit formation to be feasible, the initial habit level obviously cannot be too large. As a minimum, it cannot exceed the riskless return on the entire fund. It also makes sense to assume because otherwise the habit level would tend to rise autonomously over time, which would have required an even larger riskless portfolio to finance habit consumption over time.
We summarize these insights as:
Observation 2.
A wish to keep taxes and public services smooth over time should make risk aversion for SWF investment greater in general, and risk aversion should move in the opposite direction of the equity market. However, the extent of smoothing will have to be somewhat limited in order to be feasible.
Cochrane (2017) argues that models with habit formation and models with non-expected utility (as well as other models used in macro-finance) in many ways provide similar modifications, technically speaking, of the classical power expected-utility model in terms of providing better explanations of observed data for equity premia and riskless rates. However, in the context of optimal portfolio choice and optimal spending decisions in a SWF context, our results in Proposition 2 demonstrate that these two modifications complement rather than substitute each other. Whereas the portfolio allocation is determined by the habit level, spending is determined by habits as well as the intertemporal elasticity of substitution provided by the non-expected utility model.
4. Rebalancing and Long-Term Volatility
We furthermore note the following implication of (7a):
Observation 3.
If the government wants to maintain a smooth flow of taxes and government services, the rules for SWF portfolio rebalancing after asset price changes should be formulated so as to safeguard the funds needed to secure this smoothness.
As a response to price changes in the risky part of the asset portfolio, the portfolio has to be rebalanced to obtain the optimal portfolio weights. Recall that, without habit formation, the risky share of the portfolio should always be the constant . In this case, maintaining the optimal portfolio weights leads to counter-cyclical rebalancing: the fund buys more of the risky asset when its price falls and sells it when the price increases. With backward smoothing modelled as habit formation, counter-cyclical rebalancing may not always be optimal. Consider the following stylised example: An SWF has 100 to invest (e.g., $100 billion). It can be invested in a risky asset with price 100 or in a risk-free asset also with price 100. The price of the risky asset then falls to 98, making it necessary for the portfolio manager to rebalance the asset portfolio of the SWF. The portfolio holdings before and after rebalancing are illustrated in Table 1. In the first two cases, the price decrease makes the portfolio manager invest more in the risky asset (∆risky investment > 0). While in the first case the fraction of the wealth invested in the risky asset is constant, in the second case the optimal fraction is slightly reduced after the price decrease. In the third case, with a lower risk aversion to begin with than in the second case, the price decrease lowers the total portfolio value so much that it starts to threaten the habit level of consumption. The government investor responds to this threat by reducing the investment in the risky asset (∆risky investment < 0). As in the second case, the optimal fraction of the wealth invested in the risky asset is reduced after the price fall. This example illustrates that, under habit formation, counter-cyclical rebalancing need not always be the optimal response to a price change in the risky asset. We note that Chambers et al. (2012) also state that portfolio management based on excessively procyclical investing is a common error that should be avoided.

Table 1.
Example of portfolio rebalancing after a decline in the risky-asset price from 100 to 98. Parameter values: .
As shown by Sundaresan (1989) and Constantinides (1990), smoothing, such as modelled in Section 3, reduces the volatility of consumption on the short horizon. Indeed, habit formation has been invoked as a mechanism to help explain the empirical smoothness of consumption. The time series of consumption has lower volatility because the consumption level responds less to changes in wealth, compared to the standard model without habit formation. When the wealth increases, the consumption level increases relatively less and similarly for decreases in wealth. The direct effect of this smoothing is a higher variance for the fund value. Although this effect is partially countered by the more conservative investment portfolio, our numerical investigations indicate that the fund’s value eventually becomes more volatile. This steeper rise in the long-horizon volatility of the fund value may then even be translated into a higher long-horizon volatility of consumption itself. Thus, although the short-horizon variance is lower with habit formation, the long-horizon variance can be higher for consumption as well as for the fund itself. These insights can be gleaned from inspection of the formulae involved. However, numerical simulations presented in Figure 1 show that the variance of future log-wealth for the case of habit-formation type of smoothing rises much more quickly with the length of the horizon than in the case without such smoothing (in the figure labelled “Non-Habit”).4 The figure shows four different sets of parameter configurations. For all four configurations, the parameters are set so that the investor with habit preferences has the same initial portfolio composition as the investor without habit formation and a coefficient of relative risk aversion of .
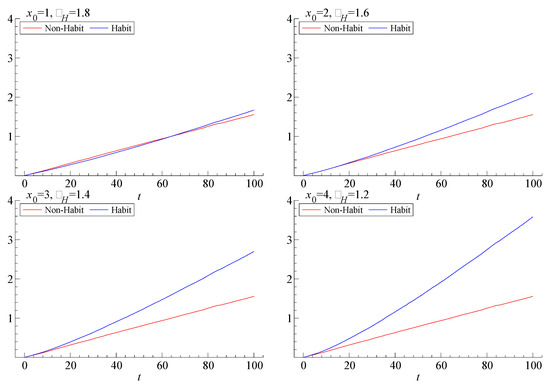
Figure 1.
Variance of log-wealth at different time horizons t for the investor with non-expected utility, non-habit preferences (Non-habit) and for the investor with non-expected utility, habit preferences (Habit). Parameter values are , and . The variances are estimated from 10,000 simulated observations at each point in time. We use 10 time points per year. The parameter shows the initial habit level, and shows the coefficient for the investor with habit preferences.
The long-horizon uncertainty of consumption is illustrated in Figure 2. Here, we plot the variances of log-consumption for different time horizons and for different parameter configurations. In three of the cases, we see lower consumption volatility for “short” horizons (say, less than 20 to 50 years) for the smoothing case than for the base case. However, for longer horizons the smoothing investor can face far more variation in consumption. This increase comes as a consequence of the riskier wealth illustrated in Figure 1.
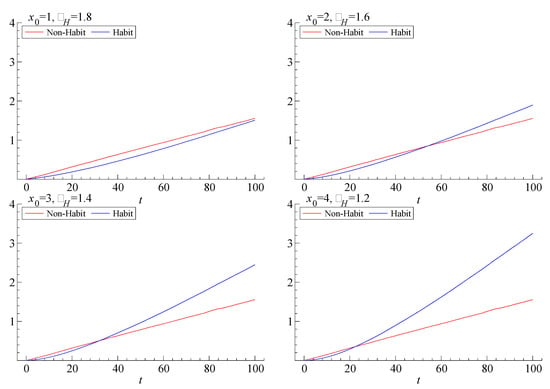
Figure 2.
Variance of log-consumption at different time horizons t for the investor with non-expected utility, non-habit preferences (Non-habit) and for the investor with non-expected utility, habit preferences (Habit). Parameter values are , and . The variances are estimated from 10,000 simulated observations at each point in time. We use 10 time points per year. The parameter shows the initial habit level and shows the coefficient for the investor with habit preferences.
This exercise teaches us an important lesson: smoothness comes at a price. We can smooth current consumption by using the fund as a buffer. But then we tamper with the fund’s principal. In so doing, we affect future consumption indirectly and hence future habit levels, which in turn influence consumption even further out. Short-term convenience carries long-term costs.
Provided the smoothing modelled as habits really is part of preferences, the trade-off between short-term smoothness and long-term uncertainty is done optimally. Figure 3 shows what would happen to the variance of log-consumption at various time horizons if the investment and spending decisions were separated so that the risky share of the portfolio were kept constant even though spending is based on the above implications of the habit model. The separation of spending and investment decisions leads to higher variability of consumption. At least as interesting is the fact that the separated rules eventually become inconsistent in all four examples, illustrated by the fact that the graph for the variance of log-consumption ends prematurely for the case of constant equity share (labelled “Habit mixed” in the figure). This phenomenon arises because keeping the risky share fixed fails to safeguard the funding of the minimal, habit-determined rates of future spending for some states of the world. Thus, the investor/consumer ends up in what Lax (2002) refers to as the insolvency range.5
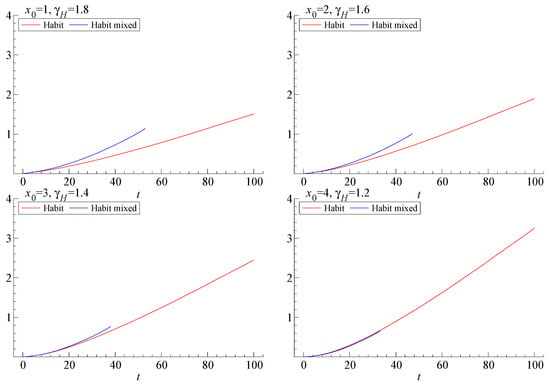
Figure 3.
Variance of log-consumption at different time horizons t for two investors. The first is for the investor with non-expected utility, habit preferences (Habit). The second is for an investor with non-expected utility, habit preferences. This investor consumes as the habit-investor, but uses the portfolio weights for the investor with non-habit preferences (Mixed habit). Parameter values are , and . The variances are estimated from 10,000 simulated observations at each point in time. We use 10 time points per year. The parameter shows the initial habit level and shows the coefficient for the investor with habit preferences.
We summarize these observations as:
Observation 4.
The smoothing of consumption tends to carry a price in the form of a wider uncertainty of the long-run prospects for consumption. This uncertainty is mitigated by the optimal modification of portfolio rebalancing, but it is not removed.
5. Time-Varying Risk-Free Rates
In this section we extend the analysis to account for interest-rate uncertainty. In practice, risk-free rates are not constant over time. In fact, recent decades have seen a long global trend of falling real interest rates since the mid-1980s, as documented, e.g., by King and Low (2014) and Rachel and Smith (2015). With a less than unit elasticity of intertemporal substitution, a permanent drop in the risk-free rate should obviously imply a corresponding reduction of the optimal draw on an SWF, as indicated by (4b). However, some authors, such as the Organization for Economic Co-operation and Development (OECD 2014), argue that the recent long decline is likely to be reversed, at least partially. We now turn to the question of what the optimal draw should be under these conditions.
For this purpose, we need a specification of the dynamically stochastic variation in the instantaneous risk-free rate. For tractability, we use the mean-reverting diffusion process introduced by Vasicek (1977):
where is a Wiener process, possibly correlated with , is the steady-state riskless return rate, the speed of return towards this rate after deviations (also known as the force of gravity), and is the instantaneous standard deviation of . This specification is consistent with the OECD’s expectation.
When the risk-free rate varies over time, the question also arises whether the equity premium stays constant or whether the expected equity return stays constant instead, so that the equity premium varies inversely with the risk-free rate. We choose to remain agnostic about this issue and use a specification of the equity premium that encompasses both cases:
where denotes the risk premium if constant () and the expected equity return if that is constant instead (). With this modification, the diffusion process for wealth now becomes,
In Appendix A.1 and Appendix A.4, we carry out the analysis of this case in the absence of habit formation. In Appendix A.5 we show that an extension to habit formation yields results that are closely approximated by those without habit formation provided that the elasticity of intertemporal substitution is small.
In the absence of habit formation, we note that the Bellman Equation (2) also needs to be modified to allow for the time variation in the riskless rate:
As shown in Appendix A.1, the time variability of the risk-free rate does not change the result that the optimal draw is proportional to the wealth level. However, the proportionality factor is now a function of the risk-free rate. This function is the solution to a non-linear, second-order differential equation. Although a closed-form solution to this equation may exist, our interest focuses on its semi-elasticity with respect to the risk-free rate. As shown in Appendix A.4, this elasticity can be approximated around the steady-state risk-free rate of return by means of the method used by Campbell and Viceira (2002) in their Chapter 5. Appendix A.1, Appendix A.4 and Appendix A.5 thus prove the following:
Proposition 3.
If the risk-free return varies over time according to (14), the optimal SWF draw, as a ratio of wealth, should respond to time variations in the risk-free rate according to:
provided, wheredenotes the value ofif the risk-free rate is constant at its steady-state value, as defined in (4b), andis the optimal equity share for. This result holds as a close approximation even with habit formation provided ε is small.
This intuitive formula shows that the reaction to dynamically stochastic variation in the risk-free rate should have the same sign as the comparative-static response, but be smaller in absolute value because of the expectation of an eventual mean reversion.6 The difference between the two responses depends positively on and negatively on . means that an increase in the risk-free rate lowers the equity premium and thus reduces the incentive for risk taking, so that the portfolio return is raised by somewhat less than the rise in the riskless rate, which in turn dampens the effect on the optimal draw rate. In contrast, means that the equity premium is unaffected by the variation in the risk-free rate, so that this dampening disappears.
As expected, the effect on the optimal draw rate is furthermore dampened by , the speed of the mean-reversion adjustment. Thus, the expectation that the risk-free rate eventually returns to normal allows for a smoothing of SWF draws relative to movements in this rate. This is true even if the return path is rocky in the sense of a large . The larger the speed of this mean-reversion adjustment, the stronger the smoothing. If the deviation from the steady state is truly ephemeral (), the smoothing is complete. If, however, the mean reversion is expected to take very long, the smoothing should be very modest.
We summarize this insight as:
Observation 5.
The rule for SWF draws should smooth over changes in the risk-free return provided they are temporary. The strength of the optimal smoothing depends on the expected speed of return to normal, even if the return path is rocky. The smoothing should be even stronger if the movements in the risk-free return leaves the expected return on equity unchanged.
Proposition 4.
If the risk-free return varies over time according to (14), the optimal equity share becomes:
wheredenotes the theoretical regression coefficient ofon.
Again, the proof is contained in Appendix A.1 and Appendix A.4. The first term indicates an inverse relationship between the risk-free rate and the equity share if a drop in the risk-free rate implies a higher equity premium. That would be the case if, as argued by Hall (2016) and Caballero et al. (2008) regarding the recent long decline in real interest rates, such a decline is due to an increase in the risk aversion of the marginal investor in global markets.
Compared to (4a), this formula furthermore has an additional term which reflects the dynamic risk of future changes in the risk-free rate. We assume because a drop in the risk-free rate tends to coincide with higher stock valuations, other things being equal. The entire second term, including the minus sign in front of it, is positive provided , which we view as the normal case. Thus, the risk of a future drop in the risk-free rate calls for a somewhat higher equity share as a dynamic hedge against such a drop. Not surprisingly, this effect is weaker if risk aversion is lower and is actually reversed if risk aversion is very low ().7
We summarize these insights as
Observation 6.
A temporary decline in the risk-free rate calls for an increase in the equity share if this change leaves the expected equity return unchanged. For a reasonably risk-averse investor, the uncertainty of future risk-free rates, furthermore, calls for a somewhat higher equity share as a dynamic hedge provided a drop in the risk-free rate is associated with a higher equity return.
6. Conclusions and Future Work
Using the proceeds of a SWF as a regular supplement to other government revenues makes sense in an advanced economy with a sizeable SWF. However, this practice offers greater complications than it may seem at first.
A rule permitting annual draws corresponding to the expected real return is optimal only under highly restrictive conditions. Our analysis uses Epstein–Zin preferences, which allows us to distinguish between risk aversion and aversion to planned changes over time. Within this framework, we find that a fiscal rule derived from the expected real return is optimal if policy makers’ elasticity of intertemporal substitution is small. However, unless risk is negligible or risk aversion extremely low, the annual draws should be considerably lower than the expected real return as an allowance for risk.
Furthermore, in the presence of risk, such a rule makes fiscal policy bumpy as either tax rates or government services (or both) must move in response to the vagaries of financial markets. This problem can be mitigated by introducing the responses to market returns gradually over time, which we refer to as backward smoothing and the model as habit formation. However, backward smoothing requires lower risk taking, which in turn implies lower return on average. Thus, smoothing can be bought at the expense of lower average SWF draws. Moreover, risk taking must not only be lower, but should move countercyclically relative to the financial markets. Rebalancing should be modified as well so that, in some instances, the SWF should sell rather than buy equity after a stock market decline. Ignoring this implication may lead to premature depletion of the fund. As a final implication, backward smoothing, although dampening short-term uncertainty about SWF draws, will typically increase long-term uncertainty about future draws.
These insights make us critical of the Norwegian fiscal rule. By allowing draws corresponding to the expected real return it ignores risk. By permitting temporary deviations from the real-return rule, it does allow backward smoothing; but it ignores its implications for risk taking and rebalancing.
Our conclusions are somewhat more upbeat in regard to the implications of stochastic movements in the riskless rate over time. When this rate declines, as has been observed in recent years, the SWF draws should decline as well; however, in this case, smoothing does indeed make sense. Moreover, dynamic risks to the instantaneously riskless rate actually call for a somewhat higher equity share as a hedge against the dynamic risk.
We believe these insights to be important food for thought for policy makers in developed countries with sizeable SWFs. However, we also realize that the analysis in this paper only scratches the surface. Just as most households receive labor income in addition to capital income, a government collects taxes. Furthermore, tax revenues as well as spending needs tend to vary with the business cycle, which in turn tends to correlate with stock returns as well as real interest rates. Active, countercyclical fiscal policy adds further volatility to these fluctuations. In the context of an SWF, this means that the policy makers not only want to smooth the draws on the fund relative to returns; they may even want the draws to fluctuate in the opposite direction. Such opposite fluctuations would translate into attacks on the fund’s principal in bad economic times, which could add to the long-term fluctuations and jeopardize the fund’s solvency if caution is not taken.
We intend to take up these and other issues in our future research. As is well known from the context of household behavior, the presence of non-capital income sources presents no new complication if markets are complete. However, this assumption is especially problematic in the context of government finances, as moral hazard, dynamic inconsistency, and poor contract enforceability mean that a government’s future tax revenues cannot be capitalized. As is well known, exact analytical solutions are then no longer available except in uninteresting cases like quadratic utility.
Viceira (2001) has worked out approximate solutions for optimal consumption and investment for an individual with stochastic labor income under the assumption that permanent changes in labor income are the main determinants of spending behavior. Benzoni et al. (2007) similarly study co-integration between stock and labor markets. However, these approaches are unsuitable for studying the implications of cyclical variations in government spending and revenues. Thus, we expect that we will need to rely on simulation exercises to obtain numerical solutions.
Author Contributions
Conceptualization, K.A.M. and S.L.; methodology, K.A.M.; software, S.L.; validation, K.A.M. and S.L.; formal analysis, K.A.M.; investigation, K.A.M. and S.L.; writing—original draft preparation, K.A.M.; writing—review and editing, S.L. and K.A.M.; visualization, S.L.
Funding
This research received no external funding.
Acknowledgments
Valuable comments by John Campbell, Espen Henriksen, Hans Jørgen Tranvåg, NTNU colleagues, and seminar participants at BI Norwegian Business School and the Norges Bank Investment Management. Egil Matsen provided valuable encouragement at the beginning of the project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Optimal Investment and Consumption with Epstein–Zin Preferences in Continuous Time, with Time-Changing Risk-Free Rate and/or Habit Formation
Appendix A.1. General Setup
We start with the value function for Epstein–Zin preferences in discrete time:
Define . Then, the value function may be rearranged and written as,
Division by and taking the limit as 0 now gives us the Bellman equation in continuous time:
where dates t have been omitted except for the expectations operator.
The dynamic budget constraints are as follows:
Here, and are Wiener processes for equity returns and the risk-free rate, respectively. is the equity premium, which is time invariant and equal to if . If , the expected equity return, is time invariant instead and equal to , so that the equity return moves one for one in opposite directions of the risk-free rate. is a consumption tax whose significance will be apparent in Appendix A.3.
We follow Campbell and Viceira (2002) by working with a second-order expansion of the value function under the conjecture that,
Then, ignoring higher-order terms, we have:
Substituting from the budget constraints, this can be further written as:
where is the correlation coefficient between and .
By Itô’s lemma, this gives us:
Using polynomial expansion, ignoring higher-order terms of , this furthermore gives us:
After dividing through by , this allows us to write the Bellman equation as:
where is the theoretical regression coefficient of on .
The first- order condition for is now easily obtained as:
Define , so that,
Then, obviously,
which implies,
Then,
Substituting, we can now write the Bellman equation as:
Maximization with respect to gives:
Define now , so that ).
After substitution of these formulae, the Bellman equation boils down to:
where is the elasticity of intertemporal substitution.
Appendix A.2. Constant Risk-Free Rate
In this case, and Thus, and are constants. From (A10) and (A11), we then find:
From (A8), we see that the optimal consumption level as a share of wealth is divided by one plus the consumption tax rate, if any. These results generalize those of Merton (1969). To our knowledge, they were first derived by Svensson (1989), with the exception of the consumption tax. However, we find our slightly different derivation method to be more amenable to applications with a time-varying riskless rate and habit formation.
Appendix A.3. Habit Formation
In this section, we assume a constant risk-free rate. We model habit formation by letting replace in the preference ordering, where is the habit level. Following Constantinides (1990), we assume that the habit level moves over time according to the constraint:
where is exogenous, which implies,
Constantinides has derived formulas for optimal consumption and equity with this specification of habit formation with expected utility. We now proceed to show that these results also hold under the specification of non-expected utility in Appendix A.1.
Our proof starts with the observation that, with our specification of habit formation, utility becomes infinitely negative if . With normally distributed equity returns, there is a non-zero probability that the return on equity at some point will be less than any arbitrarily negative number. It then follows that the habit level of consumption must be funded by investment in the safe asset only.
Thus, we may think of the investor-consumer as managing two separate portfolios. One portfolio, whose value we denote , is held for the exclusive purpose of funding the habit level . The other portfolio, denoted , is invested in order to fund the “surplus” level of consumption, . We continue to let denote total wealth, so that:
Because the habit level in general will move over time, the value of its funding portfolio, , will generally need to move as well. Thus, it is not sufficient to maintain because then the entire return on this portfolio will be absorbed by the current habit level. This means that the investor-consumer must make a regular transfer from the “surplus” portfolio to the “habit” portfolio . If these transfers may be negative, but that does not change the argument.
Let denote the transfer. We may then specify the budget constraints for the two portfolios as:
and
where now denotes the equity share of the surplus portfolio , not necessarily constant. Here, we have implicitly assumed that the consumption tax on is zero.
Based on Constantinides’ results for the case of expected utility, we conjecture that optimization requires:
Under this conjecture, (A18) implies:
This condition is equivalent to the flow condition for habit formation (A15) if and only if,
Consider now an arbitrary path for . Given (A20) and (A17), this path for is just sufficient to fund the path of the habit level as given by (A15). If, at any time, a lower value of is chosen, the implied size of the habit portfolio will be insufficient to fund the habit level implied by (A15), so it is not feasible. If, on the other hand, a higher value is chosen, it will be wasted because the habit portfolio will become excessively large. Thus, (A20) indicates the optimal path for the transfer amount v for an arbitrary path of .
Next, consider the optimal surplus consumption path . Note, then, that the optimal transfer level , given by (A20), is linear in . Thus, it has the same form as a consumption tax with:
From (A8), we then see that the optimal level of surplus consumption must be:
Thus, using (A16), the definition of , and the conjecture in (A19), we find,
For the conjecture in (A19) to hold, it suffices that the investor-consumer at time 0 sets aside:
as the initial habit portfolio.
Thus, habit formation according to (A14) requires two kinds of set-aside into the habit portfolio. First, at time 0, the investor-consumer must set aside the initial amount in (A22). Then, for , a transfer into this portfolio must continuously be made as indicated by (A20)
It is worth noting that the continuous transfers for disappear if . The reason is that the habit level then will shrink over time, as can be seen from (A15), so that the habit portfolio can be allowed to shrink as well. If both and , the habit level of consumption is given once and for all, and the habit portfolio will remain constant at .
Lastly, consider the optimal equity share in this context. From (A12), we find , so that:
This completes our proof that Constantinides’ results generalize to the case of an Epstein–Zin non-expected preference ordering in continuous time.
Appendix A.4. Time-Varying Risk-Free Rate
For this section, the consumption tax plays no role, so that we assume . We start with Equation (A11), which is a second-order non-linear differential equation in . Rather than trying to derive an exact solution, we follow Campbell and Viceira in approximating this function around as follows:
We then readily find,
Substituting this into (A11) and ignoring quadratic terms in , we obtain the following equation:
This equation must hold as an identity in , which means that we can use the method of undetermined coefficients to identify the parameters and . In particular, the coefficients multiplying must sum to zero. Thus,
where .
Appendix A.5. Time-Varying Risk-Free Rate with Habit Formation
This analysis is carried out for the simplified case of , so that:
However, the analysis carries over to the more general case. For the sub-portfolio to support the habit, we must have:
so that,
Also, as before,
Thus,
Equating the two equations for dx, we find:
This means that will not be proportional to with a fixed proportionality factor. Thus, the implicit consumption tax rate,
will not be constant, but a function of . This function is decreasing because, with a higher interest rate, the safe sub-portfolio can fund a larger habit level of consumption, so that less needs to be set aside for this purpose.
The question is the extent to which the general properties of the model are affected by this change. In Section A.1, the derivations are unaffected by this change until the first-order condition (A17), which we now write as:
If we again define , the subsequent derivations will be riddled with various terms containing the derivative ). However, we can avoid this complication by redefining:
Then, although the optimal consumption follows the somewhat more complicated formula,
Equations (A9a) and (A2) will continue to hold. Furthermore, the exponent , is the negative of the intertemporal substitution, which we have assumed to be small.
The terms involving in the Bellman Equation (A6) become:
As a result, in (A11), the first term is replaced by .
In Appendix A.4, we can use the same approximation for as before. However, we need to consider the dependence of on . For this we can use the first-order approximation:
This gives us the following first-order approximation for the product :
The equation preceding (A24) becomes:
For this equation to hold identically for all values of , the following two conditions must be satisfied:
where the inequality holds provided .
With the above re definition of , is no longer exactly the semielasticity of the consumption-wealth ratio with respect to the interest rate. Rather, we have:
Recall that the “tax” for the set-aside is a decreasing function of the interest rate, so that . Thus, the semielasticity of the consumption-wealth ratio is slightly higher than . Again, if is low, this correction will be small.
References
- Abel, Andrew B. 1990. Asset prices under habit formation and catching up with the Joneses. American Economic Review 80: 38–42. [Google Scholar]
- Alhashel, Bader. 2015. Sovereign Wealth Funds: A literature review. Journal of Economics and Business 78: 1–13. [Google Scholar] [CrossRef]
- Ang, Andrew, William N. Goetzmann, and Stephen Schaefer. 2009. Evaluation of Active Management of the Norwegian Government Pension Fund—Global. Available online: https://www0.gsb.columbia.edu/faculty/aang/papers/report%20Norway.pdf (accessed on 26 December 2018).
- Baldwin, Christopher. 2012. Sovereign Wealth Funds: The New Intersection of Money and Politics. Oxford: Oxford University Press. [Google Scholar]
- Bansal, Ravi, and Amir Yaron. 2004. Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles. Journal of Finance 59: 1481–509. [Google Scholar] [CrossRef]
- Barro, Robert J. 1979. On the determination of the public debt. Journal of Political Economy 87: 940–71. [Google Scholar] [CrossRef]
- Benzoni, Luca, Pierre Collin-Dufresne, and Robert S. Goldstein. 2007. Portfolio choice over the life-cycle when the stock and labor markets are cointegrated. Journal of Finance 62: 2123–67. [Google Scholar] [CrossRef]
- Bernstein, Shai, Josh Lerner, and Antoinette Schoar. 2013. The Investment Strategies of Sovereign Wealth Funds. Journal of Economic Perspectives 27: 219–37. [Google Scholar] [CrossRef]
- Caballero, Ricardo J., Emmanuel Farhi, and Pierre-Olivier Gourinchas. 2008. An Equilibrium Model of ‘Global Imbalances’ and Low Interest Rates. American Economic Review 98: 358–93. [Google Scholar] [CrossRef]
- Campbell, John, and John Cochrane. 1999. By force of habit: A consumption-based explanation of aggregate stock market behavior. Journal of Political Economy 107: 205–51. [Google Scholar] [CrossRef]
- Campbell, John Y., and Luis Viceira. 2002. Strategic Asset Allocation: Portfolio Choice for Long-Term Investors, 1st ed. Oxford: Oxford University Press. [Google Scholar]
- Carroll, Christopher, and Olivier Jeanne. 2009. A Tractable Model of Precautionary Reserves, Net Foreign Assets, or Sovereign Wealth Funds. NBER Working Paper No. 2824. Cambridge, CA, USA: NBER. [Google Scholar]
- Chambers, David, Elroy Dimson, and Antti Ilmanen. 2012. The Norway Model. The Journal of Portfolio Management 38: 67–81. [Google Scholar] [CrossRef]
- Choudhry, Moorad. 2007. Bank Asset and Liability Management: Strategy, Trading, Analysis, 1st ed. Singapore: Wiley Finance. [Google Scholar]
- Cochrane, John H. 2017. Macro-Finance. Review of Finance 21: 945–85. [Google Scholar] [CrossRef]
- Collier, Paul, and Jan Willem Gunning. 2005. Asset Policies During an Oil Windfall: Some Simple Analytics. The World Economy 28: 1401–15. [Google Scholar] [CrossRef]
- Constantinides, George. 1990. Habit formation: A resolution of the equity premium puzzle. Journal of Political Economy 98: 519–43. [Google Scholar] [CrossRef]
- Corden, Warner Max. 1984. Boom Sector and Dutch Disease Economics: Survey and Consolidation. Oxford Economic Papers 36: 362. [Google Scholar] [CrossRef]
- Dahlquist, Magnus, and Bernt Arne Ødegaard. 2018. A Review of Norges Bank’s Active Management of the Government Pension Fund Global. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3114175 (accessed on 26 December 2018).
- Doornik, Jurgen. 2007. Object-Oriented Matrix Programming Using Ox, 3rd ed. London: Timberlake Consultants Press and Oxford. Available online: www.doornik.com (accessed on 26 December 2018).
- Dreassi, Alberto, Stefano Miani, and Andrea Paltrinieri. 2017. Sovereign Pension and Social Security Reserve Funds: A Portfolio Analysis. Global Financial Journal 34: 43–53. [Google Scholar] [CrossRef]
- Epstein, Larry G., and Stanley E. Zin. 1991. Substitution, Risk Aversion, and the Temporal Behavior of Consumption and Asset Returns: An Empirical Analysis. Journal of Political Economy 99: 263–86. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1988. Permanent and temporary components of stock prices. Journal of Political Economy 96: 246–73. [Google Scholar] [CrossRef]
- Giovannini, Alberto, and Philippe Weil. 1989. Risk Aversion and Intertemporal Substitution in the Capital Asset Pricing Model. NBER Working Paper No. 2824. Cambridge, MA, USA: NBER. [Google Scholar]
- Guerra-Salas, Juan F. 2014. Government Investment and the Business Cycle in Oil-Exporting Countries. Bronx: Fordham University. [Google Scholar]
- Hall, Robert E. 1978. Stochastic implications of the life cycle-permanent income hypothesis: Theory and evidence. Journal of Political Economy 86: 971–87. [Google Scholar] [CrossRef]
- Hall, Robert E. 1988. Intertemporal Substitution in Consumption. Journal of Political Economy 96: 339–57. [Google Scholar] [CrossRef]
- Hall, Robert E. 2016. The Role of the Growth of Risk-Averse Wealth in the Decline of the Safe Real Interest Rate. Stanford: Stanford University. [Google Scholar]
- Johan, Sofia A., April Knill, and Nathan Mauck. 2013. Determinants of Sovereign Wealth Fund Investment in Private Equity vs. Public Equity. Journal of International Business Studies 44: 155–72. [Google Scholar] [CrossRef]
- King, Mervyn, and David Low. 2014. Measuring the ‘World’ Real Interest Rate. NBER Working Paper 19887. Cambridge, MA, USA: NBER. [Google Scholar]
- Krugman, Paul. 1987. The Narrow Moving Band, the Dutch Disease, and the Competitive Consequences of Mrs. Thatcher. Journal of Development Economics 27: 41–55. [Google Scholar] [CrossRef]
- Kunzel, Peter, Yinqiu Lu, Iva Petrova, and Jukka Pihl. 2011. Investment Objectives of Sovereign Wealth Funds—A Shifting Paradigm. IMF Working Paper WP/11/19. Available online: https://www.imf.org/en/Publications/WP/Issues/2016/12/31/Investment-Objectives-of-Sovereign-Wealth-Funds-A-Shifting-Paradigm-24598 (accessed on 26 December 2018).
- Lax, Yoel. 2002. Habit Formation and Lifetime Portfolio Selection. Available online: https://ssrn.com/abstract=325043 (accessed on 26 December 2018).
- Merton, Robert C. 1969. Lifetime portfolio selection under uncertainty: The continuous time case. Review of Economics and Statistics 51: 247–57. [Google Scholar] [CrossRef]
- Norwegian Ministry of Finance. 2015. Finanspolitikk i en oljeøkonomi (Fiscal Policy in an Oil Economy). Official Norwegian Report NOU 2015:9. Available online: https://www.regjeringen.no/no/dokumenter/nou-2015-9/id2423507/?q=2015:9 (accessed on 8 January 2019).
- Norwegian Ministry of Finance. 2016. Aksjeandelen i Statens pensjonsfond utland (The Equity Share of the Government Pension Fund Global). Official Norwegian Report NOU 2016:20. Available online: https://www.regjeringen.no/no/dokumenter/nou-2016-20/id2516269/?q=2016:20 (accessed on 8 January 2018).
- OECD. 2014. The Long-Term Global Outlook for Interest Rates. Report Commissioned by the Norwegian Ministry of Finance. Available online: https://www.regjeringen.no/no/dokumenter/nou-2015-9/id2423507/sec9 (accessed on 8 January 2019).
- Paltrinieri, Andrea, and Flavio Pichler. 2013. Asset Management Issues in Sovereign Wealth Funds: An Empirical Analysis. In Bank Performance, Risk and Securitization. Edited by Joseph Falzon. London: Palgrave Macmillan. [Google Scholar]
- Phelps, Edmund S. 1962. The accumulation of risky capital: A sequential utility analysis. Econometrica 30: 729–43. [Google Scholar] [CrossRef]
- Poterba, James M., and Lawrence H. Summers. 1988. Mean reversion in stock returns: Evidence and implications. Journal of Financial Economics 22: 27–60. [Google Scholar] [CrossRef]
- Rachel, Lukasz, and Thomas Smith. 2015. Secular Drivers of the Global Real Interest Rate. Bank of England, Staff Working Paper No. 571. Available online: https://www.bankofengland.co.uk/-/media/boe/files/working-paper/2015/secular-drivers-of-the-global-real-interest-rate.pdf?la=en&hash=AC63431DCC1F424EE322014DF858C860C148817D (accessed on 26 December 2018).
- Sá, Filipa, and Francesca Viani. 2013. Shifts in Portfolio Preferences of International Investors: An Application to Sovereign Wealth Funds. Review of International Economics 21: 868–85. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1969. Lifetime portfolio selection by dynamic stochastic programming. Review of Economics and Statistics 51: 239–46. [Google Scholar] [CrossRef]
- Sundaresan, Suresh. 1989. Intertemporally dependent preferences and the volatility of consumption and wealth. Review of Financial Studies 2: 79–89. [Google Scholar] [CrossRef]
- Svensson, Lars E. O. 1989. Portfolio Choice with Non-Expected Utility in Continuous Time. Economic Letters 30: 313–17. [Google Scholar] [CrossRef]
- Swanson, Eric. 2016. A Macroeconomic Model of Equities and Real, Nominal, and Defaultable Debt. Irvine: University of California. [Google Scholar]
- Thimme, Julian. 2016. Intertemporal Substitution in Consumption: A Literature Review. Journal of Economic Surveys 31: 226–57. [Google Scholar] [CrossRef]
- Van den Bremer, Ton, Frederick van der Ploeg, and Samuel Wills. 2016. The Elephant in the Ground: Managing Oil and Sovereign Wealth. European Economic Review 82: 113–31. [Google Scholar] [CrossRef]
- Van der Ploeg, Frederick, and Anthony J. Venables. 2011. Harnessing Windfall Revenues: Optimal Policies for Resource-Rich Developing Economies. The Economic Journal 121: 1–30. [Google Scholar] [CrossRef]
- Van Wijnbergen, Sweder. 1984. The ‘Dutch Disease’: A Disease After All? The Economic Journal 94: 41–55. [Google Scholar] [CrossRef]
- Vasicek, Oldrich. 1977. An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Viceira, Luis M. 2001. Optimal portfolio choice for long-horizon investors with nontradable labor income. Journal of Finance 56: 433–70. [Google Scholar] [CrossRef]
- Yang, Wei. 2015. Intertemporal Substitution and Equity Premium. Review of Finance 20: 403–45. [Google Scholar] [CrossRef]
| 1 | One of us participated in two government-appointed commissions related to the investment strategy and the fiscal rule associated with this SWF; Norwegian Ministry of Finance (2015, 2016). |
| 2 | The Norwegian GPFG has, despite its name, no special role in funding future pensions obligations. |
| 3 | It is also worth noting that the optimal equity share is not bounded above by unity. This is a feature of the model’s partial nature, however. |
| 4 | Calculations are performed using Ox, see Doornik (2013). |
| 5 | Out of the 10,000 simulated consumption paths used to construct each of the four graphs for the variance of log-consumption (labeled “Habit mixed”), insolvency happens in 178, 227, 288, and 387 consumption paths, respectively, with the number increasing in the initial habit level x0. |
| 6 | We also note that, in both cases, the response has the sign as 1 − ε. This is because the effect on consumption is dominated by the wealth effect when ε < 1. When ε > 1, the substitution effect dominates, so that the investor will want to postpone consumption when the risk-free rate rises, so that current consumption falls. We believe, however, that SWF decision makers tend to think mainly in terms of the wealth effect in this regard, which is consistent with our presumption that epsilon can be assumed to be quite small in the context of SWF management. |
| 7 | Indeed, if the inverse link between innovations in equity prices and the risk-free rate is strong enough, a risk neutral investor could decide to hold a short net equity position so as to take advantage of the ensuing fall in equity prices as well as the rise in the riskless rate should the latter occur. We do not pursue this extreme case, however. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).