Abstract
This paper studied the effects of credit to private non-financial sectors on income inequality. In particular, we focused on the distinction between household and firm credits, and investigated whether these two types of credit had adverse effects on income inequality. Employing cross-section augmented cointegrating regressions and using balanced panel data for 30 developed and developing countries over the period from 1995 to 2013, we showed that firm credit reduced income inequality, whereas there was no significant impact of household credit on income inequality. We concluded that it was not the size of the private credit but its composition which mattered in reducing income inequality, due to the asymmetric effects of different types of credit.
Keywords:
household credit; firm credit; income inequality; credit composition; mean group estimator JEL Classification:
G20; D31; O16; D60
1. Introduction
The impact of financial development on economic growth has long been at the center of the theoretical and empirical finance literature. Although a vast literature emphasizes that financial development contributes to subsequent economic growth1 through relaxing financial constraints, which corrects capital misallocation and mitigates productivity losses, there is a paucity of research with respect to the finance–inequality nexus. Despite the fact that income inequality has increased over the past quarter-century,2 the exact impact of financial development on income inequality has not been well-defined in both empirical studies and in the theoretical literature. The vast majority of the empirical finance–inequality studies found that financial development led to less income inequality, suggesting more finance is good for the poor.3 However, the literature has mainly focused on private credit, higher levels of which indicate more-developed financial systems and easier access to credit for entrepreneurs and households, whilst examining the linkages between financial development and income inequality (see, e.g., Clarke et al. 2006; Kappel 2010; Beck et al. 2007; Law and Tan 2009). Since these two types of borrowers, namely entrepreneurs and households, vary in terms of the use of credit, they might have different effects on the level of income inequality. Therefore, understanding whether firm credit, household credit or both contribute to reducing income inequality can help policymakers who are interested in achieving a more equitable income distribution.
In this paper, we study the link between the two components of private credit and income inequality. We argue that analyzing the separate effects of household and firm credits is more important for explaining the role of credit in income inequality than the size of total private credit per se, due to two main reasons. First, theory points to different channels through which private credit can reduce income inequality. On the one hand, household credit enables the poor to invest in their human capital and health activities, hence reducing income inequality (Galor and Zeira 1993; Banerjee and Newman 1993). On the other hand, countries with higher levels of financial development might experience a more efficient capital allocation across entrepreneurs (incumbent and new), a higher economic growth, and a lower income inequality, an effect, which can be captured by firm credit (Gine and Townsend 2004; Beck et al. 2010, 2012; Dabla-Norris et al. 2015). In that aspect, understanding the exact mechanism of generating less income inequality through providing credit requires a more nuanced analysis. Second, the ratio of household credit to firm credit is above 0.5 for many developed and developing countries in our sample, and an increasing proportion of private credit has been given to households rather than entrepreneurs over the last two decades (Figure 1). Since the proportion of household credit in total private credit has been substantially increasing and there have been increasing concerns both on the adverse effects of household debt burden and credit growth, especially in developing countries, focusing only on the size of private credit does not fully coincide with the reality. Therefore, exploring the decomposition of private credit becomes highly relevant for both economic growth and income inequality policies.
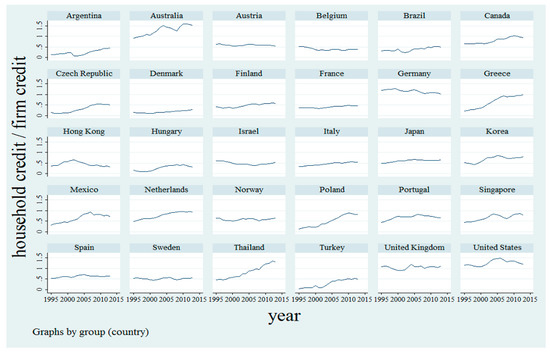
Figure 1.
The Ratio of Household Credit to Firm Credit (Annual Data, 1995–2013). Source: Bank for International Settlements (BIS) and Authors’ calculations.
In this respect, we extend finance–inequality literature by decomposing the effects of firm and household credits on income inequality. In particular, we differentiate between household credit and firm credit, while the literature has mostly focused on total credit to the private sector. Therefore, this research contributes to the literature by identifying the heterogeneous behaviors of income inequality (measured by the GINI coefficient), in response to (i) credit to non-financial corporations (firm credit), and (ii) credit to households and non-profit institutions serving households (NPISHs) (household credit), across 30 developed and developing countries. Moreover, we contribute to the literature on the finance–inequality nexus by estimating the effect of total credit to private non-financial sectors (total private credit), a common measure of financial development, on income inequality. The empirical analysis is based on balanced panel data, including annual observations for 30 selected countries over the period between 1995 and 2013. To that end, the Common Correlated Effects Mean Group (CCEMG) estimator proposed by Pesaran (2006) and Augmented Mean Group (AMG) estimator proposed by Eberhardt and Bond (2009) are employed. Contrary to the existing literature, these methods consider the cross-sectional dependence that may arise from economic integration of countries and/or common financial, political, and social shocks, and provide both the common and the country-specific estimations. We also include trade openness, foreign direct investment inward stock, government final consumption expenditure, and corruption index as control variables, which are selected from the related literature and expected to affect income inequality. We show that the response of income inequality to credit to non-financial corporations is significant and negative, whereas credit to households and NPISHs is insignificant. This may be because credit to non-financial institutions is used for investment and/or production purposes to make firms more productive, create more jobs, increase labor demand and wages, and hence, widen the income gap between rich and poor. On the other hand, household credit mostly serves to smooth consumption, and therefore, the effect of household credit on income inequality depends on the use of the credit. This evidence suggests that finance reduces income inequality through improved capital allocation and economic transformation, rather than through expanding access to credit. We also find that the effect of total private credit on income inequality is negative, but statistically insignificant. These results suggest that the composition of funds between households and firms has key implications for policies to tackle income inequality. When these two types of credits have different effects on the level of income inequality, the composition becomes even more important. This is because when policymakers are confronted with the need to restrict (or expand) credit growth, they should pay particular attention to the asymmetric effects that household and firm credits may have on income inequality. Hence, the composition of credit can support policymakers by enabling them to understand whether, and in which context, private credit is an instrument that can be used to influence income inequality, and whether the size of the total credit is always good for the poor.
Our study is further related to both the empirical and theoretical studies on the distinction between household and firm credits, all of which show that the composition of private credit matters for different macroeconomic variables. For example, Jappelli and Pagano (1994) find that an increase in household credit decreases saving rates for a sample of OECD countries. Büyükkarabacak and Krause (2009) suggest that the composition of credit does matter for the trade balance, such that lending to consumers has a negative effect on net exports, whilst firm loans contribute to a rise in net exports. Moreover, Bahadir and Gumus (2016), using a two-sector real business cycle model of a small open economy, analyze the differential effects of household and business credits dynamics on business cycles in emerging market economies. Their results suggested that two types of credit shocks generated different dynamics in sectoral input and output levels, as well as the real exchange rate.
Although there have been few systematic studies which distinguish between the components of private credit, to the best of our knowledge, the only empirical research on the finance–inequality nexus that distinguishes between household and firm credits is Beck et al. (2012). Their paper examines the differential effects of household and enterprise credits on economic growth, income inequality, and poverty. The authors find a negative relation between enterprise credit and growth of the Gini coefficient, but no statistically significant impact of household credit. However, Beck et al. (2012) use cross-country data (only 33 observations in their sample) for the period from 1992–2005. Moreover, they do not control for cross sectional dependence. The distinguishing features of our paper are that we (i) provide both country-specific and panel estimates, (ii) consider the cross-sectional dependence, (iii) use a comprehensive and updated data set, and (iv) employ cross-section augmented cointegrating regressions. Our findings are in line with the theoretical predictions of Gine and Townsend (2004) and Beck et al. (2010), which suggest that the impact of private credit on reducing income inequality goes through firm credit rather than household credit, and contradicting with theories focusing on credit for the poor by helping them to exit poverty through investing in human capital, health, and microenterprises activities (see, Galor and Zeira 1993; Banerjee and Newman 1993).
2. Data Description
We combined country-level annual data gathered from five sources: The Standardized World Income Inequality Database (SWIID), the Bank for International Settlements (BIS) Statistics, the World Bank World Development Indicators, International Country Risk Guide (ICRG) Database, and the United Nations Conference on Trade and Development (UNCTAD) Statistics. The sample consisted of 30 developed and developing countries covering 19 consecutive years, i.e., the period from 1995–2013.4 The choices of country set and data period were shaped by data availability concerns. In particular, we focused on countries having no missing values for any of our selected variables over time.
Our analysis was based on three main variables: (i) Gini coefficient, (ii) credit to non-financial corporations (TCF), and (iii) credit to households and non-profit institutions serving households (TCH). The dependent variable was the market Gini coefficient, indicated by GINIMARKET, which was drawn from the SWIID and constructed by Solt (2009), using the Luxembourg Income Study as the harmonized benchmark for comparable estimates. The SWIID was our preferred source of data on income inequality, as it provides comparable figures across countries and over a longer span of time. The market Gini coefficient was calculated on income before taxes and transfers, and it measured inequality in income distribution without considering the effect of taxes and social spending already in place in a country. We have also used the net Gini coefficient (after taxes and transfers), indicated by GININET.
Our main explanatory variables, credit to non-financial corporations and credit to households and NPISHs, which have been used interchangeably, are retrieved from the BIS Statistics. It would be helpful to briefly summarize the content of the data to better understand the structure of the BIS data on private credit. The BIS has constructed long series on credit to the private non-financial sector for both advanced and emerging economies. Credit is provided by domestic banks, and to all other sectors of the economy and non-residents. The private non-financial sector includes non-financial corporations (both private-owned and public-owned), households, and non-profit institutions serving households. In terms of financial instruments, credit covers loans and debt securities. The data for each country includes (i) credit to private non-financial sectors by domestic banks and (ii) total credit to private non-financial sectors. Moreover, total credit is broken down into (iii) credit to non-financial corporations and (iv) credit to households and non-profit institutions serving households. Hence, credit to non-financial corporations as a percentage of GDP and credit to households and non-profit institutions serving households as a percentage of GDP, both of which are in market values and adjusted for breaks, are used as explanatory variables in the analysis.
To assess the strength of the linkage between credit components and income inequality, we controlled for other potential determinants of income inequality in the regressions. We used four control variables widely employed in the related literature. These variables were also introduced into the model as a test of robustness. First, we included the ratio of trade to GDP (TRADE) to capture the degree of openness of an economy. Second, the ratio of government final consumption expenditure to GDP (GGFCE) was used to measure macroeconomic stability. Third, to measure the level of institutional quality, we used a corruption index (CORR), where lower values indicate a higher level of corruption, hence, expecting that lower values of the corruption index may be associated with lower institutional quality, higher level of corruption in the public sector, and hence a higher level of income inequality. Finally, we controlled for the foreign direct investment inward stock to GDP ratio (FDI). The source of data of TRADE and GGFCE was the World Bank DataBank. The data for CORR was compiled from the ICRG Database, whereas the data on FDI were extracted from UNCTAD Statistics.
Table 1 presents the descriptive statistics for the variables used in our empirical analysis. There are considerable variations in our variables across countries. For example, the market Gini coefficient ranges from a low of 29.66% to 58.59%. Household credit to GDP and firm credit to GDP ratios also showed significant variations, with TCH ranging from 0.9% to 118.8% and TCF from 12.2% to 197.5%. Figure 2 displays the visual evidence representing the raw correlations between our main explanatory variables (household and firm credit) and the dependent variable (the market Gini coefficient).

Table 1.
Descriptive Statistics.
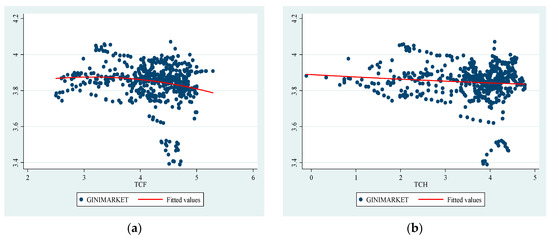
Figure 2.
Visual evidence. The figures provide a visual representation of the unconditional relationship between the firm credit to GDP ratio and the market Gini coefficient in (a), and household credit to GDP ratio and the market Gini coefficient in (b). All values are in natural logarithms.
3. Empirical Strategy
The goal was to develop an empirical strategy that would enable us to estimate the distinguished effects of household and firm credit on the level of income inequality, given the country-level data set we had. While several alternative measures of income inequality can be used in the analysis, we preferred to focus on two measures of income inequality, which were also the measures most commonly used in the literature, i.e., market Gini coefficient (GINIMARKET) and net Gini coefficient (GININET). The basic regression model that we aimed to estimate can be expressed as follows:
where and are country and time indices, represents the income inequality measure, represents, alternatively, credit to non-financial corporations (TCF) and credit to households and non-profit institutions serving households (TCH), is the vector of control variables that include , , , and , is the unobserved common factor with heterogeneous factor loadings , and is the error term. Finally, stands for the natural logarithm. Our main parameter of interest was , which approximately describes the percentage point change in income inequality measures as a response to one percentage point increase, alternatively, in firm credit and household credit.
A growing body of literature claims that panel data sets tend to show cross-sectional dependence, which may arise from economic integration of countries, common shocks (such as financial, political, and social shocks), and sometimes unobserved factors that eventually become part of the error (disturbance) term (Pesaran 2004). Since traditional estimation methods have become inconsistent or inefficient in the presence of cross-sectional dependence, new techniques have been developed in panel data econometrics for stationarity and cointegration analysis and estimation procedures, which take account of cross-sectional dependence. Assuming that cross-sectional dependence is due to common unobserved components, but that they are uncorrelated with the included regressors, the Fixed-Effects (FE) and Random-Effects (RE) estimators are consistent, although not efficient, and the estimated standard errors are biased. However, if the common unobserved components are correlated with the included regressors, the FE and RE estimators are inconsistent and biased (De Hoyos and Sarafidis 2006). To resolve this potential problem, we consecutively employed (i) Bias-Adjusted CD test developed by Pesaran et al. (2008), (ii) cross-sectionally augmented Im-Pesaran-Shin (CIPS) panel unit root test proposed by Pesaran (2007), (iii) the second generation panel cointegration tests of LM Bootstrap test from Westerlund and Edgerton (2007), and the Durbin-Hausman test of Westerlund (2008), which allow for the dependence of cross-sectional units, and (iv) Common Correlated Effects (CCE) estimator proposed by Pesaran (2006), Common Correlated Effects Mean Group (CCEMG), and Augmented Mean Group (AMG) estimator proposed by Eberhardt and Bond (2009), which allow for cross-sectional dependency arising from multiple unobserved common factors.
4. Empirical Results
As testing for cross-sectional dependence in panel data is necessary to decide on the estimation method, the first step of the empirical analysis were cross-sectional dependence (CD) tests to analyze the contemporaneous correlation across countries in the panel.5 Panel A and Panel B of Table 2 report the results of Bias-Adjusted CD test developed by Pesaran et al. (2008), for each series, and for the models, respectively.6 The results implied that for both the models with intercept, and the models with intercept and trend, the test statistics rejected the null hypothesis of no cross-sectional dependence, for all series, and for the Models 1–8.

Table 2.
Cross-sectional Dependence Tests Results.
Given the presence of cross-sectional dependence in the panel, the first generation unit root tests become invalid. Therefore, to analyze the stationarity features of the series, the cross-sectionally augmented Im-Pesaran-Shin (CIPS) panel unit root test proposed by Pesaran (2007) was employed. The CIPS test statistics are the sample averages of the individual cross-sectionally augmented ADF (CADF) statistics. The results of the CIPS test for the panel are presented in Table 3. The CIPS test results indicated the failure to reject the null hypothesis of the presence of unit root for all series, for both the model with intercept and the model with intercept and trend. In other words, all series were found to be non-stationary processes for the panel.

Table 3.
Cross-sectionally augmented Im-Pesaran-Shin (CIPS) Panel Unit Root Test Results.
After we confirmed the non-stationarity of the variables for the panel, the subsequent step was to test for cointegration among the dependent variable and the regressors. Given the presence of cross-sectional dependence in the panel, the first generation panel cointegration tests also became invalid. Hence, the second generation panel cointegration tests were employed by allowing for the dependence of cross-sectional units. Particularly, LM Bootstrap test of Westerlund and Edgerton (2007), and the Durbin-Hausman test of Westerlund (2008) were utilized to ensure the presence of cointegration in Models 1–8. Panel A and Panel B of Table 4 report the results of the LM Bootstrap and Durbin-Hausman tests, respectively. There was strong evidence of cointegration in Models 1–8, since the LM Bootstrap test results indicated failure to reject the null hypothesis of the presence of cointegration, and the Durbin-Hausman test results revealed the rejection of the null hypothesis of no cointegration.

Table 4.
Panel Cointegration Tests Results.
As we verified the presence of cointegration in our basic model, the long-run relationship in the panel regression model given in Equation (1) was further estimated by two methods for panel cointegration estimation. The cross-section augmented cointegrating regression for each country was estimated by the Common Correlated Effects (CCE) estimator proposed by Pesaran (2006), and Augmented Mean Group (AMG) estimator proposed by Eberhardt and Bond (2009). The latter allows for cross-sectional dependency, which potentially arises from multiple unobserved common factors. The CCE estimation procedure is advantageous, since it enables augmenting the basic regression with cross-section averages of the dependent variable and the observed regressors, as proxies for the unobserved common factors. The CCE estimation procedure is presented in Equation (2).
where the coefficients and represent the elasticity estimates of with respect to the cross-section averages of the observed regressors and , respectively. Accordingly, (alternatively, ) and (in Equation (1)) are contained in , and denotes the error term. This procedure allows the individual countries to respond to common time effects differently, as reflected by the country-specific coefficients on the cross-sectionally averaged variables. It also provides consistent estimates, even when the observed regressors are correlated with the common factors. Using this procedure, the individual coefficients, , can be estimated in a panel framework. The Common Correlated Effects Mean Group (CCEMG) estimation is a simple average of the individual CCE estimations. The CCEMG estimator is robust to slope heterogeneity, endogeneity, and cross-sectional dependence. It should be noted that the CCEMG estimator is also robust to structural breaks and non-stationary unobserved common factors. Therefore, the results of the CCEMG estimators provide invaluable evidence regarding the effects of credit components on income inequality. The CCEMG estimation procedure is shown in Equations (3) and (4).
where are the estimates of the coefficients in Equation (2), and are the estimated CCEMG coefficients and their standard deviations, respectively.
On the other hand, the AMG estimator considers time series data properties, as well as the differences in the impact of observables and unobservables across panel groups. This estimator considers cross-sectional dependence through the involvement of a “common dynamic effect” in the country regression, which is extracted from the year dummy coefficients of a pooled regression in first differences (FD-OLS), and represents the levels-equivalent mean evolvement of unobserved common factors across all countries (Eberhardt and Bond 2009). Provided that the unobserved common factors compose part of the country-specific cointegrating relation, the augmented country regression model embraces the cointegrating relationship that is allowed to differ across countries. In this regard, it coincides with the assumption of the CCEMG estimator (Pedroni 2007; Eberhardt and Bond 2009)7 The first stage stands for a standard FD-OLS regression with T-1 year dummies in first differences, from which the year dummy coefficients, relabeled as were collected. In the second stage, this variable was included in each of the N standard country regressions. Then, the AMG estimations were derived as averages of the individual country estimations. The first and the second stages of the AMG estimation procedure are shown in Equations (5) and (6), respectively.
where is constant, and denotes the error term of stage (i) and stage (ii). stands for cross-sectional group-specific AMG estimations, which are averaged across the panel.
We start discussing our estimates with Table 5, which presents the results of the regression of log market Gini coefficient on log firm credit to GDP ratio (in columns 1, 2, 5, and 6) and log household credit to GDP ratio (in columns 3, 4, 7, and 8), along with the controls. The regressions show that there was a statistically significant relation between firm credit to GDP ratio and the market Gini coefficient, suggesting countries with higher levels of firm credit to GDP ratio experienced lower income inequality. The results held for both the CCEMG and AMG estimates. On the other hand, both the CCEMG and AMG estimates did not suggest a statistically meaningful correlation between household credit to GDP ratio and the market Gini coefficient. Household credit and income inequality were positively associated, although we could not find a statistically significant relation between these two. The positive relationship between household credit and income inequality was not surprising when we remember what happened in the US before the global financial crisis of 2008. There had been a historic increase in American household demand relative to spendable income, whilst inequality was rising at the same time. However, the coincidence of rising income inequality and increasing access to credit provided the impetus for a debt-fueled consumption boom (Cynamon and Fazzari 2013). Consequently, the unsustainable rise in household leverage concentrated in the bottom 95 percent ultimately spawned the Great Recession in the US (see (Cynamon and Fazzari 2013), for a detailed overview of the impact of household debt on income inequality in the US). Hence, our results also showed that more credit may not always be good for the poor. Among the control variables, only government final consumption expenditure to GDP ratio, in both specifications, and the trade to GDP ratio in AMG estimate had statistically significant and positive relations with the level of income inequality.

Table 5.
Mean Group Type Estimations (the market Gini Coefficient and Credit Compositions).
In addition to the regressions with credit components, in Table 6, we present the results of the regression of log market Gini coefficient on total credit to private non-financial sectors as a percentage of GDP, which is the sum of the household credit to GDP ratio and the firm credit to GDP ratio, as defined in Section 2. This regression was estimated to examine the effect of total private credit on the level of income inequality to be able to compare our results with the existing literature on the finance–inequality nexus. Both the CCEMG and AMG estimates suggested a statistically insignificant relation between total credit to private non-financial sectors and the market Gini coefficient, though the relationship was negative. The estimates confirmed our hypothesis that the composition of total private credit was more important than its size in reducing income inequality.

Table 6.
Mean Group Type Estimations (the market Gini Coefficient and Total Private Credit).
We also explored the relation between credit components and the net Gini coefficient (GININET). The nature of analysis was same as the one executed in Table 5. Similar to Table 5, the CCEMG and AMG estimates suggested a negative and statistically significant relation between firm credit to GDP ratio and the net Gini coefficient, whilst the relationship was statistically insignificant for household credit to GDP ratio.8
In addition to the panel estimates, the cross-section augmented cointegrating regression for each country was also estimated by CCE and AMG estimators. Table A1 in Appendix A presents the signs of the coefficients regarding the regressions between (i) firm credit and income inequality, and (ii) household credit and income inequality, using CCE and AMG estimators, respectively. The results showed that though household credit was negatively and significantly associated with the market Gini coefficient in some countries (e.g., Greece, Israel, Poland, and Spain), it increased income inequality in most of the countries (e.g., Belgium, Canada, Denmark, Hong Kong, Hungary, Sweden). On the other hand, the relationship between firm credit and the market Gini coefficient was weak but negative in most of the countries. However, these evidences should be interpreted with caution due to data constraints in the sample countries.
5. Concluding Remarks
There are numerous studies investigating the link between financial development and economic growth. However, there is a scarcity of research on the relation between finance and income inequality, most of which focuses on the size of total credit given to the private sector. Although private credit is vital for the real economy, the ratio of household credit to firm credit is above 0.5 in many developed and developing countries in our sample, and an increasing proportion of private credit has been given to households rather than entrepreneurs over the last two decades. Since these two types of borrowers, namely households and entrepreneurs, vary in terms of the use of credit, they might have different effects on the level of income inequality. Therefore, the main purpose of this paper was to specifically focus on the distinction between household and firm credits, and investigate whether these two types of credit had asymmetric effects on income inequality in a sample of 30 developed and developing countries over the period from 1995 to 2013. In addition, we also tested the impact of the ratio of total credit to private non-financial sectors to GDP on the level of income inequality, to explore our main hypothesis claiming it was not the size of private credit but its composition that may matter for reducing income inequality. Our analysis also paid special attention to cross-sectional dependence issues, which are mostly ignored by the existing literature, and aims to present robust estimates on the role of credit components in reducing income inequality. We may summarize our main findings and their implications below.
First, our main finding supported by both CCEMG and AMG estimates was that firm credit reduced income inequality, whereas there was no significant impact of household credit on the level of income inequality. This suggested that countries with high levels of firm credit in the non-financial sectors may experience lower income inequality probably due to various positive externalities of firm credit expansion. Therefore, from the policy perspective, we may suggest that the policies encouraging firm credit expansion may be useful to reach a lower income inequality. However, policymakers and firms should be also careful regarding the potential drawbacks of increasing the level of corporate debts, specifically in emerging countries. Second, we found that both the CCEMG and AMG estimates did not suggest a statistically meaningful correlation between household credit to GDP ratio and the market Gini coefficient. This may be interpreted as that more credit may not always be good for the poor. Considering evidence that higher household credit may increase income inequality, countries having high levels of household credit may discourage over-expansion of private credit. The policies motivating a balanced household credit expansion may eventually result in a better income inequality picture, specifically in those countries having a volatile borrowing cost structure. Third, we also found that total credit to private non-financial sectors was negatively but insignificantly associated with the market Gini coefficient, suggesting that there was no statistically significant effect of total credit on income inequality. In addition to the above evidences, this evidence also suggested that it was not the size of private credit but its composition that may be better for reducing income inequality. Finally, the evidence also suggested that whilst the government consumption expenditure to GDP ratio and trade openness had positive associations with the level of income inequality, there was no statistically significant impact of either the corruption index or foreign direct investment to GDP ratio on income inequality. These evidences implied that higher government spending and degree of openness of an economy may increase income inequality.
Overall, since household and firm credits had different effects on the level of income inequality, the composition of private credit becomes even more important. This encourages policymakers to pay particular attention to the asymmetric effects that household and firm credits have on income inequality, when they are establishing sector-specific credit policy.
Further research on country level credit decomposition–inequality analysis may enrich the empirical literature.
Author Contributions
Conceptualization, Ü.S. and Y.C.; Methodology, Ü.S. and D.K.; Software, D.K.; Validation, Ü.S.; Formal Analysis, Ü.S. and D.K.; Data Curation, Ü.S. and D.K.; Writing-Original Draft Preparation, Ü.S. and Y.C.; Writing-Review and Editing, Ü.S. and Y.C.; Visualization, Ü.S.; Supervision, Ü.S.
Acknowledgments
We are particularly grateful to the Editor and anonymous referees for constructive comments. The views expressed here are of our own and do not necessarily reflect those of our affiliated institutions. All errors are ours.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Country-Specific Regressions (Summary of the Sign of the Coefficients).
Table A1.
Country-Specific Regressions (Summary of the Sign of the Coefficients).
| Dependent Variable: | ||||
|---|---|---|---|---|
| Country | CCE | AMG | ||
| TCF | TCH | TCF | TCH | |
| Argentina | + | + | + | − |
| Australia | + | − | + | − |
| Austria | (−) * | − | + | − |
| Belgium | − | (+) *** | − | (+) *** |
| Brazil | − | (−) *** | − | (+) *** |
| Canada | − | (+) *** | + | (+) *** |
| Czech Republic | − | − | − | − |
| Denmark | − | (+) *** | (−) ** | − |
| Finland | + | − | + | + |
| France | − | − | − | + |
| Germany | (+) *** | − | (+) ** | + |
| Greece | − | + | − | (−) *** |
| Hong Kong | (+) * | (+) ** | (−) ** | + |
| Hungary | + | − | + | (+) *** |
| Israel | − | (−) *** | + | − |
| Italy | − | − | − | − |
| Japan | + | − | − | + |
| Republic of Korea | − | − | (−) *** | + |
| Mexico | + | − | − | − |
| Netherlands | − | − | (−) ** | + |
| Norway | + | (−) ** | − | + |
| Poland | − | (−) *** | (−) *** | (−) *** |
| Portugal | − | − | − | − |
| Singapore | − | + | − | − |
| Spain | − | (−) *** | (−) *** | (−) *** |
| Sweden | − | + | + | (+) ** |
| Thailand | + | + | + | + |
| Turkey | + | − | + | (−) * |
| United Kingdom | (−) ** | + | − | (−) *** |
| United States | − | − | (−) *** | (−) *** |
Note: The superscripts ***, ** and * denote the statistical significance at 1%, 5% and 10% levels, respectively.
References
- Abosedra, Salah, Muhammad Shahbaz, and Kishwar Nawaz. 2016. Modeling Causality between Financial Deepening and Poverty Reduction in Egypt. Social Indicators Research 126: 955–69. [Google Scholar] [CrossRef]
- Bahadir, Berrak, and Inci Gumus. 2016. Credit Decomposition and Business Cycles in Emerging Market Economies. Journal of International Economics 103: 250–62. [Google Scholar] [CrossRef]
- Banerjee, Abhijit V., and Andrew F. Newman. 1993. Occupational Choice and the Process of Development. Journal of Political Economy 101: 274–98. [Google Scholar] [CrossRef]
- Beck, Thorsten, and Ross Levine. 2004. Stock Markets, Banks, and Growth: Panel Evidence. Journal of Banking & Finance 28: 423–42. [Google Scholar]
- Beck, Thorsten, Asli Demirguc-Kunt, and Ross Levine. 2007. Finance, Inequality and the Poor. Journal of Economic Growth 12: 27–49. [Google Scholar] [CrossRef]
- Beck, Thorsten, Ross Levine, and Levkov Alex. 2010. Big Bad Banks? The Impact of U.S. Branch Deregulation on Income Distribution. Journal of Finance 65: 1637–67. [Google Scholar] [CrossRef]
- Beck, Thorsten, Berrak Büyükkarabacak, Felix K. Rioja, and Neven T. Valev. 2012. Who Gets the Credit? And Does it Matter? Household vs. Firm Lending Across Countries. B.E. Journal of Macroeconomics 12. [Google Scholar] [CrossRef]
- Bencivenga, Valerie R., Bruce D. Smith, and Ross M. Starr. 1995. Transaction Costs, Technological Choice, and Endogenous Growth. Journal of Economic Theory 67: 153–77. [Google Scholar] [CrossRef]
- Breusch, Trevor Stanley, and Adrian Rodney Pagan. 1980. The Lagrange Multiplier Test and Its Applications to Model Specification in Econometrics. The Review of Economic Studies 47: 239–53. [Google Scholar] [CrossRef]
- Büyükkarabacak, Berrak, and Stefan Krause. 2009. Studying the Effects of Household and Firm Credit: The Composition of Funds Matter. Economic Inquiry 47: 653–66. [Google Scholar] [CrossRef]
- Cecchetti, Stephen, and Enisse Kharroubi. 2012. Reassessing the Impact of Finance on Growth. Working Paper No. 381. Basel, Switzerland: Monetary and Economic Department, Bank for International Settlements. [Google Scholar]
- Charlton, Andrew. 2008. Capital Market Liberalization and Poverty. In Capital Market Liberalization and Development. Edited by José Antonio Ocampo and Joseph Stiglitz. New York: Oxford Press, pp. 121–38. [Google Scholar]
- Clarke, George R.G., Lixin Colin Xu, and Heng-fu Zou. 2006. Finance and Income Inequality: What Do the Data Tell Us? Southern Economic Journal 72: 578–96. [Google Scholar] [CrossRef]
- Cynamon, Barry Z., and Steven M. Fazzari. 2013. Inequality and Household Finance during the Consumer Age. Working Paper No. 752. Annandale-On-Hudson, NY, USA: Levy Economics Institute. [Google Scholar]
- Dabla-Norris, Era, Yan Ji, Robert M. Townsend, and D. Filiz Unsal. 2015. Distinguishing Constraints on Financial Inclusion and Their Impact on GDP and Inequality. NBER Working Paper No. 20821. Cambridge, MA, USA: NBER. [Google Scholar]
- De Hoyos, Rafael E., and Vasilis Sarafidis. 2006. Testing for Cross-Sectional Dependence in Panel-Data Models. Stata Journal 6: 482–96. [Google Scholar]
- Demirguc-Kunt, Asli, and Ross Levine. 2008. Finance, Financial Sector Policies, and Long-run Growth. Working Paper No. 4469. Washington, DC, USA: The World Bank Policy Research, The World Bank. [Google Scholar]
- Dollar, David, and Aart Kraay. 2002. Growth is Good for the Poor. Journal of Economic Growth 7: 195–225. [Google Scholar] [CrossRef]
- Eberhardt, Markus, and Stephen Bond. 2009. Cross-Section Dependence in Nonstationary Panel Models: A Novel Estimator. Munich Personal RePEc Archive (MPRA) Paper No. 17692. Munich, Germany: Munich Personal RePEc Archive. [Google Scholar]
- Galor, Oded, and Joseph Zeira. 1993. Income Distribution and Macroeconomics. Review of Economic Studies 60: 35–52. [Google Scholar] [CrossRef]
- Gine, Xavier, and Robert Townsend. 2004. Evaluation of Financial Liberalization: A General Equilibrium Model with Constrained Occupational Choice. Journal of Development Economics 74: 269–307. [Google Scholar] [CrossRef]
- Goldsmith, Raymond W. 1969. Financial Structure and Development. New Haven: Yale University Press. [Google Scholar]
- Harris, Richard D. F. 1997. Stock Markets and Development: A Re-assessment. European Economic Review 41: 139–46. [Google Scholar] [CrossRef]
- Jappelli, T., and Marco Pagano. 1994. Saving, Growth, and Liquidity Constraints. The Quarterly Journal of Economics 109: 83–109. [Google Scholar] [CrossRef]
- Jauch, Sebastian, and Sebastian Watzka. 2015. Financial Development and Income Inequality: A Panel Data Approach. Empirical Economics 51: 1–24. [Google Scholar] [CrossRef]
- Kappel, Vivien. 2010. The Effects of Financial Development on Income Inequality and Poverty. CER-ETH Economics Working Paper Series. No. 10/127. Zurich, Switzerland: CER-ETH—Center of Economic Research (CER-ETH) at ETH Zurich. [Google Scholar]
- King, Robert G., and Ross Levine. 1993. Finance and Growth: Schumpeter might be right. Quarterly Journal of Economics 108: 717–37. [Google Scholar] [CrossRef]
- Law, Siong, and Hui Boon Tan. 2009. The Role of Financial Development on Income Inequality in Malaysia. Journal of Economic Development 34: 153–68. [Google Scholar]
- Levine, Ross. 2005. Finance and Growth: Theory and Evidence. In Handbook of Economic Growth. Edited by Philippe Aghion and Steven Durlauf. North-Holland: Elsevier, pp. 865–933. [Google Scholar]
- Li, Hongyi, Lyn Squire, and Heng-fu Zou. 1998. Explaining International and Intertemporal Variations in Income Inequality. The Economic Journal 108: 26–43. [Google Scholar] [CrossRef]
- Lucas, Robert E. 1988. On the Mechanics of Economic Development. Journal of Monetary Economics 22: 3–42. [Google Scholar] [CrossRef]
- McKinnon, Ronald I. 1973. Money and Capital in Economic Development. Washington, DC: Brookings Institution. [Google Scholar]
- Naceur, Samy B., and Samir Ghazouani. 2007. Stock Markets, Banks, and Economic Growth: Empirical Evidence from the MENA Region. Research in International Business and Finance 21: 297–315. [Google Scholar] [CrossRef]
- Pedroni, Peter. 2007. Social Capital, Barriers to Production and Capital Shares: Implications for the Importance of Parameter Heterogeneity from a Nonstationary Panel Approach. Journal of Applied Econometrics 22: 429–51. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem. 2004. General Diagnostic Tests for Cross Section Dependence in Panels. CESifo Working Paper Series No. 1229. Munich, Germany: CESifo Group Munich. [Google Scholar]
- Pesaran, M. Hashem. 2006. Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure. Econometrica 74: 967–1012. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem. 2007. A Simple Panel Unit Root Test in the Presence of Cross-Section Dependence. Journal of Applied Econometrics 22: 265–312. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Aman Ullah, and Takashi Yamagata. 2008. A Bias-Adjusted LM Test of Error Cross-Section Independence. The Econometrics Journal 11: 105–27. [Google Scholar] [CrossRef]
- Ravallion, Martin. 2001. Growth, Inequality and Poverty: Looking Beyond Averages. World Development 29: 1803–15. [Google Scholar] [CrossRef]
- Robinson, Joan. 1952. The Generalization of the General Theory. In The Rate of Interest and Other Essays. London: MacMillan, pp. 67–142. [Google Scholar]
- Rousseau, Peter L., and Paul Wachtel. 2000. Equity Markets and Growth: Cross-country Evidence on Timing and Outcomes 1980–1995. Journal of Banking & Finance 24: 1933–57. [Google Scholar]
- Seven, Unal, and Yener Coskun. 2016. Does Financial Development Reduce Income Inequality and Poverty? Evidence from Emerging Countries. Emerging Markets Review 26: 34–63. [Google Scholar] [CrossRef]
- Shaw, Edward Stone. 1973. Financial Deepening in Economic Development. Oxford: Oxford University Press. [Google Scholar]
- Solt, Frederick. 2009. Standardizing the World Income Inequality Database. Social Science Quarterly 90: 231–42. [Google Scholar] [CrossRef]
- Uddin, Gazi, Muhammad Shahbaz, Mohamed Arouri, and Frederic Teulon. 2014. Financial Development and Poverty Reduction Nexus: A Cointegration and Causality Analysis in Bangladesh. Economic Modelling 36: 405–12. [Google Scholar] [CrossRef]
- Westerlund, Joakim. 2008. Panel Cointegration Tests of the Fisher Effect. Journal of Applied Econometrics 23: 193–233. [Google Scholar] [CrossRef]
- Westerlund, Joakim, and Edgerton David. 2007. A Panel Bootstrap Cointegration test. Economics Letters 97: 185–90. [Google Scholar] [CrossRef]
| 1 | Papers including Goldsmith (1969); McKinnon (1973); Shaw (1973); King and Levine (1993); Bencivenga et al. (1995); Rousseau and Wachtel (2000); Beck and Levine (2004); and Demirguc-Kunt and Levine (2008) report positive association between financial development and economic growth. See Robinson (1952); Lucas (1988); Naceur and Ghazouani (2007); Harris (1997); and Cecchetti and Kharroubi (2012) for papers reporting negative or statistically insignificant association between financial development and economic growth. See Levine (2005) for comprehensive reviews of the related literature. |
| 2 | While global inequality has declined mainly thanks to the development spurt of China and India, inequality within individual countries has worsened in a remarkably consistent fashion in both the developed and developing countries over the last three decades. |
| 3 | Papers including Li et al. (1998); Clarke et al. (2006); Beck et al. (2007); Dollar and Kraay (2002); Ravallion (2001); Kappel (2010); Uddin et al. (2014); and Abosedra et al. (2016) report negative relationship between financial development and income inequality, namely that financial development reduces income inequality. On the other hand, Charlton (2008); Law and Tan (2009); Jauch and Watzka (2015) and Seven and Coskun (2016) report negative or statistically insignificant relation between finance and income inequality/poverty. See Seven and Coskun (2016) for a broad review of the related literature. |
| 4 | The sample consist of Argentina, Australia, Austria, Belgium, Brazil, Canada, Czech Republic, Denmark, Finland, France, Germany, Greece, Hong Kong SAR, Hungary, Israel, Italy, Japan, Republic of Korea, Mexico, The Netherlands, Norway, Poland, Portugal, Singapore, Spain, Sweden, Thailand, Turkey, United Kingdom, and the United States of America. |
| 5 | Note that if the time dimension (T) is larger than the cross-sectional dimension (N) in a panel data set, the CDLM1 test of Breusch and Pagan (1980) can be used to test for cross-sectional dependence. However, if N is larger than T in a panel, just as in this analysis (N = 30, T = 19), the CDLM1 test statistic does not attain desirable statistical properties as it shows considerable size distortions (Pesaran 2004). We have utilized the Bias-Adjusted CD test of Pesaran et al. (2008), since it exhibits a finite sample behavior, compared to the CDLM2 and CDLM tests of Pesaran (2004). It successfully controls the size, whilst maintaining satisfactory power in a panel with exogenous regressors. Bias-Adjusted CD test is consistent even when the CDLM2 and CDLM tests are inconsistent. |
| 6 | In Models 1, 2, 3 and 4, the dependent variable is GINIMARKET. The independent variable is TCF in Models 1 and 2; Model 2, in addition, includes control variables. The independent variable is TCH in Models 3 and 4; Model 4, in addition, includes control variables. Models 5, 6, 7 and 8 are for robustness checks, and they pursue the same ordering, where the dependent variable is GININET. |
| 7 | Eberhardt and Bond (2009) compare the performance of AMG and CCEMG estimators through Monte Carlo simulations, and find robust results for both approaches. |
| 8 | All stationary, unit-root, panel cointegration, and long-run relationship tests were employed for the regressions between credit components and the net Gini coefficient. We did not present all results here to conserve space, but available upon request from the authors. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).