Abstract
This paper investigates the predictability of exchange rate changes by extracting the factors from the three-, four-, and five-factor model of the relative Nelson–Siegel class. Our empirical analysis shows that the relative spread factors are important for predicting future exchange rate changes, and our extended model improves the model fitting statistically. The regression model based on the three-factor relative Nelson–Siegel model is the superior model of the extended models for three-month-ahead out-of-sample predictions, and the prediction accuracy is statistically significant from the perspective of the Clark and West statistic. For 6- and 12-month-ahead predictions, although the five-factor model is superior to the other models, the prediction accuracy is not statistically significant.
JEL Classification:
E47; F31; G17
1. Introduction
Analyzing the predictability of exchange rate changes is one of the concerns that market participants, policy makers, and academic scholars recognize. Many studies have analyzed the dynamics of the exchange rate and the predictability of exchange rate changes. Mussa (1976) and Frankel (1979) are well-known works of classical literature that analyze the exchange rate.
This paper investigates the predictability of future exchange rate changes, applying the yield curve model to uncovered interest rate parity in the method of the Chen and Tsang (2013) study.
The term structure model of interest rates has the information to predict the future economic activity and inflation. In particular, as Estrella and Hardouvelis (1991) and Estrella and Mishkin (1998) show, the slope factor of the term structure has the information to predict future economic changes. There are three types of term structure of interest rate models (De Rezende and Ferreira (2013)). The first type is affine equilibrium models, as proposed by Vasicek (1977) and Cox et al. (1985), and generalized later by Duffie and Kan (1996). The second type is the no-arbitrage model proposed by Christensen et al. (2009, 2011). The last type is the statistical and parametric models proposed by Nelson and Siegel (1987), Svensson (1994), and Diebold and Li (2006). As in De Rezende and Ferreira (2013), this paper focuses on the class of the Nelson–Siegel model that has the slope factor.
Chen and Tsang (2013) apply the dynamic Nelson–Siegel model to the term structure of domestic and foreign interest rate differentials. The factor in this model is called the “relative Nelson–Siegel factor”. They show that the factors predict exchange rate movements and excess currency returns. The methodological differences between Chen and Tsang (2013) and this study are as follows:
First, as in De Rezende and Ferreira (2013), the three-factor dynamic Nelson–Siegel model of Chen and Tsang (2013) is extended to a four- and -five-factor model. In the four-factor model, the model has one relative level factor, one relative spread factor, and two relative curvature factors. The five-factor model has one more relative spread factor. This paper extracts the relative Nelson–Siegel factors from these two extended models and investigates the predictability of the relative factors.
Second, we estimate the decaying parameter to which Chen and Tsang (2013) give ad hoc, the value of 0.0609, by using the method of minimizing the root mean squared errors (RMSE) of the regression model, as used by De Rezende and Ferreira (2013). Chen and Tsang (2013) use the value proposed by Diebold and Li (2006). The decaying parameter plays an important role in the Nelson–Siegel model. The smaller the parameter value becomes, the slower the decay becomes in factor loading of the Nelson–Siegel model. Diebold and Li (2006) show that the value of 0.0609 maximizes the factor loading of the spread factor at 30 months. However, as Diebold and Li (2006) mention, determining the appropriate decaying parameter is still an issue, so this paper estimates the optimal parameter by minimizing the root mean square error (RMSE), following De Rezende and Ferreira (2013).
The main results of this paper are as follows: First, the four- and five-factor models improve the re-scaled values when we regress the relative Nelson–Siegel factors on the exchange rate changes. In addition, not only the first relative spread factor, but also the second spread factor is important for predictability. Second, the five-factor model outperforms the three- and four-factor models in sample fit. Finally, these models outperform the random walk model in out-of-sample prediction and the results are statistically significant at a 1% significance level. For the three-month-ahead prediction, the three-factor model is superior relative to the other models; on the other hand, the five-factor model is superior relative to the other models, from the perspective of comparing root square mean prediction errors.
This study contributes to the literature as follows: By extending the model proposed by Chen and Tsang’s (2013) three-factor relative Nelson–Siegel model to the four- and five-factor models, this paper succeeds in improving the model fit of the future exchange rate changes in sample-fit. In addition to evaluating model accuracy in sample-fit as Chen and Tsang (2013) do, this paper investigates the prediction accuracy out-of-sample. To evaluate the out-of-sample prediction, this paper uses root mean squared prediction errors (RMSPE) and compares the RMSPE of each mode (random walk model and three-, four-, and five-factor relative Nelson–Siegel mode).
Related Literature
Concluding the Introduction, we mention the development of research on exchange rate models and Nelson–Siegel models.
The classical researches on the exchange rate are Mussa (1976) and Frankel (1979). They show that the present value of the exchange rate is determined by its expected future value and economic fundamental factor; for instance, the money stock, output, interest rate, and inflation of two countries. Engel and West (2006), Molodtsova et al. (2008), and Molodtsova and Papell (2009) emphasize the importance of monetary policy rules and extend the Taylor rule to the models for two countries. They associate domestic and foreign short interest rate differentials with future exchange rate changes. Rossi (2013) is a survey paper of the exchange rate model. Nelson and Siegel (1987) propose the parametric term structure of the interest rate model. However, since the original model was cross-sectional, Diebold and Li (2006) suggest a time-series version of the original model. In this model, called the dynamic Nelson–Siegel model, there are three factors: level, slope, and curvature factors. Svensson (1994) proposes a four-factor Nelson–Siegel model by adding a second curvature factor. The Svensson model is also a cross-sectional model. De Rezende and Ferreira (2013) extend the dynamic Svensson model by adding second slope factor, to the five-factor model. Increasing the number of factors raises the flexibility of in-sample fit, but it causes the over-parameterization problem, as Diebold and Li (2006)1 and De Rezende and Ferreira (2013) argue.
The remainder of the paper is organized as follows. In Section 2, we describe four relative Nelson–Siegel class models: the dynamic relative Nelson–Siegel model, dynamic relative Svensson model, and the relative De Rezende and Ferreira (2013) model. In Section 3, we extract the relative factors from each model. Section 4 shows the results, and Section 5 concludes.
2. Model
2.1. The Present Value Model
In the asset approach, the determination of nominal exchange rate was represented as the model depending on the discounted present value of its expected future fundamentals; for example, differences in monetary variable, output, and inflation. Mussa (1976) and Frankel (1979) show the log–linear relationship between the nominal exchange rate and the fundamentals; Mussa (1976) and Frankel (1979) derive the monetary model of the nominal exchange rate based on the money market equilibrium, uncovered interest rate parity, and purchasing power parity, and the model is represented as:
where is a log nominal exchange rate at a time , is a vector of the fundamentals,2 and denotes a mathematical expectation at time . Solving Equation (1) forward and imposing the appropriate transversality condition based on the information set at time , the nominal exchange rate is written as:
where and are parameters.
Following Chen and Tsang (2013), empirically, the nominal exchange rate was best approximated by a unit root process, so we rewrote Equation (1) in a first-differenced form:
where is an expectation error.
In this paper, we used the information in the yield curves of two cross section countries, U.S. and Japan, to proxy the expected discounted sum on the right-hand side of Equation (3). As the term structure of interest rates includes the information of future economic activity, Chen and Tsang (2013) adopt the factors extracted from the relative Nelson–Siegel model for the fundamental , which we explain shortly.
2.2. The Relative Nelson–Siegel Model
This section explains the three Relative Nelson–Siegel models: the original Chen and Tsang (2013) model, and two extended models.
2.2.1. The Original Chen and Tsang (2013) Model
To explain the Chen and Tsang (2013) model, hereafter abbreviated as the CH model, we first introduced the dynamic Nelson–Siegel model of Diebold and Li (2006) represented as:
where is a zero-coupon yield of -month maturity at time . and are factors, which are often referred to as the level, slope, and curvature factors,3 respectively. The symbol is a decaying parameter. The smaller value corresponds to the slower decay in factor loading.
The CH model that we estimated is a model for domestic and foreign interest rate differential based on the dynamic Nelson–Siegel model, which is represented as:
where the subscript “” denotes the relative factor, where “relative” means that it measures a relative impact appropriate for interest rate differentials between two countries. The subscript ”CH” refers to the CH model.
2.2.2. Extended Model 1: Four-Factor Model Based on Svensson (1994)
The second model that we estimated is a four-factor model based on Svensson (1994), which extends the Nelson–Siegel model to a four-factor model by adding a second curvature factor. The original model of Svensson (1994) is given by:
where the subscript ”SV” refers to the Svensson model, is the first curvature factor and is the second curvature factor.
Our four-factor model based on Svensson (1994), hereafter abbreviated as the SV model, extends the above equation to the context of the interest rate differential, which is represented as:
Compared to Equation (5), the second curvature factor is added in this equation. and are two different decaying parameters.
2.2.3. Extended Model 2: Five-Factor Model Based on De Rezende and Ferreira (2013)
The third model that we considered is based on the five-factor model of De Rezende and Ferreira (2013), which is an extended version of the Svensson (1994) model that has one level factor, two slope factors, and two curvature factors. The model is represented as:
The subscript “FF” denotes the five-factor model. is the first spread factor and is the second spread factor.
The extended model for the domestic and foreign interest rate differential becomes:
which we called the five-factor model, hereafter abbreviated as the FF model. The second slope factor was added to Equation (7) in this equation.
3. Estimation of Decaying Parameter and Relative Factors
In this section, we estimated the decaying parameters in the above model using the method of non-linear least squares. This paper used the yield curve data of U.S. and Japan. We obtained U.S. zero coupon yield data from the U.S. Federal Reserve Data Release, and estimated4 Japanese zero coupon yields from the prevailing interest rate data, which is published by the Ministry of Finance. Exchange rate data of USD/JPY were obtained from the database of the Bank of Japan. The period was from August 1992 to December 2016. We used the yields of 3, 6, 12, 24, 36, 48, 60, 72, 84, 96, 108, and 120 months maturity.
Diebold and Li (2006) and Chen and Tsang (2013) use the parameter value of . According to the former, this value maximizes the curvature factor at 30-month maturity. However, the value is not an optimal value, since they focus on simplicity and convenience, as Diebold and Li (2006) mention; this paper estimates that the optimal parameter minimizes the average of the root mean squared errors (RMSE). In this paper, we initially constrained the range of the value between 0.01 and 0.30, and we constructed the set and the set . Given that , we estimated the unobservable relative Nelson–Siegel factors by using ordinary least square (OLS), and then we searched for the optimal decaying parameter which minimize RMSE as follows:
where and denotes the index of the number of maturities. In the SV model and FF model, there are two decaying parameters and , so we solved the problems as follows:
where in the SV model and in the FF model.
Table 1 shows the estimated optimal parameter. is smaller than in the SV model and the FF model. Figure 1 shows the factor loadings of each relative Nelson–Siegel model in the optimal parameters.

Table 1.
The optimal decaying parameter .
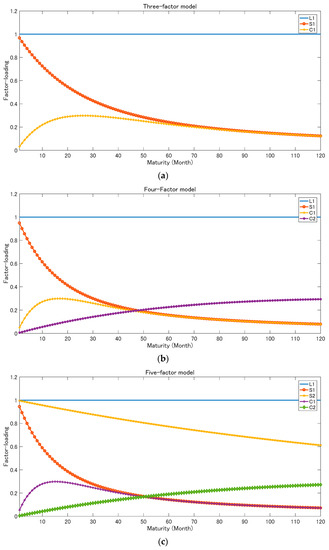
Figure 1.
Factor loadings of each model: (a) Three-factor model; (b) Four-factor model; (c) Five-factor model.
Figure 2 shows the time-series of the estimated unobservable relative Nelson–Siegel factor in each model and Table 2 reports the descriptive statistics of the estimated factors. All of the factors were persistent in one lag. The persistence of the first curvature factor of the SV model and FF model in twelve lags was weaker than the other factors. The mean of the first spread factor was only negative in the factors of each model. The volatility of the second curvature factor was larger than the volatility of the other factors.
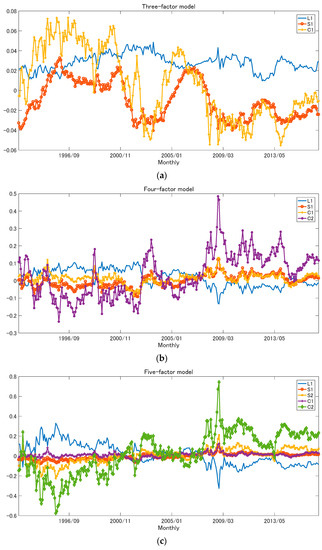
Figure 2.
Estimated factors: (a) Three-factor model; (b) Four-factor model; (c) Five-factor model.

Table 2.
Descriptive statistics of the estimated factors.
4. Modeling and Estimation Results
4.1. Uncovered Interest Rate Parity
We forecast the movement of exchange rate by using the factors affecting the interest rate differential between two countries. The relationship between the exchange rate change and the interest rate differential is specified as follows:
where is a forecast error. Equation (10) is uncovered interest rate parity (UIRP). The previous empirical literature investigates the UIRP regression model:
where denotes the error term.
Substituting the relative dynamic Nelson–Siegel model (for example, CH model in Equation (5)) into the UIRP regression model, we can rewrite the UIRP regression model as:
Defining , , , and , we have the linear regression model of Chen and Tsang (2013) as follows:
This equation is called the CH-UIRP model (or three-factor UIRP model).
We had similar linear regression models for the SV and FF model given by Equations (7) and (9) as follows:
where denotes the error term. Defining , , ,, , and . The former equation was called the SV-UIRP regression model and the latter the FF-UIRP regression model.
4.2. In-Sample-Fit Forecast Estimation
Now, we report the estimation results on the explanatory power of the future exchange rate prediction of our three models.5
The forecasting periods were 3, 6, and 12 months ahead.
Table 3 shows the estimation results of the regression model of Equations (11)–(13). The null hypothesis is . It was clear that the level factor and the spread factors had significant explanatory power for the future exchange rate change predictions of three and six months ahead. Moreover, the SV-UIRP and FF-UIRP regression models improved the re-scaled6 -value, compared to the three-factor model.

Table 3.
Estimation results of the predictability of the relative factors.
We investigated the adjusted of the three UIRP regression models (Equations (11)–(13)). In this analysis, following Chen and Tsang (2013), we generated artificial exchange rate changes using Monte Carlo experiments.7 The procedure was as follows:
- (1)
- We created error terms that affected one-month-ahead exchange rate movement. To do so, we first regressed one-month exchange rate changes on a constant term and kept the standard error of the regression as . Then, a vector of error terms of the mean zero, and the volatility was generated from the standard normal random variable.
- (2)
- We created error terms (m = 3, 6, 12) that generated m-month-ahead exchange rate movements at given time t. As Chen and Tsang (2013) mention, there was a problem with inference bias when we analyzed the longer-horizon predictability using the overlapping data. If we used 3-, 6-, and 12-month exchange rate changes, the variables overlap across observations, and the error term in Equations (11)–(13) became a moving average process of order . To solve this issue of inference bias, we constructed an error term as a moving average, i.e., . The generated data were the same length as the actual data.
- (3)
- We estimated the mean return of m-month-ahead exchange rate movement. To do so, we regressed the actual -month (m = 3, 6, 12) exchange rate changes on a constant and kept the constant term , respectively.
- (4)
- We created the artificial exchange rate changes to be . Then, we estimated the CH-UIRP, SV-UIRP, and FF-UIRP regression model (Equations (11)–(13)) using the artificial exchange rate changes as the dependent variable in rolling regressions for a five-year window.
Trials (1)–(4) were iterated 500 times.
Figure 3 plots the time-series of the adjusted for each 3, 6, and 12 months ahead. The plotted value was the average of the 500 artificial adjusted s. The adjusted- values of the relative factors of the SV model and FF model were superior to the CH model.
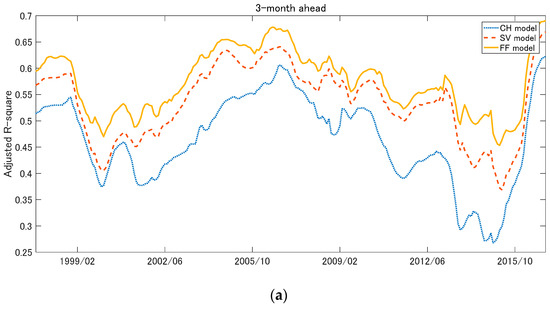
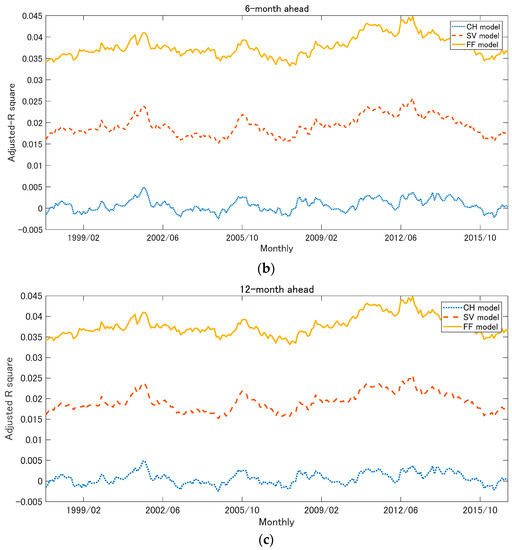
Figure 3.
Adjusted- of the rolling regression for a five-year window: (a) 3-month-ahead; (b) 6-month-ahead; (c) 12-month-ahead.
Table 4 shows the results of -test on the equality of the R-squares. Hypothesis I is that the adjusted of the CH model (ad-(CH)) is equal to the adjusted of the SV model (ad-(SV)). For example, ad-(CH) ad-(SV). The alternative hypothesis is that of the CH model (ad-(CH)) is smaller than ad-(SV). For example, ad-(CH) ad-(SV). This means that the difference is negative. Hypothesis II is that ad-(CH) ad-(FF). Hypothesis III is that ad-(SV) ad-(FF).

Table 4.
Statistical test.
In Table 4, it is clear that the regression model based on FF factors was statistically superior to the model based on CH factors and SV factors, in terms of the adjusted .
4.3. Out-of-Sample Prediction
We investigated the predictability of each model in out-of-sample by comparing root mean squared prediction errors (RMSPE). Chen and Tsang (2013) do not investigate the out-of-sample prediction accuracy of the model. This subsection presents the RMSPE of each model, while the next subsection presents the statistically significant difference by using the Clark and West test.
The RMSPE of the -th model with -month ahead predictions is defined as:
where denotes the last month of the estimation period, and represents the actual exchange rate changes at time , and represents the predicted value of the out-of-sample exchange rate changes at time .
Table 5 shows the RMSPE of each model, and we report the results of 3, 6, and 12.

Table 5.
Root mean square prediction error (RMSPE).
Table 5 provides evidence that the three-, four-, and five-factor models outperformed the random walk model for 3-, 6-, and 12-month-ahead forecasts from comparison of each RMSPE. The CH model was the most superior model for the three-month-ahead prediction, and the FF model was the most superior model for 6- and 12-month-ahead predictions.
4.4. Clark and West Test
We investigated whether the mean squared prediction errors (MSPEs) between two models had statistically significant differences. There are many statistical tests for testing out-of-sample prediction, such as the Diebold and Mariano test (Diebold and Mariano (1995)), the West test (West 1996), and the Clark and West test (Clark and West 2006). The models in this study were the nested model of random walk, following Engel et al. (2007), and we used the Clark and West test proposed by Clark and West (2006). This test investigated whether the MSPEs of two models (Model 1 and Model 2) were equivalent or not. The null hypothesis of the Clark and West test is that MSPEs of Model 1 and MSPEs of Model 2 are equivalent. For example, MSPEs(CH) = MSPEs (SV). The alternative hypothesis is MSPEs of Model 1 is larger than Model 2. For example, MSPEs(CH) > MSPEs (SV).
Table 6 shows the statistic values and -values of the Clark and West test.

Table 6.
Clark and West test for out-of-sample prediction.
As shown in Table 5, the RMSPEs of the CH, SV, and FF models were smaller than one of the random walk models. The null hypothesis was that the MSPEs of the random walk were equal to the MSPEs of the CH (SV, FF) model. In Table 6, each null hypothesis could be rejected at a 1% statistical significance level, so the CH, SV, and FF models were also superior to the random walk model from the perspective of the Clark and West test. For three-month-ahead predictions, although the RMSPE of the CH model was the smallest out of the three models, the Clark and West test could not reject the null hypothesis at statistically significant levels. For the 6- and 12-month-ahead predictions, although the RSMPE of the FF model was the smallest of the three models, the MSPEs of the FF model were statistically equal to the MSPEs of the CH model, from the results of the Clark and West test.
From these results, for the 3-, 6-, and 12-ahead predictions, all of the models outperformed the random walk model and were statistically significant at a 1% significance level. The CH model was the most statistically superior model to the SV and FF models for three-month-ahead predictions. Although the RSMPE of the FF model was the smallest of the three models for 6- and 12-ahead predictions, the MSPEs of the FF model were equal to the MSPEs of the CH model from the perspective of the Clark and West statistical test.
5. Conclusions
In this paper, we constructed a regression model to predict exchange rate changes. Chen and Tsang (2013) analyzed only the three-factor model. This paper extends their three-factor model to four (SV)- and five (FF)-factor models based on Svensson (1994), and De Rezende and Ferreira (2013).
This study provides evidence that SV and FF models improve the re-scaled statistic value of the CH model when we regress the relative Nelson–Siegel factors on exchange rate changes. Moreover, as Chen and Tsang (2013) previously show, the relative spread factors of the SV and FF models are important factors for predicting exchange rate changes.
Using the artificial exchange rate changes based on Monte Carlo experiments, we calculate the adjusted of each model in rolling regression for a five-year window. The analysis shows that the regression model based on the relative factors of the FF model is superior to the other two models. The average of the adjusted of the FF model is largest out of the three models for 3-, 6-, and 12-month-ahead predictions, and it is statistically significant from the perspective of the test.
Finally, this paper investigates the out-of-sample prediction, comparing each RMSPE and the Clark and West statistical test. We employ the random walk model as the benchmark model. The CH model, SV model, and the FF model outperform the random walk model and the results are statistically significant at a 1% significance level. The CH model is the most superior model in the three-month-ahead prediction; on the other hand, the FF model is the most superior model in 6- and 12- month-ahead predictions. Although the CH model is statistically the superior model to the SV and FF models for three-month-ahead predictions, the prediction accuracy of the FF model is not statistically significant for 6- and 12-month-ahead predictions from the perspective of the Clark and West statistical test.
Although we analyze the predictability of the factors of the extended relative Nelson–Siegel models, the models have invariant-time parameters. Recently, numerous studies have focused on the time-varying parameter model. Extending the models in this paper to allow a time-varying parameter model is a task for future research. Moreover, we did not consider the relationship among the factors of the term structure of interest rates, macroeconomic activity, and monetary policy. To extend the models to include a macro finance model is another task for future research.
Acknowledgments
I thank Katsutoshi Shimizu, Takeshi Kobayashi, and two anonymous referees, as well as participants at the 26th Nippon Finance Association Conference for helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Yu-Chin, and Kwok Ping Tsang. 2013. What does the yield curve tell us about exchange rate predictability? Review of Economics and Statistics 95: 185–205. [Google Scholar] [CrossRef]
- Christensen, Jens H. E., Francis X. Diebold, and Glenn D. Rudebusch. 2009. An arbitrage-free generalized Nelson–Siegel term structure model. Econometrics Journal 12: C33–C64. [Google Scholar] [CrossRef]
- Christensen, Jens H. E., Francis X. Diebold, and Glenn D. Rudebusch. 2011. The affine arbitrage-free class of Nelson-Siegel term structure models. Journal of Econometrics 164: 4–20. [Google Scholar] [CrossRef]
- Clark, Todd E., and Kenneth D. West. 2006. Using out-of-sample mean squared prediction errors to test the martingale difference hypothesis. Journal of Econometrics 135: 155–86. [Google Scholar] [CrossRef]
- Cox, John, Jonathan E. Ingersoll Jr., and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica 53: 385–407. [Google Scholar] [CrossRef]
- De Rezende, Rafael B., and Mauro S. Ferreira. 2013. Modeling and forecasting the yield curve by an extended Nelson-Siegel class of models; a quantile autoregression approach. Journal of Forecasting 32: 111–23. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Robert S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 134–44. [Google Scholar]
- Duffie, Darrell, and Rui Kan. 1996. A yield factor model of interest rates. Mathematical Finance 6: 379–406. [Google Scholar] [CrossRef]
- Engel, Charles, and Kenneth D. West. 2006. Taylor rules and the Deutschmark-Dollar real exchange rate. Journal of Money, Credit, and Banking 38: 1175–94. [Google Scholar] [CrossRef]
- Engel, Charles, Nelson C. Mark, and Kenneth D. West. 2007. Exchange rate models are not as bad as you think. NBER Macroeconomics Annual 22: 381–441. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Gikas A. Hardouvelis. 1991. The yield curve as a predictor of real economic activity. Journal of Finance 46: 555–76. [Google Scholar] [CrossRef]
- Estrella, Arturo, and Frederic S. Mishkin. 1998. Predicting U.S. recessions: Financial variables as leading indicators. Review of Economics and Statistics 1: 45–61. [Google Scholar] [CrossRef]
- Frankel, Jeffrey A. 1979. On the mark: a theory of floating exchange rates based on real interest differentials. American Economic Review 69: 610–23. [Google Scholar]
- Litterman, Robert, and Jose Scheinkman. 1991. Common factors affecting bond returns. Journal of Fixed Income 1: 54–61. [Google Scholar] [CrossRef]
- Mark, Nelson C. 1995. Exchange rates and fundamentals: evidence on long-horizon predictability. American Economic Review 85: 201–18. [Google Scholar]
- Molodtsova, Tanya, Alex Nikolsko-Rzhevskyy, and David H. Papell. 2008. Taylor rules with real-time data: A tale of two countries and one exchange rate. Journal of Monetary Economics 55: 63–79. [Google Scholar] [CrossRef]
- Molodtsova, Tanya, and David H. Papell. 2009. Out of-sample exchange rate predictability with Taylor rule fundamentals. Journal of International Economics 77: 167–80. [Google Scholar] [CrossRef]
- Moon, Roger, Antonio Rubia, and Rossen Valkanov. 2004. Long-Horizon Regressions when the Predictor is Slowing Varying. San Diego Working Paper. Oakland, CA, USA: University of California. [Google Scholar]
- Mussa, Michael. 1976. The exchange rate, the balance of payments and monetary and fiscal policy under a regime of controlled floating. Scandinavian Journal of Economics 78: 229–48. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Andrew F. Siegel. 1987. Parsimonious modeling of yield curves. Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Rossi, Barbara. 2013. Exchange rate predictability. Journal of Economic Literature 51: 1063–119. [Google Scholar] [CrossRef]
- Svensson, Lars E. 1994. Estimating and Interpreting Forward Interest Rates: Sweden 1992–1994. NBER Working Paper Series No.4871; Cambridge, CA, USA: National Bureau of Economic Research. [Google Scholar]
- Valkanov, Rossen. 2003. Long-horizon regressions: theoretical results and applications. Journal of Financial Economics 68: 201–32. [Google Scholar] [CrossRef]
- Vasicek, Oldrich. 1977. An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- West, Kenneth D. 1996. Asymptotic inference about predictive ability. Econometrica 64: 1067–84. [Google Scholar] [CrossRef]
| 1 | Christensen et al. (2009, 2011) impose arbitrage-free pricing theory on the dynamic Nelson–Siegel model. |
| 2 | In Mussa (1976), , where is stock money and is output. The subscript “” stands for foreign variable. In Frankel (1979), the paper records . , , and are parameters. |
| 3 | Litterman and Scheinkman (1991) show that the dynamics of the yield curve are explained well by the first three principal components. Moreover, the first, second, and third components are specified as level, slope, and curvature of the yield curve. |
| 4 | We regard the prevailing interest rates published by the Ministry of Finance as the per yields, and estimate the Japanese zero coupon yield from those of the data by using MATLAB financial toolbox and financial instrument toolbox. |
| 5 | These models are the restricted model of . |
| 6 | Following Chen and Tsang (2013), Valkanov (2003), and Moon et al. (2004), we use the rescaled statistic value . |
| 7 | Mark (1995) uses a similar method. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).