Macroeconomic Stability in a Model with Bond Transaction Services
Abstract
:1. Introduction
“Most importantly, in October 2008 the Congress gave the Federal Reserve statutory authority to pay interest on banks’ holdings of reserve balances. By increasing the interest rate on reserves, the Federal Reserve will be able to put significant upward pressure on all short-term interest rates, as banks will not supply short-term funds to the money markets at rates significantly below what they can earn by holding reserves at the Federal Reserve Banks.”
“The authority to pay interest on reserves is likely to be an important component of the future operating framework for monetary policy. For example, one approach is for the Federal Reserve to bracket its target for the federal funds rate with the discount rate above and the interest rate on excess reserves below.”
2. A Model with Bond Transaction Costs
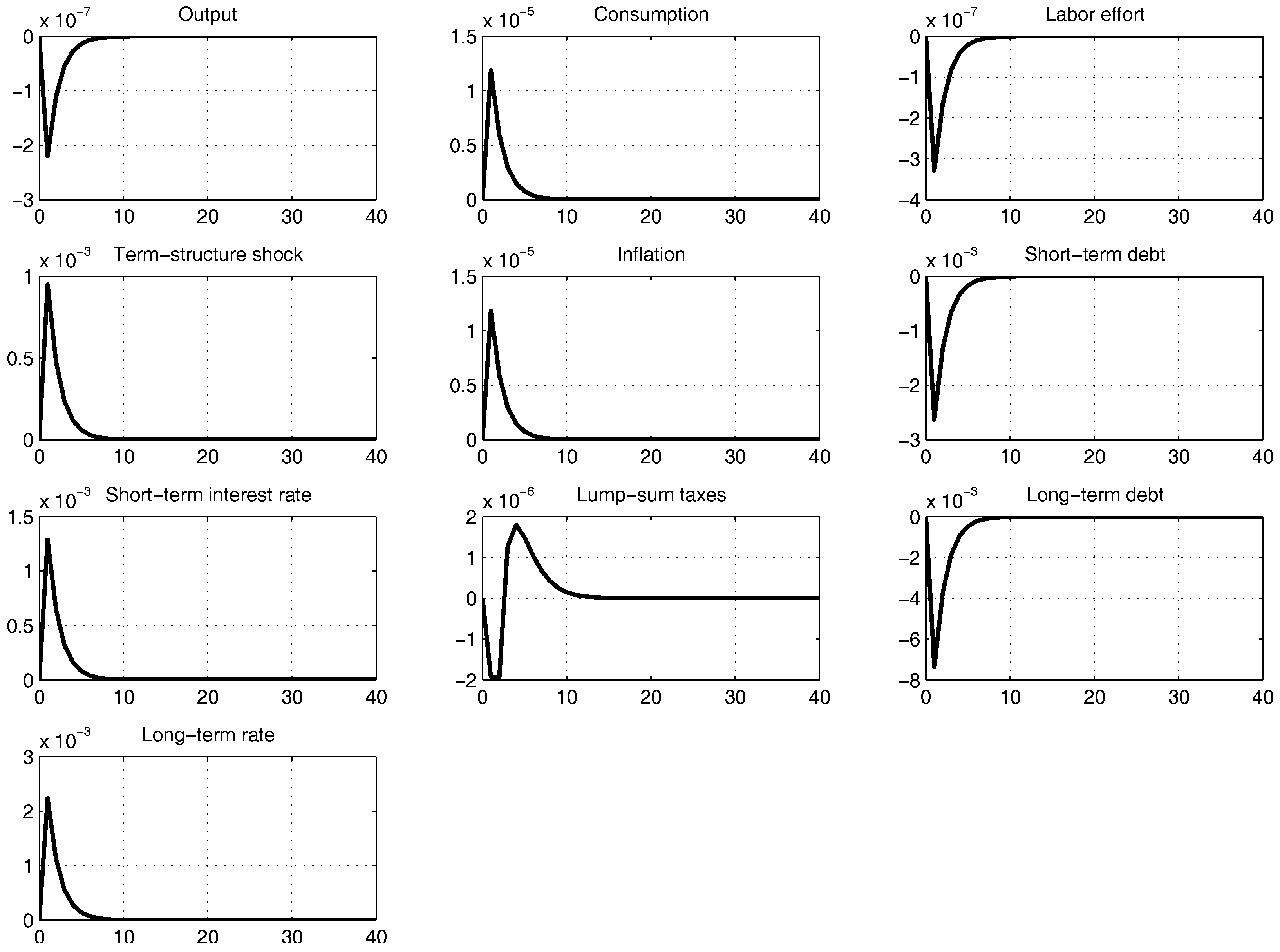
Qualitative Model Properties
3. Determinacy of Rational Expectations Equilibria
3.1. Taylor Rule
3.2. Pure Current-Inflation Targeting
3.3. Expected Inflation Targeting
3.4. Backward Inflation Targeting
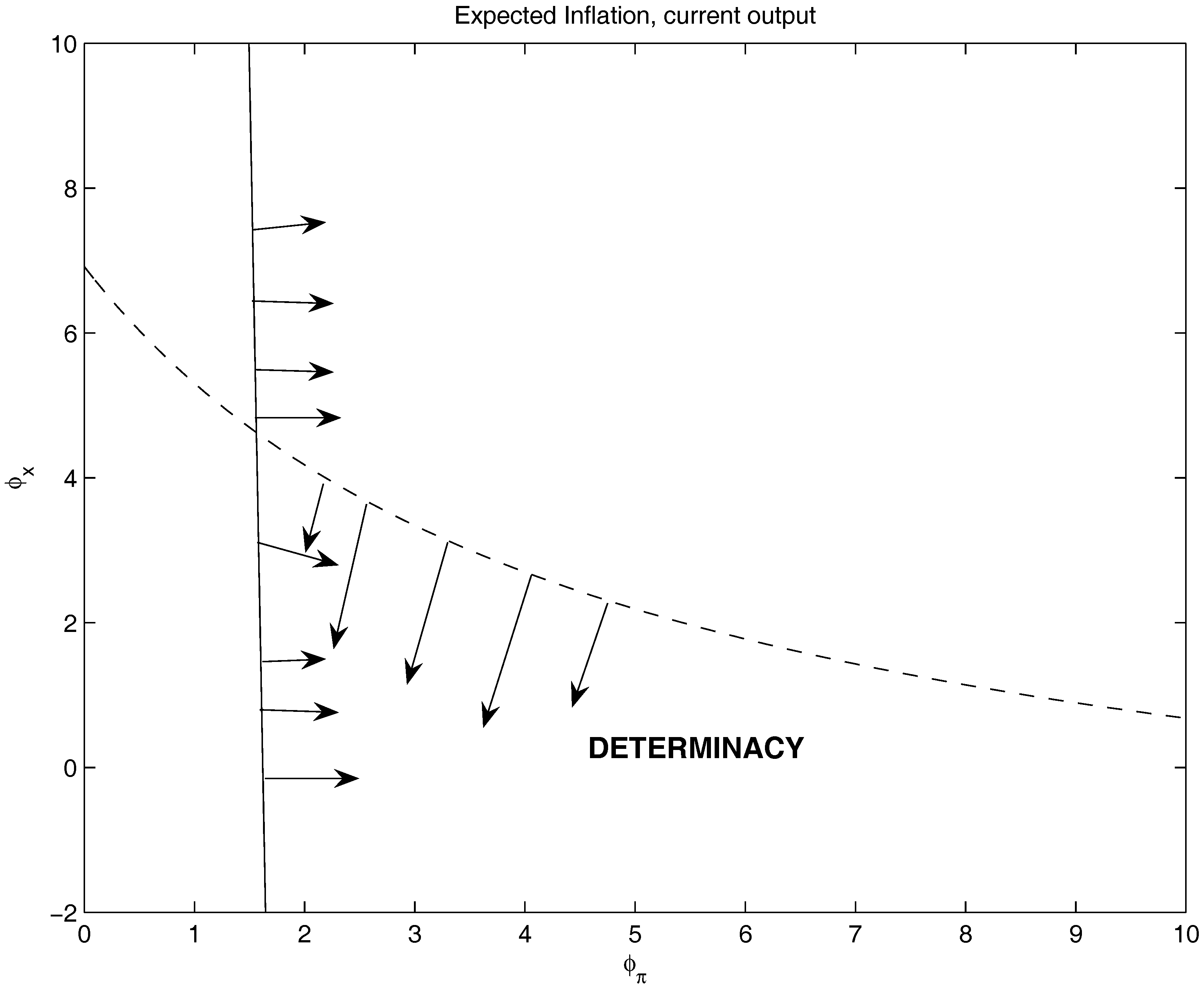
3.5. Expected Inflation and Current Output
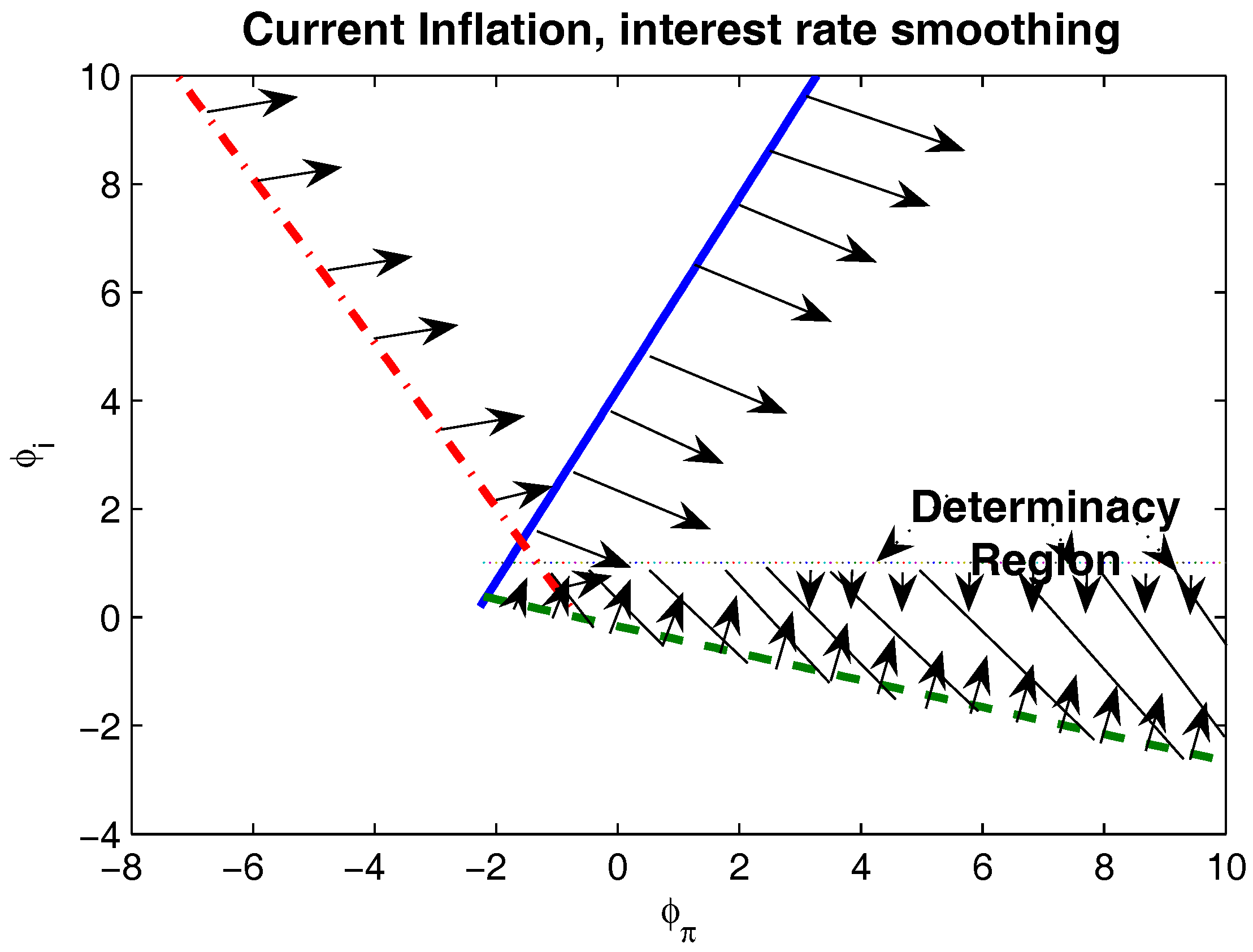
3.6. Interest-Rate Smoothing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. A Further Discussion on Model Structure and Equilibrium Conditions
Appendix A.1. Supply Side
Appendix A.2. Demand Side
Appendix A.3. Some Considerations on the Bond-Velocity Term
Appendix B. The Log-Linearized Model
Appendix C. Coefficients of the Reduced-Form Model
Appendix D. Schur-Cohn Criterion
Appendix D.1. Matrix
Appendix D.2. Matrix
Appendix E. Proof of Proposition 1
Appendix F. Proof of Proposition 2
Appendix G. Proof of Proposition 3
Appendix H. Proof of Proposition 4
Appendix I. Proof of Proposition 6
Appendix J. Proof of Proposition 7
- ; ;
- ;
References
- Aggarwal, Reena, Jennie Bai, and Luc Laeven. 2017. Safe Asset Shortages: Evidence from the European Government Bond Lending Market. Unpublished paper. August. [Google Scholar]
- Bernanke, Ben. 2008. Federal Reserve Policies in the Financial Crisis. Austin: The Greater Austin Chamber of Commerce, December 1. [Google Scholar]
- Bowman, David, Etienne Gagnon, and Mike Leahy. 2010. Interest on Excess Reserves as a Monetary Policy Instrument: The Experience of Foreign Central Banks; International Financial Discussion Paper No. 996; Washington: Federal Reserve Board.
- Canzoneri, Matthew B., and Behzad T. Diba. 2005. Interest Rate Rules and Price Determinacy: The Role of Transactions Services of Bonds. Journal of Monetary Economics 52: 329–43. [Google Scholar] [CrossRef]
- Canzoneri, Matthew B., Robert Cumby, Behzad Diba, and J. David Lopez-Salido. 2008. Monetary and Fiscal Policy Coordination when Bonds Provide Transaction Services. CEPRWorking Paper No. 6814. London, UK. [Google Scholar]
- Canzoneri, Matthew B., Robert Cumby, Behzad Diba, and J. David Lopez-Salido. 2011. The role of liquid government bonds in the great transformation of American monetary policy. Journal of Economic Dynamics and Control 35: 282–94. [Google Scholar] [CrossRef]
- Cochrane, John H. 2014. Monetary Policy with Interest on Reserves. Journal of Economic Dynamics and Control 49: 74–108. [Google Scholar] [CrossRef]
- Clarida, Richard, Jordi Galì, and Mark Gertler. 2000. Monetary Policy Rules and Macroeconomic Stability: Evidence and Some Theory. Quarterly Journal of Economics 115: 147–80. [Google Scholar] [CrossRef]
- Dixit, Avinash K., and Joseph Stiglitz. 1977. Monopolistic Competition and Optimum Product Diversity. American Economic Review 67: 297–308. [Google Scholar]
- Feenstra, Robert C. 1986. Functional Equivalence Between Liquidity Costs and the Utility of Money. Journal of Monetary Economics 17: 271–91. [Google Scholar] [CrossRef]
- Gagnon, Joseph, Matthew Raskin, Julie Remache, and Brian Sack. 2010. Large-Scale Asset Purchases by the Federal Reserve: Did They Work? Federal Reserve Bank of New York Staff Report. No. 441.
- LaSalle, Joseph P. 1986. The Stability and Control of Discrete Processes. New York and Berlin: Springer Verlag. [Google Scholar]
- Leeper, Eric M. 1991. Equilibria Under Active and Passive Monetary and Fiscal Policies. Journal of Monetary Economics 27: 129–47. [Google Scholar] [CrossRef]
- Leeper, Eric M., and Campbell Leith. 2016. Understanding Inflation as a Joint Monetary-Fiscal Phenomenon; NBER Working Papers, No. 21867; Cambridge: National Bureau of Economic Research.
- Rotemberg, Julio J. 1982. Sticky Prices in the United States. Journal of Political Economy 90: 1187–211. [Google Scholar] [CrossRef]
- Rotemberg, Julio J., and Michael Woodford. 1997. An Optimization-Based Econometric Framework for the Evaluation of Monetary Policy. In NBER Macroeconomic Annual. Edited by Ben Bernanke and Michael Woodford. Cambridge: The MIT Press. [Google Scholar]
- Sims, Christopher A. 1994. A Simple Model for Study of the Determination of the Price Level and the Interaction of Monetary and Fiscal Policy. Economic Theory 4: 381–99. [Google Scholar] [CrossRef]
- Taylor, John B. 1993. Discretion versus Policy Rules in Practice. In Carnegie-Rochester Conference Series on Public Policy. Amsterdam: Elsevier, vol. 39, pp. 195–214. [Google Scholar]
- Vayanos, Dimitri, and Jean-Luc Vila. 2009. A Preferred-Habitat Model of the Term Structure of Interest Rates; NBER Working Paper, No. 15487; Cambridge: National Bureau of Economic Research.
- Vayanos, Dimitri, and Jean-Luc Vila. 1999. Equilibrium Interest Rate and Liquidity Premium with Transaction Costs. Economic Theory 13: 509–39. [Google Scholar] [CrossRef]
- Woodford, Michael. 2003. Interest and Prices. Princeton: Princeton University Press. [Google Scholar]
- Woodford, Michael. 2012. Methods of Policy Accommodation at the Interest-Rate Lower Bound. In Federal Reserve Bank of Kansas City Proceedings, Economic Policy Symposium, Jackson Hole; Kansas City: Federal Reserve Bank of Kansas City, pp. 185–288. [Google Scholar]
- Woodford, Michael. 1995. Price Level Determinacy without Control of a Monetary Aggregate. In Carnegie-Rochester Conference Series on Public Policy. Amsterdam: Elsevier, vol. 43, pp. 1–46. [Google Scholar]
- Woodford, Michael. 2001. Fiscal Requirements for Price Stability. Journal of Money, Credit and Banking 33: 669–728. [Google Scholar] [CrossRef]
| 1 | Bowman et al. (2010) discuss the experience of other central banks characterized by policy regimes with interest rates on excess reserves. |
| 2 | This line of reasoning has already been proposed in other strands of literature. For instance, Vayanos and Vila (2009) suggests that there is a class of investors that has preferences over bond maturities, and that interact with arbitrageurs to determine market prices. This interpretation implies that changes to the maturity structure prevailing in the market unveil investor preferences. |
| 3 | Unsurprisingly, this idea is reflected by the transaction-cost approach for modelling non-zero money demand in equilibrium (e.g., see Feenstra 1986). |
| 4 | |
| 5 | |
| 6 | See Leeper and Leith (2016) for a well-organized summary of literature. |
| 7 | Since our aim is to consider the most basic form of the New Keynesian model, we abstract from the role of real capital and investment in this paper. |
| 8 | These properties make the behaviour of Equation (11) quite close to those of a traditional money demand function. |
| 9 | The model features also alternative sources of exogenous shocks to productivity and government spending. We do not discuss the impulse responses from these shocks because our model delivers macroeconomic patterns that are fairly consistent with the literature. On the other hand, a term-structure shock is not often accounted for in available microfounded models. |
| 10 | In the following sections, we make alternative assumptions for the monetary policy rule, which we discuss in greater detail. |
| 11 | An anonymous referee has suggested that the policy changes that have taken place since the beginning of the so-called ‘Great Recession’ in the U.S. could be characterized as time variation in the parameters of the Taylor rule. A similar argument might be proposed with reference to the fiscal-policy rule. We believe that the issue of parameter instability and structural change in policy formation can provide a relevant perspective on the driving forces behind the determination of macroeconomic equilibria. However, we would like to leave this discussion for another contribution. In this contribution, we intend to make a more general point that concerns that assumptions about the macroeconomic role of government bonds. |
| 12 | For the remainder of the paper, all variables are expressed as log-linear deviations from the steady state in the remainder of the paper. |
| 13 | Appendix E shows that the system is obtained by inserting (21) into (A23) and (A24) and rearranging. The terms and do not appear in the reduced-form system because they do not affect the system dynamics. |
| 14 | Appendix G demonstrates that the system is obtained by plugging Equation (35) into (A23), (A24) and (A26). |

| 0.997 | 0.22 | 0.76 | 10 | 0.1 | 8.31 | 0.05 | 0.77 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzo, M.; Zagaglia, P. Macroeconomic Stability in a Model with Bond Transaction Services. Int. J. Financial Stud. 2018, 6, 23. https://doi.org/10.3390/ijfs6010023
Marzo M, Zagaglia P. Macroeconomic Stability in a Model with Bond Transaction Services. International Journal of Financial Studies. 2018; 6(1):23. https://doi.org/10.3390/ijfs6010023
Chicago/Turabian StyleMarzo, Massimiliano, and Paolo Zagaglia. 2018. "Macroeconomic Stability in a Model with Bond Transaction Services" International Journal of Financial Studies 6, no. 1: 23. https://doi.org/10.3390/ijfs6010023
APA StyleMarzo, M., & Zagaglia, P. (2018). Macroeconomic Stability in a Model with Bond Transaction Services. International Journal of Financial Studies, 6(1), 23. https://doi.org/10.3390/ijfs6010023





