Foreign Exchange Speculation: An Event Study

Abstract

Does speculation facilitate price discovery or instability? If it is price discovery, it is beneficial and should be encouraged; if it is instability, welfare is enhanced by its reduction. This paper seeks to distinguish between these two characteristics by analysing those times when speculation in the foreign exchange market is most extreme. A series of event studies are conducted on the extremes of speculative sentiment and speculative activity. If speculation is noise, extreme sentiment and extreme positions should lead to overshooting and increase risk of subsequent reversals. The finding that speculative extremes do not provide information about subsequent returns implies that speculation is part of the process of price discovery and that efforts to reduce it would reduce the informational efficiency of financial markets.

1. Introduction

Speculation can be viewed as stabilising or destabilising. If speculation is informed, it is a stabilising force, providing liquidity and helping to ensure that markets swiftly find equilibrium. Keynes (1930) and Hicks (1946) emphasise the role that speculation plays in facilitating financial market transactions by providing liquidity that allows hedgers and other market participants to swiftly find counterparties without the need for large price concessions. In this version, speculators offer a service for a fee that is determined by the return on their activity. Friedman (1953) argued that even when speculation is a mixture of informed and uninformed, the informed would tend to buy when prices were below intrinsic value and sell when above, making profits, limiting volatility and driving the loss-making uninformed speculators out of business. However, Keynes (1936, p. 101) also had a later, more negative view of speculation. Here he regarded it as a myopic, sentient-driven activity, dominated by the desire to “beat the gun” or “outwit the crowd”. Uninformed speculators may now dominate and De Long et al. (1990) provide a model where speculative noise constrains informed traders from benefiting from their knowledge. Now speculation is an uninformed and destabilising force. We have therefore two concepts of speculation: one that is random and disruptive and one that is informed and beneficial.

The debate about the relative merit of these two concepts of speculation continues. This has been particularly evident in commodities and foreign exchange markets. Pindyck and Rotemberg (1990) find suspicious co-movement of commodities’ prices that they attribute to speculation. There has been much discussion of the role that speculation played in the boom and bust of commodity prices in the period between 2003 and 2007. This is usually called The Masters’ Thesis after Fund Manager Michael Masters testimony to the US Senate Committee on Homeland Security and Government Affairs in May 2008 that linked commodity index investors, rising food and energy prices and the so-called financialisation of commodity markets. Tang and Xiong (2012) suggest that price disruption was exacerbated by newly established commodity indices that increased the amount of speculation in the commodity markets. However, Irwin et al. (2015) dispute this thesis, citing the working of the futures market and the relationship between speculative activity and prices. Jacks (2015) document the long history of speculation being blamed for price volatilities.

Across a range of other financial markets there have been investigations of the link between speculation or noise trading and price misalignments or volatility. Verma and Verma (2007) examine noise trading in equity markets; Yan (2009) argues that speculation is not random and influential in aggregation but that behavioural biases will cause systematic deviations from intrinsic value. Foreign exchange has been a particular focus as a consequence of its liquidity, volatility and the way that speculative attacks appear to have infringed on government sovereignty. See Dornbusch (1988) in general and Eichengreen and Wypolsz (1993) for discussion of the speculative attacks on the European exchange rate system. Eichengreen et al. (1994) use a set of economic data to show that speculative attacks drove European Exchange Rate Mechanism devaluations rather than fundamentals. However, others have made the case that speculation is a key part of the foreign exchange market, providing liquidity and contributing to stability. See Mayer (1985) and Ronals (1986).

There is no consensus and the debate enters policy circles with the suggestion that a tax on financial transactions could reduce speculation and thereby limit misalignment and volatility. Tobin (1978, p. 158) and Tobin (1988) say that such a tax would “throw some sand in the well-greased wheels” of the foreign exchange market. At face value the tax has the advantage of improving market efficiency and raising funds for other welfare-enhancing activity. However, this is only the case if speculation is uninformed and destabilising. If it is informed and contributes to stability, the tax will come at a cost.

The motivation is to contribute to this debate and to specifically make the case that a tax on transactions in the foreign exchange market would not be costless. This paper evaluates the relative importance of these two concepts of speculation by investigating the relationship between the intensity of speculation and the weight of speculative positions relative to subsequent movement of foreign exchange prices. The foreign exchange market is appropriate in this study because it is central to the call for the introduction of a transaction tax as a consequence of it being the largest and most liquid financial market in the world. The latest survey taken by the Bank for International Settlements (BIS) in April 2016 estimated average daily turnover at $5.1 trn with average daily spot transactions of $1.7 trn. See BIS (2016). The cost of trading in this market, when measured in terms of the size of the bid-ask spread, is extremely low. An analysis by Chelley-Steeley and Tsorakidis (2013) of the bid-ask spreads for USD-JPY, GBP-USD and EUR-USD for the period of January 2001 to 2005 finds that the average spread for each is 0.342%, 0.305% and 0.326% respectively. This would be the cost for a round-trip (buying and selling immediately), which makes it relatively attractive for speculators.

The intensity of speculation is measured in two ways: speculative sentiment and speculative positions. Speculative sentiment is identified with the use of option risk-reversal skew. As these become more extreme they signal that expectations of future value in the foreign exchange options market have diverged significantly from the appropriate forward rate. The weight of speculative positions is identified with US regulatory data of the positions held by type of participant in the futures market. Net long and net short are open positions held by speculators relative to total speculator activity or to the total overall activity in the market. See Section 3 for full data details.

The rest of the paper proceeds as follows: Section 2 presents the framework of informed and uninformed speculation; Section 3 talks about the measurement of speculation and the event study method; Section 4 reviews the evidence; Section 5 concludes.

2. Informed and Uninformed Speculation

Speculation plays an important part in several areas of financial economics. However, there is no clear, unambiguous theory of speculation. Speculation is frequently associated with the term trading and the provision of liquidity, but trading is broader as it encompasses financial investment while liquidity provision is really market-making. Speculation and trading can be categorised as being informed or uninformed. Those trading without information are frequently called noise-traders or liquidity traders. The first implies some random quality that flows from the lack of information. However, psychologists find that the cognitive short-cuts or heuristics that are used to make decisions under uncertainty tend to have biases Kahneman and Tversky (1979) and numerous studies purport to find these biases in financial asset prices. For example, De Bondt and Thaler (1985) find evidence that representativeness causes stock prices to overshoot and Coval and Shumway (2005) identifies evidence of behavioural biases among Chicago Board of Trade proprietary traders. Liquidity trades are generally those carrying out transactions for reasons other than value. This can be passive investment funds buying stocks as money that is drawn from investors or hedging activity that does not depend on price. The terms are not fixed and Dow and Gorton (2008, p. 1) categorise noise-traders as all those trading in markets for “non-information-based reasons”. See Ramiah et al. (2015) for a recent review of the noise-trader literature.

Black (1986, p. 529) asserted that the interaction of informed and uninformed activity was essential to the smooth functioning of financial markets. Noise, he argued, was the “the arbitrary element in expectations”. Therefore, noise makes financial markets possible but imperfect: the more noise-traders that there are, the more liquidity and the easier it is to trade; the more noise-traders, the higher the level of inefficiency in the market and the more likely that price will be driven from fundamental value.

Uninformed activity provides a rationale and the opportunity for trading. Unless there is a difference of opinion about value, there is no reason to exchange. Uninformed speculation can create space between price and fundamental value that can be exploited by informed speculators. This space can encourage informed traders to pay the cost of acquiring information in the Grossman and Stiglitz (1980) model. There is equilibrium between the cost of obtaining information and the benefits that are expected to come from the use of the information.

The foreign exchange market is primarily a dealer-orientated market. It is largely consistent with the theoretical microstructure models that have been presented by the likes of Kyle (1985) and Glosten (1985). The interaction of informed and uninformed traders drives the price-discovery process: if the uninformed traders are random, the market-maker earns the bid-ask spread; if informed traders arrive to realise their informational advantage, they cause an inventory imbalance for the market-maker and drive the price towards equilibrium. Therefore, there is a link between information, orders and price.

Lyons (1995), Evans and Lyons (2002) and Rime et al. (2015) show that order flow can explain exchange rate movements much more effectively than fundamentals. The initiating or forcing orders drive the price. Therefore, deliberate speculative activity should drive the price. Speculative sentiment changes and speculative position changes would be part of the price discovery process if informed and would disrupt this process if not. Therefore, if speculators are informed, their activity drives exchange rates towards equilibrium and prices should follow a random walk after these extremes of speculative sentiment or position; if speculators are uninformed and their activity can be regarded as noise, the most extreme speculative sentiment and the time when speculators have the greatest weight in the market should correspond with the greatest deviation of prices from fundamental value, when subsequent price reversals are most likely to take place.

3. Measuring Speculation

There are two steps: identify speculation and assess what happens when it becomes extreme. If speculation is uninformed, extremes should cause a divergence from fundamental value and a price reversal should be anticipated; if informed and part of the price-discovery process, extreme speculation achieves a new equilibrium and the following price performance should be a random walk.

The measurement of speculative sentiment should identify how far speculators believe that the market will move in a particular direction. This study is about short-term movements in foreign exchange prices. The event windows are between one week and four weeks in length. While the interpretation of economic fundamentals can drive prices, market positions and liquidity trades will also be important. Even at longer horizons it is often very difficult to connect exchange rate movements to specific events. Meese and Rogoff (1983) find that forecasts using exchange rate models cannot beat a random walk while Cheung et al. (2005) updated the study to find very similar and more recent results. In the absence of a daily survey of speculators, this study uses a unique series of option risk-reversal skew as a measure of speculative sentiment. The risk-reversal data is very difficult to obtain in an over-the-counter market like foreign exchange where there is no centralised exchange to record and collect information, generally being the property of quoting institutions. The risk-reversals are the average prices quoted at 10:00 GMT by major banks on the Thomson-Reuters composite option pages (OPT1) for the period between 2 January 1996 and 6 September 2002. The risk-reversals are the spread of implied volatility for a one month 25 delta at-the-money call option relative to the equivalent put. Risk-reversal skew is the relative price of currency put and call options for the same strike price. The risk-reversal skew is the relationship between a call option and the equivalent put. Equivalence here being measured by the delta or relationship between movement of the underlying price and the movement of the option price. While the Black and Scholes (1973) model is the basis for valuing options where the price of a non-dividend paying stock trades at a discount to the forward rate equal to the risk free rate, the forward rate in a currency option is determined by the relative interest rate differential between the two currencies. The Garman and Kohlhagan (1983) adjustment that accounts for the difference in interest payments on the two currencies is used. The spot discount is determined therefore by the relative interest rate differential for the appropriate maturity, which is one month in this case. This model allows the market practice of pricing options from the volatility implied by the model. In other words, the Garman-Kohlhagan is used to extract the volatility that is implied by a specific foreign exchange option price given the strike and other parameters. It is usual to quote foreign exchange options in the form of implied volatility.

There is a widespread use of option prices to uncover market expectations. See Malick and Thomas (1997) and Shiue (2001) for the general approach that combines the implied volatility, risk-reversal and strangles to infer a mixed distribution that can be inferred as the risk-neutral probability density function for a particular asset. See Gaati and Malick (2005) an application on the Yen-dollar exchange rate where expectations are affected by central bank intervention. Using the risk-reversal is a simplified version of that where the skew is used to infer positive and expectations relative to the appropriate forward rate. See Eitrheim (1999) and ECB (2003) for previous use implied volatility data for this type of exercise.

If the risk-reversal for a 1-month USD/CAD is quoted at 0.15–0.28% and the implied volatility is 8.50%, the market-maker would be willing to buy the 1-month 25 delta USD-put-CAD-call at 8.65% and sell the USD-call-CAD-put at 8.50%. The dealer pays 0.15%. Alternatively, the dealer would sell a 25 delta call at 8.78% and buy the USD-call-CAD-put at 8.50%, earning 0.28%. See Kapner (2006) for a technical review. Therefore, the relationship between implied volatility for calls and implied volatilities for puts for the same delta and maturity strike is an indication of how much more expensive calls are relative to the equivalent put or as the market bias towards puts over calls and as an indication of market sentiment or related market positioning. The larger the absolute level of the risk-reversal skew, the greater the relative price and, if the deviation is based on information, subsequent price action should be zero on average; if the deviation is based on noise, this movement should be reversed. See Yan (2011) and Feng et al. (2015) for some analysis of implied volatility in the equity market.

Recording speculative activity in an over-the-counter market like foreign exchange is extremely difficult. However, there are some exchange-traded currency derivative markets in the US, and participants in these markets are required to report their positions to the US regulators. The Commodity Futures Trading Commission (CFTC) collects weekly information about the open positions held by private entities in the US derivative markets. A sub-set of this information is released to the public each week as the Commitment of Traders Report (CoT). The CFTC (2012) require traders to categorise themselves as being either commercial (C) or non-commercial (NC). Commercial traders must have some underlying business interest in the security, commodity or instrument that they are trading. These could be seen as natural hedgers. Non-commercial accounts are generally considered to be speculators. The data used run from 30 September 1998 when the data started to be released on a weekly basis and continue up to 31 December 2008. The Euro data runs from 3 March 1998 to 31 December 2008. There are two gaps in the Swiss Franc data for 14 September 2004 and 21 September 2004. The absence of these data seems to be a result of problems with the CFTC database. The contracts are for EUR 100,000; GBP 62,500; JPY 12,500,000; CHF 100,000 and CAD 100,000. Two new series are created from the raw data. These are labelled S1 and S2. S1 measures net non-commercial positions relative to the total non-commercial positions and S2 measures non-commercial positions relative to open interest. See Sanders et al. (2004) and Wang (2004) for examples of previous use of this data to identify speculation.

$$S1=\frac{NCL-NCS}{NCL+NCS+NCSP}$$

(1)

where NCL are the non-commercial long positions (holding non-US currency); NCS and non-commercial short positions and NCSP and the non-commercial spreading positions (spread long and short between different contract maturities). This will measure within the speculative group how biased they are towards holding long or short positions.

$$S2=\frac{NCL-NCS}{OI}$$

(2)

where NCL are the non-commercial long positions (holding non-US currency); OI is the open interest in the contract. This will measure how biased speculators are to holding long or short positions relative to the whole market. As such, S2 is the preferred measure as it picks up not only direction but also the prominence of speculators relative to other agents.

The Event Study

It is common to use series that measure market sentiment or market postitions or even proxies like moving averages as trading-rules that aim to achieve abnormal returns. See for example, Olson (2004), Papailias and Thomakos (2015), Maltz (1996) and De Bock and de Carvalho Filho (2015). It is assumed that the signals will identify times when the market is inefficient. However, in our case there is a direct test of the informational content of extreme speculative sentiment and speculative positions. A special case of the event study method will be used to identify what happens to foreign exchange prices around the time that speculative sentiment or speculative positions are extreme. If speculation is uninformed when speculative sentiment or speculative positions are extremely biased to one direction, there should be the greatest divergence from fundamental value and therefore the greatest risk of reversal; if speculation is informed these extremes are part of the adjustment to a new equilibrium. An event study will analyse the performance of security of asset prices around an event. In this case, the event is the extreme of speculative sentiment or extreme speculative activity.

Dolly (1933) is credited with the original event study method while Fama et al. (1969) developed the method to investigate the reaction of equity prices to news of a stock split. An event study will look at the evolution of asset prices in a window around an event. One of the major challenges in this process is to disentangle the effect of the event from all the other information that is around at that time. This problem is usually addressed in two ways: modelling the expected value of the asset and viewing deviations from the expected value as being influenced by the event; using a large sample that, on the condition that there are no confounding factors at that time, would tend to dilute the effect of other information.

The event is an extreme reading of risk-reversal or speculative positions. The extreme is defined as being either the top or bottom 5th or 1st percentile of all the series. The expected value should be the forward rate but given that we are looking at very short time horizons and interest rates for these currencies are relatively low, it is reasonable to take the expected value as zero and to investigate positive or negative exchange rate return. It is standard practice to call this the abnormal return to signify that it is different from the expected value. Returns are cumulated through the event window and the average recorded to give the cumulative abnormal return for the whole window (CARW) and cumulative abnormal return for after the event (CARA). The number of samples depend on the how the extreme sentiment and positions are defined. As is seen in

Table 1. Event Study: Cumulative Abnormal Returns and Extreme Risk Reversal.

		5th and 95th Percentile							1st and 99th Percentile
		1 Day			4 Day				1 Day			4 Day
		N	CARW	CARA	N	CARW	CARA		N	CARW	CARA	N	CARW	CARA
EUR	Hi	87	0.4103 *	0.1586	87	0.9442 *	0.1505		22	0.0309	−0.1748	22	0.5781 *	−0.5387 *
	Lo	106	−0.3313 *	−0.0933	106	−0.0816 *	−0.1991		21	0.3040	0.1820	21	0.7935 *	0.4377
JPY	Hi	90	0.4860 *	0.1341	90	1.5158 *	0.2531		20	0.8227 *	0.3078 *	20	2.4337 *	0.8284 *
	Lo	90	−0.3168	0.0945	90	−1.3532 *	0.1984		17	−1.6990 *	−0.9347 *	17	−3.6751 *	−1.2556 *
GBP	Hi	96	0.3303 *	0.1903 *	96	0.8966 *	0.2547		21	0.5252 *	0.1774	21	1.3131 *	0.3284
	Lo	97	−0.1894	0.0312	97	− 0.8031 *	0.1500		24	−0.2630	−0.0866	24	−0.6660	0.1888
CHF	Hi	80	0.0065	−0.0565	80	0.5624 *	0.1322		18	−0.0022	−0.1518	18	0.4887	−0.1768
	Lo	75	−0.3716 *	−0.1125	75	−1.0071 *	−0.0219		18	0.0064	0.1704	18	−0.8661 *	0.7631
CAD	Hi	113	−0.0038	−0.0489	113	0.1872	−0.1951		24	−0.1081	−0.0462	24	0.3935 *	−0.1592
	Lo	97	−0.1422 *	−0.0571	97	−0.2896 *	0.0035		26	−0.2008	−0.0146	26	0.1185	0.4560 *
AUD	Hi	101	0.2539 *	0.0125	101	0.8728 *	0.0875		33	0.5099 *	0.0682	33	1.1501 *	0.1046
	Lo	138	−0.4384 *	−0.1711	138	−1.14935 *	−0.2714 *		20	−0.4334	0.0563	20	−1.7360 *	0.1914
EURJPY	Hi	95	−0.0504	−0.1103	95	−0.0128	−0.2579		23	−0.2932	−0.4188 *	23	−0.8203	−1.0195
	Lo	97	−0.4746 *	−0.1647	97	−1.6757 *	−0.4595		20	−1.3630 *	−0.6976 *	20	−3.6849 *	−1.1999 *
EURGBP	Hi	91	0.1544	0.0696	91	0.5176 *	0.0979		28	0.2048	0.1195	28	0.4146	−0.0645
	Lo	122	0.0451	0.0996	122	−0.3097 *	0.2903 *		21	−0.07523	−0.0780	21	−0.4120	0.1290
EURCHF	Hi	77	0.1183 *	0.0690	77	0.3444 *	0.0749		31	0.1482 *	0.0739	31	0.4993 *	0.1816 *
	Lo	94	−0.0344	0.0194	94	−0.1596	0.1952 *		24	−0.3626 *	−0.1483	24	−0.7573 *	0.0875

Where Hi means extreme high in the risk-reversal skew and Lo means extreme low in the risk reversal skew; extreme is calculated as being equal or above the 95th or 99th percentile or equal or below the 5th or 1st percentile respectively; CARW is the cumulative abnormal return for the whole window, before and after the extreme event, and CARA is the cumulative abnormal return for the period after the event, which is the event day and the window; abnormal return is anything that is different from zero; the asterisk denotes significantly different from zero, where statistical significance is more than 95% of 1000 means calculated from random bootstrap samples from the events are above or below zero respectively.

taking the 5th and 95th percentile as the extreme for the risk-reversal skew will give around 100 samples for each exchange rate;

Table 2. Event Study: Cumulative Abnormal Returns and Extreme Speculative Positions.

		S1—Net Long per Speculators							S2—Net Long per Open Positions
		2 Week			4 Week				2 Week			4 Week
		N	CARW	CARA	N	CARW	CARA		N	CARW	CARA	N	CARW	CARA
EUR	Hi	27	2.9415 *	1.3163 *	27	3.8059 *	1.7341 *		27	1.0974 *	0.2896	27	1.7667 *	0.0419
	Lo	27	−2.4258 *	−1.2512 *	27	−3.9235 *	−1.9254 *		27	−2.5122 *	−1.0607 *	27	−4.4478 *	−1.9285 *
JPY	Hi	43	1.9749 *	0.7286 *	43	2.8628 *	0.7909		43	2.2463 *	1.0554 *	43	3.7125 *	1.4443 *
	Lo	43	−2.2014 *	−1.1312 *	43	−3.2488 *	−1.5758 *		43	−2.0605 *	−0.9791 *	43	−2.6865 *	−0.8318
GBP	Hi	43	0.7102	−0.2116	43	1.0172 *	−0.7902 *		43	1.2916 *	0.2370	43	1.6912 *	0.0126
	Lo	43	−0.6979 *	0.2902	43	−1.5330 *	0.1014		43	−1.8993 *	−0.1415	43	−2.8830 *	−0.0768
CHF	Hi	43	1.4400 *	−0.0988	43	2.8665 *	−0.0993		43	2.5260 *	0.5074	43	3.6060 *	0.2158
	Lo	43	−2.1816 *	−0.9770 *	43	−3.3030 *	−0.09798 *		43	−1.2605 *	−0.3070	43	−0.1.6021 *	0.0670
CAD	Hi	43	1.8658 *	1.0195 *	43	3.5298 *	1.8319 *		43	2.0160 *	0.8788 *	43	3.0995 *	0.9921 *
	Lo	43	−1.3238 *	−0.5548 *	43	−1.9151 *	−0.7859 *		43	−1.2462 *	−0.4505 *	43	−1.9390 *	−0.6195 *

Where Hi means extreme high, either S1 which is the measure of net long non-commercial (speculative) positions per total of speculators) or S2 which is the measure of net long non-commercial (speculative) positions per open interest (total outstanding open positions); high and low are above the 95th percentile or below the 5th percentile respectively; CARW is the cumulative abnormal return for the whole window, before and after the extreme event, and CARA is the cumulative abnormal return for the period after the event, which is the event day and the window; abnormal return is anything that is different from zero; the asterisk denotes significantly different from zero, where statistical significance is that more than 95% of 1000 means calculated from random bootstraps from the extreme readings are above or below zero.

shows that the 95th percentile gives just less than 50 samples for the extreme positions. The results do not seem to be sensitive to the definition of extreme. The event windows are between one and four days for the risk-reversal and between two and four weeks for the speculative positions. The results do not depend on the event window.

4. Analysis of Results

Table 1 records the result of the event studies that were carried out on extreme risk reversal. For each exchange rate, the second column distinguishes between extreme high and extreme low risk-reversals, the third column identifies the number of extreme events that were recorded while the following two columns show the cumulative average returns for the whole event window (CARW) and the cumulative average returns for the event and the period after (CARA). The windows were chosen to correspond to one day and one week of trading.

As speculators become more extreme in their opinion, exchange rates are driven in the direction of sentiment. Looking down the seventh column (the 4-day CARW) reveals the average cumulative return for the period from four days before the extreme speculative sentiment to the four days after the event. The extreme highs are those points when the risk-reversal skew is at or above the 95th percentile. For the whole event window (CARW), extreme highs (labelled “Hi”) are associated with positive returns and the extreme lows (labelled “Lo”) are associated with negative returns. In most instances these are significantly different from zero.

That sentiment drives price appears evident from the covariance of speculative sentiment with exchange rate prices. This finding is consistent with the evidence of previous research that has used order-flow or sentiment from the likes of Evans and Lyons (2002), Sanders et al. (2004) and Wang (2004). If speculation is not informed, the extreme is caused by herding or institutional features; if speculation is informed, it is facilitating the absorption of this information into the price.

Does knowledge about the extreme at event time $t=0$ provide information about the future returns? If this speculation is noise, informed traders, such as real money or long-term fundamental accounts, should take advantage of the space that has been created between the price and the fundamental value and a reversal should be seen. Whether this is the case is recorded in columns 5, 8, 11 and 14 of Table 1. A reversal is indicated by a significant negative reading for highs or positive reading for lows. Looking, for example, at the four-day window in column 8, it is clear that the extreme risk reversal skew does not provide any information about future returns. Of the 18 cases using the 5th and 95th percentiles to identify extremely negative and extremely positive sentiment respectively, 10 show a continuation (rather than a reversal) that is not significantly different from zero; one shows a significant continuation; five show reversals that are not significant; only two show significant reversal—EURCHF in each case. For the more extreme event when the 99th percentile is used, there is even less clarity. Just over half the cases with the four-day window show a reversal (8 of 18), but only two of these are statistically significant. The level of statistical significance does not make any difference. Exchange rate prices are as likely to go up as down after an extreme and there does not appear to be any information about the future from knowledge of these extremes. Extremes seem to be followed by a random walk as would be the case if the extreme were the result of information being absorbed into the price. 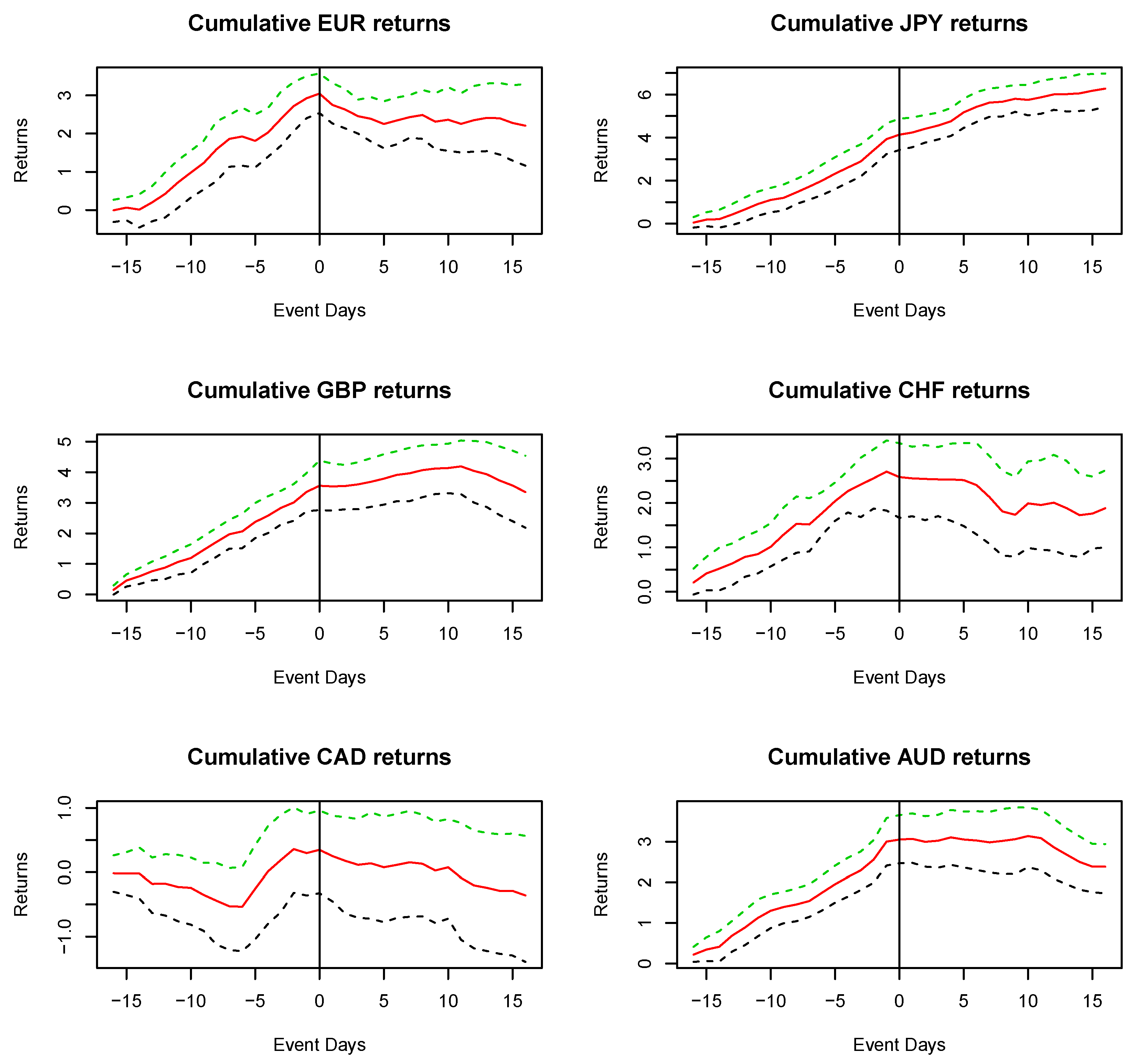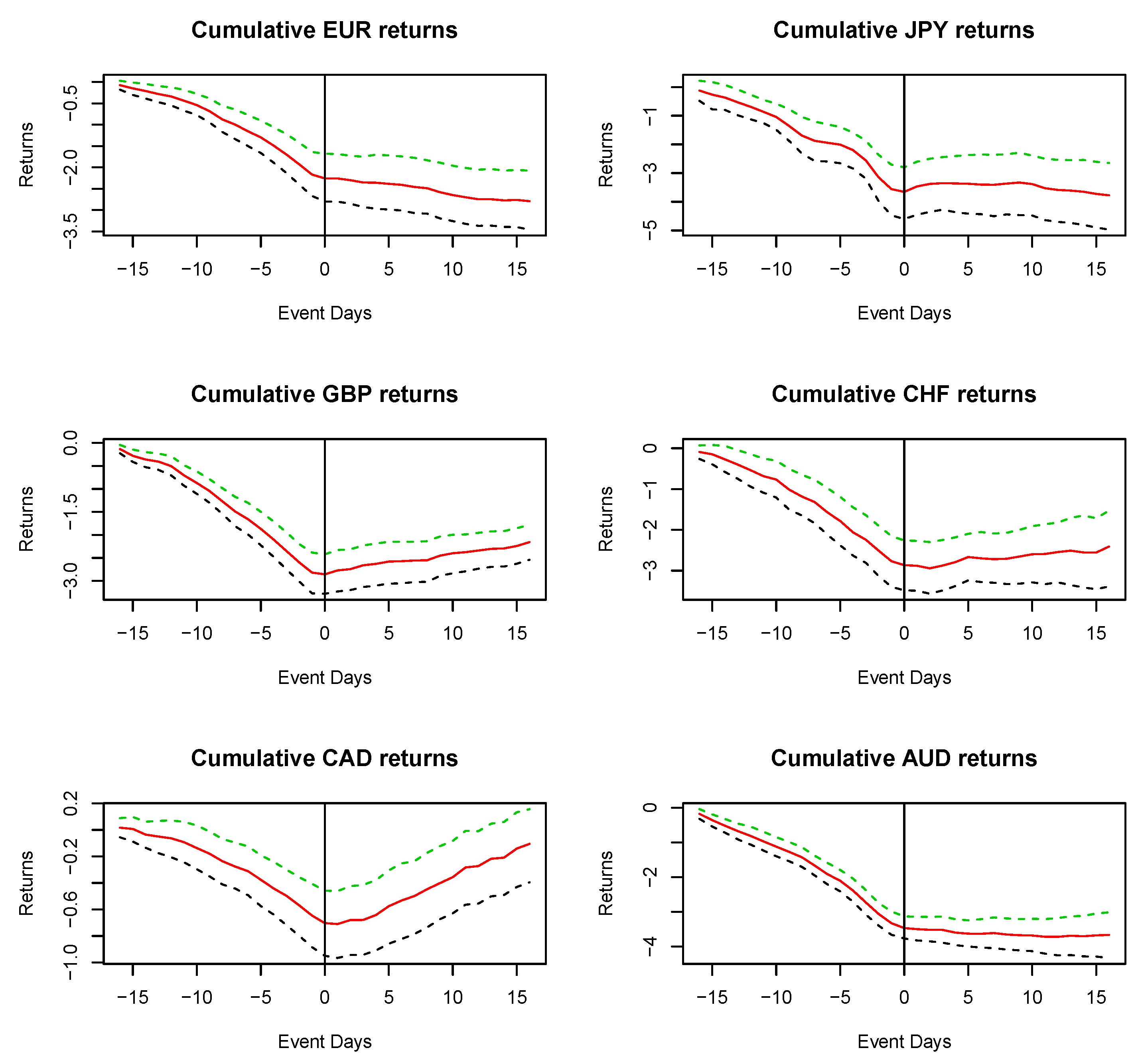Figure 1 and Figure 2 show details of a selection of the event studies. Figure 1 is the extreme high (99th percentile) with a 16 day window. There is no evidence of a reversal in any of the currency units. Figure 2 is the extreme low (10th percentile) with a 16 day event window. Only the CAD shows any evidence of reversal.

Table 2 shows the results from the event studies that were carried out using speculative positions as reported to US regulators. The table works in a similar way to Table 1. The first column is the exchange rate, defined as units per US dollar. The table is then split into two parts. The first part uses the S1 measure, the net non-commercial (speculative) positions relative to total non-commercial (speculative) positions; the second is S2 as the net non-commercial position relative to open interest or the total outstanding open positions. Therefore, the first captures the balance of speculative positions while the second captures the balance of speculative positions relative to the whole market. If speculators become more prevalent or dominant in the market, this will show up in S2 but not in S1. S1 is more sensitive to changes in sentiment and more volatile. Each of these sections is broken into the results for a two week window and a four week window. There is a row for extreme high and extreme low which represents extreme long positions or extreme short positions; the first column identifies the number of cases; CARW is the cumulative abnormal return for the whole event window; CARA is the cumulative abnormal return for the period after the event to the end of the window.

Once again, there is a very strong association between returns and the activity of speculators. For the 4-day window and the S1 and S2 measures, every one of the currencies studied, high and low, had a mean cumulative return for the whole of the event window that was in the same direction as sentiment. When re-sampled 1000 times, more than 95 percent of the means calculated were greater than zero in all cases but one (GBP). There is evidence here of momentum and of prices following the movement of speculator positions. Once again, it appears that orders from speculators drive the price.

There is little evidence that these self-reported speculators are driving prices away from fundamentals with their activity. Sixty percent of the S1 cases still show a significant abnormal return in the direction of the extreme four weeks after the extreme has been reached; only 30 percent of the cases show a reversal and in only one of those do 95 percent of the means calculated after re-sampling remain above zero. For S2 there is even less clarity, with 95 percent of the cases showing a continuation and 40 percent of them showing significant continuation. The evidence here with speculative positions is the same as that of speculative sentiment. Prices move in the direction of speculative activity but speculative extremes do not provide information about the future. The price action of the event study is consistent with speculation being informed rather than uninformed. 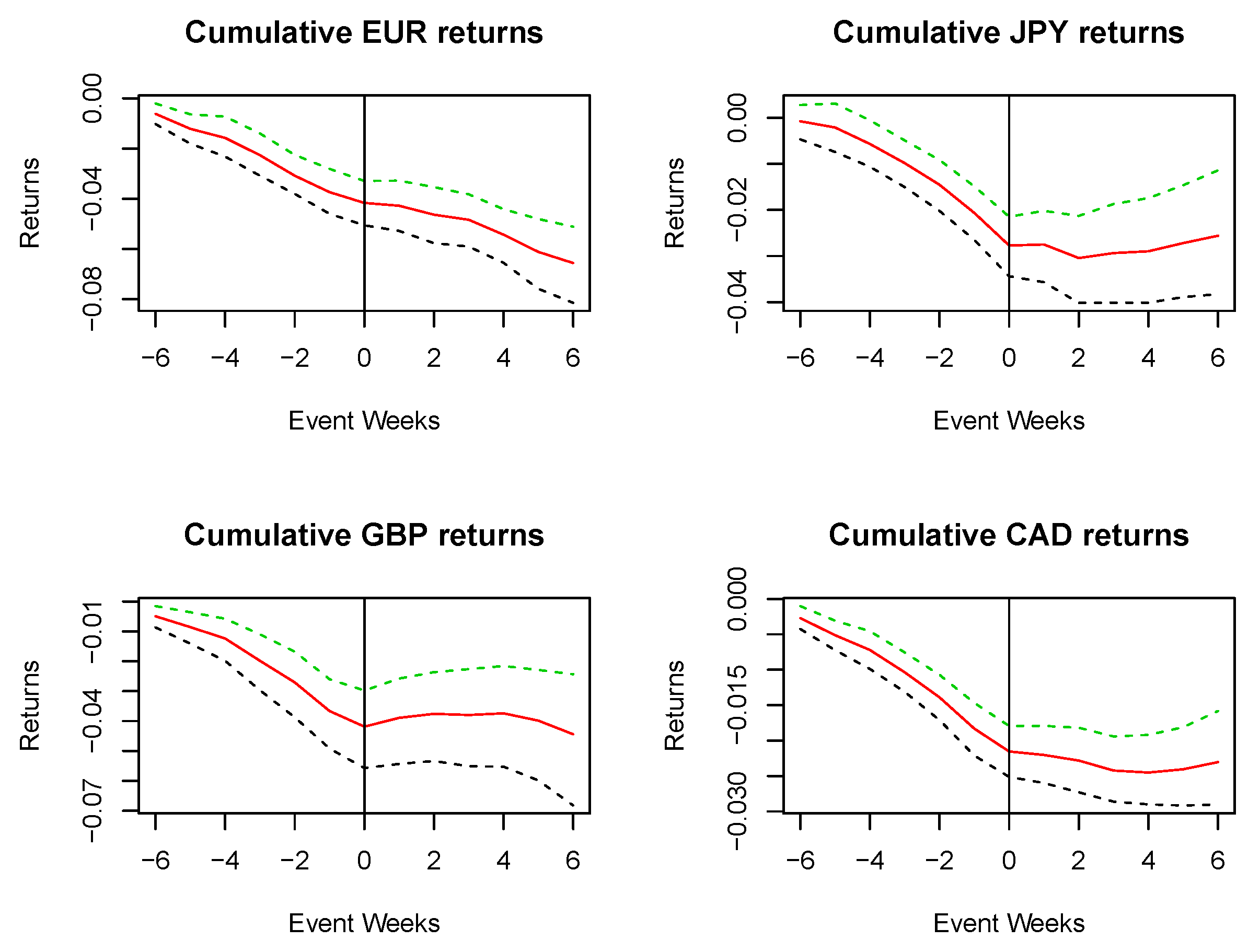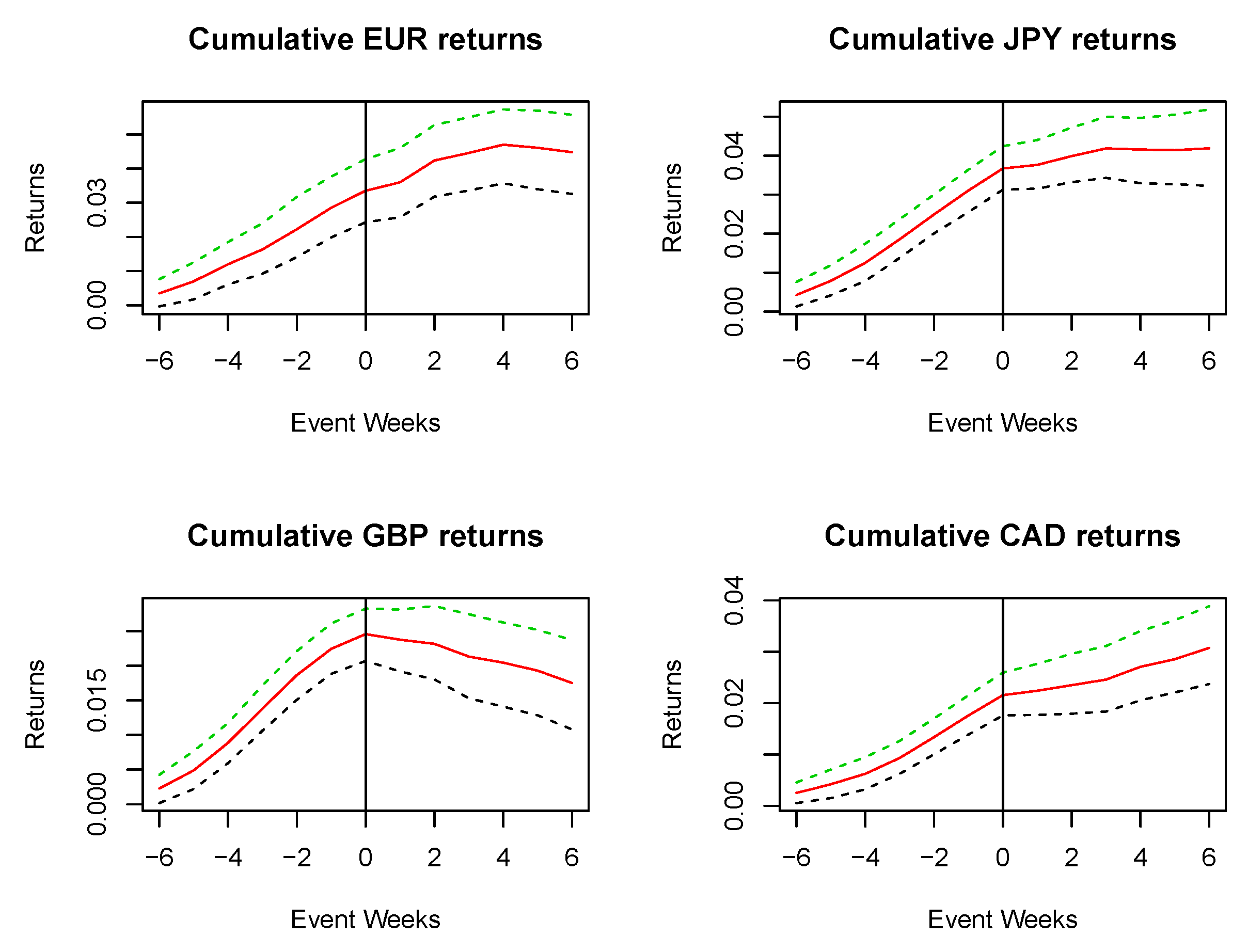Figure 3 and Figure 4 show a selection of event studies that were carried out. Figure 3 is the extreme low (10th percentile) with a 13 week window. There is no evidence of a reversal in any of the currency units. Figure 4 is the extreme high (90th percentile) with a 13 week event window. Only the GBP shows any evidence of reversal. It is not statistically significant.

5. Speculation and Foreign Exchange Returns

If foreign exchange speculation is uninformed noise, extreme speculation, whether measured by sentiment or weight of activity, will coincide with deviations from fundamental value; if speculation is informed, speculation is part of the process of price discovery and extremes will provide no information about future prices. It appears that speculation drives prices towards equilibrium and that speculation is informed. An event study showed that exchange rates move in the direction of speculative sentiment and activity. However, once extreme speculative sentiment or extreme speculative positions are established, prices are as likely to continue as to reverse. The random moves after the extreme is indicative of foreign exchange prices having absorbed available information: the next information and movement is random.

The results do not depend on the design of the event study. The event window and the quantiles that are chosen to measure the extreme can be changed. Alternative measures produced very similar results. Alternative quantiles from 1% and 99% to 20% and 80% have been assessed; Figure 1, Figure 2, Figure 3 and Figure 4 have much wider windows and do not find any alternative to the view that extreme speculation is followed by a random walk.

It is possible to raise some questions about the measures of speculation that are used here, though the fact that two different measures show very similar results for daily and weekly data is encouraging. For example, it may be disputed that there is a link between risk reversal and market sentiment. However, the co-movement of this measure of sentiment with the exchange rate is consistent with the findings of numerous studies that have used actual survey data to measure sentiment and expectations, see for example Frankel and Froot (1987a) and Frankel and Froot (1987b). Nonetheless, future research might try to consider the link between risk-reversals and other measures of expectations. It may also be questioned whether speculative positions in the foreign exchange futures market can be used to understand speculation in the much larger spot market. There are some private sources of information about spot market speculation and future research might try to establish whether they show the same results.

The foreign exchange market has a particular microstructure that is dominated by over-the-counter transactions in the spot market. It is not clear whether these results could be used to make assertions about other markets where there are alternative institutions. Future research might look at risk-reversals in financial markets that are traded on electronic exchanges to see if these results can be replicated. The data on speculative positions are from the exchange traded futures market.