An Econometric Analysis of ETF and ETF Futures in Financial and Energy Markets Using Generated Regressors †
Abstract
1. Introduction
“Fifty-one North American oil-and-gas producers have already filed for bankruptcy since the start of 2015, cases totaling $17.4 billion in cumulative debt, according to law firm Haynes and Boone LLP. That trails the number from September 2008 to December 2009 during the global financial crisis, when there were 62 filings, but is expected to grow: About 175 companies are at high risk of not being able to meet loan covenants, according to Deloitte LLP.”
- (i)
- ETFs offer greater transparency compared with mutual funds in the sense that ETFs are required to reveal their holdings data on a daily basis, whereas mutual funds are mandated only to disclose holdings data on a quarterly basis.
- (ii)
- ETFs are more flexible than mutual funds because investors can short sell them when they are bearish on the market. Although short selling may be considered risky compared with conventional investing, it can be a useful strategy if executed by savvy investors when the market is overvalued.
2. Brief Literature Review
3. Methodology
- (1)
- a brief discussion of the most widely-used univariate conditional volatility model;
- (2)
- the definition of three novel spillover effects;
- (3)
- a discussion of the most widely-used multivariate model of conditional volatility.
3.1. Univariate Conditional Volatility Models
Random coefficient autoregressive process and GARCH
3.2. Multivariate Conditional Volatility Models
3.3. Full and Partial Volatility and Co-Volatility Spillovers
- (1)
- Full volatility spillovers:
- (2)
- Full co-volatility spillovers:
- (3)
- Partial co-volatility spillovers:
3.4. Diagonal and Scalar BEKK
3.5. Triangular, Hadamard and Full BEKK
3.6. Generated Regressors
- (1)
- Financial Select Sector SPDR Fund (XLF);
- (2)
- Generic 1st S&P 500 index futures (SP1); and
- (3)
- Generic 1st FTSE 100 index futures (Z1).
- (1)
- Energy Select Sector SPDR Fund (XLE);
- (2)
- Generic 1st Crude Oil WTI futures (CL1); and
- (3)
- Generic 1st Natural Gas futures (NG1).
4. Data and Variables
 where XLFf is financial ETF futures, XLF is the Financial Select Sector SPDR® Fund, SP1 is Generic 1st S&P 500 index futures, Z1 is Generic 1st FTSE 100 index futures, and t-ratios are shown in parentheses. As stated previously, the t-ratios do not have the standard asymptotic normal distribution as the variables are non-stationary, but the extremely high value of suggests that the generated variable is a useful construction of the latent variable.
where XLFf is financial ETF futures, XLF is the Financial Select Sector SPDR® Fund, SP1 is Generic 1st S&P 500 index futures, Z1 is Generic 1st FTSE 100 index futures, and t-ratios are shown in parentheses. As stated previously, the t-ratios do not have the standard asymptotic normal distribution as the variables are non-stationary, but the extremely high value of suggests that the generated variable is a useful construction of the latent variable.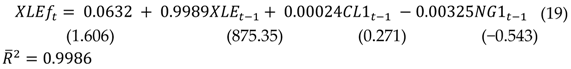 where XLEf is Energy ETF futures, XLE is Energy Select Sector SPDR® Fund, CL1 is Generic 1st Crude Oil WTI futures, NG1 is Generic 1st Natural Gas futures, and t-ratios are shown in parentheses. As stated previously, the t-ratios do not have the standard asymptotic normal distribution as the variables are non-stationary, but the extremely high value of suggests that the generated variable is a useful construction of the latent variable.
where XLEf is Energy ETF futures, XLE is Energy Select Sector SPDR® Fund, CL1 is Generic 1st Crude Oil WTI futures, NG1 is Generic 1st Natural Gas futures, and t-ratios are shown in parentheses. As stated previously, the t-ratios do not have the standard asymptotic normal distribution as the variables are non-stationary, but the extremely high value of suggests that the generated variable is a useful construction of the latent variable.5. Empirical Results for Co-Volatility Spillovers
5.1. Hypothesis Testing of Co-Volatility Spillovers
5.2. Calculating Average Co-Volatility Spillovers

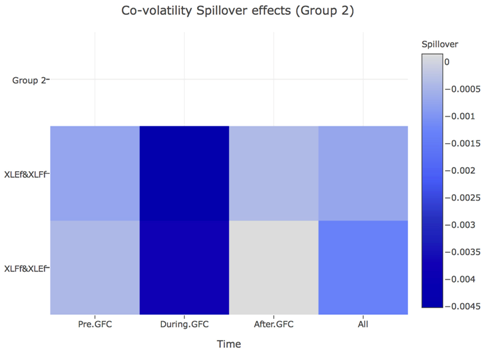


- Asymmetric spillover effects were found in all cases of spot-spot and futures-futures across sectors (see Groups 1 and 2).
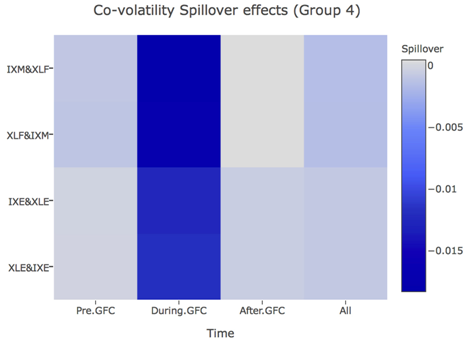
- Symmetric spillover effects were found in all cases of spot-spot between the financial ETF and financial index, as well as between the energy ETF and energy index in all periods (see Group 4).
- Asymmetric spillover effects were found in all cases of spot-futures ETF within sectors. Moreover, in all cases, spillover effects of ETF futures on its co-volatility with the corresponding ETF are stronger than in the reverse case (see Group 5).
- The co-volatility spillovers in all groups over all time periods are statistically significant, except for Cases 3.c.1 to 3.d.2 during-GFC.
- Additionally, with the exception of the insignificant cases, the co-volatility spillovers are stronger during-GFC than for the other time periods (see Groups 1, 2 and 4).
- In terms of the current relationship between the financial and energy sectors, the After-GFC spillovers are of greater relevance than the spillovers of the three sub-periods combined into a single sample.
6. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Baba, Yoshi, Robert F. Engle, Dennis F. Kraft, and Kenneth F. Kroner. 1985. Multivariate Simultaneous Generalized ARCH. San Diego: Department of Economics, University of California. [Google Scholar]
- Baffes, John, M. Ayhan Kose, Franziska Ohnsorge, and Marc Stocker. 2015. The Great Plunge in Oil Prices: Causes, Consequences, and Policy Responses. Policy Rsearch Note. Washongton: World Bank Group. [Google Scholar]
- Bollerslev, Tim. 1986. Generalised Autoregressive Conditional Heteroscedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the Coherence in Short-Run Nominal Exchange Rate: A Multivariate Generalized ARCH Approach. The Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert F. Engle, and Jeffrey M. Wooldridge. 1988. A Capital Asset Pricing Model with Time Varying Covariance. Journal of Political Economy 96: 116–31. [Google Scholar] [CrossRef]
- Chang, Chia-Lin. 2015. Modelling a Latent Daily Tourism Financial Conditions Index. International Review of Economics & Finance 40: 113–26. [Google Scholar]
- Chang, Chia-Lin, and Yu-Pei Ke. 2014. Testing Price Pressure, Information, Feedback Trading, and Smoothing Effects for Energy Exchange Traded Funds. Annals of Financial Economics 9: 1–26. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, and Michael McAleer. 2017a. The correct condition and interpretation of asymmetry in EGARCH. Economics Letters 161: 52–55. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, and Michael McAleer. 2017b. A Simple Test for Causality in Volatility. Econometrics 5: 15. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, Yiying Li, and Michael McAleer. 2015. Volatility Spillovers between Energy and Agricultural Markets: A Critical Appraisal of Theory and Practice. Tinbergen Institute Discussion Papers 15–077/III. Amsterdam: Tinbergen Institute. [Google Scholar]
- Chang, Chia-Lin, Tai-Lin Hsieh, and Michael McAleer. 2016. How are VIX and Stock Index ETF Related? Tinbergen Institute Discussion Paper 16–010/III. Amsterdam and Rotterdam: Tinbergen Institute. [Google Scholar]
- Chang, Chia-Lin, Hui-Kuang Hsu, and Michael McAleer. 2017. A Tourism Financial Conditions Index forTourism Finance. Challenges 8: 23. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, Michael McAleer, and Yu-Ann Wang. 2018. Modelling Volatility Spillovers for Bio-ethanol, Sugarcane and Corn Spot and Futures Prices. Renewable and Sustainable Energy Reviews 81: 1002–18. [Google Scholar] [CrossRef]
- Chen, J. -H., and C. -Y. Huang. 2010. An Analysis of the Spillover Effects of Exchange Traded Funds. Applied Economics 42: 1155–68. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert. 2002. Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Autoregressive Conditional Hereoskedasticity Models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate Simultaneous Generalized ARCH. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Fiebig, Denzil G., Michael McAleer, and Robert Bartels. 1992. Properties of Ordinary Least Squares Estimators in Regression Models with Non-Spherical Disturbances. Journal of Econometrics 54: 321–34. [Google Scholar] [CrossRef]
- Jeantheau, Thierry. 1998. Strong Consistency of Estimators for Multivariate ARCH Models. Econometric Theory 14: 70–86. [Google Scholar] [CrossRef]
- Krause, Timothy, and Yiuman Tse. 2013. Volatility and Return Spillovers in Canadian and U.S. Industry ETFs. International Review of Economics and Finance 25: 244–59. [Google Scholar] [CrossRef]
- Lau, Marco Chi Keung, Samuel A. Vigne, Shixuan Wang, and Larisa Yarovaya. 2017. Return spillovers between white precious metal ETFs: The role of oil, gold, and global equity. International Review of Financial Analysis 52: 316–32. [Google Scholar] [CrossRef]
- Ling, Shiqing, and Michael McAleer. 2003. Asymptotic Theory for a Vector ARMA-GARCH Model. Econometric Theory 19: 278–308. [Google Scholar] [CrossRef]
- Martinet, Guillaume, and Michael McAleer. 2018. On the Invertibility of EGARCH(p,q). Econometric Reviews, 1–26. [Google Scholar] [CrossRef]
- McAleer, Michael. 1992. The Rao-Zyskind Condition, Kruskal’s Theorem and Ordinary Least Squares. Economic Record 68: 65–72. [Google Scholar] [CrossRef]
- McAleer, Michael. 2005. Automated Inference and Learning in Modeling Financial Volatility. Econometric Theory 21: 232–61. [Google Scholar] [CrossRef]
- McAleer, Michael, and Christian M. Hafner. 2014a. A One Line Derivation of DCC: Application of a Vector Random Coefficient Moving Average Process. Tinbergen Institute Discussion Paper. Amsterdam: Tinbergen Institute. [Google Scholar]
- McAleer, Michael, and Christian M. Hafner. 2014. A One Line Derivation of EGARCH. Econometrics 2: 92–97. [Google Scholar] [CrossRef]
- McAleer, Michael, and Colin Ross McKenzie. 1991. When are Two-Step Estimators Efficient? Econometric Reviews 10: 235–52. [Google Scholar] [CrossRef]
- McAleer, Michael, Felix Chan, Suhejla Hoti, and Offer Lieberman. 2008. Generalized Autoregressive Conditional Correlation. Econometric Theory 24: 1554–83. [Google Scholar] [CrossRef]
- McAleer, Michael, Suhejla Hoti, and Felix Chan. 2009. Structure and Asymptotic Theory for Multivariate Asymmetric Conditional Volatility. Econometric Reviews 28: 422–40. [Google Scholar] [CrossRef]
- McAleer, Michael, Juan-Ángel Jiménez-Martín, and Teodosio Pérez-Amaral. 2013. Has the Basel Accord Improved Risk Management During the Global Financial Crisis? North American Journal of Economics and Finance 26: 250–65. [Google Scholar] [CrossRef]
- McLannahan, Ben, and Alistair Gray. 2016. Big U.S. Banks Reveal Oil Price Damage. Financial Times, January 15. [Google Scholar]
- Olson, B., E. Glazer, and M. Jarzemsky. 2016. Coming to the Oil Patch: Bad Loans to Outnumber the Good. The Wall Street Journal. Available online: https://www.wsj.com/articles/coming-to-the-oil-patch-bad-loans-to-outnumber-the-good-1458840050 (accessed on 24 March 2016).
- Sawik, Bartosz. 2008. A Three Stage Lexicographic Approach for Multi-Criteria Portfolio Optimization by Mixed Integer Programming. Przegląd Elektrotechniczny 84: 108–12. [Google Scholar]
- Sawik, Bartosz. 2012a. Bi-Criteria Portfolio Optimization Models with Percentile and Symmetric Risk Measures by Mathematical Programming. Przegląd Elektrotechniczny 88: 176–80. [Google Scholar]
- Sawik, Bartosz. 2012b. Downside Risk Approach for Multi-Objective Portfolio Optimization. In Operations Research Proceedings 2011. Edited by Diethard Klatte, Hans-Jakob Lüthi and Karl Schmedders. Berlin and Heidelberg: Springer-Verlag, pp. 191–96. [Google Scholar]
- Smith, Grant. 2014. U.S. Seen as Biggest Oil Producer after Overtaking Saudi. Bloomberg News, July 4. [Google Scholar]
- Tsay, Ruey S. 1987. Conditional Heteroscedastic Time Series Models. Journal of the American Statistical Association 82: 590–604. [Google Scholar] [CrossRef]
- Tse, Yiu K., and Albert K. C. Tsui. 2002. A Multivariate GARCH Model with Time-Varying Correlations. Journal of Business and Economic Statistics 20: 351–62. [Google Scholar] [CrossRef]
- Van Vactor, S.A. 2009. Financial Crisis Impacts Energy Industry. Oil and Gas Financial Journal. Available online: http://www.ogfj.com/articles/print/volume-6/issue-1/capital-perspectives/financial-crisis-impacts-energy-industry.html (accessed on 1 January 2009).
| Variable Name | Definitions | Exchange | Source |
|---|---|---|---|
| IXM | Financial Select Sector Index | Non-tradable | Bloomberg |
| IXE | Financial Select Sector Index | Non-tradable | Bloomberg |
| XLF | Financial Select Sector SPDR Fund | NYSE | Yahoo Finance |
| XLE | Energy Select Sector SPDR Fund | NYSE | Yahoo Finance |
| XLFf | financial ETF futures | Generated Regressors | |
| XLEf | energy ETF futures | Generated Regressors | |
| Constituents of Financial ETF futures (XLFf) | |||
| XLF | Financial Select Sector SPDR Fund | NYSE | Yahoo Finance |
| SP1 | Generic 1st S&P 500 futures | CME | Bloomberg |
| Z1 | Generic 1st FTSE 100 futures | LIFFE | Bloomberg |
| Constituents of Energy ETF futures (XLEf) | |||
| XLE | Energy Select Sector SPDR Fund | NYSE | Yahoo Finance |
| CL1 | Generic 1st Crude Oil WTI futures | NYMEX | Bloomberg |
| NG1 | Generic 1st Natural Gas futures | NYMEX | Bloomberg |
| Variables | Mean | Maximum | Minimum | Std. Dev. | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Return (%) | ||||||
| IXM_Return | −0.00001 | 7.47123 | −8.09431 | 0.85274 | −0.07166 | 18.32649 |
| IXE_Return | 0.00992 | 7.61806 | −7.51765 | 0.75370 | −0.37323 | 12.69031 |
| XLF_Return | 0.00324 | 11.85519 | −8.28167 | 0.86750 | 0.33284 | 24.25198 |
| XLE_Return | 0.01286 | 6.62314 | −6.77485 | 0.75686 | −0.41494 | 12.02135 |
| XLFf_Return | 0.00329 | 11.83412 | −8.26734 | 0.86482 | 0.33368 | 24.23240 |
| XLEf_Return | 0.01290 | 6.61355 | −6.76537 | 0.75571 | −0.41562 | 12.02699 |
| ADF Test | |||
| Variables | No Trend and Intercept | With Intercept | With Trend and Intercept |
| IXM_Return | −74.8746 * | −74.8663 * | −74.8584 * |
| IXE_Return | −52.3193 * | −52.3291 * | −52.3299 * |
| XLF_Return | −75.4704 * | −75.4632 * | −75.4554 * |
| XLE_Return | −52.2382 * | −52.2581 * | −52.2579 * |
| XLFf_Return | −75.5023 * | −75.4951 * | −75.4872 * |
| XLEf_Return | −52.2497 * | −52.2692 * | −52.2693 * |
| PP Test | |||
| Variables | No Trend and Intercept | with Intercept | with Trend and Intercept |
| IXM_Return | −76.5683 * | −76.5589 * | −76.5513 * |
| IXE_Return | −72.0880 * | −72.1263 * | −72.1402 * |
| XLF_Return | −77.5130 * | −77.5103 * | −77.5032 * |
| XLE_Return | −71.8730 * | −71.9392 * | −71.9946 * |
| XLFf_Return | −77.5604 * | −77.5577 * | −77.5502 * |
| XLEf_Return | −71.9054 * | −72.0151 * | −72.0267 * |
| Group 1: Cross-Sector Spot-Spot | |||||||
| Case | Asset 1 | Asset 2 | A | Before-GFC | During-GFC | After-GFC | All |
| 1.a | IXE | IXM | A1(1,1) | 0.191 * | 0.310 * | 0.225 * | 0.227 * |
| A1(2,2) | 0.262 * | 0.226 * | 0.247 * | 0.253 * | |||
| 1.b | XLE | XLF | A1(1,1) | 0.202 * | 0.290 * | 0.224 * | 0.235 * |
| A1(2,2) | 0.320 * | 0.230 * | 0.244 * | 0.272 * | |||
| 1.c | XLE | IXM | A1(1,1) | 0.192 * | 0.290 * | 0.225 * | 0.227 * |
| A1(2,2) | 0.261 * | 0.227 * | 0.249 * | 0.253 * | |||
| 1.d | IXE | XLF | A1(1,1) | 0.204 * | 0.312 * | 0.224 * | 0.236 * |
| A1(2,2) | 0.323 * | 0.228 * | 0.243 * | 0.273 * | |||
| Group 2: Cross-Sector Futures-Futures | |||||||
| Case | Asset 1 | Asset 2 | A | Before-GFC | During-GFC | After-GFC | All |
| 2.a | XLEf | XLFf | A1(1,1) | 0.202 * | 0.291 * | 0.224 * | 0.234 * |
| A1(2,2) | 0.320 * | 0.230 * | 0.242 * | 0.271 * | |||
| Group 3: Cross-Sector Spot-Futures | |||||||
| Case | Asset 1 | Asset 2 | A | Before-GFC | During-GFC | After-GFC | All |
| 3.a | IXM | XLEf | A1(1,1) | 0.267 * | 0.254 * | 0.301 * | 0.286 * |
| A1(2,2) | 0.178 * | 0.272 * | 0.188 * | 0.191 * | |||
| 3.b | XLF | XLEf | A1(1,1) | 0.352 * | 0.249 * | 0.297 * | 0.337 * |
| A1(2,2) | 0.174 * | 0.275 * | 0.185 * | 0.191 * | |||
| 3.c | IXE | XLFf | A1(1,1) | 0.165 * | 0.313 * | 0.260 * | 0.234 * |
| A1(2,2) | 0.365 * | −0.037 | 0.189 * | 0.251 * | |||
| 3.d | XLE | XLFf | A1(1,1) | 0.161 * | 0.307 * | 0.259 * | 0.233 * |
| A1(2,2) | 0.362 * | −0.041 | 0.187 * | 0.250 * | |||
| Group 4: Within-Sector Spot-Spot | |||||||
| Case | Asset 1 | Asset 2 | A | Before-GFC | During-GFC | After-GFC | All |
| 4.a | IXM | XLF | A1(1,1) | 0.301 * | 0.471 * | 0.313 * | 0.299 * |
| A1(2,2) | 0.299 * | 0.439 * | 0.313 * | 0.300 * | |||
| 4.b | IXE | XLE | A1(1,1) | 0.187 * | 0.408 * | 0.278 * | 0.257 * |
| A1(2,2) | 0.186 * | 0.403 * | 0.271 * | 0.253 * | |||
| Group 5: Within-Sector Spot-Futures | |||||||
| Case | Asset 1 | Asset 2 | A | Before-GFC | During-GFC | After-GFC | All |
| 5.a | IXM | XLFf | A1(1,1) | 0.267 * | 0.272 * | 0.256 * | 0.277 * |
| A1(2,2) | 0.331 * | 0.531 * | 0.373 * | 0.321 * | |||
| 5.b | XLF | XLFf | A1(1,1) | 0.321 * | 0.171 * | 0.296 * | 0.315 * |
| A1(2,2) | 0.306 * | 0.477 * | 0.257 * | 0.291 * | |||
| 5.c | IXE | XLEf | A1(1,1) | 0.211 * | 0.274 * | 0.233 * | 0.228 * |
| A1(2,2) | 0.192 * | 0.609 * | 0.336 * | 0.304 * | |||
| 5.d | IXM | XLEf | A1(1,1) | 0.267 * | 0.254 * | 0.301 * | 0.286 * |
| A1(2,2) | 0.178 * | 0.272 * | 0.188 * | 0.191 * | |||
| Group 1: Cross-Sector Spot-Spot | |||||
| Case | Asset | Before-GFC | During-GFC | After-GFC | All |
| 1.a | IXE | −0.011204 | −0.071687 | −0.008686 | −0.011357 |
| IXM | −0.006777 | −0.072454 | 0.001743 | −0.020297 | |
| 1.b | XLE | −0.011494 | −0.065577 | −0.007675 | −0.011257 |
| XLF | −0.007065 | −0.065807 | 0.002071 | −0.020948 | |
| 1.c | XLE | −0.010616 | −0.062126 | −0.008207 | −0.010482 |
| IXM | −0.006639 | −0.069262 | 0.001767 | −0.019909 | |
| 1.d | IXE | −0.012103 | −0.074886 | −0.008168 | −0.012156 |
| XLF | −0.007285 | −0.069917 | 0.002027 | −0.02138 | |
| Group 2: Cross-Sector Futures-Futures | |||||
| Case | Asset | Before-GFC | During-GFC | After-GFC | All |
| 2.a | XLEf | −0.01166 | −0.067914 | −0.007756 | −0.011694 |
| XLFf | −0.007 | −0.057135 | 0.002322 | −0.021018 | |
| Group 3: Cross-Sector Spot-Futures | |||||
| Case | Asset | Before-GFC | During-GFC | After-GFC | All |
| 3.a | IXM | −0.010596 | −0.08784 | −0.000715 | −0.0222 |
| XLEf | −0.005352 | −0.043396 | −0.009213 | −0.000729 | |
| 3.b | XLE | −0.012874 | −0.091973 | −0.001053 | −0.024498 |
| XLEf | −0.005131 | −0.04453 | −0.008712 | −0.000712 | |
| 3.c | IXE | −0.009224 | −0.071131 | −0.009599 | −0.014442 |
| XLFf | −0.003639 | 0.001534 | 0.006691 | −0.013987 | |
| 3.d | XLE | −0.010088 | −0.064578 | −0.009295 | −0.014803 |
| XLFf | −0.004424 | 0.000471 | 0.006743 | −0.014104 | |
| Group 4: Within-Sector Spot-Spot | |||||
| Case | Asset | Before-GFC | During-GFC | After-GFC | All |
| 4.a | IXM | −0.011165 | −0.08912 | 0.003486 | −0.018308 |
| XLF | −0.012522 | −0.086464 | 0.003553 | −0.01781 | |
| 4.b | IXE | −0.007966 | −0.075882 | −0.007843 | −0.014385 |
| XLE | −0.007481 | −0.072072 | −0.007864 | −0.014581 | |
| Group 5: Within-Sector Spot-Futures | |||||
| Case | Asset | Before-GFC | During-GFC | After-GFC | All |
| 5.a | IXM | −0.010662 | −0.066578 | 0.005485 | −0.020032 |
| XLFf | −0.000539 | 0.001660 | −0.000476 | 4.67E-06 | |
| 5.b | XLF | −0.014975 | −0.045831 | 0.002275 | −0.024073 |
| XLFf | 2.41E-05 | 0.000424 | −6.16E-05 | 1.01E-05 | |
| 5.c | IXE | −0.005847 | −0.064652 | −0.007429 | −0.012769 |
| XLEf | 0.000311 | 0.003213 | −0.000369 | −0.000497 | |
| 5.d | XLE | −0.009237 | −6.82E-06 | −3.66E-08 | −0.016685 |
| XLEf | 1.10E-06 | −2.69E-05 | −3.84E-07 | −6.85E-06 | |
| Group 1: Cross-Sector Spot-Spot Spillover Effects | ||||||
| Case | Asset i | Asset j | Before-GFC | During-GFC | After-GFC | All |
| 1.a.1 | IXE | IXM | −0.000561 | −0.005022 | −0.000483 | −0.000652 |
| 1.a.2 | IXM | IXE | −0.000339 | −0.005076 | 0.000097 | −0.001166 |
| 1.b.1 | XLE | XLF | −0.000743 | −0.004374 | −0.000419 | −0.000720 |
| 1.b.2 | XLF | XLE | −0.000457 | −0.004389 | 0.000113 | −0.001339 |
| 1.c.1 | XLE | IXM | −0.000532 | −0.004090 | −0.000460 | −0.000602 |
| 1.c.2 | IXM | XLE | −0.000333 | −0.004560 | 0.000099 | −0.001143 |
| 1.d.1 | IXE | XLF | −0.000797 | −0.005327 | −0.000445 | −0.000783 |
| 1.d.2 | XLF | IXE | −0.000480 | −0.004974 | 0.000110 | −0.001377 |
| Group 2: Cross-Sector Futures-Futures Spillover Effects | ||||||
| Case | Asset i | Asset j | Before-GFC | During-GFC | After-GFC | All |
| 2.a.1 | XLEf | XLFf | −0.000754 | −0.004545 | −0.000420 | −0.000742 |
| 2.a.2 | XLFf | XLEf | −0.000452 | −0.003824 | 0.000126 | −0.001333 |
| Group 3: Cross-Sector Spot-Futures Spillover Effects | ||||||
| Case | Asset i | Asset j | Before-GFC | During-GFC | After-GFC | All |
| 3.a.1 | IXM | XLEf | −0.000504 | −0.006069 | −0.000040 | −0.001213 |
| 3.a.2 | XLEf | IXM | −0.000254 | −0.002998 | −0.000521 | −0.000040 |
| 3.b.1 | XLF | XLEf | −0.000789 | −0.006298 | −0.000058 | −0.001577 |
| 3.b.2 | XLEf | XLF | −0.000314 | −0.003049 | −0.000479 | −0.000046 |
| 3.c.1 | IXE | XLFf | −0.000556 | Insignificant | −0.000472 | −0.000848 |
| 3.c.2 | XLFf | IXE | −0.000219 | Insignificant | 0.000329 | −0.000822 |
| 3.d.1 | XLE | XLFf | −0.000588 | Insignificant | −0.000450 | −0.000862 |
| 3.d.2 | XLFf | XLE | −0.000258 | Insignificant | 0.000327 | −0.000822 |
| Group 4: Within-Sector Spot-Spot Spillover Effects | ||||||
| Case | Asset i | Asset j | Before-GFC | During-GFC | After-GFC | All |
| 4.a.1 | IXM | XLF | −0.001005 | −0.018427 | 0.000342 | −0.001642 |
| 4.a.2 | XLF | IXM | −0.001127 | −0.017878 | 0.000348 | −0.001598 |
| 4.b.1 | IXE | XLE | −0.000277 | −0.012477 | −0.000591 | −0.000935 |
| 4.b.2 | XLE | IXE | −0.000260 | −0.011850 | −0.000592 | −0.000948 |
| Group 5: Within-Sector Spot-Futures Spillover Effects | ||||||
| Case | Asset i | Asset j | Before-GFC | During-GFC | After-GFC | All |
| 5.a.1 | IXM | XLFf | −0.000942 | −0.009616 | 0.000383 | −0.001781 |
| 5.a.2 | XLFf | IXM | −0.000048 | 0.000240 | −0.000033 | 0.000000 |
| 5.b.1 | XLF | XLFf | −0.001471 | −0.003738 | 0.000173 | −0.002207 |
| 5.b.2 | XLFf | XLF | 0.000002 | 0.000035 | −0.000005 | 0.000001 |
| 5.c.1 | IXE | XLEf | −0.000237 | −0.010788 | −0.000582 | −0.000885 |
| 5.c.2 | XLEf | IXE | 0.000013 | 0.000536 | −0.000029 | −0.000034 |
| 5.d.1 | XLE | XLEf | −0.000615 | −0.000001 | −2.25E-09 | −0.001069 |
| 5.d.2 | XLEf | XLE | 7.32E-08 | −0.000003 | −2.36E-08 | −4.39E-07 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-L.; McAleer, M.; Wang, C.-H. An Econometric Analysis of ETF and ETF Futures in Financial and Energy Markets Using Generated Regressors. Int. J. Financial Stud. 2018, 6, 2. https://doi.org/10.3390/ijfs6010002
Chang C-L, McAleer M, Wang C-H. An Econometric Analysis of ETF and ETF Futures in Financial and Energy Markets Using Generated Regressors. International Journal of Financial Studies. 2018; 6(1):2. https://doi.org/10.3390/ijfs6010002
Chicago/Turabian StyleChang, Chia-Lin, Michael McAleer, and Chien-Hsun Wang. 2018. "An Econometric Analysis of ETF and ETF Futures in Financial and Energy Markets Using Generated Regressors" International Journal of Financial Studies 6, no. 1: 2. https://doi.org/10.3390/ijfs6010002
APA StyleChang, C.-L., McAleer, M., & Wang, C.-H. (2018). An Econometric Analysis of ETF and ETF Futures in Financial and Energy Markets Using Generated Regressors. International Journal of Financial Studies, 6(1), 2. https://doi.org/10.3390/ijfs6010002







