Model Selection Test for the Heavy-Tailed Distributions under Censored Samples with Application in Financial Data
Abstract
:1. Introduction
2. Main Definitions and Assumptions
3. New Model Selection Test (NMST) For HTDC
Decision Rule
- (i)
- If the calculated interval includes zero, it can be concluded that both proposed models ( and ) are equivalent.
- (ii)
- If both bounds of are negative, which indicates that is better than to estimate the true model.
- (iii)
- Finally, if both bounds of are negative, then we conclude that is better than to estimate the true model.
4. Heavy Tail Properties
- i.
- Based on definition 4, if only some or if none of the moments of distributions exist, then it has the heavy tail.
- ii.
- If , then the distribution has the heavy tail. Here, is the hazard function.
- iii.
- If is the decreasing function for increasing value of t, then the distribution has the heavy tail, where .
- iv.
- If the distribution is heavy tail, then . Note that the converse does not hold.
- v.
- The distribution has the heavy tail, if
4.1. Heavy-Tailed Distributions
4.1.1. Generalized Extreme Value Distribution (GEVD)
- Weibull distribution (),
- Ferechet distribution (),
- Gumbel distribution ().
4.1.2. Pareto Distribution
4.1.3. Log-Normal Distribution
4.1.4. Burr Type XII Distribution
4.1.5. Dugum and Singh-Maddala Distribution
5. Application of the NMST of Tehran Stock Exchange
- (1)
- Da (f) and LN (g),
- (2)
- Da (f) and We (g),
- (3)
- We (f) and S-M (g),
- (4)
- Da (f) and S-M (g).
- Scheme 1: (The first 5 pieces of data are not observed).
- Scheme 2: (The first 20 pieces of data are not observed).
- Scheme 3: (The first 60 pieces of data are not observed).
6. Conclusions
Conflicts of Interest
Appendix A
Appendix B
References
- S. Ahna, H.T. Kim Joseph, and V. Ramaswami. “A new class of models for heavy tailed distributions in finance and insurance risk.” Insur. Math. Econ. 51 (2012): 43–52. [Google Scholar] [CrossRef]
- K. Burnecki, A. Wylomanska, and A. Chechkin. “Discriminating between light- and heavy-tailed distributions with limit theorem.” PLoS ONE 10 (2015): e0145604. [Google Scholar] [CrossRef] [PubMed]
- X. Hao, and Q. Tang. “Asymptotic ruin probabilities for a bivariate Leavy-driven risk model with heavy-tailed claims and risky investments.” J. Appl. Probab. 49 (2012): 939–953. [Google Scholar]
- G. Pastor, I. Mora-Jiménez, J. Caamaño Antonio, and R. Jäntti. “Asymptotic expansions for heavy-tailed data.” IEEE Signal Process. Lett. 23 (2016): 444–448. [Google Scholar] [CrossRef]
- O.E. Barndor-Nielsen. “Superposition of Ornstein-Uhlenbeck type processes.” Theory Probab. Appl. 45 (2001): 175–194. [Google Scholar] [CrossRef]
- S.R. Chandra, D. Mukherjee, and I. SenGupta. “PIDE and solution related to pricing of levy driven arithmetic type floating Asian options.” Stoch. Anal. Appl. 33 (2015): 630–652. [Google Scholar] [CrossRef]
- I. Sen Gupta. “Generalized BN-S stochastic volatility model for option pricing.” Int. J. Theor. Appl. Financ. 19 (2016): 1650014. [Google Scholar] [CrossRef]
- O.E. Barndor-Nielsen, and N. Shephard. “Non-Gaussian Ornstein-Uhlenbeck based models and some of their uses in financial economics.” J. R. Stat. Soc. Ser B 63 (2001): 167–241. [Google Scholar] [CrossRef]
- D. Kundu, R.D. Gupta, and A. Manglick. “Discriminating between the log-normal and generalized exponential distribution.” J. Stat. Plan. Inference 127 (2005): 213–227. [Google Scholar] [CrossRef]
- A.K. Dey, and D. Kundu. “Discriminating among the Log-Normal, Weibull and Generalized Exponential distributions.” IEEE Trans. Reliab. 58 (2009): 416–424. [Google Scholar] [CrossRef]
- D.R. Cox. “Test of Separate Families of Hypothesis.” In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Statistical Laboratory of the University of California, Berkeley, CA, USA, 20 June–30 July 1960; pp. 105–123.
- Q.H. Vuong. “Likelihood ratio tests for model selection and non-nested hypothesis.” Econometrica 57 (1989): 307–333. [Google Scholar] [CrossRef]
- Q.H. Vuong, and W. Wang. “Minimum chi-square estimation and tests for model selection.” J. Econom. 56 (1993): 141–168. [Google Scholar] [CrossRef]
- D. Commenges, B. Liquet, and C. Proust-Lima. “Choice of prognostic estimators in joint models by estimating differences of expected conditional Kullback-Leibler risks.” Biometrics 68 (2012): 380–387. [Google Scholar] [CrossRef] [PubMed]
- H. Panahi, and S. Asadi. “A model selection test with application to the censored data of carbon nanotubes coating.” Prog. Color Colorants Coat. 9 (2016): 17–28. [Google Scholar]
- H. Panahi, and A. Sayyareh. “Parameter estimation and prediction of order statistics for the Burr Type XII distribution with Type II censoring.” J. Appl. Stat. 41 (2014): 215–232. [Google Scholar] [CrossRef]
- H. Panahi, and A. Sayyareh. “Estimation and prediction for a unified hybrid-censored Burr Type XII distribution.” J. Stat. Comput. Simul. 86 (2016): 55–73. [Google Scholar] [CrossRef]
- H. Panahi, and A. Sayyareh. “Tracking interval for type II hybrid censoring scheme.” JIRSS 13 (2014): 187–208. [Google Scholar]
- K.C. Cain, S.D. Harlow, R.J. Little, B. Nan, M. Yosef, J.R. Taffe, and M.R. Elliott. “Bias due to left truncation and left censoring in longitudinal studies of developmental and disease processes.” Am. J. Epidemiol. 25 (2011): 1–7. [Google Scholar] [CrossRef] [PubMed]
- S. Mitra, and D. Kundu. “Analysis of left censored data from the generalized exponential distribution.” J. Stat. Comput. Simul. 78 (2008): 669–679. [Google Scholar] [CrossRef]
- U. Singh, and A. Kumar. “Bayesian estimation of the exponential parameter under a multiply type-II Censoring scheme.” Aust. J. Stat. 36 (2007): 227–238. [Google Scholar]
- E.M. Thompson, J.B. Hewlett, L.G. Baise, and R.M. Voge. “The Gumbel hypothesis test for left censored observations using regional earthquake records as an example.” Nat. Hazards Earth Syst. Sci. 11 (2011): 115–126. [Google Scholar] [CrossRef] [Green Version]
- T.A. Louis. “Finding the observed information matrix when using the EM algorithm.” J. R. Stat. Soc. Ser. B 44 (1982): 226–233. [Google Scholar]
- I.W. Burr. “Cumulative frequency functions.” Ann. Math. Stat. 13 (1942): 215–232. [Google Scholar] [CrossRef]
- H. Panahi, and A. Sayyareh. “Tracking interval for doubly censored data with application of plasma droplet spread samples.” J. Stat. Res. Iran 11 (2015): 147–176. [Google Scholar] [CrossRef]
- H. Cramér. Mathematical Methods of Statistics. Princeton, NJ, USA: Princeton University Press, 1946. [Google Scholar]
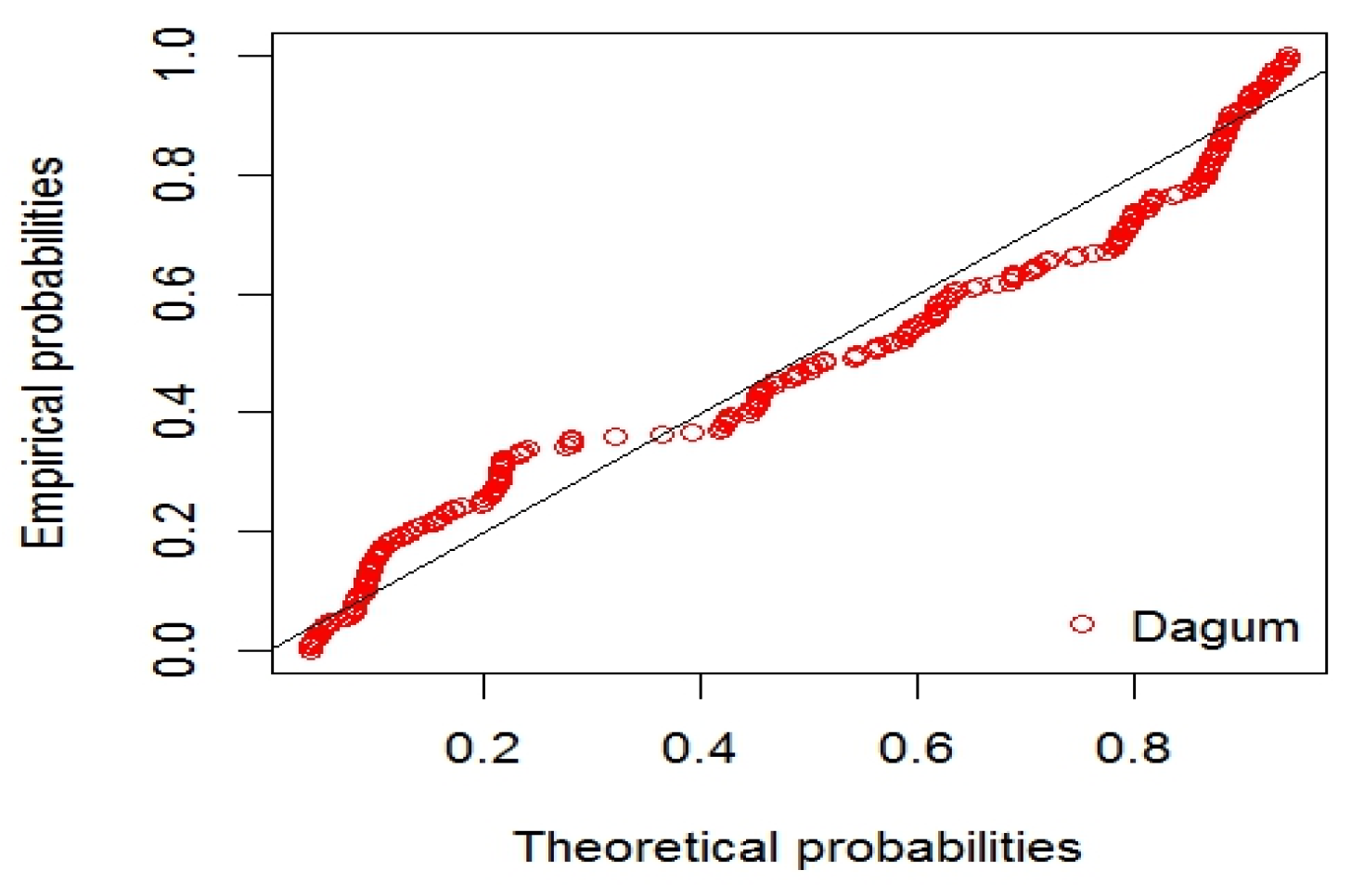
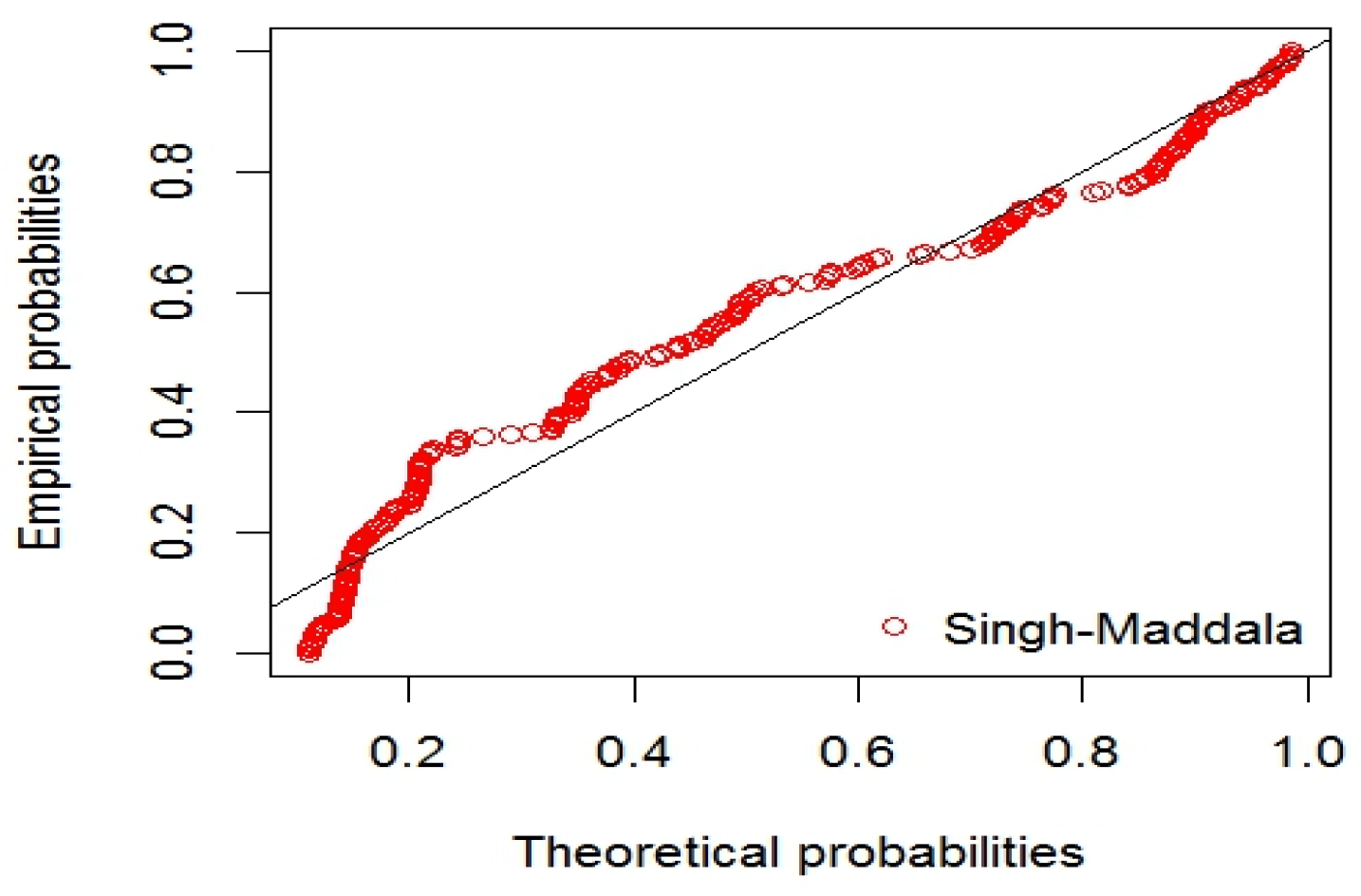
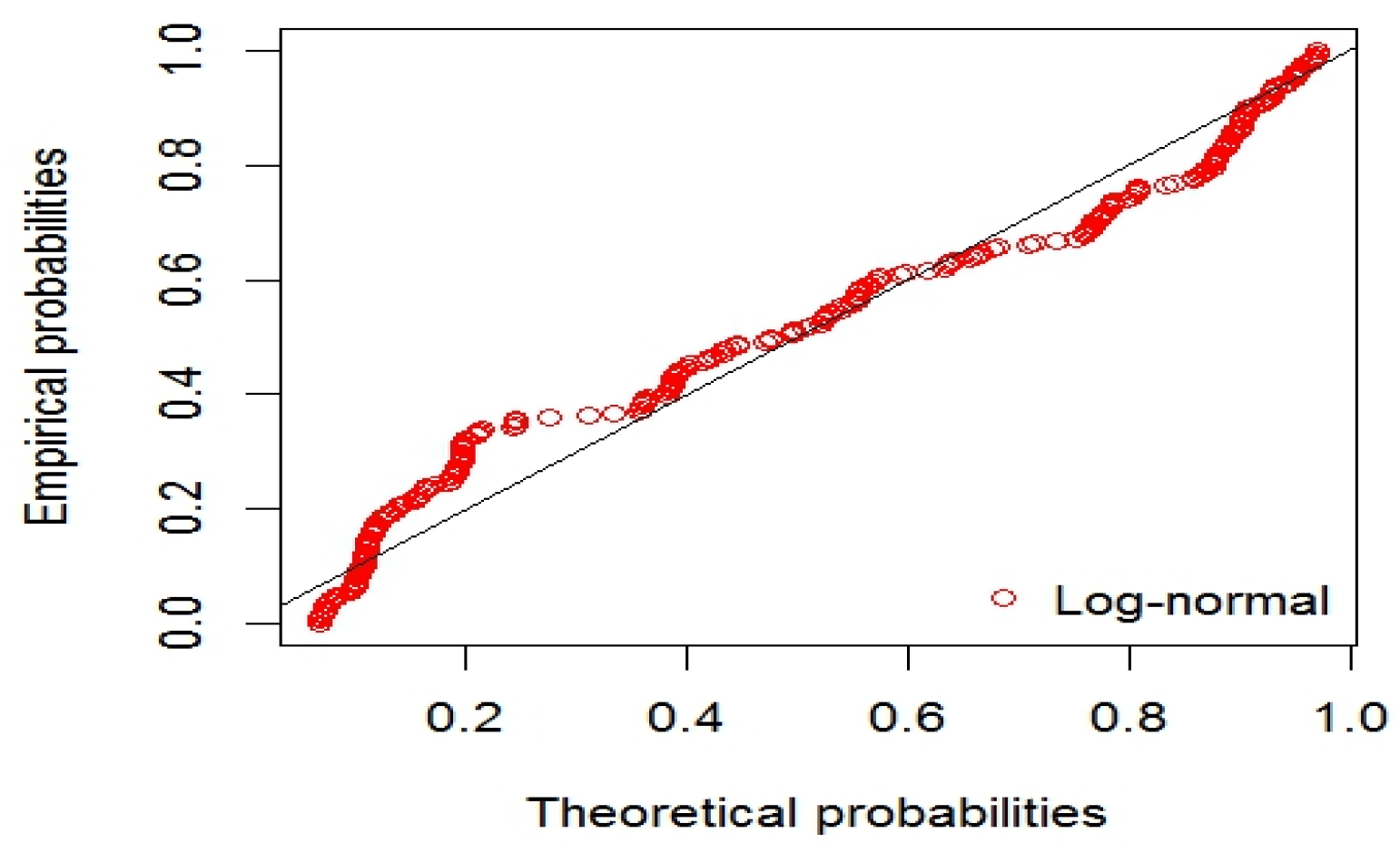
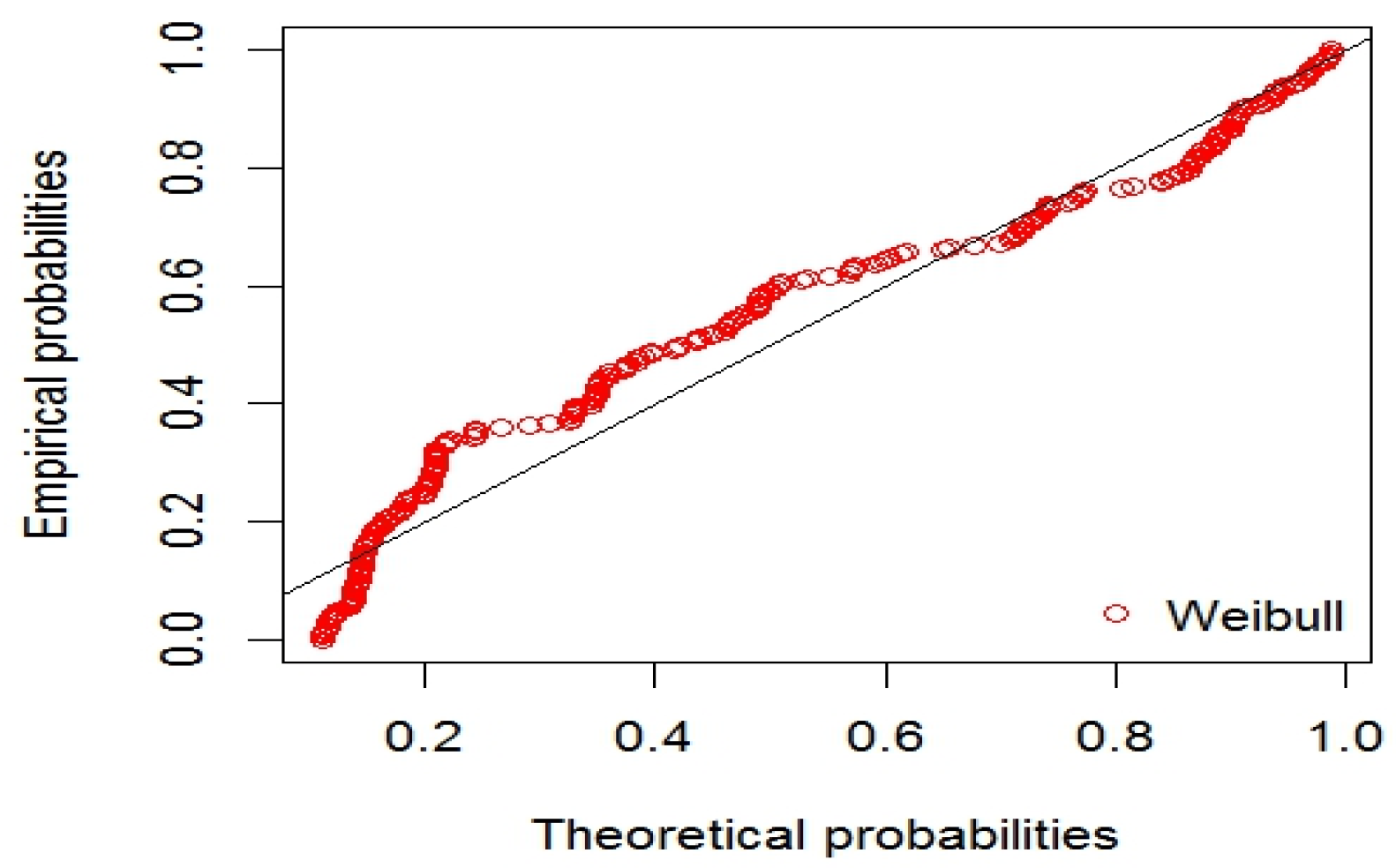
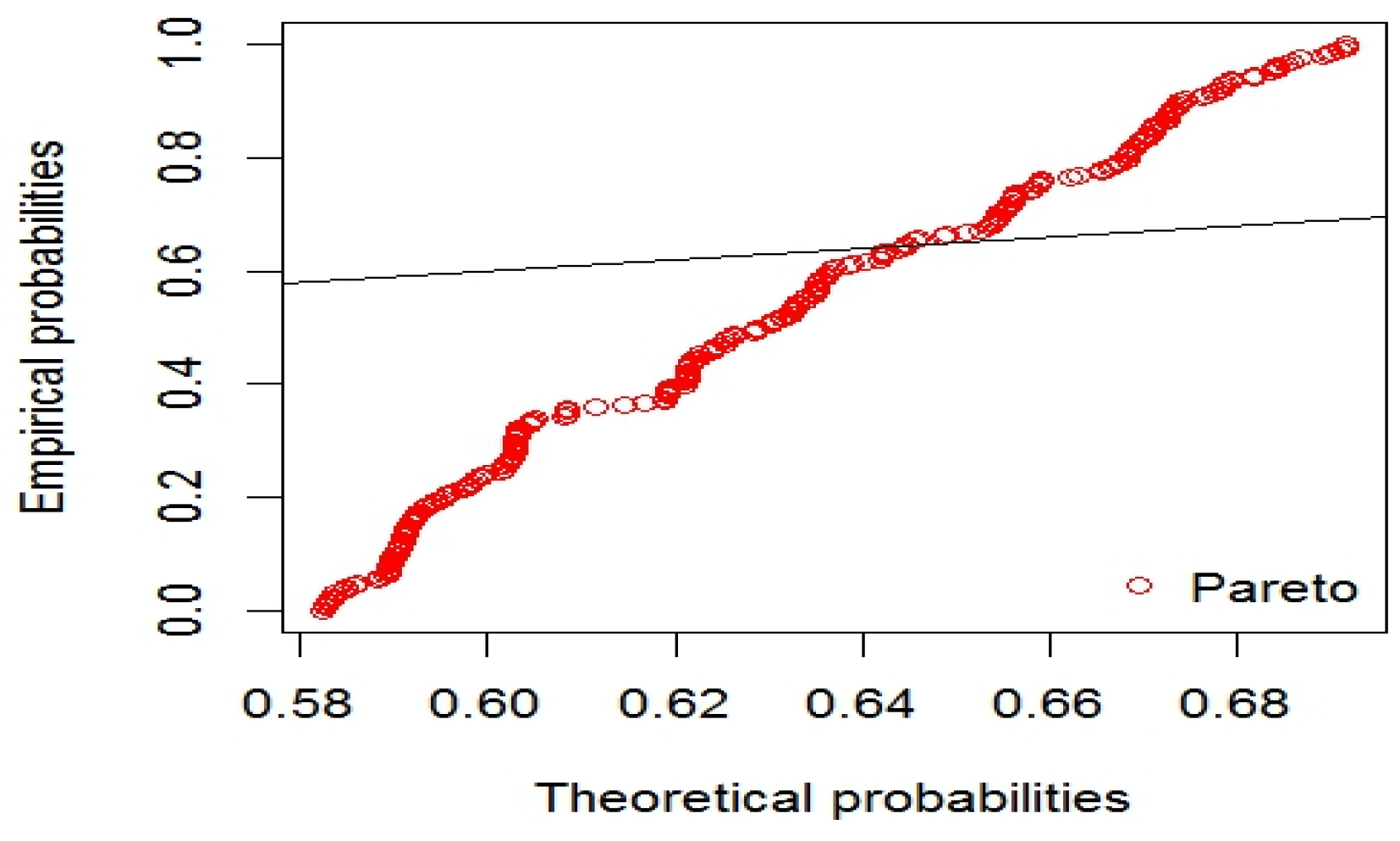
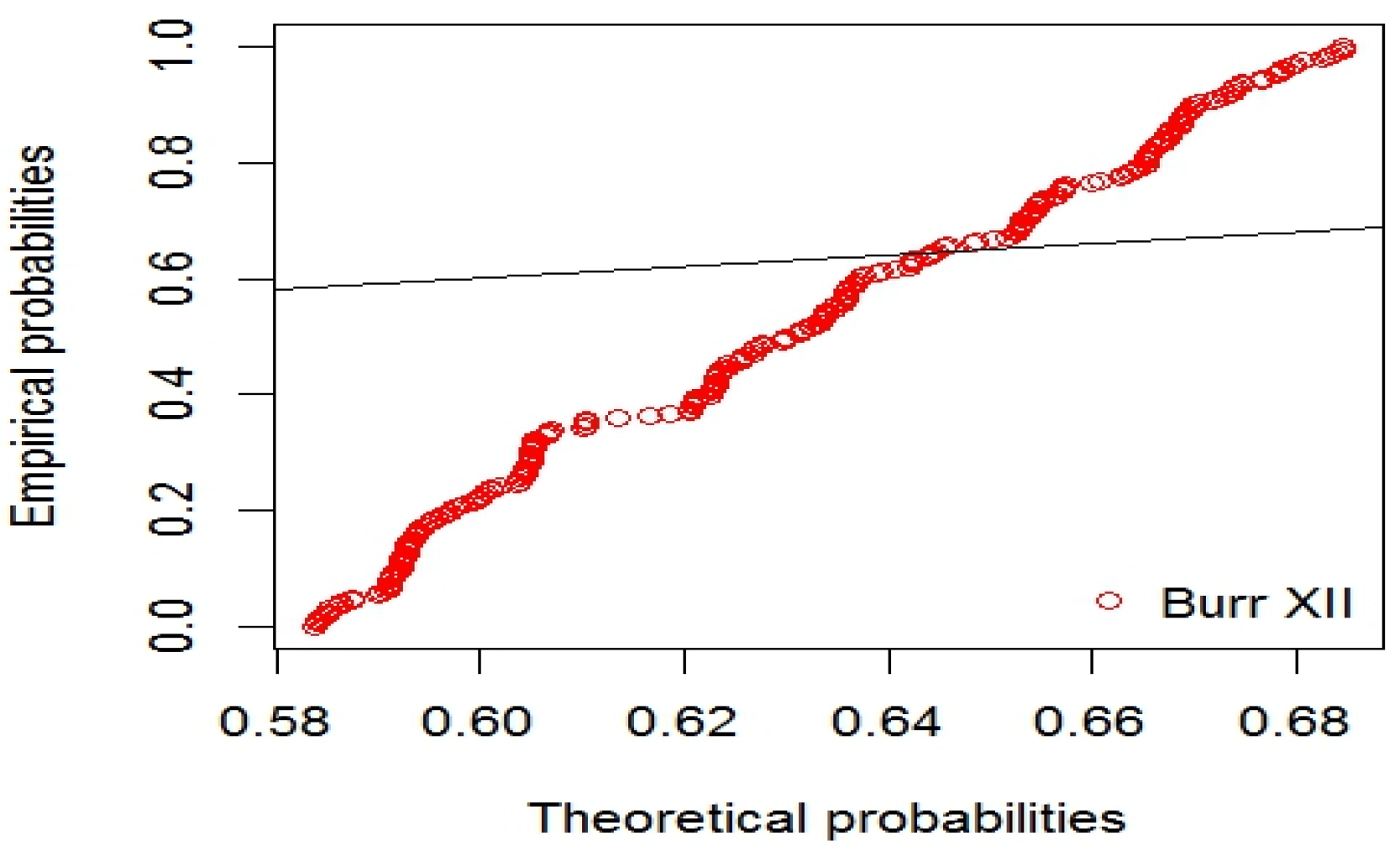
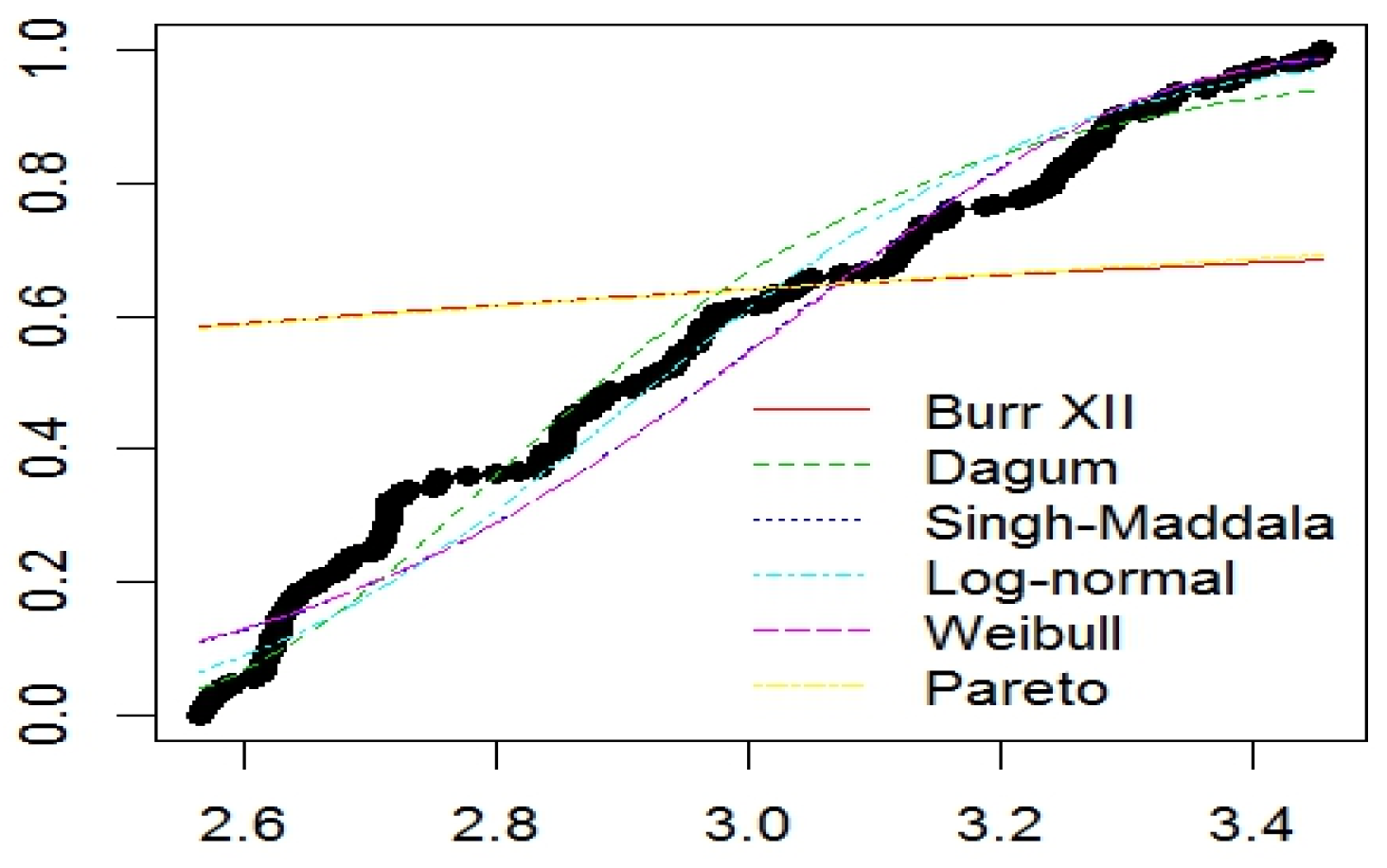
| S-W | K-S | A-D | J-B | |
|---|---|---|---|---|
| Value of test | 0.4659 | 0.2957 | 6.0576 | 953.5819 |
| p-value | 9.605 × 10−11 | 2.493 × 10−9 | 3.471 × 10−15 | <2.2 × 10−16 |
| Models | Parameters | MLE | AIC | BIC | LL |
|---|---|---|---|---|---|
| We | 12.07339 | 64.83431 | 71.86922 | −30.41716 | |
| 3.059887 | |||||
| Pa | 5037634 | 1038.656 | 1045.691 | −517.3281 | |
| k | 1715197 | ||||
| BXII | 0.071667 | 1072.124 | 1079.159 | −534.0619 | |
| 12.98343 | |||||
| LN | mean | 1.073703 | 36.6373 | 43.67221 | −16.31865 |
| s.d. | 0.088294 | ||||
| Da | 13.39737 | 36.8876 | 47.43996 | −17.4438 | |
| 2.142820 | |||||
| 37.14274 | |||||
| S-M | 12.22984 | 66.50122 | 77.05358 | −30.25061 | |
| 4.134818 | |||||
| 40.52715 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panahi, H. Model Selection Test for the Heavy-Tailed Distributions under Censored Samples with Application in Financial Data. Int. J. Financial Stud. 2016, 4, 24. https://doi.org/10.3390/ijfs4040024
Panahi H. Model Selection Test for the Heavy-Tailed Distributions under Censored Samples with Application in Financial Data. International Journal of Financial Studies. 2016; 4(4):24. https://doi.org/10.3390/ijfs4040024
Chicago/Turabian StylePanahi, Hanieh. 2016. "Model Selection Test for the Heavy-Tailed Distributions under Censored Samples with Application in Financial Data" International Journal of Financial Studies 4, no. 4: 24. https://doi.org/10.3390/ijfs4040024
APA StylePanahi, H. (2016). Model Selection Test for the Heavy-Tailed Distributions under Censored Samples with Application in Financial Data. International Journal of Financial Studies, 4(4), 24. https://doi.org/10.3390/ijfs4040024





