Impacts of Credit Default Swaps on Volatility of the Exchange Rate in Turkey: The Case of Euro
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Hatemi-J and Roca (2014) [24] Asymmetric Causality Test
3.2. Frequency Domain Causality Test
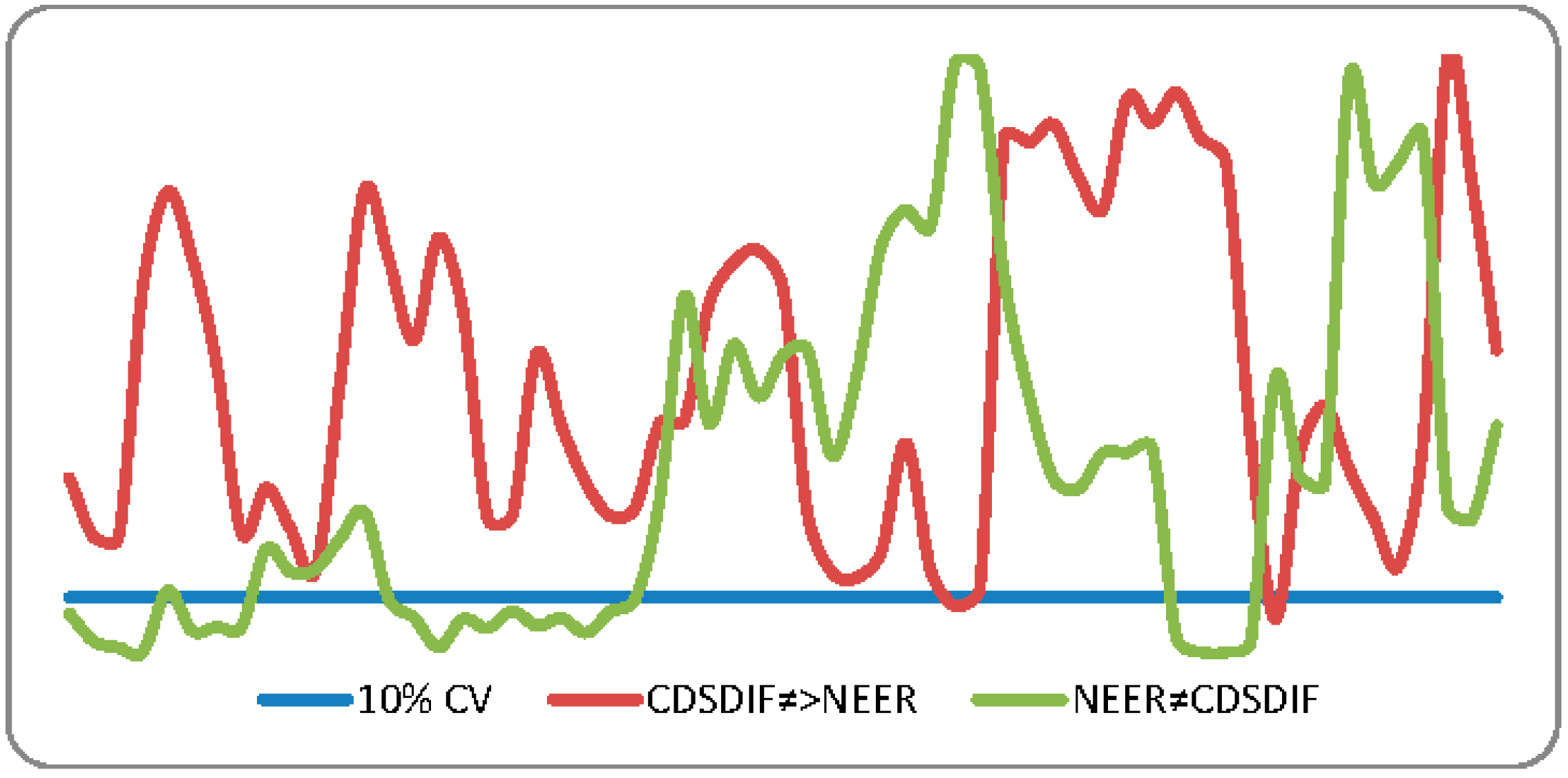
3.3. Balcilar et al. (2010) [26] Bootstrap Rolling Window Causality Test
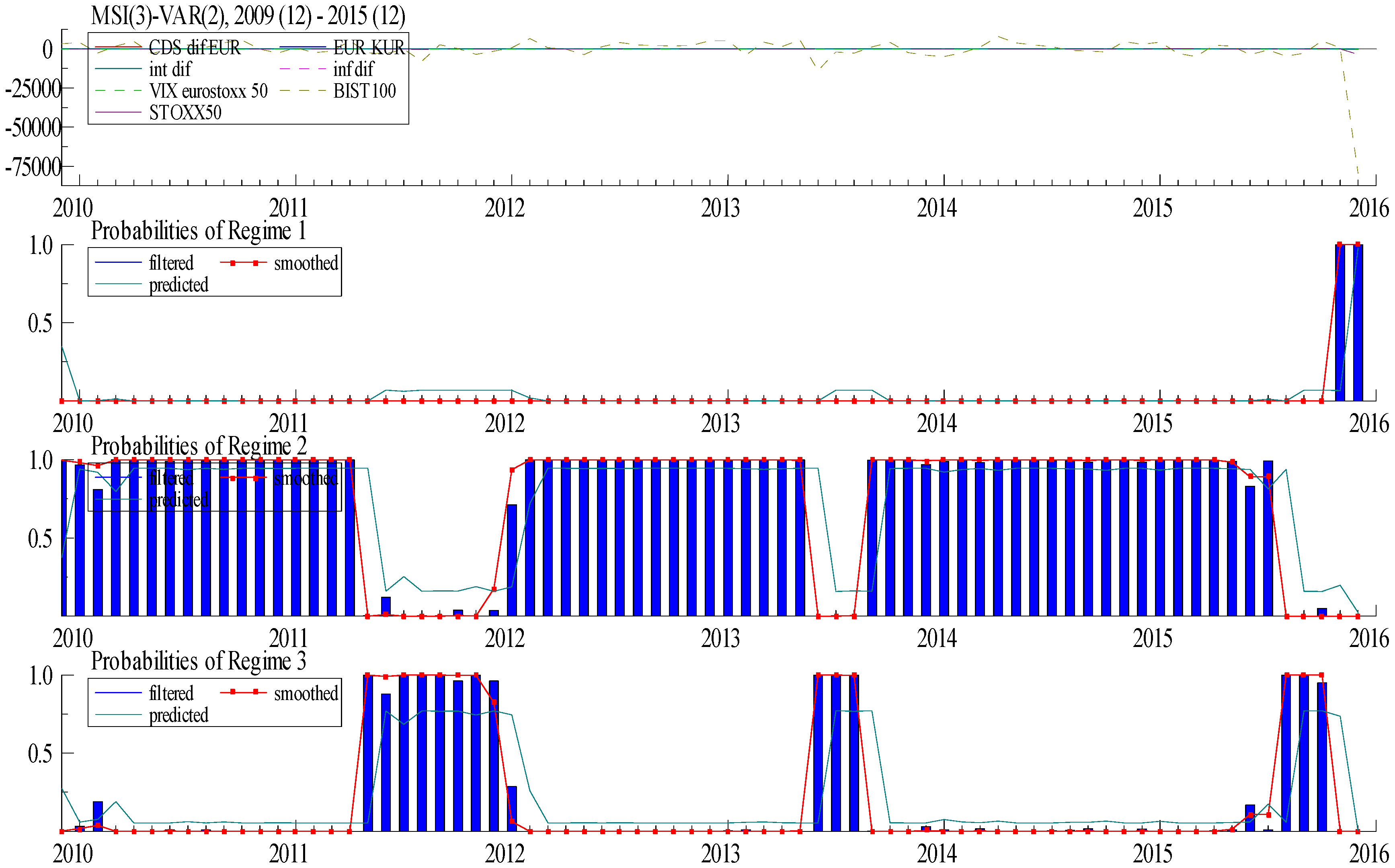
3.4. Markov Switching VAR Methodology
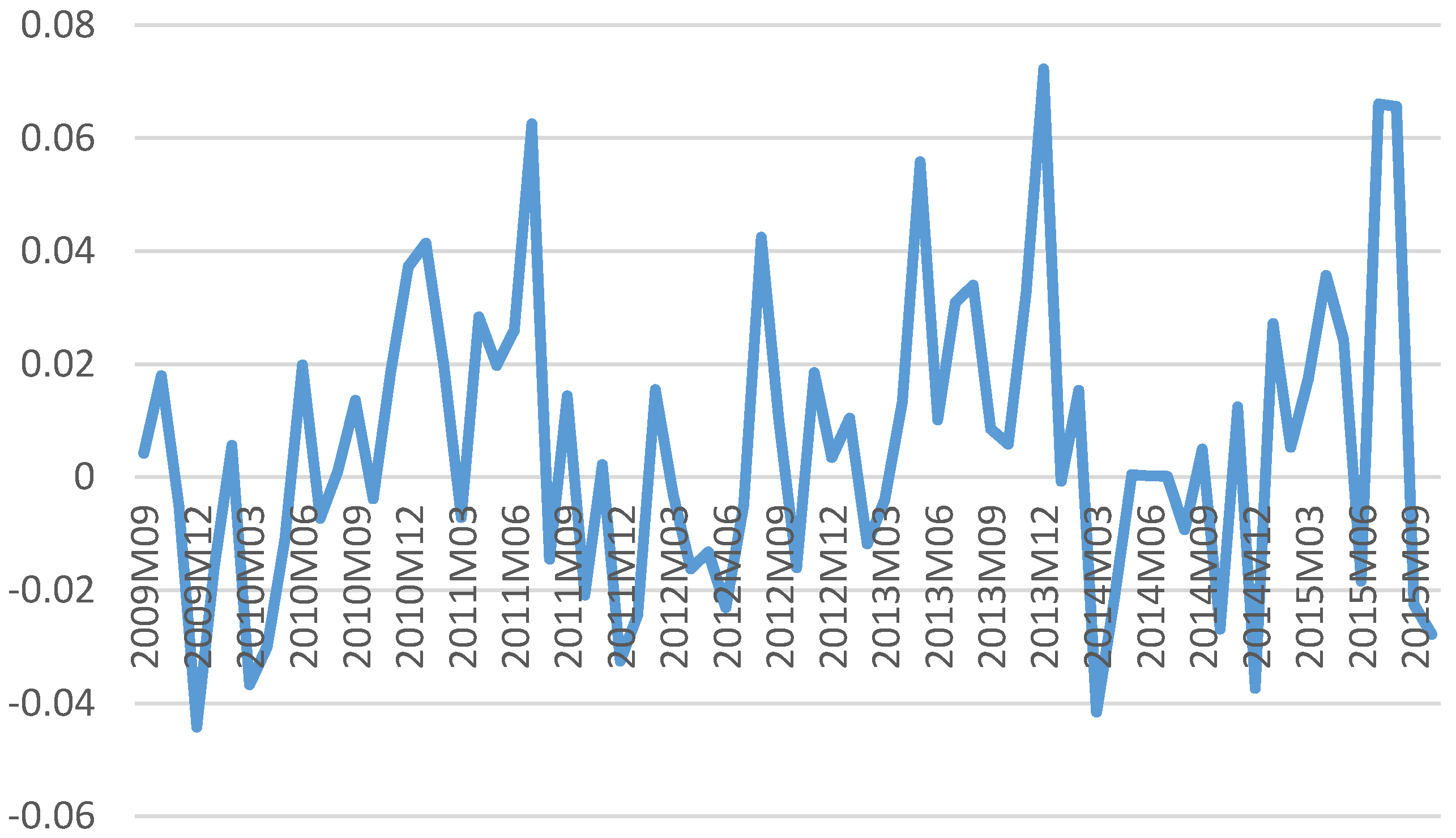
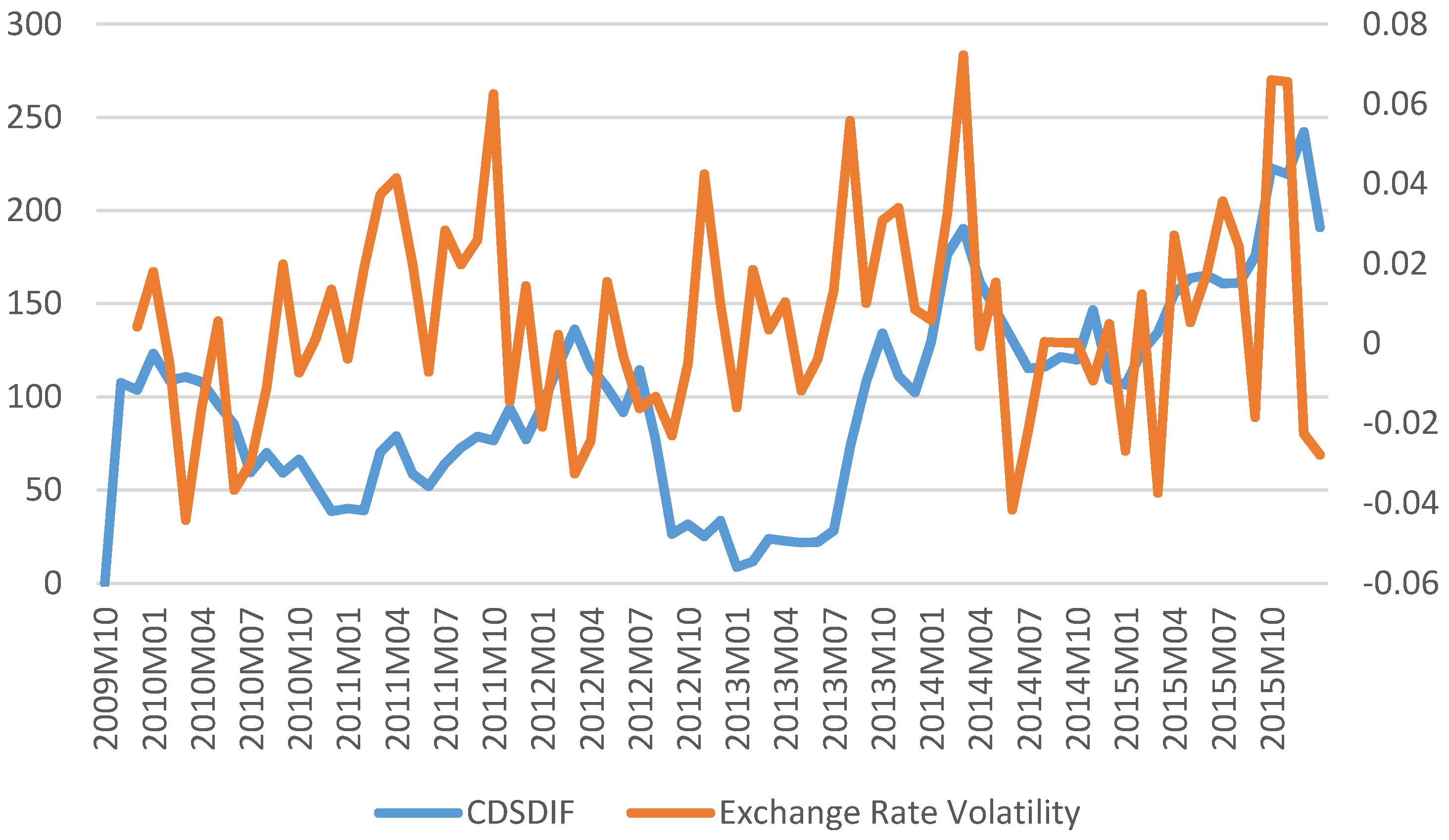
4. Data Description
5. Empirical Results
6. Conclusions
Author Contributions
Conflicts of Interest
References
- R. Dornbusch. “Exchange Rate Economics: Where Do We Stand? ” Brookings Pap. Econ. Activity 11 (1980): 143–206. [Google Scholar] [CrossRef]
- W.H. Branson. “Macroeconomic Determinants of Real Exchange Rates.” NBER Working Paper No. 801. 1981. Available online: http://www.nber.org/papers/w0801 (accessed on 15 February 2016).
- R.S. Pindyck, and J.J. Rotemberg. “The excess co-movement of commodity prices.” Econ. J. 100 (1990): 1173–1189. [Google Scholar] [CrossRef]
- J.H. Bergstrand. “Structural determinants of real exchange rates and national price levels: Some empirical evidence.” Am. Econ. Rev. 81 (1991): 325–334. [Google Scholar]
- H. Faruqee. “Long-run determinants of the real exchange rate: A stock-flow perspective.” Int. Money Fund Staff Pap. 42 (1995): 80–107. [Google Scholar] [CrossRef]
- R. Clarida, and J. Gali. “Sources of real exchange rate fluctuations: How important are nominal shocks.” Carnegie Rochester Conf. Ser. Public Policy 41 (1994): 1–56. [Google Scholar] [CrossRef]
- N.C. Mark, and D.Y. Choi. “Real exchange rate prediction over long horizons.” J. Int. Econ. 43 (1997): 29–60. [Google Scholar] [CrossRef]
- M.D. Chinn. “Real Exchange Rates.” Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.363.1561&rep=rep1&type=pdf (accessed on 15 February 2016).
- J. Zalduendo. “Determinants of Venezuela’s Equilibrium Real Exchange Rate.” IMF Working Paper. 2006. Available online: http://www.imf.org/external/pubs/ft/wp/2006/wp0674.pdf (accessed on 15 February 2016).
- S.S. Golub. “Oil prices and exchange rates.” Econ. J. 93 (1983): 576–593. [Google Scholar] [CrossRef]
- P. Krugman. “Oil and the dollar.” NBER Working Paper No. 554. 1980. Available online: http://www.nber.org/papers/w0554.pdf (accessed on 23 April 2015).
- S. Nazlioglu, T. Bayat, and S. Kayhan. “Exchange rate and oil price interactions in transition economies: Czech Republic, Hungary and Poland.” Panoeconomicus 62 (2015): 267–285. [Google Scholar]
- G. Zhang, Y. Jot, and H.G. Fung. “Do credit default swaps predict currency values? ” Appl. Financ. Econ. 20 (2010): 439–458. [Google Scholar] [CrossRef]
- B. Eichengreen, A.K. Rose, and C. Wyplosz. “Exchange market mayhem: The antecedents and aftermath of speculative attacks.” Econ. Policy 21 (1995): 249–312. [Google Scholar] [CrossRef]
- B. Eichengreen, and R. Hausmann. “Exchange Rates and Financial Fragility.” NBER Working Paper 7418. 1999. Available online: www.nber.org/papers/w7418.pdf (accessed on 10 February 2016).
- M. Obstfeld, and K. Rogoff. “The six major puzzles in international macroeco-nomics: Is there a common cause? ” 2000. Available online: www.nber.org/papers/w7777 (accessed 10 February 2016).
- C.H. Hui, and T.K. Chung. “Crash risk of the euro in the sovereign debt crisis of 2009–2010.” J. Bank. Financ. 35 (2011): 2945–2955. [Google Scholar] [CrossRef]
- C. Hui, and T.P. Fong. “Price cointegration between sovereign CDS and currency option markets in the financial crises of 2007–2013.” Int. Rev. Econ. Finance 40 (2015): 174–190. [Google Scholar] [CrossRef]
- L. Yang, B. Morley, and J. Hudson. “A study of the causal relationships between sovereign CDS spreads, risk-free interest rates and exchange rates.” In Proceedings of the 8th INFINITI Conference on International Finance, Dublin, Ireland, 14–15 May 2010.
- L. Bekkour, X. Jin, T. Lehnert, F. Rasmouki, and C. Wolff. “Euro at risk: The impact of member countries’ credit risk on the stability of the common currency.” J. Empir. Finance 33 (2015): 67–83. [Google Scholar] [CrossRef]
- TIM (Türkiye İhracatçılar Meclisi). Ekonomi ve dış ticaret raporu 2014. İstanbul, Turkey: Türkiye İhracatçılar Meclisi Yayını, 2015. [Google Scholar]
- G. Ozgur, and H. Ozel. “Kuresellesme, finansal genisleme ve bunalim.” Amme Idaresi Dergisi 43 (2010): 33–56. [Google Scholar]
- J. Pan, and K.J. Singleton. “Default and recovery implicit in the term structure of sovereign CDS spreads.” J. Finance 13 (2008): 2345–2385. [Google Scholar] [CrossRef]
- A. Hatemi-J, and E. Roca. “BRICs and PIGS in the presence of Uncle Sam and big brothers: Who drive who? Evidence based on asymmetric causality tests.” 2014. Available online: http://econpapers.repec.org/paper/griapaper/finance_3a201401.htm (accessed on 10 October 2015).
- J. Breitung, and B. Candelon. “Testing for short and long-run causality: A frequency domain approach.” J. Econom. 12 (2006): 363–378. [Google Scholar] [CrossRef]
- M. Balcilar, Z.A. Ozdemir, and Y. Arslanturk. “Economic growth and energy consumption causal nexus viewed through a bootstrap rolling window.” Energy Econ. 32 (2010): 1398–1410. [Google Scholar] [CrossRef]
- K. Galil, O.M. Shapir, D. Amiram, and U. Ben-Zion. “The determinants of CDS spreads.” J. Bank. Finance 41 (2014): 271–282. [Google Scholar] [CrossRef]
- P. Ehlers, and P. Schonbucher. “The influence of FX risk on credit spreads.” Available online: http://www.actuaries.org/afir/colloquia/zurich/ehlers_schoenburcher.pdf (accessed on 10 February 2016).
- D. Duffie. “Credit default valuation.” Financ. Anal. J. 55 (1999): 73–87. [Google Scholar] [CrossRef]
- M. Singh. A New Methodology to Proxy Recovery Value in CDS Contracts. IMF Working Paper No. 03/242; Washington, D.C., USA: IMF, 2003. [Google Scholar]
- T.S. Kim, Y.J. Park, and J. Park. “Macroeconomic conditions and credit default swap spread changes.” In Proceedings of the European Financial Management Association 2015 Annual Meetings, Amsterdam, The Netherlands, 24–27 June 2015.
- P. Carr, and L. Wu. “Theory and evidence on the dynamic interactions between sovereign credit default swaps and currency options.” J. Bank. Finance 31 (2007): 2383–2403. [Google Scholar] [CrossRef]
- M. Omachel, and M. Rudolf. “The Linkage between Sovereign Defaults and Exchange Rate Shocks in the Eurozone: A Measure for Systemic Risk.” 2015. Available online: http://ssrn.com/abstract=2513178 (accessed on 10 February 2016).
- P. Della Corte, L. Sarno, M. Schmeling, and C. Wagner. “Exchange Rates and Sovereign Risk.” 2015. Available online: http://ssrn.com/abstract=2354935 (accessed on 10 February 2016).
- A. Hatemi-J. “A new method to choose optimal lag order in stable and unstable VAR models.” Appl. Econ. Lett. 10 (2003): 135–137. [Google Scholar] [CrossRef]
- A. Hatemi-J. “Forecasting properties of a new method to choose optimal lag order in stable and unstable VAR models.” Appl. Econ. Lett. 15 (2008): 239–243. [Google Scholar] [CrossRef]
- H. Lütkepohl. New Introduction to Multiple Time Series Analysis. Berlin, Germany: Springer, 2005. [Google Scholar]
- C. Ciner. “Eurocurrency interest rate linkages: A frequency domain analysis.” Int. Rev. Econ. Finance 10 (2011): 498–505. [Google Scholar] [CrossRef]
- J. Geweke. “Measurement of linear dependence and feedback between multiple time series.” J. Am. Stat. Assoc. 77 (1982): 304–313. [Google Scholar] [CrossRef]
- Y. Hosoya. “The decomposition and measurement of the interdependence between second-order stationary process.” Probab. Theory Relat. Fields 88 (1991): 429–444. [Google Scholar] [CrossRef]
- A. Koutris, M.S. Heracleous, and A. Spanos. “Testing for nonstationarity using maximum entropy resampling: A misspecification testing perspective.” Econom. Rev. 27 (2008): 363–384. [Google Scholar] [CrossRef]
- G. Shukur, and P. Mantalos. “A simple investigation of the Granger-causality test in integrated-cointegrated VAR systems.” J. Appl. Stat. 27 (2000): 1021–1031. [Google Scholar] [CrossRef]
- M. Binder, and M. Gross. “Regime-switching global vector autoregressive models.” ECB Working Paper No. 1569. 2013. Available online: https://www.ecb.europa.eu/pub/pdf/scpwps/ecbwp1569.pdf?d2d0799b7984bf9aa815ed4192419033 (accessed on 20 April 2015).
- J.D. Hamilton. “A new approach to the economic analysis of nonstationary time series and the business cycle.” Econometrica 57 (1989): 357–384. [Google Scholar] [CrossRef]
- J.D. Hamilton. “Analysis of time series subject to regime changes.” J. Econom. 45 (1990): 39–70. [Google Scholar] [CrossRef]
- J.D. Hamilton. Time Series Analysis. Princeton, NJ, USA: Princeton University Press, 1994, Chapter 22. [Google Scholar]
- J.D. Hamilton. “Specification testing in Markov-switching time-series models.” J. Econom. 70 (1996): 127–157. [Google Scholar] [CrossRef]
- C.J. Kim, and G. Nelson. State-Space Models with Regime-Switching: Classical and Gibbs-Sampling Approaches with Applications. Cambridge, MA, USA: MIT Press, 1998. [Google Scholar]
- H.M. Krolzig. Markov Switching Vector Autoregressions. Modelling, Statistical Inference and Application to Business Cycle Analysis. Berlin, Germany: Springer, 1997. [Google Scholar]
- H.M. Krolzig. Econometric Modelling of Markov-Switching Vector Autoregressions Using MSVAR for Ox. New York, NY, USA: Oxford University Press, 1998. [Google Scholar]
- H.M. Krolzig. Predicting Markov-Switching Vector Autoregressive Processes. New York, NY, USA: Oxford University Press, 2000. [Google Scholar]
- H.M. Krolzig. Estimation, Structural Analysis and Forecasting of Regime-Switching Model with MSVAR for Ox. New York, NY, USA: Oxford University Press, 2001. [Google Scholar]
- T.I. Mohd, and I. Zahid. “Modelling exchange rates using regime switcing models.” Sains Malaysiana 35 (2006): 55–62. [Google Scholar]
- F. Fallahi, and G. Rodriguez. Using Markov-switching models to identify the link between unemployment and criminality. Working Paper. No #0701E, 1–53; Ottowa, Canada: Faculty of Social Sciences, University of Ottawa, 2007. [Google Scholar]
- S. Kayhan, T. Bayat, and A. Kocyigit. “Enflasyon hedeflemesi rejiminde ogrenme sureci ve asimetri: Markov switching yaklasimi.” Eskiseh. Osman. Univ. IIBF Dergisi 8 (2013): 191–212. [Google Scholar]
- S. Owen. “A Markov Switching Model for UK Acquisition Levels.” School of Banking and Finance, University of New South Wales, Working Paper No. 2004-1. 2004. Available online: http://wwwdocs.fce.unsw.edu.au/banking/workpap/wp%2001%202004.pdf (accessed on 15 June 2014).
- L. Ferrara. “A three-regime real-time indicator for the US economy.” Econ. Lett. 80 (2003): 373–378. [Google Scholar] [CrossRef]
- M. Bildirici, and U. Bozoklu. Bireysel Beklentiler ve Çoklu Ekonomik Denge: Markov Geçiş Modeli. 8. Malatya, Turkey: Türkiye Ekonometri ve İstatistik Kongresi, İnönü Üniversitesi, 2007, pp. 1–10. [Google Scholar]
- C.H. Hui, C.-F. Lo, and T. Fong. “A quasi-bounded model for Swiss Franc’s one-sided target zone during 2011–2015.” Available online: http://www.hkimr.org/uploads/publication/421/wp-no-15_2015-final-.pdf (accessed on 10 February 2016).
- D. Dickey, and W. Fuller. “Distribution of the estimators for autoregressive time series with a unit root.” J. Am. Stat. Assoc. 74 (1979): 427–431. [Google Scholar]
- D. Dickey, and W. Fuller. “Likelihood ratio statistics for autoregressive time series with a unit root.” Econometrica 49 (1981): 1057–1072. [Google Scholar] [CrossRef]
- P.C. Phillips, and P. Perron. “Testing for a unit root in time series regression.” Biometrika 75 (1988): 335–346. [Google Scholar] [CrossRef]
- J.G. MacKinnon. “Numerical distribution functions for unit root and co-integration tests.” J. Appl. Econom. 11 (1996): 601–618. [Google Scholar] [CrossRef]
- R.B. Davies. “Hypothesis testing when a nuisance parameter is present only under the alternative.” Biometrika 4 (1977): 247–254. [Google Scholar] [CrossRef]
- R.B. Davies. “Hypothesis testing when a nuisance parameter is present only under the alternative.” Biometrika 74 (1987): 33–43. [Google Scholar]
- R. Garcia, and P. Perron. “An analysis of the real interest rate under regime shifts.” Rev. Econ. Stat. 78 (1996): 111–125. [Google Scholar] [CrossRef]
| ETFs | Mean | Max. | Min. | Standard Dev. | Skewness | Kurtosis | Jarque-Bera (p-value) |
|---|---|---|---|---|---|---|---|
| CDSDIF | 100.16 | 242.31 | 8.647 | 53.627 | 0.3719 | 2.7819 | 1.8778 |
| NEER | 2.4947 | 3.3809 | 1.9273 | 0.3745 | 0.3965 | 2.1684 | 4.1270 |
| INTDIF | 4.822 | 7.85 | 0.00 | 2.2424 | −0.4402 | 2.4001 | 3.5478 |
| INFDIF | 6.4644 | 9.2807 | 1.3109 | 1.8701 | −0.8339 | 3.2796 | 8.9368 |
| BIST100 | 68,442.9 | 90,094.5 | 46,533.5 | 11,182.7 | −0.0505 | 1.9276 | 3.6256 |
| VIX | 23.878 | 46.68 | 6.95 | 6.5534 | 0.6996 | 4.0491 | 9.5589 |
| EURTRX | 2865.1 | 3697.4 | 2118.9 | 377.24 | 0.2264 | 2.4073 | 1.7384 |
| Levels | - | Variables | ADF | PP | First Differences | Variables | ADF | PP |
| Constant | BIST100 | −1.848 (0) [0.354] | −1.898 (3) [0.331] | BIST100 | −7.445 (0) [0.00] *** | −7.393 (6) [0.00] *** | ||
| CDSDIF | −0.680 (0) [0.844] | −0.728 (2) [0.832] | CDSDIF | −8.002 (0) [0.00] *** | −7.927 (3) [0.00] *** | |||
| NEER | 0.350 (0) [0.979] | 0.045 (3) [0.959] | NEER | −6.771 (0) [0.00] *** | −6.771 (1) [0.00] *** | |||
| INFDIF | −2.186 (0) [0.212] | −2.312 (1) [0.170] | INFDIF | −7.790 (0) [0.00] *** | −7.789 (1) [0.00] *** | |||
| INTDIF | −1.400 (0) [0.577] | −1.650 (3) [0.452] | INTDIF | −7.477 (0) [0.00] *** | −7.470 (1) [0.00] *** | |||
| EURTRX | −1.133 (0) [0.698] | −1.133 (0) [0.698] | EURTRX | −8.779 (0) [0.00] *** | −8.819 (2) [0.00] *** | |||
| VIX | −3.019 (1) [0.038] ** | −5.057 (4) [0.00] *** | VIX | −14.695 (0) [0.00] *** | −15.693 (3) [0.00] *** | |||
| Constant + Trend | BIST | −2.352 (0) [0.400] | −2.529 (1) [0.313] | BIST | −7.414 (0) [0.00] *** | −7.357 (6) [0.00] *** | ||
| CDSDIF | −1.767 (0) [0.710] | −1.730 (3) [0.727] | CDSDIF | −8.205 (0) [0.00] *** | −8.191 (6) [0.00] *** | |||
| NEER | −1.980 (0) [0.602] | −2.279 (3) [0.439] | NEER | −6.832 (0) [0.00] *** | −6.833 (1) [0.00] *** | |||
| INF DIF | −2.445 (0) [0.353] | −2.706 (2) [0.237] | INF DIF | −7.735 (0) [0.00] *** | −7.734 (1) [0.00] *** | |||
| INT DIF | −2.278 (0) [0.439] | −2.437 (3) [0.357] | INT DIF | −7.504 (0) [0.00] *** | −7.499 (1) [0.00] *** | |||
| EURTRX | −2.202 (0) [0.481] | −2.210 (1) [0.476] | EURTRX | −8.788 (0) [0.00] *** | −8.832 (2) [0.00] *** | |||
| VIX | −3.357 (1) [0.065] * | −5.820 (4) [0.00] *** | VIX | −14.593 (0) [0.00] *** | −15.604 (3) [0.00] *** |
| Direction of Causality | Mwald | 1% | 5% | 10% | Direction of Causality | Mwald | 1% | 5% | 10% |
|---|---|---|---|---|---|---|---|---|---|
| (CDSDIF)+ ≠> (NEER)+ | 0.052 (0.819) | 7.525 | 4.487 | 2.262 | (NEER)+ ≠> (CDSDIF)+ | 3.782 (0.052) * | 9.023 | 5.064 | 3.319 * |
| (CDSDIF)+ ≠> (NEER)− | 3.699 (0.157) | 12.168 | 6.793 | 4.922 | (NEER)+ ≠> (CDSDIF)− | 11.058 (0.004) *** | 14.074 | 8.048 ** | 5.804 * |
| (CDSDIF)− ≠> (NEER)− | 3.224 (0.073) * | 8.477 | 4.902 | 3.318 | (NEER)− ≠> (CDSDIF)− | 0.210 (0.646) | 8.381 | 4.283 | 2.745 |
| (CDSDIF)− ≠> (NEER)+ | 6.529 (0.038) ** | 12.251 | 7.061 | 5.090 * | (NEER)− ≠> (CDSDIF)+ | 3.284 (0.194) | 10.817 | 6.539 | 4.801 |
| Direction of Causality | Long Term | Medium Term | Short Term | |||
|---|---|---|---|---|---|---|
| ωi | 0.01 | 0.05 | 1.00 | 1.50 | 2.0 | 2.50 |
| CDSDIF ≠> NEER | 3.762 ** | 3.817 ** | 5.947 ** | 0.344 | 1.574 | 2.744 |
| NEER ≠> CDSDIF | 6.863 ** | 6.819 ** | 6.115 ** | 9.898 ** | 6.128 ** | 0.553 |
| No. of Regime | Log Prob | LR Linearity | Davies | AIC | SC |
|---|---|---|---|---|---|
| MS(2) | −1724.8929 | 239.3154 | 0.00 | 53.8327 | 61.3630 |
| MS(3) | −1464.7980 | 759.5052 | 0.00 | 49.6931 | 60.6434 |
| MS(4) | −1782.8227 | 123.4558 | 0.00 | 53.3924 | 58.6008 |
| No. of Regime | Number of Observations | Duration | Regime 1 | Regime 2 | Regime 3 |
|---|---|---|---|---|---|
| Regime 1 | 14.2 | 1.90 | 0.4734 | 0.3803 | 0.1462 |
| Regime 2 | 38.8 | 3.76 | 0.1371 | 0.7342 | 0.1287 |
| Regime 3 | 20.0 | 2.83 | 0.1046 | 0.2491 | 0.6463 |
| No. of Periods | CDS | EXC | INTDIF | INFDIF | VIX | BIST100 | EURSTX |
|---|---|---|---|---|---|---|---|
| 1 | 0.2786 | 0.3660 | 0.7254 | 0.0368 | −0.4410 | 0.1207 | 0.3886 |
| 2 | −0.2324 | 0.1349 | 0.4230 | 0.2944 | −0.2058 | −0.7039 | 0.8148 |
| 3 | −0.1719 | 0.4970 | 0.1698 | 0.1742 | −0.8476 | −0.2401 | 0.3690 |
| 4 | −0.7918 | 0.1830 | 0.6494 | 0.7382 | −0.3256 | −0.1094 | 0.1088 |
| 5 | −0.3104 | 0.6738 | 0.2431 | 0.2886 | −0.1221 | −0.3334 | 0.4420 |
| 6 | −0.1188 | 0.2481 | 0.9009 | 0.1089 | −0.4531 | −0.1240 | 0.1509 |
| 7 | −0.4413 | 0.9133 | 0.3327 | 0.4054 | −0.1674 | −0.4104 | 0.5778 |
| 8 | −0.1638 | 0.3362 | 0.1226 | 0.1499 | −0.6171 | −0.1500 | 0.2074 |
| 9 | −0.6035 | 0.1238 | 0.4518 | 0.5531 | −0.8371 | −0.5278 | 0.7745 |
| 10 | −0.2226 | 0.4557 | 0.1664 | 0.2038 | −0.2273 | −0.1936 | 0.2826 |
| No. of Periods | CDS | EXC | INTDIF | INFDIF | VIX | BIST100 | EURSTX |
|---|---|---|---|---|---|---|---|
| 1 | 0.3480 | 0.0392 | −0.8609 | 0.1550 | −0.2108 | 0.2108 | 0.8910 |
| 2 | 0.6355 | 0.0019 | −0.0639 | 0.1371 | −0.4697 | −0.0801 | −0.7709 |
| 3 | 0.1799 | 0.0011 | 0.0019 | 0.0341 | −0.2903 | −0.3207 | 0.6165 |
| 4 | 0.0951 | 0.0009 | 0.0011 | 0.0588 | −0.2171 | −0.1817 | −0.1581 |
| 5 | 0.0676 | 0.0007 | 0.0019 | 0.0330 | −0.1875 | −0.1154 | 0.1739 |
| 6 | 0.0573 | 0.0006 | 0.0011 | 0.0266 | −0.1129 | −0.0805 | −0.0085 |
| 7 | 0.0357 | −0.0004 | 0.0010 | 0.0162 | −0.0840 | −0.0589 | 0.0559 |
| 8 | 0.0261 | −0.0003 | 0.0006 | 0.0125 | −0.0563 | −0.0402 | 0.0091 |
| 9 | 0.0170 | −0.0002 | 0.0005 | 0.0082 | −0.0407 | −0.0283 | 0.0207 |
| 10 | 0.0126 | −0.0001 | 0.0003 | 0.0060 | −0.0277 | −0.0196 | 0.0076 |
| No. of Periods | CDS | EXC | INTDIF | INFDIF | VIX | BIST | EURSTX |
|---|---|---|---|---|---|---|---|
| 1 | −0.3133 | 0.0191 | 0.3631 | 0.2300 | 0.2248 | −0.2445 | −0.9750 |
| 2 | −0.2018 | 1.4169 | 0.8915 | −0.8888 | 0.5330 | 1.0345 | −0.6896 |
| 3 | −0.4793 | 0.4666 | −0.8428 | −1.2259 | 0.9432 | 1.7000 | 1.3800 |
| 4 | 1.3500 | 0.9955 | −0.4793 | 1.2341 | −0.7429 | −2.3980 | −3.6180 |
| 5 | −1.1108 | 1.9018 | 1.3085 | −1.4134 | 0.3527 | −0.6751 | −0.9711 |
| 6 | −0.5380 | 3.9310 | 2.0110 | −0.8771 | 5.2710 | 1.8212 | 1.1912 |
| 7 | 1.1212 | 1.4511 | −0.7341 | 0.7471 | −1.2911 | 3.0715 | 3.8415 |
| 8 | 2.4415 | 1.7914 | −0.8991 | 3.4613 | −2.0814 | −1.0716 | −1.1516 |
| 9 | −0.7045 | −0.7744 | 4.1414 | −8.3313 | −0.0406 | −1.3419 | −1.7519 |
| 10 | −1.0719 | −0.7842 | 3.9517 | −1.5817 | 0.9141 | 6.0919 | 6.3419 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, M.; Bayat, T.; Kayhan, S. Impacts of Credit Default Swaps on Volatility of the Exchange Rate in Turkey: The Case of Euro. Int. J. Financial Stud. 2016, 4, 14. https://doi.org/10.3390/ijfs4030014
Kar M, Bayat T, Kayhan S. Impacts of Credit Default Swaps on Volatility of the Exchange Rate in Turkey: The Case of Euro. International Journal of Financial Studies. 2016; 4(3):14. https://doi.org/10.3390/ijfs4030014
Chicago/Turabian StyleKar, Muhsin, Tayfur Bayat, and Selim Kayhan. 2016. "Impacts of Credit Default Swaps on Volatility of the Exchange Rate in Turkey: The Case of Euro" International Journal of Financial Studies 4, no. 3: 14. https://doi.org/10.3390/ijfs4030014
APA StyleKar, M., Bayat, T., & Kayhan, S. (2016). Impacts of Credit Default Swaps on Volatility of the Exchange Rate in Turkey: The Case of Euro. International Journal of Financial Studies, 4(3), 14. https://doi.org/10.3390/ijfs4030014






