Debunking Two Myths of the Weekend Effect
Abstract
:“What do you believe that is actually false?”Ken Fisher, Author of The Only Three Questions That Count.
1. Introduction
2. Literature
3. Empirical Analysis
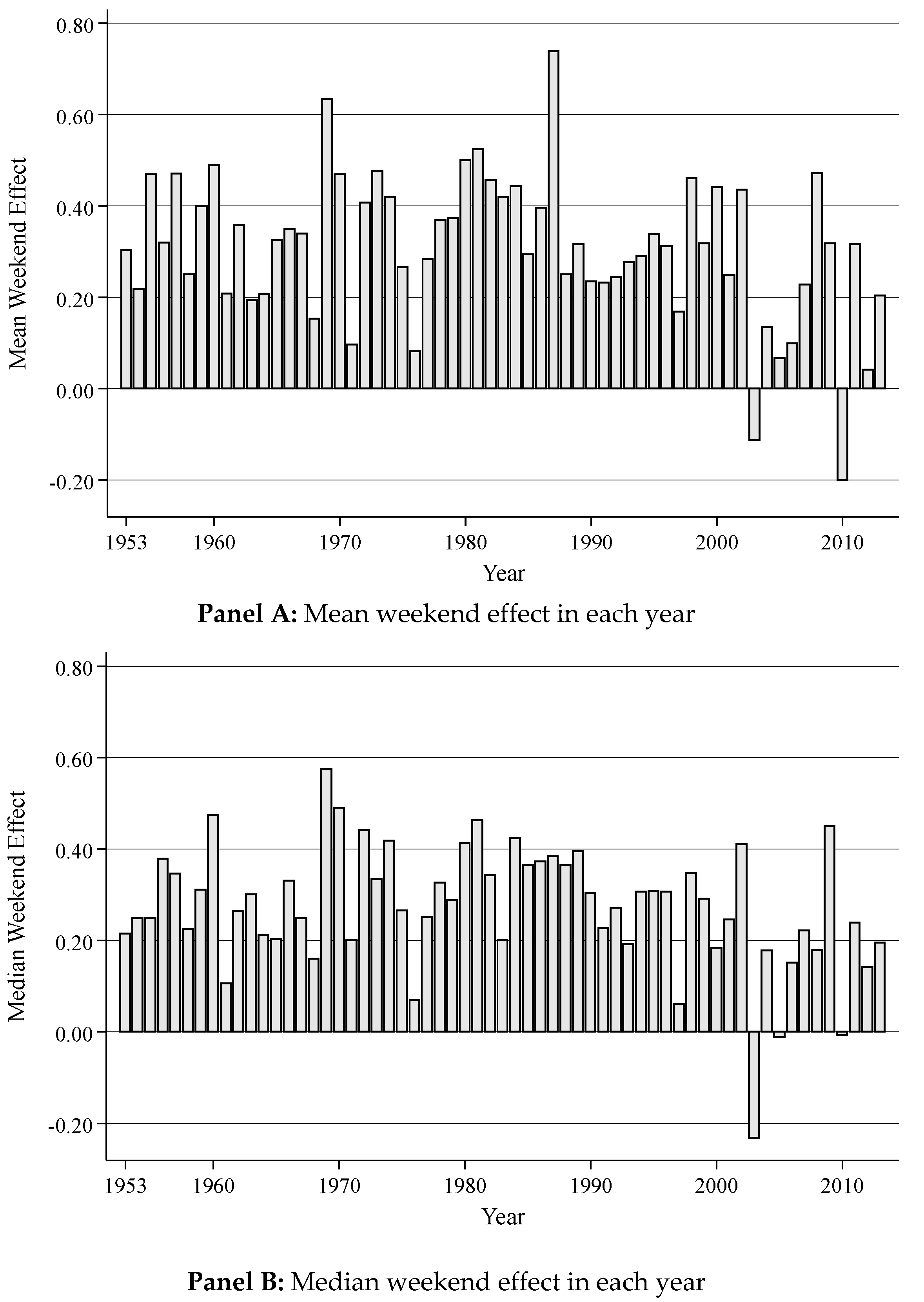
3.1. Is the Weekend Effect Due to Data-Mining?
3.2. Reconciliation with Prior Studies
3.3. Is the Weekend Effect Driven by Unusual/Rare Events (Such as the Yearly Change in Daylight Saving)?
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- F. Cross. “The Behavior of Stock Prices on Fridays and Mondays.” Financ. Anal. J. 29 (1973): 67–69. [Google Scholar] [CrossRef]
- K. French. “Stock Returns and the Weekend Effect.” J. Financ. Econ. 8 (1980): 55–69. [Google Scholar] [CrossRef]
- D. Keim, and R. Stambaugh. “A Further Investigation of the Weekend Effect in Stock Returns.” J. Finance 39 (1984): 819–835. [Google Scholar] [CrossRef]
- D.B. Keim. “Trading patterns, bid-ask spreads, and estimated security returns: The case of common stocks at calendar turning points.” J. Financ. Econ. 25 (1989): 75–97. [Google Scholar] [CrossRef]
- M. Gibbons, and P. Hess. “Day of the Week Effects and Asset Returns.” J. Bus. 54 (1981): 579–596. [Google Scholar] [CrossRef]
- J. Lakonishok, and M. Levi. “Weekend Effects on Stock Returns: A Note.” J. Finance 37 (1982): 883–889. [Google Scholar] [CrossRef]
- E. Dyl, and S. Martin Jr. “Weekend Effects on Stock Returns: A Comment.” J. Finance 40 (1985): 347–349. [Google Scholar] [CrossRef]
- J. Lakonishok, and M. Levi. “Weekend Effects on Stock Returns: A Comment.” J. Finance 40 (1985): 351–352. [Google Scholar] [CrossRef]
- A. Abraham, and D. Ikenberry. “The Individual Investor and the Weekend Effect.” J. Financ. Quant. Anal. 29 (1994): 263–277. [Google Scholar] [CrossRef]
- K. Wang, Y. Li, and J. Erickson. “A New Look at the Monday Effect.” J. Finance 52 (1997): 2171–2186. [Google Scholar] [CrossRef]
- A. Damodaran. “The Weekend Effect in Information Releases: A Study of Earnings and Dividend Announcements.” Rev. Financ. Stud. 2 (1989): 607–623. [Google Scholar] [CrossRef]
- R. Thaler. “Anomalies: Seasonal Movements in Security Prices II: Weekend, Holiday, Turn of the Month, and Intraday Effects.” J. Econom. Perspect. 1 (1987): 169–177. [Google Scholar] [CrossRef]
- M. Rubinstein. “Rational Markets: Yes or No? The Affirmative Case.” Financ. Anal. J. 57 (2001): 15–29. [Google Scholar] [CrossRef]
- G.W. Schwert. “Anomalies and Market Efficiency.” In Handbook of the Economics of Finance. North Holland, The Netherlands: Elsevier, 2003. [Google Scholar]
- R. Sullivan, A. Timmermann, and H. White. “Dangers of Data-Mining: The Case of Calendar Effects in Stock Returns.” J. Econom. 105 (2001): 249–286. [Google Scholar] [CrossRef]
- M. Kamstra, L. Kramer, and M. Levi. “Losing Sleep at the Market: The Daylight Saving Anomaly.” Am. Econ. Rev. 90 (2000): 1005–1011. [Google Scholar] [CrossRef]
- R.W. Banz. “The relationship between return and market value of common stocks.” J. Financ. Econ. 9 (1981): 3–18. [Google Scholar] [CrossRef]
- J. Lakonishok, and S. Smidt. “Are seasonal anomalies real? A ninety-year perspective.” Rev. Financ. Stud. 1 (1988): 403–425. [Google Scholar] [CrossRef]
- K.L. Fisher, J. Chou, and L. Hoffmans. The Only Three Questions that Still Count: Investing by Knowing What Others Don’t. Hoboken, NJ, USA: John Wiley & Sons, 2012. [Google Scholar]
- H. Chen, and V. Singal. “Role of Speculative Short Sales in Price Formation: The Case of the Weekend Effect.” J. Finance 58 (2003): 685–706. [Google Scholar] [CrossRef]
- B.M. Blau, B.F. van Ness, and R.A. van Ness. “Short Selling and the Weekend Effect for NYSE Securities.” Financ. Manag. 38 (2009): 603–630. [Google Scholar] [CrossRef]
- H. White. “A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity.” J. Econom. Soc. 48 (1980): 817–838. [Google Scholar] [CrossRef]
- J. Campbell, A. Lo, and A. MacKinlay. The Econometrics of Financial Markets. Princeton, NJ, USA: Princeton University Press, 1997. [Google Scholar]
- 1If expected returns on non-trading days and trading days are similar, then Monday’s return should be three times higher than Friday. Alternatively, if expected return on non-trading days (i.e., weekends) is zero, then Monday’s return should be the same as Friday.
- 2p-value < 0.000001 using a binomial probability test.
- 3Consider a volatile stock whose price rises from $1 to $2, and falls back to $1. If raw return is used (i.e., 100% and –50%, respectively), then the mean return will be spuriously positive and correlated with return volatility.
| Panel A: Time-series regression of equal-weighted daily indices return (EWRETD) on day of the week dummies, and whether that date precedes, or follows, a holiday. | ||||
| EWRETD = α1 MONDAY + α2 TUESDAY + α3 WEDNESDAY + α4 THURSDAY + α5 FRIDAY + α6 PREHOLIDAY + α7 POSTHOLIDAY + ε. | ||||
| French [2] Sample Period 1953–1977 | Schwert [14] Sample Period 1978–2002 | |||
| (1) | (2) | (3) | (4) | |
| Variables | EWRETD | EWRETD | EWRETD | EWRETD |
| MONDAY | −0.14 *** | −0.15 *** | −0.10 *** | −0.11 *** |
| (−5.98) | (−6.62) | (−4.25) | (−4.33) | |
| TUESDAY | −0.01 | −0.03 * | −0.00 | −0.00 |
| (−0.50) | (−1.72) | (−0.06) | (−0.09) | |
| WEDNESDAY | 0.13 *** | 0.11 *** | 0.14 *** | 0.13 *** |
| (6.91) | (6.10) | (7.23) | (6.91) | |
| THURSDAY | 0.10 *** | 0.08 *** | 0.16 *** | 0.15 *** |
| (5.52) | (4.53) | (8.15) | (7.73) | |
| FRIDAY | 0.20 *** | 0.17 *** | 0.25 *** | 0.24 *** |
| (11.87) | (10.30) | (13.29) | (12.02) | |
| PREHOLIDAY | 0.29 *** | 0.23*** | ||
| (7.54) | (5.34) | |||
| POSTHOLIDAY | 0.21 *** | −0.02 | ||
| (4.21) | (−0.38) | |||
| Observations | 6273 | 6273 | 6313 | 6313 |
| R-squared | 0.03 | 0.04 | 0.03 | 0.03 |
| Panel B: Time-series regression of change in daily return (ΔEWRETD) on day of the week dummies, and whether that date precedes, or follows, a holiday | ||||
| ΔEWRETD = α1 MONDAY + α2 TUESDAY + α3 WEDNESDAY + α4 THURSDAY + α5 FRIDAY + α6 PREHOLIDAY + α7 POSTHOLIDAY + ε | ||||
| where ΔEWRETDt = EWRETDt – EWRETDt–1 | ||||
| French [2] Sample Period (1953–1977) | Schwert [14] Sample Period (1978–2002) | |||
| (1) | (2) | (3) | (4) | |
| Variables | ΔEWRETD | ΔEWRETD | ΔEWRETD | ΔEWRETD |
| MONDAY | −0.33 *** | −0.33 *** | −0.35 *** | −0.34 *** |
| (−16.17) | (−16.07) | (−14.75) | (−14.26) | |
| TUESDAY | 0.11 *** | 0.10 *** | 0.07 *** | 0.10 *** |
| (4.19) | (4.20) | (2.72) | (3.76) | |
| WEDNESDAY | 0.14 *** | 0.14 *** | 0.14 *** | 0.14 *** |
| (6.42) | (6.15) | (5.73) | (5.67) | |
| THURSDAY | −0.02 | −0.03 | 0.02 | 0.02 |
| (−1.09) | (−1.44) | (0.81) | (0.68) | |
| FRIDAY | 0.09 *** | 0.08 *** | 0.10 *** | 0.10 *** |
| (4.95) | (4.10) | (4.52) | (4.21) | |
| PREHOLIDAY | 0.28 *** | 0.19 *** | ||
| (4.55) | (3.90) | |||
| POSTHOLIDAY | −0.13 ** | −0.38 *** | ||
| (−2.54) | (−6.21) | |||
| Observations | 6273 | 6273 | 6313 | 6313 |
| R-squared | 0.05 | 0.05 | 0.04 | 0.05 |
| Panel A: Mean weekend effect in each size decile (1953–1977) | ||||||
| Size Decile | Mon Return | Tue Return | Wed Return | Thu Return | Fri Return | Weekend Effect |
| 1 (smallest) | −0.09 *** | −0.06 *** | 0.11 *** | 0.12 *** | 0.23 *** | 0.32 *** |
| 2 | −0.13 *** | −0.06 *** | 0.11 *** | 0.11 *** | 0.23 *** | 0.35 *** |
| 3 | −0.16 *** | −0.04 * | 0.12 *** | 0.09 *** | 0.21 *** | 0.35 *** |
| 4 | −0.15 *** | −0.04 ** | 0.12 *** | 0.10 *** | 0.22 *** | 0.37 *** |
| 5 | −0.17 *** | −0.03 | 0.13 *** | 0.08 *** | 0.20 *** | 0.36 *** |
| 6 | −0.17 *** | −0.02 | 0.13 *** | 0.09 *** | 0.18 *** | 0.34 *** |
| 7 | −0.16 *** | −0.01 | 0.12 *** | 0.09 *** | 0.17 *** | 0.32 *** |
| 8 | −0.15 *** | −0.00 | 0.12 *** | 0.07 *** | 0.15 *** | 0.29 *** |
| 9 | −0.14 *** | 0.01 | 0.11 *** | 0.08 *** | 0.14 *** | 0.29 *** |
| 10 (largest) | −0.15 *** | 0.03 | 0.11 *** | 0.06 *** | 0.11 *** | 0.26 *** |
| D10–D1 | −0.06 | 0.09 *** | −0.01 | −0.06 ** | −0.12 *** | −0.05 |
| (−1.64) | (3.08) | (−0.27) | (−2.05) | (−4.38) | (−1.51) | |
| Panel B: Mean weekend effect in each size decile (1978–2002) | ||||||
| Size Decile | Mon Return | Tue Return | Wed Return | Thu Return | Fri Return | Weekend Effect |
| 1 (smallest) | −0.12 *** | −0.11 *** | 0.07 *** | 0.15 *** | 0.34 *** | 0.45 *** |
| 2 | −0.16 *** | −0.09 *** | 0.08 *** | 0.14 *** | 0.29 *** | 0.45 *** |
| 3 | −0.17 *** | −0.09 *** | 0.08 *** | 0.14 *** | 0.27 *** | 0.44 *** |
| 4 | −0.17 *** | −0.07 *** | 0.09 *** | 0.12 *** | 0.24 *** | 0.41 *** |
| 5 | −0.17 *** | −0.05 ** | 0.10 *** | 0.13 *** | 0.22 *** | 0.39 *** |
| 6 | −0.16 *** | −0.05 ** | 0.11 *** | 0.12 *** | 0.20 *** | 0.36 *** |
| 7 | −0.15 *** | −0.03 | 0.12 *** | 0.11 *** | 0.17 *** | 0.32 *** |
| 8 | −0.13 *** | −0.01 | 0.13 *** | 0.10 *** | 0.15 *** | 0.28 *** |
| 9 | −0.11 *** | −0.00 | 0.13 *** | 0.10 *** | 0.12 *** | 0.24 *** |
| 10 (largest) | −0.01 | 0.05 * | 0.10 *** | 0.03 | 0.06 ** | 0.08 * |
| D10–D1 | 0.11 ** | 0.16 *** | 0.02 | −0.12 *** | −0.28 *** | -0.38 *** |
| (2.57) | (4.53) | (0.73) | (-3.71) | (−8.20) | (−8.29) | |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheong, F.S. Debunking Two Myths of the Weekend Effect. Int. J. Financial Stud. 2016, 4, 7. https://doi.org/10.3390/ijfs4020007
Cheong FS. Debunking Two Myths of the Weekend Effect. International Journal of Financial Studies. 2016; 4(2):7. https://doi.org/10.3390/ijfs4020007
Chicago/Turabian StyleCheong, Foong Soon. 2016. "Debunking Two Myths of the Weekend Effect" International Journal of Financial Studies 4, no. 2: 7. https://doi.org/10.3390/ijfs4020007
APA StyleCheong, F. S. (2016). Debunking Two Myths of the Weekend Effect. International Journal of Financial Studies, 4(2), 7. https://doi.org/10.3390/ijfs4020007





