Performance of the Multifractal Model of Asset Returns (MMAR): Evidence from Emerging Stock Markets
Abstract
:1. Introduction
2. Literature Reviews
3. Theory of the Econometric Model
3.1. Multiscaling Property
3.2. The Multifractal Model of Asset Returns
3.3. FIGARCH Model and Scaling
4. Empirical Analysis
4.1. Descriptive Statistics
4.2. Parameter Estimations
4.3. Simulations and Construction of the Models
5. Conclusions
Conflicts of Interest
Abbreviations
| MMAR | Multifractal Model of Asset Returns |
| ARCH | Autoregressive Conditional Heteroscedasticity |
| GARCH | Generalized Autoregressive Conditional Heteroscedasticity |
| EGARCH | Exponential Generalized Autoregressive Conditionally Heteroscedasticity |
| FIGARCH | Fractionally Integrated Generalized Autoregressive Conditionally Heteroscedasticity |
| MRS-GARCH | Markov Regime Switching Generalized Autoregressive Conditional Heteroscedasticity |
| EMH | Efficient Market Hypothesis |
| FMH | Fractal Market Hypothesis |
| ARFIMA | Autoregressive Fractionally Integrated Moving Average |
| MF-DFA | Multifractal Detrended Fluctuation Analysis |
| FIEGARCH | Fractionally Integrated Exponential Generalized Autoregressive Conditionally Heteroskedasticity |
| FIEGARCH-M | Fractionally Integrated Exponential Generalized Autoregressive Conditional Heteroskedastic-in-mean |
| CAC40 | Cotation Assistée en Continu 40 |
| GBM | Geometric Brownian Motion |
| DFA | Detrended Fluctuation Analysis |
| GED | Generalized Error Distribution |
| AIC | Akaike Information Criterion |
| SIC | Schwartz Information Criterion |
References
- E. Fama. “Random Walks in Stock Market Prices.” Financ. Anal. J. 21 (1965): 55–59. [Google Scholar] [CrossRef]
- E. Fama. “Efficient Capital Markets: A Review of Theory and Empirical Work.” J. Financ. 25 (1970): 383–417. [Google Scholar] [CrossRef]
- B.B. Mandelbrot. “The Pareto-Lévy law and the distribution of income.” Int. Econ. Rev. 1 (1960): 79–106. [Google Scholar] [CrossRef]
- B.B. Mandelbrot. “The variation of certain speculative prices.” J. Bus. 36 (1963): 392–417. [Google Scholar] [CrossRef]
- B.B. Mandelbrot, and J.R. Wallis. “Some Long-Run Properties of Geophysical Records.” Water Resour. Res. 5 (1969): 321–340. [Google Scholar] [CrossRef]
- H.E. Hurst. “Long-term storage capacity of reservoirs.” Trans. Am. Soc. Civ. Eng. 116 (1951): 770–808. [Google Scholar]
- M.S. Taqqu. “Benoit Mandelbrot and Fractional Brownian Motion.” Stat. Sci. 28 (2013): 131–134. [Google Scholar] [CrossRef]
- E.E. Peters. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York, NY, USA: John Wiley and Sons, 1994. [Google Scholar]
- J. Beran, Y. Feng, S. Ghosh, and R. Kulik. Long-Memory Processes: Probabilistic Properties and Statistical Methods. New York, NY, USA: Springer, 2013. [Google Scholar]
- A.B. Schmidt. Financial Markets and Trading: An Introduction to Market Microstructure and Trading Strategies. New York, NY, USA: John Wiley & Sons, 2011. [Google Scholar]
- J. Goddard, and E. Onali. “Self-affinity in financial asset returns.” Int. Rev. Financ. Anal. 24 (2012): 1–11. [Google Scholar] [CrossRef]
- R. Engle. “Autorregressive Conditional Heteroskedasticity with Estimates of United Kingdom Inflation.” Econometrica 50 (1982): 987–1008. [Google Scholar] [CrossRef]
- T. Bollerslev. “Generalized Autorregressive Conditional Heteroskedasticity.” J. Econom. 31 (1986): 307–327. [Google Scholar] [CrossRef]
- B.B. Mandelbrot, A. Fisher, and L. Calvet. “A multifractal model of asset returns.” Cowles Foundation Discussion Paper No. 1164; New Haven, CT, USA: Yale University, 1997, pp. 1–33. [Google Scholar]
- F.C. Drost, and J.C. Werker. “Closing the GARCH gap: Continuous GARCH modelling.” J. Econom. 74 (1996): 31–57. [Google Scholar] [CrossRef]
- B.B. Mandelbrot. “Statistical Methodology for Nonperiodic Cycles from Covariance to R/S Analysis.” In Annals of Economic and Social Measurement. Cambridge, MA, USA: National Bureau of Economic Research, 1972, Volume 1, pp. 259–290. [Google Scholar]
- A.W. Lo. “Long-term memory in stock market prices.” Econometrica 59 (1991): 1279–1313. [Google Scholar] [CrossRef]
- C.K. Peng, S.V. Buldyrev, S. Havlin, M. Simons, H.E. Stanley, and A.L. Goldberger. “Mosaic organization of DNA nucleotides.” Phys. Rev. E 49 (1994): 1685–1689. [Google Scholar] [CrossRef]
- M. Taqqu, V. Teverovsky, and W. Willinger. “Estimators for long-range dependence: An empirical study.” Fractals 3 (1995): 785–798. [Google Scholar] [CrossRef]
- M.S. Taqqu, and V. Teverovsky. “Robustness of Whittle type estimators for time series with long-range dependence.” Stoch. Models 13 (1997): 723–757. [Google Scholar] [CrossRef]
- P. Abry, and D. Veitch. “Wavelet analysis of long-range-dependent traffic.” IEEE Trans. Inf. Theory 44 (1998): 2–15. [Google Scholar] [CrossRef]
- C.W.J. Granger, and R. Joyeux. “An introduction to loag memory time series models and fractional differencing.” J. Time Ser. Anal. 1 (1980): 5–39. [Google Scholar]
- J.R.M. Hosking. “Fractional differencing.” Biometrika 68 (1981): 165–176. [Google Scholar] [CrossRef]
- J. Geweke, and S. Porter-Hudak. “The estimation and Appication of Long Memory Time Series Models.” J. Time Seri. Anal. 4 (1983): 221–238. [Google Scholar] [CrossRef]
- P.M. Robinson. “Log-periodogram regression of time series with long range dependence.” Ann. Stat. 23 (1995): 1048–1072. [Google Scholar] [CrossRef]
- P.C.B. Phillips. “Discrete Fourier Transforms of Fractional Processes; 1999.” New Haven, CT, USA; Unpublished Working Paper No. 1243. : Cowles Foundation for Research in Economics; Yale University. Available online: http://cowles.yale.edu/sites/default/files/files/pub/d12/d1243.pdf (accessed on 23 July 2014).
- P.C.B. Phillips. “Unit Root Log Periodogram Regression; 1999.” Cowles Foundation for Research in Economics; Yale University; Unpublished Working Paper No. 1244. Available online: http://cowles.yale.edu/sites/default/files/files/pub/d12/d1244.pdf (accessed on 23 July 2014).
- A. Smith. “Level Shifts and the Illusion of Long Memory in Economic Time Series.” J. Bus. Econ. Stat. 23 (2005): 321–335. [Google Scholar] [CrossRef]
- K. Shimotsu, and P.C.B. Phillips. “Exact Local Whittle estimation of fractional integration.” Ann. Stat. 33 (2005): 1890–1933. [Google Scholar] [CrossRef]
- K.M. Abadir, W. Distaso, and L. Giraitis. “Non-stationarity extended Local Whittle estimation.” J. Econom. 141 (2007): 1353–1384. [Google Scholar] [CrossRef]
- K. Shimotsu. Simple (but Effective) Tests of Long Memory versus Structural Breaks. Queen’s Economics Department Working Paper No. 1101; Kingston, ON, Canada: Queen’s University, 2006. [Google Scholar]
- R.T. Baillie, T. Bollerslev, and H.O. Mikkelsen. “Fractionally integrated Generalized Autoregressive Conditional Heteroscedasticity.” J. Econom. 74 (1996): 3–30. [Google Scholar] [CrossRef]
- T. Bollerslev, and H.O. Mikkelsen. “Modeling and pricing long memory in stock market volatility.” J. Econom. 73 (1996): 151–184. [Google Scholar] [CrossRef]
- B.J. Christensen, M.Ø. Nielsen, and J. Zhu. “Long memory in stock market volatility and the volatility-in-mean effect: The FIEGARCH-M Model.” J. Empir. Financ. 17 (2010): 460–470. [Google Scholar] [CrossRef]
- R. Kilic. “Long memory and nonlinearity in conditional variances: A smooth transition FIGARCH model.” J. Empir. Financ. 18 (2011): 368–378. [Google Scholar] [CrossRef]
- J. Davidson, and P. Sibbertsen. “Generating schemes for long memory processes: Regimes, aggregation and linearity.” J. Econom. 128 (2005): 253–282. [Google Scholar] [CrossRef]
- T. Andersen, and T. Bollerslev. “Heterogeneous information arrivals and return volatility dynamics: Uncovering the long-run in high frequency returns.” J. Finance 52 (1997): 975–1005. [Google Scholar] [CrossRef]
- P. Zaffaroni. “Aggregation and memory of models of changing volatility.” J. Econom. 136 (2007): 237–249. [Google Scholar] [CrossRef]
- T. Mikosch, and C. Starica. “Change of Structure in Financial Time Series, Long Range Dependence and the GARCH Model.” Available online: http://citeseerx.ist.psu.edu/viewdoc/versions?doi=10.1.1.56.5517 (accessed on 5 September 2014).
- F.X. Diebold, and A. Inoue. “Long Memory and Regime Switching.” J. Econom. 105 (2001): 131–159. [Google Scholar] [CrossRef]
- M. Balcilar. “Long Memory and Structural Breaks in Turkish Inflation Rates.” In Proceedings of the National Econometrics and Statistics Symposium VI, Gazi University, Ankara, Turkey, May 2003; pp. 1–13.
- R.T. Baillie, and C. Morana. “Modelling long memory and structural breaks in conditional variances: An adaptive FIGARCH approach.” J. Econ. Dyn. Control 33 (2009): 1577–1592. [Google Scholar] [CrossRef]
- A. Fisher, L. Calvet, and B.B. Mandelbrot. “Multifractality of Deutschemark/US Dollar Exchange Rates.” Cowles Foundation Discussion Paper No.1165; New Haven, CT, USA: Yale University, 1997, pp. 1–77. [Google Scholar]
- L. Calvet, and A. Fisher. “Multifractality in Asset Returns: Theory and Evidence.” Rev. Econ. Stat. 84 (2002): 381–406. [Google Scholar] [CrossRef]
- J. Fillol. “Multifractality: Theory and Evidence an Application to the French Stock Market.” Econ. Bull. 3 (2003): 1–12. [Google Scholar]
- S. Jamdee, and C.A. Los. “Multifractal Modeling of the US Treasury Term Structure and Fed Funds Rate.” 2005. Available online: http://econpapers.repec.org/paper/wpawuwpfi/0502021.htm (accessed on 5 September 2014).
- S. Jamdee, and C.A. Los. “Multifractal Modeling of the Japanese Treasury Term Structure.” In Japanese Fixed Income Markets: Money, Bond and Interest Rate Derivatives. Edited by J.A. Batten, T.A. Fetherston and P.G. Szilagyi. Amsterdam, The Netherlands: Elsevier Science, 2006, Chapter 12; pp. 285–320. [Google Scholar]
- J.A. Batten, H. Kinateder, and N. Wagner. “Multifractality and value-at-risk forecasting of exchange rates.” Phys. A Stat. Mech. Appl. 401 (2014): 71–81. [Google Scholar] [CrossRef]
- W. Palma. Long-Memory Time Series: Theory and Methods. Hoboken, NJ, USA: John Wiley & Sons, 2007. [Google Scholar]
- K. Sheppard. “MFE MATLAB Function Reference Financial Econometrics.” 2009. Available online: www.kevinsheppard.com/images/9/95/MFE_Toolbox_Documentation.pdf (accessed on 7 August 2014).
- J. Marcucci. “Forecasting stock market volatility with regime switching GARCH models.” Stud. Nonlinear Dyn. Econom. 9 (2005): 1–53. [Google Scholar] [CrossRef]
- T. Chuffart. “Readme RSGARCH Toolbox.” Available online: www.thomaschuffart.fr/?page_id=12 (accessed on 13 August 2014).
- E.A.F. Ihlen. “Introduction to multifractal detrended fluctuation analysis in Matlab.” Front. Physiol. 3 (2012): 1–18. [Google Scholar] [CrossRef] [PubMed]
- C. Wengert. “Multifractal Model of Asset Returns (MMAR).” Available online: http://www.mathworks.com/matlabcentral/fileexchange/29686-multifractal-model-of-asset-returns--mmar- (accessed on 2 September 2014).
- C. Martineau. “Partition Function for Scaling Moment.” Available online: www.charlesmartineau.com/?page_id=1196 (accessed on 13 August 2014).
- B.S. Kim, H.S. Kim, and S.H. Min. “Hurst’s Memory for Chaotic, Tree Ring, and SOI Series.” Appl. Math. 5 (2013): 175–195. [Google Scholar] [CrossRef]
- S. Günay. “Are the Scaling Properties of Bull and Bear Markets Identical? Evidence from Oil and Gold Markets.” Int. J. Financ. Stud. 2 (2014): 315–334. [Google Scholar] [CrossRef]
- R.F. Engle, and T. Bollerslev. “Modelling the Persistence of Conditional Variances.” Econom. Rev. 5 (1986): 1–50. [Google Scholar] [CrossRef]



| Models | Model Parameters | Model Simulation |
|---|---|---|
| GARCH, EGARCH, FIGARCH | Ox-Metrics | Sheppard [50] |
| Matlab MFE Toolbox | ||
| MRS-GARCH | Marcucci [51] | Chuffart [52] |
| MRS-GARCH MATLAB toolbox | MRS-GARCH toolbox | |
| MMAR | Ihlen [53] | Wengert [54] |
| MF-DFA MATLAB toolbox | MMAR MATLAB codes | |
| Partition Function | Martineau [55] | - |
| MATLAB codes |
| Statistics | Croatia | Greece | Poland | Turkey |
|---|---|---|---|---|
| Mean | 0.000104 | −0.00018 | 0.0000423 | 0.000178 |
| SD | 0.00581 | 0.007811 | 0.006685 | 0.009988 |
| Skewness | 0.097397 | −0.02117 | −0.13425 | −0.06851 |
| Kurtosis | 16.5597 | 7.639252 | 5.761347 | 9.77734 |
| Jarque-Bera | 27,838 *** | 3258 *** | 1165 *** | 6956 *** |
| Methods | Croatia | Greece | Poland | Turkey |
|---|---|---|---|---|
| Detrended Fluctuation Analysis | 0.5397 *** | 0.5166 *** | 0.4805 *** | 0.4832 *** |
| (−0.0199) | (−0.0152) | (−0.0201) | (−0.0094) | |
| Aggregated Variance | 0.6294 *** | 0.5878 *** | 0.5435 *** | 0.5084 *** |
| (0.0297) | (0.0294) | (0.0513) | (0.0444) |
| Countries | |||
|---|---|---|---|
| Croatia | 0.292444 | 0.085159 ** | 0.911678 ** |
| (0.17881) | (0.026237) | (0.027485) | |
| Greece | 0.516918 * | 0.090307 ** | 0.905742 ** |
| (0.23256) | (0.01795) | (0.019015) | |
| Poland | 0.380276 ** | 0.061464 ** | 0.930645 ** |
| (0.12473) | (0.0082957) | (0.0089465) | |
| Turkey | 0.013341 * | 0.103096 ** | 0.886660 ** |
| (0.0053819) | (0.021269) | (0.023662) |
| Countries | ||||
|---|---|---|---|---|
| Croatia | −0.305014 ** | 0.197241 ** | −0.008751 * | 0.984521 ** |
| (0.015919) | (0.007293) | (0.004147) | (0.001323) | |
| Greece | −0.273209 ** | 0.163630 ** | −0.043302 ** | 0.984898 ** |
| (0.021986) | (0.009035) | (0.004873) | (0.001950) | |
| Poland | −0.227455 ** | 0.125215 ** | −0.036094 ** | 0.987054 ** |
| (0.025928) | (0.009624) | (0.005910) | (0.002256) | |
| Turkey | −0.376273 ** | 0.208343 ** | −0.052680 ** | 0.977284 ** |
| (0.027994) | (0.010824) | (0.006009) | (0.002656) |
| Countries | Asymmetry | Tail | GED | ||||
|---|---|---|---|---|---|---|---|
| Croatia | 0.5652 | 0.4498 ** | 0.4124 ** | 0.6391 ** | - | - | 1.0075 |
| (0.3075) | (0.0712) | (0.1262) | (0.1314) | (0.0441) | |||
| Greece | 2.5724 ** | 0.3566 ** | 0.1015 | 0.3849 ** | - | - | 1.2322 |
| (0.7623) | (0.0429) | (0.0733) | (0.0891) | (0.0513) | |||
| Poland | 0.5307 * | 0.5753 ** | 0.2108 ** | 0.7476 ** | - | - | 1.2948 ** |
| (0.2361) | (0.1134) | (0.0488) | (0.0756) | (0.0489) | |||
| Turkey | 3.6399 ** | 0.3523 ** | 0.1235 | 0.3802 ** | −0.0617 ** | 7.7344 ** | - |
| (1.3372) | (0.0426) | (0.0993) | (0.1140) | (0.0227) | (0.9032) |
| Parameters | Croatia | Greece | Poland | Turkey |
|---|---|---|---|---|
| 0.4705 | 0.0554 | 0.0371 | −1.3797 | |
| (0.0619) | (0.0234) | (0.0201) | (0.5813) | |
| 0.0000 | −0.0425 | −1.9493 | 0.1519 | |
| (0.0082) | (0.0408) | (0.4761) | (0.0294) | |
| 0.7287 | 0.0729 | 0.0338 | 0.9673 | |
| (0.4098) | (0.0247) | (0.0119) | (0.4796) | |
| 0.0201 | 0.4484 | 0.0758 | 0.0633 | |
| (0.0061) | (0.1344) | (0.9568) | (0.0213) | |
| 0.2965 | 0.0742 | 0.0458 | 0.0470 | |
| (0.1782) | (0.0187) | (0.0107) | (0.0394) | |
| 0.0981 | 0.1037 | 0.0320 | 0.0677 | |
| (0.0151) | (0.0225) | (0.1764) | (0.0118) | |
| 0.1757 | 0.8627 | 0.9177 | 0.9497 | |
| (0.3783) | (0.0326) | (0.0114) | (0.0735) | |
| 0.8868 | 0.8002 | 0.9537 | 0.8861 | |
| (0.0139) | (0.0419) | (0.3109) | (0.0122) | |
| 0.9341 | 0.9991 | 0.9916 | 0.7518 | |
| (0.0247) | (0.0007) | (0.0034) | (0.0904) | |
| 0.9922 | 0.9995 | 0.6206 | 0.9839 | |
| (0.0034) | (0.0006) | (0.1313) | (0.0069) |
| Croatia | Greece | Poland | Turkey | |
|---|---|---|---|---|
| 1.6331 | 1.8368 | 1.8595 | 2.0000 |
| Countries | H | |||
|---|---|---|---|---|
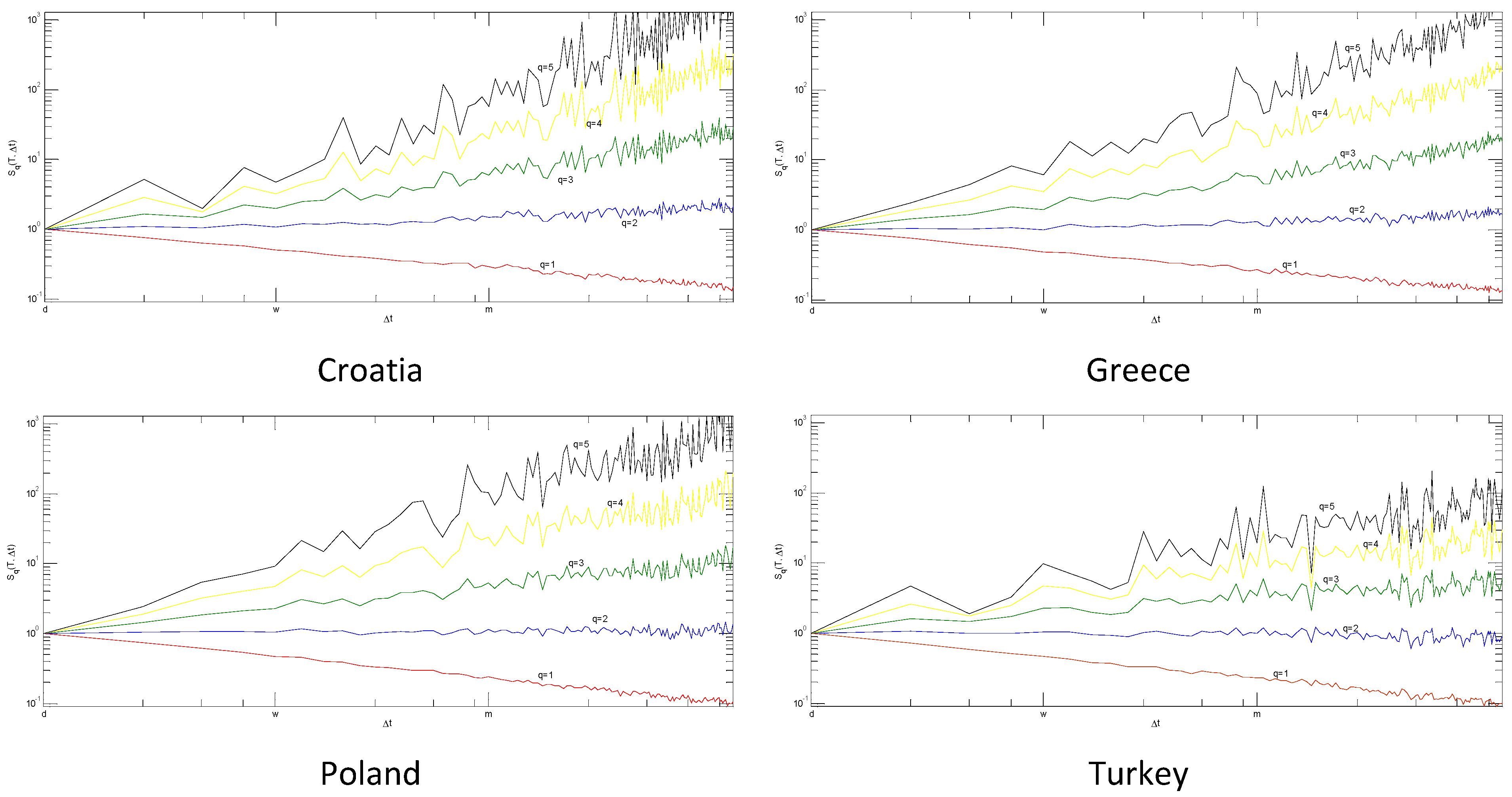
| Croatia | 0.6123 | 0.6392 | 1.0439 | 0.1268 |
| Greece | 0.5444 | 0.5522 | 1.0143 | 0.0411 |
| Poland | 0.5378 | 0.5524 | 1.0272 | 0.0783 |
| Turkey | 0.5000 | 0.5455 | 1.0910 | 0.2597 |
| MMAR | GARCH (1.1) | EGARCH (1.1) | FIGARCH (1.1) | MRS-GARCH | |||
|---|---|---|---|---|---|---|---|
| Simulation Results | |||||||
| Croatia | 1 | −0.39 | −0.38 | −0.48 | −0.49 | −0.48 | −0.53 |
| 2 | 0.21 | 0.20 | −0.01 | −0.01 | −0.01 | −0.09 | |
| 3 | 0.76 | 0.76 | 0.40 | 0.42 | 0.41 | 0.32 | |
| 4 | 1.27 | 1.28 | 0.76 | 0.81 | 0.79 | 0.71 | |
| 5 | 1.74 | 1.77 | 1.09 | 1.18 | 1.13 | 1.08 | |
| Greece | 1 | −0.45 | −0.45 | −0.48 | −0.49 | −0.49 | −0.46 |
| 2 | 0.09 | 0.08 | −0.01 | −0.01 | −0.01 | 0.07 | |
| 3 | 0.59 | 0.59 | 0.39 | 0.43 | 0.43 | 0.59 | |
| 4 | 1.05 | 1.08 | 0.75 | 0.83 | 0.82 | 1.09 | |
| 5 | 1.47 | 1.54 | 1.07 | 1.20 | 1.18 | 1.56 | |
| Poland | 1 | −0.46 | −0.45 | −0.49 | −0.50 | −0.49 | −0.50 |
| 2 | 0.07 | 0.07 | −0.01 | −0.02 | -0.01 | −0.01 | |
| 3 | 0.57 | 0.57 | 0.44 | 0.44 | 0.42 | 0.46 | |
| 4 | 1.04 | 1.05 | 0.85 | 0.86 | 0.81 | 0.92 | |
| 5 | 1.48 | 1.51 | 1.23 | 1.26 | 1.17 | 1.36 | |
| Turkey | 1 | −0.47 | −0.47 | −0.48 | −0.49 | −0.49 | −0.48 |
| 2 | 0.00 | 0.00 | −0.01 | −0.02 | −0.02 | −0.01 | |
| 3 | 0.42 | 0.42 | 0.40 | 0.42 | 0.42 | 0.41 | |
| 4 | 0.80 | 0.81 | 0.76 | 0.82 | 0.81 | 0.78 | |
| 5 | 1.14 | 1.16 | 1.09 | 1.18 | 1.17 | 1.13 | |
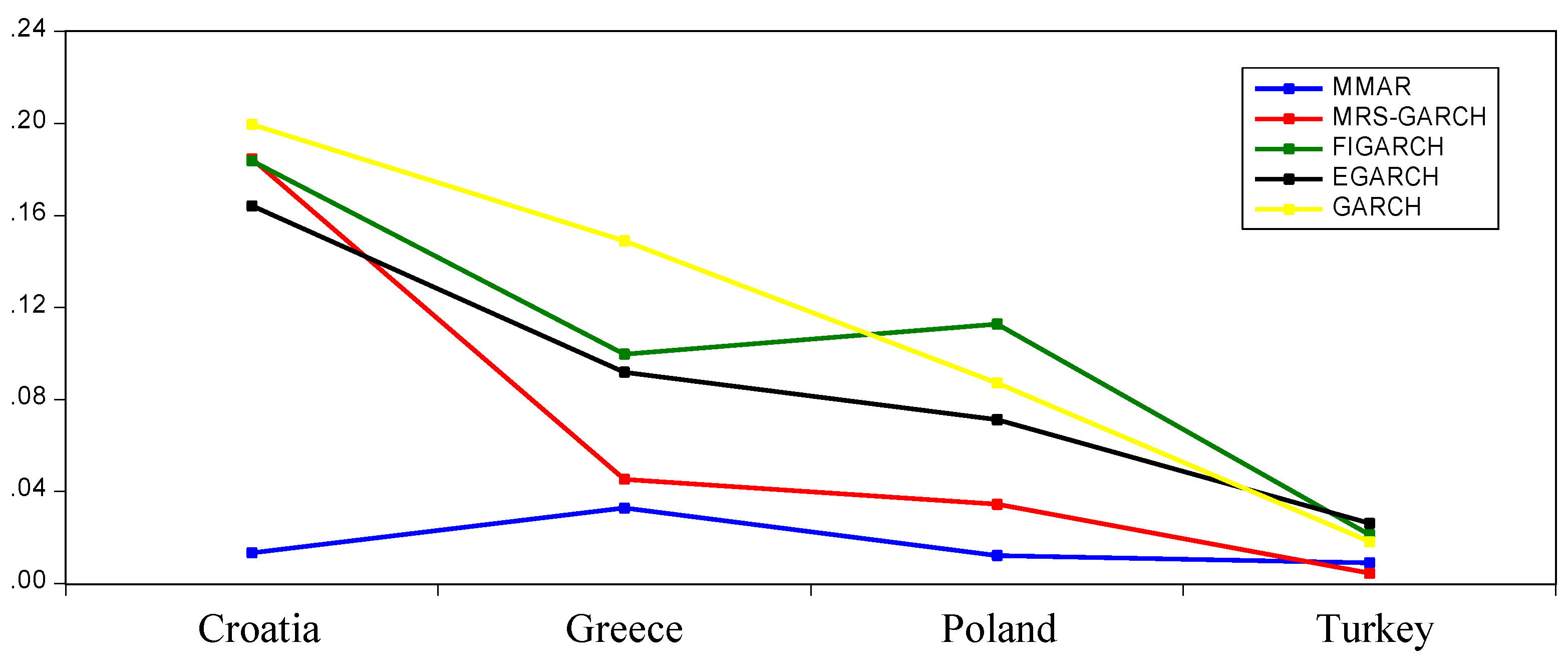
| Countries | MMAR | GARCH (1.1) | EGARCH (1.1) | FIGARCH (1.1) | MRS-GARCH |
|---|---|---|---|---|---|
| Croatia | 0.0133 | 0.1995 | 0.1641 | 0.1838 | 0.1846 |
| Greece | 0.0327 | 0.1489 | 0.0918 | 0.0996 | 0.0453 |
| Poland | 0.0122 | 0.0871 | 0.0712 | 0.1127 | 0.0344 |
| Turkey | 0.0089 | 0.0182 | 0.0261 | 0.0212 | 0.0045 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Günay, S. Performance of the Multifractal Model of Asset Returns (MMAR): Evidence from Emerging Stock Markets. Int. J. Financial Stud. 2016, 4, 11. https://doi.org/10.3390/ijfs4020011
Günay S. Performance of the Multifractal Model of Asset Returns (MMAR): Evidence from Emerging Stock Markets. International Journal of Financial Studies. 2016; 4(2):11. https://doi.org/10.3390/ijfs4020011
Chicago/Turabian StyleGünay, Samet. 2016. "Performance of the Multifractal Model of Asset Returns (MMAR): Evidence from Emerging Stock Markets" International Journal of Financial Studies 4, no. 2: 11. https://doi.org/10.3390/ijfs4020011
APA StyleGünay, S. (2016). Performance of the Multifractal Model of Asset Returns (MMAR): Evidence from Emerging Stock Markets. International Journal of Financial Studies, 4(2), 11. https://doi.org/10.3390/ijfs4020011





