Abstract
In this paper, a level set analysis is proposed which aims to analyze the S&P 500 return with a certain magnitude. It is found that the process of large jumps/drops of return tend to have negative serial correlation, and volatility clustering phenomenon can be easily seen. Then, a nonparametric analysis is performed and new patterns are discovered. An ARCH model is constructed based on the patterns we discovered and it is capable of manifesting the volatility skew in option pricing. A comparison of our model with the GARCH(1,1) model is carried out. The explanation of the validity on our model through prospect theory is provided, and, as a novelty, we linked the volatility skew phenomenon to the prospect theory in behavioral finance.
Keywords:
level set analysis; nonparametric regression; ARCH/GARCH model; prospect theory; behavioral finance; agent-based modeling JEL:
C14; C58; G02
1. Introduction
Building a good mathematical or statistical model is fundamental to modern financial studies. Although the geometric Brownian Motion plays an important role in the modeling of modern financial studies due to its conciseness, it has become common sense that the log returns in the stock market are not i.i.d. (independent and identically distributed) normal random variables. New patterns on the stock returns have been discovered and new models have been constructed in the past three decades—for example, the phenomenon of volatility skew in the equity market and volatility smile in the currency market, and the ARCH models [1] and GARCH models [2] that were proposed to capture the clustering property of highly volatile periods in stock returns, although they lack the characterization of serial correlations in the return process. Stochastic volatility (SV) models, e.g., [3,4], were presented as an extension to the ARCH/GARCH models and they are shown, under some situations, to be capable of reproducing the volatility skew phenomenon [5]. The statistical aspects on ARCH and SV models was analyzed in [6]. In [7], Barndorff–Nielsen and Shephard constructed positive OU processes for the volatility processes and carried out extensive model calibration. The modelling with Lévy processes is presented in [8] and theoretical analysis on related processes can be found in [9]. Interested readers are referred to [10] for a comprehensive literature on financial time series analysis. Besides the traditional time domain analysis, other methods include the spectrum analysis and wavelet analysis [11,12], the analysis through P/E ratio [13], and some other recent progress [14].
Another major branch of study to capture the volatility skew/smile phenomenon is the so-called regime switching models, e.g., [15,16]. The parameters in these models vary due to the changing of market or economic states, and it can be shown that these models can replicate the volatility skew/smile phenomenon. However, the biggest challenge to this explanation is that volatility skew/smile phenomenon is seen only from market data after the 1987 crash but is not seen from market data before 1987. Therefore, the 1987 crash must have brought some fundamental change to the market and, very likely, in the behavior of investors.
Most of the aforementioned models are proposed to mimic the evolution of asset price in a statistical or mathematical point of view, and there is a tendency toward complication in these models. Furthermore, little work has been found to explain why these models are valid in a practical and realistic point of view. On the contrary, behavioral finance often provides an explanation from a different aspect. For example, Chen et al. [17] studied the price effects of changes to the S&P 500 Index and discovered an asymmetric price response around additions to and deletions from the S&P 500 Index. In [18] and also in [19], the authors presented an agent based model, where the agents’ trading behavior consists of a fundamental component and a trend chasing component. The final trading decision is a random combination of these two components, and the price is thus determined by the market clearing condition. A limiting diffusion model is derived, which is a random regime switching dynamic process.
Frey and Stremme [20] modeled the market participants as reference traders and program traders, where the former make decisions based on their utility function and investigated the effect of dynamic hedging on volatility. They showed that the heterogeneity of the distribution of hedged contracts is one of the key determinants for the transformation of volatility. Heemeijer et al. [21] showed that when the economic agents have positive expectations about the market development, due to the feedback effect, large fluctuations in realized prices and persistent deviations from the fundamental are likely; when they have negative expectations, prices converge quickly to their equilibrium values. According to the work of Danilova [22], the main explanation of the volatility of asset returns is the volume of trade. Lyengar and Ma [23] linked the asset price and trading volume through the study of behavioral finance, and proposed a logistic regression model for jointly predicting stock price and volume at the tick-by-tick level. This work provided a novel path for the search for more comprehensive results.
Furthermore, in order to explain the volatility smile and skewness phenomenon, Platen and Schweizer [24] assumed that the market participants consist of arbitrage-based agents (or speculators) and hedgers (or technical agents), and the volatility smile effect is obtained through the Black–Scholes hedging of European call options from the technical component. This research work through behavioral finance provides evidence that feedback effects from the traders’ behavior play an important role in the study of price fluctuations.
Market fluctuations are accompanied with the activities of investors, especially those of large financial agents who often have information advantages. Therefore, studying the market fluctuations such as large jumps or drops in the stock market can provide us with information about the patterns of activities of participating financial agents. In this paper, we propose a level set analysis on the S&P500 return in Section 2. We discovered that the magnitude of the return has patterns of correlations, and a volatility clustering property can be easily seen in this method. Furthermore, we find that the return process tends to have negative/oscillating serial correlation. Then, in Section 3, a nonparametric analysis is performed and new patterns on the data are discovered which are in accordance with our findings in Section 2. After that, an ARCH model is constructed which is capable of manifesting the volatility skew in option pricing, and a comparison of this model with the GARCH(1,1) model is carried out. Section 4 proposes an explanation on the validity of our model through the prospect theory [25] in behavioral finance, and the connection between the volatility skew phenomenon and prospect theory is novel to the best of our knowledge. The contributions and discoveries of this paper are summarized in Section 5.
2. Level Set Analysis
The term level set in this paper refers to the set of stock returns whose magnitudes exceed a certain level/threshold. Large jumps or drops in stock market are often associated with the actions of large financial agents, who usually have information advantages over individual investors. Therefore, we are very interested in finding out if there are patterns in large fluctuations in the stock market.
Figure 1 shows the log return of the daily S&P 500 Index and its histogram of the market data from Jan 2, 1990 to May 2, 2013. The normal distribution density curves are provided as well.
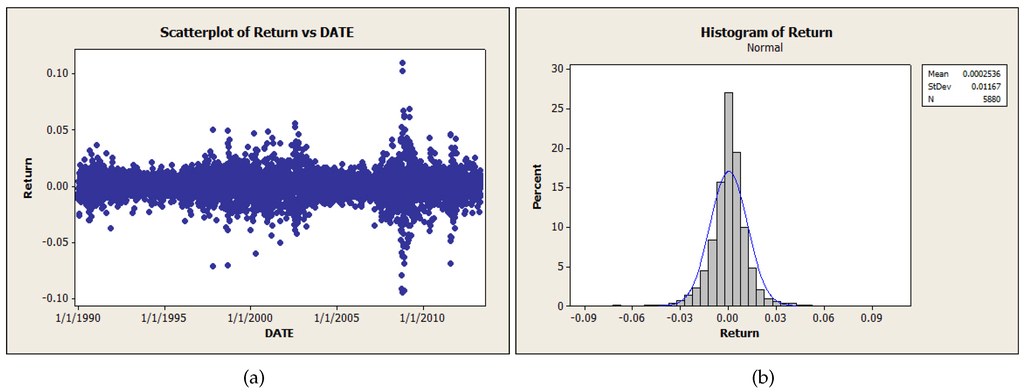
Figure 1.
Market Data. (a) daily Returns; (b) histogram of Return Data.
In fact, the i.i.d. normal assumption on returns can be easily challenged. For example, a simple normality test is provided in Figure 2 for the original return data.

Figure 2.
Normal probability plot.
In this section, we are especially interested in these questions such as “Does the magnitude of the log returns correlate with the return process?”, “What is the distribution of the log returns with a certain magnitude?”, and “Is there any pattern in the return process in consideration of the magnitude?”, etc. The reason we did this is that large jumps in the financial market are believed to contain special information.
For the same set of data as in Figure 1, we first remove the mean of the return and get the excessive return data. Notice that the all time mean of the original data is 0.000254, which is very close to zero. Table 1 provides some basic statistics on the excessive return with a certain minimum magnitude. For example, the variable “Return0.01” represents the return with absolute magnitude of at least 0.01, which indicates a daily index change being greater than or equal to 1% over the all time average. Thus, the entire observations are grouped into several level sets. The box plots for these groups of variables are shown in Figure 3.

Table 1.
Basic statistics on excessive returns.

Figure 3.
Box plots.
It can be seen that, starting from the variable “Return 0.008” in the excessive return data, the group means begin to show large deviation from zero, and actually, most of the means are negative except the last group (“Return 0.1”) which has only two observations. In some sense, this mimics the so called “pump and dump” phenomenon. Although the “pump and dump” phenomenon is often associated with penny stocks, it seems that this phenomenon is also associated with the S&P 500 Index. To the best of the authors’ knowledge, looking into the daily S&P 500 return in this way is novel.
Then, how about the serial correlation in each group? Let us first look at the scatter plots of some groups in Figure 4, and the rest are omitted due to similarity.

Figure 4.
Scatter plots.
An interesting question is that, if a return with a certain magnitude has been observed one day, what is the distribution of the number of days until the next occurrence with the same or larger magnitude? We call this time interval the waiting time. An observation with large magnitude indicates a shock on the market, and, therefore, this distribution is of much interest. Using the given data, we plot in Figure 5 the histograms of the waiting time for some of these groups with considerably large numbers of observations.
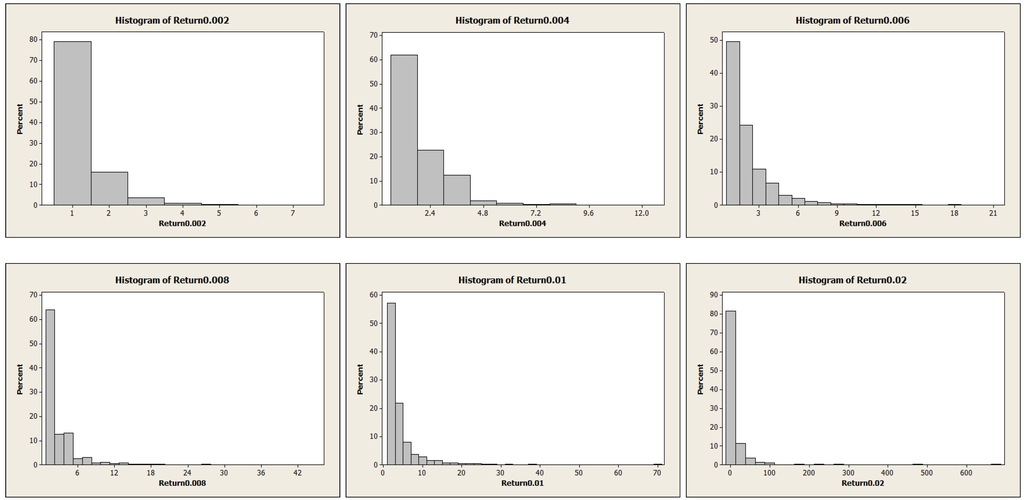
Figure 5.
Histogram of waiting time.
From Figure 5, it can be clearly seen that the probability density concentrates on the region of short waiting time, and this phenomenon is especially notable for returns with large magnitude. This phenomenon certainly agrees with the volatility clustering property in GARCH models or stochastic volatility models.
However, there is a feature that the traditional ARCH/GARCH models or stochastic volatility models might have missed, which is, besides the volatility clustering, would the observations tend to have positive or negative serial correlation? We run the Durbin–Waston (DW) test on some of the groups of data with considerably large numbers of observations, and the result is shown in Table 2. Since we are only interested in the serial correlation of the data in each group where the data tend to have a clustering manner, the time interval (or waiting time) between any two consecutive observations in a group is ignored for now.

Table 2.
Durbin–Watson test.
It should not be a surprise that all of the data examined in Table 2 exhibit negative serial correlations (DW > 2). To further strengthen our findings, we perform a Run Test on the data to test the randomness. Once again, the time intervals are ignored temporarily so that we can focus on the serial correlation. The results are shown in Figure 6.
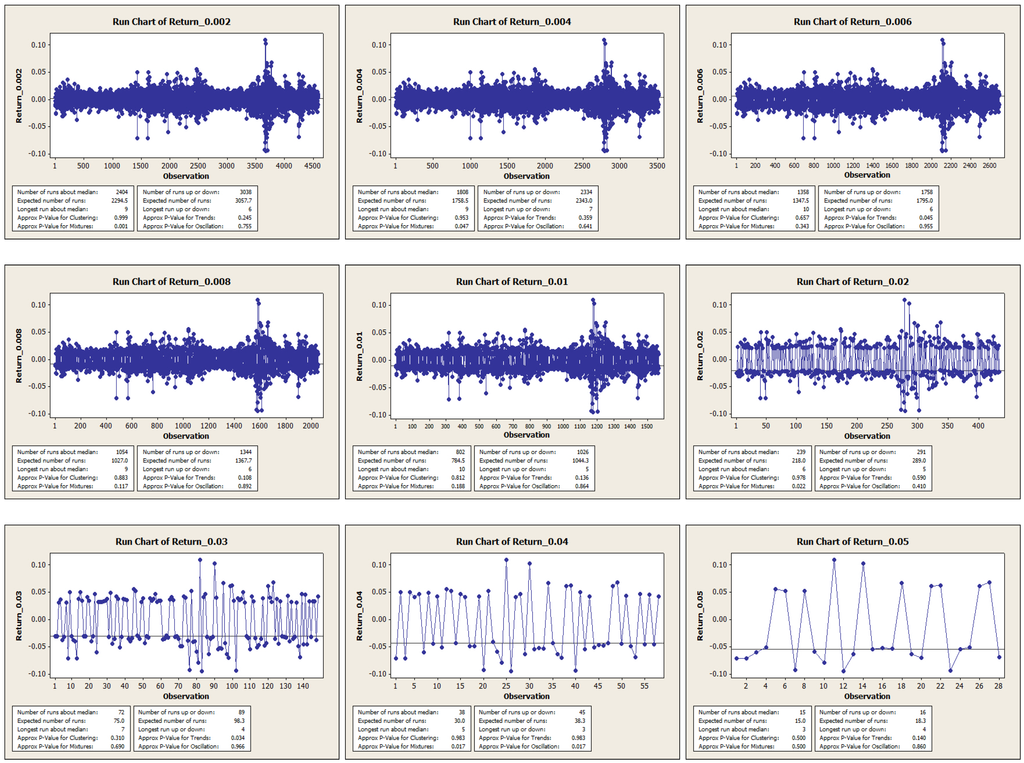
Figure 6.
Run charts.
We notice that the oscillation in the group “Return 0.04” is especially significant (p-Value = 0.017). In the meantime, we understand that if we change the cutoff of the magnitude, a few observations are inserted into or discarded from the original set. Recall that the Run Test for randomness is very sensitive to the order of observations, and, as a consequence, the test results for randomness could be very different from group to group.
Then here comes a natural question: would the negative serial correlation be more manifest during economic crisis? We take the piece of data from Jan 2, 2008 to Dec 31, 2009 and perform the Durbin–Watson Test on the level sets, and the result is shown in Table 3.

Table 3.
Durbin–Watson Test on 2008 Crisis.
If we compare Table 2 to Table 3, we see that the negative serial correlation in the level sets is more manifest during the 2008 crisis.
As a short summary of what we have found so far, the S&P 500 daily return, based on the given data, tends to have negative serial correlation as well as a volatility clustering property. Therefore, the assumption of independence of daily returns, which is the basis of much research work, is challenged. In the next section, we perform a nonparametric regression on the daily data and the results are consistent with our findings.
3. Nonparametric Regression
The level set analysis in Section 2 gives us a new insight into the S&P 500 daily return, yet we hope to build a time series model on this process that is capable of capturing the features we have found, and we accomplish this task through a nonparametric regression technique.
3.1. Local Polynomial Regression
Let be a time series (of the return process), we want to fit an ARCH model so that
where are i.i.d. random variables. Local polynomial regression [26,27] is used to estimate the drift (f) and volatility (g) functions. An early work on the application of this technique on financial time series can be found in [28]. The procedure is as follows: we seek a function which satisfies
Let n be the size of , then for each x, consider the following two minimization problems:
where denotes a nonnegative weight function and h is a positive number called the bandwidth. We choose K to be the standard normal p.d.f. Then, is estimated at , and the estimation of f is given by .
Let be the daily data of S&P500 index where the last date is May 2, 2013, and let be the yield process, i.e., . For each data size S, we choose the bandwidth h to be , where all ’s belong to this set and γ is a chosen positive constant. In what follows, we shall pick different data sizes and different values of γ, and plot the graphs of and .
From Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, we can observe the following phenomena.
Observations:
- There is a pattern of . If , is slightly negative. If , is positive. This represents a mean reverting pattern, or negative serial correlation on .
- If is large, i.e., there is a big gain at time , then on expectation, tends to be slightly negative. However, if is large negative, then on expectation, tends to be largely positive. So, there is an obvious bend in the curve of .
- All the graphs of show U-shaped “smiling faces”, and the minimum is achieved at a point of close to zero. In fact, a point that is slightly to the right of zero. Thus, large magnitude of corresponds to large volatility. What is more, on each “smiling face”, the left side of the curve is higher than the right side of the curve. Thus, these are tilted “smiling faces”, or skew.
- When γ is big, we observe the boundary effect on the boundaries of the interval, see, e.g., the graphs of . This phenomenon was also observed in [26] where an explanation was provided.
- These discoveries are pretty robust in view of various data sizes.
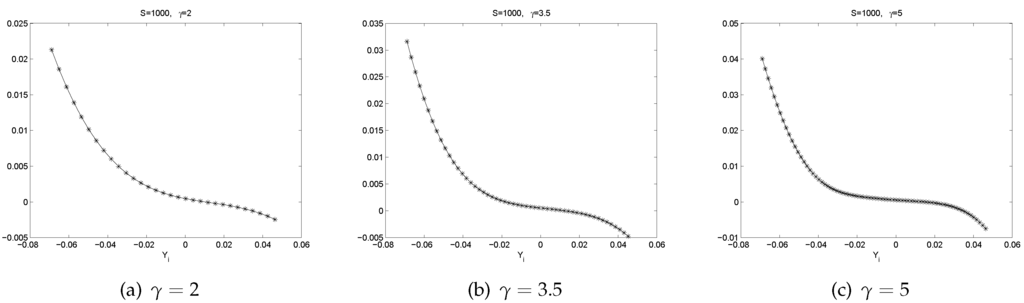
Figure 7.
.

Figure 8.
.
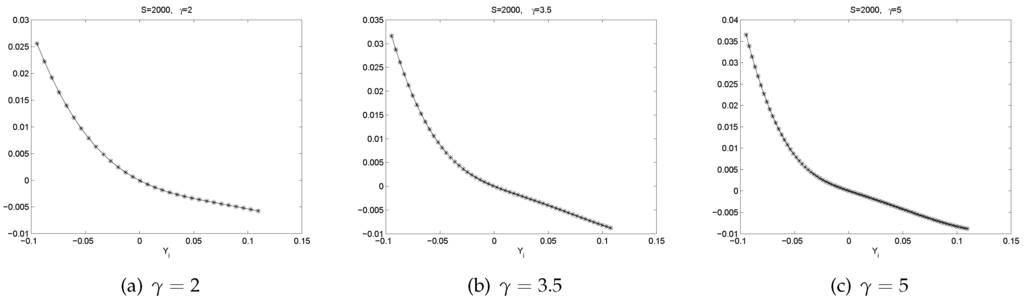
Figure 9.
.
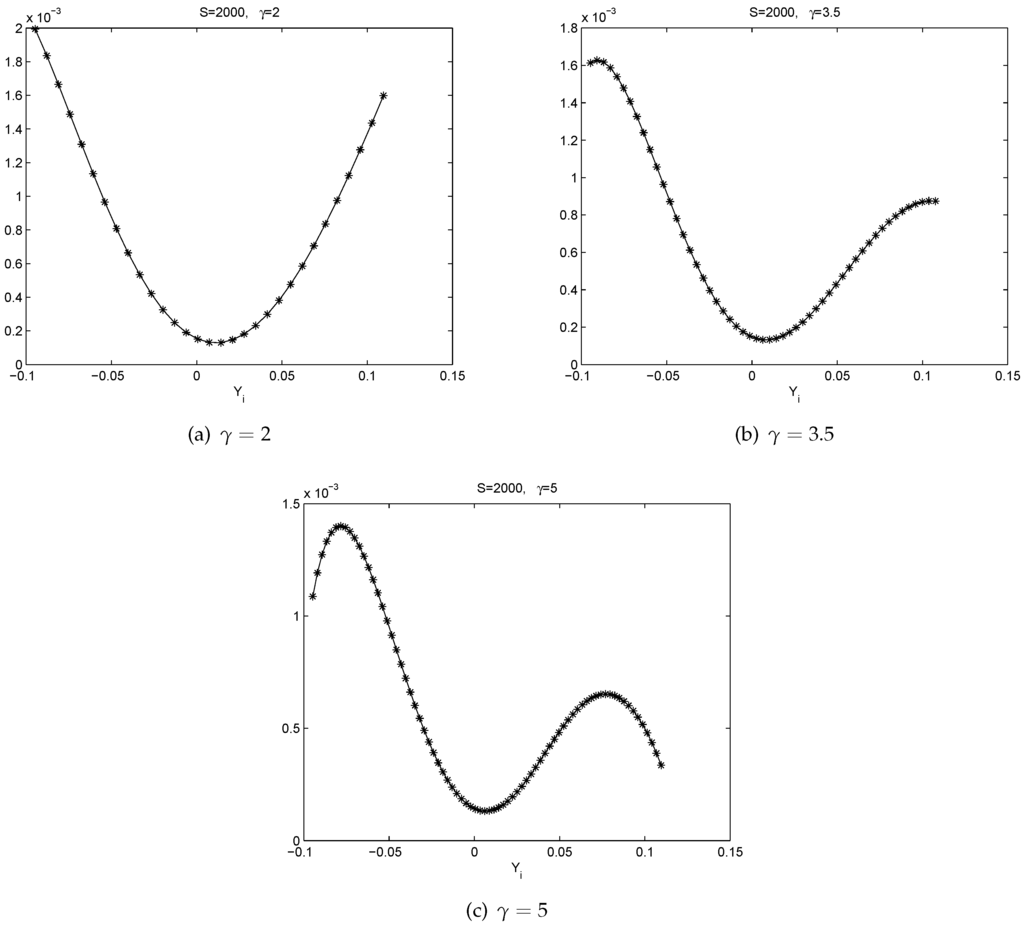
Figure 10.
.
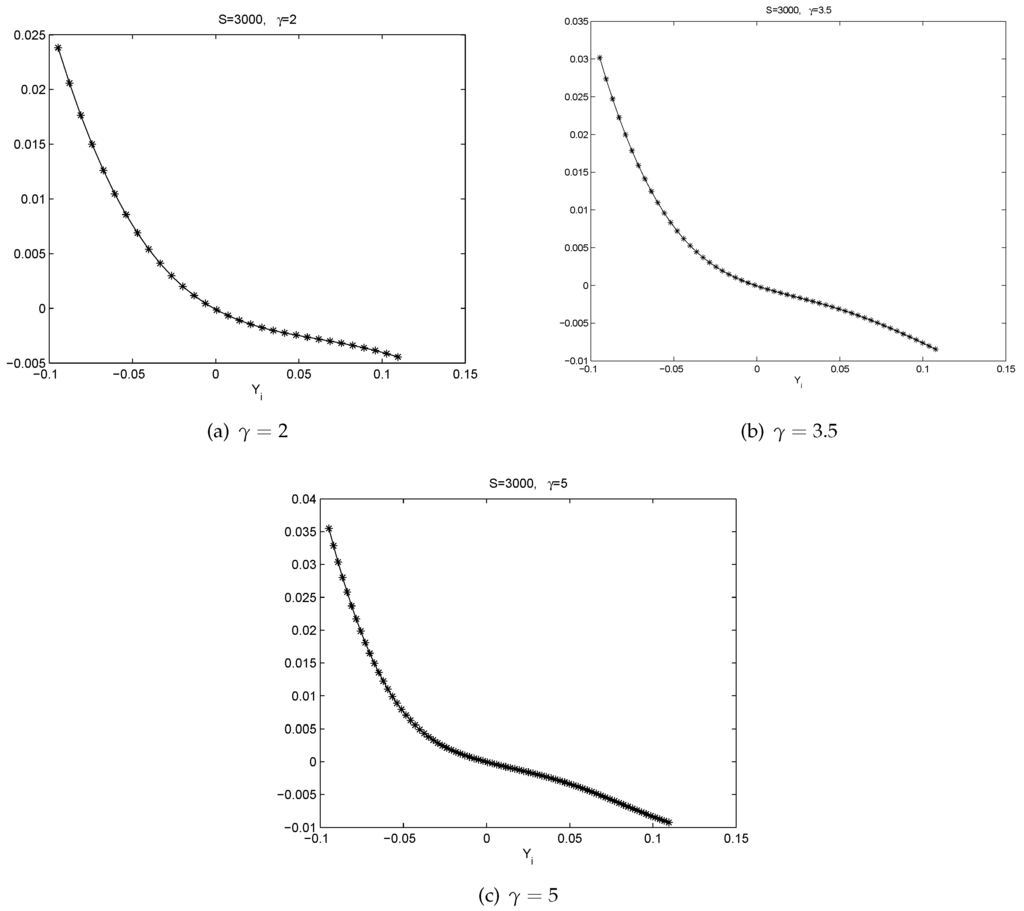
Figure 11.
.

Figure 12.
.
The results from local regression methods agree with our conclusions in Section 2, i.e., the return process tends to be negatively serially correlated and has volatility clustering. Furthermore, these results enable us to build a time series model on the S&P 500 Index. The steps are shown in the next section.
3.2. An ARCH Model
Then, it is not hard to find polynomial approximations to f and g, respectively, and we get the following ARCH model
where . That is,
where represent the polynomial approximations of , respectively. Figure 13 shows the graphs of and .
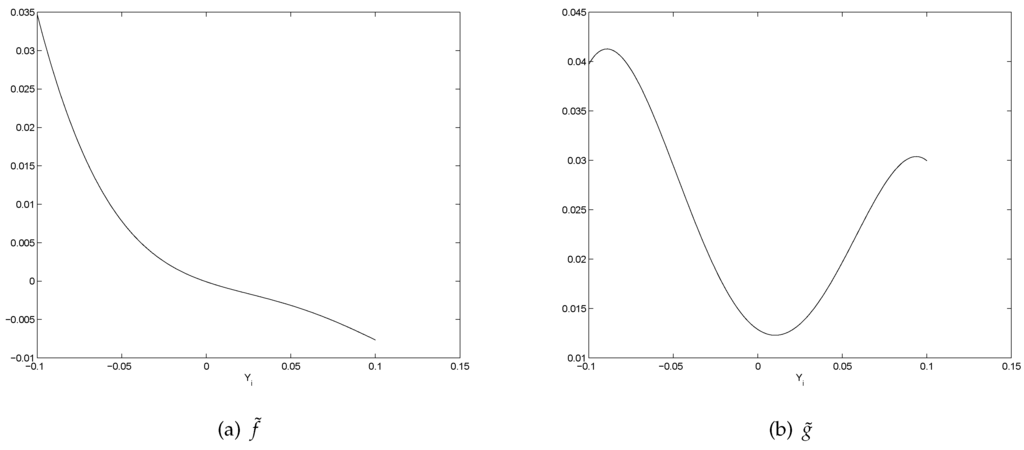
Figure 13.
Polynomial Approximations of .
It can be seen that this model is a local volatility model, but, different from most well known local volatility models which aim to replicate the implied volatility surface only, our model replicates both the drift term and volatility term through real data calibration using the technique of local polynomial regression. Our model is also different from most of the SV models, such as [7], in that the volatility term is a special function of the return. We believe that general linear regression is incapable, if not impossible, of achieving such a model. Figure 14 shows some sample paths of this ARCH model.
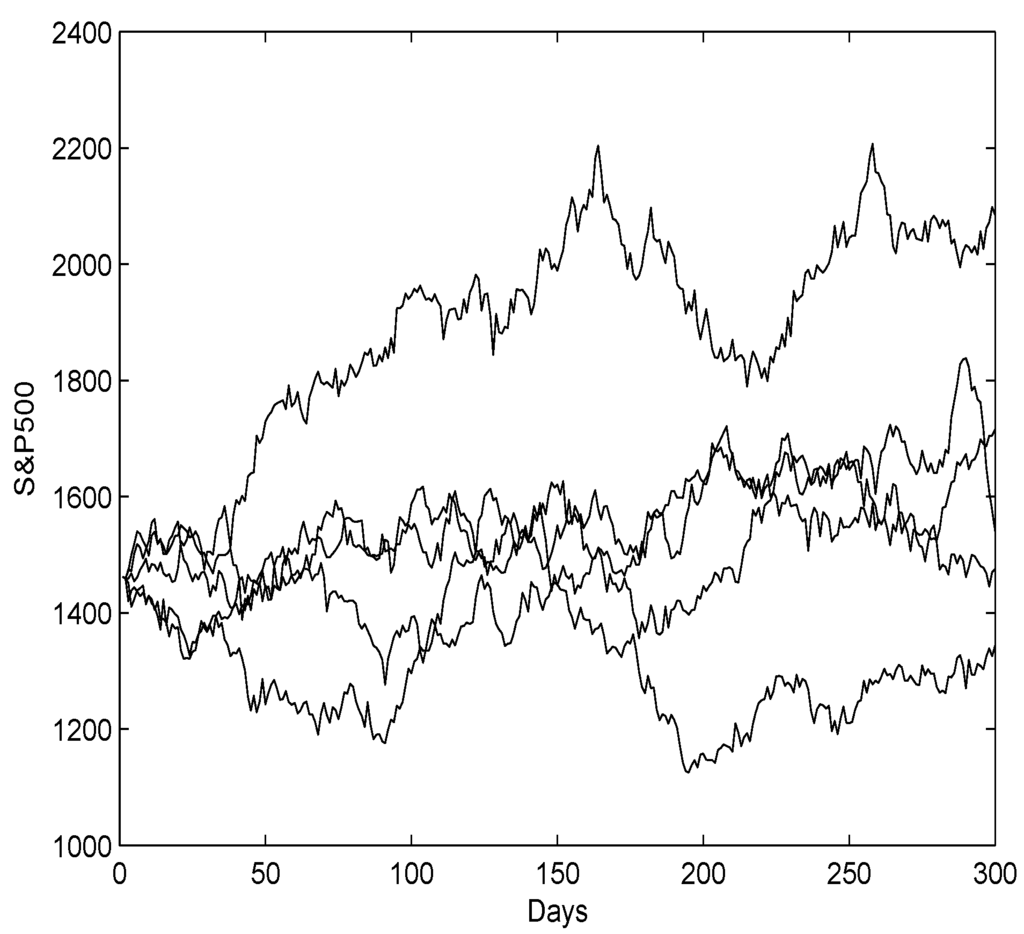
Figure 14.
Sample Paths.
3.3. Model Comparison
In order to check the performance of model (5), we compare it to an GARCH(1,1) model. The GARCH(1,1) model is estimated, using our market data as in Table 1, at
where is the excessive daily return and ’s are i.i.d. standard normal random variables (lower case letters are used to indicate that they come from a different model). This model can be obtained through standard techniques. We used the fGarch package in R (version 3.2.3).
A random path with 5880 daily returns is generated using model (5) with initial values and as of Jan 2, 1990 and Jan 3, 1990, respectively, and the DW test on the level sets is shown in Table 4.

Table 4.
Durbin–Watson Test on model (5).
We can see that model (5) shows a pattern of negative serial correlation in the return process. Due to Equation (6), the GARCH model assumes that the return process is white noise, and now we believe that there is large space to improve.
Then, using the GARCH(1,1) model (6) and (7), we generate a random path of the same length and compare the distributions of daily returns with model (5) and the market data. The normal fits and the density functions are also shown in Figure 15.
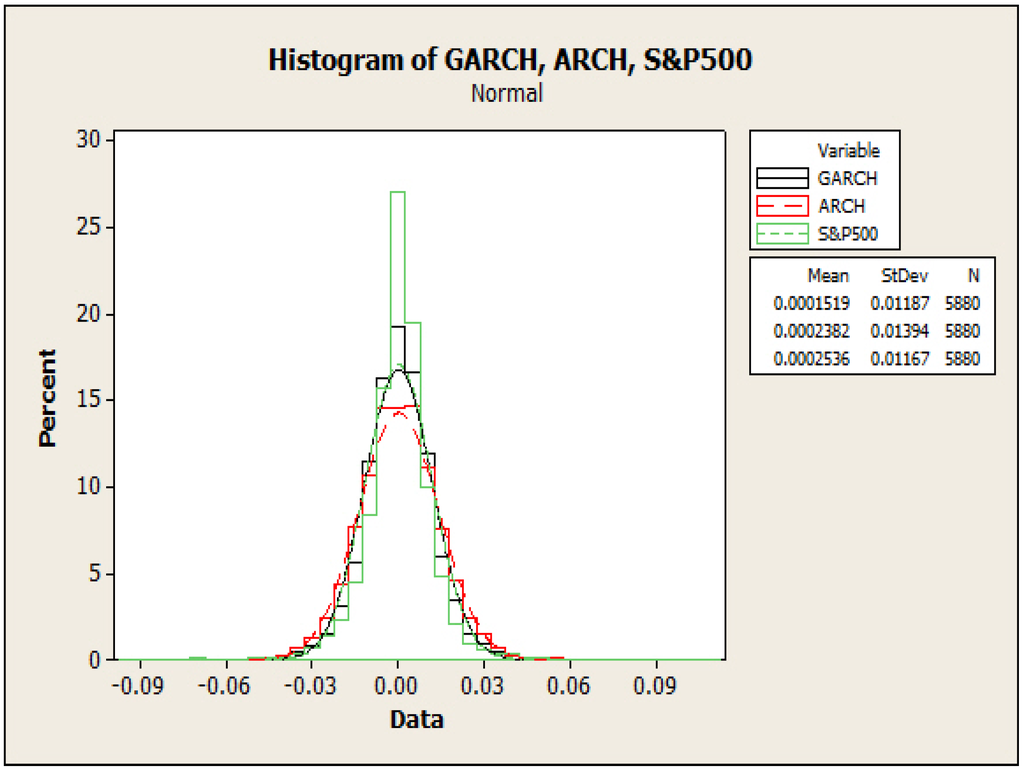
Figure 15.
Density functions.
It can be seen from Figure 15 that both the GARCH(1,1) model (6) and (7) and the ARCH model (5) have “fatter” distribution than that of the market data, but the histogram of GARCH(1,1) model fits the histogram of S&P 500 return a little better. We believe that this is due to the natural advantage of GARCH models over ARCH models. A promising future research topic is to incorporate the GARCH model into the nonparametric regression in order to capture more features of the market data.
Finally, recall that Figure 14 shows only five random paths of the ARCH model (5), and we are now interested in the terminal distribution of the stock index using this model. Thus, we generated 10,000 random paths with length 300 using model (5) and examine the terminal distribution. The initial values are . For the purpose of comparison, we did the same for the GARCH(1,1) model. The results and the log-normal fits are provided in Table 5 and Figure 16.

Table 5.
Terminal distribution.

Figure 16.
Terminal distribution.
Table 5 and Figure 16 show that the GARCH(1,1) model has a slightly larger mean, smaller deviation but very large maximum. Recall that the GARCH model (6) and (7) captures the volatility clustering very well but ignores the negative serial correlation (or mean reverting) in the return, so it could generate very extreme values. Future research may focus on incorporating the mean reverting property and volatility clustering property of GARCH models into the nonparametric regression.
3.4. Option Pricing and Implied Volatility
To see if the model (5) could replicate the volatility skew in option pricing, we use Monte Carlo simulations. Other numerical methods solving option pricing problem with SV models or stochastic interest rate via partial differential equations can be seen, e.g., in [31,32].
In order to get the price of the European call options, we rewrite this model under the risk neutral measure and get
where r is the risk free interest rate, , is the standard normal random variable under the risk neutral measure, and
In order to find the proper number of paths, we use Monte Carlo simulation to price a European call option with the following parameter settings: annual interest rate , time to maturity months, strike price and underlying price . We chose this option because it has the largest variance in our model. The number of paths ranges from 10,000 to 1,000,000, and for each setting, 20 trials are run and the standard deviation of the option prices are calculated. The result is shown in Figure 17.

Figure 17.
Standard deviation.
We can now set the number of paths to be 500,000. Figure 18 shows a Monte Carlo simulation on call option prices with 500,000 sample paths.
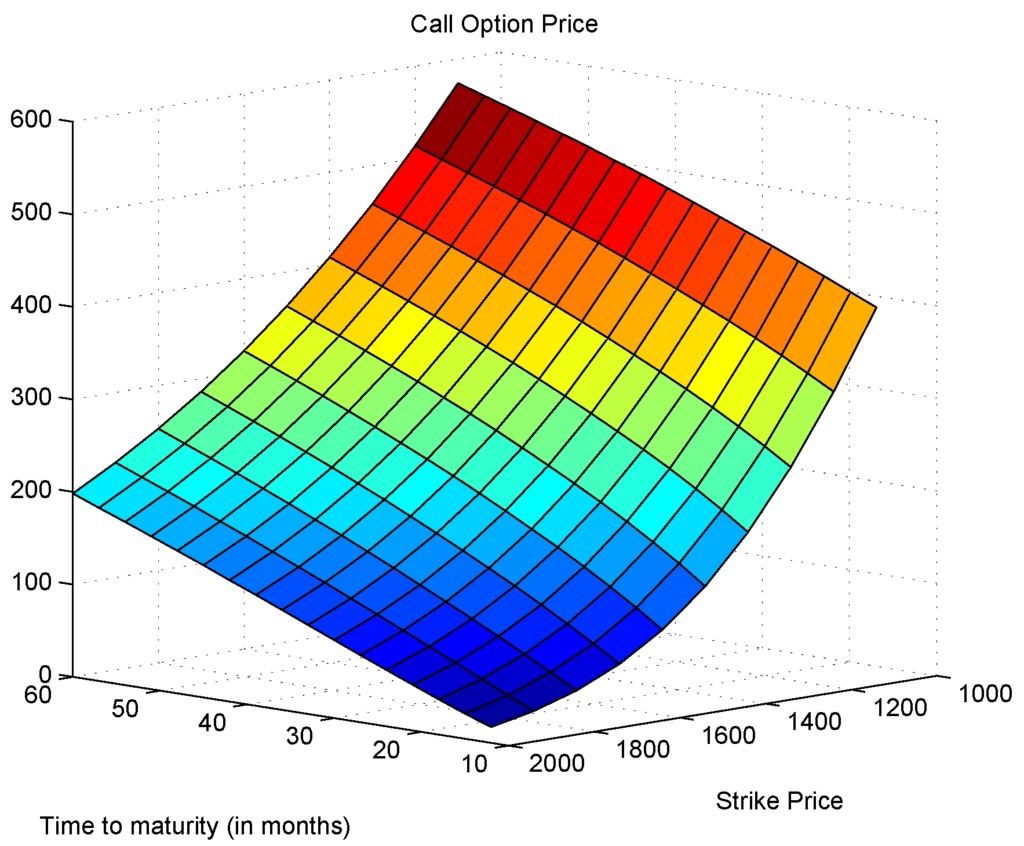
Figure 18.
Call options prices.
We pick the region and (months) to recover the implied volatility surface from the Black–Scholes formula. The reason is that, on this region the computation is considered to be stable because is not too close to zero. Figure 19 shows the implied volatility surface through the Black–Scholes formula. Thus, the volatility skew can be clearly seen.

Figure 19.
Implied volatility surface–S&P 500.
4. Price Fluctuation and Market Participants
In this section, we shall give a tentative explanation of our findings in Section 3. As is widely accepted, asset price is determined by the temporary balance between demand and supply. Excessive demand would push the price high and excessive supply would press it down, with the market clearing condition being held. This effect is determined by the traders’ actions. In this approach, understanding the behavior of the interacting traders is the key to model the price process. In the agent-based model presented in [18,19] as introduced in Section 1, the reference of a fundamentalist is given by
where is an agent’s reference level. The idea is that the agent believes that the asset price will finally go to its fundamental value F. While by the trend chasing component, the agent believes that the asset price forms a trend and hence the reference is given by
The final trading decision is a random combination of these two components, and the price is thus determined by the market clearing condition. The model in [24] assumed that the cumulative demand of the asset up to time t is given by
where is a Brownian Motion with drift m and volatility v. The part corresponds to the demand of speculators where is a constant, and is the cumulative demand of hedgers. The dynamics of was then obtained by differentiating, using Ito’s formula, the equation , which is due to the market clearing condition.
Although there is no agreement yet what kind of market participants and what kind of behavior there are, it should be noticed that, besides the noisy demand in the market, there are usually more than one types of agents (traders or components) in the market. Observing the phenomenon that market participants often have expectations on their investment, either arbitrage or hedging, and they behave differently when they feel a gain vs. a loss of their investments, we present in this paper the prospect agents. Through this model, we are able to derive a stochastic price process that explains the volatility skew phenomena that is observed from real market data.
4.1. Prospect Agents
In this section, we shall derive the asset price dynamics through feedback effect via market clearing conditions. As in [19], we assume the noisy demand and trend chasing demand as part of the market component, yet our method is different from [19,24] in that we model the behavior of the other traders through a different point of view.
It has been widely observed that whenever there is a big jump or drop of a stock price, there is a large volume of transactions associated with it, see, e.g., [23], together with large volatilities, see, e.g., [33] where this phenomenon is “possibly explained by behavior factors influencing the stock markets on or near dates of extreme events”. It is commonly accepted that the decisions of the investors to buy or to sell the asset depend on the gains or losses of this asset, see, e.g., [34]. By means of gain and loss, we mean the difference between the return of the asset and a reference rate of return, for example, a rate of return close to zero or comparable to the daily interest rate. That is, if is bigger than a threshold, investors feel gains of the investment, and if is less than this threshold, investors feel losses of their wealth. These different feelings result in different trading behaviors. If is above the reference rate, the excessive demand of this asset will increase. However, the investors who long the asset feel a gain and some of them try to realize the profit by selling some shares. In other words, they show a risk-averse behavior. For investors who short the asset, some of them feel that they have already missed the chance to make profit, and therefore some of them do not want to buy the asset. As a result, the excessive demand of this asset does not increase linearly with but shows a concave pattern.
When is lower than the reference return, the excessive demand of this asset will decrease. However, the investors will show different behaviors. For holders, since they feel a loss, some of them tend to hold rather than bail out. This can be explained by their unwillingness to realize a loss, and so they hold in the hope that they will have a gain later. That is, they show a risk-seeking behavior. For those who short the asset, some of them tend to buy the asset due to the reduced price with the hope that the asset will gain soon. Consequently, the excessive demand does not decrease linearly with but shows a convex pattern. A similar phenomenon has been observed in many articles, see, e.g., [35]. This phenomenon can be perfectly explained by the prospect theory [25].
Since Kahneman and Tversky [25] introduced the prospect theory to economics, it has been playing an important role in explaining many phenomena in economics and finance. The key idea of the prospect theory is that, in a risky situation, when people feel gains, they show risk-averse behavior and when people feel losses, they show risk-seeking behavior, and this theory can be readily applied to investment. In short, when the investors feel a gain, they show risk-averse behavior and when they feel a loss, they show risk-seeking behavior.
To illustrate this idea, consider the utility as a function of the yield, see Figure 20.

Figure 20.
Prospect agents.
In the second sub figure in Figure 20, Scenario 1 corresponds to a positive yield of the investment. In Scenario 2, there is a possible further jump and a possible further drop of the return in the investment. By the prospect theory, this type of investors would show a risk averse behavior in this case, so the utility of Scenario 1 is bigger than the utility of Scenario 2. Therefore, once Scenario 1 happens, these investors tend to secure the gain by selling the risky asset, and as a result, the supply of this asset on the market increases.
In the third sub figure in Figure 20, Scenario 1 corresponds to a negative yield while Scenario 2 corresponds to a possible further jump and a possible further drop. Due to the prospect theory, these investors show a risk seeking behavior. Therefore, Scenario 2 has a bigger utility, and these type of investors tend to hold but not to sell the asset. As a result, the supply of this asset on the market decreases.
Many research works have discovered this phenomenon, for example, Fiegenbaum and Thomas [36] pointed out that “For returns below target, a large majority of individuals appear to be risk seeking; for returns above target, a large majority appear to be risk averse.” ; and Odean [37] showed that individual investors are reluctant to sell stocks with short-term prior losses, preferring to sell prior short-term winner stocks. This is also known as the disposition effect.
We shall extend the prospect theory to the extreme case to model the behavior of these traders, that is, when is much bigger (or much lower) than the threshold. If is much bigger than the threshold, for example, the stock price jumps by in one day, then the investors show extreme risk averse behavior: more holders tend to sell the shares to realize the profit, and less buyers are willing to buy the shares since they feel having missed the best chance. As a result, the net demand of this asset decreases. A similar argument can be given to the case when the yield is way below the threshold. Figure 21 illustrates a typical graph of the excessive demand as a function of return.
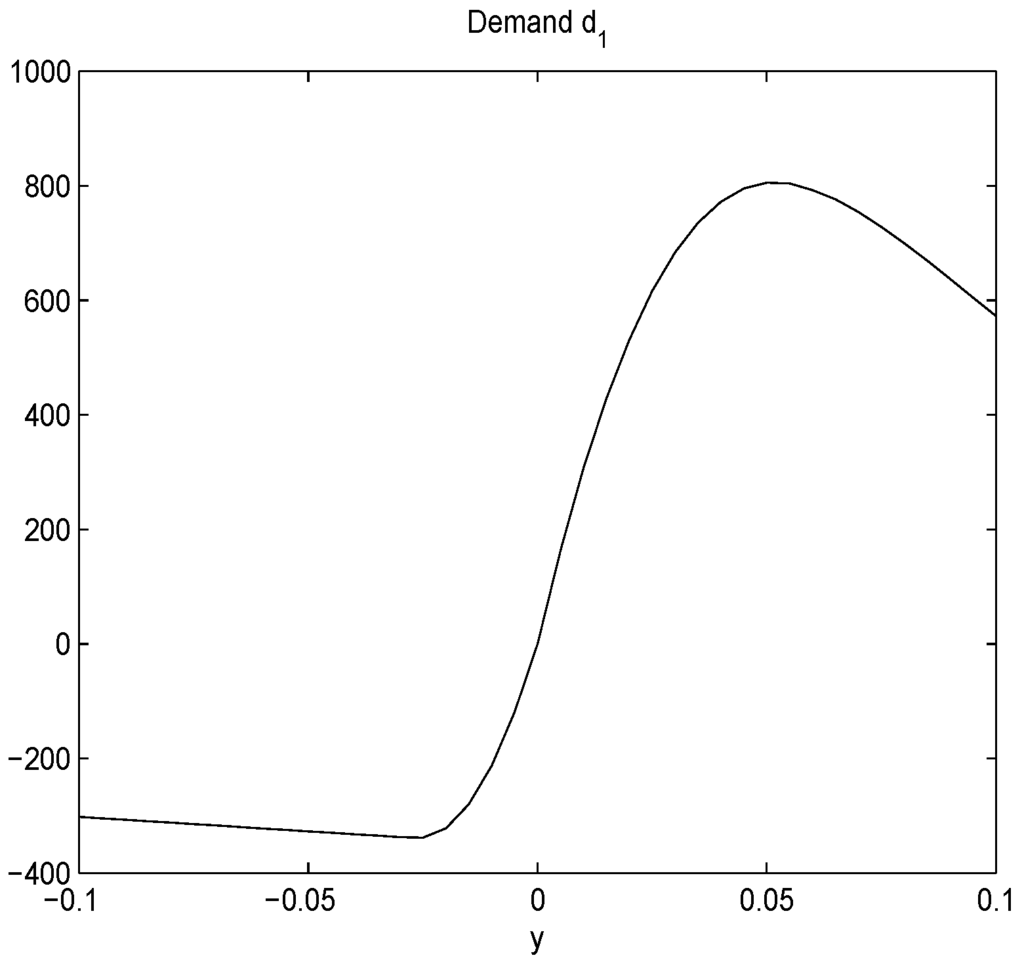
Figure 21.
Excessive demand as a function of return.
We use to represent this instant demand as a function of the current return y, and the cumulative demand from this type of investors is thus given by . Later, if we need a discrete model, we use index i to denote the sample at time , and then will be the corresponding excessive demand function at time .
We believe that the types of investors that we have proposed so far, namely the noisy traders, trend chasers, and prospect investors, are not uncommon. Yao and Li [38] studied the market interaction between prospect theory-investors and regular CRRA investors and investigated their trading patterns. In this work, since we hope to replicate both the drift and volatility terms in the model (1), we need another type of investor. The actual market participants are certainly much more complicated, and this topic could go on for ever. In this paper, we want to contribute a model that could possibly explain what we have discovered from the real market data, and we hope this model could shed some light on future research in financial studies.
These last types of investors are assumed to behave in the following way. In one aspect, they are trend chasers on the return process (not the price process) since their instant demand of the asset is proportional to . On the other hand, they believe that the return process should be mean reverting, thus their instant demand is assumed to have the form , where achieves the maximum when y is close to zero and decreases whenever y is away from zero. An illustrative graph on is shown in Figure 22.

Figure 22.
Excessive demand as a function of return.
With these proposed market participants, we shall construct an ARCH model for the return process in the next section.
4.2. An ARCH Model from Prospect Theory
Let be the cumulative noisy demand and be the cumulative trend chasing demand as in [19], where is a Wiener process, and , are constants. The market clearing condition states that
where M is a constant. Define , , , and is assumed to follow the normal distribution. Since we are interested in the daily yield process, we choose . The associated difference equation can be easily written as follows:
Now, it is a simple step to derive a recursive equation for by rewriting (9) as (that is, solve this equation for )
where
and are i.i.d random variables.
With properly chosen functions of that have the properties as shown in Figure 21 and Figure 22, respectively, we are capable of replicating the drift and volatility terms. For example, if we choose
and
and the parameter settings , then the graphs of and are shown in Figure 23, compared to Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 as well as Figure 13.
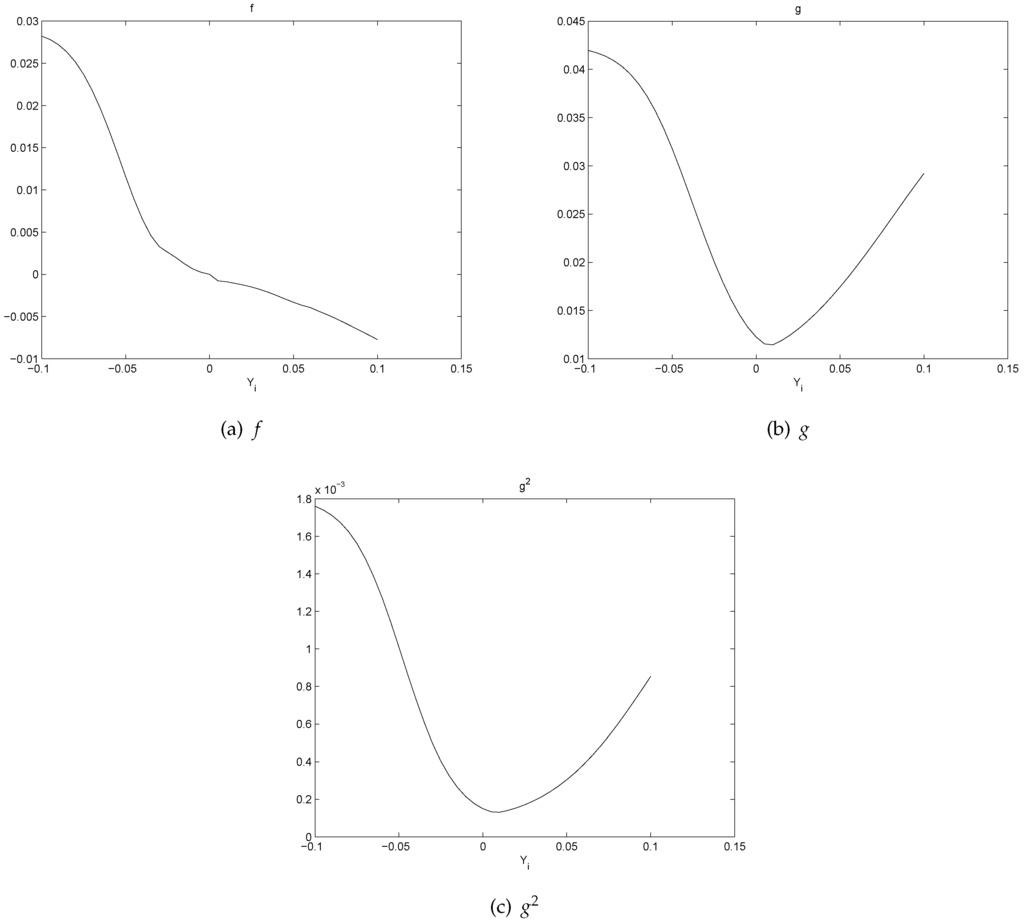
Figure 23.
Drift and volatility functions.
There are many stochastic models that tried to explain the volatility skew/smile, although they lack the explanation of why the asset prices fluctuate in that way. For example, if the price process is modeled as regime switching process [15,16] that are due to the changing of market or economic states, then it is reasonable to construct the same model for price process before the year 1987 since market states kept changing all the time. However, the volatility skew/smile phenomenon is not seen from the market data before 1987. Because volatility smile/skew is only seen from the market data after 1987, it is reasonable to argue that the crash in 1987 fundamentally changed the behaviors of investors, and as a consequence, the evolution of the asset price has been changed. As we have mentioned, the actual market participants are much more complicated, and we hope that our model can bring new insights to future research in financial studies.
5. Conclusions
The contributions of this paper are as follows:
- We proposed a level set analysis and performed a nonparametric analysis on the S&P 500 return, and the results showed that this return process has negative serial correlation and volatility clustering property.
- We found new patterns on the S&P 500 return through local polynomial regression and constructed an ARCH model that replicates both the drift and volatility terms.
- We brought in the prospect theory to explain the mechanism of our model and linked it to the volatility skew phenomenon observed in the actual stock market.
Acknowledgments
Author Yipeng Yang is supported by Faculty Research and Support Funds #1123 from University of Houston-Clear Lake.
Author Contributions
Author Yipeng Yang proposed the linkage between volatility skew(smile) and behavioral finance, and performed the data analysis, model calibration and the writing of this paper; author Allanus Tsoi gave important instructions such as to verify our theory through real market data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- R. Engle. “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of U.K. Inflation.” Econometrica 50 (1982): 987–1008. [Google Scholar] [CrossRef]
- T. Bollerslev. “Generalized Autoregressive Conditional Heteroscedasticity.” J. Econom. 31 (1986): 307–327. [Google Scholar] [CrossRef]
- E. Jacquier, N.G. Polson, and P.E. Rossi. “Bayesian Analysis of Stochastic Volatility Models.” J. Bus. Econ. Stat. 12 (1994): 371–417. [Google Scholar]
- S.J. Taylor. “Financial Returns Modelled by the Product of Two Stochastic Processes-A Study of Daily Sugar Prices, 1961–1979.” In Time Series Analysis: Theory and Practice. Edited by O.D. Anderson. New York, NY, USA: Elsevier/North-Holland, 1982, Volume 1, pp. 203–226. [Google Scholar]
- J.P. Fouque, G. Papanicolaou, and K.R. Sircar. Derivatives in Financial Markets with Stochastic Volatility. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- N. Shephard. “Statistical Aspects of ARCH and Stochastic Volatility.” In Time Series Models in Econometrics, Finance and Other Fields. Edited by D.R. Cox, D.V. Hinkley and O.E. Barndorff-Nielson. London, UK: Chapman and Hall, 1996, pp. 1–100. [Google Scholar]
- O.E. Barndorff-Nielsen, and N. Shephard. “Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics.” J. R. Stat. Soc. Ser. B Stat. Methodol. 63 (2001): 167–241. [Google Scholar] [CrossRef]
- O.E. Barndorff-Nielsen, and N. Shephard. “Modelling by Lévy Processes for Financial Econometrics.” In Lévy Processes: Theory and Applications. Edited by O.E. Barndorff-Nielsen, T. Mikosch and S. Resnick. New York, NY, USA: Birkhäuser, 2001, pp. 283–318. [Google Scholar]
- J. Rosiński. “Tempering stable processes.” Stoch. Process Appl. 117 (2007): 677–707. [Google Scholar] [CrossRef]
- R.S. Tsay. Analysis of Financial Time Series, 3rd ed. Hoboken, NJ, USA: John Wiley and Sons, 2010. [Google Scholar]
- E. Bayraktar, H.V. Poor, and K.R. Sircar. “Estimating the Fractal Dimension of the S&P500 Index Using Wavelet Analysis.” Int. J. Theor. Appl. Financ. 7 (2004): 615–643. [Google Scholar]
- J. McCarthy, and A.G. Orlov. “Time-frequency Analysis of Crude Oil and S&P500 Futures Contracts.” Quant. Financ. 12 (2012): 1893–1908. [Google Scholar]
- R. Becker, J. Lee, and B.E. Gup. “An Empirical Analysis of Mean Reversion of the S&P500’s P/E Ratio.” J. Econ. Financ. 36 (2012): 675–690. [Google Scholar]
- Y.S. Kim, S.T. Rachev, M.L. Bianchi, I. Mitov, and F.J. Fabozzi. “Time series analysis for financial market meltdowns.” J. Bank. Financ. 35 (2011): 1879–1891. [Google Scholar] [CrossRef]
- N.P.B. Bollen. “Valuing Options in Regime-Switching Models.” J. Deriv. 6 (1998): 38–49. [Google Scholar] [CrossRef]
- A. Papanicolaou, and R. Sircar. “A Regime-Switching Heston Model for VIX and S&P 500 Implied Volatilities.” Quant. Financ. 14 (2013): 1811–1827. [Google Scholar]
- H. Chen, G. Noronha, and V. Singal. “The Price Response to S&P 500 Index Additions and Deletions: Evidence of Asymmetry and a New Explanation.” J. Financ. 59 (2004): 1901–1930. [Google Scholar]
- H. Föllmer, and M. Schweizer. “A Microeconomic Approach to Diffusion Models for Stock Prices.” Math. Financ. 3 (1993): 1–23. [Google Scholar] [CrossRef]
- U. Horst. “Financial Price Fluctuations in A Stock Market Model with Many Interacting Agents.” Econ. Theory 25 (2005): 917–932. [Google Scholar] [CrossRef]
- R. Frey, and A. Stremme. “Market Volatility and Feedback Effects from Dynamic Hedging.” Math. Financ. 7 (1997): 351–374. [Google Scholar] [CrossRef]
- P. Heemeijer, C. Homoes, J. Sonnemans, and J. Tuinstra. “Price Stability and Volatility in Markets with Positive and Negative Expectations Feedback: An Experimental Investigation.” J. Econ. Dyn. Control 33 (2009): 1052–1072. [Google Scholar] [CrossRef]
- A. Danilova. “Emergence of Stochastic Volatility from Informational Heterogeneity.” Doctoral Dissertation, Princeton University, Princeton, NJ, USA, 2005. [Google Scholar]
- G. Lyengar, and A.K.C. Ma. “A Behavioral Finance-based Tick-by-tick Model for Price and Volume.” J. Comput. Financ. 14 (2010): 57–80. [Google Scholar]
- E. Platen, and M. Schweizer. “On Feedback Effects from Hedging Derivatives.” Math. Financ. 8 (1998): 67–84. [Google Scholar] [CrossRef]
- D. Kahneman, and A. Tversky. “Prospect Theory: An Analysis of Decision under Risk.” Econometrica 47 (1979): 263–292. [Google Scholar] [CrossRef]
- W. Härdle, and A.B. Tsybakov. “Local Polynomial Estimators of the Volatility Function in Nonparametric Autoregression.” J. Econom. 81 (1997): 223–242. [Google Scholar] [CrossRef]
- E. Masry, and J. Fan. “Local Polynomial Estimation of Regression functions for mixing processes.” Scand. J. Stat. 24 (1997): 165–179. [Google Scholar] [CrossRef]
- W.S. Cleveland. “Robust Locally Weighted Regression and Smoothing Scatterplots.” J. Am. Stat. Assoc. 74 (1979): 829–836. [Google Scholar] [CrossRef]
- T. Bollerslev, U. Kretschmer, C. Pigorsch, and G. Tauchen. “A Discrete-time Model for Daily S&P 500 Returns and Realized Variations: Jumps and Leverage Effects.” J. Econom. 150 (2009): 151–166. [Google Scholar]
- P. Christoffersen, B. Feunou, and Y. Jeon. “Option Valuation with Observable Volatility and Jump Dynamics.” J. Bank. Financ. 61 (2015): S101–S120. [Google Scholar] [CrossRef]
- M.C. Mariani, I. SenGupta, and G. Sewell. “Numerical methods applied to option pricing models with transaction costs and stochastic volatility.” Quant. Financ. 15 (2015): 1417–1424. [Google Scholar] [CrossRef]
- I. SenGupta. “Option pricing with transaction costs and stochastic interest rate.” Appl. Math. Financ. 21 (2014): 399–416. [Google Scholar] [CrossRef]
- F.B. Slimane, M. Mehanaoui, and I.A. Kazi. “How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets? ” Int. J. Financ. Stud. 1 (2013): 81–101. [Google Scholar] [CrossRef]
- B.M. Barber, and T. Odean. “The Behavior of Individual Investors.” In Handbook of the Economics of Finance. Edited by G.M. Constantinides, M. Harris and R.M. Stulz. North-Holland, The Netherlands: Elsevier, 2013, Volume 2, pp. 1533–1570. [Google Scholar]
- H. Shefrin, and M. Statman. “The Disposition to Sell Winners Too Early and Ride Losers Too Long: Theory and Evidence.” J. Financ. 40 (1985): 777–790. [Google Scholar] [CrossRef]
- A. Fiegenbaum, and H. Thomas. “Attitudes Toward Risk and the Risk-Return Paradox: Prospect Theory Explanations.” Acad. Manag. J. 31 (1988): 85–106. [Google Scholar] [CrossRef]
- T. Odean. “Are Investors Reluctant to Realize Their Losses? ” J. Financ. 53 (1998): 1775–1798. [Google Scholar] [CrossRef]
- J. Yao, and D. Li. “Prospect Theory and Trading patterns.” J. Bank. Financ. 37 (2013): 2793–2805. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).