1. Introduction
A common goal in studying investor sentiment is to find whether sentiment can explain returns. Or, do irrational investors cause mispricing that predictably reverses itself in the next period? The key to confirming this hypothesis is finding the right measure of irrational behavior, or investor sentiment. There are many different measures of investor sentiment in the literature, the most popular recently being Baker and Wurgler’s [
1] index. As Baker and Wurgler [
1] state, mispricing can occur when there are sufficient limits to arbitrage, and uninformed demand shocks occur. Therefore, the ideal sentiment measure would consist entirely of irrational (non-fundamental) investor behavior. Then, this pure measure of investor sentiment should have significant predictive power for future returns. This paper argues that the existing proxies of sentiment fall short in this regard.
The sentiment index used in Baker and Wurgler [
1] may be the most complete measure in the current literature. They create a composite measure of investor sentiment using principal-components analysis. They use six components: closed-end fund discount, market turnover, number of IPOs, average first-day return of IPOs [
2,
3,
4,
5], gross equity share, and a dividend premium measure. However, if one wants a purer measure of sentiment that better captures mispricing, then their sentiment index should be altered. They create a principal-components index based on existing sentiment proxies in the literature, but there are likely to be some rational or fundamental components involved. In order to arrive at a better sentiment measure, the non-fundamental component should be separated from the fundamental components of the Baker and Wurgler index (BW hereafter). However, properly removing as much of the fundamental component as possible is tricky. Baker and Wurgler do attempt to do this by removing what they call business cycle variation from their sentiment measure. They regress each individual component against a dummy variable for NBER recessions, industrial production index growth, and growth in consumer durables, nondurables, and services, and then run principal-components on these six residuals. The sentiment index is still likely to contain rational reactions to fundamentals that do not move with the business cycle. This paper provides empirical confirmation that indeed the BW procedure may not fully remove fundamentals.
A measure of investor sentiment that fully removes fundamentals should do a superior job of forecasting returns due to the following: prices move away from fundamentals when noise trading is correlated and arbitrage is limited, and then deviations are eventually reversed. The basic hypothesis is that mispricing due to sentiment shows up in the aggregate so that market returns are predictable by a pure irrational sentiment measure.
1 This assumes that sentiment drives predictability of returns more than fundamentals, which admittedly may not have a strong prior. However, the evidence in this paper supports the idea of return predictability being due to sentiment and not fundamentals. If sentiment predicts returns only because it captures fundamental factors, then the new sentiment index created in this paper should perform worse in forecasting. However, the opposite is true. Thus, evidence in contrast with some of the literature in this area is provided. It should be noted, though, that Campbell and Kyle [
6] find that mispricing can affect aggregate returns, and Lemmon and Portniaguina [
7] mention that rational and behavioral hypotheses are not mutually exclusive.
It is also important here to note the difference between in-sample explanatory power and out-of-sample predictability. It is common for a model to perform well in sample but poor out-of-sample. As shown in
Section 4, the BW index is more significant in sample than the Baker and Wurgler [
1] index that removes business cycle variation. When moving out of sample, though, the BW index performs poorly. The new sentiment index is not intended to fully explain market returns. Rather, the intent is to capture deviations in expected return which are due to irrational mispricing (sentiment). An index that successfully does this should work better out of sample but not necessarily in sample.
This paper removes fundamentals from BW in a way similar to Lemmon and Portniaguina [
7]. Lemmon and Portniaguina [
7] use a set of fundamentals that is sufficiently different (and arguably more complete) from Baker and Wurgler’s [
1] business cycle variables. Lemmon and Portniaguina [
7] separate the fundamental and non-fundamental components of consumer confidence (CC hereafter). They use the non-fundamental component as a proxy for investor sentiment. This paper follows their methodology, but applies it to the Baker and Wurgler [
1] index by first regressing CC on a set of fundamentals, then regressing BW on the fitted (fundamental/rational) value from this initial regression, and finally using the residuals from this regression as a proxy for pure sentiment.
Basically, the Lemmon and Portniaguina [
7] measure of fundamental consumer confidence is removed from the Baker and Wurgler [
1] index. Thus, a composite index of fundamentals based on consumer confidence is removed from Baker and Wurgler’s [
1] composite index of sentiment. This composite index of fundamentals should limit any measurement errors or over-fitting of fundamentals when removing them from BW.
2 Also, Lemmon and Portniaguina’s [
7] set of fundamentals (which this paper uses with some minor changes) is a more complete measure of overall fundamentals compared to Baker and Wurgler’s [
1] business cycle variables. This paper shows that, empirically, following this methodology allows investor sentiment to forecast market returns better.
Instead of directly following Lemmon and Portniaguina [
7], this paper uses BW for forecasting instead of CC, as it is a market measure of investor sentiment.
3 Market measures of sentiment are composed of real actions by investors directly involved in the market. For surveys (especially consumer confidence surveys), a participant may feel overly optimistic but may not actually act on this optimism. Surveys are also open to problems such as dishonesty, bias, and incomplete responses. A market measure of sentiment (such as BW) will match investors’ actions as it relates to their overall feeling of the stock market. Thus, this paper proposes that a market measure of investor sentiment will forecast market returns better than a survey-based measure. Empirical evidence is presented in support of this hypothesis, as the new index performs better in forecasting market returns than both Baker and Wurgler’s [
1] index and their alternative sentiment index that removes business cycle variations (BWA hereafter).
To measure the predictive power of the new index, a linear forecasting model is used to forecast one-month-ahead market returns. The sample runs from July 1978, when the University of Michigan consumer sentiment survey became available in a monthly frequency, to December 2010. A simple investment strategy is used: if the one-month-ahead predicted excess market return is higher than the historical average of all previous months in the sample at the time of forecasting, then the investor will invest in the market. Otherwise, she invests in a risk-free asset (T-bills). Essentially, the goal is to time the market. This differs from both Baker and Wurgler [
1] and Lemmon and Portniaguina [
7], where no market timing is involved. Market timing is considered here for two reasons. First, it is a practical application of investor sentiment, in that it is usable by practitioners. Since a common goal in the sentiment literature is predicting returns, market timing is a natural extension. The second reason for using a market timing approach is that it provides economic significance (via realized returns) in addition to statistical significance. Following the investment strategy (essentially switching between stocks and bonds), the forecast model that removes the fundamental component of CC from BW provides average realized excess returns of around 10.6% annually compared to around 5.3% annually for BW and 8.0% annually for BWA. This new sentiment index also has significant market timing ability, as will be shown later. The excess market return average over the forecasting sample is around 6.7% annually (the return from a buy-and-hold strategy), so a forecast model utilizing only BW would not beat the market on average. This new index performs significantly better than both CC and Lemmon and Portniaguina’s [
7] sentiment component of CC (by itself) as well. Since sentiment is typically thought to affect small, young, and volatile stocks the most, forecasting is also performed on a small-size portfolio. Again, removing the fundamental component increases the realized returns an investor could obtain. The evidence supports the hypothesis that investor sentiment should have no fundamental (rational) component, and that the existing measures of sentiment do not properly remove fundamentals. It should be noted that predictability in returns may be driven somewhat by time-varying risk and risk aversion, and not entirely by sentiment. However, this paper provides evidence that creating a better measure of irrationality increases predictability in returns.
The paper proceeds as follows:
Section 2 reviews the existing literature on investor sentiment and consumer confidence as a proxy for sentiment;
Section 3 discusses the data and methodology used;
Section 4 discusses the results; and
Section 5 concludes the paper.
2. Literature Review
DeLong
et al. [
8] show that returns of assets mostly held by noise traders can be predictable as mispricing caused by correlated sentiment (with limited arbitrage) will eventually correct itself.
4 Most studies (Baker and Wurgler [
1], Lemmon and Portniaguina [
7],
etc.) show that small and young firms (and closed-end funds, discussed shortly) are predominantly held by noise traders and thus are more susceptible to sentiment. However, Campbell and Kyle [
6] show that overreaction can impact aggregate stock values as well. Hence sentiment may also be able to predict market returns.
Lee, Shleifer, and Thaler [
2] show that closed-end fund discounts may be due to investor sentiment. In their study, the returns of ten size-ranked portfolios are regressed against market returns and the change in a value-weighted closed-end fund discount variable. They find that the smallest size-ranked portfolio moves closely with closed-end funds, while the largest size-ranked portfolio moves in the opposite direction of closed-end funds.
The papers that follow Lee, Shleifer, and Thaler [
2] are at the core of the field of investor sentiment. Barberis, Shleifer, and Vishny [
10] present a model of investor sentiment that supports the findings that stock prices underreact to earnings announcements and overreact to successive good or bad news. Elton, Gruber, and Busse [
11] show that changes in closed-end fund discounts do not explain common stock returns when including a value-weighted industry return index. They also find that investor sentiment is not a priced factor in common stocks as well as closed-end funds. Neal and Wheatley [
3] find that closed-end fund discounts can predict the size premium, but nothing else.
Other authors have considered proxies or measures of investor sentiment outside of closed-end fund discounts. Lee, Jiang, and Indro [
12] use a GARCH-mean model and the Investor’s Intelligence survey as their sentiment proxy to show that sentiment is a priced systematic risk. Lowry [
4] shows that investor sentiment may impact IPO volume. Cai
et al. [
13], find that sentiment affects variation in straight debt IPO volume, and Derrien [
5] shows that sentiment may play a role in the initial return of IPOs. Baker and Stein [
14] create a model in which high market liquidity indicates that the market is dominated by irrational investors, creating a role for sentiment.
There is a wide range of literature in which consumer confidence indices are used to proxy for investor sentiment. Fisher and Statman [
15] find that consumer confidence impacts individual investors’ sentiment, but not institutional investors’ sentiment. They also find that consumer confidence will rise significantly when stock returns (using many different indices) are high, and that consumer confidence may have some predictive power for returns. Schmeling [
16] uses consumer confidence to try to predict returns for 18 different countries. He finds that consumer confidence has predictive power up to 6 months, but dies out after that. Also, some countries’ consumer confidence measure has no predictive power whatsoever.
Lemmon and Portniaguina [
7] use consumer confidence as a proxy for investor sentiment. As mentioned earlier, Lemmon and Portniaguina [
7] create a sentiment proxy from consumer confidence by removing nine quarterly fundamentals and their lags. They point out that the rational hypothesis and sentiment hypothesis are not mutually exclusive. Therefore, by removing fundamentals they create a sentiment index similar to what this paper creates: an index where mispricing could only be due to sentiment, so that prices will reverse and be predictable. They use a quarterly index of the University of Michigan Consumer Sentiment Index (CC). They mention that from 1978–2002 their sentiment component and the Baker and Wurgler [
1] index have a very small correlation and that their index does not support Baker and Wurgler’s [
1] findings mentioned below. They do not attempt to predict market returns as this paper does. The other key difference in this paper is that here their fundamental component of CC (using monthly data) is then removed from BW (a more direct market measure) to be used in market timing.
As discussed in the previous section, Baker and Wurgler [
1] create a composite investor sentiment index using principal-component analysis. They use their index to run a predictive regression on various long-short portfolios. Their main findings are that small, young, and volatile firms have low returns for the following year when current sentiment is high. Baker and Wurgler [
17] create a first-differenced series of their 2006 sentiment indices, whereby they first-difference the individual components and then run principal-components analysis. They use the change index to test for return co-movement with sentiment, while using their 2006 levels index to forecast returns. Their findings are that speculative, difficult-to-arbitrage stocks and stocks with high volatility are impacted greatly by sentiment. They also find that high sentiment leads to lower future market returns (overreaction). This paper builds on this finding, and attempts to forecast market returns.
3. Data and Methodology
The sample period used in this paper runs from July 1978 (when the Michigan Survey began to consistently use monthly frequencies) to December 2010, using monthly data. Market return is the value-weighted CRSP measure that includes dividends.
5 The risk-free rate used is the rate on 3-month Treasury bills, obtained from the St. Louis Federal Reserve (FRED) website [
19]. Excess market return is the difference between these two. The University of Michigan Consumer Sentiment Index (CC, or consumer confidence) is also obtained from the FRED website [
19]. The Baker and Wurgler [
1] index and its alternative that removes business cycle variation, along with the individual components, are obtained from Jeffrey Wurgler’s website [
20].
Table 1 shows the descriptive statistics for these variables.
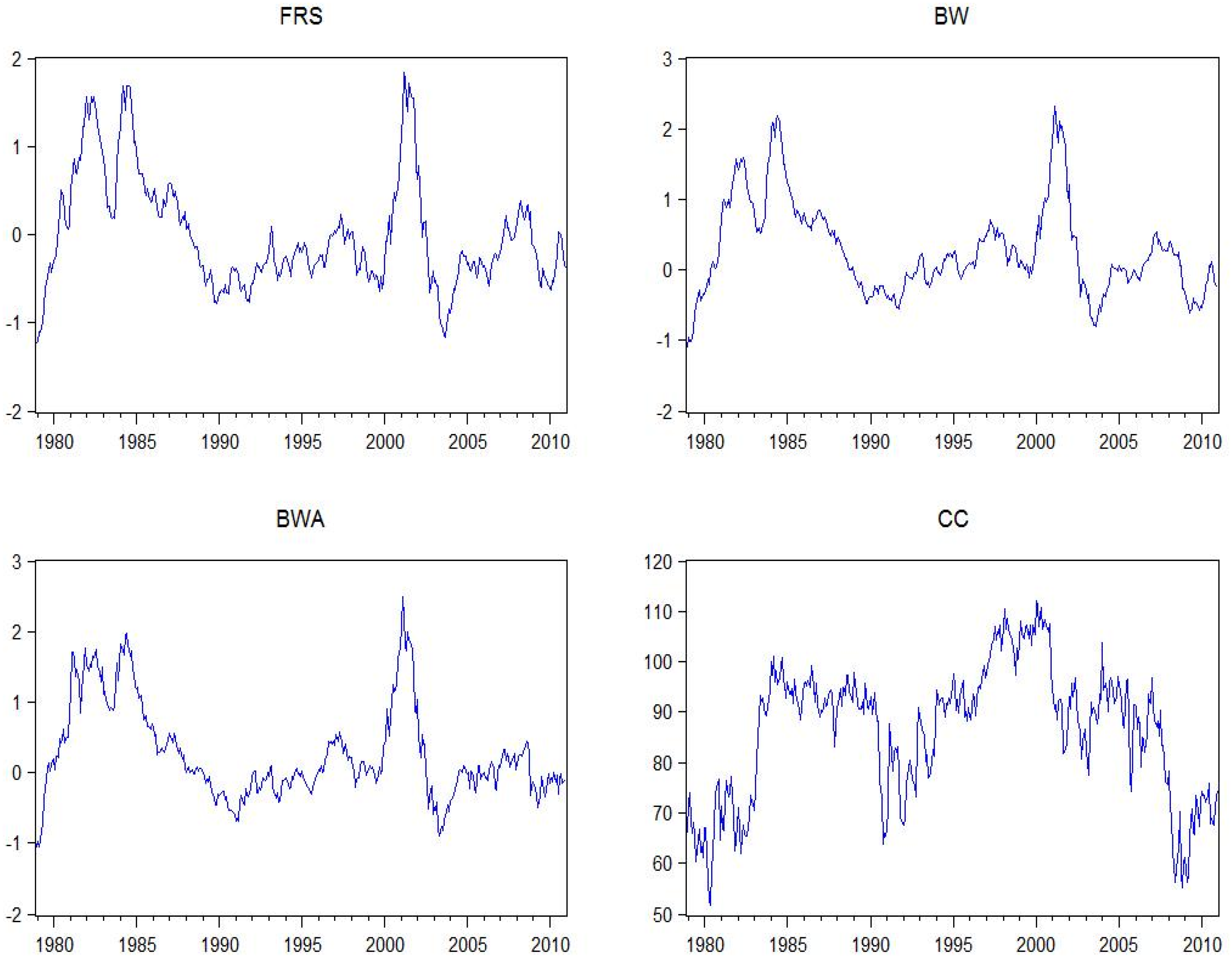
Figure 1 provides time-series graphs of the excess market return, CC, BW, and BWA over the sample for comparison purposes.
Table 1.
Descriptive Statistics.
Table 1.
Descriptive Statistics.
| Statistics | RF | MKTRET | CC | BW | BWA |
|---|
| Mean | 0.004560 | 0.010268 | 86.18487 | 0.260882 | 0.245618 |
| Median | 0.004242 | 0.014399 | 90.2 | 0.1135 | 0.054 |
| Maximum | 0.013583 | 0.12967 | 112 | 2.321 | 2.497 |
| Minimum | 0.000025 | −0.219503 | 51.7 | −1.333 | −1.273 |
| Std. Dev. | 0.002836 | 0.044035 | 13.18374 | 0.677739 | 0.68605 |
| CV | 0.621882 | 4.288566 | 0.152970 | 2.597876 | 2.793166 |
| Skewness | 0.666981 | −0.778491 | −0.436221 | 0.765964 | 0.861307 |
| Kurtosis | 0.465557 | 5.695326 | 2.408766 | 3.624503 | 3.405068 |
As can be seen from
Table 1, the average market return for the sample used here is about 12.3% annually (1.027% monthly). The average excess market return is slightly less than 7% annually. CC uses 1966 as its base year, with CC = 100. BW is from a standardized principal-component analysis, so that the series (although not necessarily in the sample used here) has a unit variance and a mean of zero. As described in the literature review, BW is comprised of six individual sentiment components and employs both leads and lags.
While CC is definitively non-stationary, BW’s stationarity is ambiguous using Dickey-Fuller, Dickey-Fuller GLS, and Phillips-Perron tests. For BW, the Dickey-Fuller GLS test shows that it is non-stationary, but the other tests are inconclusive. It appears that BW may be non-stationary due to the non-stationarity of just one component, the turnover component. Further, CC and BW may be cointegrated, using the Johansen integration test. The results are not definitive, as would be expected since BW may or may not be non-stationary.
Figure 1.
This figure shows time-series graphs of the paper’s modified BW index (FRS), BW, BWA, and CC. FRS is fundamental-removed-sentiment, BW is Baker and Wurgler’s [
1] sentiment index, BWA is Baker and Wurgler’s [
1] sentiment index that removes business cycle variation, and CC is the University of Michigan Consumer Sentiment Index. Sample is from July 1978–December 2010.
Figure 1.
This figure shows time-series graphs of the paper’s modified BW index (FRS), BW, BWA, and CC. FRS is fundamental-removed-sentiment, BW is Baker and Wurgler’s [
1] sentiment index, BWA is Baker and Wurgler’s [
1] sentiment index that removes business cycle variation, and CC is the University of Michigan Consumer Sentiment Index. Sample is from July 1978–December 2010.
Initially, Lemmon and Portniaguina’s [
7] methodology is implemented, with some minor changes. Primarily, Lemmon and Portniaguina [
7] use quarterly data and this paper uses monthly data. Lemmon and Portniaguina [
7] use the following nine fundamentals: default spread (DEF), as measured by the difference between the yields to maturity on Moody’s Baa-rated bonds and Aaa-rated bonds; yield on 3-month Treasury bills (RF); dividend yield (DIV), following Fama and French [
21]; real GDP growth (GDP); growth in personal consumption expenditures (CONS); labor income growth (LABOR), as measured by the per capita growth in total personal income minus dividend income, deflated by the PCE deflator; the Bureau of Labor Statistics unemployment rate (URATE), seasonally adjusted; inflation rate (INF), measured by the change in the consumer price index; and the consumption-to-wealth ratio (CAY) from Lettau and Ludvigson [
22]. The dividend yield measure can be obtained from the difference between CRSP’s value-weighted return index and its value-weighted return index excluding dividends. The CAY measure is obtained from Martin Lettau’s website [
23]. The seven other fundamental variables can be obtained from FRED’s website [
19].
This paper makes two changes to Lemmon and Portniaguina’s [
7] choice of fundamentals: instead of using the unemployment rate the prime rate on bank loans (PRIME) is used, and CAY and GDP are interpolated to monthly data. PRIME is obtained from FRED. The prime rate is essentially a benchmark for other loan rates, so it should broadly capture fundamental economic activity. Also, the unemployment rate is a survey measure, while the other fundamentals (and the prime rate) are directly observable.
6 The prime rate is more quickly accessible to investors than is the unemployment rate as well. Following Lemmon and Portniaguina [
7], CC is regressed against these 9 fundamentals and their lags using monthly data. Since Lemmon and Portniaguina [
7] use quarterly indices with one lead and one lag (giving six months of data), the lead on each fundamental along with 5 monthly lags is used. Since CAY and GDP are converted to monthly, only a lead and one 3-month lag can be used for these two variables to avoid multicollinearity. This gives the following:
is a constant,
is a vector of coefficients:
,
is the fitted value of the regression, and
is the error term (noting that CAY and GDP only have one lag at
t − 3).
The fitted value from the above equation is obtained by multiplying the coefficient by the respective value for that variable (from i = 0 to 5) and summing them together with the intercept for each particular month. This produces the “fundamental” or “rational” component of CC, whereas the residual is the sentiment component as in Lemmon and Portniaguina [
7]. As discussed in the introduction, the idea is to weight the fundamentals on the non-market survey measure of consumer confidence before removing it from BW. The aim is to remove the rational, fundamental component of BW, leaving only irrational investor sentiment (which produces market mispricing).
7Each regression is rolled forward one month, while anchoring the starting point. This is done so that only information from time 1 to
t is utilized in forecasting at month
t + 1. Therefore, the coefficients will change as the regression updates forward each month in a stepwise fashion. The fitted values of Equation (1) are saved each time so that a series is created to be used in forecasting. That is, Equation (1) is run from time 1 to time
t, with
t fitted values created. This series can be used to then forecast at
t + 1, as will be explained later. To forecast the next month (
t + 2), Equation (1) is then run from time 1 to
t + 1, creating
t + 1 values in each series. Thus, Equation (1) is updated each month as forecasting moves from the halfway point to the last period in the sample. When running Equation (1) for the entire sample, the adjusted R-squared value is 0.78, which is very close to the value that Lemmon and Portniaguina [
7] obtain.
The fitted (fundamental) CC values are then used to properly remove fundamentals from BW. Again, BW is used to forecast as it is a market-based measure and should forecast market returns better. Lemmon and Portniaguina’s [
7] methodology has been used up to this point in order to get a proper measure of fundamentals. Now, after obtaining the series of fitted values from Equation (1), the following is run:
CC
fit is the fitted value of CC from Equation (1). The procedure in Equation (2) is the same as in Equation (1). The residual from Equation (2),
, is hereafter referred to as FRS (fundamental-removed sentiment). Note that using only CC
fit eliminates any endogeneity issues that would arise from using CC in Equation (2). The reason is that since CC also has a sentiment component, it would be correlated with the residual from Equation (2), or FRS.
8 CC
fit is used as a composite index of fundamentals which should help prevent potential over-fitting or measurement errors when removing fundamentals from sentiment.
Table 2 shows the descriptive statistics for FRS, when forecasting starts at the one-third mark of the sample as will be done later. Note that this is the series of only time
t residual from Equation (2), where time
t is used to forecast excess market return at time
t + 1. Since FRS contains residuals from different regressions, it is not necessarily expected that its mean be zero (as opposed to a series of residuals from one regression). It should also be noted that FRS is unambiguously stationary when BW is modified using this methodology. As discussed at the beginning of this section, BW is found to be non-stationary using some statistical tests.
Table 2.
FRS Descriptive Statistics.
Table 2.
FRS Descriptive Statistics.
| Statistics | FRS |
|---|
| Mean | −0.319224 |
| Median | −0.398 |
| Maximum | 1.815 |
| Minimum | −1.254 |
| Std. Dev. | 0.53787 |
| Skewness | 1.452870 |
| Kurtosis | 6.435207 |
The regression in Equation (2) is run in a stepwise fashion with an anchored starting point, with the end point starting from the halfway point (October 1994) updating each time to include the next month. Equation (2) can be thought of as running simultaneously with Equation (1). The residuals from Equation (2) are then used in forecasting excess market returns, with each month in which forecasting is done having its own unique series of the residuals from Equation (2) that does not include any future information. The R-squared value from Equation (2) is 8% for the full sample, although it ranges from 3%–8% over the sample.
The following forecasting models are employed:
is the predicted excess market return and
is the appropriate sentiment measure, lagged one month, for model i. For Model I (i = 1) BW is used for “sent”, for Model II (i = 2) BWA is used, and for Model III (i = 3) FRS is used. BWA is included for comparison purposes; this also shows that BW removes some fundamentals but ultimately falls short. Forecasting is done from October 1994 to December 2010 and also from May 1989 to December 2010. Therefore, out-of-sample forecasts for the second half of the sample are obtained, and also for the last two-thirds of the sample for comparison and robustness. So when forecasting starts at the halfway point of the sample, the forecasting equations above start by running from July 1978–September 1994, and finish by running from July 1978–November 2010. Ordinary least squares is used in the forecasting equations, and one-month-ahead forecasts of the excess market returns,
, are obtained using the residuals of the forecasting equations.