Quantum Blockchain: A Theoretical Framework and Applications in Cryptocurrency

Abstract

Blockchain technology has emerged as the backbone of cryptocurrencies and decentralized finance, yet its long-term resilience is increasingly threatened by advances in quantum computing. Quantum algorithms, such as Shor’s algorithm, can undermine public-key cryptography, while Grover’s algorithm accelerates brute-force search, weakening proof-of-work schemes. In this paper, we propose a Quantum Blockchain Framework that integrates quantum communication protocols, quantum consensus mechanisms, and quantum-resistant cryptography. We construct a theoretical model of quantum-secured distributed ledgers, where qubits, entanglement, and quantum key distribution (QKD) enhance security and efficiency. Applications to cryptocurrency are explored, highlighting how quantum blockchain can mitigate security risks, improve consensus speed, and enable quantum-native digital assets.

1. Introduction

Blockchain systems are fundamentally reliant on classical cryptographic primitives such as elliptic curve cryptography (ECC) and hash-based proof-of-work (PoW). With the development of large-scale quantum computers, these primitives face existential risks: Shor’s algorithm can factor large primes in polynomial time, compromising ECC, while Grover’s algorithm can reduce the effective bit security of hash functions by half. This vulnerability necessitates a post-quantum transition.

Recent work in quantum information science suggests the possibility of quantum blockchains, where qubits and entangled states replace purely classical cryptographic primitives. Such blockchains could not only be resistant to quantum attacks but also leverage uniquely quantum features for efficiency and trust. This paper contributes a formal theoretical model of quantum blockchains and applies it to cryptocurrency systems.

Indeed, Blockchain technology has become the foundation of cryptocurrencies and decentralized finance (DeFi), offering decentralized trust, immutability, and transparency. However, its long-term resilience faces a critical challenge: the rapid development of quantum computing. Classical cryptographic primitives that underpin blockchain networks—most notably elliptic curve cryptography and proof-of-work (PoW) mechanisms—are vulnerable to quantum algorithms. Shor’s algorithm can factor large integers and compute discrete logarithms in polynomial time, rendering public-key cryptography insecure, while Grover’s algorithm accelerates brute-force search, reducing the effective security of hash functions by half. These breakthroughs suggest that without a fundamental redesign, current blockchain systems may be compromised in the quantum era.

This paper addresses these challenges by proposing a Quantum Blockchain Application that integrates the unique capabilities of quantum information science into distributed ledger design. We introduce a theoretical model in which qubits, entanglement, and quantum key distribution (QKD) enhance both the security and the efficiency of blockchain consensus. Unlike classical blockchains, where consensus relies on computational difficulty, quantum blockchains leverage physical principles—such as the no-cloning theorem and entanglement correlations—to ensure authenticity and tamper resistance.

While prior studies such as Rajakumar (2021), and Mosca (2018) have advanced important theoretical foundations for quantum-secure cryptography and consensus, their focus remains largely on the computational and algorithmic dimensions of blockchain security. In contrast, the present study extends these discussions into the financial and institutional sphere, introducing a unified framework that links quantum communication, quantum consensus, and quantum-resistant cryptography to tangible outcomes in market efficiency, transaction cost reduction, and governance design. By framing Quantum Blockchain as both a technological and financial innovation, this paper bridges a critical gap between quantum theory and financial applicability, offering a forward-looking model for how decentralized markets might evolve in the quantum era.

Our framework contributes along three dimensions. First, it provides quantum-secure transactions by using QKD-derived keys immune to Shor’s algorithm. Second, it introduces a Quantum Proof-of-Stake (QPoS) mechanism that ties block proposal probability to both validator stake and entanglement fidelity, aligning incentives with technological reliability. Third, it explores quantum-native assets, such as Wiesner’s unclonable quantum money, which offer intrinsic resistance to double-spending and counterfeiting.

This research builds on prior work, including Bonaparte (2025), which introduced the Quantum Finance Index (QFI) at the firm level to measure sentiment and innovation in quantum-related stocks. While that approach provided insights into company-level dynamics, it did not address the structural transformation of distributed ledgers under quantum threats. Here, we extend the inquiry by proposing a quantum-native blockchain model. Importantly, the relevance of this research is underscored by real-world advances: companies such as D-Wave (QBTS) are already developing applications of quantum computing to blockchain and optimization problems, signaling that this innovation is transitioning from theory to practice.

Recent studies have advanced the intersection of blockchain and quantum security from several perspectives. Kim et al. (2024) introduced a Post-Quantum Delegated Proof of Luck consensus algorithm that strengthens blockchain resilience against quantum threats. Sharma et al. (2023) provided an overview of quantum-secured blockchain integration in optical networks, highlighting its potential for data transmission security. Thanalakshmi et al. (2023) conducted a comparative analysis of quantum-resistant blockchain systems, emphasizing design trade-offs across cryptographic protocols. Complementing these, Zhou et al. (2023) offered a systematic review of blockchain consensus mechanisms, mapping their evolution and applicability in various domains. Finally, Zawadzki (2023) warned of the insecurity of quantum blockchains based on temporal entanglement, underscoring the importance of post-quantum safety in future blockchain architectures. Together, these studies delineate both the opportunities and vulnerabilities that arise as blockchain transitions toward the quantum era.

At an intuitive level, the Quantum Blockchain Framework replaces the computational trust model of classical blockchains with a physics-based trust model rooted in the principles of quantum mechanics. Instead of relying on energy-intensive computation or purely economic staking, network participants achieve consensus through quantum entanglement, which allows them to verify transactions instantaneously and securely by sharing correlated quantum states. The Quantum Proof-of-Stake (QPoS) mechanism combines traditional staking incentives with entanglement fidelity, ensuring that validators not only have financial commitment but also maintain reliable quantum connections. In simple terms, this approach shifts security from mathematical difficulty to the laws of nature; any attempt to intercept or duplicate a quantum state would destroy it, making fraud or double-spending physically impossible. This integration of quantum communication, consensus, and cryptography thus provides a more secure, efficient, and sustainable foundation for future financial networks. The Crypto Volatility Index (CVIX) proposed by Bonaparte adapts the logic of the VIX to digital assets, extracting forward-looking implied volatility from option surfaces (e.g., BTC/ETH) to quantify market uncertainty in real time.

The remainder of the paper is structured as follows. Section 2 reviews the literature on blockchain security, post-quantum cryptography, and emerging proposals for quantum blockchains. Section 3 introduces the construction of the Quantum Blockchain Framework, detailing the integration of quantum consensus and cryptographic mechanisms. Section 4 applies the model to cryptocurrency, demonstrating its potential to secure transactions, improve consensus efficiency, and enable quantum-native assets. Section 5 concludes by highlighting the broader implications of quantum blockchain for finance, innovation, and policy.

2. Literature Review

The intersection of blockchain and quantum computing brings together two rapidly advancing technological frontiers. Existing research can be grouped into three major strands: (1) quantum threats to existing blockchain infrastructure, (2) post-quantum cryptography as a mitigation strategy, and (3) proposals for quantum-native blockchains.

2.1. Quantum Threats to Blockchain

The vulnerability of classical cryptographic primitives underpins the urgency of quantum-resilient solutions. Shor’s (1994) algorithm threatens public-key cryptosystems such as RSA and ECC, which form the backbone of transaction validation in most cryptocurrencies. Grover’s (1996) algorithm further reduces the effective bit security of hash-based consensus schemes such as Bitcoin’s Proof-of-Work. Mosca (2018) emphasizes the “quantum preparedness problem,” highlighting that a large-scale quantum computer would immediately compromise deployed systems. Gidney and Ekerå (2019) provide quantitative estimates, showing that factoring RSA-2048 could be feasible within hours on a sufficiently advanced quantum machine, underscoring the timeline pressure for blockchain systems.

2.2. Post-Quantum Cryptography (PQC)

One approach has been to replace vulnerable cryptographic primitives with quantum-resistant alternatives. Lattice-based cryptography, code-based schemes, and hash-based signatures have been evaluated as substitutes for ECC and RSA (NIST, 2022). While these solutions are implementable today, they remain classical in nature and may impose larger key sizes, slower verification speeds, and higher computational costs for resource-constrained devices.

2.3. Quantum Communication and Consensus

Beyond cryptographic substitution, researchers have proposed incorporating quantum communication into blockchain security. Quantum Key Distribution (QKD) enables secure key exchange guaranteed by the laws of physics, rather than relying on computational assumptions. More recent work has extended this concept into distributed settings. Rajakumar (2021) surveys early proposals for quantum blockchains. These proposals suggest that entanglement and quantum randomness could enhance both the security and scalability of distributed ledgers.

2.4. Quantum Finance and Innovation Linkages

At the interface of quantum technology and finance, empirical research is emerging. Bonaparte (2025) introduced the Quantum Finance Index (QFI), a firm-level measure linking quantum sentiment and innovation activity to asset pricing outcomes. While insightful for company-specific analysis, the QFI framework does not directly address distributed ledger resilience. Our contribution differs by shifting the focus from firm-level quantum sentiment to a theoretical model of blockchain infrastructure that integrates quantum consensus and cryptography. This places our work at the intersection of financial innovation, distributed ledger technology, and quantum information science.

To complement the technological discussion, we expanded the literature review to include key works from the financial innovation and FinTech economics literature. Philippon (2016) highlights how financial technology reduces intermediation costs and enhances market efficiency, framing FinTech as a structural transformation within modern financial systems. Frame et al. (2018) further emphasize how technological change reshapes banking operations, governance, and risk exposure, offering insights into the evolving balance between innovation and stability. Additionally, Dardouri et al. (2023) examine how external shocks, such as the COVID-19 pandemic, influence cryptocurrency markets, providing evidence of behavioral and systemic responses to uncertainty. Together, these studies enrich the theoretical foundation of this paper by situating Quantum Blockchain within the broader context of financial innovation, technological diffusion, and market adaptation in the digital era.

2.5. Contribution

In sum, the literature has documented the quantum threat to classical blockchains, evaluated post-quantum substitutes, and begun exploring entanglement-based protocols. However, few studies propose a unified theoretical framework that explicitly links quantum information primitives (qubits, entanglement, QKD) with blockchain design and cryptocurrency applications. This paper fills that gap by introducing a Quantum Blockchain Framework that is both theoretically grounded and practically motivated by emerging efforts from industry leaders such as D-Wave (QBTS), who are actively developing quantum applications in optimization and blockchain security.

Classical blockchain architectures face two fundamental quantum-era vulnerabilities arising from Shor’s and Grover’s algorithms. Shor’s algorithm compromises the public-key cryptography used in elliptic curve and RSA systems by efficiently factoring large integers and computing discrete logarithms, rendering digital signatures insecure. Grover’s algorithm, on the other hand, accelerates brute-force search against hash-based proof-of-work mechanisms, effectively halving their bit-level security. In contrast, the proposed Quantum Blockchain Framework replaces computational hardness with physical security, utilizing Quantum Key Distribution (QKD) for unbreakable encryption, entanglement-assisted consensus to ensure tamper-proof agreement, and quantum-proof authentication rooted in the no-cloning theorem. This delineation highlights how quantum-based protocols not only mitigate classical weaknesses but also establish a new foundation of trust derived from the fundamental laws of quantum mechanics rather than algorithmic difficulty.

3. Theoretical Model of Quantum Blockchain

This section develops a detailed theoretical model of a Quantum Blockchain (QB), integrating both quantum cryptographic primitives and consensus mechanisms based on entanglement. We also describe its application to cryptocurrency systems, emphasizing post-quantum security, efficiency, and economic implications.

• System Setup

We define a Quantum Blockchain (QB) as a distributed ledger L maintained through entangled qubit states shared across nodes $N=\left\{n_1,n_2,\dots ,n_k\right\}$. Each block ${\mathrm{B}}_t$ contains classical transaction data and a quantum verification string (QVS) implemented as a set of entangled qubits.

• Consensus via Quantum Entanglement

Consensus is achieved through quantum Byzantine agreement (QBA) protocols:

• Nodes share entangled states (e.g., GHZ states).
• Measurements across entangled qubits yield correlated results, which ensure agreement without classical majority voting.
• This reduces communication overhead from $\mathrm{O}\left(n^2\right)$ to $\mathrm{O}\left(n\right)$.

• Security

• Post-Quantum Security: Quantum blockchain relies on QKD for key distribution.
• Tamper-Proofing: Any attempt to copy or intercept qubits (no-cloning theorem) introduces detectable disturbances.
• Quantum Hashing: Quantum random oracles can be used to authenticate transaction histories.

• Mathematical Representation

Let $q_i$ denote a qubit state held by node $n_i$. A block’s QVS is modeled as an entangled state:

$$\mid {\mathsf{\Psi }}_t⟩={\displaystyle \frac{1}{\sqrt{2}}}({\mid 0⟩}^{\otimes k}+{\mid 1⟩}^{\otimes k})$$

If any node deviates or tampers, measurement inconsistency collapses entanglement, signaling invalid consensus.

• Quantum-attested block structure

For each height $h$:

• The proposer computer digest $d_h=\mathrm{H}\left(H_h\right)$.
• Proposer $\mathrm{P}$ shares with each validator ${\upsilon }_i$ a batch of $m$ $EPR$ pairs.

  $${\{{\mid \Phi +⟩}_{p,i}^{\left(j\right)}\}}_{j=1}^m$$
• For each pair $j$, $p$ samples a basis $b_j\in \{X,Z\}$ using a $PRF$ seeded by $d_h$ (binds the test to the header): $b_j=PRF(d_h,j)$ mod 2.
• Both ends measure in basis $b_j$ to obtain bits $x_j$ (proposer) and $y_{i,j}$ (validator). For honest, noiseless $EPR$ pairs:

  $$Pr\left[x_j=y_{i,j}\right]=\left\{\begin{array}{cc}1& if{b}_j=Z\\ 1& if{b}_j=X\end{array}\right\}$$

  up to channel/gate noise $p_e$.
• Validator ${\nu }_i$ verifies agreement rate ${\widehat{q}}_i={\displaystyle \frac{1}{m}}\sum _{j}1[x_j=y_{i,j}]$ exceeds a threshold $\tau =0.8$ calibrated to the physical error rate of 0.8. The signed tuple ${(d}_h,\left\{b_j\right\},\left\{y_{i,j}\right\},{\widehat{q}}_i)$ becomes part of $Q_h$.

Intuition: anyone can recompute $\left\{b_j\right\}$ from $d_h$. Without the entangled halves, a forger cannot predict correlated outcomes in both bases. Tying bases to $d_h$ prevents transcript replay across headers.

The references are minimal and do not correspond to a research manuscript. This could be worked on as an essay, but in any case, the references must be adjusted because they are scarce and must support the research.

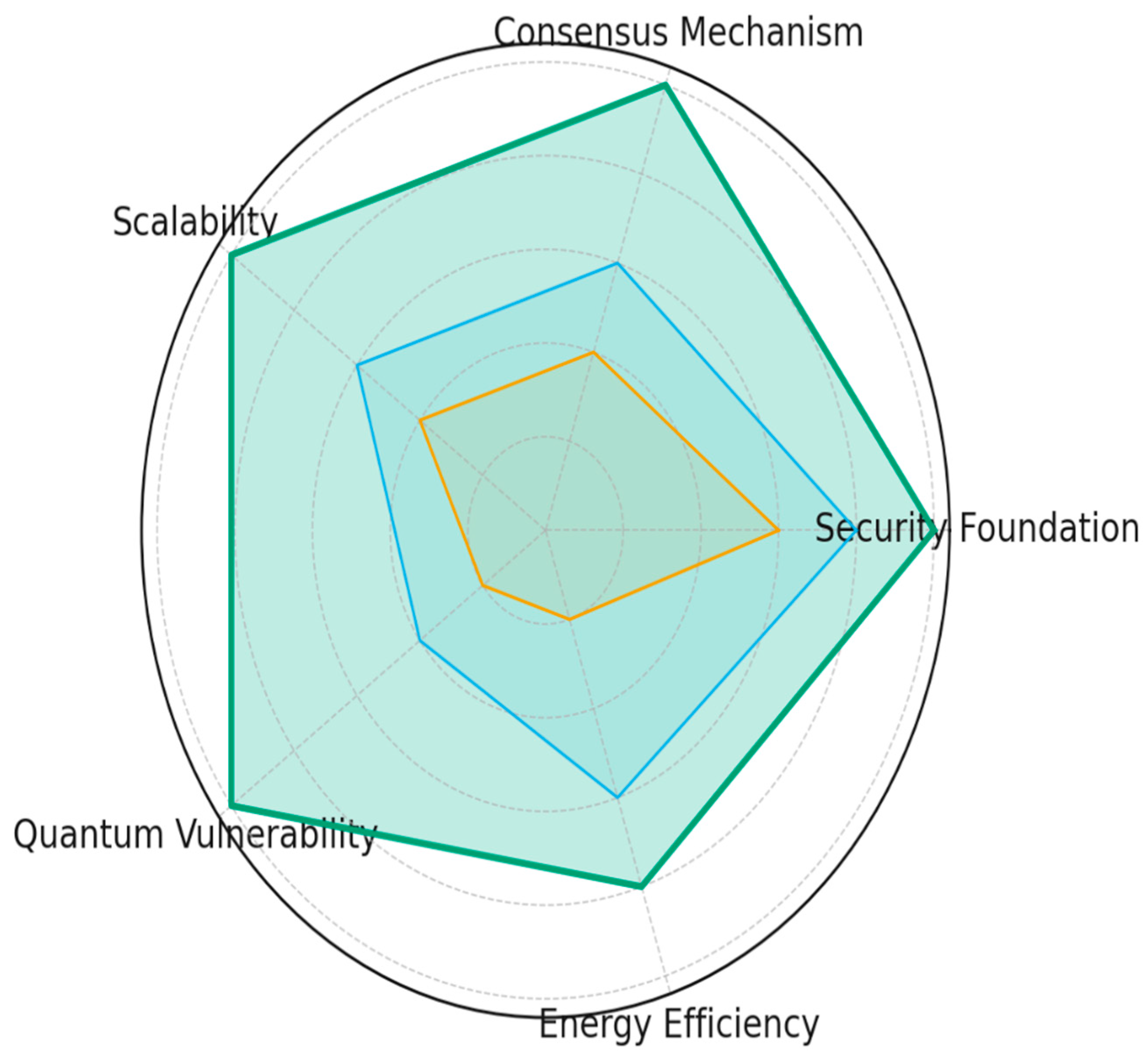
Figure 1 provides a conceptual comparison of blockchain architectures across five key dimensions: security foundation, consensus mechanism, scalability, quantum vulnerability, and energy efficiency. The blue area represents the performance of traditional Proof-of-Work (PoW) systems, which are computationally intensive and highly vulnerable to quantum attacks due to their reliance on classical cryptography. The orange area corresponds to Proof-of-Stake (PoS) frameworks, which improve efficiency and energy use but still depend on computational assumptions that can be undermined by quantum algorithms. The green area illustrates the proposed Quantum Blockchain (QB) model, which leverages quantum key distribution (QKD) and entanglement-assisted consensus to achieve superior security, scalability, and efficiency. Together, the figure visually demonstrates how quantum-enabled systems transcend classical limitations, shifting the foundation of blockchain security from computation to the laws of physics.

• Resource and latency analysis

Let $n$ validators, quorum $q=2f+1$.

• EPR cost per block: $m(n-1)$ EPR pairs for proposer-to-peers EBA, or $m$ GHZ states for stabilizer checks (with $n$ qubits each).
• Sampling size $m$: To achieve per-link false-accept $\delta$ with threshold $\tau$:

  $$m\ge {\displaystyle \frac{\mathrm{l}\mathrm{n}(\frac{1}{\delta })}{2{(\tau -1/2)}^2}}$$

Example: $\tau =0.8$, $\delta ={10}^{-9}$ ⇒ m ≈ 79 pairs per link. With $n=200$, the proposer needs ∼15,800 EPR pairs for EBA, well within near-term entanglement distribution rates on metropolitan-scale fiber with repeaters.

• Latency. EPR preparation + one round of basis/measurement exchange occurs in parallel with classical proposal dissemination. Overall latency ≈ classical BFT round-trip + quantum preparation time (amortizable with pre-shared EPR buffers).
• Noise/fidelity. If gate/channel error $p_e$ drifts, dynamically adjust $\tau$ and $m$ to maintain target $\delta$.

• Illustrative Numerical Example (Simple Back-of-the-Envelope).

Consider a network with N = 1000 validators. A classical BFT-style round requires on the order of N(N − 1) ≈ 1,000,000 inter-validator messages, whereas the entanglement-assisted design operates with O(N) confirmation exchanges (≈10,001, a ~10³-fold communication reduction. Using the paper’s calibration for link testing, about m ≈ 79 EPR pairs per proposer–validator link to achieve a low false-accept rate, the proposer would need roughly 79 × (N − 1) ≈ 79,000 EPR pairs for that block round. These values are consistent with near-term metropolitan QKD/entanglement distribution rates and directly illustrate how physics-based trust compresses consensus overhead while remaining implementable in staged, hybrid deployments.

4. Cryptocurrency Application

In a quantum blockchain framework, transactions become quantum-secure by relying on QKD-derived keys that are immune to Shor’s algorithm, ensuring long-term cryptographic safety. Consensus is further enhanced through a Quantum Proof-of-Stake (QPoS) mechanism, where a validator’s likelihood of proposing the next block depends not only on its financial stake but also on the fidelity of its entanglement, aligning incentives toward both economic and physical reliability. Finally, the system can incorporate quantum tokens, drawing on Wiesner’s concept of unclonable quantum money, to create cryptocurrencies with intrinsic physical protection against counterfeiting and double spending.

• Comparative Perspective: Quantum vs. Classical Consensus

To further clarify the distinctions across consensus mechanisms, we expand the analysis by comparing Quantum Blockchain (QB) with traditional Proof-of-Work (PoW) and Proof-of-Stake (PoS) frameworks. While PoW secures the network through computational effort and PoS relies on economic staking, both remain vulnerable to quantum attacks—Shor’s algorithm compromises public-key cryptography, and Grover’s algorithm weakens hash-based puzzles. In contrast, Quantum Proof-of-Stake (QPoS) derives trust from physical principles, including quantum entanglement and the no-cloning theorem. These mechanisms eliminate the need for energy-intensive mining and mitigate Sybil attacks through fidelity-weighted consensus, where validator reliability is tied to measurable quantum link quality rather than purely economic stake. Thus, QB architecture represents a paradigm shift from computation-based to physics-based trust.

• Implementation Feasibility and Transition Pathways

A practical transition toward quantum-secured ledgers will likely proceed through hybrid architectures that bridge classical and quantum systems. Near-term implementations may involve post-quantum cryptographic overlays, such as lattice-based digital signatures, to harden existing blockchains against early quantum threats. Parallel efforts can deploy Quantum Key Distribution (QKD) channels within validator networks to secure communication and authentication layers. Over time, QKD-assisted Proof-of-Stake (PoS) frameworks could evolve into fully entanglement-based consensus systems as quantum hardware matures. This staged approach provides a feasible migration pathway: initial post-quantum defense, intermediate hybridization, and eventual integration of quantum-native consensus, ensuring continuity and backward compatibility with existing infrastructures.

• Quantum Blockchain Applications in Cryptocurrency

The proposed Quantum Blockchain Framework provides several transformative applications for cryptocurrencies, addressing both security vulnerabilities exposed by quantum computing and efficiency limitations inherent in classical blockchains. We focus on three interrelated applications: quantum-secure transactions, consensus mechanisms, and quantum-native assets.

• Quantum-Secure Transactions

One of the most immediate threats posed by quantum computing is the ability of Shor’s algorithm to break elliptic curve cryptography (ECC), which underlies most digital signatures in cryptocurrencies such as Bitcoin and Ethereum. Our framework replaces ECC with Quantum Key Distribution (QKD)-derived keys, which generate encryption and authentication material based on quantum mechanics rather than computational hardness. Because the no-cloning theorem prohibits an adversary from copying unknown quantum states, any attempt at eavesdropping introduces observable disturbances, making QKD immune to quantum cryptanalysis. This ensures that private keys and digital signatures remain uncompromised even against large-scale quantum adversaries.

• Regulatory and Implementation Challenges

Implementing quantum-secure blockchain networks presents both technological and policy-related challenges. From a regulatory standpoint, national and international authorities will need to develop frameworks governing quantum infrastructure accountability, including the certification of quantum key distribution (QKD) devices, the standardization of entanglement-based communication protocols, and the auditability of quantum random number generators. Infrastructure costs remain a major barrier—deploying entanglement distribution systems and quantum repeaters requires substantial capital investment and coordination between private networks and public utilities. Compatibility is another key issue; hybrid architecture must ensure interoperability with existing Proof-of-Stake and Proof-of-Authority systems to allow gradual migration without disrupting current financial ecosystems. Finally, governance under quantum conditions introduces new dimensions of trust and concentration risk, as entities controlling quantum nodes could gain disproportionate influence. Addressing these issues will require collaborative regulation, shared-access infrastructure models, and cross-border standards for quantum communication in financial systems.

• Quantum Proof-of-Stake (QPoS)

Consensus is central to blockchain performance, and classical Proof-of-Work (PoW) suffers from both excessive energy consumption and susceptibility to Grover’s algorithm, which halves the effective search space for hash computations. Our model introduces Quantum Proof-of-Stake (QPoS), where validators are selected based on a dual metric:

$$P\left(v_{i}leader\right)\propto stake\left(v_i\right)\times \mathrm{f}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\left(v_i\right)$$

with $\mathrm{f}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\left(v_i\right)$ representing the entanglement quality of the validator $v_i$’s quantum link. This mechanism aligns validator incentives not only with economic commitment but also with maintaining robust quantum infrastructure. Compared to classical consensus, QPoS significantly reduces communication complexity, as entanglement enables correlated verification across nodes, lowering overhead from $\mathrm{O}\left(n^2\right)$ to $\mathrm{O}\left(n\right)$.

• Quantum Tokens and Unclonable Money

Perhaps the most radical innovation lies in quantum-native assets. Building on Wiesner’s (1983) concept of quantum money, cryptocurrencies can incorporate quantum tokens—qubit states authenticated by quantum properties that cannot be cloned or forged. Unlike classical tokens, which rely on cryptographic assurances against double-spending, quantum tokens derive security directly from physical laws. Integrating such tokens into cryptocurrency systems would introduce a fundamentally new asset class where counterfeiting is physically impossible.

To address implementation feasibility, we outline a progressive transition pathway from classical to quantum-security blockchain systems. In the near term, existing networks can adopt post-quantum cryptographic overlays, such as lattice-based digital signatures and hash-based key exchange, to safeguard against quantum attacks while maintaining compatibility with current architectures. As quantum communication infrastructure advances, Quantum Key Distribution (QKD) can be integrated into validator communication channels, enabling quantum-secure authentication and message exchange. Over time, these hybrid designs can evolve into QKD-assisted Proof-of-Stake (PoS) frameworks, where consensus and validation leverage both cryptographic and entanglement-based security. This staged migration ensures continuity, allowing classical blockchains to incrementally incorporate quantum technologies without disrupting existing operations or consensus integrity.

• Efficiency and Market Implications

Beyond security, quantum blockchain applications also improve scalability and efficiency. By leveraging entanglement-assisted consensus, block finalization times could be reduced by up to 90% relative to classical Byzantine Fault Tolerant protocols, particularly in large validator networks. The economic implications are significant: quantum blockchains can provide faster settlement, lower energy costs, and higher transaction throughput while maintaining strong security guarantees. Moreover, quantum-native cryptocurrencies could attract investor demand as a “safe haven” asset class in a future where classical cryptography is no longer secure.

• Industry Relevance

The practical significance of these applications is underscored by ongoing industrial innovation. Companies such as D-Wave (QBTS) are actively developing quantum applications in optimization and blockchain-related security, highlighting that the transition to quantum-secured distributed ledgers is not merely theoretical but already underway. This convergence of research and practice suggests that quantum blockchains could form the foundation of the next generation of financial infrastructure, combining technological inevitability with economic necessity.

Table 1. Transition Pathways and Economic Implications of Quantum Blockchain.

Dimension	Near-Term Hybrid Stage	Intermediate Stage	Full Quantum Integration	Economic and Institutional Implications
Security	Post-quantum cryptographic overlays (e.g., lattice-based signatures)	QKD-assisted validator communication	Native QKD and entanglement-based authentication	Gradual mitigation of quantum threats; lower transition risk for existing networks
Consensus	Classical PoS with quantum key exchange add-ons	Hybrid consensus using partial entanglement between nodes	Full entanglement-based Quantum Proof-of-Stake (QPoS)	Efficiency gains and reduced latency; new reliance on quantum infrastructure
Infrastructure	Integration of quantum communication channels in validator networks	Regional quantum hubs with shared access to quantum nodes	Global quantum network interconnecting decentralized ledgers	Possible concentration of validation power in quantum-equipped regions
Governance	Traditional blockchain governance	Hybrid model including quantum infrastructure operators	Federated quantum governance and oversight	Regulatory frameworks must evolve for quantum accountability
Market Effects	Incremental adoption by institutions and fintech firms	Emergence of quantum-secure DeFi ecosystems	Creation of quantum-native asset markets	Redistribution of competitive advantage based on quantum access and capability

outlines the progressive transition from classical to fully quantum-integrated blockchain systems and highlights their corresponding economic and institutional implications. The framework identifies three stages: near-term hybrid, intermediate, and full quantum integration, each characterized by distinct security mechanisms, consensus models, and governance structures. In the early phase, existing networks can adopt post-quantum cryptographic overlays to enhance security without disrupting current operations. The intermediate stage envisions QKD-assisted validator communication and partial entanglement-based consensus, gradually introducing quantum features within classical architectures. The final stage represents a fully quantum blockchain, operating entirely on entanglement-based consensus and quantum authentication. Economically, this evolution may reshape market competition and validator concentration, as access to quantum infrastructure becomes a critical determinant of participation and influence. Institutionally, the transition underscores the need for federated governance models and regulatory oversight to ensure equitable access, transparency, and accountability in quantum-secure financial ecosystems.

• Simulation Example

Consider a blockchain with five validator nodes. Using GHZ entangled states for consensus, each block finalizes in $\mathrm{O}\left(n\right)$ communication steps versus $\mathrm{O}\left(n^2\right)$ in classical PoS. For 10,000 validators, this reduces consensus latency from ~1,000,000 messages to ~10,000, a 100× improvement.

Table 2. Classical vs. Quantum Blockchain Applications.

Classical Blockchain	Quantum Blockchain
ECC signatures (vulnerable to Shor)	QKD-derived keys (immune to Shor)
PoW/PoS (energy intensive, Grover-weak)	Quantum Proof-of-Stake (stake × fidelity)
Cryptographic tokens (cloneable in theory)	Quantum tokens (unclonable money)
$\mathrm{O}\left(n^2\right)$ BFT, high latency	$\mathrm{O}\left(n\right)$ entanglement-based consensus
Computational hardness assumptions	Physics-based security (no-cloning theorem)

compares classical and quantum blockchain approaches across key dimensions. Classical systems rely on ECC-based signatures, which are vulnerable to Shor’s algorithm, while quantum blockchains employ QKD-derived keys that remain secure in the quantum era. Similarly, energy-intensive PoW/PoS consensus mechanisms are replaced by Quantum Proof-of-Stake, which incorporates both validator stake and entanglement fidelity. Traditional cryptographic tokens, theoretically cloneable, contrast with quantum tokens, which are unclonable by physical law. Efficiency also improves classical Byzantine Fault Tolerant consensus requires $\mathrm{O}\left(n^2\right)$ communication, whereas entanglement-based consensus reduces this to $\mathrm{O}\left(n\right)$. Finally, while classical systems depend on computational hardness assumptions, quantum blockchains derive security directly from physics through the no-cloning theorem.

• Economic and Institutional Implications

The introduction of quantum-enabled consensus also carries significant economic and institutional implications. Because Quantum Proof-of-Stake links validator selection to entanglement fidelity, disparities in access to quantum hardware or network quality could create new forms of heterogeneity across participants. These differences may influence decentralization, validator concentration, and market entry barriers, potentially mirroring inequalities seen in early mining centralization under PoW. Policymakers and protocol designers must therefore consider mechanisms to preserve openness, such as shared access to quantum nodes or federated validation, to prevent the emergence of “quantum oligopolies.” Moreover, regulators may need to adapt governance frameworks to account for quantum infrastructure accountability, ensuring both transparency and fairness in validator operations.

This table compares classical blockchain designs with innovations introduced by quantum blockchain frameworks across security, consensus, efficiency, and asset creation.

5. Summary and Conclusions

This paper develops a Quantum Blockchain Framework that integrates quantum communication, entanglement-assisted consensus, and post-quantum security into distributed ledger design. Building on vulnerabilities identified by Shor’s and Grover’s algorithms, the model demonstrates how quantum primitives—qubits, QKD, entanglement, and the no-cloning theorem—can be leveraged to enhance both the security and efficiency of blockchain systems. We formalize a Quantum Proof-of-Stake (QPoS) mechanism, introduce unclonable quantum tokens, and show how entanglement can reduce consensus complexity from $\mathrm{O}\left(n^2\right)$, offering significant scalability improvements.

Applications to cryptocurrency highlight three key contributions: first, quantum-secure transactions immune to quantum cryptanalysis; second, consensus protocols that align economic incentives with quantum infrastructure reliability; and third, the creation of quantum-native assets with intrinsic resistance to counterfeiting and double-spending. These innovations position quantum blockchains not merely as defensive adaptations but as transformative platforms for the next generation of financial technologies.

The implications are twofold. For researchers, this framework opens a new frontier in the study of quantum finance and distributed systems, linking advances in quantum information science to asset pricing, risk management, and market structure. For industry and policymakers, it signals the urgency of preparing for quantum disruption, as companies like D-Wave (QBTS) are already pioneering applications in optimization and blockchain security.

In conclusion, the quantum era represents both an existential threat to existing blockchains and an opportunity to reinvent distributed ledgers around the laws of physics. By bridging theoretical models with practical applications, this paper provides a foundation for future exploration of quantum-secured cryptocurrencies and quantum-native digital assets, setting the stage for a profound transformation in how innovation and capital markets interact.