Has US (Un)Conventional Monetary Policy Affected South African Financial Markets in the Aftermath of COVID-19? A Quantile–Frequency Connectedness Approach
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Quantile Connectedness Component
2.2.2. Frequency Connectedness Component
2.2.3. Connectedness and Spillover Effects in Quantile–Frequency Framework
3. Empirical Analysis
3.1. Descriptive Statistics of Time Series
3.2. Overview of Empirical Analysis
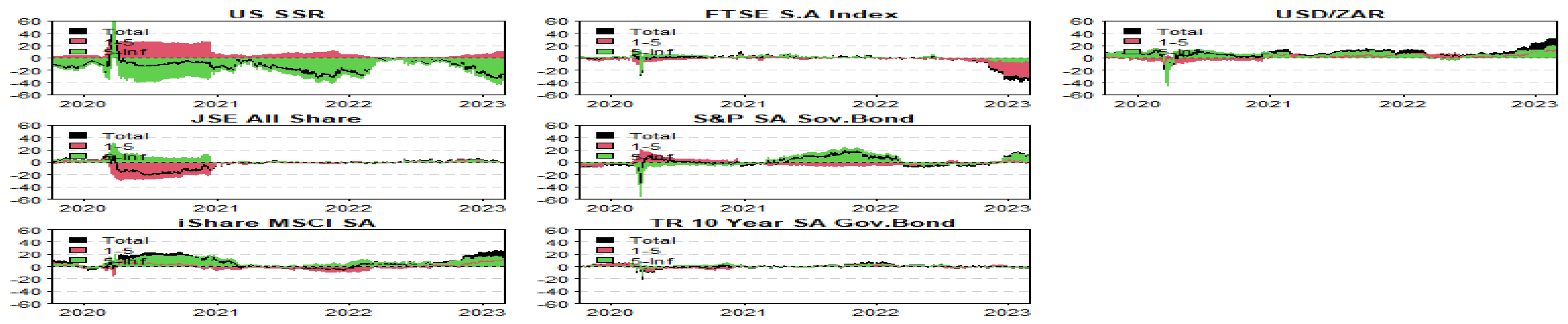
3.3. Frequency Connectedness Analysis
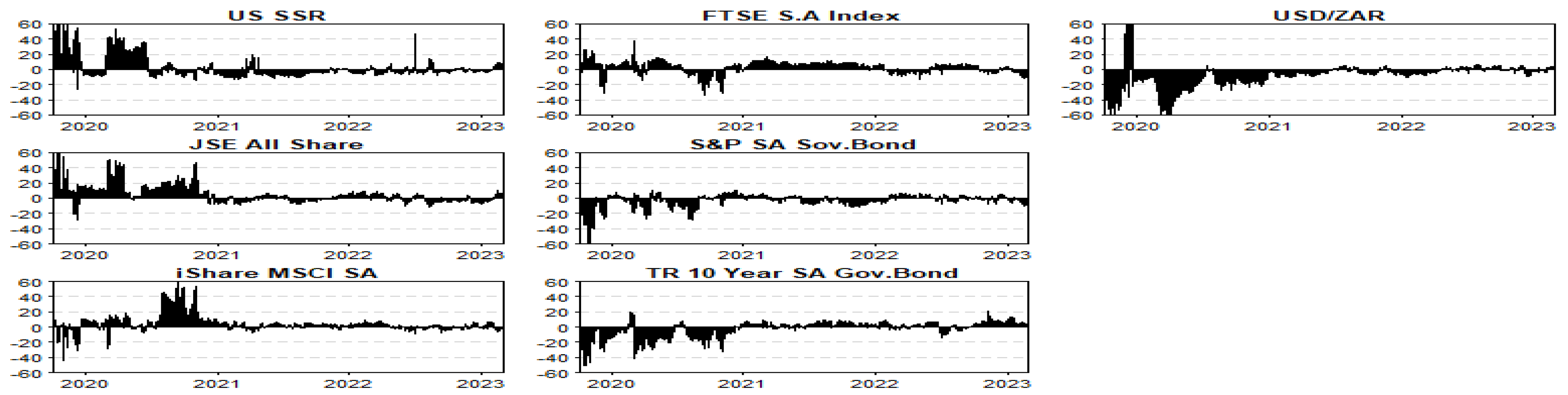
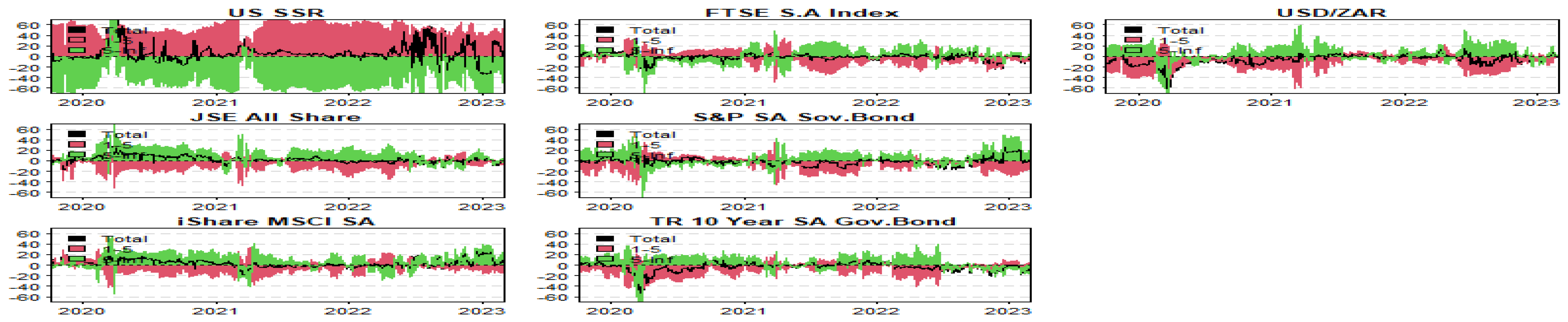
3.4. Quantile Connectedness Analysis
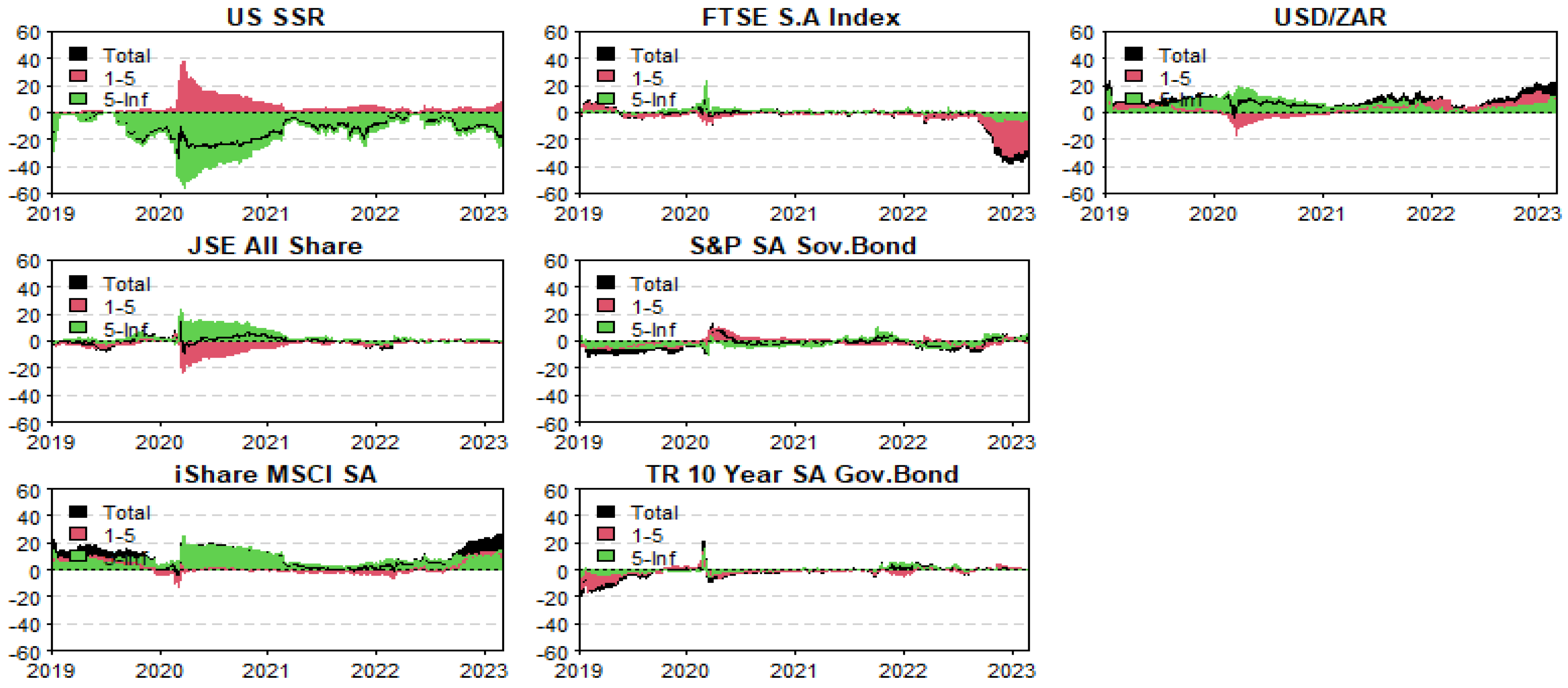
3.5. Quantile–Frequency Connectedness Analysis
4. Further Discussion of Results
4.1. Comparison to Previous Literature
4.2. Implications of Findings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Author | Measure of UMP | Country | Period | Method | Result |
| Lavigne et al. (2014) | Asset purchase, and bond and equity inflows to EMEs | 23 EMEs and 8 AE | 2005–2013 | Event study and dynamic stochastic general equilibrium mode | UMP as implemented by AE increases capital flow, and volatility in the financial market during the tapering period |
| Bowman et al. (2015) | Policy announcements, maturity extension program (MEP) and FOMC speeches | 17 EMEs | 2006:M01–2013:M12 | VAR and event study | US UMP significantly affects the sovereign bond of EMEs. Lower US sovereign yields also lower sovereign yields in most EMEs. |
| Aizenman et al. (2016) | FOMC QE and tapering announcements | 10 robust and 15 fragile emerging economies | 27 November 2012 – 3 March 2013 | Event study | Full sample: significant drop in stock indices during tapering |
| Estrada et al. (2016) | Taper tantrum dummy | 22 developing countries | 2013:M05–2013:M06 | Regression analysis/event study | Taper tantrum had negative effect on South African equity prices |
| Anaya et al. (2017) | Fed balance sheet | 19 EMEs | 2008M01–2014M12 | GVAR and event study | US UMP has increased capital flows from the US to EMEs for almost 6 months. This is accompanied by a persistent increase in real and financial variables (exchange rate). |
| Gupta et al. (2017) | FOMC announcements and 2/10-year Treasury yield | 20 EMEs, including South Africa | 1 October 2008–1 September 2016. | Event study and OLS | US UMP results in exchange rate appreciation, increase in equity prices and decrease in bond yields in EME. The spillover effects of other AE are weaker than US. |
| Apostolou and Beirne (2019) | Fed balance sheet | 13EMEs | 2003:M01–2018:M12 | GARCH-in-mean | UMP has negative impact on equity, debt and exchange rate markets |
| Naape and Masoga (2019) | Asset Purchase | US and SA | 25 November 2008–12 December 2012 | Event study, AR and (CAR) | US UMP has a positive impact in the short run and a negative impact in the long run on treasury bonds |
| Kabundi et al. (2020) | FRED Policy Interest Rate (PIR) and Asset Purchase | US and SA | 1990M01–2018M02 | BVAR and event study | US CMP and UMP expansion has a positive impact on the SA financial market, except for industrial production and credit to the private sector, which respond differently. |
| Kalu et al. (2020) | US 10-year bond and Treasury Bill | 6 African countries | 01/05/2013–31/12/2018 | FE, RE and PMG | US UMP has a negative effect on African equities |
| Meszaros and Olson (2020) | St. Louis Adjusted Monetary Base; and Divisia M4 measure of money | SA | 1960:Q1–2008:Q3 and 2008:Q4–2018:Q3 | VAR | US UMP, particularly the quantitative easing programs, had only slight overall effects on South Africa’s economy |
| Ono (2020) | SSR | SA | 09/01/2004–29/12/2017 | VARX | US UMP has negative impact on stock markets but positive on exchange rates |
| Bhattarai et al. (2021) | US Treasuries, debt and mortgage-backed securities | 13EMEs | 2008:M01–2014:M11 | SVAR and PVAR | US UMP increases stock prices and yet weakens the exchange rates in the EMEs |
| Lubys and Panda (2021) | FOMC policy announcements | BRICS | 1 January 2008–1 January 2017 | Event study, AR, CAR and CAPM | US UMP announcements have a negative impact on the SA financial markets (stock and bond) |
| Wei and Han (2021) | FOMC policy announcements | 37 countries | 1 January 2011–30 January 2020 | Event study | USP announcements have negative impact on equities and exchange rates and yet insignificant for bonds |
| Yildirim and Ivrendi (2021) | US Mortgage spread and US Term spread | 20 EMEs and 20 AEs | 1 June 2007–1 February 2013 | SVAR | US UMP resulted in a decrease in country risk premiums and long-term yields. An upswing in stock prices and appreciation of local currencies across AEs, especially in EMEs. |
| Ntshangase et al. (2023) | Dummy variable as a proxy for United States’ QE | 12 EMEs | 2000:Q1–2020:Q4 | Panel VAR | US UMP increases volatility in exchange rate of EMEs, decreases interest rate and has no significant impact on stock prices |
| Cui et al. (2024) | SSR | 33 emerging and advanced countries | 2002:Q2–2021:Q4 | TGVAR | EMEs are more vulnerable to spillover effects than AEs, and EMs are much more exposed to monetary policy shocks than AEs |
Appendix B
| US SSR | JSE All Share | iShare MSCI SA Index | FTSE South Africa Index | S&P SA Sovereign Bond Index | TR SA 10 Years Gov. Bond Index | Exchange Rate USD/ZAR | FROM | |
| Panel A: D-Y | ||||||||
| US SSR | 82.15 | 3.92 | 4.46 | 1.73 | 2.70 | 0.67 | 4.36 | 17.85 |
| JSE All Share | 1.81 | 90.20 | 4.26 | 0.83 | 0.84 | 0.77 | 1.29 | 9.80 |
| iShare MSCI SA Index | 1.16 | 2.69 | 54.00 | 0.47 | 11.04 | 0.59 | 30.04 | 46.00 |
| FTSE South Africa Index | 0.47 | 1.09 | 2.63 | 89.83 | 3.05 | 1.12 | 1.81 | 10.17 |
| S&P SA Sovereign Bond Index | 0.59 | 0.55 | 14.34 | 1.50 | 65.38 | 1.01 | 16.63 | 34.62 |
| TR SA 10 Years Gov. Bond Index | 0.94 | 1.13 | 0.72 | 1.61 | 1.25 | 93.40 | 0.95 | 6.60 |
| Exchange Rate USD/ZAR | 1.00 | 0.61 | 29.81 | 0.71 | 13.17 | 0.87 | 53.83 | 46.17 |
| TO | 5.97 | 9.99 | 56.22 | 6.85 | 32.06 | 5.03 | 55.09 | 171.21 |
| Inc.Own | 88.12 | 100.19 | 110.22 | 96.68 | 97.44 | 98.43 | 108.93 | |
| Net | −11.88 | 0.19 | 10.22 | −3.32 | −2.56 | −1.57 | 8.93 | |
| TCI = 24.46 | ||||||||
| Panel B: High frequency | ||||||||
| US SSR | 0.09 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.05 |
| JSE All Share | 1.52 | 71.57 | 3.20 | 0.74 | 0.71 | 0.63 | 1.00 | 7.80 |
| iShare MSCI SA Index | 0.97 | 1.94 | 44.76 | 0.35 | 9.33 | 0.53 | 25.22 | 38.34 |
| FTSE South Africa Index | 0.35 | 0.89 | 2.06 | 72.30 | 2.15 | 0.83 | 1.42 | 7.71 |
| S&P SA Sovereign Bond Index | 0.44 | 0.43 | 10.19 | 0.99 | 50.56 | 0.72 | 12.07 | 24.85 |
| TR SA 10 Years Gov. Bond Index | 0.70 | 0.79 | 0.54 | 1.39 | 0.89 | 72.63 | 0.70 | 5.00 |
| Exchange Rate USD/ZAR | 0.83 | 0.51 | 24.07 | 0.56 | 10.94 | 0.69 | 44.25 | 37.61 |
| TO | 4.81 | 4.57 | 40.07 | 4.02 | 24.03 | 3.41 | 40.43 | 121.35 |
| Inc.Own | 4.90 | 76.14 | 84.83 | 76.32 | 74.59 | 76.04 | 84.68 | |
| Net | 4.76 | −3.22 | 1.73 | −3.68 | −0.81 | −1.59 | 2.82 | |
| TCI = 17.34 | ||||||||
| Panel C: Low frequency | ||||||||
| US SSR | 82.07 | 3.91 | 4.46 | 1.72 | 2.69 | 0.67 | 4.35 | 17.80 |
| JSE All Share | 0.29 | 18.63 | 1.06 | 0.10 | 0.13 | 0.14 | 0.29 | 2.00 |
| iShare MSCI SA Index | 0.19 | 0.75 | 9.24 | 0.12 | 1.71 | 0.06 | 4.82 | 7.66 |
| FTSE South Africa Index | 0.12 | 0.20 | 0.56 | 17.53 | 0.90 | 0.28 | 0.39 | 2.46 |
| S&P SA Sovereign Bond Index | 0.16 | 0.11 | 4.16 | 0.51 | 14.82 | 0.28 | 4.56 | 9.78 |
| TR SA 10 Years Gov. Bond Index | 0.24 | 0.34 | 0.18 | 0.22 | 0.36 | 20.78 | 0.25 | 1.60 |
| Exchange Rate USD/ZAR | 0.17 | 0.10 | 5.74 | 0.15 | 2.23 | 0.18 | 9.58 | 8.56 |
| TO | 1.16 | 5.41 | 16.15 | 2.82 | 8.03 | 1.61 | 14.67 | 49.86 |
| Inc.Own | 83.23 | 24.05 | 25.39 | 20.35 | 22.84 | 22.39 | 24.25 | |
| Net | −16.63 | 3.41 | 8.49 | 0.36 | −1.75 | 0.02 | 6.11 | |
| TCI = 7.12 |
Appendix C
| US SSR | JSE All Share | iShare MSCI SA Index | FTSE South Africa Index | S&P SA Sovereign Bond Index | TR SA 10 Years Gov. Bond Index | Exchange Rate USD/ZAR | FROM | |
| Panel A: 5th quantile | ||||||||
| US SSR | 24.24 | 14.21 | 12.94 | 13.35 | 10.63 | 12.63 | 12.00 | 75.76 |
| JSE All Share | 13.05 | 21.08 | 14.66 | 12.83 | 13.20 | 12.80 | 12.39 | 78.92 |
| iShare MSCI SA Index | 13.08 | 14.21 | 22.64 | 13.52 | 15.37 | 12.71 | 8.47 | 77.36 |
| FTSE South Africa Index | 12.84 | 13.54 | 13.88 | 22.05 | 13.34 | 12.21 | 12.15 | 77.95 |
| S&P SA Sovereign Bond Index | 12.32 | 13.54 | 16.47 | 13.59 | 21.63 | 12.78 | 9.67 | 78.37 |
| TR SA 10 Years Gov. Bond Index | 12.94 | 14.11 | 13.69 | 13.07 | 12.56 | 20.90 | 12.74 | 79.10 |
| Exchange Rate USD/ZAR | 13.83 | 14.27 | 9.65 | 14.10 | 10.38 | 13.73 | 24.04 | 75.96 |
| TO | 78.08 | 83.87 | 81.27 | 80.46 | 75.49 | 76.86 | 67.41 | 543.43 |
| Inc.Own | 102.32 | 104.95 | 103.91 | 102.50 | 97.12 | 97.76 | 91.45 | |
| Net | 2.32 | 4.95 | 3.91 | 2.50 | −2.88 | −2.24 | −8.55 | |
| TCI = 77.63 | ||||||||
| Panel B: 50th quantile | ||||||||
| US SSR | 75.39 | 2.91 | 5.65 | 2.05 | 6.33 | 0.91 | 6.77 | 24.61 |
| JSE All Share | 2.90 | 88.95 | 3.30 | 1.18 | 1.60 | 0.89 | 1.17 | 11.05 |
| iShare MSCI SA Index | 2.03 | 2.13 | 54.99 | 0.63 | 9.93 | 1.24 | 29.05 | 45.01 |
| FTSE South Africa Index | 1.19 | 0.92 | 2.13 | 89.76 | 3.02 | 1.26 | 1.71 | 10.24 |
| S&P SA Sovereign Bond Index | 1.94 | 0.78 | 12.25 | 1.79 | 67.38 | 1.16 | 14.71 | 32.62 |
| TR SA 10 Years Gov. Bond Index | 1.42 | 1.05 | 0.89 | 1.13 | 0.98 | 93.62 | 0.91 | 6.38 |
| Exchange Rate USD/ZAR | 2.50 | 0.72 | 28.19 | 0.90 | 12.20 | 1.40 | 54.09 | 45.91 |
| TO | 11.99 | 8.52 | 52.40 | 7.68 | 34.06 | 6.86 | 54.32 | 175.83 |
| Inc.Own | 87.37 | 97.47 | 107.40 | 97.44 | 101.44 | 100.48 | 108.41 | |
| Net | −12.63 | −2.53 | 7.40 | −2.56 | 1.44 | 0.48 | 8.41 | |
| TCI = 25.12 | ||||||||
| Panel C: 95th quantile | ||||||||
| US SSR | 28.41 | 12.31 | 14.17 | 12.29 | 11.05 | 10.91 | 10.86 | 71.59 |
| JSE All Share | 13.22 | 23.30 | 13.93 | 12.26 | 12.55 | 12.28 | 12.46 | 76.70 |
| iShare MSCI SA Index | 12.96 | 13.57 | 23.71 | 12.72 | 16.40 | 12.17 | 8.48 | 76.29 |
| FTSE South Africa Index | 13.52 | 12.86 | 13.33 | 21.74 | 13.15 | 12.32 | 13.09 | 78.26 |
| S&P SA Sovereign Bond Index | 12.32 | 13.15 | 16.53 | 13.15 | 22.41 | 12.25 | 10.21 | 77.59 |
| TR SA 10 Years Gov. Bond Index | 12.56 | 13.40 | 12.80 | 13.00 | 12.44 | 21.93 | 13.88 | 78.07 |
| Exchange Rate USD/ZAR | 13.71 | 13.93 | 9.53 | 13.68 | 10.51 | 14.06 | 24.57 | 75.43 |
| TO | 78.28 | 79.22 | 80.29 | 77.10 | 76.08 | 73.99 | 68.97 | 533.93 |
| Inc.Own | 106.69 | 102.52 | 104.00 | 98.84 | 98.49 | 95.92 | 93.54 | |
| Net | 6.69 | 2.52 | 4.00 | −1.16 | −1.51 | −4.08 | −6.46 | |
| TCI = 76.28 |
Appendix D
| US SSR | JSE All Share | iShare MSCI SA Index | FTSE South Africa Index | S&P SA Sovereign Bond Index | TR SA 10 Years Gov. Bond Index | Exchange Rate USD/ZAR | FROM | |
|---|---|---|---|---|---|---|---|---|
| Panel A: Low Frequency | ||||||||
| US SSR | 23.59 | 13.56 | 12.26 | 12.84 | 10.17 | 12.19 | 11.58 | 72.59 |
| JSE All Share | 5.42 | 7.95 | 5.45 | 5.07 | 5.20 | 4.74 | 4.62 | 30.51 |
| iShare MSCI SA Index | 4.77 | 4.56 | 5.99 | 4.50 | 4.46 | 3.67 | 2.80 | 24.76 |
| FTSE South Africa Index | 4.60 | 4.55 | 4.53 | 6.87 | 4.40 | 3.66 | 3.42 | 25.17 |
| S&P SA Sovereign Bond Index | 3.96 | 3.83 | 4.20 | 3.69 | 5.00 | 2.88 | 2.29 | 20.85 |
| TR SA 10 Years Gov. Bond Index | 4.80 | 4.89 | 4.60 | 4.49 | 4.19 | 6.28 | 4.09 | 27.06 |
| Exchange Rate USD/ZAR | 3.95 | 3.56 | 2.66 | 3.48 | 2.68 | 3.14 | 4.80 | 19.46 |
| TO | 27.51 | 34.95 | 33.70 | 34.06 | 31.09 | 30.28 | 28.82 | 220.40 |
| Inc.Own | 51.10 | 42.90 | 39.69 | 40.93 | 36.09 | 36.55 | 33.62 | |
| TCI = 31.49 | ||||||||
| Net | −45.09 | 4.44 | 8.93 | 8.89 | 10.24 | 3.22 | 9.36 | |
| Panel B: High Frequency | ||||||||
| US SSR | 0.65 | 0.65 | 0.68 | 0.51 | 0.47 | 0.44 | 0.41 | 3.17 |
| JSE All Share | 7.64 | 13.12 | 9.21 | 7.75 | 8.00 | 8.05 | 7.77 | 48.42 |
| iShare MSCI SA Index | 8.31 | 9.65 | 16.65 | 9.02 | 10.92 | 9.04 | 5.66 | 52.60 |
| FTSE South Africa Index | 8.23 | 8.99 | 9.35 | 15.18 | 8.94 | 8.55 | 8.72 | 52.78 |
| S&P SA Sovereign Bond Index | 8.36 | 9.71 | 12.26 | 9.91 | 16.63 | 9.90 | 7.38 | 57.52 |
| TR SA 10 Years Gov. Bond Index | 8.14 | 9.22 | 9.09 | 8.58 | 8.37 | 14.62 | 8.65 | 52.04 |
| Exchange Rate USD/ZAR | 9.89 | 10.71 | 6.99 | 10.62 | 7.70 | 10.60 | 19.24 | 56.50 |
| TO | 50.57 | 48.93 | 47.57 | 46.39 | 44.40 | 46.58 | 38.59 | 323.03 |
| Inc.Own | 51.22 | 62.05 | 64.23 | 61.57 | 61.03 | 61.20 | 57.83 | |
| Net | 47.40 | 0.51 | −5.02 | −6.39 | −13.13 | −5.46 | −17.91 | |
| TCI = 46.15 |
Appendix E
| US SSR | JSE All Share | iShare MSCI SA Index | FTSE South Africa Index | S&P SA Sovereign Bond Index | TR SA 10 Years Gov. Bond Index | Exchange Rate USD/ZAR | FROM | |
| Panel A: Low Frequency | ||||||||
| US SSR | 75.17 | 2.90 | 5.62 | 2.04 | 6.30 | 0.91 | 6.74 | 24.50 |
| JSE All Share | 0.52 | 17.56 | 0.37 | 0.20 | 0.14 | 0.14 | 0.17 | 1.54 |
| iShare MSCI SA Index | 0.34 | 0.52 | 9.60 | 0.11 | 1.61 | 0.19 | 4.41 | 7.18 |
| FTSE South Africa Index | 0.36 | 0.22 | 0.37 | 18.44 | 0.66 | 0.23 | 0.32 | 2.16 |
| S&P SA Sovereign Bond Index | 0.66 | 0.20 | 3.18 | 0.54 | 14.36 | 0.32 | 3.61 | 8.50 |
| TR SA 10 Years Gov. Bond Index | 0.35 | 0.34 | 0.15 | 0.14 | 0.24 | 20.47 | 0.20 | 1.42 |
| Exchange Rate USD/ZAR | 0.83 | 0.17 | 5.35 | 0.23 | 1.94 | 0.28 | 8.86 | 8.81 |
| TO | 3.07 | 4.35 | 15.04 | 3.26 | 10.89 | 2.07 | 15.44 | 54.12 |
| Inc.Own | 78.24 | 21.90 | 24.64 | 21.69 | 25.26 | 22.54 | 24.30 | |
| Net | −21.43 | 2.81 | 7.86 | 1.09 | 2.39 | 0.65 | 6.63 | |
| TCI = 7.73 | ||||||||
| Panel B: High Frequency | ||||||||
| US SSR | 0.21 | 0.02 | 0.02 | 0.01 | 0.03 | 0.01 | 0.03 | 0.11 |
| JSE All Share | 2.38 | 71.40 | 2.93 | 0.98 | 1.46 | 0.75 | 1.01 | 9.51 |
| iShare MSCI SA Index | 1.69 | 1.61 | 45.39 | 0.52 | 8.32 | 1.05 | 24.65 | 37.83 |
| FTSE South Africa Index | 0.83 | 0.70 | 1.76 | 71.32 | 2.37 | 1.03 | 1.38 | 8.07 |
| S&P SA Sovereign Bond Index | 1.28 | 0.58 | 9.07 | 1.24 | 53.02 | 0.84 | 11.10 | 24.12 |
| TR SA 10 Years Gov. Bond Index | 1.06 | 0.71 | 0.74 | 1.00 | 0.74 | 73.15 | 0.71 | 4.96 |
| Exchange Rate USD/ZAR | 1.67 | 0.55 | 22.84 | 0.68 | 10.26 | 1.11 | 45.23 | 37.11 |
| TO | 8.92 | 4.17 | 37.36 | 4.42 | 23.17 | 4.79 | 38.88 | 121.71 |
| Inc.Own | 9.13 | 75.56 | 82.76 | 75.75 | 76.18 | 77.94 | 84.11 | |
| Net | 8.80 | −5.34 | −0.47 | −3.65 | −0.95 | −0.17 | 1.77 | |
| TCI = 17.39 |
Appendix F
| US SSR | JSE All Share | iShare MSCI SA Index | FTSE South Africa Index | S&P SA Sovereign Bond Index | TR SA 10 Years Gov. Bond Index | Exchange Rate USD/ZAR | FROM | |
| Panel A: Low Frequency | ||||||||
| US SSR | 27.97 | 11.90 | 13.68 | 11.89 | 10.62 | 10.53 | 10.46 | 69.08 |
| JSE All Share | 3.24 | 4.92 | 2.98 | 2.88 | 2.64 | 2.78 | 2.78 | 17.30 |
| iShare MSCI SA Index | 3.71 | 3.43 | 5.21 | 3.12 | 3.76 | 3.13 | 2.56 | 19.71 |
| FTSE South Africa Index | 4.81 | 4.20 | 4.30 | 6.18 | 4.21 | 3.88 | 3.82 | 25.22 |
| S&P SA Sovereign Bond Index | 3.71 | 3.52 | 4.15 | 3.34 | 5.03 | 2.96 | 2.55 | 20.24 |
| TR SA 10 Years Gov. Bond Index | 3.74 | 3.37 | 3.23 | 3.42 | 3.17 | 5.07 | 3.36 | 20.29 |
| Exchange Rate USD/ZAR | 3.65 | 3.36 | 2.21 | 3.05 | 2.38 | 3.23 | 5.14 | 17.88 |
| TO | 22.86 | 29.78 | 30.56 | 27.70 | 26.77 | 26.50 | 25.54 | 189.71 |
| Inc.Own | 50.83 | 34.71 | 35.76 | 33.89 | 31.80 | 31.57 | 30.68 | |
| Net | −46.22 | 12.48 | 10.85 | 2.48 | 6.53 | 6.21 | 7.66 | |
| TCI = 27.10 | ||||||||
| Panel B: High Frequency | ||||||||
| US SSR | 0.44 | 0.42 | 0.49 | 0.40 | 0.42 | 0.38 | 0.40 | 2.51 |
| JSE All Share | 9.98 | 18.37 | 10.95 | 9.38 | 9.91 | 9.51 | 9.67 | 59.41 |
| iShare MSCI SA Index | 9.24 | 10.14 | 18.51 | 9.60 | 12.64 | 9.04 | 5.93 | 56.58 |
| FTSE South Africa Index | 8.71 | 8.66 | 9.03 | 15.56 | 8.94 | 8.44 | 9.26 | 53.04 |
| S&P SA Sovereign Bond Index | 8.61 | 9.62 | 12.38 | 9.81 | 17.38 | 9.29 | 7.65 | 57.36 |
| TR SA 10 Years Gov. Bond Index | 8.81 | 10.03 | 9.57 | 9.58 | 9.27 | 16.86 | 10.52 | 57.78 |
| Exchange Rate USD/ZAR | 10.07 | 10.58 | 7.31 | 10.63 | 8.13 | 10.84 | 19.43 | 57.55 |
| TO | 55.41 | 49.44 | 49.73 | 49.40 | 49.31 | 47.49 | 43.43 | 344.22 |
| Inc.Own | 55.86 | 67.81 | 68.24 | 64.96 | 66.69 | 64.35 | 62.86 | |
| Net | 52.90 | −9.97 | −6.85 | −3.64 | −8.04 | −10.28 | −14.12 | |
| TCI = 49.17 |
References
- Aizenman, J., Binici, M., & Hutchison, M. (2016). The transmission of Federal Reserve tapering news to emerging financial markets. International Journal of Central Banking, 12(2), 317–356. [Google Scholar]
- Anaya, P., Hachula, M., & Offermanns, C. (2017). Spillovers of U.S. unconventional monetary policy to emerging markets: The role of capital flows. Journal of International Money and Finance, 73(B), 275–295. [Google Scholar] [CrossRef]
- Ando, T., Greenwood-Nimmo, M., & Shin, Y. (2022). Quantile connectedness: Modeling tail behavior in the topology of financial networks. Management Science, 68(4), 2401–2431. [Google Scholar] [CrossRef]
- Antonakakis, N., Gabauer, D., & Gupta, R. (2019). International monetary policy spillovers: Evidence from a time-varying parameter vector autoregression. International Review of Financial Analysis, 65, 101382. [Google Scholar] [CrossRef]
- Anyikwa, I., & Phiri, A. (2023). Connectedness and spillover between African equity, commodity, foreign exchange and cryptocurrency markets during the COVID-19 and Russia-Ukraine conflict. Future Business Journal, 9(1), 48. [Google Scholar] [CrossRef]
- Apostolou, A., & Beirne, J. (2019). Volatility spillovers of unconventional monetary policy to emerging market economies. Economic Modelling, 79, 118–129. [Google Scholar] [CrossRef]
- Baruník, J., & Křehlík, T. (2018). Measuring the frequency dynamics of financial connectedness and systemic risk. Journal of Financial Econometrics, 16(2), 271–296. [Google Scholar] [CrossRef]
- Bhattarai, S., Chatterjee, A., & Park, W. (2021). Effects of US quantitative easing on emerging market economies. Journal of Economic Dynamics and Control, 122, e104031. [Google Scholar] [CrossRef]
- Bowman, D., Londono, J., & Sapriza, H. (2015). U.S. unconventional monetary policy and transmission to emerging market economies. Journal of International Money and Finance, 55, 27–59. [Google Scholar] [CrossRef]
- Breitenlechner, M., Gründler, D., & Scharler, J. (2021). Unconventional monetary policy announcements and information shocks in the U.S. Journal of Macroeconomics, 67, 103283. [Google Scholar] [CrossRef]
- Cepni, O., Gupta, R., & Ji, Q. (2023). Sentiment regimes and reaction of stock markets to conventional and unconventional monetary policies: Evidence from OECD countries. Journal of Behavioral Finance, 24(3), 365–381. [Google Scholar] [CrossRef]
- Chatziantoniou, I., Abakah, E., Gabauer, D., & Tiwari, A. (2021). Quantile time–frequency price connectedness between green bond, green equity, sustainable investments and clean energy markets. Journal of Cleaner Production, 361, 132088. [Google Scholar] [CrossRef]
- Chatziantoniou, I., Gabauer, D., & Gupta, R. (2023). Integration and risk transmission in the market for crude oil: New evidence from a time-varying parameter frequency connectedness approach. Resources Policy, 84, 103729. [Google Scholar] [CrossRef]
- Choi, S., Phiri, A., Teplova, T., & Umar, Z. (2024). Connectedness between (un) conventional monetary policy and islamic and advanced equity markets: A returns and volatility spillover analysis. International Review of Economics & Finance, 91, 348–363. [Google Scholar] [CrossRef]
- Cui, B., Li, J., & Zhang, Y. (2024). Asymmetries in the international spillover effects of monetary policy: Based on TGVAR model. The North American Journal of Economics and Finance, 69, 102029. [Google Scholar] [CrossRef]
- Dedola, L., Georgiadis, G., Gräb, J., & Mehl, A. (2020). Does a big bazooka matter? Quantitative easing policies and exchange rates. Journal of Monetary Economics, 117, 489–506. [Google Scholar] [CrossRef]
- de Rezende, R., & Ristiniemi, A. (2023). A shadow rate without a lower bound constraint. Journal of Banking & Finance, 146, 106686. [Google Scholar]
- Diebold, F., & Yilmaz, K. (2009). Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal, 119(534), 158–171. [Google Scholar] [CrossRef]
- Diebold, F., & Yilmaz, K. (2012). Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of forecasting, 28(1), 57–66. [Google Scholar] [CrossRef]
- Diebold, F., & Yılmaz, K. (2014). On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics, 182(1), 119–134. [Google Scholar] [CrossRef]
- Diebold, F. X., & Yilmaz, K. (2023). On the past, present, and future of the Diebold–Yilmaz approach to dynamic network connectedness. Journal of Econometrics, 234, 115–120. [Google Scholar] [CrossRef]
- Estrada, G., Park, D., & Ramayandi, A. (2016). Taper tantrum and emerging equity market slumps. Emerging Markets Finance and Trade, 52(5), 1060–1071. [Google Scholar] [CrossRef]
- Fausch, J., & Sutter, D. (2024). Monetary policy spillovers: The impact of ECB conventional and unconventional monetary policies on the Swiss stock market. Applied Economics Letters, 31(2), 122–127. [Google Scholar] [CrossRef]
- Gertler, M., & Karadi, P. (2015). Monetary policy surprises, credit costs, and economic activity. American Economic Journal: Macroeconomics, 7(1), 44–76. [Google Scholar] [CrossRef]
- Gupta, P., Masetti, O., & Rosenblatt, D. (2017). Should emerging markets worry about US monetary policy announcements? World Bank Policy Research Working Paper, (8100). World Bank Group. [Google Scholar]
- Hong-Vo, D., & Dang, T. (2024). The geopolitical risk spillovers across BRICS countries: A quantile frequency connectedness approach. Scottish Journal of Political Economy, 71(1), 132–143. [Google Scholar] [CrossRef]
- Huertas, G. (2022). Why follow the fed? Monetary policy in times of US tightening. IMF Working Paper No. 2022-2243, September. International Monetary. [Google Scholar]
- Iyke, B., & Ho, S. (2021). Exchange rate exposure in the South African stock market before and during the COVID-19 pandemic. Finance Research Letters, 43, 102000. [Google Scholar] [CrossRef]
- Kabundi, A., Loate, T., & Viegi, N. (2020). Spillovers of the Conventional and Unconventional Monetary Policy from the US to South Africa. South African Journal of Economics, 88(4), 435–471. [Google Scholar] [CrossRef]
- Kalu, E., Okoyeuzu, C., Ukemenam, A., & Ujunwa, A. (2020). Spillover effects of the US monetary policy normalization on African stock markets. Journal of Economics and Development, 22(1), 3–19. [Google Scholar] [CrossRef]
- Krippner, L. (2013). Measuring the stance of monetary policy in zero lower bound environments. Economic Letters, 118(1), 135–138. [Google Scholar] [CrossRef]
- Krippner, L. (2019). A note of caution on shadow rate estimates. Journal of Money, Credit, and Banking, 52(4), 952–962. [Google Scholar] [CrossRef]
- Lavigne, R., Sarker, S., & Vasishtha, G. (2014). Spillover effects of quantitative easing on emerging-market economies. Bank of Canada Review, 2014, 23–33. [Google Scholar]
- Le, T. (2023). Quantile time-frequency connectedness between cryptocurrency volatility and renewable energy volatility during the COVID-19 pandemic and Ukraine-Russia conflicts. Renewable Energy, 202, 613–625. [Google Scholar] [CrossRef]
- Lubys, J., & Panda, P. (2021). US and EU unconventional monetary policy spillover on BRICS financial markets: An event study. Empirica, 48(2), 353–371. [Google Scholar] [CrossRef]
- Marco, T., Mighri, Z., Tiwari, A., & Sarwar, S. (2023). A quantile-time-frequency connectedness investigation through the dirty and clean cryptocurrencies spillover. Journal of Cleaner Production, 425, 138889. [Google Scholar] [CrossRef]
- Maurer, T., & Nitschka, T. (2023). Stock market evidence on the international transmission channels of US monetary policy surprises. Journal of International Money and Finance, 136, 102866. [Google Scholar] [CrossRef]
- Meszaros, J., & Olson, E. (2020). The effects of US quantitative easing on South Africa. Review of Financial Economics, 38(2), 321–331. [Google Scholar] [CrossRef]
- Mkhombo, T., & Phiri, A. (2022). Investigating Fisher effect in SACU countries: A wavelet coherence approach. Cogent Economics & Finance, 10(1), 2142308. [Google Scholar] [CrossRef]
- Mkhombo, T., & Phiri, A. (2023). Wavelet-Based Analysis of the Comovement Between Exchange Rate and Stock Returns in SACU Countries. The Journal of Developing Areas, 57(4), 29–53. [Google Scholar] [CrossRef]
- Naape, B., & Masoga, M. (2019). An Address of the Global Financial Crises with Unconventional Monetary Policies. Journal of Economics and Behavioral Studies, 11(6(J)), 23–31. [Google Scholar] [CrossRef]
- Narayan, P., Phan, D., & Liu, G. (2021). COVID-19 lockdowns, stimulus packages, travel bans, and stock returns. Finance Research Letters, 38, 101732. [Google Scholar] [CrossRef]
- Nong, H., & Liu, H. (2023). Measuring the frequency and quantile connectedness between policy categories and global oil price. Resources Policy, 83, 103565. [Google Scholar] [CrossRef]
- Ntshangase, L., Zhou, S., & Kaseeram, I. (2023). The Spillover effects of US unconventional monetary policy on inflation and non-inflation targeting emerging markets. Economies, 11(5), 138. [Google Scholar] [CrossRef]
- Ono, S. (2020). Impacts of conventional and unconventional US monetary policies on global financial markets. International Economics and Economic Policy, 17(1), 1–24. [Google Scholar] [CrossRef]
- Papadamou, S., Kyriazis, N., & Tzeremes, P. (2019). Spillover effects of US QE and QE tapering on African and middle eastern stock indices. Journal of Risk and Financial Management, 12(2), 57. [Google Scholar] [CrossRef]
- Phan, D. H. B., & Narayan, P. K. (2021). Country responses and the reaction of the stock market to COVID-19—A preliminary exposition. In Research on pandemics (pp. 6–18). Routledge. [Google Scholar]
- Phiri, A. (2015). Asymmetric cointegration and causality effects between financial development and economic growth in South Africa. Studies in Economics and Finance, 32(4), 464–484. [Google Scholar] [CrossRef]
- Phiri, A. (2020). Structural changes in exchange rate-stock returns dynamics in South Africa: Examining the role of crisis and new trading platform. Economic Change and Restructuring, 53(1), 171–193. [Google Scholar] [CrossRef]
- Phiri, A., Anyikwa, I., & Moyo, C. (2023). Co-movement between COVID-19 and G20 stock market returns: A time and frequency analysis. Heliyon, 9(3), e14195. [Google Scholar] [CrossRef]
- Qabhobho, T., Wait, C., & Le Roux, P. (2020). Exchange rate volatility, the contagion and spillover effect from South African to other SADC currency markets: 2007–2015. African Journal of Business and Economic Research, 15(2), 7–23. [Google Scholar] [CrossRef]
- Rigobon, R. (2019). Contagion, spillover, and interdependence. Economía, 19(2), 69–100. [Google Scholar] [CrossRef]
- Stiassny, A. (1996). A spectral decomposition for structural VAR models. Empirical Economics, 21, 535–555. [Google Scholar] [CrossRef]
- Strohsal, T., Proaño, C., & Wolters, J. (2019). Characterizing the financial cycle: Evidence from a frequency domain analysis. Journal of Banking & Finance, 106, 568–591. [Google Scholar] [CrossRef]
- Taleb, N. (2007). Black swans and the domains of statistics. The American Statistician, 61(3), 198–200. [Google Scholar] [CrossRef]
- Tumala, M., Salisu, A., Atoi, N., & Yaaba, B. (2021). International monetary policy spillovers to emerging economies in Sub-Saharan Africa: A global VAR analysis. Scientific African, 14, e00976. [Google Scholar] [CrossRef]
- Umar, Z., Sayed, A., Gubareva, M., & Vo, X. (2023). Influence of unconventional monetary policy on agricultural commodities futures: Network connectedness and dynamic spillovers of returns and volatility. Applied Economics, 55(22), 2521–2535. [Google Scholar] [CrossRef]
- Wang, X., Liu, J., & Xie, Q. (2024). Quantile frequency connectedness between energy tokens, crypto market, and renewable energy stock markets. Heliyon, 10(3), e25068. [Google Scholar] [CrossRef]
- Wei, X., & Han, L. (2021). The impact of COVID-19 pandemic on transmission of monetary policy to financial markets. International Review of Financial Analysis, 74, 101705. [Google Scholar] [CrossRef]
- Wei, Y., Bai, L., & Li, X. (2022). Normal and extreme interactions among nonferrous metal futures: A new quantile-frequency connectedness approach. Finance Research Letters, 47, 102855. [Google Scholar] [CrossRef]
- Wu, J., & Xia, F. (2016). Measuring the macroeconomic impact of monetary policy at zero lower bound. Journal of Money and Central Banking, 48(2–3), 253–291. [Google Scholar] [CrossRef]
- Wu, J., & Xia, F. (2020). Negative interest rate policy and the yield curve. Journal of Applied Econometrics, 35(6), 653–796. [Google Scholar] [CrossRef]
- Yildirim, Z., & Ivrendi, M. (2021). Spillovers of US unconventional monetary policy: Quantitative easing, spreads, and international financial markets. Financial Innovation, 7(1), 86. [Google Scholar] [CrossRef]
- Zhao, M., & Park, H. (2024). Quantile time-frequency spillovers among green bonds, cryptocurrencies, and conventional financial markets. International Review of Financial Analysis, 93, 103198. [Google Scholar] [CrossRef]
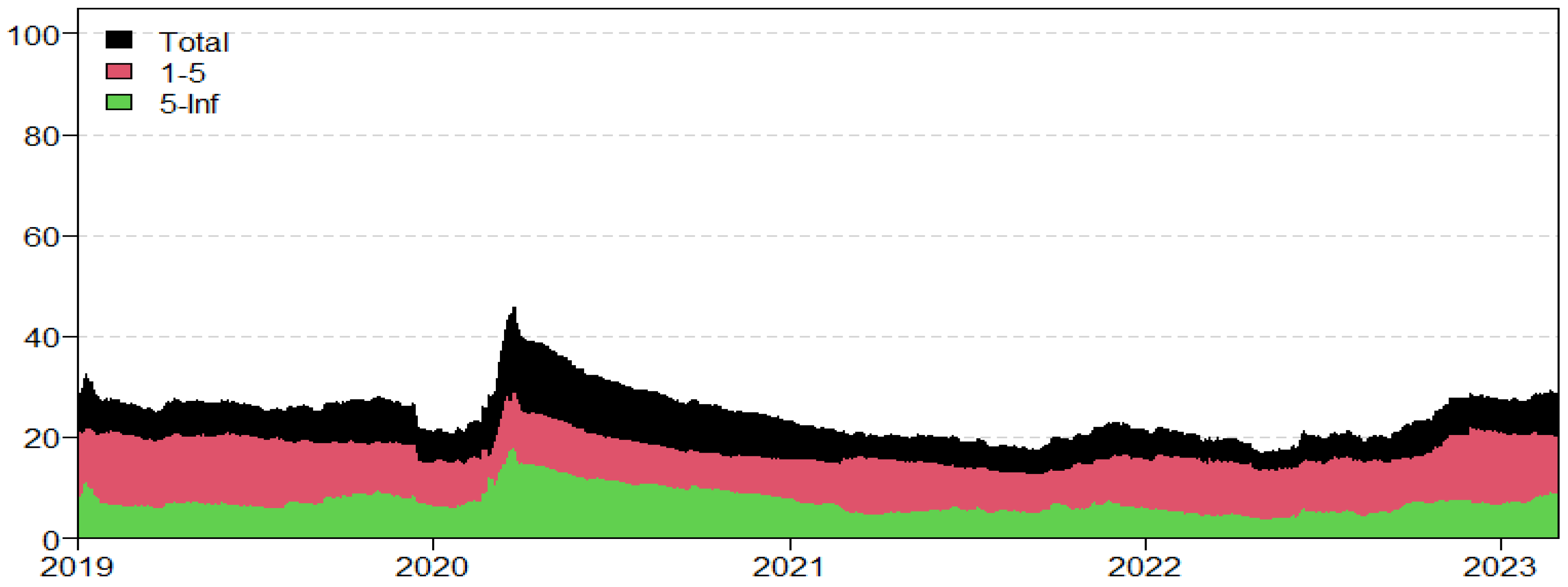
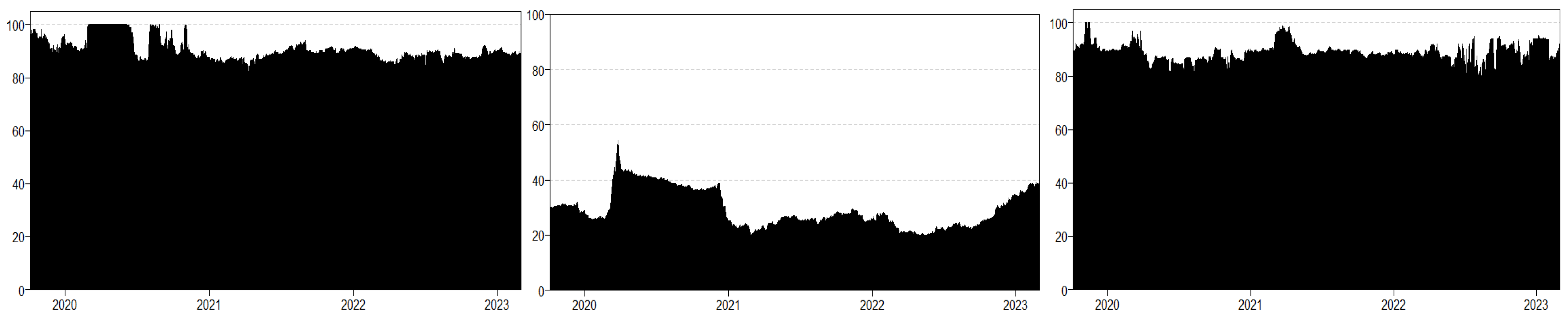
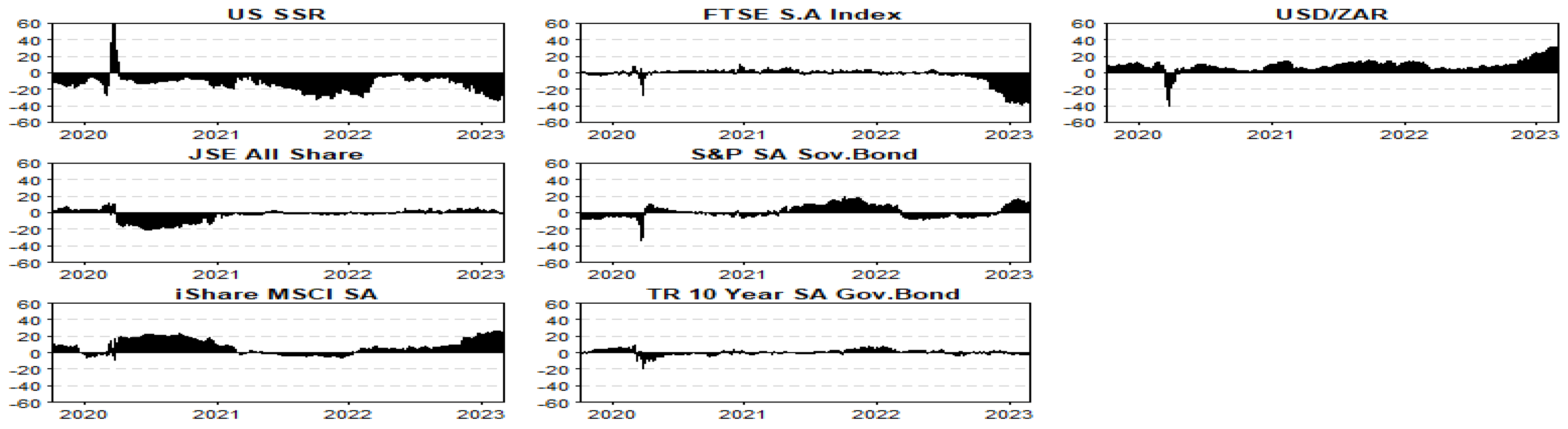
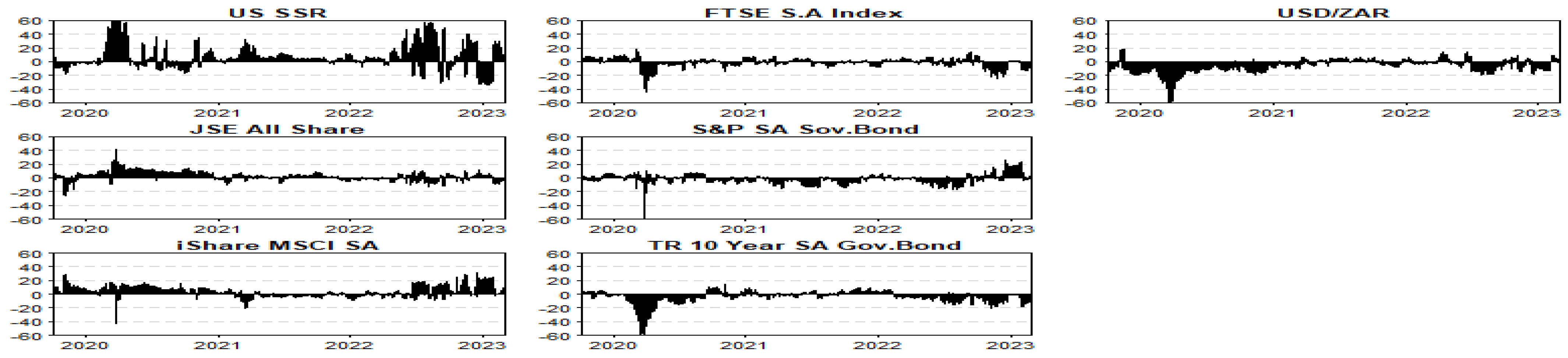
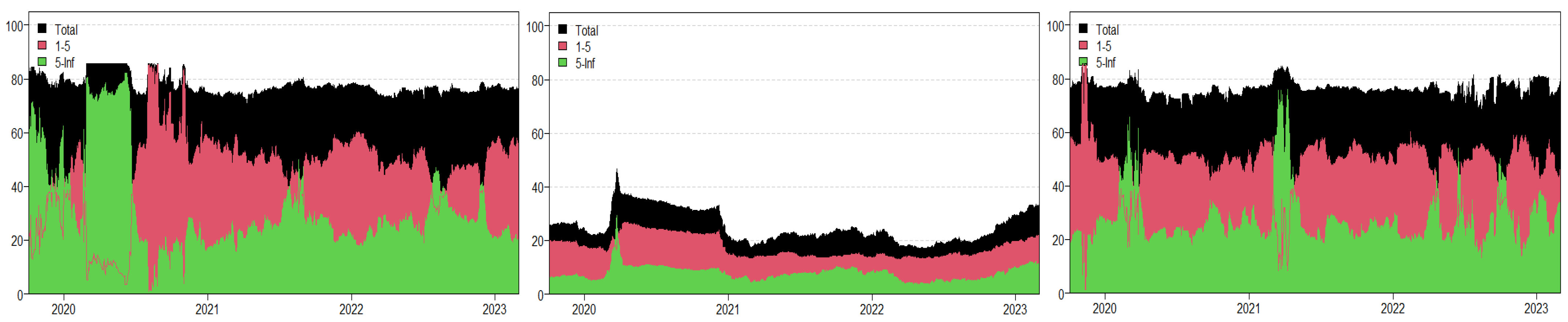
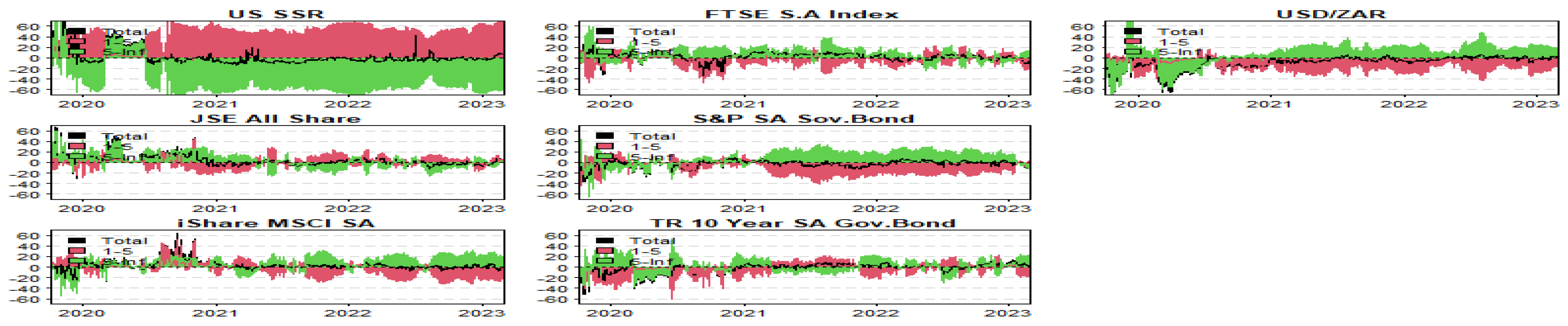
| Series | Mean | Std Dev | Skew | Kurt | JB (prob) | ADF | PP |
|---|---|---|---|---|---|---|---|
| US SSR | 0.74 | 2.17 | 0.21 | 2.10 | 0.00 | −0.369 | −0.285 |
| All Share Index | 0.032 | 1.28 | −0.82 | 11.01 | 0.00 | −32.98 *** | −32.99 *** |
| FTSE SA Index | 0.018 | 1.35 | −0.86 | 11.81 | 0.00 | −32.78 *** | −32.79 *** |
| iShares MSCI Index | −0.017 | 2.12 | −0.94 | 11.63 | 0.00 | −36.72 *** | −36.63 *** |
| S&P SA Sovereign Bond | 0.029 | 0.06 | −0.52 | 15.59 | 0.00 | −11.55 *** | −28.69 *** |
| TR SA 10 yr Gov. Bond | 0.033 | 0.62 | −0.46 | 14.78 | 0.00 | −29.27 *** | −29.47 *** |
| USD/ZAR Exchange Rate | 0.022 | 0.94 | 0.30 | 3.62 | 0.00 | −34.04 *** | −34.04 *** |
| Receivers | Transmitters | TCI | |
|---|---|---|---|
| Total frequency | US SSR, FTSE SA index, S&P sovereign bond, 10-year gov bond | JSE all share, MSCI SA index, USD-ZAR | 24.46 |
| High frequency | JSE all share, FTSE SA index, S&P sovereign bond, 10-year gov bond | US SSR, MSCI SA index, USD-ZAR | 17.34 |
| Low frequency | US SSR, S&P sovereign bond | JSE all share, MSCI SA index, FTSE SA index, 10-year gov bond, USD-ZAR | 7.12 |
| Receivers | Transmitters | TCI | |
|---|---|---|---|
| 5th quantile | S&P sovereign bond, 10-year gov bond, USD-ZAR | US SSR, JSE all share, MSCI SA index, FTSE SA index. | 77.63 |
| 50th quantile | US SSR, JSE all share, FTSE SA index | MSCI SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | 25.12 |
| 95th quantile | FTSE SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | US SSR, JSE all share, MSCI SA index | 76.28 |
| Receivers | Transmitters | TCI | |
|---|---|---|---|
| Panel A: 5th quantile | |||
| Low frequency | US SSR | JSE all share, MSCI SA index, FTSE SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR. | 31.49 |
| High frequency | FTSE SA index, MSCI SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | US SSR, JSE all share | 46.15 |
| Panel B: 50th quantile | |||
| Low frequency | US SSR | JSE all share, MSCI SA index, FTSE SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | 7.73 |
| High frequency | JSE all share, MSCI SA index, FTSE SA index, S&P sovereign bond, 10-year gov bond | US SSR, USD-ZAR | 17.39 |
| Panel C: 95th quantile | |||
| Low frequency | US SSR | JSE all share, MSCI SA index, FTSE SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | 27.10 |
| High frequency | JSE all share, MSCI SA index, FTSE SA index, S&P sovereign bond, 10-year gov bond, USD-ZAR | US SSR | 49.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngondo, M.; Phiri, A. Has US (Un)Conventional Monetary Policy Affected South African Financial Markets in the Aftermath of COVID-19? A Quantile–Frequency Connectedness Approach. Int. J. Financial Stud. 2025, 13, 153. https://doi.org/10.3390/ijfs13030153
Ngondo M, Phiri A. Has US (Un)Conventional Monetary Policy Affected South African Financial Markets in the Aftermath of COVID-19? A Quantile–Frequency Connectedness Approach. International Journal of Financial Studies. 2025; 13(3):153. https://doi.org/10.3390/ijfs13030153
Chicago/Turabian StyleNgondo, Mashilana, and Andrew Phiri. 2025. "Has US (Un)Conventional Monetary Policy Affected South African Financial Markets in the Aftermath of COVID-19? A Quantile–Frequency Connectedness Approach" International Journal of Financial Studies 13, no. 3: 153. https://doi.org/10.3390/ijfs13030153
APA StyleNgondo, M., & Phiri, A. (2025). Has US (Un)Conventional Monetary Policy Affected South African Financial Markets in the Aftermath of COVID-19? A Quantile–Frequency Connectedness Approach. International Journal of Financial Studies, 13(3), 153. https://doi.org/10.3390/ijfs13030153






