Exchange Rate Forecasting: A Deep Learning Framework Combining Adaptive Signal Decomposition and Dynamic Weight Optimization
Abstract
1. Introduction
2. Literature Review
2.1. Exchange Rate Forecasting Based on Statistical Model
2.2. Exchange Rate Forecasting Based on an Artificial Intelligence Model
2.3. Exchange Rate Forecasting Based on a Hybrid Model
2.4. Research Gaps and Contributions
- Although CEEMDAN is an effective method for signal processing and analysis, its practical application is limited by manual parameter adjustment. This manual adjustment process not only increases the computational complexity but also introduces the subjectivity of model implementation. Existing research has yet to solve the problem of automatic optimization of CEEMDAN parameters, which leaves an important gap in the application of financial time series prediction.
- Within the decomposition-integration framework, although individual prediction models can effectively forecast exchange rate prices, the inherent nonlinearity and complexity of exchange rates pose challenges in fully extracting the information embedded in the original data. Therefore, it is essential to choose an appropriate combination of prediction models that addresses the limitations of individual models.
- An innovative OCEEMDAN method has been introduced, applying GWO to the automatic optimization of key parameters in CEEMDAN. Unlike previous studies that relied on manual parameter adjustment, this method optimizes the accuracy and elasticity of signal decomposition by optimizing the information entropy of the intrinsic mode function (IMFs), thereby gaining a deeper understanding of the intrinsic structure and complexity of the signal.
- A dynamic integrated weight optimization framework based on ZOA was proposed. Different from the fixed-weight integration method, this method adjusts the weights of Bi-LSTM, GRU, and FNN according to the current market conditions. ZOA simulates the foraging and defense behaviors of zebras, providing effective optimization capabilities and rapid convergence, thereby enhancing the overall prediction performance.
- An advanced predictive model for the closing prices of the EUR/USD, GBP/USD, and USD/JPY currency pairs is developed using enhanced signal decomposition techniques and intelligent parameter optimization. The model exhibits substantial prediction accuracy and robustness through simulation trials on historical data of various currency pairs, providing great support for decision-making in the foreign exchange market.
3. Methodology and Proposed Model Framework
3.1. The Proposed OCEEMDAN Method
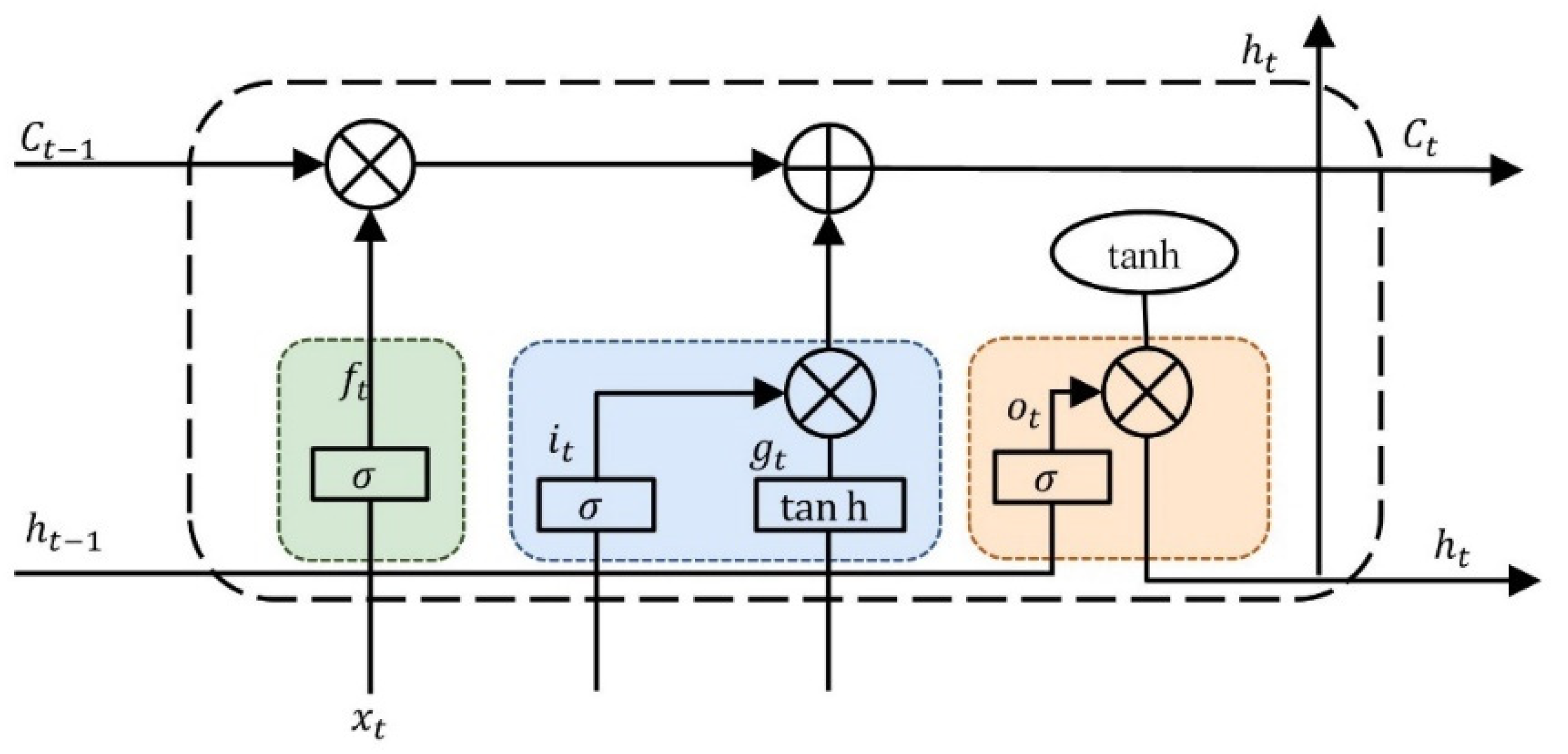
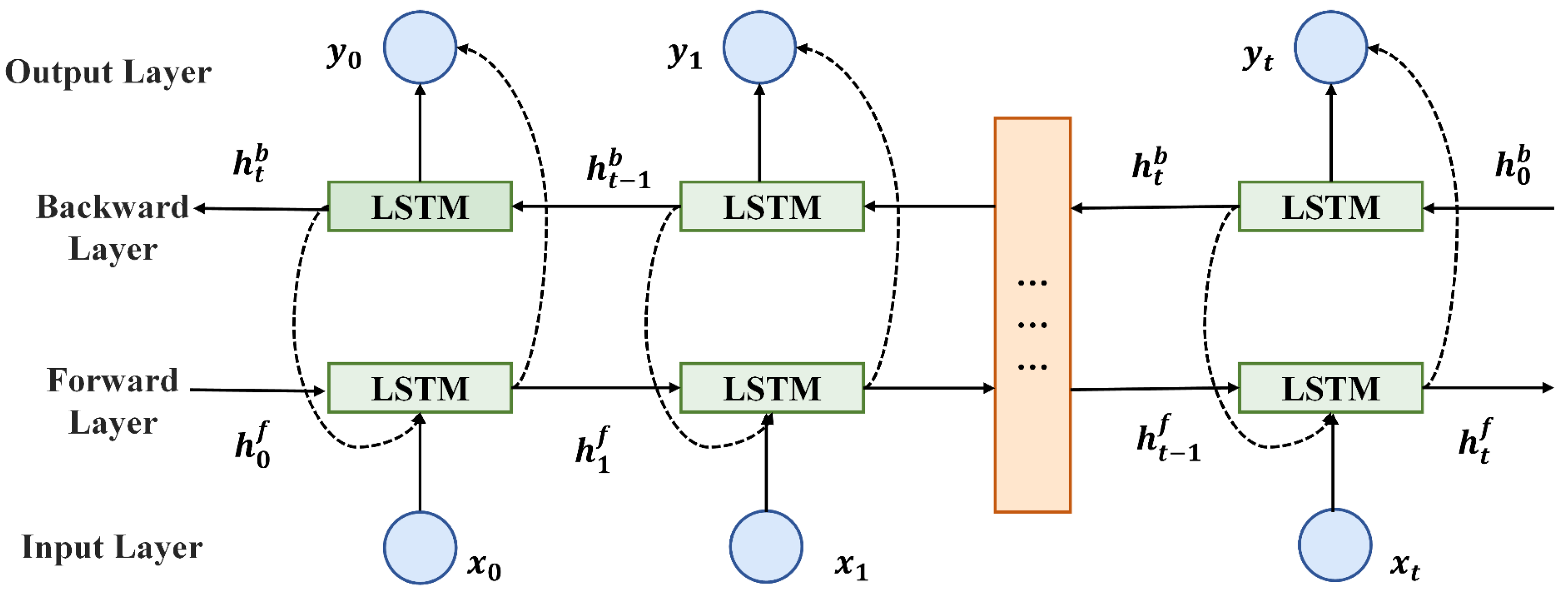
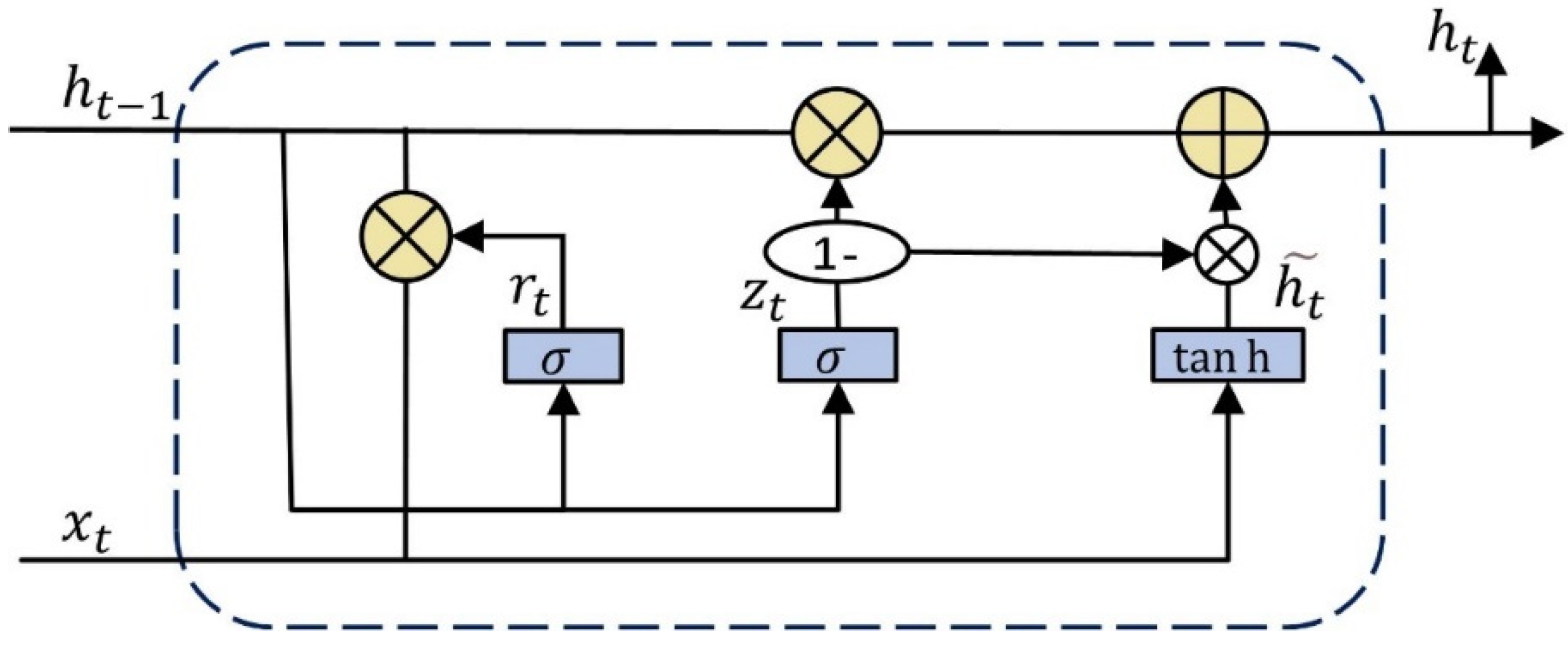
3.2. Deep Learning Prediction Models
- (1)
- Bi-LSTM
- (2)
- GRU
- (3)
- FNN
- (4)
- ZOA
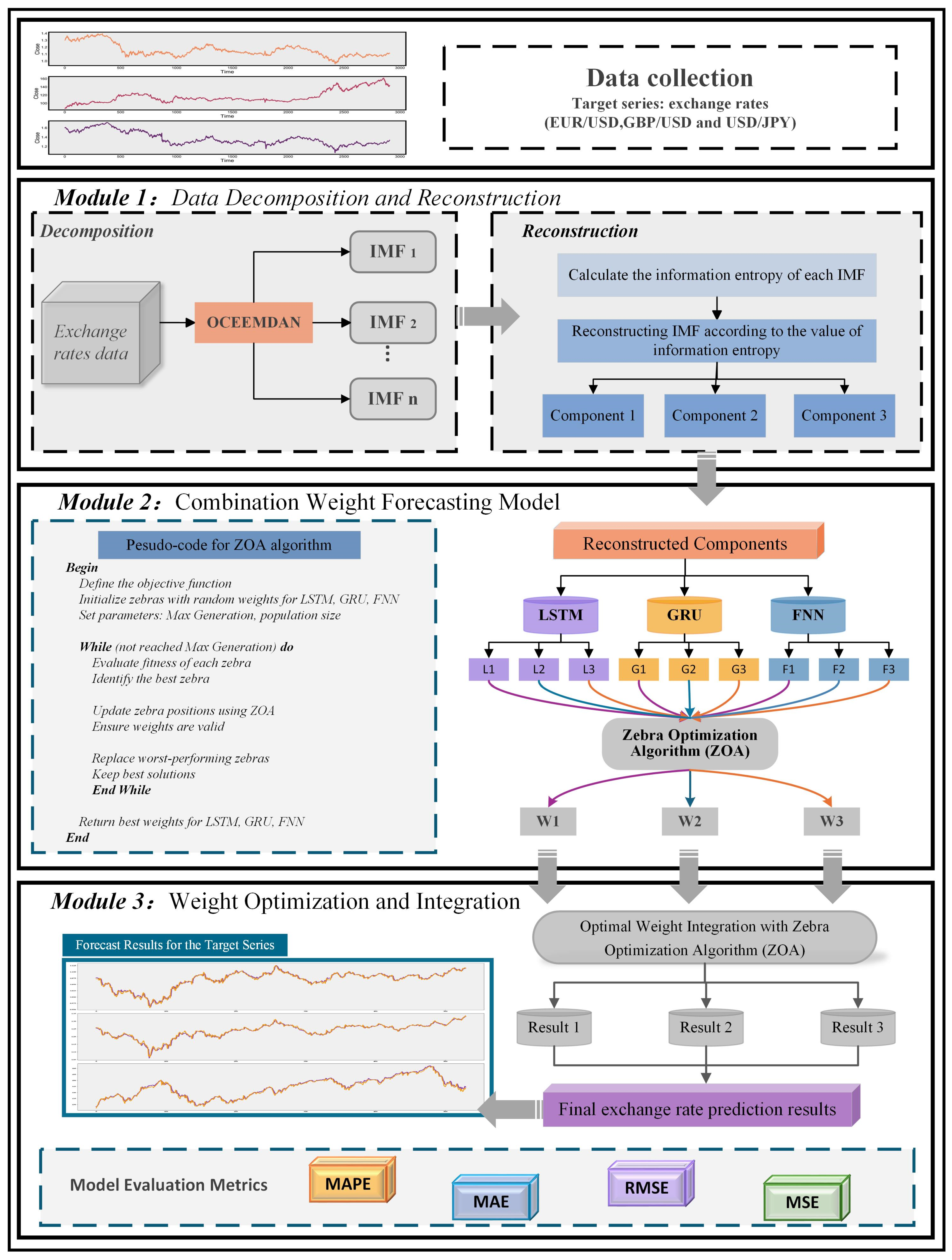
3.3. Proposed Model Framework
- Module 1: Data Decomposition and Reconstruction
- Module 2: Combination Weight Forecasting Model
- Module 3: Model Integration and Evaluation Metrics
4. Empirical Analysis
4.1. Experimental Dataset
4.1.1. Data Source
4.1.2. Normalized Processing
4.2. Decomposition and Reconstruction of Exchange Rate Series
- (1)
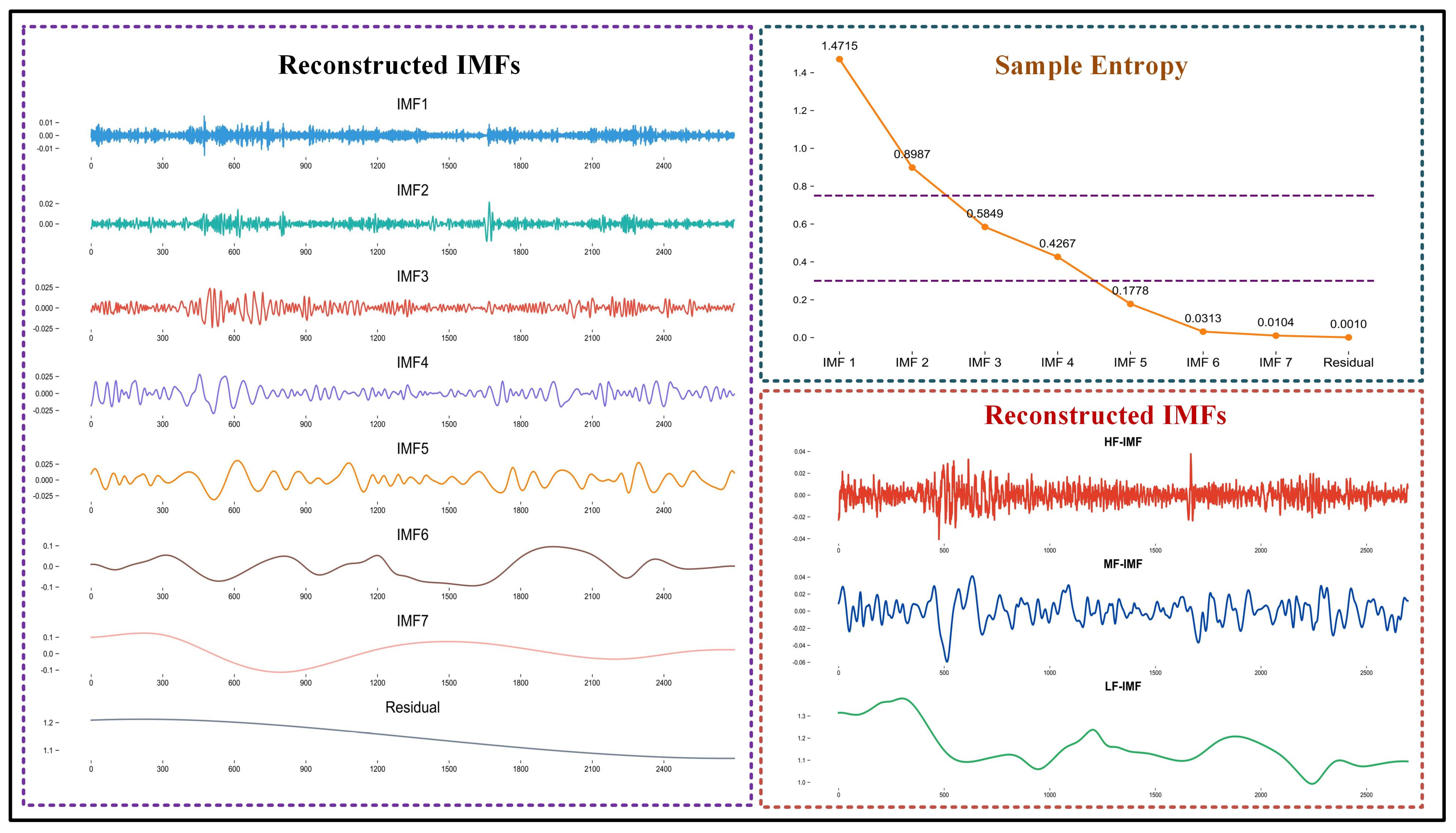
- IMF1 and IMF2 are combined to form the high-frequency component (HF-IMF), which captures random fluctuations in exchange rates and currency pair prices driven by complex trading activities, short-term macroeconomic data releases, and unexpected international financial events (Engle, 2000). Although these high-frequency components contribute to short-term volatility, they typically do not influence long-term trends.
- (2)
- IMF3 and IMF4 are combined to form the mid-frequency component (MF-IMF), reflecting periodic fluctuations in exchange rates and currency pair prices caused by macroeconomic cycles, monetary policy changes, or international trade dynamics (Borio & Lowe, 2002; Taylor, 1993).
- (3)
- IMF5, IMF6, IMF7, and the residual are combined to form the low-frequency component (LF-IMF), which is more stable and effectively represents long-term trends in exchange rates and currency pair prices, influenced by global economic structural changes and long-term demographic shifts (Lucas, 2004; Reinhart & Rogoff, 2009).
4.3. Results of the Proposed Model
5. Further Analysis and Discussion
5.1. Ablation Study of Key Components
5.1.1. Ablation Study on Baseline Model Selection
5.1.2. Ablation Study on Decomposition Methods
5.1.3. Ablation Study on Sample Entropy Thresholding
5.1.4. Ablation Study on Dynamic Weight Optimization
5.2. Risk-Management Applications and Value
- (a)
- High-frequency volatility signals extracted from the model’s components, combined with a zero-order allocation (ZOA) weighting scheme, enable real-time adjustment of hedge ratios. When the model anticipates short-term turbulence, derivative exposures can be increased automatically, shielding portfolios from market swings and enhancing risk-adjusted performance.
- (b)
- Low-frequency trend components extracted via OCEEMDAN, in conjunction with a historical extreme events database, are used to construct a complex systems-based early warning model. This approach facilitates the early detection of nonlinear risk signals, such as exchange rate overshooting or abrupt policy changes, providing valuable data for regulators and firms to initiate stress tests and contingency plans in advance.
- (c)
- By integrating multiple models and optimizing with information entropy, the predictive framework significantly reduces parameter sensitivity inherent in single models. By quantifying forecast confidence intervals, financial institutions can more accurately assess the uncertainty boundaries of exchange rate predictions, preventing decision-making biases caused by model overfitting and enhancing the scientific rigor and adaptability of risk management practices.
6. Conclusions
- We proposed applying the GWO to the automatic optimization of key parameters of CEEMDAN for financial time series prediction.
- A framework for exchange rate prediction using the zebra optimization algorithm for dynamic integrated weight optimization was proposed. ZOA’s two-stage behavior of simulating zebra foraging and defense strategies makes it particularly suitable for balancing exploration and development in a weighted space.
- The developed exchange rate prediction model, verified through historical simulations, has demonstrated its stability and reliability under various market conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADF | Augmented dickey-fuller |
| ALSTM | Attention-based long short-term memory |
| APSO | Accelerated particle swarm optimization |
| ARIMA | Autoregressive integrated moving average |
| CEEMD | Complete ensemble empirical mode decomposition |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CNN | Convolutional neural network |
| DE | Differential evolution |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| GAN | Generative adversarial network |
| GARCH | Generalized autoregressive conditional heteroskedasticity |
| GRU | Gated recurrent unit neural network |
| GWO | Grey wolf optimizer |
| IE | Information entropy |
| IMF | Intrinsic mode function |
| IWOA | Improved whale optimization algorithm |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| OCEEMDAN | Optimal complete ensemble empirical mode decomposition with adaptive noise |
| PSO | Particle swarm optimization |
| RMSE | Root-mean-square error |
| RNN | Recurrent neural networks |
| R2 | Coefficient of determination |
| SE | Sample entropy |
| SSA | Singular spectrum analysis |
| VAR | Vector autoregression |
| WT | Wavelet transform |
| ZOA | Zebra optimization algorithm |
Appendix A. Neural Network Model Hyperparameter Configurations for Three Exchange Rates
| Model | Parameter | EUR/USD | GBP/USD | USD/JPY |
| Bi-LSTM | Hidden layers | 2 | 3 | 2 |
| Units per layer | 100 | 128 | 256 | |
| Dropout rate | 0.15 | 0.3 | 0.25 | |
| Learning rate | 0.001 | 0.0005 | 0.0015 | |
| Batch size | 64 | 32 | 48 | |
| Gradient clipping | 1 | 2 | 1.5 | |
| L2 regularization | 0.0001 | 0.0003 | 0.0002 | |
| GRU | Hidden layers | 2 | 2 | 3 |
| Units per layer | 128 | 100 | 200 | |
| Dropout rate | 0.2 | 0.25 | 0.3 | |
| Learning rate | 0.0008 | 0.0007 | 0.0005 | |
| Batch size | 32 | 48 | 24 | |
| Gradient clipping | 1.2 | 1 | 1.8 | |
| L2 regularization | 0.00015 | 0.0002 | 0.00025 | |
| FNN | Hidden layers | 3 | 4 | 3 |
| Neurons per layer | [256,128,64] | [300,150,75,38] | [400,200,100] | |
| Dropout rate | 0.3 | 0.4 | 0.35 | |
| Hidden layer activation | ReLU | LeakyReLU | ReLU | |
| Output activation | Linear | Linear | Linear | |
| Learning rate | 0.001 | 0.0006 | 0.0012 | |
| Batch size | 64 | 32 | 48 | |
| L2 regularization | 0.0001 | 0.00025 | 0.00015 |
Appendix B. Statistical Analysis of the Proposed Model
| MAPE (%) | MAE | MSE | R2 | |
| EUR/USD | 3.3581 ± 0.1245 (3.2336–3.4826) | 2.6501 ± 0.0937 (2.5564–2.7438) | 2.1076 ± 0.0745 (2.0331–2.1821) | 0.9551 ± 0.0042 (0.9509–0.9593) |
| GBP/USD | 3.1683 ± 0.1032 (3.0651–3.2715) | 1.5493 ± 0.0508 (1.4985–1.5999) | 1.6174 ± 0.0530 (1.5644–1.6704) | 0.9231 ± 0.0040 (0.9191–0.9271) |
| USD/JPY | 2.0945 ± 0.0723 (2.0222–2.1668) | 1.1659 ± 0.0403 (1.1256–1.2062) | 1.0945 ± 0.0379 (1.0566–1.1324) | 0.9180 ± 0.0035 (0.9145–0.9215) |
References
- Alexandridis, A. K., Panopoulou, E., & Souropanis, I. (2024). Forecasting exchange rate volatility: An amalgamation approach. Journal of International Financial Markets, Institutions and Money, 97, 102067. [Google Scholar] [CrossRef]
- Borio, C. E. V., & Lowe, P. W. (2002). Asset prices, financial and monetary stability: Exploring the nexus. SSRN Journal. [Google Scholar] [CrossRef]
- Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv. [Google Scholar] [CrossRef]
- Ding, H., Zhao, X., Jiang, Z., Abdullah, S. N., & Dewi, D. A. (2024). EUR-USD exchange rate forecasting based on information fusion with large language models and deep learning methods. arXiv. [Google Scholar] [CrossRef]
- Du, P., Ye, Y., Wu, H., & Wang, J. (2025). Study on deterministic and interval forecasting of electricity load based on multi-objective whale optimization algorithm and transformer model. Expert Systems with Applications, 268, 126361. [Google Scholar] [CrossRef]
- Engle, R. F. (2000). Dynamic conditional correlation—A simple class of multivariate GARCH models. Journal of Business & Economic Statistics, 20(3), 339–350. [Google Scholar] [CrossRef]
- Fang, T., Zheng, C., & Wang, D. (2023). Forecasting the crude oil prices with an EMD-ISBM-FNN model. Energy, 263, 125407. [Google Scholar] [CrossRef]
- Ghosh, I., & Dragan, P. (2023). Can financial stress be anticipated and explained? Uncovering the hidden pattern using EEMD-LSTM, EEMD-prophet, and XAI methodologies. Complex & Intelligent Systems, 9, 4169–4193. [Google Scholar] [CrossRef]
- Gong, M., Zhao, Y., Sun, J., Han, C., Sun, G., & Yan, B. (2022). Load forecasting of district heating system based on Informer. Energy, 253, 124179. [Google Scholar] [CrossRef]
- Gui, Z., Li, H., Xu, S., & Chen, Y. (2023). A novel decomposed-ensemble time series forecasting framework: Capturing underlying volatility information. arXiv. [Google Scholar] [CrossRef]
- Hochreiter, S., & Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lee, M.-C. (2022). Research on the feasibility of applying GRU and attention mechanism combined with technical indicators in stock trading strategies. Applied Sciences, 12, 1007. [Google Scholar] [CrossRef]
- Liu, P., Wang, Z., Liu, D., Wang, J., & Wang, T. (2023). A CNN-STLSTM-AM model for forecasting USD/RMB exchange rate. Journal of Engineering Research, 11, 100079. [Google Scholar] [CrossRef]
- Liu, S., Huang, Q., Li, M., & Wei, Y. (2024). A new LASSO-BiLSTM-based ensemble learning approach for exchange rate forecasting. Engineering Applications of Artificial Intelligence, 127, 107305. [Google Scholar] [CrossRef]
- Lu, H., Ma, X., Huang, K., & Azimi, M. (2020). Carbon trading volume and price forecasting in China using multiple machine learning models. Journal of Cleaner Production, 249, 119386. [Google Scholar] [CrossRef]
- Lucas, R. (2004). The industrial revolution: Past and future. Available online: https://www.aier.org (accessed on 20 May 2025).
- Luo, J., & Gong, Y. (2023). Air pollutant prediction based on ARIMA-WOA-LSTM model. Atmospheric Pollution Research, 14, 101761. [Google Scholar] [CrossRef]
- Mroua, M., & Lamine, A. (2023). Financial time series prediction under COVID-19 pandemic crisis with long short-term memory (LSTM) network. Humanities and Social Sciences Communications, 10, 530. [Google Scholar] [CrossRef]
- Nanthakumaran, P., & Tilakaratne, C. D. (2018). Financial time series forecasting using empirical mode decomposition and FNN: A study on selected foreign exchange rates. International Journal on Advances in ICT for Emerging Regions, 11, 1–12. [Google Scholar] [CrossRef]
- Oreshkin, B. N., Carpov, D., Chapados, N., & Bengio, Y. (2020). N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv. [Google Scholar] [CrossRef]
- Pfahler, J. F. (2021). Exchange rate forecasting with advanced machine learning methods. Journal of Risk and Financial Management, 15, 2. [Google Scholar] [CrossRef]
- Reinhart, C. M., & Rogoff, K. S. (2009). This time is different: Eight centuries of financial folly. Princeton University Press. [Google Scholar] [CrossRef]
- Ren, Y., Huang, Y., Wang, Y., Xia, L., & Wu, D. (2025). Forecasting carbon price in Hubei Province using a mixed neural model based on mutual information and multi-head self-attention. Journal of Cleaner Production, 494, 144960. [Google Scholar] [CrossRef]
- Ren, Y., Wang, Y., Xia, L., & Wu, D. (2024). An innovative information accumulation multivariable grey model and its application in China’s renewable energy generation forecasting. Expert Systems with Applications, 252, 124130. [Google Scholar] [CrossRef]
- Rezaei, H., Faaljou, H., & Mansourfar, G. (2021). Stock price prediction using deep learning and frequency decomposition. Expert Systems with Applications, 169, 114332. [Google Scholar] [CrossRef]
- Semenov, A. (2024). Overreaction and underreaction to new information and the directional forecast of exchange rates. International Review of Economics & Finance, 96, 103676. [Google Scholar] [CrossRef]
- Taylor, J. B. (1993). Discretion versus policy rules in practice. Carnegie-Rochester Conference Series on Public Policy, 39, 195–214. [Google Scholar] [CrossRef]
- Torres, M. E., Colominas, M. A., Schlotthauer, G., & Flandrin, P. (2011, May 22–27). A complete ensemble empirical mode decomposition with adaptive noise. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 4144–4147), Prague, Czech Republic. [Google Scholar] [CrossRef]
- Trojovska, E., Dehghani, M., & Trojovsky, P. (2022). Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access, 10, 49445–49473. [Google Scholar] [CrossRef]
- Wang, J., & Zhang, Y. (2025). A hybrid system with optimized decomposition on random deep learning model for crude oil futures forecasting. Expert Systems with Applications, 272, 126706. [Google Scholar] [CrossRef]
- Wang, X., Li, C., Yi, C., Xu, X., Wang, J., & Zhang, Y. (2022). EcoForecast: An interpretable data-driven approach for short-term macroeconomic forecasting using N-BEATS neural network. Engineering Applications of Artificial Intelligence, 114, 105072. [Google Scholar] [CrossRef]
- Wu, F., Cattani, C., Song, W., & Zio, E. (2020). Fractional ARIMA with an improved cuckoo search optimization for the efficient Short-term power load forecasting. Alexandria Engineering Journal, 59, 3111–3118. [Google Scholar] [CrossRef]
- Wu, P., Zou, D., Zhang, G., & Liu, H. (2024). An improved NSGA-II for the dynamic economic emission dispatch with the charging/discharging of plug-in electric vehicles and home-distributed photovoltaic generation. Energy Science & Engineering, 12, 1699–1727. [Google Scholar] [CrossRef]
- Yang, Q., & Li, J. (Eds.). (2025). The proceedings of the 11th Frontier Academic Forum of Electrical Engineering (FAFEE2024): Volume I, lecture notes in electrical engineering. Springer Nature. [Google Scholar] [CrossRef]
- Yao, D., Chen, S., Dong, S., & Qin, J. (2024). Modeling abrupt changes in mine water inflow trends: A CEEMDAN-based multi-model prediction approach. Journal of Cleaner Production, 439, 140809. [Google Scholar] [CrossRef]
- Yeh, J.-R., Shieh, J. S., & Huang, N. E. (2010). Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Advances in Data Science and Adaptive Analysis, 2, 135–156. [Google Scholar] [CrossRef]
- Zhang, X. (2023). An enhanced decomposition integration model for deterministic and probabilistic carbon price prediction based on two-stage feature extraction and intelligent weight optimization. Journal of Cleaner Production, 415, 137791. [Google Scholar] [CrossRef]
- Zhang, Y., Zhong, K., Xie, X., Huang, Y., Han, S., Liu, G., & Chen, Z. (2025). VMD-ConvTSMixer: Spatiotemporal channel mixing model for non-stationary time series forecasting. Expert Systems with Applications, 271, 126535. [Google Scholar] [CrossRef]
- Zhou, H., Zhang, S., Peng, J., Zhang, S., Li, J., Xiong, H., & Zhang, W. (2021). Informer: Beyond efficient transformer for long sequence time-series forecasting. arXiv. [Google Scholar] [CrossRef]
- Zhou, M. (2024). Predict stock price fluctuations using realized volatility, CEEMDAN, LSTM models. SHS Web of Conferences, 196, 02003. [Google Scholar] [CrossRef]
- Zhou, T., Ma, Z., Wen, Q., Wang, X., Sun, L., & Jin, R. (2022). FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting. arXiv. [Google Scholar] [CrossRef]
- Zhou, Y., & Zhu, X. (2025). Forecasting USD/RMB exchange rate using the ICEEMDAN-CNN-LSTM model. Journal of Forecasting, 44, 200–215. [Google Scholar] [CrossRef]
- Zinenko, A. (2023). Forecasting financial time series using singular spectrum analysis. Business Informatics, 17, 87–100. [Google Scholar] [CrossRef]
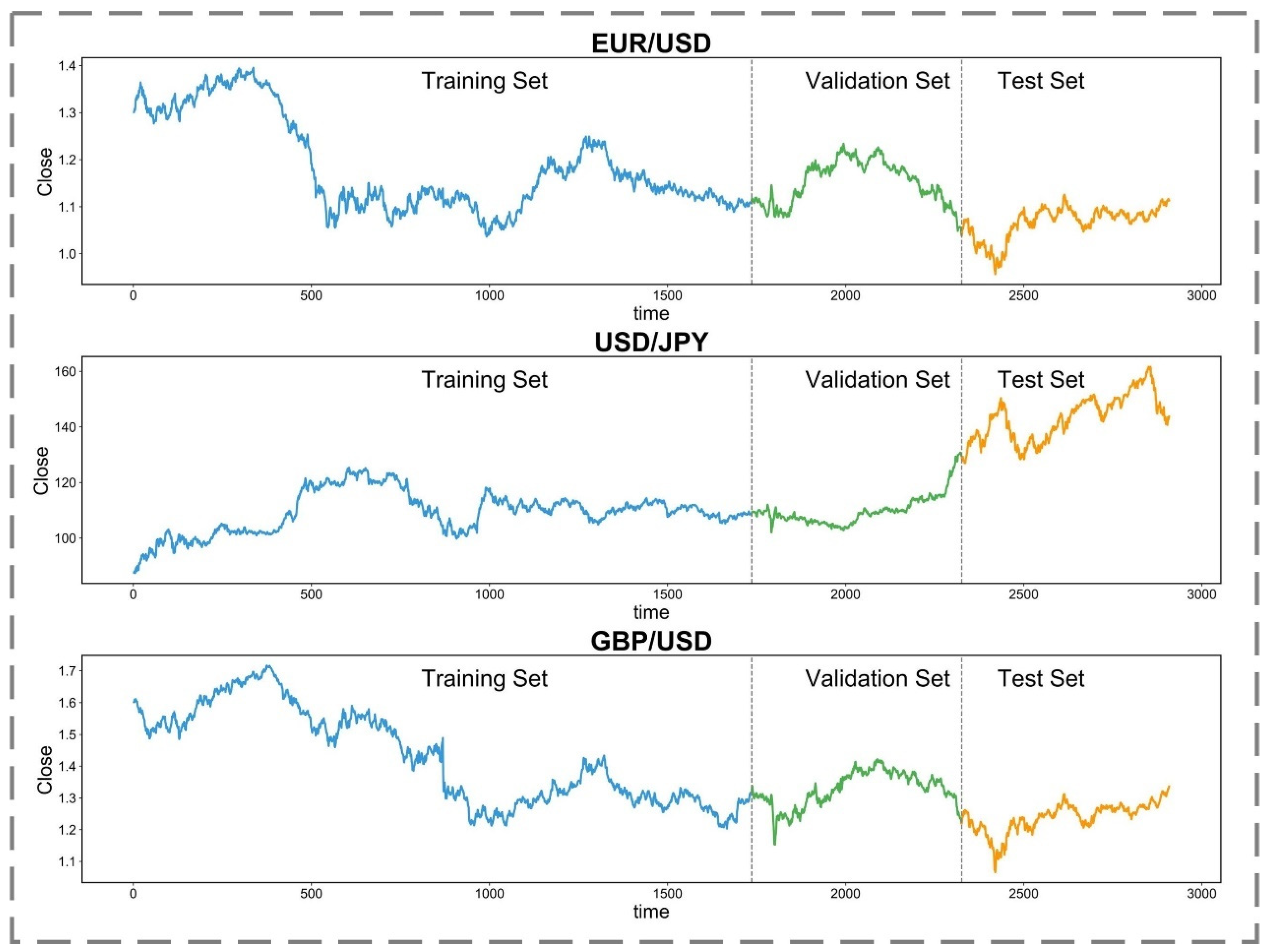



| Currency Pair | Sample Size | Training Set | Validation Set | Test Set |
|---|---|---|---|---|
| EUR/USD | 2909 | 1745 | 582 | 582 |
| USD/JPY | 2909 | 1745 | 582 | 582 |
| GBP/USD | 2909 | 1745 | 582 | 582 |
| Currency Pair | Max | Min | Mean | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| EUR/USD | 1.3953 | 0.9565 | 1.1560 | 0.0934 | 0.9258 | 0.1019 |
| USD/JPY | 161.6400 | 87.4500 | 116.2198 | 15.4047 | 1.1137 | 0.3684 |
| GBP/USD | 1.7161 | 1.4883 | 1.3703 | 0.1404 | 0.7550 | −0.5028 |
| Currency Pair | T-Statistic | Prob. |
|---|---|---|
| EUR/USD | −1.96 | 0.30 |
| USD/JPY | −1.30 | 0.63 |
| GBP/USD | −1.95 | 0.31 |
| Currency Pair | Statistic | Z-Statistic | p-Value |
|---|---|---|---|
| EUR/USD | BDS (2) | 5.50 | 0.00 |
| BDS (3) | 9.27 | 0.00 | |
| BDS (4) | 15.11 | 0.00 | |
| BDS (5) | 21.00 | 0.00 | |
| GBP/USD | BDS (2) | 6.20 | 0.00 |
| BDS (3) | 11.54 | 0.00 | |
| BDS (4) | 18.31 | 0.00 | |
| BDS (5) | 24.40 | 0.00 | |
| USD/JPY | BDS (2) | 8.59 | 0.00 |
| BDS (3) | 7.33 | 0.00 | |
| BDS (4) | 15.82 | 0.00 | |
| BDS (5) | 19.48 | 0.00 |
| Exchange Rate Pairs | MAPE (%) | MAE | MSE | |
|---|---|---|---|---|
| Daily EUR/USD exchange rate | 3.3581 | 2.6501 | 2.1076 | 0.9551 |
| Daily GBP/USD exchange rate | 3.1683 | 1.5493 | 1.6174 | 0.9231 |
| Daily USD/JPY exchange rate | 2.0945 | 1.1659 | 1.0945 | 0.9180 |
| Exchange Rate Pairs | Model | MAPE (%) | MAE | MSE | |
|---|---|---|---|---|---|
| Daily EUR/USD exchange rate | Bi-LSTM | 7.6894 | 4.1572 | 4.4891 | 0.8751 |
| GRU | 7.8392 | 6.5027 | 5.1743 | 0.9401 | |
| FNN | 8.4738 | 5.3265 | 3.9524 | 0.9804 | |
| SSA-ACWM | 5.9872 | 4.0143 | 4.5638 | 0.8946 | |
| VMD-ACWM | 5.0814 | 3.4729 | 3.1095 | 0.7457 | |
| EEMD-ACWM | 4.2034 | 3.7582 | 3.6291 | 0.8947 | |
| CEEMDAN-ACWM | 4.8173 | 3.0392 | 3.0845 | 0.9104 | |
| CEEMDAN-CEEMDAN-ACWM | 3.6019 | 3.4821 | 2.8467 | 0.8142 | |
| OCEEMDAN-FCWM | 5.2751 | 3.7594 | 2.2305 | 0.9238 | |
| OCEEMDAN-ACWM(NT) | 3.9183 | 2.6022 | 4.0549 | 0.8628 | |
| Proposed model | 3.3581 | 2.6501 | 2.1076 | 0.9551 | |
| Daily GBP/USD exchange rate | Bi-LSTM | 5.9145 | 5.6187 | 3.9854 | 0.8942 |
| GRU | 7.1254 | 5.6147 | 4.9076 | 0.7193 | |
| FNN | 9.2890 | 6.7309 | 5.1348 | 0.9728 | |
| SSA-ACWM | 5.1571 | 2.4823 | 3.1958 | 0.9074 | |
| VMD-ACWM | 4.5619 | 3.8246 | 2.4397 | 0.8728 | |
| EEMD-ACWM | 6.8124 | 3.1943 | 3.5389 | 0.8067 | |
| CEEMDAN-ACWM | 3.9735 | 2.2518 | 2.3081 | 0.9426 | |
| CEEMDAN-CEEMDAN-ACWM | 3.1979 | 2.5083 | 1.8945 | 0.9698 | |
| OCEEMDAN-FCWM | 5.3926 | 3.6214 | 2.2173 | 0.8047 | |
| OCEEMDAN-ACWM(NT) | 4.1854 | 3.8624 | 2.9839 | 0.8841 | |
| Proposed model | 3.1683 | 1.5493 | 1.6174 | 0.9231 | |
| Daily USD/JPY exchange rate | Bi-LSTM | 4.1053 | 4.4025 | 3.1269 | 0.9027 |
| GRU | 5.7931 | 7.8412 | 4.6783 | 0.9115 | |
| FNN | 8.5627 | 5.9576 | 4.5194 | 0.8461 | |
| SSA-ACWM | 4.6853 | 3.8471 | 3.1934 | 0.8428 | |
| VMD-ACWM | 2.3842 | 2.6298 | 2.4105 | 0.9057 | |
| EEMD-ACWM | 3.2063 | 4.7349 | 3.4812 | 0.7257 | |
| CEEMDAN-ACWM | 2.6308 | 2.7841 | 1.5739 | 0.9149 | |
| CEEMDAN-CEEMDAN-ACWM | 3.0859 | 2.0735 | 1.5382 | 0.8561 | |
| OCEEMDAN-FCWM | 5.8812 | 3.1496 | 2.3948 | 0.7939 | |
| OCEEMDAN-ACWM(NT) | 3.1158 | 2.0904 | 1.5827 | 0.8267 | |
| Proposed model | 2.0945 | 1.1659 | 1.0945 | 0.9180 |
| Exchange Rate Pairs | Model | (%) | (%) | (%) | |
|---|---|---|---|---|---|
| Daily EUR/USD exchange rate | Bi-LSTM | 128.06% | 57.08% | 112.67% | −8.37% |
| GRU | 133.60% | 146.56% | 145.93% | −1.57% | |
| FNN | 152.72% | 101.34% | 87.56% | 2.66% | |
| SSA-ACWM | 78.19% | 51.42% | 116.50% | −6.34% | |
| VMD-ACWM | 51.12% | 31.11% | 47.55% | −21.97% | |
| EEMD-ACWM | 25.13% | 41.84% | 72.15% | −6.33% | |
| CEEMDAN-ACWM | 43.41% | 14.72% | 46.37% | −4.69% | |
| CEEMDAN-CEEMDAN-ACWM | 7.25% | 31.42% | 35.03% | −14.74% | |
| OCEEMDAN-ACWM(NT) | 25.72% | 30.78% | −81.79% | −6.60% | |
| OCEEMDAN-FCWM | 56.94% | 41.88% | 5.82% | −3.29% | |
| Daily GBP/USD exchange rate | Bi-LSTM | 86.91% | 262.44% | 146.50% | −8.13% |
| GRU | 125.07% | 262.42% | 203.48% | −26.07% | |
| FNN | 192.82% | 334.84% | 217.72% | −0.03% | |
| SSA-ACWM | 62.83% | 60.24% | 97.65% | −6.77% | |
| VMD-ACWM | 44.04% | 147.49% | 50.87% | −10.28% | |
| EEMD-ACWM | 114.91% | 106.82% | 118.94% | −17.13% | |
| CEEMDAN-ACWM | 25.41% | 45.44% | 42.77% | −3.13% | |
| CEEMDAN-CEEMDAN-ACWM | 0.94% | 62.04% | 17.15% | −0.34% | |
| OCEEMDAN-ACWM(NT) | 38.56% | 37.59% | 49.08% | 1.73% | |
| OCEEMDAN-FCWM | 70.18% | 133.63% | 37.13% | −17.28% | |
| Daily USD/JPY exchange rate | Bi-LSTM | 96.02% | 278.99% | 185.57% | −1.66% |
| GRU | 177.57% | 573.74% | 327.27% | −0.71% | |
| FNN | 309.77% | 411.83% | 313.78% | −7.82% | |
| SSA-ACWM | 123.71% | 230.78% | 192.02% | −8.18% | |
| VMD-ACWM | 13.84% | 125.34% | 120.61% | −1.34% | |
| EEMD-ACWM | 53.24% | 305.62% | 218.96% | −21.00% | |
| CEEMDAN-ACWM | 25.58% | 138.00% | 44.02% | −0.33% | |
| CEEMDAN-CEEMDAN-ACWM | 47.43% | 78.01% | 40.67% | −6.74% | |
| OCEEMDAN-ACWM(NT) | 64.35% | 62.98% | 54.30% | 15.63% | |
| OCEEMDAN-FCWM | 180.53% | 170.72% | 118.73% | −13.54% |
| Comparison | Currency Pair | DM Statistic | DM p-Value | Wilcoxon Statistic | Wilcoxon p-Value |
|---|---|---|---|---|---|
| Ensemble Model vs. Bi-LSTM | EUR/USD | 3.842 | 0.0001 | 26,342 | 0.0002 |
| GBP/USD | 1.634 | 0.1022 | 14,327 | 0.1128 | |
| USD/JPY | 2.768 | 0.0057 | 21,894 | 0.0048 | |
| Ensemble Model vs. GRU | EUR/USD | 2.357 | 0.0183 | 18,561 | 0.0165 |
| GBP/USD | 4.105 | <0.0001 | 27,178 | <0.0001 | |
| USD/JPY | 1.215 | 0.2243 | 11,245 | 0.2468 | |
| Ensemble Model vs. FNN | EUR/USD | 4.721 | <0.0001 | 29,875 | <0.0001 |
| GBP/USD | 4.102 | <0.0001 | 27,436 | <0.0001 | |
| USD/JPY | 3.956 | <0.0001 | 28,145 | <0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Xie, Y. Exchange Rate Forecasting: A Deep Learning Framework Combining Adaptive Signal Decomposition and Dynamic Weight Optimization. Int. J. Financial Stud. 2025, 13, 151. https://doi.org/10.3390/ijfs13030151
Tang X, Xie Y. Exchange Rate Forecasting: A Deep Learning Framework Combining Adaptive Signal Decomposition and Dynamic Weight Optimization. International Journal of Financial Studies. 2025; 13(3):151. https://doi.org/10.3390/ijfs13030151
Chicago/Turabian StyleTang, Xi, and Yumei Xie. 2025. "Exchange Rate Forecasting: A Deep Learning Framework Combining Adaptive Signal Decomposition and Dynamic Weight Optimization" International Journal of Financial Studies 13, no. 3: 151. https://doi.org/10.3390/ijfs13030151
APA StyleTang, X., & Xie, Y. (2025). Exchange Rate Forecasting: A Deep Learning Framework Combining Adaptive Signal Decomposition and Dynamic Weight Optimization. International Journal of Financial Studies, 13(3), 151. https://doi.org/10.3390/ijfs13030151





