Abstract
As a colossal developing economy, irrational, and inefficient trades broadly exist in China’s stock market and are intensified by the once-in-a-century COVID-19 pandemic. This atypical but prominent event enhances systemic risk and requires a more effective analysis tool that adapts to the investors’ sentiment and behavior. Based on the behavioral asset pricing model, this paper verifies the existence of noise traders in China’s stock market, measures the intensity of the noise with the NTR indicator, and examines the market noise with IANM. Furthermore, the mechanism of how COVID-19 influences the market noise through investors’ behaviors is analyzed with the event study method. The findings show that, based on 92 Chinese companies, the market noise significantly exists, and the noise is associated with psychological biases including over-confidence, herding effects and regret aversion. These biases are affected to varying degrees by COVID-19-related events, leading to notable implications for market stability and investor behavior during crises. Our study provides critical insights for policymakers and investors on managing market risks and understanding behavioral impacts during unprecedented events.
1. Introduction
COVID-19 first hit China in early 2020 and forced several cities, such as Wuhan, to shut down entirely. Then, the pandemic spread globally, infecting 546 million people and causing over 6.3 million deaths as of 3 July 2022, according to the statistics of the World Health Organization. The influences of COVID-19 are severe and pervasive on the economy, including but not limited to employment shortages, logistics disruptions, and decreasing demands (Wang et al. 2022). The pandemic significantly affects the stock market, which acts as an economic barometer since it reflects investors’ expectations for the economy (Sun et al. 2021). The most direct impact is reflected by the declined market return and sharper stock price fluctuation (Gao et al. 2021). According to Spyrou (2013), the herding effect plays a key role in the malfunction of the stock market when significant exogenous factors occur. Further studies reveal the mechanism of the herding effect, which can be summarized into the investors’ sentiment, mainly fear and confusion (Wu et al. 2020).
According to Shefrin and Statman (1994), investors who do not follow the Bayesian learning rule are called “noise traders”. Ramiah and Davidson (2007) pointed out that noise traders are market participants who are not fully rational and make decisions that are not based on the information. Their behaviors are not captured well by the classic capital asset pricing model (CAPM) as the theory assumes that investors are primarily risk-averse and have free access to all available information (Efficient market hypothesis, EMH). However, some anomalies in the market suggest that CAPM malfunctions occasionally because these noise traders’ actions are not adapted to the model (Kholdy and Sohrabian 2014). To adjust the noise in the market, the behavioral portfolio theory and behavioral asset pricing model (BAPM) were proposed in 1994 (Shefrin and Statman 1994) based on the behavioral portfolio theory (Roy 1952). BAPM theory suggests that the investors have diverse and variable preferences, rather than only risk-aversion, and they usually pursue a satisfactory solution, not necessarily the optimal one. This theory offers a practical and new perspective for studying China’s stock market.
The investors in China’s stock market have several structural characteristics, which are more prone to market noise. Firstly, individual investors are the majority in the market. As of September 2021, individual investors in China exceeded 190 million, and small and medium-sized investors accounted for 97%. Secondly, more investments are made directly by individuals (more than 30%) than funds and wealth management products. These properties meet the prerequisites and create a great demand for behavioral finance research in China. Thus, this paper aims to test the existence of market noise by comparing the empirical results of CAPM and BAPM. De Long et al. (1990) defines the risk caused by market noise as noise trader risk, which leads to a large divergence between the market price and fundamental value. Afterward, several measurements and models are proposed to quantify and price this risk, such as a model based on the open-ended fund (Sias et al. 2001) and the information-adjusted noise model (Ramiah and Davidson 2007). To measure the noise intensity in the daily frequency, the paper adapts the information-adjusted noise model and builds the noise trader risk (NTR) index by applying the moving average method. Based on the NTR index, it can study the mechanism of how the COVID-19 event affects the noise intensity and influences the stock price and its volatility.
The contribution of this paper is three-fold. Firstly, the return volatility is estimated based on CAPM and BAPM for 92 companies with the highest market value in China. It comes out that the existence of market noise is significant by comparing the betas of CAPM and BAPM. Secondly, an innovative measure of market noise with daily frequency is proposed, which suggests a new factor for quantitative finance research. Thirdly, this paper studies how specific events, such as the COVID-19 pandemic, affect market noise and stock returns by applying an event study.
2. Theory and Model
The initial asset pricing models are based on the basic assumption of agents’ desire to maximize utility, which is reflected by assuming the market is efficient and traders are rational. The most famous CAPM (Sharpe) was built in 1964 and is widely used in the asset pricing area for its simplicity and the multi-factor form. Undoubtedly, CAPM inspires a series of explorations of new models that get closer to the real situation in the market, such as Arbitrage Pricing Theory (Ross 1976), Investment-based CAPM (Cochrane 1991), and Conditional CAPM (Lewellen and Nagel 2006). Unlike the assumption and foundation on which CAPM relies, BAPM follows the prospect theory (Kahneman and Tversky 1979), which is an alternative to the utility theory and suggests that investors have different investment goals based on psychological factors. Recent research includes investors’ irrational sentiment in the integrated mechanism of asset pricing and adapted to the model in different market scenarios. Considering investors’ sentiment as the main variable in asset pricing, various mental effects are studied, such as the effects of pessimism and doubt (Abel 2002), the effects of optimism, over-confidence, and self-attribution (Kahneman and Riepe 1998; Daniel et al. 1998), behaviors under overreaction and underreaction (Barberis et al. 1998; Daniel et al. 1998), the influences of loss aversion on investment decisions (Barberis et al. 2001), mimicking and herding (Hirshleifer et al. 1994), and the effects of culture and social status (Bender et al. 2013).
BAPM labels traders in the market as information traders and noise traders. The former is consistent with CAPM; the latter is not, but both can be expressed by probability distributions . According to the basic model of BAPM, which assumes traders in the market, and a period is described by discrete time . At the beginning of a date, new information denoted by is disclosed, and then, the information revealed at can be denoted as , and transitions from to are governed by an irreducible Markov chain with transition matrix (Beja 1979). Different types of traders have different probability distributions in response to the flow of information, and this probability distribution is something that becomes an attribute of these traders (Kahneman and Tversky 1979). Information traders receive and process all the information rationally as described in CAPM and obtain the estimable yield, while for noise traders, there are two types: one type is the person who misestimates information, overweighs recent events, and underweighs distant events (Shefrin and Statman 2000). This makes them more likely to over-evaluate recent events and behave accordingly in the stock market. The other is mismapping, which is described as the information flow mismap to the wrong probability distribution due to the specific psychological factors of the person. For example, if a person tosses a coin and the first five times are all positive, the probability of the sixth time that he thinks will be negative is higher. In fact, the probability of the negative is still one in two (Shefrin and Statman 1994). This is the correspondence of the probability of error caused by subjective factors in human psychology. These noise traders make us misestimate an asset in the market, so we need to analyze it. In traditional financial theory models, traders are rational, and the expected one-period net return to i asset is as follows:
where is the return rate for the i asset, is the risk-free rate of return for the market, is the rate of return for the effective combination of the market, and is the sensitive index of the return of the i asset to the effective market portfolio. We used this traditional CAPM to obtain betas without including other factors to keep our focus on the measurement of NTR and subsequent behavior effects, and the bias caused by other factors can cancel out in the NTR measurement. The formation of beta is as follows:
However, the market with noise traders tends to be different from the market described in CAPM. In this case, the mean-variance factor and the beta value of the market will be slightly varied (Sias et al. 2001). BAPM is described as follows:
where is the return rate of i assets, is the risk-free return rate of the market, is the rate of return of the behavioral market portfolio, and is the sensitive index of the return of the i asset to the behavioral effective market portfolio. The beta is calculated as follows:
In the BAPM, an SDF-based behavioral beta performs and explains better than the traditional CAPM beta according to Blitz’s (2014) research, since it captures return dynamics better in most of the return quantiles. Based on Shefrin and Statman’s (1994) model, the BAPM beta corresponds to the mean-variance efficient portfolio, which excludes the noise traders in the market, and it provides a measurement of the efficiency of the market, while CAPM beta is the “true beta” of the capital market encompassing both information traders and noise traders. The different construction of the market portfolio leads to the disparity of betas between the two models. Thus, realizing the existence of noise trading in the BAPM and excluding it to build a real efficient portfolio, the behavior beta is supposed to be less than that of the conventional beta ( < ). Hence, the difference between the two betas represents the degree of noise trading in the market.
So, we define the difference between and as NTR:
In practice, the construction of the rate of return for the behavioral portfolio requires a complex calculation process. Taking the purpose of variables control into consideration at the same time, we chose the SSE Composite Index as the efficient market based on CAPM and the SSE 380 Momentum Index as the behavioral market.
The construction of a behavioral portfolio based on Shefrin and Statman’s (1994) definition of a mean-variance efficient portfolio should follow several standards: (1) compared with the “true” capital market portfolio (CAPM), the behavioral portfolio should be composed of information traders only; (2) the behavioral portfolio needs to be as close as possible to the market portfolio in terms of the number of component stocks, market capitalization, and inter-correlation to achieve variable control. Empirically, Ramiah and Davidson (2007) use a sentiment index, the “Mums and Dads” Index (MDI), to build the behavioral portfolio, and Xu et al. (2016) chooses the top ten popular stocks by market capitalization as a Dragon Index to represent the behavioral portfolio.
The SSE 380 Momentum Index consists of the top 380 stocks on the Shanghai Stock Exchange, screened and weighted based on the momentum indicator, trading quantity to the stock price. The chosen stocks have high price momentum while keeping a moderate turnover rate, and typically, a large number of these stocks are owned by long-term investors and strategic investors. The dominance of information traders in the SSE 380 Momentum Index fulfills the standard (1) of the behavioral portfolio selection. Meanwhile, the SSE 380 Momentum Index shares the same constituent stocks with the SSE Composite Index and consequently similar stock numbers, market capitalization, and inter-correlation, thus meeting the requirement of the standard (2).
In modern finance, the behavioral error is stated to be zero as it should be offset by arbitrage, indicating that E(NTR) = 0 in an efficient market. In terms of behavioral finance, the market is behaviorally efficient when E(NTR) ≠ 0 and the variation of NTR can be explained by information. The information-adjusted noise model describes this phenomenon:
where is the variation of NTR, and is treated as a dummy variable, equal to 1 when the information happens on that date and equal to 0 when no information is released. The information includes transactions, performance disclosures, major projects, operation business, outbound investment, etc. On no information days, Equation (4) will collapse to the following:
There are three reactions that information traders have to the noise in the stock market: underreaction (U), overreaction (O), and information pricing error (IPE) (Ramiah and Davidson 2007). The underreaction indicates that the information traders do not clear all errors in the market, while the overreaction demonstrates that the information traders overestimate the intensity of the errors and causes the price to move away from its intrinsic value. A more serious case occurs when information traders fail to realize the errors and so augment the noise in the market. This type of error is referred to as IPE. Specifically, each type of error is divided into positive and negative reactions to show the resulting noise taking both noise traders and information traders into consideration (Barberis et al. 1998). , the sum of and is used to show this consequent noise:
Table 1 summarizes the conditions of , , and for each reaction.

Table 1.
Conditions for each reaction.
3. Empirical Results
In this section, firstly, we examine whether there is significant noise in the Chinese stock market and measure the noise with the moving average method. Second, we compare the suitability of BAPM and CAPM in China’s stock market. Finally, we test the IANM with company-related information obtained from Wind (a provider of financial information services in China) to understand the behaviors of both information traders and noise traders.
We take 92 component stocks of the CSI 100 (top 100 stocks in China’s stock market) as the sample with three-year transaction data from 1 January 2019 to 31 December 2021, eliminating the eight securities listed after 2019. We choose the daily return of the SSE Index (stock market index of all stocks traded at the Shanghai Stock Exchange) as the market return following a vast amount of literature related to China’s stock market.1 The data source is Wind2.
3.1. Market Noise
Noise has an intimate connection with trader’s emotions, and many studies focus on people’s sentiment to measure the noise in the market. Black (1986) and Trueman (1988) studied the role of fund managers in asset pricing and adopted the trading volume of the mutual fund to measure the market noise as the noise in their model is generated between investors and fund managers who are able to receive private information. Another commonly used method for measuring market noise is proposed by Baker and Wurgler (2006), who applied principal component analysis to filter out trait components unrelated to emotion and obtain more pure emotion-related elements. Specifically, the market price of risk is regressed on various fundamental variables. Verma and Soydemir (2009) studied the effect of individual and institutional investors’ sentiment on the market price of risk, which follows Baker’s method to capture the irrational component of investor sentiment by regressing sentiment indicators to a set of risk factors and calculating residuals. Besides, a specific index, the American Association of Individual Investors Index (AAII) is built based on surveys to individual investors and is widely used by Brown and Cliff (2004), Verma and Soydemir (2006), and Sayim et al. (2013) to represent the market noise. However, these measurements either rely on third-party data based on surveys from individual investors or only capture partial market noise. Meanwhile, BAPM provides a noise measurement of the entire market with transaction data from the market itself, which is believed to represent the market noise well and is straightforward for measuring.
Whether noise can be offset itself or it plays a noticeable role in the movements of a stock price is a crucial issue. If the noise exists in the stock market, an apparent gap can be discerned by the betas of CAPM and BAPM. According to Equations (1) and (2), regression based on the 729 observations generates an estimate of coefficients and , which reflect the volatility of a security or portfolio compared to the market. Table 2 shows the result of regression based on the whole period of three years. It is clear that the beta calculated with CAPM is larger than that of BAPM for all stocks, which is consistent with the hypothesis.

Table 2.
Regression results of BAPM and CAPM.
To ensure the robustness of the results, we test the betas based on every year data (2019, 2020, and 2021), rank the BAPM betas in ascending order, and plot the CAPM betas correspondingly, as shown in Figure 1. For most of the stocks, the result is robust; however, some abnormal results may occur due to the mismapping issues or the luck component (De Long et al. 1990), and it happens on a few stocks in one-year-period testing.
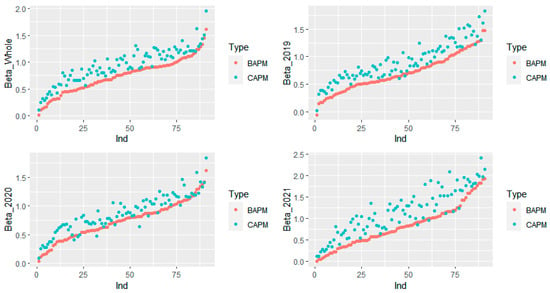
Figure 1.
Beta of BAPM and CAPM.
We apply the two-sample t-test to examine whether the difference between the mean value of and is statistically significant and positive. First, both groups of and pass the S-W test, indicating that both conform to the normal distribution. Then, we perform a two-sample t-test, and the results show that the is significantly smaller than . Figure 2 illustrates the test results.
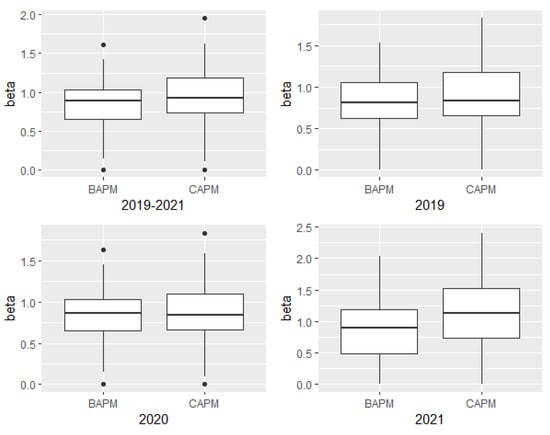
Figure 2.
Box plots of beta.
To further test the existence of market noise, we applied the Monte-Carlo method to examine whether NTR is statistically positive. As a prerequisite of the Monte-Carlo method, the normality of NTR is tested with the Shapiro–Wilk normality test (Shapiro and Wilk 1965). The W-statistic is 0.972, suggesting that NTR follows a normal distribution at a 95% confidence level. Figure 3 shows the pdf for NTR with 10,000 times stimulation, of which only 296 times is the NTR value less than 0. This result is consistent with the previous tests of BAPM beta and CAPM beta; at a 95% confidence level, the NTR is statistically positive.
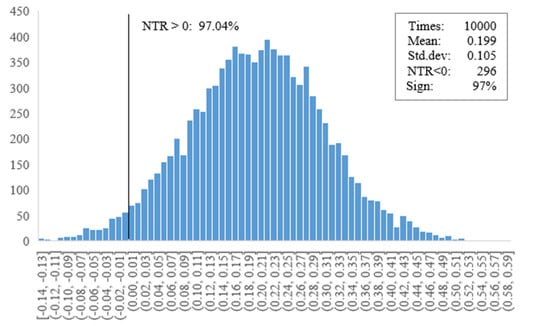
Figure 3.
Graphic presentation of pdf for NTR.
We apply the moving average method based on Equation (3) to obtain a calculable and sequential measure of market noise, as called the NTR indicator. The intensity of NTR shows the influence of noise trading on the whole stock market, and the variation in intensity reflects the psychological changes of investors. The NTR indicator also acts as a signal of the systemic risk of the stock market as it represents the extent of deviation from the efficient market hypothesis. Equation (7) provides a calculation method for the NTR indicator:
where N is the total number of securities in the sample; F represents the length of the moving average window in days.
In our research, N is equal to 92 as the number of component stocks in the CSI100 after eliminating the eight newly listed stocks; 100-days is chosen as the length of the moving average window to both ensure the reliability of the regression and to reduce the loss of data as much as possible. Time starts from 0 (15 January 2019) to 630 (30 December 2021), only counting the stock trading days.
In 2019, the NTR indicator was kept at a lower level and fluctuated around 0.05, and the SSE Composite Index showed a similar oscillation. By mid-2020, the market noise decreased, accompanied by a stable rise in the index to a high position of 4852. At the beginning of 2021, the SSE Composite Index continued the ascending trend until it reached the highest, 5808, on 10 February 2021; correspondingly, the market noise became stronger. In the second half of 2021, the market noise gradually fell to return to its year 2019 level, and the index seesawed to the position of 4500.
3.2. Suitability of BAPM in China’s Stock Market
Since the market noise significantly exists in China’s stock market and its intensity reached nearly 0.4 in 2021, the market shows the main characteristics of a behavioral market that is largely affected by noise traders. Thus, we analyze whether BAPM has a better performance based on interpreting the stock returns than CAPM.
We perform a regression of stock returns on the two groups of beta estimates to compare which model better explains the stock return in China’s stock market. We perform regression and a t-test on and obtained in Section 3.1. The regression model is as follows:
As can be seen from Table 3 below, stands for slope, and refers to the intercept. The R-squared values obtained in our regressions are relatively low, because the independent variables used in our regressions are proxies for broader market phenomena. While they are significant, they may not fully capture all the determinants of stock market movements during the studied period. The low R-squared values suggest that other unmeasured factors likely played a role. Furthermore, the period under study includes the COVID-19 pandemic, a time of unprecedented market volatility and uncertainty. Such extreme conditions can lead to increased noise and erratic market behavior, reducing the explanatory power of standard financial models. The model with a larger can explain the return better. Then, we can find that > holds for all three years, which indicates a better interpretation of BAPM in stock yields during the period. In addition, R-squared of the regression with is also greater than that of and all the regression results are significant at a 99% confidence level.

Table 3.
Regression based on beta.
3.3. Test of IANM
Over the entire 2019–2021 period, there were 5480 information days for the 92 companies investigated. This study analyzes every single day and checks if the market is efficient or if there is some underreaction, IPE, or overreaction occurring in the market. Each of these three abnormal effects is then divided into two directions, namely positive and negative. Table 4 reports the number of days of O (+), O (−), IPE (+), IPE (−), U (+), U (−), and EMH that happened on the information days in different periods, the entire period 2019–2021, and 2019, 2020, and 2021 separately.

Table 4.
Test of IANM.
Underreaction happens with the least frequency among the three, accounting for about 7.90% for three years, which is due to the rarer events, which can cause such a reaction. Underreaction occurs when information traders capture the existed noise in the market but reacted too slowly and mildly to eliminate the noise in the market. Usually, the events that cause investors to react this way are generally when a company that is doing well and has been continuously releasing positive news but suddenly announces a loss or a company that has been in the doldrums suddenly rises and has an unexpected high rate of return. Since this kind of sudden event tends to be inherently rare, the underreaction happens less frequently and its impacts on the general market are limited.
The happening of IPE is in the middle of the three effects, and it shows a continuously increasing trend over the three years, reaching 33.50% in 2021, which is roughly consistent with Ramiah and Davidson’s (2007) findings of 35% IPE in the Australian stock market. Compared with underreaction, the events that lead to the occurrence of IPE are much more commonplace, as not all information can be clearly and correctly captured and processed by traders in the market (Wang et al. 2021). Thus, information traders may unconsciously follow the opinions in the market, mistakenly strengthening the noise, rather than adjusting the noise. An increasing IPE sometimes is taken as a signal of market malfunction as the noise in the market is fostering the formation of a bubble or serious crashing. We believe that the more frequent IPE since 2019 is probably related to the influence of the COVID-19 pandemic since this global event makes it hard for information transmission, such as the shutting down of a stock exchange or transportation restrictions due to the government policies. In addition, the psychological bias of over-confidence is believed to be associated with the increasing IPE, which will be discussed in the Section 4.2.
In our model, overreaction happens when information traders detect the existence of noise in the market but react excessively and lead the market towards another pole. Overreaction takes the largest proportion with 33.85% for the whole period. This proportion of overreaction is reasonable compared with the empirical result of Xu et al.’s (2016) research of the Shenzhen stock market. In the absence of information flow, people will be over-prepared for the unknown due to panic, anxiety, and other emotions, which also leads to overreaction (Brown 1999). In China’s stock market, which is dominated by individual investors, it is normal to observe that overreaction happens from time to time in the market.
In general, 27.63% of the data supports the EMH, while 4544 inefficient days out of 5480 information days cannot be explained well by the EMH. The number and proportion of inefficient days in our research surpass the historical measurements, compared with Xu et al.’s (2016) tests over the period from 2002 to 2010. Among the inefficient days, IPE and overreaction occurs more frequently in China’s stock market, which suggests an obvious inefficiency and mispricing caused by investors’ reaction to news in the market. Meanwhile, it occurs to us that the more frequent happening of IPE is related to the COVID-19 pandemic, which will be further discussed in the next part.
4. Influences of COVID-19
In this part, we analyze how the COVID-19 pandemic influences the noise and yields based on the event study method and excel into the micro investment behaviors to understand how investors respond to this serious event. In behavioral finance, there are four common psychological biases of investment decision-making: over-confidence, regret aversion, herding, and loss aversion (Daniel et al. 1998). During the COVID-19 pandemic, access to information has become more difficult, and the cost of living for investors has become higher and more stressful (Chen 2020). These influences lead to changes in investment behaviors, such as mitigating confidence and increasing herding effects (Wu et al. 2020), thus causing sharper volatility in the stock price. Figure 4 illustrates this mechanism.
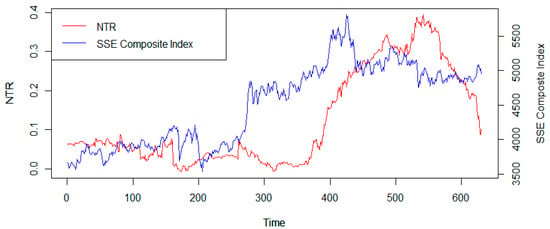
Figure 4.
NTR Indicator and SSE Composite Index.
In response to the COVID-19 event, with psychological biases playing a crucial role in investors’ decision making, which is of significance for us to have a deeper understanding of investment behaviors. However, the difficult part is to find an appropriate measurement for these psychological activities. Based on previous research in behavioral finance, these activities have their corresponding mappings on stock trading, so we choose three indicators based on stock information to represent the psychological activities respectively, which helps make this process more observable and calculable.
The COVID-19 pandemic had a profound impact on global stock markets, as explored in several recent studies, and stock markets in different regions were affected to varying degrees. Gao et al. (2021) compared the responses of the Chinese and U.S. markets and found that the stock market in China, where the initial outbreak was more severe, experienced a greater impact. More general comparisons between emerging markets and developed markets were also thoroughly examined (Harjoto et al. 2021; Harjoto and Rossi 2023). The market fluctuations are widely believed to be caused by investor sentiment and risk aversion, as indicated by Cox et al. (2020). However, to the best of our knowledge, few studies empirically measure the noise trading during the COVID-19 and comprehensively associate the noise with various behavioral factors, such as herding and overconfidence. This paper aims to fill this gap using an event–study framework. Comparing different behavioral factors and finding the dominant effect play a significant role in understanding the mechanism and channel of how an exogenous event affects the stock market.
4.1. COVID-19, Market Noise, and Stock Return
Event study is a widely used statistical methodology to estimate the impact of a specific event on the explained variable by calculating its abnormal return (Schmeling 2009). A model window, usually before the event, is chosen to construct the estimation model. Correspondingly, AR windows are selected to measure the influence of the event. The abnormal return is calculated by the following:
where represents the mean of the explained variable in the AR window; is the estimate of the explained variable based on the model window.
In our research, COVID-19 events are divided into the directions positive and negative. We choose four momentous events during the COVID-19 pandemic, including the outbreak of COVID-19 on 31 December 2019, the announcement of a free vaccine, the global COVID-19 deaths surpassing 1 million, and the vaccination rate reaching 20%. The first one and the third one are believed to be negative influences while the second and fourth one are positive. And the model window is selected from 30 days to 10 days before the event date to avoid being affected by other unrelated events. Table 5 shows the time reference of the model window and AR window. To measure the abnormal return of both the NTR and yield, we calculate by assigning the mean of the model window. Figure 5 shows the performance of the NTR indicator and SSE Composite Index during these events.

Table 5.
Time reference of model window and AR window.
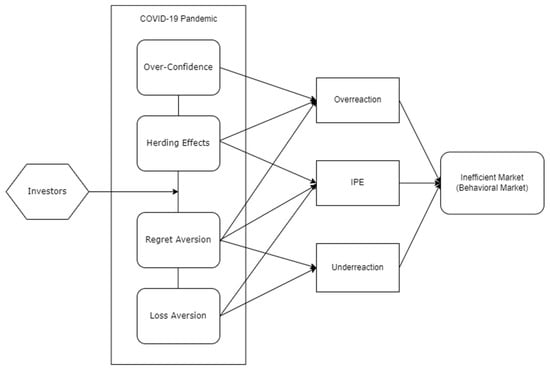
Figure 5.
COVID-19 affects investors’ behaviors.
In the face of the COVID-19 outbreak and the rising deaths, the stock market responded with increased noise and lower yields (Beirne et al. 2021). The stock market had a delay in reacting to the outbreak of the pandemic. The market noise increased significantly in the fourth AR window, while the yield started to decrease in the third window, because the virological nature, fatality rate, and the spread of COVID-19 were not very clear during the first month.
Table 6 shows the event study of NTR and stock return, The outbreak, and some news described COVID-19 as the second SARS. Similarly, when the global death surpassed 1 million, which represented a stronger sense of fear in life, the market noise rose quickly from the first window, and the yield fell from the second window.

Table 6.
Tests of the abnormal return of different events.
The market response to the vaccination was a drop in noise and a recovery in yield, though the response was less salient than the pandemic itself. The news that free vaccination was available led to higher yields in the whole event windows, and the global availability of vaccination was linked to a significant decrease in market noise for nearly one month.
4.2. Over-Confidence
Over-confidence describes a psychological bias that investors overestimate their ability for investments or the accuracy of their private information (Daniel et al. 1998). Usually, this psychological factor is negatively associated with investor’s performance (Odean 1998), as investors tend to behave irrationally and to perform poorly. Trinugroho and Sembel (2011) provide evidence that over-confidence consequently leads investors to buy a stock at a high price or sell at a low price, overconfidently thinking the stock price might rise or fall. In our opinion, over-confidence is associated with overreaction and IPE, and over-confidence is reinforced by the COVID-19 pandemic, as confidence is an attribute that repeatedly self-verifies in various events (Coopersmith 1967).
The measurement of the over-confidence index (OCI) is based on the actual average number of transactions (AANT) (Ho 2011), by multiplying the degree of private information and the turnover rate. An over-confident investor tends to make trading behaviors more frequently and to believe that the private information is accurate; thus, the OCI will become greater if the over-confidence is stronger. Thus, the OCI is calculated by the following:
where is measured by the number of trades over the period divided by number of trades over the whole sampling period; the degree of private information is calculated by the number of over-the-counter trades divided by the public trades in the secondary market.
We apply the event study method on the OCI and find that this index is apparently associated with the market noise represented by the NTR indicator. This suggests that the market noise is related to the psychological action of over-confidence. Figure 6 shows the trends in OCI and NTR during the four COVID-19-related events.
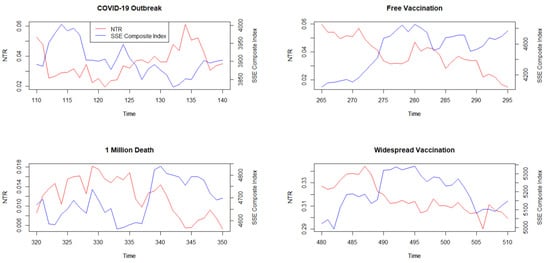
Figure 6.
Influence of COVID-19 events on NTR and SSE Composite Index.
Consistent with Apergis’s (2022) and Azam et al.’s (2022) findings that COVID-19 contributes to a stronger over-confidence sentiment, during the negative events of the COVID-19 outbreak or the number of deaths surpassing one million, we can observe that the over-confidence phenomenon becomes fiercer, accompanied by an increasing market noise. A time lag of 10 days occurs between the two indicators, which suggests that the over-confidence of investors firstly causes the trading behaviors in the market, then is reflected by the market noise. Therefore, OCI can serve as a signal for market noise as the price increase is not driven by the higher fundamental value but by the inaccurate information and judgement of investors. However, for positive events, such as widespread vaccination, both indicators seesawed to a lower level, as investors restore to a more calm and rational psychological state and make reasonable investment decisions.
4.3. Herding Effect
The herding effect was first proposed by Keynes in 1936, describing the phenomenon of blindly following other people’s behaviors without thinking carefully and rationally. This phenomenon has been tested to be significant in China’s stock market (Tan et al. 2008) mainly due to the large group of individual investors in the stock market of China. We believe that COVID-19 will reinforce the intensity of herding effects in China’s stock market as the information transmission is negatively influenced by the pandemic and the life pressure of the investors is more serious. The increasing intensity of the herding effect leads to a less efficient market and more market noise as investors blindly follow the news on the market without thinking carefully and analyzing the news.
To measure the herding behaviors, there are two common methods. One is the CH method by calculating the difference between the variance in the stock return and market return, and another is the CSAD indicator (Chang et al. 2000), which measures the herding effect by calculating the deviation of the stock return to the market return with cross-section data. We adopt the CSAD indicator to measure the herding effects as it solves the problem of measuring herding effects when the volatility is not large enough. The CSAD indicator is as follows:
where refers to the stock return of an individual stock and refers to the market return. N is equal to 92 stocks in the sample.
Then, we apply the event study method to the CSAD indicator, and we find that the indicator shares a similar trend with NTR, which indicates that market noise is related to the herding effect and CSAD tends to show the trend before NTR does. Figure 7 shows the trends of the two indicators during the four COVID-19-related events.
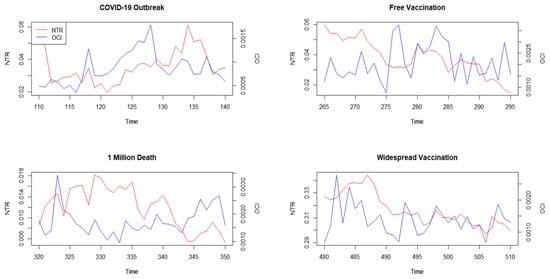
Figure 7.
Influence of COVID-19 events on OCI and NTR.
Similarly, when COVID-19 happened, the herding effect was observed to be more intensive, accompanied by the increasing NTR, which further proves Espinosa-Méndez and Arias’s (2021) opinions that fear and uncertainty over the pandemic drive less informed investors to follow more informed ones, while the positive news during COVID-19, such as the development of vaccination, which helped to mitigate the herding in the market, consequently decreased noise in the market.
4.4. Loss Aversion and Regret Aversion
Loss aversion and regret aversion happen less frequently than over-confidence and herding, but these two effects describe very typical investors’ mental activities, such as bottom fishing and selling at the top. Both being part of the prospect theory, loss aversion indicates that investors feel fretful at loss and make decisions based on obviating loss as much as they can, while regret aversion suggests that investors make decisions to avoid feeling regretful after knowing the outcome (Köbberling and Wakker 2005). Based on the prospect theory, we map the investors’ behaviors to stock trading information and construct the aversion index as follows:
where is the change in the stock price i at time t, and refers to the trading quantity of stock i at time t + 1. When the aversion index turns into the regret aversion index, and when it becomes the loss aversion index.
Then, we apply the event study method to the AI and find that this index in some occasions moves in the same direction with the NTR and moves in the opposite direction in other occasions. This indicates that loss aversion and regret aversion may have different influences on the market noise. Figure 8 shows the trends in AI and NTR during the four COVID-19-related events.
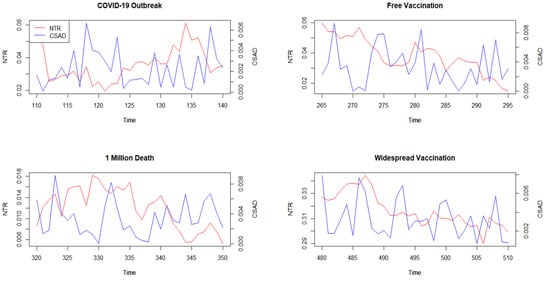
Figure 8.
Influence of COVID-19 events on CSAD and NTR.
During the negative events of COVID-19, the aversion index had different performances, but it shared the same direction of movement with the NTR (Figure 9). We think the reason is due to other events during these periods as the psychological aversion weighed less in investors’ decision-making. Similarly, during the positive event, AI moves towards the same direction of NTR but itself has different directions.
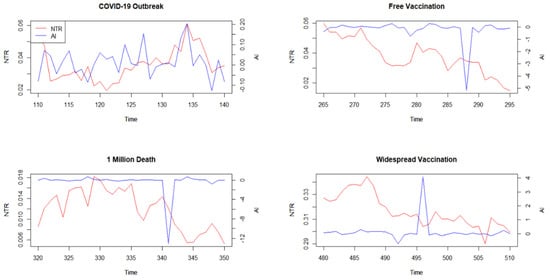
Figure 9.
Influence of COVID-19 events on AI and NTR.
However, we acknowledged that there were some limitations in our models and measures. The reliance on the CSI 100 index, while capturing the performance of major market players, may overlook the dynamics of smaller firms or specific sectors that were disproportionately impacted by the pandemic. This limitation means that our findings might not fully represent the broader market effects experienced by these overlooked segments. Additionally, the use of the moving average method to calculate the NTR indicator, though effective for smoothing short-term fluctuations, could introduce autocorrelation issues. However, since our study did not perform regression analysis, these autocorrelation concerns do not directly affect our results.
5. Conclusions
The first conclusion is that the pandemic is not a simple black swan to the stock market. In fact, it affects the stock price, volatility, and market noise by changing people’s expectations and investment behaviors. When positive signals occur, investors’ confidence can be rebuilt, and the stock price rebounds accordingly. For investors, this encourages them to look at the market objectively, rather than blindly following other people’s opinions or the general trend, thus leading to weakening market noise. For enterprises, during the pandemic, it is more necessary to actively communicate with investors and make them fully aware of the enterprises’ operation under the pandemic, which effectively helps clear the sense of fear and bewilderment when they make investment decisions.
From the perspective of behavioral finance, our paper conducts an empirical study of the BAPM and the behavioral portfolio theory. The evidence shows that BAPM provides a better explanation for the returns of stocks or portfolios in China’s stock market, a major emerging market. This conclusion also holds true before the COVID-19 pandemic. This may be due to the less completed regulations, the relatively less experienced investors, and the transparency and accessibility of information (Li et al. 2022). These common characteristics of developing markets make the BAPM more effective and significant in explaining and predicting the yield. Furthermore, based on the IANM, we estimate that the inefficient market holds for 70% of information days, while EMH is true for only 30%. In addition, we find that the market noise is associated with the investors’ psychological biases, such as over-confidence and regret aversion. Our results are consistent with the empirical literature but found more pronounced influences in China’s market due to the higher severity of the COVID-19 pandemic in China.
Noise not only exists significantly in China’s market but also has a great impact on the stock return and volatility. Of the 92 listed companies with the largest capital market value, most of them had significant noise trading. For quantitative trading, the intensity of noise, to some extent, determines the size of their profitable exposure. With stronger noise, more arbitrage opportunities appear to them. For less experienced and rational investors, they face higher uncertainty in a pervasive noise market. This paper proposes a new method of measuring noise based on BAPM theory and several indicators of investment behaviors, such as CSAD for the herding effect. However, these indicators still have some shortcomings, such as a certain time lag, which makes it difficult for high-frequency trading.
However, there are some questions still being unanswered. Is the intensity of the noise also related to the industry? What is the mechanism of noise generation? Are there more effective ways to build the behavioral portfolio? Will long-term value investment reduce market noise? How can quantitative factors based on noise traders’ risk be applied to real practice? Thus, more research about investment behaviors is needed to figure them out.
Author Contributions
Conceptualization, X.J.; Methodology, K.L. and X.J.; Software, K.L.; Validation, K.L.; Formal analysis, K.L.; Investigation, K.L.; Resources, X.J.; Writing—original draft, K.L. and X.J.; Supervision, X.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | While indices like the CSI 300 and CSI 500 do include stocks from both exchanges, they are primarily based on market capitalization and focus on the largest and most liquid companies. |
| 2 | https://www.wind.com.cn/mobile/WFT/en.html, accessed on 1 January 2024. |
References
- Abel, Andrew B. 2002. An exploration of the effects of pessimism and doubt on asset returns. Journal of Economic Dynamics and Control 26: 1075–92. [Google Scholar] [CrossRef]
- Apergis, Nicholas. 2022. Overconfidence and US stock market returns. Finance Research Letters 45: 102186. [Google Scholar] [CrossRef]
- Azam, Md Qamar, Nazia Iqbal Hashmi, Iqbal Thonse Hawaldar, Md Shabbir Alam, and Mirza Allim Baig. 2022. The COVID-19 Pandemic and Over-confidence Bias: The Case of Cyclical and Defensive Sectors. Risks 10: 56. [Google Scholar] [CrossRef]
- Baker, Malcolm, and Jeffrey Wurgler. 2006. Investor Sentiment and the Cross-Section of Stock Returns. The Journal of Finance (New York) 61: 1645–80. [Google Scholar] [CrossRef]
- Barberis, Nicholas, Andrei Shleifer, and Robert Vishny. 1998. A model of investor sentiment. Journal of Financial Economics 49: 307–43. [Google Scholar] [CrossRef]
- Barberis, Nicholas, Ming Huang, and Tano Santos. 2001. Prospect theory and asset prices. The Quarterly Journal of Economics 116: 1–53. [Google Scholar] [CrossRef]
- Beirne, John, Renzhi Nuobu, Sugandi Eric, and Volz Ulrich. 2021. COVID-19, asset markets and capital flows. Pacific Economic Review (Oxford, England) 26: 498–538. [Google Scholar] [CrossRef]
- Beja, Avraham. 1979. State Preference and the Riskless Interest Rate: A Markov Model of Capital Markets. The Review of Economic Studies 46: 435–46. [Google Scholar] [CrossRef]
- Bender, Jennifer C., Carol L. Osler, and David Simon. 2013. Noise Trading and Illusory Correlations in US Equity Markets. Review of Finance 17: 625–52. [Google Scholar] [CrossRef]
- Black, Fischer. 1986. Noise. The Journal of Finance 41: 528–43. [Google Scholar] [CrossRef]
- Blitz, David. 2014. Agency-Based Asset Pricing and the Beta Anomaly. European Financial Management: The Journal of the European Financial Management Association 20: 770–801. [Google Scholar] [CrossRef]
- Brown, Gregory W. 1999. Volatility, Sentiment, and Noise Traders. Financial Analysts Journal 55: 82–90. [Google Scholar] [CrossRef]
- Brown, Gregory W., and Michael T. Cliff. 2004. Investor sentiment and the near-term stock market. Journal of Empirical Finance 11: 1–27. [Google Scholar] [CrossRef]
- Chang, Eric C., Joseph W. Cheng, and Ajay Khorana. 2000. An examination of herd behavior in equity markets: An international perspective. Journal of Banking & Finance 24: 1651–79. [Google Scholar]
- Chen, Tao. 2020. Country herding in the global market. The Journal of Behavioral Finance 21: 174–85. [Google Scholar] [CrossRef]
- Cochrane, John H. 1991. Volatility tests and efficient markets: A review essay. Journal of Monetary Economics 27: 463–85. [Google Scholar] [CrossRef]
- Coopersmith, Stanley. 1967. The Antecedents of Self-Esteem. Palo Alto: Consulting Psychologists Press Inc. [Google Scholar]
- Cox, Josue, Daniel L. Greenwald, and Sydney C. Ludvigson. 2020. What Explains the COVID-19 Stock Market? NBER Working Paper Series; Cambridge, MA: National Bureau of Economic Research. [Google Scholar]
- Daniel, Kent, Hirshleifer David, and Avanidhar Subrahmanyam. 1998. Investor Psychology and Security Market Under- and Overreactions. The Journal of Finance 53: 1839–85. [Google Scholar] [CrossRef]
- De Long, J. Bradford, Andrei Shleifer, Lawrence H. Summers, and Robert J. Waldmann. 1990. Noise trader risk in financial markets. The Journal of Political Economy 98: 703–38. [Google Scholar] [CrossRef]
- Espinosa-Méndez, Christian, and Jose Arias. 2021. COVID-19 effect on herding behaviour in European capital markets. Finance Research Letters 38: 101787. [Google Scholar] [CrossRef]
- Gao, Xue, Yixin Ren, and Muhammad Umar. 2021. To what extent does COVID-19 drive stock market volatility? A comparison between the U.S. and China. Economic Research-Ekonomska Istraživanja 35: 1686–706. [Google Scholar] [CrossRef]
- Harjoto, Maretno Agus, and Fabrizio Rossi. 2023. Market reaction to the COVID-19 pandemic: Evidence from emerging markets. International Journal of Emerging Markets 18: 173–99. [Google Scholar] [CrossRef]
- Harjoto, Maretno Agus, Fabrizio Rossi, Robert Lee, and Bruno S. Sergi. 2021. How do equity markets react to COVID-19? Evidence from emerging and developed countries. Journal of Economics and Business 115: 105966. [Google Scholar] [CrossRef]
- Hirshleifer, David, Avanidhar Subrahmanyam, and Sheridan Titman. 1994. Security Analysis and Trading Patterns When Some Investors Receive Information Before Others. The Journal of Finance (New York) 49: 1665–98. [Google Scholar] [CrossRef]
- Ho, Chi Ming. 2011. Does Over-confidence Harm Individual Investors? An Empirical Analysis of the Taiwanese Market. Asia-Pacific Journal of Financial Studies 40: 658–82. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263–91. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Mark W. Riepe. 1998. Aspects of investor psychology. Journal of Portfolio Management 24: 52–65. [Google Scholar] [CrossRef]
- Kholdy, Shady, and Ahmad Sohrabian. 2014. Noise traders and the rational investors: A comparison of the 1990s and the 2000s. Journal of Economic Studies (Bradford) 41: 849–62. [Google Scholar] [CrossRef]
- Köbberling, Veronika, and Peter P. Wakker. 2005. An index of Loss Aversion. Journal of Economic Theory 122: 119–31. [Google Scholar] [CrossRef]
- Lewellen, Jonathan, and Stefan Nagel. 2006. The conditional CAPM does not explain asset-pricing anomalies. Journal of Financial Economics 82: 289–314. [Google Scholar] [CrossRef]
- Li, Jianhui, Xinfeng Ruan, Sebastian A. Gehricke, and Jin E. Zhang. 2022. The COVID-19 risk in the Chinese option market. International Review of Finance 22: 346–55. [Google Scholar] [CrossRef]
- Odean, Terrance. 1998. Are Investors Reluctant to Realize Their Losses? The Journal of Finance (New York) 53: 1775–98. [Google Scholar] [CrossRef]
- Ramiah, Vikash, and Sinclair Davidson. 2007. Information-Adjusted Noise Model: Evidence of Inefficiency on the Australian Stock Market. The Journal of Behavioral Finance 8: 209–24. [Google Scholar] [CrossRef]
- Ross, Stephen A. 1976. The arbitrage theory of capital asset pricing. Journal of Economic Theory 13: 341–60. [Google Scholar] [CrossRef]
- Roy, Andrew Donald. 1952. Safety First and the Holding of Assets. Econometrica 20: 431–49. [Google Scholar] [CrossRef]
- Sayim, Mustafa, Pamela D. Morris, and Hamid Rahman. 2013. The effect of US individual investor sentiment on industry-specific stock returns and volatility. Review of Behavioral Finance 5: 58–76. [Google Scholar] [CrossRef]
- Schmeling, Maik. 2009. Investor sentiment and stock returns: Some international evidence. Journal of Empirical Finance 16: 394–408. [Google Scholar] [CrossRef]
- Shapiro, Samuel Sanford, and Martin B. Wilk. 1965. An analysis of variance test for normality (complete samples). Biometrika 52: 591–611. [Google Scholar] [CrossRef]
- Shefrin, Hersh, and Meir Statman. 1994. Behavioral Capital Asset Pricing Theory. The Journal of Financial and Quantitative Analysis 29: 323. [Google Scholar] [CrossRef]
- Shefrin, Hersh, and Meir Statman. 2000. Behavioral Portfolio Theory. Journal of Financial and Quantitative Analysis 35: 127–51. [Google Scholar] [CrossRef]
- Sias, Richard W., Laura T. Starks, and Seha M. Tiniç. 2001. Is noise trader risk priced? The Journal of Financial Research 24: 311–29. [Google Scholar] [CrossRef]
- Spyrou, Spyros. 2013. Herding in financial markets: A review of the literature. Review of Behavioral Finance 5: 175–94. [Google Scholar] [CrossRef]
- Sun, Yunchuan, Mengyuan Wu, Xiaoping Zeng, and Zihan Peng. 2021. The impact of COVID-19 on the Chinese stock market: Sentimental or substantial? Finance Research Letters 38: 101838. [Google Scholar] [CrossRef] [PubMed]
- Tan, Lin, Thomas C. Chiang, Joseph R. Mason, and Edward Nelling. 2008. Herding behavior in Chinese stock markets: An examination of A and B shares. Pacific-Basin Finance Journal 16: 61–77. [Google Scholar] [CrossRef]
- Trinugroho, Irwan, and Roy Sembel. 2011. Over-confidence and Excessive Trading Behavior: An Experimental Study. International Journal of Business and Management 6: 147–52. [Google Scholar] [CrossRef]
- Trueman, Brett. 1988. A Theory of Noise Trading in Securities Markets. The Journal of finance (New York) 43: 83–95. [Google Scholar] [CrossRef]
- Verma, Rahul, and Gökçe Soydemir. 2006. The impact of U.S. individual and institutional investor sentiment on foreign stock markets. Journal of Behavioral Finance 7: 128–44. [Google Scholar] [CrossRef]
- Verma, Rahul, and Gökçe Soydemir. 2009. The impact of individual and institutional investor sentiment on the market price of risk. The Quarterly Review of Economics and Finance 49: 1129–45. [Google Scholar] [CrossRef]
- Wang, Yenan, Di Yu, Junjie Ye, and Wenbin Wei. 2021. Study on the public psychological states and its related factors during the outbreak of coronavirus disease 2019 (COVID-19) in some regions of China. Psychology, Health & Medicine 26: 13–22. [Google Scholar]
- Wang, Zhixuan, Yanli Dong, and Ailan Liu. 2022. How does China’s stock market react to supply chain disruptions from COVID-19? International Review of Financial Analysis 82: 102168. [Google Scholar] [CrossRef]
- Wu, Guosong, Boxian Yang, and Ningru Zhao. 2020. Herding behavior in Chinese stock markets during COVID-19. Emerging Markets Finance and Trade 56: 3578–87. [Google Scholar] [CrossRef]
- Xu, Xiaoming, Vikash Ramiah, Imad Moosa, and Sinclair Davidson. 2016. An application of the information-adjusted noise model to the Shenzhen stock market. International Journal of Managerial Finance 12: 71–91. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).