Abstract
Using the volatility spillover index method based on the quantile vector autoregression (QVAR) model, this paper systematically examines structural changes and corresponding spillover effects within 20 major stock markets under both extreme and normal market conditions, using data spanning from January 2005 to January 2023. The results show that, compared to the traditional volatility spillover index method, which focuses mainly on average spillover effects, the QVAR model-based spillover index better captures spillover effects under extreme and various market conditions among global stock markets. The connections between stock markets are closer in extreme market conditions. The total spillover index of major global stock markets significantly increases in extreme conditions compared to normal conditions. In extreme market conditions, inflow indices show varying degrees of increase, with emerging economy stock markets displaying more significant increases. The outflow indices exhibit heterogeneity; emerging economies show consistent increases, while developed economies show mixed changes.
1. Introduction
With the deepening of economic globalization and the integration of financial markets, the connectedness across stock markets of various countries has significantly increased, which also exacerbates the transmission of risks across diverse economies (Nyakurukwa and Seetharam 2023; Balcilar et al. 2023). The sharp fluctuations in one stock market can spread and amplify across markets, thereby engendering substantial volatility in the global stock market and potentially precipitating systemic financial crises on a global scale. A paradigmatic illustration of this phenomenon unfolded in March 2020 when the U.S. stock market, grappling with the repercussions of the COVID-19 pandemic, encountered four circuit breakers. Stock markets in numerous countries experienced precipitous declines, culminating in an epic shock to the global market (Hassan and Riveros Gavilanes 2021; Chowdhury et al. 2022). In extreme situations such as this, the volatility spillover effect within global stock markets becomes significantly intensified. Thangamuthu et al. (2022) showed how volatility spread from major economies like the U.S., China, Japan, and others to the Indian market. Similarly, in an analysis of multiple markets, studies observed heightened spillover effects among markets during COVID-19 compared to prior periods (Hassan and Riveros Gavilanes 2021; Balcilar et al. 2023). Therefore, being able to accurately gauge the spillover effects across varying conditions is essential for understanding the characteristics of global stock market risk transmission, identifying the focus of risk prevention, and is of great practical significance for countries to take targeted measures to prevent imported risks and maintain financial stability (Bae and Karolyi 1994; Thangamuthu et al. 2022).
This paper selects 20 major global economies’ stock markets as a sample and utilizes the Volatility Spillover Index method based on the framework of Quantile Vector Autoregressive Model (QVAR) to measure the spillover effects among global stock markets under various conditions. The main contributions of the study are as follows. First, we employ the latest Volatility Spillover Index method based on the Quantile Vector Autoregressive (QVAR) model to measure spillover indices and investigate variations in spillover effects among the 20 major global stock markets, assessing both normal and extreme conditions. Second, this paper analyzes changes in total spillover and directional spillover from both static and dynamic perspectives. Furthermore, this comprehensive approach aligns with other studies that emphasize the importance of continuous monitoring and strategic measures to minimize global financial contagion (Bae and Karolyi 1994; Bhargava et al. 2012; Gamba-Santamaria et al. 2017). By leveraging these insights, policymakers can better mitigate the cascading risks that threaten global financial stability.
The rest of the paper is organized as follows: Section 2 briefly reviews the literature; Section 3 describes the data and presents the empirical methods employed; Section 4 discusses the results; Section 5 includes discussion, limitations, and future research direction; and Section 6 concludes and provides policy implications.
2. Literature Review
The study of global stock market interconnectivity has been significantly influenced by two primary theoretical frameworks: the economic foundation theory and the market contagion theory (Liang et al. 2015; Sun et al. 2017). The tangible economic foundation theory, grounded in the Efficient Market Hypothesis, posits that the fundamentals of economies are interconnected through international trade and cross-border capital flows, leading to increased asset price interconnectivity. This theory suggests that stock market correlations are stronger within regions or among countries with close economic ties. Conversely, the market contagion theory focuses on psychological factors and investor behavior, particularly during times of market stress. It proposes that irrational herding behavior and psychological expectations drive “herd behavior”, resulting in convergence effects in markets that increase the interconnectivity and spread of risk across global stock markets. This, in turn, causes risk to spread between markets and increases the interconnectivity of global stock markets. Such occurrences may transpire irrespective of any underlying changes in fundamentals (King and Wadhwani 1990; Forbes and Rigobon 2002). Zheng and Liu (2018) found that both economic fundamentals and market contagion can effectively explain spillover effects among international stock markets.
Empirical research on global stock market interconnectivity initially focused on mature markets within developed economies, reflecting the systems’ established financial infrastructures. Early studies, such as those by Hamao et al. (1990), Kanas (1998), and Baele (2005), identified critical patterns of volatility spillovers among major markets, such as the United States, Japan, and key European countries, uncovering both unidirectional and bidirectional effects. As the global landscape evolved with economic globalization, the research expanded to include the dynamic between developed and emerging markets, which have exhibited rapid growth. This shift is exemplified by studies from Miyakoshi (2003) and Zhang et al. (2010), which explored the interplay between markets like the U.S. and China, highlighting significant changes in volatility spillovers as markets liberalized.
The methodological approaches in this field have also seen considerable evolution. From initial techniques that measured market connectedness through correlation coefficients (King and Wadhwani 1990) and cointegration methods (Bessler and Yang 2003), research has moved towards more sophisticated tools such as the volatility spillover index. This method was notably advanced by Diebold and Yilmaz (2009, 2012) and has been widely adopted for more rigorous analyses, as seen in the work of Zhou et al. (2012), which has not only incorporated a broader array of markets into their analyses but have also emphasized the growing interdependence of global markets intensified (Alter and Schüler 2012), particularly in response to financial crises. However, most of the above-mentioned studies focused on log returns or volatility of stock indices as their starting point. The calculated correlation coefficients or spillover levels could only reflect the average level of information spillover between stock markets. However, scholars have grown more interested in exploring how information flows between global stock markets during extreme events such as financial crises. Recent approaches have integrated advanced risk assessment methods, such as EVT-Copula-CoVaR and MVMQ-CAViaR, to explore the nuances of how markets interact during extreme financial events. This line of inquiry, pursued by researchers like Liu et al. (2011), Zeng et al. (2017), has provided deeper insights into the behavior of markets under various market conditions, further enriching our understanding of global financial volatility.
In summary, the global stock markets exhibit significant spillover effects driven by both economic fundamentals and risk contagion mechanisms, especially during extreme market conditions. While measurements based on conditional means provide insights into the general spillover landscape, it is also important to understand whether there exist significant differences in the level and structure of such spillovers among global stock markets under different market conditions. Our paper fills this gap. To address these, this paper employs the framework of the Quantile Vector Autoregressive Model (QVAR) to measure spillover indices under various conditional quantiles. The approach utilizes relative spillover indices and directional spillover networks to examine changes in spillover structures among global stock markets from normal to extreme market conditions.
3. Data and Methodology
Our sample includes stock markets from 20 countries and regions, including China, Hong Kong, Singapore, Japan, South Korea, Indonesia, India, the United States, Canada, Mexico, Brazil, Australia, Russia, Germany, France, the United Kingdom, the Netherlands, Italy, Spain, and Switzerland1. Among them, six are emerging economies and fourteen are developed economies. These countries and regions are represented by the following abbreviations CHN, HK, SGP, JPN, KOR, IDN, IND, US, CAN, MEX, BRA, AUS, RUS, DEU, FRA, UK, NED, ITY, ESP, and CHE. Collectively, these markets accounted for over 90% of the global market capitalization at the end of 2021, making them highly representative. Given that the official publication of the CSI 300 Index began in 2005, the sample period spans from 7 January 2005 to 27 January 2023. To mitigate the impact of asynchronous trading across global stock markets, weekly data are used. In addition, to account for any missing data resulting from holidays and weekends, we replace them with data from the previous trading day. The final dataset comprises a total of 943 sets of weekly observations, and the primary data source utilized is the WIND database.
In recent years, there has been a growing adoption of the volatility spillover index approach, primarily based on the conventional VAR model. However, this model focuses on assessing conditional mean and faces challenges in precisely quantifying the spillover effects during extreme market conditions, for example, the bull and bear markets. To address this limitation, the quantile vector autoregressive model (QVAR) is applied to investigate spillover effects across conditional quantiles. The distribution of the stock index’s logarithmic return rates captures the various levels of shock in the stock market. For instance, the conditional median (τ = 0.50) represents the normal condition of the market, τ = 0.05 represents an extreme downturn (a bear market), and τ = 0.95 represents an extreme upturn (a bull market).
In this section, we initially employ a QVAR model with N variables and then apply the Diebold and Yilmaz (2012, 2014) method to compute the volatility spillover index. This allows us to analyze how the characteristics of information spillover effects in major global stock markets evolve under different conditions. First, we construct a conditional quantile τ-based N-dimensional QVAR (p) model:
where τ ∈ (0, 1), yt is an N-dimensional column vector of weekly index log returns, c(τ) is an N × 1 dimensional intercept column vector, Ai(τ) is an N × N dimensional QVAR coefficient matrix, p illustrates the lag length of the QVAR model, εt(τ) ~ (0, Σ(τ)) are N × 1 dimensional independent and identically distributed error vectors, and Σ(τ) is the covariance matrix. When Equation (1) satisfies the stability conditions, it can be transformed into a moving average form:
where and represents the coefficient matrix corresponding to the conditional quantile τ. When s > 0, + ; when s = 0, ; and when , .
Next, we perform a generalized variance decomposition to measure the degree to which each variable in the VAR system is affected by shocks from other variables or itself. The proportion of the generalized forecast error variance of variable i over the past H periods caused by variable j is denoted as and is defined as follows:
where represents the covariance matrix of the error vector is the th element on the diagonal of , denotes a column vector of dimension , where the th element is 1 and all other elements are 0, H represents the forecast horizon, and represents the coefficients of the moving average model (Equation (2)). Due to the generalized variance decomposition not orthogonalizing the error terms, the variance decomposition results calculated in Equation (3) may not necessarily satisfy the requirement that the sum of elements in each row of the variance decomposition table equals 1. To compute the volatility spillover index values, we standardized as follows:
where N represents the number of variables and is the spillover level of variable j on variable i over the forecast period H, which implies that and . Then, we calculate the total spillover index and directional spillover indices (inflow and outflow) at the quantile τ based on the results of the generalized variance decomposition:
Finally, we follow Adrian and Brunnermeier (2016) to construct the following net indices:
where and are the net inflow indices for the left tail and right tail, respectively, which measure changes in the inflow levels of each stock market during extreme downturns and upturns compared to the normal market condition, and , represent the net outflow indices for the left tail and right tail, respectively, which measure the changes in the outflow levels of each stock market during extreme downturns and upturns compared to the normal condition.
4. Results
Table 1 shows the summary statistics of the logarithmic returns for each stock market. The logarithmic return for each stock index is calculated as , where represents the closing price of the th stock market index at time t. During the sample period, emerging markets such as India, Indonesia, Brazil, Mexico, and China exhibit higher average returns for their respective stock markets. Meanwhile, Russia, China, and Brazil have relatively larger standard deviations in stock market returns, reflecting higher returns usually accompanied by greater volatility in emerging economies and also highlighting their immaturity (Li et al. 2011). Among developed economies, Italy and Spain’s stock market returns exhibit relatively low average values, even turning negative, with relatively large standard deviations, indicating that these two markets displayed characteristics of low returns and high risks. Germany and the United States rank just below the aforementioned emerging market countries in terms of average returns, and they exhibit relatively lower standard deviations. This observation reflects the “safe haven” aspect of these two stock markets (Liang et al. 2015). Furthermore, the kurtosis of the returns for all 20 stock markets is significantly greater than 3, aligning with the financial characteristic of “fat-tailed” distributions. ADF unit root tests suggest that the return series for all 20 stock indices are stationary, meeting the assumptions of VAR models.

Table 1.
Sample characteristics.
4.1. Static Analysis of the Information of Spillover among Global Major Stock Markets
We calculate the global volatility spillover index for the entire sample at different quantiles: (1) the traditional VAR model based on conditional means, (2) the QVAR model based on conditional medians (τ = 0.50), and (3) the QVAR model based on tail quantiles (τ = 0.05 and τ = 0.95). Table 2 presents the change in information spillover effects among major global stock markets under these different market conditions. Using model selection criteria, we set the lag order of the models to 1 and the forecast horizon for generalized forecast variance decomposition to 6.

Table 2.
Information spillover of global major stock markets under different conditions (%).
Columns (1) and (2) in Table 2 indicate the effect under normal market conditions, where several patterns are found. First, the total spillover index based on the traditional VAR model is 85.51%, suggesting strong connectedness among major global stock markets. Second, there are variations in the outflow (to) levels and inflow (from) levels across different stock markets, indicating an uneven distribution of information spillover among major global stock markets. The range of outflow levels varies from 63.76% (China) to 90.37% (France), while the range of inflow levels varies from 26.49% (China) to 116.31% (France). The stock markets of emerging economies exhibit relatively lower levels of inflow and outflow in comparison to the stock markets of developed economies. Third, stock markets with higher (lower) outflow levels tend to have higher (lower) inflow levels. For instance, the stock markets of France, the Netherlands, Germany, the United Kingdom, and the United States exhibit higher spillover and spillback levels, while China and India have relatively lower levels. Furthermore, when examining net spillover levels, the stock markets of major developed economies significantly show positive net spillover. Specifically, France, the Netherlands, Germany, the United Kingdom, the United States, and Italy lead as net givers, whereas the stock markets of emerging economies all demonstrate negative net spillover. China, India, and Indonesia rank among the leading net recipients. This indicates that under normal conditions, stock markets in Europe and the United States, among others, exert a stronger influence on other markets, reflecting the relatively mature status of developed economy stock markets and their dominant position in the global economic and financial system. In contrast, emerging economies’ stock markets exhibit a relatively weaker external influence and are more susceptible to external influence, making them net recipients of risk. Columns (3) and (4) of Table 2 show the effect based on the conditional median, and the values closely align with those of the traditional VAR model. Specifically, the total spillover index based on the conditional median is 84.25%, slightly lower than the 85.51% obtained from the conditional mean model.
Columns (5) and (6) represent directional spillover and total indices during extreme downturns (τ = 0.05), while columns (9) and (10) show the corresponding net inflow and outflow indices. The results indicate that during extreme downturns, the total spillover index is 93.91%, much higher than the conditional median of 84.25%, indicating stronger international market linkages. Second, the levels of spillover rise and the differences in spillover levels among different stock markets diminish. The range of changes in spillover level is from 93.36% to 94.25%, with a standard deviation of 0.20%, significantly lower than the standard deviation of spillover levels at the conditional median of 5.76%. Compared to spillover levels based on the conditional median, the spillover levels are higher during extreme downturns. Additionally, the increase is more pronounced for emerging economy stock markets than for developed economy stock markets. Overall, there are varying degrees of underestimation in the spillover levels of the 20 stock markets. Third, in a state of extreme decline, the spillover levels of stock markets exhibit differentiation globally. The range of spillover level changes is from 84.86% to 101.1%, with a standard deviation of 5.25%, significantly lower than the standard deviation of 22.10% at the median level. Compared to spillover levels based on the conditional median, the spillover levels of emerging economy stock markets increase significantly, with China experiencing the largest increase followed by India. For developed economies, the spillover levels of the stock markets in the Netherlands, France, the United Kingdom, and Germany show significant declines, while Canada’s and the United States’ stock markets experience slight declines. Other developed economy stock markets show small increases, with Australia’s, South Korea’s, and Japan’s stock markets having relatively larger increases in spillover indices. Furthermore, in terms of the changes in net spillover levels, developed economy stock markets, such as those in Europe and the United States, remain in the risk net spillover category compared to normal conditions. Although emerging economy stock markets all experience significant increases in both inflow and outflow levels, they still fall into the risk net recipient category. An exception is Russia, where China, Brazil, and Indonesia rank as the top three net recipients.
Columns (7) and (8) represent directional spillover and total indices based on the condition quantiles at τ = 0.95. These indices reflect the level of spillover in the stock market during extremely bullish conditions. Columns (11) and (12) show their corresponding relative inflow and outflow indices. The results show that, in extreme upward market conditions, the overall connectedness among major global stock markets significantly increases. The total spillover index based on the 0.95 quantile is 93.00%, much higher than the conditional median of 84.25%. In highly bullish market conditions, spillover into various countries’ stock markets rises, reducing the differences in spillover levels between them. The spillover level changes range from 90.99% to 93.62%, with a standard deviation of 0.58%, significantly lower than the standard deviation of spillover levels at the conditional median of 5.76%. Overall, there are varying degrees of underestimation in the spillover levels of the 20 stock markets in extreme upward market conditions compared to the median case.
In summary, the volatility spillover index based on conditional mean and median cannot be extrapolated to the extreme market states. These methods tend to underestimate the linkages between major stock markets, as well as the directional spillover levels, leading to inaccurate assessments of their importance in the global major stock market spillover network.
4.2. Dynamic Analysis of Information Spillover among Global Major Stock Markets
The static analysis above can only reflect the general level of spillover effects among major global stock markets, but it has limitations in capturing dynamic changes in spillover levels. In this section, we will introduce the rolling window analysis method, which has been used in the literature (Chatziantoniou et al. 2021; Chishti et al. 2023; Shahzad et al. 2023), with the rolling window set to 104 weeks (approximately containing 2 years of data). The spillover index of the QVAR model is calculated separately for τ = 0.50, τ = 0.05, and τ = 0.95, covering three aspects: total spillover index, directional spillover index, and directional spillover index between pairs.
4.2.1. Total Spillover Index
The trend of the total volatility spillover index for all 20 stock markets is shown in Figure 1. Compared to normal conditions, the total spillover index is larger and less volatile in extreme conditions. Throughout the sample period, the index’s magnitude in extreme conditions significantly surpasses that in normal conditions, with diminished variability. Specifically, in normal conditions, the index varies from 73.34% to 90.32%, with a mean and standard deviation of 84.25% and 3.97%. In contrast, during extreme conditions, the index consistently exceeds 90%, with a standard deviation below 0.75%. When contrasting extreme downturns and upturns, the former displayed a higher volatility spillover level, ranging between 91.80% and 96.79%, against the latter’s 90.87% to 95.51%. The average index during downturns was marginally higher at 93.91%, compared to 93.00% in upturns, with standard deviations of 0.745% and 0.742%, respectively, suggesting slightly lower volatility during extreme upturns.

Figure 1.
Changes in the total spillover levels of major global stock markets under normal and extreme conditions.
Figure 2 exhibits a U-shaped pattern in the total spillover index, indicating stronger information spillover among the world’s major stock markets under extreme conditions, attributed to increased panic and irrational risk transmission, which strengthens market linkages. Additionally, the index’s asymmetry in extreme conditions, with a higher one on the left tail, signifies a more potent spillover effect during extreme downtowns. This phenomenon is linked to a widespread loss of confidence and the amplification of negative sentiment, leading to a pronounced market “overshoot”. On the contrary, despite extreme upturns also facilitating market resonance, the response to positive shocks is tempered, as evidenced by a smaller index on the right tail. This pattern suggests that median-based spillover indices fall short of accurately capturing the extent of spillover in extreme conditions, making the case for an extreme quantile-based volatility spillover index essential for a comprehensive assessment of market interconnections during such conditions.

Figure 2.
Total spillover levels in different quantiles.
4.2.2. Directional Spillover Index
Figure 3 and Figure 4 illustrate the variations in stock market inflow and outflow under different conditions, respectively. According to Figure 3, the inflow index (From) for the 20 analyzed economies shows a U-shaped distribution, highlighting significantly increased inflow levels in extreme versus normal condition. This suggests that estimations based on conditional mean and median tend to underestimate the inflow index in extreme states, potentially overlooking intensified risk inputs. Additionally, the degree of concavity in the inflow curves varies by economy, with emerging economies like China and Indonesia showing a more pronounced concavity than developed economies such as the Netherlands, France, Germany, the UK, and the US. Furthermore, the disparity between the left- and right-tail inflow indices underlines the necessity of heightened attention to risk inputs during significant downturns.
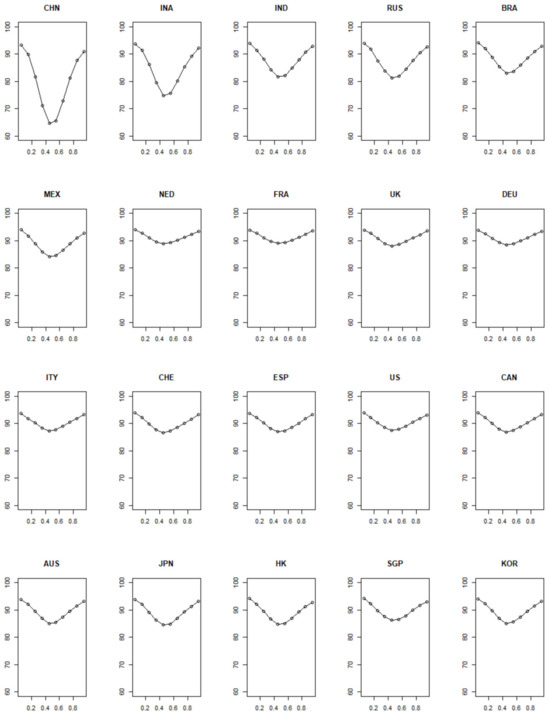
Figure 3.
Spillover index (From) of 20 stock markets in different states. The horizontal axes represent different percentiles and the vertical axes represents the spillover index in percentage.
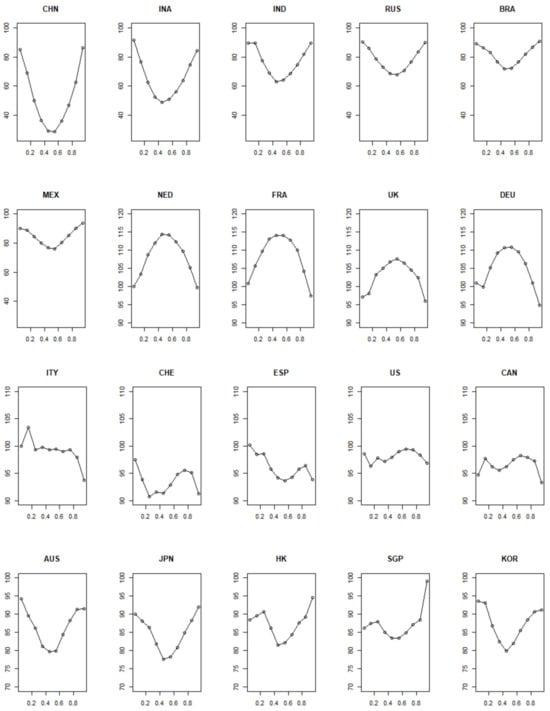
Figure 4.
Spillover index (To) of 20 stock markets in different states. The horizontal axes represents different percentiles and the vertical axes represents the spillover index in percentage.
In terms of the outflow index (To), Figure 4 highlights the significant heterogeneity in spillover effects under varying conditions. Emerging markets exhibit a U-shaped distribution, with spillover levels peaking in extreme conditions over normal ones. In contrast, developed markets show different patterns, with Australia, Japan, and South Korea exhibiting a U-shaped distribution, while the Netherlands, France, the United Kingdom, and Germany show an inverted U-shaped distribution. Hong Kong and Singapore exhibit an irregular N-shaped distribution, characterized by fluctuating spillover levels. Moreover, the distinction in the left and right tail spillover indices among these economies indicates divergent trends. Specifically, among emerging economies, Mexico, China, and Brazil show a predilection for higher spillover levels during extreme upward movements, whereas Indonesia, Russia, and India show an opposite pattern, with a more significant spillover during extreme downward trends. Among developed economies, most exhibit a greater left tail than a right tail, with the exception of Singapore, Hong Kong, and Japan, which have stronger external impacts during extreme upward trends. Recognizing these nuanced risk contagion characteristics across different economies under varied conditions is essential for implementing precise systemic risk prevention strategies and facilitating proactive and targeted measures.
To quantify the differences in outflow and inflow index between extreme and normal conditions, we further construct relative indices for the left and right tails, as shown in Table 3.

Table 3.
Relative outflow and inflow indices (%) and rankings of the left and right tails of 20 economic entity stock markets.
Regarding the inflow index (), the mean of the stock markets of 20 economies is significantly greater than 0. This indicates varying degrees of increase for each economy’s stock market in extreme conditions, with emerging economies showing a more significant increase. In terms of the mean and rankings of the left and right tail relative inflow index, emerging economies lead the way, especially China and Indonesia, taking the top two positions. Compared to the right tail relative inflow index ((∆From_R), emerging economies and developed economies such as Spain, the United States, Australia, Japan, Hong Kong (China), and Singapore have a larger left tail relative Inflow Index (((∆From_L). This suggests that the inflow levels in the stock markets of these economies have increased to a greater extent in extreme downward conditions.
Compared to the inflow index, the outflow index (∆To) in different economic entities displays heterogeneity in extreme conditions. Emerging markets tend to experience varying degrees of increase, while developed economy stock markets are exposed to both rises and falls. The mean of ∆To in emerging economy stock markets is significantly greater than 0, with China and Indonesia leading in the relative outflow index. When looking at the left-tail relative outflow index (∆To_L), the mean value for developed economies such as the Netherlands, France, the United Kingdom, Germany, the United States, and Canada is negative, while the rest of the economies are positive. Conversely, when examining the right-tail relative outflow index (∆To_R), the mean value for developed economies like France, the Netherlands, Germany, the United Kingdom, Italy, and the United States is negative, while the rest of the economies are positive, also indicating an increase in outflow levels. These findings suggest that results based on conditional median underestimate the overflow levels of stock markets in extreme states for emerging economies and some developed economies (ranking from 1st to 14th) while overestimating the outflow levels of stock markets in developed economies like the Netherlands, France, the United Kingdom, Germany, and the United States (ranking from 15th to 20th).
4.2.3. Net Spillover Index
The net spillover index results, presented in Table 4, reveal the top three economic market stocks in terms of spillover during normal and extreme states. Figure 5, Figure 6 and Figure 7 illustrate directional spillover networks among global stock markets. In these diagrams, larger nodes signify higher spillover levels to external markets, and arrows indicate the direction and strength of information spillover between economic market stocks. Only edges with spillover levels greater than the mean are retained, with thicker lines denoting greater spillover strength.

Table 4.
Directed spillover index.
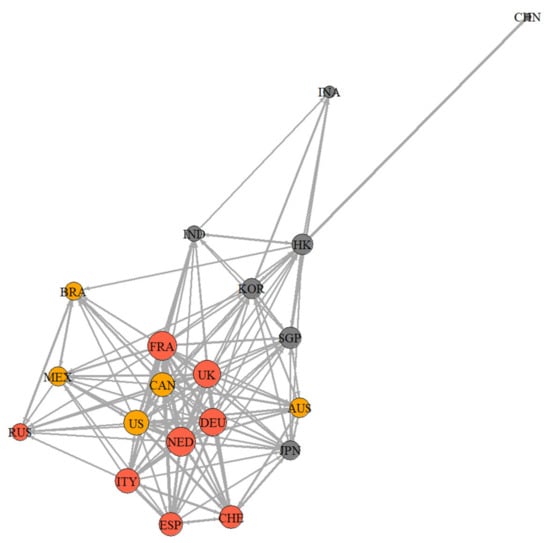
Figure 5.
Spillover network diagram of major stock markets under normal condition. Larger nodes signify higher spillover levels to external markets, and arrows indicate the direction and strength of information spillover between economic market stocks. Three different colors represent different regions: gray represents the Asian market, orange represents the European market, and since Oceania only includes Australia (AUS), it is incorporated into the American market, represented by yellow.
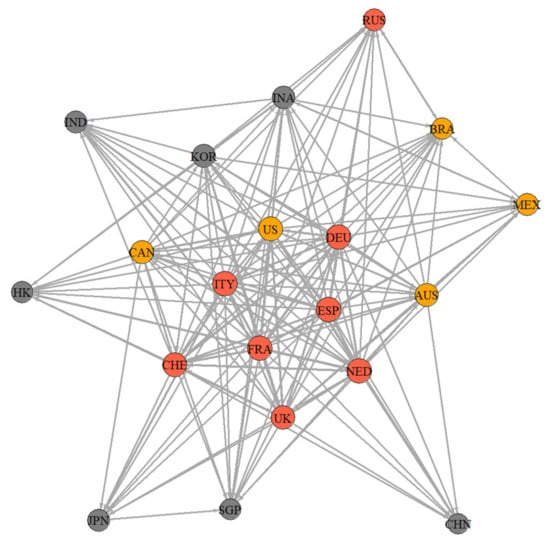
Figure 6.
Spillover network diagram of major stock markets under an extreme downward condition. Larger nodes signify higher spillover levels to external markets, and arrows indicate the direction and strength of information spillover between economic market stocks. Three different colors represent different regions: gray represents the Asian market, orange represents the European market, and since Oceania only includes Australia (AUS), it is incorporated into the American market, represented by yellow.
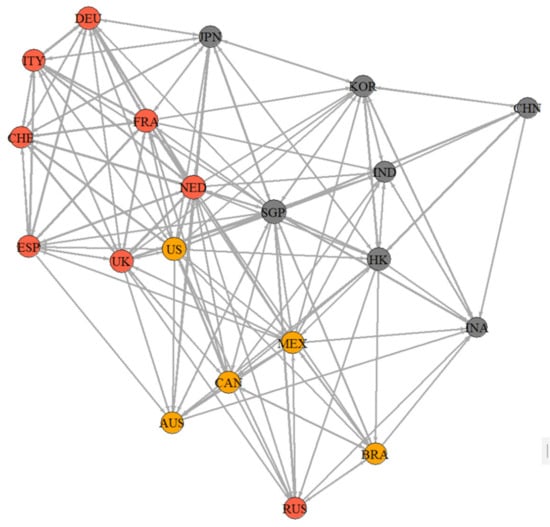
Figure 7.
Spillover network diagram of major stock markets under an extreme upward condition. Larger nodes signify higher spillover levels to external markets, and arrows indicate the direction and strength of information spillover between economic market stocks. Three different colors represent different regions: gray represents the Asian market, orange represents the European market, and since Oceania only includes Australia (AUS), it is incorporated into the American market, represented by yellow.
In normal market conditions, spillovers are primarily driven by economic fundamentals, with risk contagion being less influential. There is a noticeable trend of heightened directional spillovers within regional markets; in Asia, for instance, the Chinese stock market significantly influences Hong Kong, Singapore, and India. European markets show similar trends, with the UK stock market notably influencing Switzerland, the Netherlands, and France and, in turn, receiving significant inflows from the Netherlands, France, and Germany, reflecting close economic connections within regions.
Cross-regional risk spillovers are predominantly driven by mature stock markets; for instance, the Netherlands, France, and Germany are the primary sources of inflows into the Japanese stock market, while Canada, the UK, and the Netherlands are the major sources of inflows into the Australian stock market. This is related to the strong overseas influence of mature stock markets. In general, major developed economies have control over the allocation of global liquidity, allowing them to export risk to other economies due to their economic strength and financial status (Bu et al. 2020). Developing economies, on the other hand, have limited influence on other economies’ stock markets due to lower market openness and limited maturity.
In normal conditions, the network structure of major global stock markets (Figure 5) reveals stronger interconnections within regions, particularly within Europe, followed by the Americas and Asia. Russia, despite being part of Europe, has stronger connections with stock markets in the Americas, such as Brazil, Canada, and Mexico. Japan, while being an Asian country, is more connected to European and U.S. stock markets, reflecting its status as a developed economy. The spillover network displays a clear core–periphery pattern, with six developing economies on the periphery and developed economies like Europe and the U.S. at the core, further confirming the dominance of mature stock markets in global risk spillover (Bu et al. 2020).
In extreme downturn conditions, information related to risk contagion takes precedence, with mature stock markets in Europe and the United States emerging as primary sources of risk spillover for various economies. In Asia, economies primarily spill over within the region, but risk spillover stems mainly from mature economies like Europe and the United States. For instance, the Chinese stock market influences Hong Kong, India, and Australia, reflecting the economic fundamentals. Spain, the United States, and France are the major sources of risk spillover to the Chinese stock market, indicating information-related risk contagion. In Europe, targeted spillovers among economies remain significant, with mature stock markets in Europe and the United States not only dominating regional risk spillover but also serving as the main sources for other economies. In extreme downturns, the spillover network (Figure 6) among major global stock markets becomes denser. Mature stock markets in Europe and the United States continue to sit at the center of the spillover network, while emerging economies and the stock markets of Japan, Singapore, and Hong Kong are on the periphery. The interconnections among stock markets of economies within Asia and the Americas weaken, and the risk output from mature stock markets in Europe and the United States gains prominence. The dominance of mature stock markets in global stock market risk spillover becomes more pronounced in extreme downturn conditions compared to normal states.
In extreme upward conditions, targeted spillovers among stock markets are mainly driven by economic fundamentals, leading to a significant increase in spillovers to Singapore and Hong Kong. In Europe, substantial targeted spillovers persist, but there have been structural changes compared to the extreme downturn conditions. Apart from Germany and Spain, the top three destinations for spillovers for other economies have changed. For instance, the UK stock market’s spillover destinations shifted from France, the United States, and the Netherlands during the extreme downturn to Switzerland, the Netherlands, and Germany in extreme upturn conditions. Similarly, the sources of spillover to the UK stock market changed from France, Germany, and the Netherlands to the Netherlands, France, and the United States. In Asia, regional targeted spillovers take precedence. Using the example of the Chinese stock market, it primarily spills over to Hong Kong, Singapore, and South Korea. Additionally, it is essential to note that the Singaporean stock market not only serves as the primary source of spillover for major Asian economies, but also for the Russian, Brazilian, and Mexican stock markets during extreme upturn conditions. In extreme upturn conditions, the spillover network among major global stock markets (Figure 7) is less dense than in extreme downturn conditions. However, interconnections within regions, particularly in Asia, Europe (excluding Russia), and the Americas (including Oceania), are more pronounced. The stock markets of the Netherlands, the United States, and Singapore are at the center of the spillover network, while China, Indonesia, Brazil, and Russia are on the periphery, but notably closer to the center of the spillover network.
4.2.4. Robustness Checks
To test the reliability of our results, we conducted a series of robustness checks. The discussions above are based on 0.05 and 0.95 as extreme market conditions. We redefined them using more extreme criteria, 0.01 and 0.99, respectively. The results were very similar and did not affect our conclusions. Additionally, we redefined the rolling window value to 52 and 200 days, down and up from the previous 104 days, to construct the indices of inflow and outflow, and found that the results did not change significantly.
5. Discussion and Limitations
This study investigates spillover effects among global stock markets under various market conditions using the QVAR model and the Volatility Spillover Index method. The findings indicate that the QVAR model provides a more accurate measurement of spillover effects, especially under extreme conditions, capturing nuances missed by traditional method. During extreme market conditions, connectivity among global stock markets intensifies significantly, with emerging economies showing more pronounced increases in spillover levels than developed economies. The study also reveals a U-shaped distribution in spillover indices, indicating dynamic risk contagion patterns that vary between normal and extreme conditions. Developed economies often act as net givers of risk, while emerging economies are net recipients, with notable regional differences in spillover dynamics. Our paper offers critical insights for policymakers to develop effective risk mitigation strategies and for investors to better manage portfolio risks. Unlike previous studies, it uses a more sophisticated analytical approach, covers a broader scope of 20 major global economies, incorporates dynamic analysis, and focuses on spillover effects during extreme market conditions, providing a deeper understanding of global financial stability and risk transmission mechanisms.
We acknowledge that our study faces potential limitations arising from restrictions on free capital flows between certain countries in our sample. For instance, Russia’s economic isolation following the invasion of Ukraine in February 2022 has substantially impacted capital flows. Such geopolitical events can lead to unique market conditions, altering the global investment landscape and potentially affecting the spillover effects captured in our study. To account for this limitation, we performed sensitivity analyses by excluding Russia from the sample. Our results remained consistent, indicating that the spillover effects are robust even in the absence of Russian data2. However, we recognize that similar events could create unaccounted-for biases, particularly if such situations affect the flow of international capital disproportionately.
Moreover, these geopolitical restrictions underscore the importance of understanding the dynamic nature of global markets. While the spillover effects remain a general phenomenon, they can be influenced by external factors. Therefore, future research could explore market spillovers with a focus on geopolitical risks, providing a more comprehensive assessment of their implications.
6. Conclusions and Policy Implications
This paper examines stock market returns in the top 20 global economies, using data from January 2005 to January 2023. Employing the QVAR model and the Volatility Spillover Index method, we construct Volatility Spillover Indices under various conditions to explore the spillover effects in global major stock markets from static and dynamic perspectives, comparing both normal and extreme conditions. Additionally, we analyze the degree of difference through the relative spillover index and directional spillover network maps. There are several main findings: (1) The results of the total spillover index measurement based on mean and median methods consistently capture effects in major global stock markets during normal conditions but prove less effective in extreme conditions. (2) In extreme conditions, the total spillover index of major global stock markets significantly increases compared to normal conditions, highlighting a substantial enhancement in the linkage between stock markets of various economies. The spillover index for emerging economies rises substantially, while for the Netherlands, France, the United Kingdom, Germany, and the United States, it varies. (3) The total spillover and inflow indices of major global stock markets exhibit a U-shaped distribution in different conditions, showing divergent trends in the spillover indices. In extreme conditions, inflow indices are significantly higher, with the left-tail inflow index consistently exceeding the right-tail inflow index, indicating greater risk input during extreme downturns. Among emerging and developed economies, Australia, Japan, and South Korea’s spillover indices show a U-shaped trend, while the Netherlands, France, the United Kingdom, and Germany exhibit an inverted U-shaped pattern. Hong Kong and Singapore follow an irregular N-shaped pattern on the spillover indices, with other developed economies displaying irregular patterns. There is significant heterogeneity in the relationship between the left and right tail spillover index across different economic markets. (4) The analysis of the relative outflow and inflow indices indicates heterogeneity in the impact of extreme shocks. The inflow index for stock markets in various economies showed varying degrees of increase in extreme conditions, with emerging economies stock markets experiencing a more significant impact. The outflow index for different economic marketplaces exhibited heterogeneity in extreme conditions. It always shows an increasing trend for the emerging economies’ stock markets, while developed economies’ stock markets show mixed performance. The directional overflow index for the Chinese stock market experiences the highest increase, displaying significant time-varying characteristics with sharp spikes at certain points during the sample period. (5) The directed spillover index and associated network analysis reveal primary sources of risk spillovers in various stock markets. In normal conditions, spillovers between stock markets are primarily driven by economic fundamentals, with information linkages playing a secondary role. In extreme downward conditions, risk contagion takes the lead, and mature markets like Europe and the United States become the primary sources of risk overflow for various economies. In extreme upward conditions, directed spillovers between stock markets are primarily influenced by economic fundamentals, with Singapore and Hong Kong exhibiting a significant increase.
We provide several points of policy advice based on our findings: (1) We should develop a comprehensive understanding of the characteristics of information spillovers among major global stock markets. Traditional spillover index methods face challenges in accurately characterizing spillover features in extreme conditions. It is necessary to introduce a spillover index measurement method based on conditional quantiles to measure the network characteristics of correlations among major global stock markets under different conditions. (2) Prioritizing the impact of extreme risk events on the stock market is crucial. The impact of extreme, unforeseen events can lead to significant stock market volatility, increased inter-market connections, and a notable rise in overall market contagion levels. Regulatory authorities should strengthen their measurement and monitoring of external risks entering the stock market, continually enhance risk prevention and resolution mechanisms, and, in extreme circumstances, policymakers can implement temporary administrative measures to guard against systemic risks. (3) Investors should pay attention to the dynamic changes in the correlation between major stock markets and promptly assess and optimize their investment portfolios to mitigate risks. In extreme market conditions, the correlation between stock markets significantly increases, indicating a reduced level of portfolio diversification and increased investment risk. Investors need to scientifically assess the impact of changes in correlation between stock markets on their investment portfolios, especially in extreme market situations.
Author Contributions
Q.L.: Conceptualization, Methodology, Formal Analysis, Investigation. C.X.: Formal Analysis, Investigation, and Writing. J.X.: Investigation, and Writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable because the study did not involve humans.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors are grateful to the editor and anonymous reviewers for their constructive comments and valuable suggestions, which certainly improved the presentation and quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | The selected indices are as follows: the CSI 300 Index (China), the Hang Seng Index (Hong Kong), the Straits Times Index (Singapore), the Nikkei 225 Index (Japan), the KOSPI Index (South Korea), the Jakarta Composite Index (Indonesia), the BSE Sensex 30 Index (India), the S&P 500 Index (United States), the S&P/TSX Composite Index (Canada), the IPC Index (Mexico), the Ibovespa Index (Brazil), the ASX 200 Index (Australia), the RTS Index (Russia), the DAX Index (Germany), the CAC 40 Index (France), the FTSE 100 Index (United Kingdom), the AEX Index (Netherlands), the MIB Index (Italy), the IBEX 35 Index (Spain), and the SMI Index (Switzerland). |
| 2 | The sensitivity results are available upon request. |
References
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. CoVaR. American Economic Review 106: 1705–41. [Google Scholar] [CrossRef]
- Alter, Adrian, and Yves S. Schüler. 2012. Credit spread interdependencies of European states and banks during the financial crisis. Journal of Banking & Finance 36: 3444–68. [Google Scholar]
- Bae, Kee-Hong, and G. Andrew Karolyi. 1994. Good news, bad news and international spillovers of stock return volatility between Japan and the US. Pacific-Basin Finance Journal 2: 405–38. [Google Scholar] [CrossRef]
- Baele, Lieven. 2005. Volatility Spillover Effects in European Equity Markets. Journal of Financial & Quantitative Analysis 40: 373–401. [Google Scholar]
- Balcilar, Mehmet, Ahmed H. Elsayed, and Shawkat Hammoudeh. 2023. Financial connectedness and risk transmission among MENA countries: Evidence from connectedness network and clustering analysis. Journal of International Financial Markets Institutions and Money 82: 101656. [Google Scholar] [CrossRef]
- Bessler, David A., and Jian Yang. 2003. The Structure of Interdependence in International Stock Markets. Journal of International Money and Finance 22: 261–87. [Google Scholar] [CrossRef]
- Bhargava, Vivek, Akash Dania, and Davinder Kumar Malhotra. 2012. Industry effects and volatility transmission in portfolio diversification. Journal of Asset Management 13: 22–33. [Google Scholar] [CrossRef]
- Bu, Lin, Xuejie Wang, and Zhiqiang Liu. 2020. Research on the Systemic Risk Transmission Network in Global Stock Markets. International Financial Research 395: 87–96. [Google Scholar]
- Chatziantoniou, Ioannis, David Gabauer, and Alexis Stenfors. 2021. Interest rate swaps and the transmission mechanism of monetary policy: A quantile connectedness approach. Economics Letters 204: 109891. [Google Scholar] [CrossRef]
- Chishti, Muhammad Zubair, Avik Sinha, Umer Zaman, and Umer Shahzad. 2023. Exploring the dynamic connectedness among energy transition and its drivers: Understanding the moderating role of global geopolitical risk. Energy Economics 119: 106570. [Google Scholar] [CrossRef]
- Chowdhury, Emon Kalyan, Iffat Ishrat Khan, and Bablu Kumar Dhar. 2022. Catastrophic impact of Covid-19 on the global stock markets and economic activities. Business and Society Review 127: 437–60. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring Financial Asset Return and Volatility Spillovers, with Application to Global Equity Markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to Give than to Receive: Predictive Directional Measurement of Volatility Spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yılmaz. 2014. On the Network Topology of Variance Decompositions: Measuring the Connectedness of Financial Firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No Contagion, Only Interdependence: Measuring Stock Market Comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Gamba-Santamaria, Santiago, Jose Eduardo Gomez-Gonzalez, Jorge Luis Hurtado-Guarin, and Luis Fernando Melo-Velandia. 2017. Stock market volatility spillovers: Evidence for Latin America. Finance Research Letters 20: 207–16. [Google Scholar] [CrossRef]
- Hamao, Yasushi, Ronald W. Masulis, and Victor Ng. 1990. Correlations in Price Changes and Volatility across International Stock Markets. The Review of Financial Studies 3: 281–307. [Google Scholar] [CrossRef]
- Hassan, Sherif M., and John M. Riveros Gavilanes. 2021. First to react is the last to forgive: Evidence from the stock market impact of COVID 19. Journal of Risk and Financial Management 14: 26. [Google Scholar] [CrossRef]
- Kanas, Angelos. 1998. Volatility Spillovers Across Equity Markets: European Evidence. Applied Financial Economics 8: 245–56. [Google Scholar] [CrossRef]
- King, Mervyn A., and Sushil Wadhwani. 1990. Transmission of Volatility between Stock Markets. Review of Financial Studies 3: 5–33. [Google Scholar] [CrossRef]
- Li, Hongquan, Yongmiao Hong, and Shouyang Wang. 2011. Research on the Interactive Relationship between China’s A-Share Market and the U.S. Stock Market, Hong Kong Stock Market: Based on the Perspective of Information Overflow. Economic Research Journal 46: 15–25. [Google Scholar]
- Liang, Qi, Zheng Li, and Xiangchao Hao. 2015. Research on the Internationalization of the Chinese Stock Market: A Perspective Based on Information Spillover. Economic Research Journal 50: 150–64. [Google Scholar]
- Liu, Xiaoxing, Bin Duan, and Fuzuo Xie. 2011. Research on Risk Spillover Effects in the Stock Market: An Analysis Based on the EVT-Copula-CoVa Model. World Economy 399: 145–59. [Google Scholar]
- Miyakoshi, Tatsuyoshi. 2003. Spillovers of Stock Return Volatility to Asian Equity Markets from Japan and the US. Journal of International Financial Markets Institutions & Money 13: 383–99. [Google Scholar]
- Nyakurukwa, Kingstone, and Yudhvir Seetharam. 2023. Quantile and asymmetric return connectedness among BRICS stock markets. The Journal of Economic Asymmetries 27: e00303. [Google Scholar] [CrossRef]
- Shahzad, Umer, Mahdi Ghaemi Asl, and Marco Tedeschi. 2023. Is there any market state-dependent contribution from Blockchain-enabled solutions to ESG investments? Evidence from conventional and Islamic ESG stocks. International Review of Economics & Finance 86: 139–54. [Google Scholar]
- Sun, Yanan, Caixia Xiao, and Huajun Liu. 2017. The International Position of China’s Stock Market in the Post-Financial Crisis Era—A Network Analysis of Stock Market Linkages Based on a Nonlinear Perspective. Southern Economy 333: 1–21. [Google Scholar]
- Thangamuthu, Mohanasundaram, Suneel Maheshwari, and Deepak Raghava Naik. 2022. Volatility spillover effects during pre-and-post COVID-19 outbreak on Indian market from the USA, China, Japan, Germany, and Australia. Journal of Risk and Financial Management 15: 378. [Google Scholar] [CrossRef]
- Zeng, Yufeng, Huwei Wen, and Xuebin Chen. 2017. Stock Market Interconnectedness, Tail Risk Contagion, and Systemically Important Markets—An Analysis Based on Multivariate Quantile Regression Model. International Financial Research 365: 86–96. [Google Scholar]
- Zhang, Bing, Zhizhen Fan, and Xindan Li. 2010. A Study on the Linkage of the Chinese and American Stock Markets. Economic Research Journal 45: 141–51. [Google Scholar]
- Zheng, Tingguo, and Tangyong Liu. 2018. Analysis of Stock Market Volatility Spillover Effects and Their Influencing Factors. Economic Research (Quarterly) 17: 669–92. [Google Scholar]
- Zhou, Xiangyi, Weijin Zhang, and Jie Zhang. 2012. Volatility Spillovers between the Chinese and World Equity Markets. Pacific Basin Finance Journal 20: 247–70. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).