Predicting Healthcare Mutual Fund Performance Using Deep Learning and Linear Regression
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
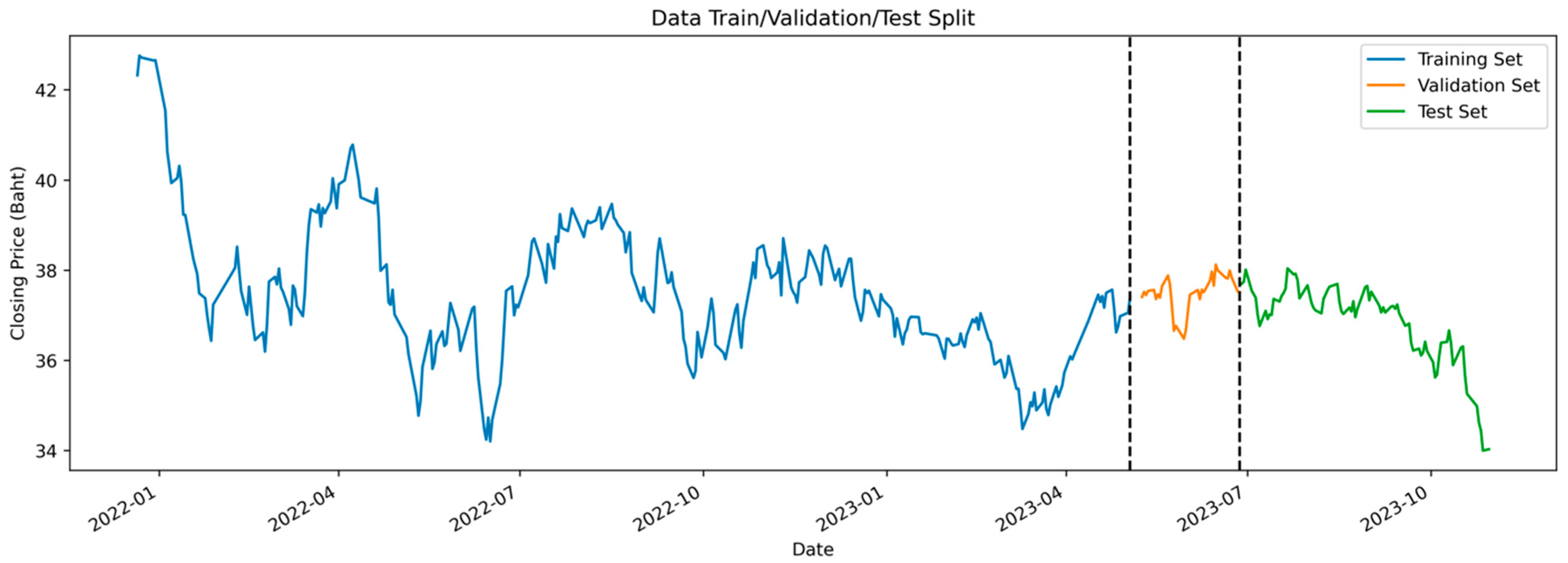
3.1. Data Collection and Descriptive Statistics
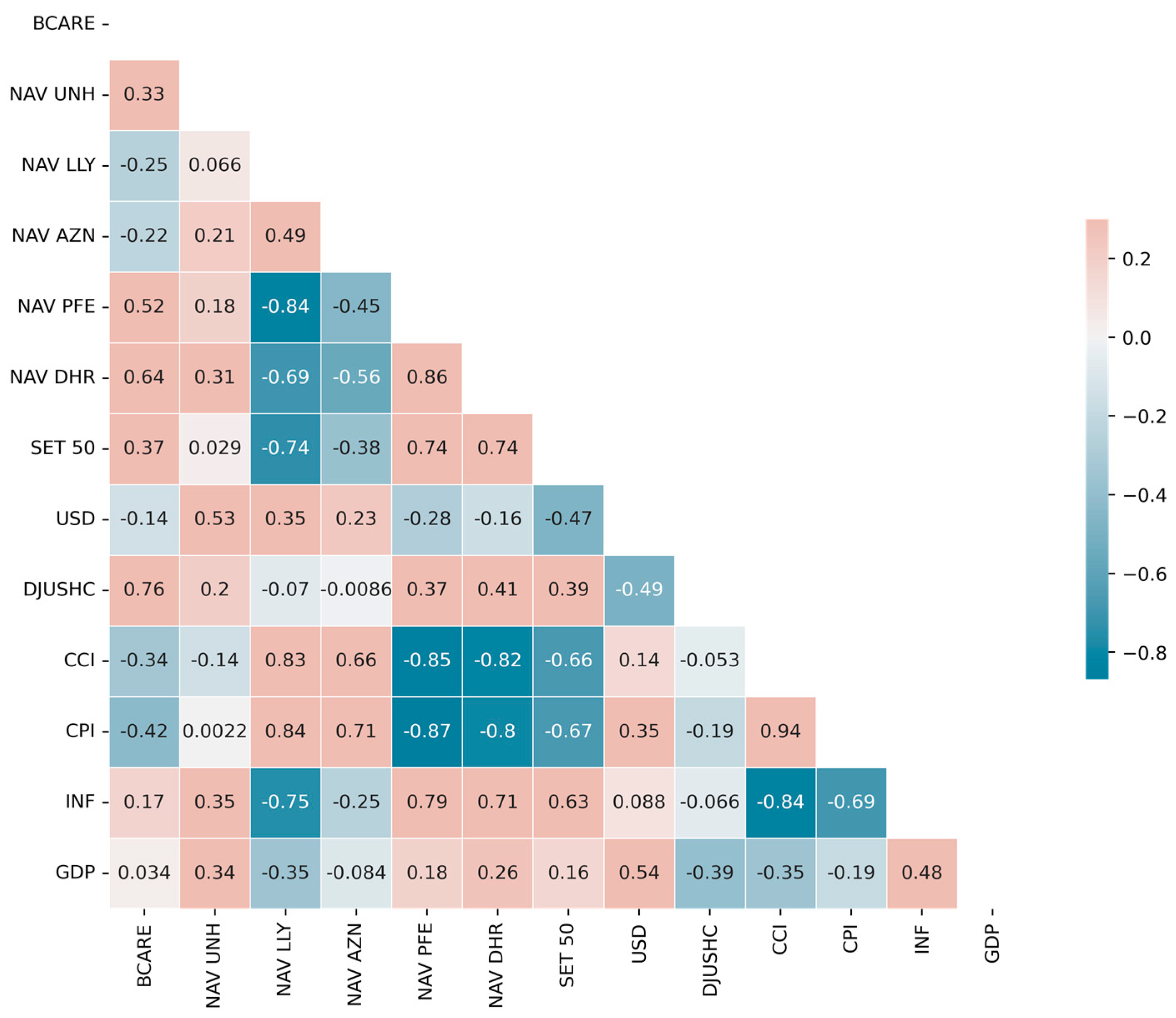
3.2. Principal Component Analysis
3.3. Multiple Linear Regression
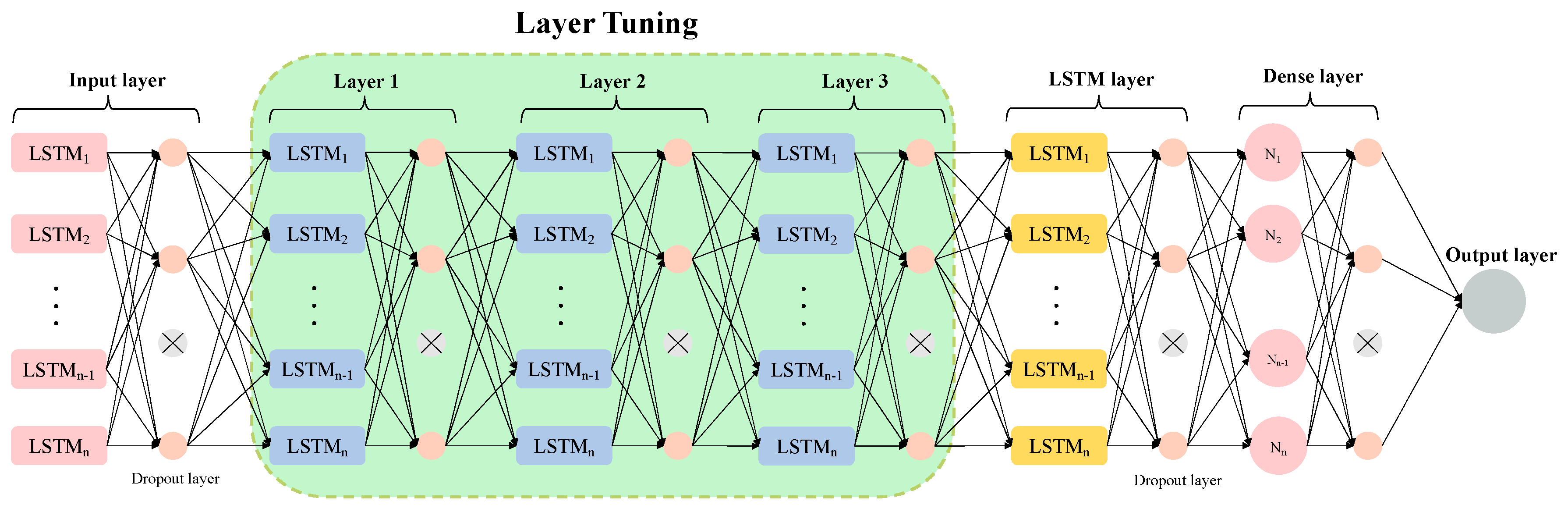
3.4. Long Short-Term Memory
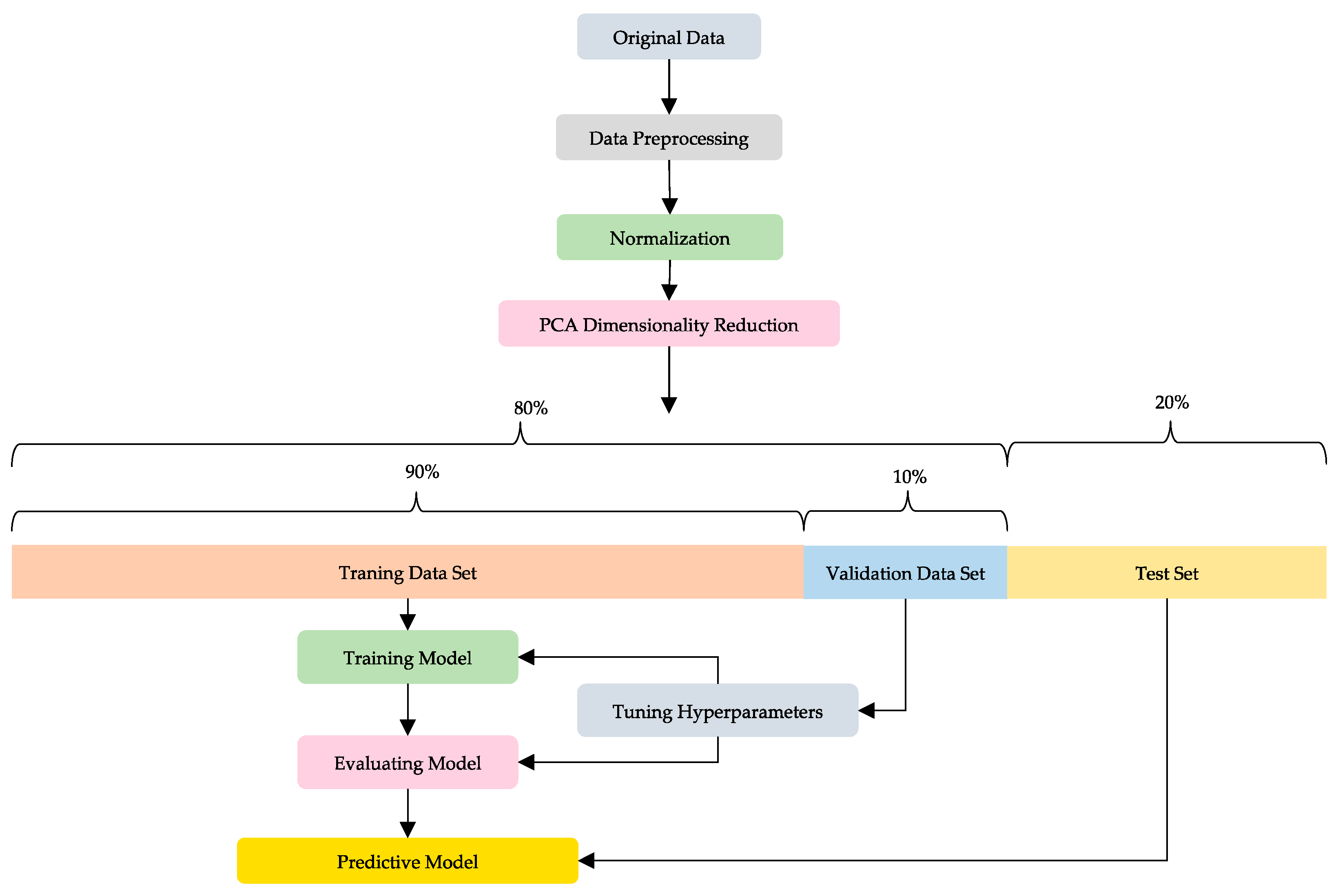
3.5. Data Preprocessing
3.5.1. Normalization
3.5.2. Standardization
3.6. Performance Metrics
3.7. Diebold–Mariano Test
4. Results and Discussion
4.1. Dimensionality Reduction
4.2. MLR Prediction Results
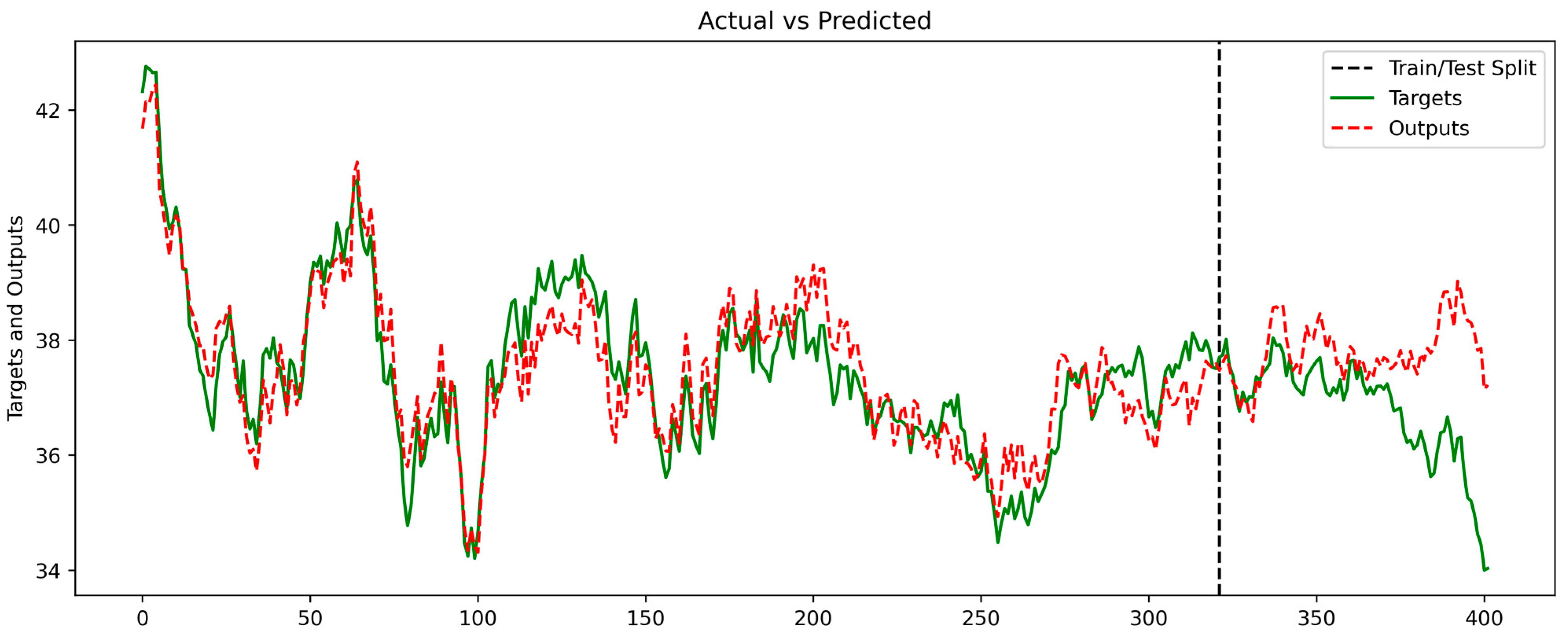
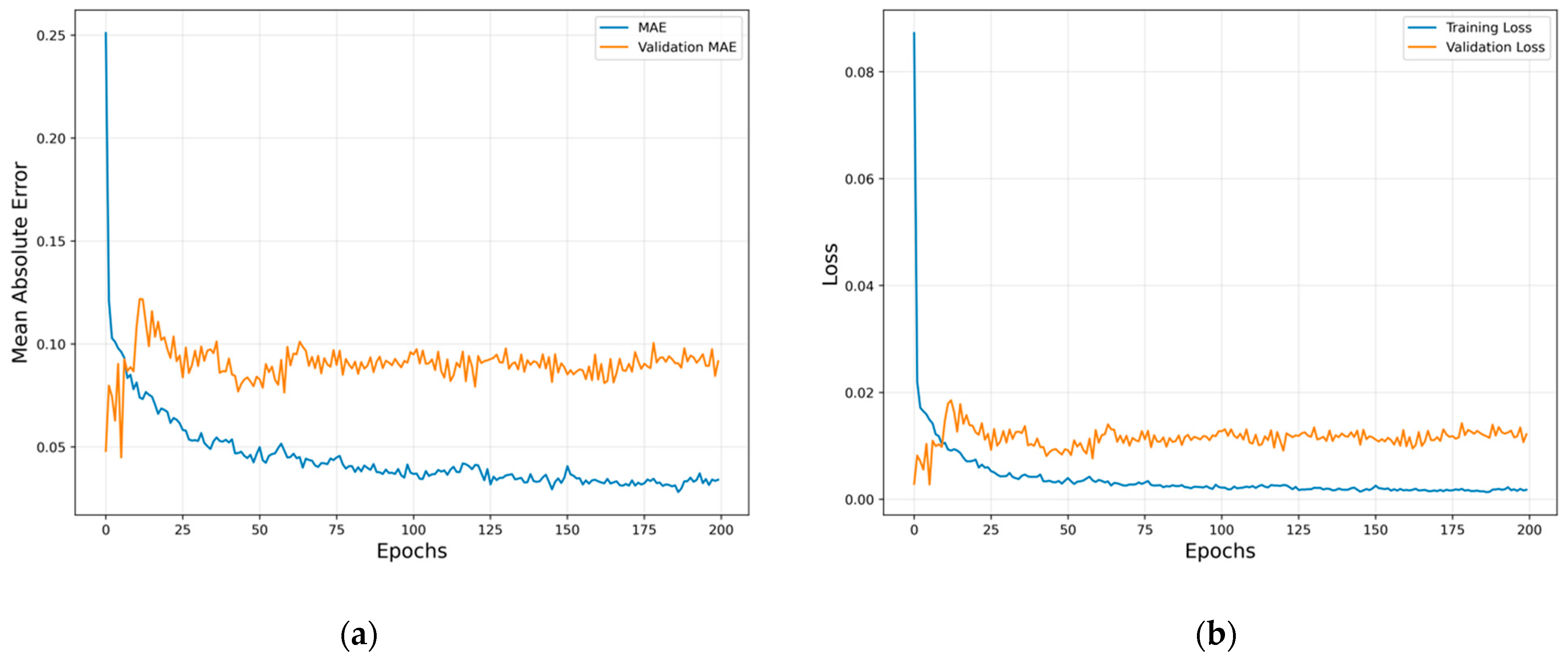
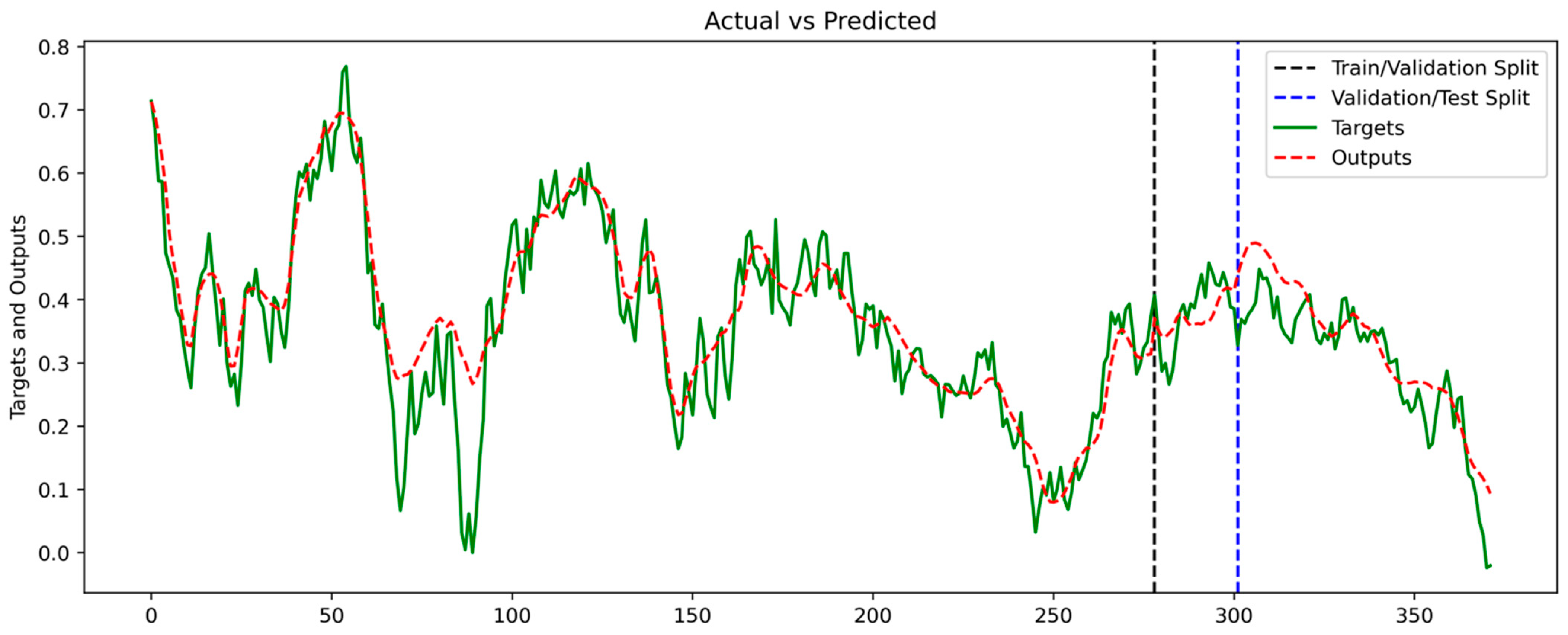
4.3. LSTM Prediction Results
4.4. Diebold–Mariano Test
5. Conclusions and Future Work
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, Daiyaan, Ronhit Neema, Nishant Viswanadha, and Ramani Selvanambi. 2022. Analysis and Prediction of Healthcare Sector Stock Price Using Machine Learning Techniques: Healthcare Stock Analysis. International Journal of Information System Modeling and Design (IJISMD) 13: 1–15. [Google Scholar] [CrossRef]
- Alnabulsi, Khalil, Emira Kozarević, and Abdelaziz Hakimi. 2023. Non-Performing Loans and Net Interest Margin in the MENA Region: Linear and Non-Linear Analyses. International Journal of Financial Studies 11: 64. [Google Scholar] [CrossRef]
- Alzubi, Jafar, Anand Nayyar, and Akshi Kumar. 2018. Machine learning from theory to algorithms: An overview. Journal of Physics: Conference Series 1142: 012012. [Google Scholar] [CrossRef]
- Anzanello, Michel Jose, and Flavio Sanson Fogliatto. 2011. Learning curve models and applications: Literature review and research directions. International Journal of Industrial Ergonomics 41: 573–83. [Google Scholar] [CrossRef]
- Banegas, Ayelen, Gabriel Montes-Rojas, and Lucas Siga. 2022. The effects of US monetary policy shocks on mutual fund investing. Journal of International Money and Finance 123: 102676. [Google Scholar] [CrossRef]
- Berry, William Dale, and Stanley Feldman. 1985. Multiple Regression in Practice. Newcastle upon Tyne: Sage. [Google Scholar]
- Bolaman, Özge, and Pınar EVRİM. 2014. Effect of investor sentiment on stock markets. Finansal Araştırmalar ve Çalışmalar Dergisi 6: 51–64. [Google Scholar] [CrossRef][Green Version]
- Bolboacă, Roland, and Piroska Haller. 2023. Performance Analysis of Long Short-Term Memory Predictive Neural Networks on Time Series Data. Mathematics 11: 1432. [Google Scholar] [CrossRef]
- Brogaard, Jonathan, and Abalfazl Zareei. 2023. Machine learning and the stock market. Journal of Financial and Quantitative Analysis 58: 1431–72. [Google Scholar] [CrossRef]
- Chatterjee, Ananda, Hrisav Bhowmick, and Jaydip Sen. 2021. Stock price prediction using time series, econometric, machine learning, and deep learning models. Paper presented at the 2021 IEEE Mysore Sub Section International Conference (MysuruCon), Hassan, India, October 24–25. [Google Scholar]
- Cheng, Leonardo, and Kartika Dewi. 2020. The effects of inflation, risk, and money supply on mutual funds performance. Journal of Applied Finance and Accounting 7: 29–34. [Google Scholar] [CrossRef]
- Chimmula, Vinay Kumar Reddy, and Lei Zhang. 2020. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos, Solitons & Fractals 135: 109864. [Google Scholar]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business and Economic Statistics 13: 253–63. [Google Scholar]
- Dillender, Marcus, Andrew Friedson, Cong Gian, and Kosali Simon. 2021. Is healthcare employment resilient and “recession proof”? INQUIRY: The Journal of Health Care Organization, Provision, and Financing 58: 00469580211060260. [Google Scholar]
- Ersin, Özgür Ömer, and Melike Bildirici. 2023. Financial Volatility Modeling with the GARCH-MIDAS-LSTM Approach: The Effects of Economic Expectations, Geopolitical Risks and Industrial Production during COVID-19. Mathematics 11: 1785. [Google Scholar] [CrossRef]
- Gu, Shihao, Bryan Kelly, and Dacheng Xiu. 2020. Empirical asset pricing via machine learning. The Review of Financial Studies 33: 2223–73. [Google Scholar] [CrossRef]
- Gülmez, Burak. 2023. Stock price prediction with optimized deep LSTM network with artificial rabbits optimization algorithm. Expert Systems with Applications 227: 120346. [Google Scholar] [CrossRef]
- Gyamfi Gyimah, Adjei, Bismark Addai, and George Kwasi Asamoah. 2021. Macroeconomic determinants of mutual funds performance in Ghana. Cogent Economics & Finance 9: 1913876. [Google Scholar]
- Heshmaty, Behrooz, and Abraham Kandel. 1985. Fuzzy linear regression and its applications to forecasting in uncertain environment. Fuzzy Sets and Systems 15: 159–91. [Google Scholar] [CrossRef]
- Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. Long short-term memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef] [PubMed]
- Janiesch, Christian, Patrick Zschech, and Kai Heinrich. 2021. Machine learning and deep learning. Electronic Markets 31: 685–95. [Google Scholar] [CrossRef]
- Jariyapan, Prapatchon, Jittima Singvejsakul, and Chukiat Chaiboonsri. 2022. A Machine Learning Model for Healthcare Stocks Forecasting in the US Stock Market during COVID-19 Period. Journal of Physics: Conference Series 2287: 012018. [Google Scholar] [CrossRef]
- Jasra, Javed Mahmood, Rauf I Azam, and Muhammad Asif Khan. 2012. Impact of macroeconomic variables on stock prices: Industry level analysis. Actual Problems of Economics 134: 403–12. [Google Scholar]
- Jolliffe, Ian T., and Jorge Cadima. 2016. Principal component analysis: A review and recent developments. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 374: 20150202. [Google Scholar] [CrossRef]
- Kang, Yushan, Jian Xing, and Shanhui Zhao. 2022. Influencing Factors of Investment for Companies. Paper presented at the 2022 7th International Conference on Financial Innovation and Economic Development (ICFIED 2022), Harbin, China, January 21–23. [Google Scholar]
- Kittichotsatsawat, Yotsaphat, Nakorn Tippayawong, and Korrakot Yaibuathet Tippayawong. 2022. Prediction of arabica coffee production using artificial neural network and multiple linear regression techniques. Scientific Reports 12: 14488. [Google Scholar] [CrossRef]
- Kumar, P. Rajendra, and E. Bala Krishna Manash. 2019. Deep learning: A branch of machine learning. Journal of Physics: Conference Series 1228: 012045. [Google Scholar]
- Li, Zheming. 2020. Economic Policy Uncertainty and Mutual Fund’s Risk Adjusting Behavior in China. Modern Economy 11: 609–19. [Google Scholar] [CrossRef]
- Lin, Eric C. 2018. The effect of Dow Jones industrial average index component changes on stock returns and trading volumes. The International Journal of Business and Finance Research 12: 81–92. [Google Scholar]
- Mokhlis, Nur Hanis Mohd, Nur Anira Ahmad Burhan, Nur Fatin Ainsyah Roeslan, Siti Nur Aishah Zainal Moin, and Ummu Aiman Mohd Nur. 2021. Forecasting healthcare stock price using arima-garch model and its value at risk. International Journal of Business and Economy 3: 127–42. [Google Scholar]
- Ouyang, Qi, Yongbo Lv, Jihui Ma, and Jing Li. 2020. An LSTM-based method considering history and real-time data for passenger flow prediction. Applied Sciences 10: 3788. [Google Scholar] [CrossRef]
- Panigrahi, Ashok, Pradhum Karwa, and Pushkin Joshi. 2019. Impact of macroeconomic variables on the performance of mutual funds: A selective study. Journal of Economic Policy & Research October 15: 1–13. [Google Scholar]
- Qureshi, Fiza, Ali M Kutan, Izlin Ismail, and Chan Sok Gee. 2017. Mutual funds and stock market volatility: An empirical analysis of Asian emerging markets. Emerging Markets Review 31: 176–92. [Google Scholar] [CrossRef]
- Sarker, Iqbal H. 2021. Deep Learning: A Comprehensive Overview on Techniques, Taxonomy, Applications and Research Directions. SN Computer Science 2: 420. [Google Scholar] [CrossRef] [PubMed]
- Sen, Jaydip, Sidra Mehtab, Abhishek Dutta, and Saikat Mondal. 2021. Precise stock price prediction for optimized portfolio design using an LSTM model. Paper presented at the 2021 19th OITS International Conference on Information Technology (OCIT), Bhubaneswar, India, December 16–18. [Google Scholar]
- Shah, Jaimin, Darsh Vaidya, and Manan Shah. 2022. A comprehensive review on multiple hybrid deep learning approaches for stock prediction. Intelligent Systems with Applications 16: 200111. [Google Scholar] [CrossRef]
- Slinker, Bryan K., and Stanton A Glantz. 1988. Multiple linear regression is a useful alternative to traditional analyses of variance. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology 255: R353–R367. [Google Scholar] [CrossRef] [PubMed]
- Sonkavde, Gaurang, Deepak Sudhakar Dharrao, Anupkumar M Bongale, Sarika T Deokate, Deepak Doreswamy, and Subraya Krishna Bhat. 2023. Forecasting stock market prices using machine learning and deep learning models: A systematic review, performance analysis and discussion of implications. International Journal of Financial Studies 11: 94. [Google Scholar] [CrossRef]
- Subhani, Muhammad Imtiaz, Amber Osman, and Ameet Gul. 2010. Relationship between Consumer Price Index (CPI) and KSE-100 Index Trading Volume in Pakistan and Finding the Endogeneity in the Involved Data. MPRA Paper 26375. Available online: https://mpra.ub.uni-muenchen.de/29712/ (accessed on 1 November 2023).
- Van Houdt, Greg, Carlos Mosquera, and Gonzalo Nápoles. 2020. A review on the long short-term memory model. Artificial Intelligence Review 53: 5929–55. [Google Scholar] [CrossRef]
- Wanaset, Apinya. 2018. The relationship between capital market and economic growth in Thailand. Journal of Economics and Management Strategy in Thailand 5: 25–38. [Google Scholar]
- Wong, Hock Tsen. 2022. The impact of real exchange rates on real stock prices. Journal of Economics, Finance and Administrative Science 27: 262–76. [Google Scholar] [CrossRef]
- Zhou, Xianzheng, Hui Zhou, and Huaigang Long. 2023. Forecasting the equity premium: Do deep neural network models work? Modern Finance 1: 1–11. [Google Scholar] [CrossRef]
| Factors | Mean | Maximum | Minimum | SD | Description of Each Factor |
|---|---|---|---|---|---|
| BCARE (THB) | 37.340 | 42.762 | 34.002 | 1.373 | The historical data for the fund’s prices, denoted as the variable ‘y’ for prediction by the model, are available on a daily basis and are stated in Thai Baht. |
| UNH (USD) | 500.471 | 555.15 | 447.75 | 24.201 | The historical stock price data for UnitedHealth Group Incorporated, which holds the top-ranking position within the fund’s portfolio, are provided on a daily basis and are denominated in US dollars. |
| LLY (USD) | 369.611 | 616.64 | 234.69 | 96.155 | The historical stock price data for Eli Lilly and Company, the asset ranked second within the fund’s portfolio, are provided on a daily basis and are denominated in US dollars. |
| AZN (USD) | 10,593.664 | 12294 | 8282 | 905.072 | The historical stock price data for AstraZeneca PLC, the asset ranked third within the fund’s portfolio, are available on a daily basis and are denominated in US dollars. |
| PFE (USD) | 44.538 | 59.55 | 30.11 | 6.968 | The historical stock price data for Pfizer Inc., which is the fourth-ranked asset held within the fund, are provided on a daily basis and are denominated in US dollars. |
| DHR (USD) | 247.868 | 328.47 | 185.1 | 30.178 | The historical stock price data for Danaher Corporation, the asset ranked fifth within the fund’s holdings, are available on a daily basis and are denominated in US dollars. |
| SET50 Index | 965.682 | 1035.94 | 846.89 | 35.164 | Index data referencing the top 50 highest-valued Thai stocks in the securities market, computed as a daily index. |
| US Dollars Exchange Rate (THB) | 34.887 | 38.24 | 32.1 | 1.377 | Daily exchange rate records detailing the conversion rate from US dollars to Thai Baht. |
| Dow Jones U.S. Health Care Index | 1398.889 | 1540.53 | 1271.73 | 45.249 | A market capitalization-weighted index that tracks the performance of the healthcare sector in the United States, presented on a daily basis. |
| Consumer Confidence Index | 49.879 | 56.6 | 43.8 | 4.391 | An economic indicator gauging consumer confidence and overall economic sentiment, including financial conditions. These data are reported on a monthly frequency. |
| Consumer Price Index for Health Care and Personal Care Services | 102.345 | 103.6 | 100.71 | 0.948 | The retail price index, which measures alterations in the prices of goods and services in equivalent quantities over a specified period, relative to the prices of the same commodities in the base year. This index specifically focuses on changes in the prices of medical treatment and services within the country. Monthly data are provided. |
| Inflation Rate | 3.915 | 7.86 | −0.31 | 2.691 | The consumer price index, which quantifies the percentage increase in the general price level of goods and services within an economy over a specific period, reflecting the erosion of purchasing power of a currency. Monthly data are available. |
| Gross Domestic Product (GDP) | 2.359 | 4.5 | 1.4 | 0.984 | Gross Domestic Product (GDP), denoting the total monetary value of all finished goods and services produced within a nation’s borders during a particular timeframe. This dataset is presented on a quarterly basis. |
| Principal Component | Explained Variance | Explained Variance Ratio | Cumulative Explained Variance Ratio |
|---|---|---|---|
| 1 | 6.27746 | 0.52182 | 0.52182 |
| 2 | 2.37639 | 0.19754 | 0.71936 |
| 3 | 1.46909 | 0.12211 | 0.84147 |
| 4 | 0.76288 | 0.06341 | 0.90489 |
| 5 | 0.44540 | 0.03702 | 0.94191 |
| 6 | 0.24519 | 0.02038 | 0.96230 |
| 7 | 0.17680 | 0.01469 | 0.97699 |
| 8 | 0.09612 | 0.00799 | 0.98498 |
| 9 | 0.07860 | 0.00653 | 0.99152 |
| 10 | 0.05038 | 0.00418 | 0.99570 |
| 11 | 0.03661 | 0.00304 | 0.99875 |
| 12 | 0.01501 | 0.00124 | 1.00000 |
| Factors | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 |
|---|---|---|---|---|---|---|
| UNH | −0.05395 | 0.39391 | −0.58507 | 0.2138 | 0.11052 | −0.0905 |
| LLY | 0.35898 | 0.01049 | −0.17060 | 0.31135 | 0.02323 | −0.33053 |
| AZN | 0.24575 | 0.11064 | −0.36409 | −0.67845 | 0.22114 | 0.18960 |
| PFE | −0.37475 | −0.02941 | −0.13328 | −0.06051 | 0.23523 | 0.27940 |
| DHR | −0.36112 | 0.02441 | −0.20098 | 0.22107 | −0.13946 | −0.11840 |
| SET50 | −0.32792 | −0.13587 | −0.11733 | −0.32707 | −0.38088 | −0.65376 |
| USD | 0.11597 | 0.58036 | −0.03926 | 0.25511 | 0.048396 | −0.05818 |
| DJUSHC | −0.10143 | −0.35613 | −0.60917 | 0.13878 | −0.27575 | 0.31157 |
| CCI Index | 0.37847 | −0.09041 | −0.11985 | −0.13022 | −0.20164 | 0.01365 |
| CPI Index | 0.37481 | 0.06522 | −0.13017 | −0.16696 | −0.16590 | −0.24640 |
| Inflation Rate | −0.32748 | 0.26784 | −0.03579 | −0.28068 | 0.36433 | −0.2438 |
| GDP Growth | −0.12131 | 0.51451 | 0.13735 | −0.17183 | −0.6627 | 0.32604 |
| Training Set | Testing Set | ||
|---|---|---|---|
| RMSE Train | MSE Train | RMSE Test | MSE Test |
| 0.5585 | 0.3119 | 1.4158 | 2.0046 |
| Window Size | LSTM Layer 1 | LSTM Layer 2 | LSTM Layer 3 | Number of Neurons | MSE Train | MSE Validation |
|---|---|---|---|---|---|---|
| 10 days | 1 | 1 | 1 | 256 | 0.00301 | 0.00942 |
| 1 | 0 | 1 | 256 | 0.00361 | 0.01004 | |
| 1 | 1 | 0 | 256 | 0.00619 | 0.01089 | |
| 1 | 1 | 0 | 32 | 0.01047 | 0.01149 | |
| 1 | 1 | 1 | 64 | 0.00383 | 0.01175 | |
| 0 | 1 | 1 | 64 | 0.00379 | 0.01199 | |
| 0 | 1 | 1 | 256 | 0.00534 | 0.01210 | |
| 0 | 0 | 1 | 256 | 0.00372 | 0.01246 | |
| 0 | 1 | 0 | 2256 | 0.00310 | 0.01275 | |
| 0 | 1 | 1 | 32 | 0.00459 | 0.01426 | |
| 12 days | 1 | 1 | 1 | 128 | 0.00347 | 0.00954 |
| 0 | 1 | 1 | 256 | 0.00370 | 0.01039 | |
| 1 | 1 | 0 | 256 | 0.00306 | 0.01288 | |
| 1 | 1 | 1 | 256 | 0.00302 | 0.01298 | |
| 1 | 0 | 1 | 256 | 0.00380 | 0.01328 | |
| 1 | 1 | 1 | 32 | 0.00502 | 0.01363 | |
| 1 | 1 | 1 | 64 | 0.00369 | 0.01440 | |
| 0 | 0 | 1 | 256 | 0.00613 | 0.01512 | |
| 0 | 1 | 0 | 64 | 0.00443 | 0.01523 | |
| 1 | 0 | 0 | 128 | 0.00537 | 0.01579 | |
| 15 days | 1 | 1 | 1 | 128 | 0.00409 | 0.01394 |
| 1 | 1 | 1 | 256 | 0.00452 | 0.01467 | |
| 1 | 1 | 1 | 64 | 0.00353 | 0.01623 | |
| 1 | 1 | 0 | 256 | 0.00380 | 0.01684 | |
| 1 | 0 | 1 | 256 | 0.00470 | 0.01734 | |
| 0 | 0 | 1 | 256 | 0.00375 | 0.01774 | |
| 1 | 1 | 0 | 32 | 0.00428 | 0.01803 | |
| 0 | 0 | 0 | 256 | 0.00421 | 0.01954 | |
| 0 | 1 | 1 | 64 | 0.00315 | 0.01978 | |
| 1 | 1 | 1 | 32 | 0.00421 | 0.02021 | |
| 20 days | 1 | 1 | 1 | 256 | 0.00329 | 0.01175 |
| 1 | 1 | 0 | 256 | 0.00397 | 0.01207 | |
| 0 | 1 | 1 | 256 | 0.00322 | 0.01450 | |
| 1 | 1 | 1 | 128 | 0.00293 | 0.01451 | |
| 1 | 0 | 1 | 256 | 0.00445 | 0.01461 | |
| 1 | 1 | 1 | 64 | 0.00338 | 0.01552 | |
| 0 | 1 | 0 | 256 | 0.00517 | 0.01670 | |
| 1 | 0 | 0 | 256 | 0.00516 | 0.01721 | |
| 0 | 0 | 1 | 256 | 0.00465 | 0.01816 | |
| 0 | 0 | 0 | 256 | 0.00416 | 0.01876 |
| Training Set | Validation Set | Testing Set | |||
|---|---|---|---|---|---|
| RMSE Train | MSE Train | RMSE Validation | MSE Validation | RMSE Test | MSE Test |
| 0.0617 | 0.0038 | 0.0458 | 0.0021 | 0.0547 | 0.0030 |
| Diebold–Mariano Test Statistic | p-Value | |
|---|---|---|
| DM test based on MLR and LSTM | −2.2334 | 0.02867 |
| References | Subject | Description of Data | Model | RMSE | Accuracy |
|---|---|---|---|---|---|
| Ahmed et al. (2022) | The paper incorporates various machine learning algorithms, including SVM, reinforcement learning, ANN, and RNN, to forecast stock prices within the healthcare sector. | The dataset encompasses healthcare stock price data spanning the years 2016 to 2019, comprising fields such as opening and closing prices, alongside features such as price volatility and momentum. | Linear Regression | 0.080 | - |
| RNN with GRU | 0.051 | - | |||
| SVM | 0.079 | - | |||
| Random Forest | 0.065 | - | |||
| Jariyapan et al. (2022) | Supervised learning algorithms such as Linear Discriminant Analysis (LDA), k-Nearest Neighbors (kNN), and Support Vector Machine (SVM) are employed to explore the cycle regimes of healthcare stocks over the next five years. | Monthly stock price data from 2015 to 2020 for five healthcare sector stock price indexes, specifically sourced from the Nasdaq index, were utilized in the paper. | LDA | - | 0.8138 |
| k-NN | - | 0.5223 | |||
| SVM | - | 0.7847 | |||
| Chatterjee et al. (2021) | Six models are developed, integrating time series, econometric, and learning-based techniques, specifically tailored for stock price prediction across three major sectors, with a particular focus on the healthcare sector. | Data pertaining to SUN Pharmaceuticals, covering the period from January 2004 to December 2019, were employed in the study. | Holt–Winters | 0.056 | - |
| ARIMA | 0.020 | - | |||
| Random Forest | 0.009 | - | |||
| MARS | 0.017 | - | |||
| RNN | 0.0209 | - | |||
| LSTM | 0.022 | - | |||
| Mokhlis et al. (2021) | Time series models such as ARIMA, GARCH, and TGARCH are utilized to predict the IHH stock price, and their performances are evaluated using RMSE. | The paper leverages daily data of the IHH stock price to forecast its future trends and volatility, encompassing the period from September 2015 to September 2021. | ARIMA (4,1,5) -GARCH (1,1) | 0.02289412 | - |
| ARIMA (4,1,5) -TGARCH (1,1) | 0.02289852 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boonprasope, A.; Tippayawong, K.Y. Predicting Healthcare Mutual Fund Performance Using Deep Learning and Linear Regression. Int. J. Financial Stud. 2024, 12, 23. https://doi.org/10.3390/ijfs12010023
Boonprasope A, Tippayawong KY. Predicting Healthcare Mutual Fund Performance Using Deep Learning and Linear Regression. International Journal of Financial Studies. 2024; 12(1):23. https://doi.org/10.3390/ijfs12010023
Chicago/Turabian StyleBoonprasope, Anuwat, and Korrakot Yaibuathet Tippayawong. 2024. "Predicting Healthcare Mutual Fund Performance Using Deep Learning and Linear Regression" International Journal of Financial Studies 12, no. 1: 23. https://doi.org/10.3390/ijfs12010023
APA StyleBoonprasope, A., & Tippayawong, K. Y. (2024). Predicting Healthcare Mutual Fund Performance Using Deep Learning and Linear Regression. International Journal of Financial Studies, 12(1), 23. https://doi.org/10.3390/ijfs12010023






