Abstract
Economic disruptions can alter the likelihood of defaults on peer-to-peer loans, causing those impacted to adjust. The option to declare economic hardship and temporarily reduce the payment burden can provide some relief. When this occurs, the borrower’s financial qualifications have changed. The qualities instrumental in successfully securing the original loan terms must be reanalyzed to manage risk. This is a critical point in the life of the loan because the declaration of financial hardship can signal that the borrower’s ability to repay has diminished. We present a novel default detection scheme for borrowers experiencing an economic disruption based on the Two-Class Support Vector Machine, a data classification algorithm for supervised learning problems. The method utilizes data from actual loan records (15,355 loans from 2016 through 2020), specifically from borrowers who declared economic hardship. We provide a detailed description of the default detection process and present results that show defaults among borrowers experiencing financial hardship can be predicted accurately.
1. Introduction
Peer-to-peer loans aim to fill in the gaps for people where there may be financial remedies to problematic shortcomings. The alternative nature of the peer lending space, combined with its recent accessibility and popularity, has given us vast amounts of data that can be used to answer many questions. Economic data captured at the granularity of the individual has value and is one of the many benefits provided by the analysis of peer-to-peer data. Among many other borrower attributes commonly studied in other work, there is also less considered economic hardship data for those who have experienced disruptions during the life of their loan. While many other groups have studied and made contributions to repayment predictions, researching the economic hardship data points reported at an individual level seems uncommon. Economic disruption in an individual’s life has the potential to be an indication of a larger issue in the local economy. This larger issue is apparent when and if there is a situation that affects more than just that one individual. News of a large employer shuttering, a trend of population migration, an increase in the cost of living, a natural disaster, a public health emergency, and social unrest are a few examples of possible events that can cause an economic disruption (Yao and Liu 2023). When something along these lines occurs, the people affected can report economic disruption in their lives in multiple ways. One of the ways these individuals can report this is by declaring economic hardship with a creditor.
A borrower with a peer-to-peer loan experiencing an economic hardship can report this hardship through the lending platform by utilizing a special process. The borrower must apply for the hardship, reporting various attributes such as the hardship reason and approximate date. If successfully granted hardship status, relief such as short-term loan deferment or short-term interest-only payments will be applied to the borrower’s agreement of repayment. This creates an opportunity for meaningful research because other attributes become available when this occurs. Attributes such as the relief type, the duration of the hardship relief, and the reduced amount of payment during the hardship plan will be populated in the borrower’s record. One of the more interesting attributes is the relief status, which indicates if the plan was successfully completed. Relief status is important, as this could show the severity of the impact on the borrower’s situation. The data captured can be utilized for analysis of the economic disruption.
In times when economic disruption is common or expected, lending risks can be heightened. A process that aids the peer lender in dealing with the fallout occurring in existing loans could be beneficial to the peer-to-peer lending market. The disruption can cause an adverse chain reaction in peer-to-peer loans, such as early repayment, late payments, partial payments, or a complete failure to make any further payments. Disruptions in a few peer-to-peer loans have the potential to bubble up to more serious issues if not contained or detected beforehand. Many methods are used to track these disruptions, but peer-to-peer lending data allows for analyzing the alternative lending space in more of a “boots on the ground” nature. The data gives information at a granular individual economic level, which can be aggregated to visualize any disruptions that have occurred. Machine learning can be utilized to detect situations across various types of borrowers, specifically those who have experienced economic hardship. Economic hardship data could prove useful in the detection of smaller-scale problems with borrowers having similar attributes in specific geographic regions (Mueller et al. 2022).
There is not much published work using hardship data from peer-to-peer loans to analyze how economic disruptions play a role in that market. Research in this area can propel the peer lending space to a more reputable level by exposing insightful ways to deal with problematic situations that will inevitably occur. Examples of useful findings such as patterns in hardships by type, job sector, or credit level would help with risk management for peer lenders and could even be used as cautionary information for the general public (Yao and Liu 2023). Machine learning algorithms can also aid in accurately predicting defaults when these disruptions occur. These predictions could have the viability and usefulness to prevent greater losses that would occur by not knowing the probable outcome. This research could strengthen the adoption of the alternative lending market by providing a reliable method for identifying qualities in applicants that indicate a level of resilience to economic disruptions.
Peer-to-peer lending is still regarded as an alternative lending option that is gaining popularity. There is economic diversity in the types of borrowers that take peer-to-peer loans. This economic diversity can be utilized as an advantage in the data when disruptions occur because of the range of coverage in the makeup of borrower types. There is value in the ability to see how different borrowers in different industries and locations with various credit scores and income levels are impacted and respond to disruptions because future lending decisions can rely on this information. The peer lenders could decide to give more favorable terms to attract a certain type of borrower or could limit their exposure to less desirable profiles based on how similar peers performed in previous economic rifts (Fitzpatrick and Mues 2021).
Traditionally, lending decisions on applications were and are still based mainly on credit profiles and income. The credit profile, income, and other factors give a lender a decent picture of the applicant’s ability to repay. These attributes can be negatively impacted by an economic disruption. In severe cases, the applicant, who would later become the borrower, would not get the same repayment terms if they applied at a point of hardship. In a much more severe scenario, this borrower would not qualify for the loan due to a blemished credit profile or diminished income (Boiko Ferreira et al. 2017). Knowing that the borrower’s situation has changed, we can also assume that the ability to repay the loan has changed. In this scenario, the peer lender’s investment is now at an unanalyzed risk, and tools should be used to give the borrower some indication of the anticipated outcome. This can result in a peer lender tightening, relaxing, or deciding to stay consistent with the criteria future applicants must meet to align with their risk profile for investment. One advantage of peer-to-peer lending is that one peer’s investment criteria may not be the same as another, so there is a diverse footprint allowing for the possibility of a match (Liu et al. 2020).
The hardship process offers a set term where the borrower gets the opportunity to either make reduced payments or skip payments to get back on track financially. The terms of this period can be broken or completed based on how the borrower performs. If the terms are broken, this is captured in the data. Since the original loan terms still apply after the hardship period ends, the attributes capturing the status of the original loan are available to give an indication of the overall outcome of the loan. By having the detailed hardship information and the original loan information, decisions can be made utilizing historical data that supports these decisions with actual evidence. The common issue would remain the same: the return on investment is not guaranteed, and the borrower can still default. Peer lenders taking risks on applicants with attributes shown to be problematic during a disruption would need some incentive to make the investment worthwhile. An example of a problematic attribute could be the length of employment in an applicant’s profile. If the work is seasonal or in an inconsistent industry, a disruption could have a negative impact. There could also be positive impacts on income from disruption as well. One example of a positive impact would be a disruption causing hardship and requiring the borrower to change industries, resulting in better income and an increased ability to repay. Peer lenders must also be mindful enough to analyze an applicant’s income situation or utilize a method that will do this for them prior to deciding to lend. This is important because if the income is a moving target, the financial snapshot taken when applying will likely be different throughout the course of the loan term (Guo et al. 2015).
The decision-making capability of a peer lender can lean on the support of data-driven predictions from actual data when applying machine learning techniques to the data offered on these platforms. This enabler allows for different approaches compared with the traditional lending construct because the individual peer can use their own method to determine fit. There is already research on the prediction and decision-making capabilities of individual peer lenders with access to information on their potential borrowers before lending. The peer lender can benefit from consistent performance and a proven level of repeatable accuracy in the predictions a model achieves (Kriebel and Stitz 2021). The missing piece to much of the research work on peer-to-peer default prediction is the element of financial disruption, which should not be ignored. In this work, the prediction capability given a hardship from a disruption will be analyzed. This analysis can be used to establish a level of accuracy for a peer lender to make confident decisions with economic hardship in mind. Giving economic hardship more weight in the decision process is just one of the many alternative methods that should be explored in developing fintech arenas, such as the peer-to-peer lending space. Alternative data like the digital footprint and free-form text-based information provided by the applicant have been used in the analysis of loan applications, with noteworthy results (Kriebel and Stitz 2021) that expose some of the innovative approaches to lending decisions. Non-traditional methods such as these can aid in making the alternative lending space use an alternative lending process instead of relying on the same decision-making methods used in traditional lending. From work like this, a lender gains the ability to focus on certain types of applicants with attributes that show them to be resilient to economic disruptions, which could prove to be more beneficial in risk avoidance. Analysis of historical repayment performance during times of financial hardship in combination with proven machine learning models can give peer lenders the confidence to make decisions on funding requests.
The performance results from our work will contribute information to support either recommending or discouraging peer lenders from utilizing this method. The results of the experiment will provide a basis for individual peer lenders to determine if utilizing the Support Vector Machine algorithm is viable for detecting potential default among borrowers claiming hardship due to disruption. Confidence is important when identifying applications in times when disruption can occur. Alternative lending spaces like this exist to provide benefits to borrowers and lenders that are not achieved through the traditional space. These benefits become one-sided or cease to exist when loans are not approved and repaid successfully. An increase in the rate at which we identify promising loan applicants based on attributes that show resiliency to disruptions can encourage more peer lenders to participate in the space, possibly providing more opportunities. Through our work, we intend to provide answers to two research questions:
- (a)
- Which attributes show to have the greatest impact on default or repayment among borrowers with economic hardship?
- (b)
- Using these attributes, can machine learning algorithms such as the Support Vector Machine be used to predict defaults among borrowers with hardships?
Beyond this introduction, our paper is organized in the following manner: Section 2 contains topics related to our work in loan repayment prediction with a peer-to-peer lending focus. In Section 3, we walk through an explanation of the empirical study, including the sample data and data analysis. Included in the study is an explanation of the machine learning algorithm utilized in the experiment and the experiment results. In Section 4, we further the work with a discussion, including the practical implications and how the work applies to the problem. We conclude in Section 5, where the objectives are revisited and assessed based on the findings from our work.
2. Related Work
Repayment predictions in lending have been extensively studied in various research studies. The common model in the U.S. uses credit-based attributes to compile a score for determining the ability to repay (Berg et al. 2019). In an economically developed country like the United States or Canada, many lending organizations will use the borrowing history or credit report, which displays the borrower’s repayment history and score, as the basis for determining an individual’s tendency and ability to repay (Oh and Rosenkranz 2020). These previous financial interactions involve and require a lender that reports performance to any of the three major bureaus. Conventionally, predicting loan repayment via the credit report is the most widely used method today. Focusing on aspects of a borrower’s previous economic situation gives the lender a good indication of the type of borrower they may be analyzing if all things stay consistent in the borrower’s life. Kim and Cho provided a promising model built using a convolutional neural network that predicts repayment on peer-to-peer loans with 5-fold cross-validation (Kim and Cho 2019). In their model, they were able to automatically retrieve complex features more effectively than many other machine learning methods used for prediction (Kim and Cho 2019). In their work, they developed rules to apply to neural network algorithms using similar data to efficiently identify patterns. These patterns were ultimately used to point out potentially defaulting borrowers. An interesting part of their work was that none of the features were extracted in their analysis, which showed to be a benefit in the development of the many layers of the network. This is an alternative approach because there are many attributes that bloat the peer-to-peer lending dataset. Many models often remove redundant and unimpactful attributes for model efficiency (Kim and Cho 2019).
Machine learning is commonly used in credit analysis and repayment prediction. The work completed by Bhattacharya et al. provided a model developed to analyze competing risk hazards. In the work, default and repayment data were used in combination with Markov Chain Monte Carlo methods. This model used the duration of loans and similarly analyzed statistical differences in repayment and default probabilities. One notable difference in their work was the analysis of an outcome they named “prepayment” which was categorized as a competing risk to the lender. The model essentially made predictions of which outcome would be more likely to occur earliest for a borrower. One aspect of their results showed that the rate of default in relation to the debt-to-income ratio was identical to the rate of prepayment in relation to the occupancy attribute. Due to an imbalance in the outcomes resulting in a lower number of defaults observed, they experienced difficulty in estimating default times (Bhattacharya et al. 2018). This is a common problem in lending datasets because more loans result in repayment, as there are consequences to default that a borrower wants to avoid. In many cases, the number of defaults and successful repayments will be different since we are using data from a lender/source with specific qualifying criteria and a quality threshold for their borrower. Despite the imbalance, the total number of defaults across the entire population dataset serves as a baseline for a performance benchmark when filtering and analyzing specific groups.
In a work published by Lui et al., data analysis and machine learning techniques were utilized to discover relationships between the probability of default and the timing of default. The research, which made use of mixture models to show unidentified subpopulations, successfully predicted borrower default times. A mix of hierarchical and non-hierarchical models showed how useful the model can be for lenders to better understand borrower activity. The findings made a solid contribution by providing a method for time-based risk management markers for lenders (Liu et al. 2015). Their method utilized Markov Chain Monte Carlo without a variable selection phase, instead using mostly time-based variables with the prime interest rate to provide a useful system for effectively timing default.
Chen et al. have published peer-to-peer lending work focused on imbalanced datasets. The referenced work provided a very detailed analysis of dataset imbalance as a common problem among publicly available peer-to-peer lending datasets often published by prominent, reputable platforms. Their contribution showed how analyzing performance data after the funding decision has the potential to skew the dataset with only the candidates that meet the desired criteria. This skewing excludes applicants, which denies the model all data for balanced training (Chen et al. 2021). Removing the applicants deemed unfit leaves a hole in the data. While lenders are seeking funding only when presented with a promising candidate, the data can become imbalanced if the same criteria are used for each applicant. The dataset can also become imbalanced when proximity or location is taken into account. In the case of a peer-to-peer lending platform restricted to a specific country, state, city, or town, there could be an underrepresentation of certain groups with distinct qualities. On the other hand, there could be a strong representation among other groups just based on the location in which the boundaries are set. Relationships among borrowers and lenders could also exist when location restrictions are involved. In a situation where a lender-borrower relationship exists among the majority of the observations, a dataset imbalance is possible due to the individual’s knowledge of their counterpart (Galema 2020). On many peer-to-peer lending platforms, a grade is given to a candidate to provide a quality ranking based on a proprietary recommendation method. Using this method can lead to a dataset imbalance as more loans with similar attributes are approved and the other applications are discarded (Chen et al. 2021). The imbalance can present issues if the sampling rate and the class frequency are not equal in representation, resulting in a skewed analysis. This problem is the focal point of their research, and they address the challenges with cost-sensitive learning, under-sampling, and other methods used to classify imbalanced datasets.
An analysis of existing literature in the peer-to-peer lending space reveals that there is a wide range of issues that multiple groups have published work trying to solve. Surveying the landscape of published work can reveal a list of common topics from various domains. The summarized information in Table 1 shows a sample of multiple references, the methods used in the work, the nature of the data used in the experiment, and if the work addresses or explicitly accounts for disruptions in their experiment. Though not an exhaustive list of all the work published in the space, with this sampling, we can clearly see that a gap exists in the field of peer-to-peer lending research, specifically in disruption analysis.

Table 1.
Example of the research gap showing a need for analysis of default predictions involving disruptions due to hardship.
3. Hypotheses
Other work shows the relationship among attributes in a borrower’s credit profile and the ability to predict repayment outcomes, but this work distinguishes itself from the others as it focuses on how economic disruptions alter this outcome. With the available work analyzed, we propose the following hypotheses to be tested:
Hypothesis 1.
There are specific job titles that are more resilient to hardships which will show above average repayment counts.
Hypothesis 2.
There are specific job titles that are less resilient to hardships which will show below average repayment counts.
Hypothesis 3.
There are specific significant attributes in the hardship dataset that can be used to accurately predict repayment/default using the Two Class Support Vector Machine.
4. Empirical Study
4.1. Sample and Data
The official historical data are publicly offered online and made accessible for analysts and peers in the statistics and data section of the Lending Club website. Though no longer being consistently updated, these datasets were published quarterly in the past, and the hardship data was included from 2016 through 2020. Many data analysis platforms (Source: https://www.kaggle.com/ethon0426/lending-club-20072020q1; accessed on 3 April 2023) have included this dataset for research purposes, allowing for a collaborative effort to increase our understanding of the peer-to-peer lending space.
Along with a term or end date for the loan, all loans that enter hardship have a set date when the hardship repayment term period ends. These loans that have both ended the hardship term and reached the end or full term of the loan are expired. Among expired loans, there are those that have been fully paid and those that resulted in a default. Figure 1 shows the number of expired loans with a hardship term that were repaid in comparison to the number of expired loans with a hardship term that ended in default. The fact that just under 40% of loans with hardships end in default is cause for concern enough to dig into the details. A lender seeing this statistic without any other analysis would be uneasy if one of their loan investments went into a hardship repayment agreement. Peer lenders need the ability to factor hardship into their default potential. When a hardship occurs, they should be able to review data suggestions about the attributes that impact their loan.
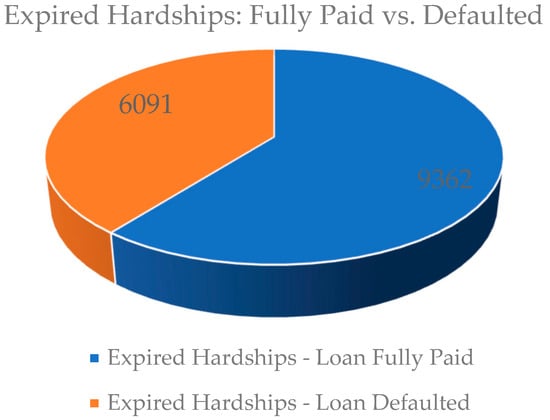
Figure 1.
Total expired hardships resulting in default in relation to all expired hardships.
There are various reasons for declaring financial hardship resulting from an economic disruption. We are not given insight into the method used to approve or deny the hardship claim, but we can retrieve the approved hardships by capturing the start and end dates of the hardship term. In Figure 2, we get a more detailed breakdown of the total number of expired hardships, the year they occurred, and the result of the loan. The data available spans from the 1st quarter of 2016 through and including the 1st quarter of 2020. From this data, we attempt to achieve the study’s first objective, which is to identify, quantify, examine, and understand the attributes in the financial hardship data that prove to be factors in the prediction of default among borrowers experiencing financial hardship. From the specific segment of borrowers with financial hardships, we intend to analyze the defaults and repaid loans to find attributes specific to each group. We will use the Two-Class Support Vector Machine, a machine learning algorithm that performs supervised learning for the classification of data groups. This machine learning method will be used to train a model for predicting default, specifically for this group of borrowers who experienced financial hardship. Our second objective is to determine whether default predictions can be accurately made using the attributes found from the work in the first objective. Upon achieving this, we can contribute a model for default prediction among hardship-experiencing borrowers with peer-to-peer loans.
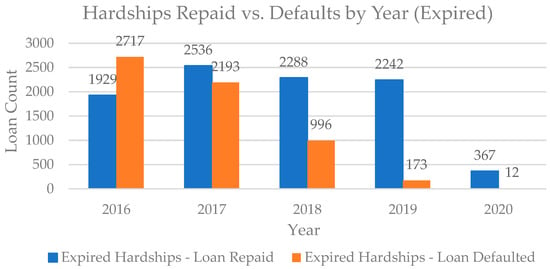
Figure 2.
Comparison of expired hardship agreements through the years (Only Q1 of 2020).
As shown in Table 2, the dataset contains loan details, including amount, rate, term, payment, and status. There are also details about the borrower, such as income, employment, credit, housing, and open accounts. The attributes or features listed in Table 2 are some of the typical attributes analyzed for lending decisions and credit activity. This set of features displayed is only a sample of the common features used in the lending space, as there are many features captured in the dataset that are not shown here. In this work, we will find the set of features that prove to be of most value to the predictability of the loan outcome.

Table 2.
Notable features and descriptions of peer-to-peer loans.
A key difference in the subset of data used in the experiment is the availability and inclusion of the financial hardship details. We extract the details of each historical loan having a borrower that experienced an economic disruption due to financial hardship. The fields in the dataset that were populated for borrowers who declared financial hardship are listed in Table 3 along with their descriptions. In Table 4, we expand on the types of hardships that were reported in the dataset and give an explanation of the nature of the reported disruption. With the extracted group, we prepared the data for analysis and classification performance using the associated method. Next, the data had to be put in the proper format to fit specific data types (categorical, numeric, date/time, string, or binary) to process in the next step. The data was separated into a training group and a testing group with a randomized split function. An incremental approach was used to adjust the ratio of training to test data to tune the model. The Two-Class Support Vector Machine was selected because this is essentially a binary classification problem with two available classes for prediction. The loan attributes, along with the hardship-related features, are used in the experiment to test the prediction capabilities of the Two-Class Support Vector Machine when used with this data.

Table 3.
Hardship related attributes populated for borrowers with an approved hardship agreement.

Table 4.
Common hardship reasons and explanations used in the data.
4.2. Exploratory Analysis
This work is focused on the portion of the population of borrowers that experienced economic hardship. By filtering the dataset to only include the hardship-experiencing population of borrowers, the results will be tailored to that group. The aim is to determine which features show a statistically provable impact on loan default predictions within this hardship-experiencing group. We analyze the relationship between the attributes and the outcome to make the case. For each feature, we test for the difference in mean, so = The attribute has no statistical role in the loan default of a peer-to-peer loan with a borrower experiencing economic hardship. This test will assist in finding the attributes that show statistical significance in default prediction and can exclude those that show no significance or impact. The classification is binary, resulting in only default or repaid outcomes. The dataset is comprised of a combination of numerical and categorical input, and we must utilize a method that can handle the removal of non-informative fields as predictors. We must analyze the features separately to determine their impact on the prediction capability of the model. A supervised filter will be implemented to make model training faster and more interpretable.
The Chi-Square test will be used for the analysis of correlation. Chi-Square will also allow us to determine if there is a relationship between a variable and the binary class. This test, which is a determination of independence, attempts to achieve classification accuracy by keeping the original class distribution and utilizing the smallest subset of features. Chi-Square is calculated with the following formula, where = degrees of freedom, = observed value, and = expected value.
The resulting p-values from the test performed on the data were used in determining the attributes that show predictive capability to be used in the classification experiment. The Chi-Square test revealed that a distinct subset of the available features were showing statistical influence on the classification of an observation. These attributes can theoretically provide a simpler approach to the prediction of default. Table 5 displays these categorical features with promising p-values, which we must reject and assume have statistical significance for the classification of the data. Table 5 also displays their corresponding p-values for reference. From the test performed, the employment length, deferral term, hardship reason, grade, verification of application information, term of loan, hardship type, public records, and loan purpose were attributes that had p-values lower than the level of significance. These attributes will be included in the next steps of the analysis.

Table 5.
Resulting analysis of statistically important categorical features.
We utilized the t-test to test the variation in group mean to further the determination of relationships in the continuous attributes. We must utilize a method to analyze continuous attributes because there are many continuous variables in the lender profile. To understand which attributes have a bearing on repayment outcomes, all continuous variables were tested. We took random samplings of these variables in our data to perform the comparison to the corresponding class value of each individual random observation. These comparisons of the random samples will be used to determine the goodness of independence. In the independent-sample t-test, we compared the group mean of independent, continuous variables amongst the two separate class groups, which were ‘Repaid’ and ‘Default’. In the t-test, calculated with the formula where = observed mean of sample 1, = observed mean of sample 2, = standard deviation of sample 1, = standard deviation of sample 2, = size of sample 1, and = size of sample 2.
We observed statistically significant differences among the group means of samples classified as repayments and samples with a defaulted classification. Table 6 lists the findings, including the continuous attributes displaying statistical significance using the t-test. Features with lower p-values (below 0.05) were then earmarked to be utilized in the loan default prediction experiment.

Table 6.
Resulting analysis of statistically important continuous features.
4.3. Text Analysis
One difficulty faced during the feature selection process was handling free-form text. The job title, a key categorical feature, did not show statistical significance to the class straightaway because of its representation in the dataset. This data was captured in a free-form text field on the loan application with no standardization in place. Many of the job titles were variations of the same role, and there was no specific rule in place for capturing this important data from the applicant. Figure 3 shows the outline of the steps in the text classification experiment performed on the free-form job title field. There were 6010 unique job titles among the total hardship population of 15,355, and of the 6010, the most common terms are shown in the word cloud in Figure 4, with the most frequent having the larger font size. A lender lacking insight such as how the borrower consistently makes a living is at a disadvantage when analyzing the effect of economic disruption on peer-to-peer loans. For this reason, we find it extremely important to include the job title as a feature in the experiment.
To aid in predictive capabilities, we employed a common text classification technique, the bag-of-words model, to capture the frequency of occurrences of each word, which can produce scores for training a classifier. The bag-of-words model was selected due to the size of the corpus. There were a total of 2775 unique words extracted, and the most frequently found words can be found in Figure 5. In the data set, the job title field is a free form and has variable-length input. This technique is often used on large sets of text, such as paragraphs, emails, or customer reviews. In our case, the large set of text is the job title field. We also utilize a N-gram model to represent our text vectors for performance comparison. In the text processing step of the experiment, the ability to aggregate individual words amongst the job titles gave insight that could produce a high-level view of frequently used words in this field. Prior to this aggregation, a number of optional text processing and cleaning methods had to be used. These methods include replacing punctuation marks with spaces, removing special characters, and avoiding case sensitivity by lower casing all observations. Word stemming was not utilized because of the high sensitivity of the job title. For example, with word stemming, the word ‘operations’ and the word ‘operator’ would be reduced to the word ‘operate’ and would represent both cases. Using this method would result in a loss of the existing detail needed to differentiate between two different roles. The loss of detail in the previously mentioned scenario applies to many cases where the stem of the word would result in undesirable groupings. In this experiment, the cost of an incorrectly grouped or classified word is high because that word will impact a prediction and possibly a decision. For the reasons mentioned, we attempted to avoid ambiguity in relation to job titles, making the inconvenience of duplicate representation less of a concern.
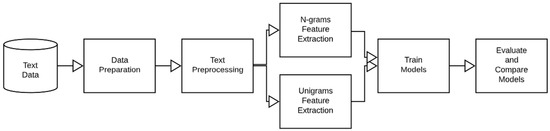
Figure 3.
Text analysis process used on free form job title field in the borrower application.

Figure 4.
Word Cloud of most frequent terms in the job title feature in repaid loans and defaults respectively (larger font means more representation).
The job title field is not restricted to a certain word length in the dataset, which requires a method for handling a combination of N-gram mappings. This is a text classification problem for a field in which conditioning, context, and probabilities of subsequent word occurrences do not apply. For these reasons and the existence of many single-word job titles, we intend to compare the performance of a unigram model to a bigram, trigram, and N-gram model. Each of these was used for the text classification problem to determine how each would handle the classification of the observations. A unigram model would give the ability to analyze terms independently in the corpus, but combining words could present a performance advantage.
In the comparison of unigrams to bigrams, trigrams, and N-grams, there were clear performance advantages to using unigrams for prediction capability. The results of this comparison in Table 7 shows that the unigram (1-g) model outscored all other models in each of the performance metrics used. The next best-performing model was the bigram (2-g) model, and performance showed a decrease with an increase in N-grams from 1 to 4. Using the ROC-based performance visualization shown in Figure 6, we can show the comparison of the best and next closest performance. The largest area under curve was achieved using the unigram approach, and the next best model was the bigram model. The performance decreased further for the trigram and 4-g models. In this scenario, the ability to predict default increased with a lower N value, showing no benefit from dimensionality reduction.

Table 7.
Performance comparison of 1-g, 2-g, 3-g, & N-gram models.
The time and complexity of the classification model are tied to the input space dimensionality. For the support vector machine, a linear model, complexity is linear and correlated to N (the number of features). In text classification models such as this, the feature count is high since the number of features resulting from word extraction builds the vocabulary, and each N-gram is mapped to a feature.
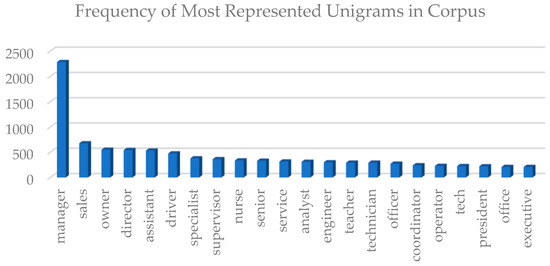
Figure 5.
Frequency of Most Represented Unigrams in Corpus. Only unigrams with a frequency over 200 are displayed.
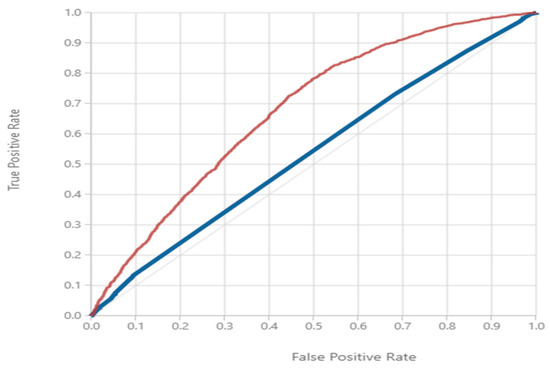
Figure 6.
Comparison of ROC Curves for Unigram and Bigram Model. The red line shows the Unigram Model’s ROC Curve and the blue line shows the Bigram Model’s ROC Curve.
Here we take a string of one or more words and extract each individual word contained in the job title, which is free-form text. Each term extracted is then mapped to a corresponding feature to represent the word as an attribute of the observation. The output from this mapping is the text frequency, which represents the number of times a word appears across the entire corpus dataset.
To work with a more statistically significant list of features instead of the entire unigram list of extracted words, we utilize a suitable filter-based selection method. A test was then applied to attempt to reduce the computational complexity and the effects of high dimensionality. From the list of 2775 unique terms, we captured those that showed statistical significance with a p-value below the threshold of 0.001. There were a total of 36 words that showed statistical significance with p-values lower than the 0.001 level of significance. We then compared the performance of just the job titles containing the statistically significant terms to the performance of the entire unigram set. This comparison would determine if the statistically significant terms can be used as a basis for default predictions among those loans with borrowers experiencing financial hardships.
The comparison of the classification performance between the unigram model with every unigram included and the model with only the unigrams of statistical significance shows that there is an advantage in classification capability when using terms with lower p-values. The list shown in Table 8 gives the lender a count of repayments and defaults by unigram, which shows if a job title containing that unigram is skewed towards one class or the other historically. In the comparison shown in Table 9, we found that the accuracy improved significantly, and the ROC-based visualization in Figure 7 shows the difference in area under the curve. This comparison suggests that when analyzing free-form text in the job titles, loans with borrower job titles containing any terms with statistical significance will have more accurate class predictions than those loans that do not have borrower job titles containing terms showing no statical significance. As a result of the work leading up to the comparison, we are also able to contribute a list of statistically significant unigrams that a lender may utilize for repayment predictions in situations involving a borrower experiencing a financial hardship during the repayment term. When comparing the list of statistically significant terms to the list of most popular terms found in the dataset, we see a positive correlation. Almost all of the terms that were found to be statistically significant also had stronger representation in the number of occurrences. This relationship shows that the more representation a term has in the corpus, the greater the opportunity for this term to provide accuracy in prediction. The lesser represented terms have fewer occurrences, so the sampling can be imbalanced based on a lack of representation. This does not mean that the term is not useful, but rather that the test used to prove significance did not have enough to meet the qualification of use for prediction using the applied method.

Table 8.
Results of Chi-square test with p-values for extracted unigrams.
Table 8.
Results of Chi-square test with p-values for extracted unigrams.
| Word/Feature | Repaid | Default | Expected | p-Value | |
|---|---|---|---|---|---|
| Observed | Observed | ||||
| Manager | 1444 | 840 | 1142 | 159.727 | 1.29821 × 10−36 |
| Director | 343 | 199 | 271 | 38.258 | 6.19728 × 10−10 |
| Engineer | 199 | 101 | 150 | 32.013 | 1.53118 × 10−8 |
| Owner | 339 | 210 | 274 | 30.311 | 3.57262 × 10−8 |
| Attendant | 40 | 9 | 24 | 19.612 | 7.57731 × 10−6 |
| Assistant | 316 | 216 | 266 | 18.797 | 1.45396 × 10−5 |
| Sales | 393 | 283 | 338 | 17.899 | 2.32894 × 10−5 |
| Lead | 101 | 50 | 75 | 17.225 | 3.11444 × 10−5 |
| Office | 134 | 74 | 104 | 17.308 | 3.17897 × 10−5 |
| Dentist | 19 | 1 | 10 | 16.200 | 5.69941 × 10−5 |
| Ceo | 49 | 17 | 33 | 15.515 | 8.18466 × 10−5 |
| Process | 23 | 3 | 13 | 15.385 | 8.76994 × 10−5 |
| Server | 71 | 32 | 51 | 14.767 | 0.000112074 |
| Technician | 179 | 113 | 146 | 14.918 | 0.000112298 |
| Therapist | 60 | 25 | 42 | 14.412 | 0.000133251 |
| Stylist | 32 | 8 | 20 | 14.400 | 0.000147802 |
| Practice | 13 | 0 | 6 | 13.000 | 0.000167308 |
| Senior | 199 | 131 | 165 | 14.012 | 0.000181636 |
| Specialist | 225 | 153 | 189 | 13.714 | 0.000212829 |
| Supervisor | 215 | 146 | 180 | 13.188 | 0.000275831 |
| Coordinator | 148 | 92 | 120 | 13.067 | 0.000300598 |
| Dental | 44 | 16 | 30 | 13.067 | 0.000300598 |
| Cashier | 28 | 7 | 17 | 12.600 | 0.000311491 |
| Banquet | 18 | 2 | 10 | 12.800 | 0.000346619 |
| Agent | 76 | 38 | 57 | 12.667 | 0.000372233 |
| Pilot | 17 | 2 | 9 | 11.842 | 0.00039503 |
| Clinical | 38 | 13 | 25 | 12.255 | 0.000402619 |
| corporate | 12 | 0 | 6 | 12.000 | 0.000532006 |
| service | 188 | 127 | 157 | 11.813 | 0.00057553 |
| registered | 114 | 68 | 91 | 11.626 | 0.000650232 |
| Tech | 138 | 87 | 112 | 11.560 | 0.000653844 |
| electrician | 35 | 12 | 23 | 11.255 | 0.00068787 |
| mechanic | 65 | 32 | 48 | 11.227 | 0.000752789 |

Table 9.
Performance comparison when using all unigrams vs. just the statistically significant unigrams.
Table 9.
Performance comparison when using all unigrams vs. just the statistically significant unigrams.
| All Unigrams | Unigrams with p-Value < 0.001 | |
|---|---|---|
| Accuracy | 0.634 | 0.846 |
| Precision | 0.539 | 0.784 |
| Recall | 0.411 | 0.837 |
| F1 Score | 0.466 | 0.810 |
| AUC | 0.678 | 0.918 |
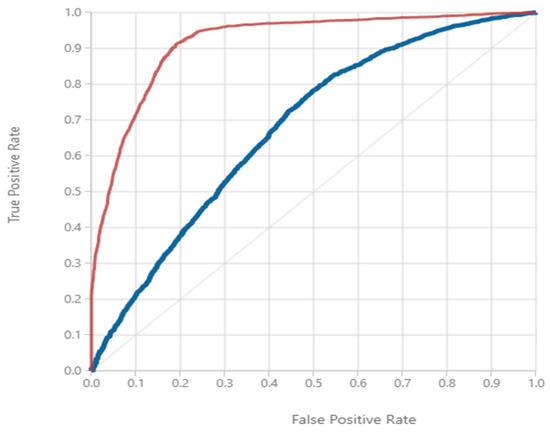
Figure 7.
ROC curve comparison when using all unigrams (blue) vs. just the statistically significant unigrams (red).
4.4. Two Class Support Vector Machine
The data classification method used in this work is based on the Support Vector Machine, which is an algorithm that determines a hyperplane in an N-dimensional space to classify data. This is relevant to our work as this classification problem involves two classes: loans that are fully paid and loans that are defaulted. To make a separation into class A or class B predictions, there will be many possible hyperplanes, but the algorithm chooses the hyperplane with the largest distance of separation in classes, also known as the margin. The algorithm maximizes margin to allow future classification confidence. The decision boundaries give classification suggestions for data points falling on a particular side of the hyperplane, representing class A or class B. The complexity of the dimensions is determined by the complexity of the data involved. If the data is simple or uses fewer variables, then the complexity will be simple. In cases where the data uses many features, the dimensionality of the hyperplane increases.
Data points falling closest to the boundaries form the support vector and thus greatly impact the position of the hyperplane. Some data points are easier to classify than others. The data points that are the most difficult to classify make up the decision surface edge. When data points or observations that make up the hyperplane are removed or non-existent, the positioning of the hyperplane is influenced to use the next closest data point in its place, altering the space of the support vector. A thresholding approach is used with a linear function to assign a value to the data used as input. The range of values produced by the linear function is ([−1,1]). The assigned value -1 refers to the classification, and the assignment of 1 identifies with the other class.
For a simplified example, say the input set of sample features is , which are features in the dataset. The algorithm would produce a set of weights for each feature, where a combination could be used to predict the class. One key aspect of the SVM is that the weight reduction results in fewer features of importance to optimize the margin of the hyperplane. These difficult points close to the boundary line help to find the optimal hyperplane and are critical to the positioning of the division of classes.
In Figure 8, notice the and which are the support vectors, and which is a measure half the width of the hyperplane.
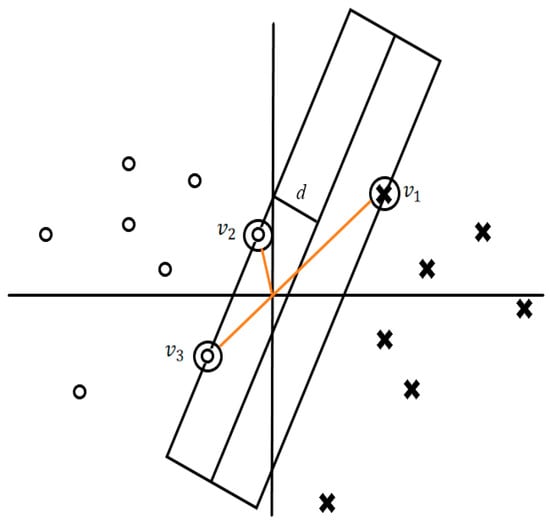
Figure 8.
Data Points on the Boundary Line Forming a Division. For a sample binary classification problem, circles indicate class 0, while crosses indicate class 1.
Define the hyperplanes :
and are the planes: , .
The points on the planes and are the edges of the Support Vectors. The plane sits between and at which .
If the shortest distance to the closest positive point, and if the shortest distance to the closest negative point, then is the margin of the hyperplane, as shown in Figure 9. There are infinite solutions for the hyperplane. To find the optimal solution, move the support vector and recalculate the decision boundary by using the optimization algorithm to generate weights that will obtain the biggest margin possible.
In cases such as the classification problem at hand, the separation is nonlinear and thus would need to be mapped to a higher dimensionality because of the number of features in an observation.
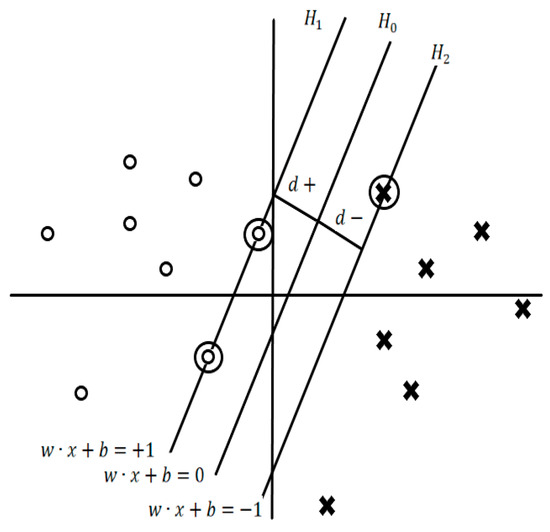
Figure 9.
Example of Hyperplanes with Support Vectors and Margin. Shapes are a graphical representation of sample class. Circles indicate class 0, while crosses indicate class 1.
We must optimize using a function similar to: = ∑ − ½∑ where is the dot product of just the two feature vectors. For consideration, take two vectors, and in a dimensional space of . A mapping of or to transform and into a higher dimension. In a case where there are more than two feature vectors, we could instead use )), for a way to handle more than two features. The issue is that this is an inefficient computation for a situation involving many features, so instead of doing this, we can use a kernel trick function such as: = ∑ − ½∑ where and is tunable. This will define similarity in the converted data space in a more efficient manner, as solving for only adds one exponent and some addition. We employ a nonlinear support vector machine using sigmoid and tanh for transformation: .
4.5. Results
The experiment was based on the cited dataset, which spans from 2016 through 2020. The results of the model’s performance on this dataset were analyzed using multiple performance indicators for scoring the model, such as precision, accuracy, recall, and F1. These metrics are a commonly used set of measurements for scoring machine learning models. The classification problem in the experiment involved predicting loan default among borrowers who had experienced an economic disruption and entered into a financial hardship agreement with the lender. The experiment targeted the records in the dataset that have evidence of a hardship agreement only.
In this experiment, we compared the performance outcomes of the support vector machine to those of other machine learning algorithms and analyzed the results. We used the actual outcomes as a comparison for scoring classification performance since the data used is historical. Though the actual loan outcomes were available in the dataset, some assumptions still had to be made to justify the use of the actual loan performance. We assumed that any peer lender involved in a funded loan had the intention of being repaid in full, at least in principle investment, and with interest as a profit in the best-case scenario. We assumed that the lender anticipated the loan to perform as agreed with the borrower, complying with the terms for the full duration of the life of the loan. In summary, any loan given by a peer lender was completed with the intention of returning a profit. In the event of a disruption, we assumed that a hardship agreement was given to the borrower because the intention of the lender did not change from the original point of funding. This means that we assume the peer lender continued to have the belief of a full repayment despite the economic disruption. These assumptions led to our reasoning that any loan that was not repaid was an incorrect prediction of repayment made by the lender, thus negatively impacting the benchmark performance for comparison.
There were 15,355 expired loans with hardship agreements analyzed in the dataset. Among the hardships, there were 5993 loans that defaulted and 9362 with successful repayments. We used these expired loans in our supervised learning experiment as the actual outcome is available as a baseline. This 39% default rate serves as a baseline benchmark when isolating this group because 15,355 lenders entered into hardship agreements expecting to resume repayment with the borrower as originally agreed.
When using accuracy (true positives and true negatives) as a performance metric, the average accuracy achieved by the model based on the Two-Class Support Vector Machine was 0.855 across evenly distributed samplings of train-to-test ratios. Our model, which used the Two-Class Support Vector Machine, accurately classified 85.5% of the overall total number of observations. The true positives identified are loans that were actual defaults that the model predicted to be defaults. On the other hand, the true negatives were loans that were non-default and predicted to be non-default. The other 14.5% of the data was incorrectly classified. These incorrect classifications fell into either the false negative or false positive groups. The false negative count of 502 reflects the number of incorrectly predicted non-defaults that occurred during the experiment. The false negatives were the loans that were classified as non-default when the loan was in fact a default. For false negatives, the cost is that the lender using the model would see a negative prediction reading for default (non-default), but the actual outcome would be a default. This cost results in a loss of investment for the lender and will eventually result in a borrower having derogatory marks on their credit. A lower than normal false negative rate is an incentive to use this model because false negatives have a costly impact on the lender’s anticipation and preparation for default. These false negatives can be misleading in classification applications such as these because the lender would be expecting a default not to occur, hence a costly outcome. The false positive count reflected those loans that were predicted as defaults but were incorrectly classified. The model did produce a total of 613 false-positive predictions. Though slightly higher than the false negative count, the impact of these false positives is less costly to the lender. In our classification scenario for predicting default, we assume that a lender would much rather lose an opportunity to a false positive than to lose their investment to a false negative. A predicted default that ends up being a non-default costs more to a borrower than a false negative because the lender would not engage with the borrower if using the advice of the model. In the case of this model, there is a very high accuracy (true positive and true negative) and a low misclassification count. One drawback is that the false positive could have caused the hardship terms to be different if the decisions were made based on the model’s predictions prior to entering the hardship agreement. When comparing the impact of both types of misclassifications, there is a higher cost associated with false negatives because a loss of money occurs in these scenarios, causing negative experiences for lenders in the peer-to-peer market (Havrylchyk and Verdier 2018). These false negatives will result in an unanticipated loss of capital due to the loan defaulting without the model’s detection.
The original dataset without the hardship filter in place is extremely imbalanced. The total repaid loans were 838,429 loans, with 216,625 defaulting. After adding a filter for loans experiencing hardship, there were 5993 loans that defaulted and 9362 with successful repayments among the group of hardships. Most of the hardship observations still have a repayment as an outcome, but the balance ratio of default to repayment improves with the hardship filter in place. With an improvement on the imbalance, we have the justification for using accuracy as a metric for validation. There is a slight imbalance, so the F1 score should also be utilized to expand on the performance analysis of the model. Given the data used, in a scenario where no skill can be achieved by the model, a classification output comprised of all positive predictions would accurately classify 5993 observations out of 15,355. In this hypothetical case, the model would still correctly predict 39% of all observations by simply classifying all hardship loans as defaults. This is an ineffective strategy for default prediction that would not be used in an actual experiment, but the inverse case for repayment prediction would achieve a correct prediction rate of 69%. The effectiveness of any model using this dataset should at least be measured with respect to a “blanket case” baseline, such as the scenario mentioned. A model with prediction capabilities that are not able to exceed the baseline rate should be considered a model ‘of no skill’. Other metrics can be used in conjunction with accuracy for performance analysis. The ROC, which uses the true and false positive rates to formulate an area under curve, is another output from the experiment showing the accuracy of the classification model.
The Two-Class Support Vector Machine achieved an AUC of 0.93, which is shown in Figure 10. This AUC implies that the model achieved excellent levels of discrimination on the given set of hardship data to predict defaults. This AUC is indicative of there being no direct effect from the class imbalance, as the true positive rate exceeds the false positive rate for default predictions. Though this AUC is far beyond the threshold referenced, previous work has found that an AUC of 60% or higher is desirable in information-scarce scenarios, and an AUC of 70% or more would be the goal in information-rich scenarios (Berg et al. 2019).
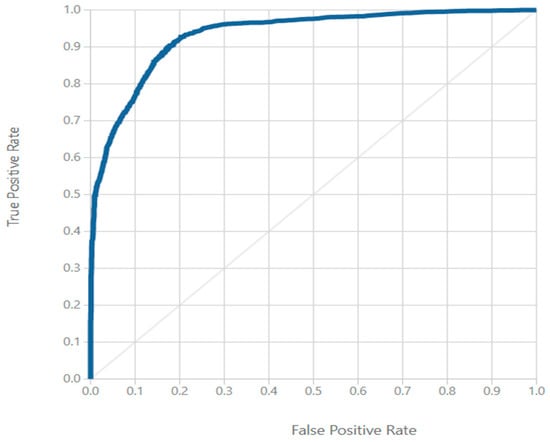
Figure 10.
ROC for Default Predictions in the Hardship Population using Two Class Support Vector Machine.
Due to the slight class imbalance of the hardship plan data, we can also justify the use of another method of classification performance evaluation, the PR curve. The precision and recall will be used to analyze the output of the precision-recall curve. Figure 10 displays the achieved precision, a measure that represents the ratio of relevant positives to the total positive classifications retrieved. The average retrieval rate for relevant defaults was around 80%, which is the precision score for the model. Table 9 also shows the recall of the model, which is the fraction of defaults retrieved from the dataset. On average, the model achieved a recall score of 83% in the experiment.
This experiment is a simulation of a peer lender using the Two-Class Support Vector Machine to predict defaults on loans that have entered a hardship plan. There are three different ways to look at how the lender would want to proceed with the classification problem. The lender may want to receive as many hardship default predictions as possible, no matter how many actually result in repayment, as they intend to cast a wide net. In this case, precision is of less importance because they would only want to maximize recall. A peer lender can also look at the situation differently, being okay with seeing a lesser number of default predictions in hardships if it means they want to only receive predictions that result in actual defaults in the future. This would mean precision would be much more important than recall and would be heavily relied upon. There are also peer lenders that would be interested in possible defaults among hardships while still avoiding misclassifications. This scenario would rely on a balance of both precision and recall maximization, which is ideal for the classification problem at hand.
From the PR curve shown in Figure 11, we see that there is a tradeoff in positive predictive value and sensitivity achieved where an increase in recall gradually diminishes the precision. The recall for a model “of no skill” is in the range of {0.5, 1}, which is far from the plotted curve. The curve shape in Figure 11 indicates that the data is very randomized and complex, but some imbalance in class does still exist.
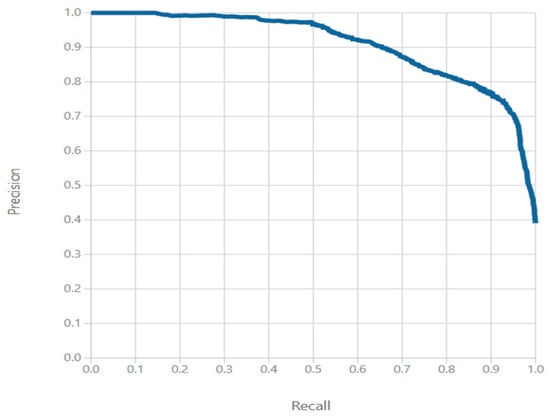
Figure 11.
PR Curve for Hardship Disrupted Loan Population using Two Class Support Vector Machine.
To compute the F1 Score, our recall and precision metrics will be used. The F1 of the model:
The F1 Score takes the overall recall and precision and gives a score that balances the two. Our F1 of 0.817 is the score achieved when balancing precision and recall on our imbalanced dataset. A peer lender would use this score if they were interested in receiving information on as many of the potentially problematic loans predicted as defaults while still avoiding the loans that have a good chance of being repaid. The higher or closer the F1 score of the model is to 1, the better for the peer lender. In this imbalanced dataset, our F1 is not measuring correct classifications; it is giving an edge by placing higher importance on false negatives and false positives. These false negatives equate to defaulted loans, where the model is incorrectly classified as non-default. The false positives equate to non-default loans where the model is incorrectly classified as default. The cost of a false negative is that the borrower takes an unanticipated loss. On the other hand, the cost of a false positive is a surprise repayment when a default is expected. The lender analyzing hardship loans would prioritize accurate predictions, but in cases where misclassifications occur, false positives would be more beneficial because a lender only loses time, as opposed to losing time and a portion of their investment in the case of a false negative.
For comparison of the results shown in Table 10, we included the performance of a few other machine learning algorithms to justify the use of the Two-Class Support Vector Machine for this data classification problem. Though we are not performing a comparative analysis of algorithms, these comparisons can serve as performance benchmarks for the method used in the experiment. The performance of the Decision Tree, Two-Class Bayes Point Machine, Logistic Regression, and Neural Network algorithms was analyzed using the same data with the same statistically significant variables. There are many other algorithms that we can use for comparison, but this is just a small look at a few of the more well-known. As shown in Table 11, the Two-Class Support Vector Machine did not outperform in all areas, but it did lead in accuracy, precision, and area under curve (which is directly related to accuracy).

Table 10.
Experiment Results using Two Class Support Vector Machine.

Table 11.
Performance Comparison Using Other Machine Learning Algorithms.
5. Discussion
This section is not mandatory but can be added to the manuscript if the discussion is unusually long or complex. Economic disruptions can be unexpected and untimely, with the potential to affect many different markets. With the uncertainty that comes from an economic disruption, a peer lender needs the ability to have a decisional system available to manage the hardships that a peer borrower can claim as a result of the economic disruption impacting their ability to repay their peer-to-peer loan as initially agreed. Accuracy is crucial to prediction capabilities in this market, and the work performed provides an accurate model for predicting defaults in the scenario mentioned above. The characteristics of a borrower profile that were proven to be resilient to economic disruptions were presented, along with a machine learning algorithm accurately making predictions with these features. Utilizing the method proposed, peer lenders may select loans to maximize the probability of repayment during uncertain times because the data suggests resiliency. For example, in the case analyzed, a simple rule that can be derived from the analysis of the attributes: “borrowers experiencing financial hardships with the word ‘dental’ in their job title, no more than 3 days past due on their hardship payment, who declared hardship because of income curtailment, having a loan graded ‘D’ or better” tend to repay their loans despite the economic disruption. Having a rules-based method with supporting historical data for analyzing what outcomes are probable during an economic disruption strengthens the argument for peer lenders to engage with borrowers more confidently. This is important because economic disruptions have proven to be devastating financially on many occasions. With an approach that assists the lender in making decisions based on avoiding problematic repayment situations, the financial assistance needed during an economic disruption can come from peer lenders.
In Hypothesis 1, we stated that there are specific job titles that are more resilient to hardships and will show above-average repayment counts. For this hypothesis, we used the test of independence: = The job title has no statistical role or relationship to the loan repayment of a peer-to-peer loan with a borrower experiencing economic hardship. Based on the text analysis performed in conjunction with the test for independence, we found that the terms in many of the job titles show statistical significance. We further solidified our findings by taking these terms and analyzing their predictive capability with the Two-Class Support Vector Machine. Based on the accuracy achieved with these tests, we must reject as the job titles were found to be statistically significant and show differences in repayment/default prediction. We found a 72.3% average observed repayment frequency among the group of job titles containing significant terms. When analyzing the highest observed repayment-to-default ratio, the top-scoring job titles contained the following terms: pilot, dentist, practice, and processer. These job titles all had repayment rates higher than 88%, proving to be more resilient to the disruption experienced by economic hardships.
In Hypothesis 2, we stated that there are specific job titles that are less resilient to hardships, which will show below-average repayment counts. In our experiment, we tested for independence of the terms in the job title and the repayment/default in the same manner as previously mentioned.
= The job title has no statistical role or relationship to default in a peer-to-peer loan with a borrower experiencing economic hardship. We found a 28.5% average observed default frequency among the group of job titles containing significant terms. When analyzing the highest observed default to repayment ratio, the top-scored job titles contained the following terms: assistant, sales, specialist, supervisor, and service. These job titles all had default rates higher than 40.4%, showing that these specific job titles are less resilient to economic disruptions. For this reason, we reject as there is a relationship between the job title and the possibility of default when a borrower claims financial hardship.
For Hypothesis 3, we stated that there are specific attributes in the borrower profile that will prove to be statistically significant in predicting default among borrowers who have declared hardship. We provide the evidence of the work to determine this outcome in Table 5 and Table 6. Each of these attributes makes a statistical contribution to the predictive capability of the machine learning algorithm utilized. We must reject the null hypothesis based on the test for statistical significance and further validation coming from the resulting performance of the Support Vector Machine utilizing only these attributes. The list of categorical attributes that proved to be important to prediction includes employment length, deferral term, hardship reason, grade, verification, term, hardship type, public records, and purpose. The list of continuous attributes that proved to be important to prediction includes loan amount, annual income, payment, rev balance, interest rate, delinquencies, debt to income, fico, inquiries, hardship length, hardship days past due, hardship amount, hardship payoff balance amount, and hardship last payment amount. When utilizing only the attributes listed as significant, the Two-Class Support Vector machine achieved an accuracy of 0.855, a recall of 0.0832, precision of 0.802, an f1 score of 0.817, and a 0.933 area under curve.
This study demonstrates that certain attributes in a borrower application can be used to determine how the loan will perform if the economic situation negatively changes for the borrower during the repayment term. The lender should screen the application knowing that the borrower’s application attributes could change during the next 36- or 60-month loan term. If an economic disruption occurs in the borrower’s line of work, they could claim economic hardship. In addition to the significant attributes for default detection among hardships, we analyzed the free-form job title field. This field had no standardization and proved to be difficult to analyze in the same manner as the other attributes. In the loan application, any standardization for the job title would result in an aggregation of data that would only give summarized categories. While categories would be useful, having the job title captured with free form text allowed for more granularity. For this reason, we performed text analysis and broke the job tiles into unigrams. From the study, we can contribute a resulting list of terms that show predictive capability. These terms, their repaid percentage, and the percentile ranking of the repayment rate are displayed in Table 12. In Table 12, the terms are listed with the repayment rate in ascending order. The same rates show default prediction capabilities, as the lower the repayment rate, the higher the term on the list. In Table 12, the terms that show statistical significance and have higher default prediction capability are shown in the lower ranking percentiles.
While many of the factors in the borrower profile can change, we can use the list of features that show statistical significance to assist in decisions when the loan enters hardship status. This information utilizes the data that the applicant gives to the lender when hardship occurs, which is a process the borrower must initiate. Those borrowers who do not initiate the hardship status will not communicate any changes in their profile and cannot be included in the hardship discussion.

Table 12.
Statistically significant unigrams of job titles along with repayment rate and percentile ranking.
Table 12.
Statistically significant unigrams of job titles along with repayment rate and percentile ranking.
| Unigram | Repayment Rate | Percentile |
|---|---|---|
| Sales | 0.58 | 10 |
| Assistant | 0.59 | |
| Specialist | 0.60 | 20 |
| Supervisor | 0.60 | |
| Service | 0.60 | |
| Senior | 0.60 | |
| Technician | 0.61 | |
| Tech | 0.62 | 30 |
| Coordinator | 0.62 | |
| Owner | 0.62 | |
| Registered | 0.63 | 40 |
| Manager | 0.63 | |
| Director | 0.63 | |
| Office | 0.64 | |
| Engineer | 0.66 | 50 |
| Agent | 0.67 | |
| Lead | 0.67 | |
| Mechanic | 0.68 | 60 |
| Server | 0.70 | |
| Therapist | 0.71 | |
| Dental | 0.73 | 70 |
| CEO | 0.74 | |
| Clinical | 0.76 | |
| Electrician | 0.76 | |
| Stylist | 0.80 | 80 |
| Cashier | 0.82 | |
| Attendant | 0.83 | 90 |
| Process | 0.88 | |
| Banquet | 0.90 | |
| Pilot | 0.94 | |
| Dentist | 0.95 | |
| Practice | 1.00 | |
| Corporate | 1.00 |
Some key factors that were shown to be statistically significant in determining repayment outcomes were based on the amount to be repaid. We observed that the group of borrowers who repaid their loans despite the economic disruption had a lower group average loan amount than the group who defaulted on the loans. These borrowers with higher loan amounts had a higher chance of defaulting when entering hardship status. We also observed that the borrowers who defaulted had a higher group average interest rate. Though there is not an apparent reason for this higher likelihood of default, one possibility is the financial strain caused by the burden of the loan. The larger the loan amount, the higher the payment in principal alone. Since interest is also a factor in the payment amount, it does make sense that a higher payment would warrant more of the borrower’s available funds. This would cause a strain in a financial hardship. A lower loan amount would equate to a lower payment, but a higher interest rate increases the payment amount from an already diminished income.
Another attribute that showed statistical significance was the borrower’s income. We observed that the group who repaid their loans had a higher average annual income. From the annual income metrics, we can assume that an income lower than the group mean among defaulting borrowers would be of interest to a lender trying to predict the chance of default for a borrower who entered hardship status. The lower group mean among defaulting borrowers with hardships could possibly be due to the income level reported at the time of applying for the loan being the obtainable income level for the borrower after the hardship-causing event is no longer making an impact. A higher income could have a positive effect on the borrower’s ability to repay in the future, and having this higher income could also mean that there is a possibility of obtaining a similar income during or after experiencing an economic disruption.
Income is important for analyzing the ability to pay, but for determining a borrower’s tendency to repay, many use their past credit history. To estimate future repayment outcomes, there are certain attributes in the borrower profile that can give an indication of how the borrower could possibly perform. In the scenario used in the experiment, we are using the credit profiles of borrowers claiming financial hardship on an existing loan. The credit-based attributes that showed statistical significance were the number of delinquencies, the debt-to-income ratio, the revolving balance, the number of days past due, and the number of credit inquiries. These factors also play a part in calculating the overall FICO score of the borrower, which also showed statistical importance to the predictability of borrower default. We observed that the group mean for borrowers who repaid their loan despite having a hardship was higher than the group mean for those who defaulted. A lender would proceed with caution when analyzing a hardship agreement for a borrower experiencing a hardship with a score lower than the group mean. A higher amount of delinquencies, a higher debt-to-income ratio, a higher number of credit inquiries, a higher revolving balance, and more days past due are all situations that negatively impact the credit score. Though each of these metrics has an inverse relationship with the credit score, only the revolving balance was observed to have a higher group mean among borrowers who repaid their loans despite experiencing financial hardship. The revolving balance could have been higher due to this group having higher credit limits because of a higher group mean credit score (the higher the score, the more access to revolving credit). In our analysis, we found that debt consolidation and credit cards were the top two loan purposes listed by most of the borrowers sampled. Debt consolidation and credit card payoffs are two of the benefits of using peer-to-peer loans because they give the borrower a fixed rate for a defined term, providing relief from revolving debt balances with variable interest rates and an indefinite term.
Economic disruptions can cause a borrower to completely stop earning money to repay loans. In the experiment, we observed that the most common hardship terms were the COVID-19 skip and the interest-only 3-month deferral. In the COVID-19 skip hardship agreement, the borrower was able to skip payments to provide some financial breathing room until the borrower was able to resume making payments as promised. These skipped payments are added to the end of the loan for the borrower to make up in the future. The interest-only 3-month deferral hardship agreement allows the borrower to make a payment only on the interest accrued, which drastically reduces the payment amount for the borrower. This provides relief in the short term but also allows the lender to receive the interest that they would have normally been paid. The missing principal amount is to be repaid later by the borrower. There is a time factor and a payment amount factor in all cases of hardship agreements. These two factors proved to be statistically significant for default predictions. The group mean for the hardship length was lower for the group of borrowers who repaid their loans at 2.35 months, compared with 2.96 months for defaulting borrowers. A lender analyzing hardship requests could use a generalized rule that cautions against approving hardship requests exceeding the group mean for the historic default population. The group mean for the hardship payment amount was lower for the group of borrowers who repaid their loans at $58.94 per month, compared with $267.97 per month for defaulting borrowers. A lender analyzing hardship requests may see the benefit in providing more relief in the form of an overall lower payment during the hardship period since the group mean was significantly higher among the defaulting borrowers.
Our study did have limitations on the quality of the data. The data used was limited to a single peer-to-peer platform. This sampling limitation can be mitigated when more platforms make their data accessible for analysis. This work could be extended with the inclusion of more data from other sources. This work was also limited due to the relevance of the time period. Economic disruptions can occur in any time period, so the analysis is only relevant for the time period in which the data exists. One key finding is that the prediction capability of terms in the job title can be greatly affected by the time period of data collection and recording. Disruptions that occur in one decade may align with certain types of jobs, while disruptions in another decade could align with a completely different set of industries. There are also limitations on the type of data collected. The data used is from a U.S.-based peer-to-peer platform basing lending decisions on criteria normal for the local market in the U.S. This study could possibly render different results if applied to another market with different scoring models and lending criteria acceptable for that localized economy. Future work to extend this study should take into account the need for more data collection in other parts of the world. Other areas could have different disruption catalysts like climate and weather, political situations, and economic factors that are not found in this study. Any U.S.-focused study will have the same limitations in analyzing peer-to-peer loans.
6. Conclusions
In this work, we have given an example of how a peer lender can handle a case where an economic disruption causes financial hardships in peer-to-peer loans. Decision-making in the peer-to-peer loan market during times of economic disruption can be aided by accurate default predictions with a machine learning approach such as the Support Vector Machine. The model achieved an accuracy of 0.85 and showed an ability to handle a slight class imbalance by achieving an F1 score of 0.817 on the dataset used. We have tested the viability and usefulness of default predictions among actual peer-to-peer loan data where the borrower experienced economic hardship. We have made the contribution of analyzing experiment results, providing evidence of the benefits of using the listed important features along with the Two-Class Support Vector Machine to build a model for default prediction. We found that, when applied to historical loan records with hardship agreements, this model proved to be accurate in the prediction of the positive class (true positives vs. false positives). In the default prediction circumstance, less focus must be given to true negatives, which has a large impact on the accuracy metric. True negatives, though useful, have less of a cost than false negatives and false positives when predicting loan repayment. In this case, a different metric, the F1 score, must be used due to the uneven class distribution. After adjusting for the imbalance of classes, the focus on precision and recall showed that the model performed well. A precision of 0.802 implies that out of all of the loans that were predicted to be repaid, the model correctly identified slightly over 80% of repayments. The cost of false positives is high in the peer lending market, but we must also look at the rate of correctly identified defaults out of the total number of defaults that occurred because the cost of false negatives is also high in default prediction. The model achieved a 0.997 recall, which shows its coverage of actual repayments. This means that the model was successfully able to recommend slightly over 99% of the applications that resulted in actual defaults. A lender would want to balance the two metrics to have confidence in using the model. A balance between the two metrics was found in the F1 score of the model, which was 0.856, which is a positive result as this gives another measure of the model’s effectiveness. In addition, our findings in analyzing job titles showed that the loans with borrowers having the terms Pilot, Dentist, Practice, or Corporate were resilient to economic disruptions as these terms had repayment rates in the 90th percentile. When looking for default predictions, job titles containing the terms Sales or Assistant should be handled with caution when using the same financial hardship context. These roles ranked in the bottom 10th percentile for repayment rates.
Author Contributions
Conceptualization, B.N. and S.-C.H.; methodology, D.M.; software, D.M.; validation, S.-C.H., B.N. and D.M.; formal analysis, D.M.; investigation, D.M.; resources, S.-C.H.; data curation, D.M.; writing—original draft preparation, D.M.; writing—review and editing, S.-C.H., B.N. and D.M.; visualization, B.N.; supervision, B.N. and S.-C.H.; project administration, B.N. and S.-C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.kaggle.com/datasets/ethon0426/lending-club-20072020q1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Babaei, Golnoosh, and Shahrooz Bamdad. 2020. A Multi-Objective Instance-Based Decision Support System for Investment Recommendation in Peer-to-Peer Lending. Expert Systems with Applications 150: 113278. [Google Scholar] [CrossRef]
- Berg, Tobias, Valentin Burg, Ana Gombović, and Manju Puri. 2019. On the Rise of Fintechs: Credit Scoring Using Digital Footprints. The Review of Financial Studies 33: 2845–97. [Google Scholar] [CrossRef]
- Bhattacharya, Arnab, Simon P. Wilson, and Refik Soyer. 2018. A Bayesian Approach to Modeling Mortgage Default and Prepayment. European Journal of Operational Research 274: 1112–24. [Google Scholar] [CrossRef]
- Boiko Ferreira, Luis Eduardo, Jean Paul Barddal, Heitor Murilo Gomes, and Fabricio Enembreck. 2017. Improving Credit Risk Prediction in Online Peer-To-Peer (P2P) Lending Using Imbalanced Learning Techniques. Paper presented at 2017 IEEE 29th International Conference on Tools with ArtificialIntelligence (ICTAI), Boston, MA, USA, 6–8 November 2017. [Google Scholar] [CrossRef]
- Chen, Yen-Ru, Jenq-Shiou Leu, Sheng-An Huang, Jui-Tang Wang, and Jun-Ichi Takada. 2021. Predicting Default Risk on Peer-to-Peer Lending Imbalanced Datasets. IEEE Access 9: 73103–9. [Google Scholar] [CrossRef]
- Fitzpatrick, Trevor, and Christophe Mues. 2021. How Can Lenders Prosper? Comparing Machine Learning Approaches to Identify Profitable Peer-to-Peer Loan Investments. European Journal of Operational Research 294: 711–22. [Google Scholar] [CrossRef]
- Galema, Rients. 2020. Credit rationing in P2P lending to SMEs: Do lender-borrower relationships matter? Journal of Corporate Finance 65: 101742. [Google Scholar] [CrossRef]
- Guo, Yanhong, Wenjun Zhou, Chunyu Luo, Chuanren Liu, and Hui Xiong. 2015. Instance-based credit risk assessment for investment decisions in P2P lending. European Journal of Operational Research 249: 417–26. [Google Scholar] [CrossRef]
- Havrylchyk, Olena, and Marianne Verdier. 2018. The financial intermediation role of the P2P lending platforms. Comparative Economic Studies 60: 115–30. [Google Scholar] [CrossRef]
- Junior, Leopoldo Melo, Franco Maria Nardini, Chiara Renso, Roberto Trani, and Jose Antonio Macedo. 2020. A novel approach to define the local region of dynamic selection techniques in imbalanced credit scoring problems. Expert Systems with Applications 152: 113351. [Google Scholar] [CrossRef]
- Kim, Ji-Yoon, and Sung-Bae Cho. 2019. Towards repayment prediction in Peer-to-Peer social lending using deep learning. Mathematics 7: 1041. [Google Scholar] [CrossRef]
- Kriebel, Johannes, and Lennart Stitz. 2021. Credit Default Prediction from User-Generated Text in Peer-to-Peer Lending using Deep Learning. European Journal of Operational Research 302: 309–23. [Google Scholar] [CrossRef]
- Liu, Fan, Zhongsheng Hua, and Andrew Lim. 2015. Identifying Future Defaulters: A Hierarchical Bayesian Method. European Journal of Operational Research 241: 202–11. [Google Scholar] [CrossRef]
- Liu, Zhengchi, Jennifer Shang, Shin-Yi Wu, and Pei-Yu Chen. 2020. Social Collateral, Soft Information and Online Peer-to-Peer Lending: A Theoretical Model. European Journal of Operational Research 281: 428–38. [Google Scholar] [CrossRef]
- Ma, Lin, Xi Zhao, Zhili Zhou, and Yuanyuan Liu. 2018. A New Aspect on P2P Online Lending Default Prediction Using Meta-Level Phone Usage Data in China. Decision Support Systems 111: 60–71. [Google Scholar] [CrossRef]
- Mueller, J. Tom, Alexis Merdjanoff, Kathryn McConnell, Paul Burow, and Justin Farrell. 2022. Elevated serious psychological distress, economic disruption, and the COVID-19 pandemic in the nonmetropolitan American West. Preventive Medicine 155: 106919. [Google Scholar] [CrossRef] [PubMed]
- Oh, Eun Young, and Peter Rosenkranz. 2020. Determinants of Peer-to-Peer Lending Expansion: The Roles of Financial Development and Financial Literacy. Asian Development Bank Economics Working Paper Series, 613; Mandaluyong: Asian Development Bank. [Google Scholar] [CrossRef]
- Yao, Zhigang, and Yao Liu. 2023. How COVID-19 impacts the financing in SMEs: Evidence from private firms. Economic Analysis and Policy 79: 1046–56. [Google Scholar] [CrossRef]
- Yu, Haihong, MengHan Dan, Qingguo Ma, and Jia Jin. 2018. They all do it, will you? Event-Related Potential Evidence of Herding Behavior in Online Peer-to-Peer Lending. Neuroscience Letters 681: 1–5. [Google Scholar] [CrossRef] [PubMed]
- Zanin, Luca. 2020. Combining multiple probability predictions in the presence of class imbalance to discriminate between potential bad and good borrowers in the peer-to-peer lending market. Journal of Behavioral and Experimental Finance 25: 100272. [Google Scholar] [CrossRef]
- Zhou, Yimin, and Xu Wei. 2018. Joint Liability Loans in Online Peer-to-Peer Lending. Finance Research Letters 32: 101076. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).