The Dynamic Return and Volatility Spillovers among Size-Based Stock Portfolios in the Saudi Market and Their Portfolio Management Implications during Different Crises
Abstract
:1. Introduction
2. Institutional Background and Review of Related Literature
2.1. Institutional Background
2.2. Review of Related Literature
2.2.1. Interdependencies among the MENA and GCC Regions and Other Financial Markets
2.2.2. Interdependencies among Size-Based Portfolios in Other Advanced and Emerging Markets
3. Data and Methodology
3.1. Data and Preliminary Analysis
3.2. Methodology
4. Empirical Results
4.1. Regression Estimation Results and Their Interpretation
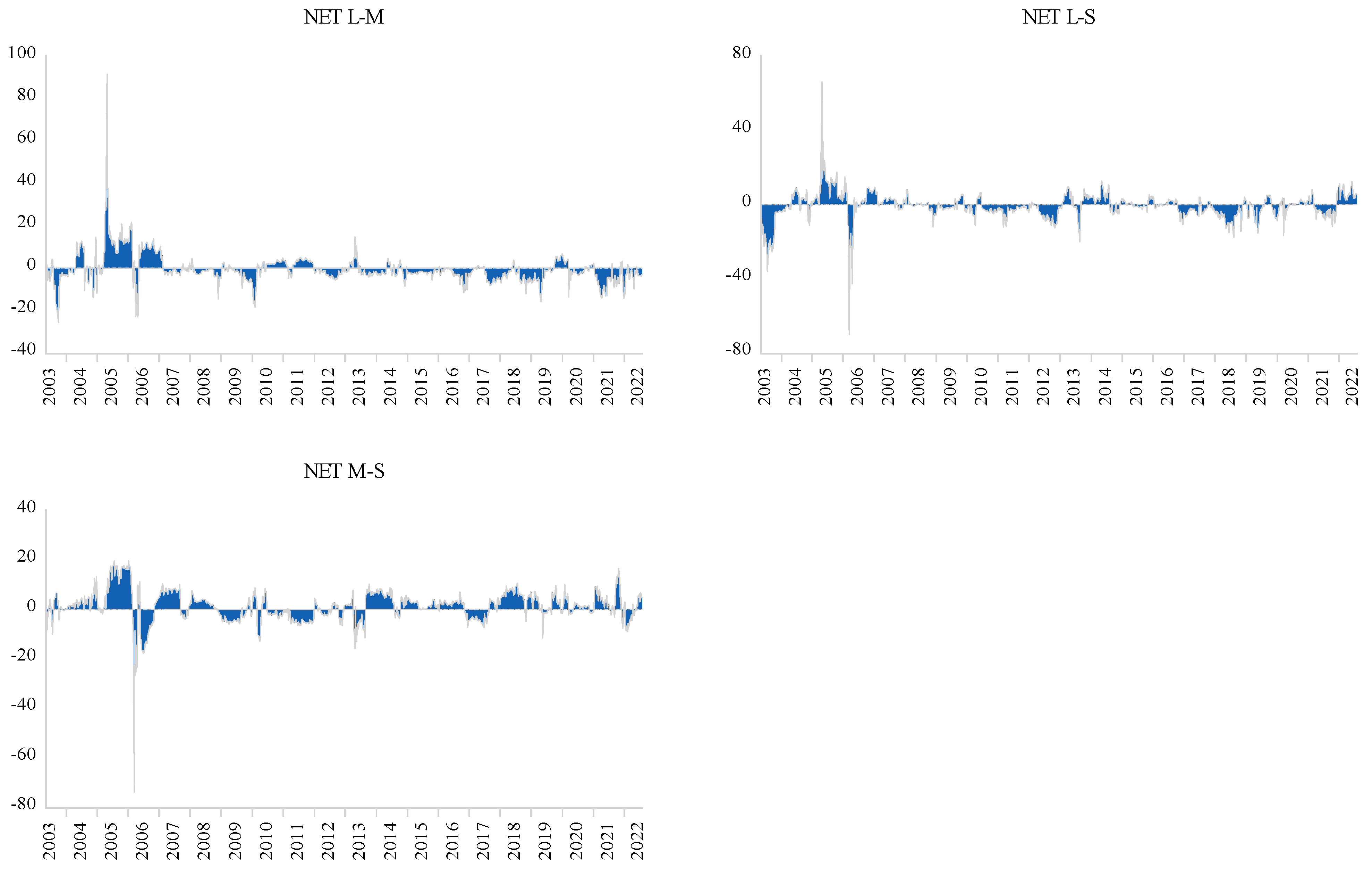
4.2. Time-Varying Conditional Correlation
5. Portfolio and Risk Management Implications
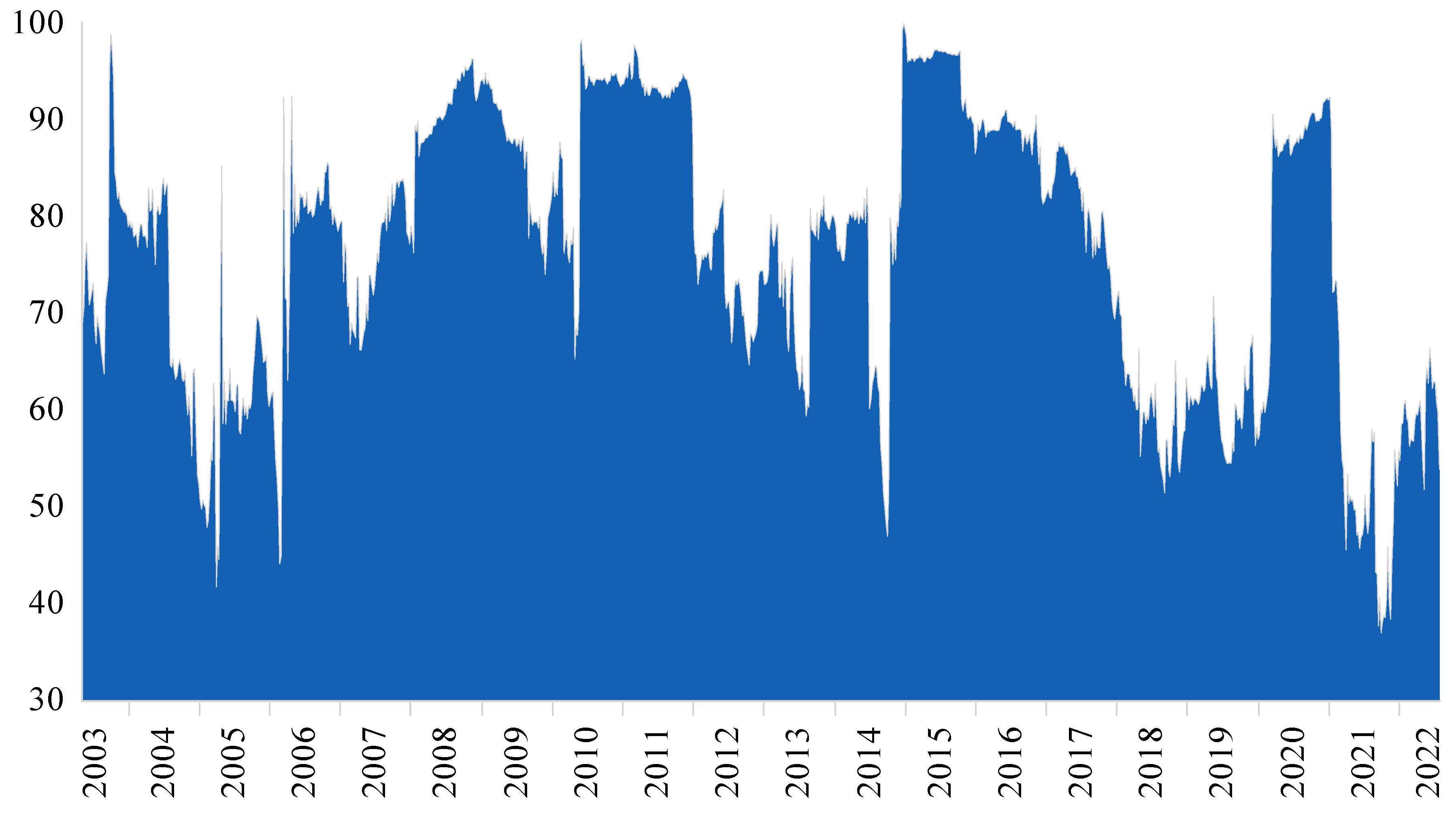
5.1. Fund Allocation
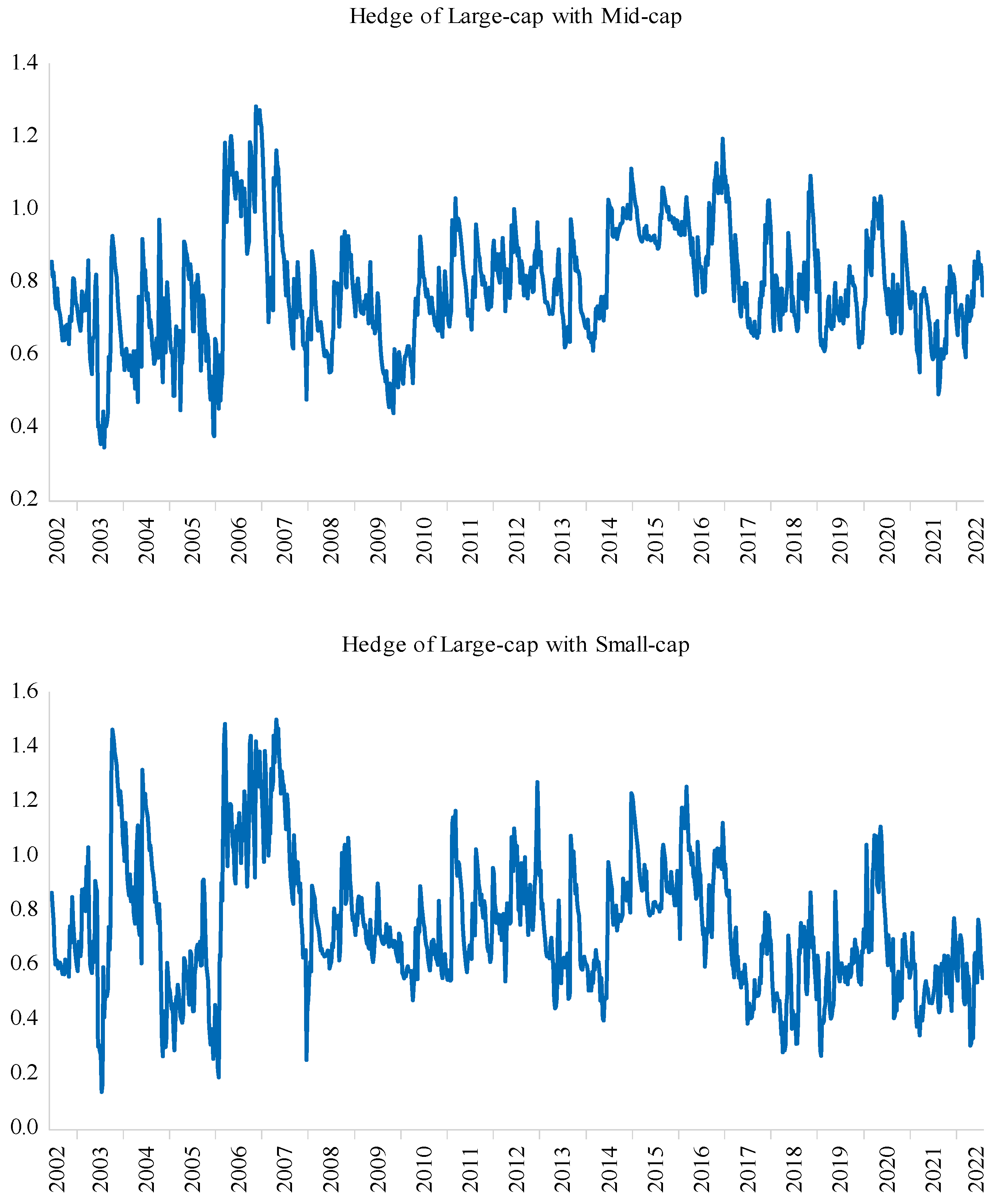
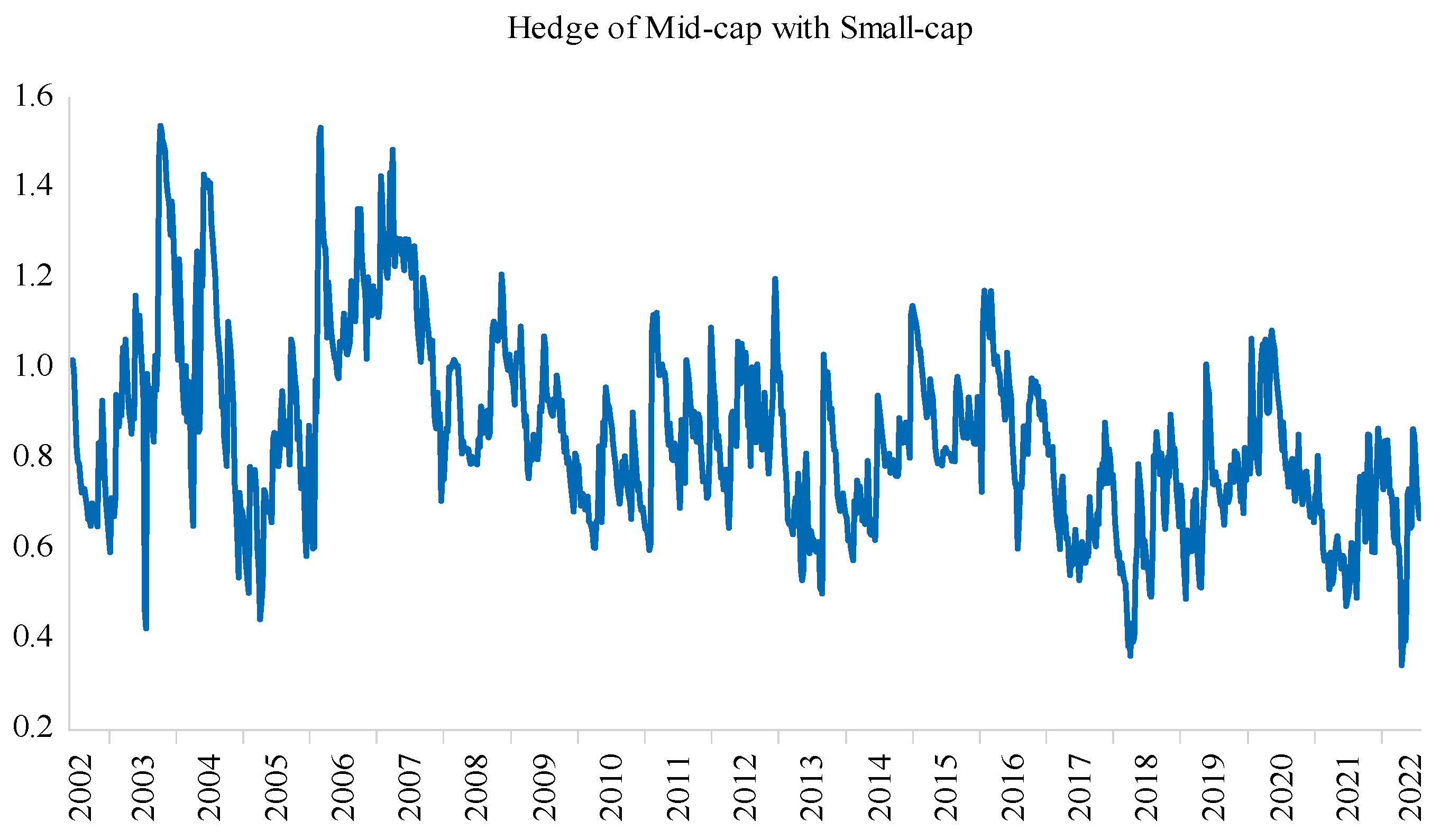
5.2. Hedge Ratios
6. Robustness Check
7. Discussion and Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Half Life | LL | |||||
|---|---|---|---|---|---|---|
| Large | 0.74 | 0.27 | 0.71 | 0.977 | 30.12 | −2652.441 |
| [0.00] | [0.00] | [0.00] | ||||
| Mid | 0.86 | 0.33 | 0.65 | 0.983 | 39.46 | −2610.8265 |
| [0.00] | [0.00] | [0.00] | ||||
| Small | 0.66 | 0.28 | 0.72 | 1.00 | −2668.8324 | |
| [0.00] | [0.00] | [0.00] |
| Lag Order | AIC | SC | HQ |
|---|---|---|---|
| 0 | 14.51531 | 14.52950 * | 14.52069 |
| 1 | 14.48388 | 14.54065 | 14.50541 * |
| 2 | 14.49634 | 14.59570 | 14.53402 |
| 3 | 14.45710 * | 14.59904 | 14.51092 |
| 4 | 14.46312 | 14.64764 | 14.53309 |
| 1 | The estimation results of the GARCH model used to obtain the residuals on the basis of which the is calculated are relegated to the Appendix A (Table A1) to conserve space. |
| 2 | The student distribution is used because the return series for small mid- and large caps do not follow the normal distribution (see Fiorentini et al. 2003). |
| 3 | On the basis of Nyblom’s individual test statistics, the endogenously determined shift dummies coincide with bursting of the Saudi stock market bubble in 2006, the GFC, and the 2014–2016 crude oil price plunge. The first dummy spans the period from 21 February 2006 to 18 August 2009, while the second dummy falls between 17 June 2014 and 29 December 2015. |
| 4 | The time-varying conditional correlations are based on the BEKK model with shift dummies. The time-varying conditional correlation values for the first model are not reported for the sake of brevity, but the corresponding author will make them available upon reasonable request. |
| 5 | The dynamic weights are based on the BEKK model with shift dummies. The dynamic weights for the first model are not reported for the sake of brevity, but the corresponding author will make them available upon reasonable request. |
| 6 | The dynamic hedge ratios are based on the BEKK model with shift dummies. The dynamic hedge ratios for the first model are not reported for the sake of brevity, but the corresponding author will make them available upon reasonable request. |
| 7 | To conserve space, we did not include a self-contained description of the model. For a comprehensive description of this methodology, see Dieobold and Yilmaz (2012). |
References
- Abakah, Emmanuel Joel Aikins, Aviral Kumar Tiwari, Imhotep Paul Alagidede, and Shawkat Hammoudeh. 2023. Nonlinearity in the causality and systemic risk spillover between the OPEC oil and GCC equity markets: A pre- and post-financial crisis analysis. Empirical Economics 65: 1027–103. [Google Scholar] [CrossRef]
- Abuzayed, Bana, and Nedal Al-Fayoumi. 2021. Risk spillover from crude oil prices to GCC stock market returns: New evidence during the COVID-19 outbreak. The North American Journal of Economics and Finance 58: 101476. [Google Scholar] [CrossRef]
- Ahmad, Wasim. 2017. On the dynamic dependence and investment performance of crude oil and clean energy stocks. Research in International Business and Finance 42: 376–89. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, and Ahmet Sensoy. 2021a. Financial contagion during COVID-19 crisis. Finance Research Letters 38: 101604. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, Brian M. Lucey, and Ahmet Sensoy. 2021b. Is gold a hedge or a safe-haven asset in the COVID-19 crisis? Economic Modelling 102: 105588. [Google Scholar] [CrossRef]
- Al-Nassar, Nassar S., and Beljid Makram. 2022. The COVID-19 Outbreak and Risk–Return Spillovers between Main and SME Stock Markets in the MENA Region. International Journal of Financial Studies 10: 6. [Google Scholar] [CrossRef]
- Al-Nassar, Nassar S., Sabri Boubaker, Anis Chaibi, and Beljid Makram. 2022. In search of hedges and safe havens during the COVID-19 pandemic: Gold versus Bitcoin, oil, and oil uncertainty. The Quarterly Review of Economics and Finance 90: 318–32. [Google Scholar] [CrossRef]
- Alotaibi, Abdullah R., and Anil V. Mishra. 2017. Time varying international financial integration for GCC stock markets. The Quarterly Review of Economics and Finance 63: 66–78. [Google Scholar] [CrossRef]
- Al-Rodhan, Khalid R. 2005. The Saudi and Gulf Stock Markets: Irrational Exuberance or Markets Efficiency. Washington, DC: Center for Strategic and International Studies CSIS. Available online: https://www.csis.org/analysis/saudi-and-gulf-stock-markets-irrational-exuberance-or-markets-efficiency (accessed on 19 June 2022).
- Al-Yahyaee, Khamis Hamed, Walid Mensi, Ahmet Sensoy, and Sang Hoon Kang. 2019. Energy, precious metals, and GCC stock markets: Is there any risk spillover? Pacific-Basin Finance Journal 56: 45–70. [Google Scholar] [CrossRef]
- Andreou, Elena, and Eric Ghysels. 2002. Detecting multiple breaks in financial market volatility dynamics. Journal of Applied Econometrics 17: 579–600. [Google Scholar] [CrossRef]
- Apostolakis, George N., Christos Floros, Konstantinos Gkillas, and Mark Wohar. 2021. Political uncertainty, COVID-19 pandemic and stock market volatility transmission. Journal of International Financial Markets, Institutions and Money 74: 101383. [Google Scholar] [CrossRef]
- Arouri, Mohamed El Hedi, Amine Lahiani, and Duc Khuong Nguyen. 2011. Return and volatility transmission between world oil prices and stock markets of the GCC countries. Economic Modelling 28: 1815–25. [Google Scholar] [CrossRef]
- Asness, Clifford, Andrea Frazzini, Ronen Israel, Tobias J. Moskowitz, and Lasse H. Pedersen. 2018. Size matters, if you control your junk. Journal of Financial Economics 129: 479–509. [Google Scholar] [CrossRef]
- Awartani, Basel, and Aktham Issa Maghyereh. 2013. Dynamic spillovers between oil and stock markets in the Gulf Cooperation Council Countries. Energy Economics 36: 28–42. [Google Scholar] [CrossRef]
- Badrinath, Swaminathan G., Jayant R. Kale, and Thomas H. Noe. 1995. Of Shepherds, Sheep, and the Cross-autocorrelations in Equity Returns. The Review of Financial Studies 8: 401–30. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Ahmed H. Elsayed, and Shawkat Hammoudeh. 2023. Financial connectedness and risk transmission among MENA countries: Evidence from connectedness network and clustering analysis1. Journal of International Financial Markets, Institutions and Money 82: 101656. [Google Scholar] [CrossRef]
- Balcılar, Mehmet, Rıza Demirer, and Shawkat Hammoudeh. 2015. Regional and global spillovers and diversification opportunities in the GCC equity sectors. Emerging Markets Review 24: 160–87. [Google Scholar] [CrossRef]
- Balli, Faruk, Syed Abul Basher, and Rosmy Jean Louis. 2013. Sectoral equity returns and portfolio diversification opportunities across the GCC region. Journal of International Financial Markets, Institutions and Money 25: 33–48. [Google Scholar] [CrossRef]
- Bani-Khalaf, Omar, and Nigar Taspinar. 2022. Oil and gold return spillover and stock market elasticity during COVID-19 pandemic: A comparative study between the stock markets of oil-exporting countries and oil-importing countries in the Middle East. Resources Policy 79: 102935. [Google Scholar] [CrossRef]
- Banz, Rolf W. 1981. The relationship between return and market value of common stocks. Journal of Financial Economics 9: 3–18. [Google Scholar] [CrossRef]
- Baruník, Jozef, and Tomáš Křehlík. 2018. Measuring the Frequency Dynamics of Financial Connectedness and Systemic Risk. Journal of Financial Econometrics 16: 271–96. [Google Scholar] [CrossRef]
- Basher, Syed Abul, Alfred A. Haug, and Perry Sadorsky. 2018. The impact of oil-market shocks on stock returns in major oil-exporting countries. Journal of International Money and Finance 86: 264–80. [Google Scholar] [CrossRef]
- Bauwens, Luc, Sébastien Laurent, and Jeroen V. K. Rombouts. 2006. Multivariate GARCH models: A survey. Journal of Applied Econometrics 21: 79–109. [Google Scholar] [CrossRef]
- Boldanov, Rustam, Stavros Degiannakis, and George Filis. 2016. Time-varying correlation between oil and stock market volatilities: Evidence from oil-importing and oil-exporting countries. International Review of Financial Analysis 48: 209–20. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the Coherence in Short-Run Nominal Exchange Rates: A Multivariate Generalized Arch Model. The Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Boubaker, Sabri, and Jamel Jouini. 2014. Linkages between emerging and developed equity markets: Empirical evidence in the PMG framework. The North American Journal of Economics and Finance 29: 322–35. [Google Scholar] [CrossRef]
- Boubaker, Sabri, Jamel Jouini, and Amine Lahiani. 2016. Financial contagion between the US and selected developed and emerging countries: The case of the subprime crisis. The Quarterly Review of Economics and Finance 61: 14–28. [Google Scholar] [CrossRef]
- Boubaker, Sabri, John W. Goodell, Dharen Kumar Pandey, and Vineeta Kumari. 2022. Heterogeneous impacts of wars on global equity markets: Evidence from the invasion of Ukraine. Finance Research Letters 48: 102934. [Google Scholar] [CrossRef]
- Boudoukh, Jacob, Matthew Richardson, and Robert Whitelaw. 1994. A tale of three schools: Insights on autocorrelations of short-horizon stock returns. The Review of Financial Studies 7: 539–73. [Google Scholar] [CrossRef]
- Bouri, Elie, Rami Hammoud, and Christina Abou Kassm. 2023. The effect of oil implied volatility and geopolitical risk on GCC stock sectors under various market conditions. Energy Economics 120: 106617. [Google Scholar] [CrossRef]
- Butler, Kirt C., and Saleh Jameel Malaikah. 1992. Efficiency and inefficiency in thinly traded stock markets: Kuwait and Saudi Arabia. Journal of Banking & Finance 16: 197–210. [Google Scholar] [CrossRef]
- Caporin, Massimiliano, and Michael McAleer. 2012. Do we really need both BEKK and DCC? A tale of two multivariate GARCH models. Journal of Economic Surveys 26: 736–51. [Google Scholar] [CrossRef]
- Chan, Louis K. C., Jason Karceski, and Josef Lakonishok. 2000. New Paradigm or Same Old Hype in Equity Investing? Financial Analysts Journal 56: 23–36. [Google Scholar] [CrossRef]
- Charfeddine, Lanouar, and Hisham Al Refai. 2019. Political tensions, stock market dependence and volatility spillover: Evidence from the recent intra-GCC crises. The North American Journal of Economics and Finance 50: 101032. [Google Scholar] [CrossRef]
- Chelley-Steeley, Patricia L., and James M. Steeley. 1996. Volatility, leverage and firm size: The UK evidence. The Manchester School 64: 83–103. [Google Scholar] [CrossRef]
- Conrad, Jennifer, Mustafa N. Gultekin, and Gautam Kaul. 1991. Asymmetric Predictability of Conditional Variances. The Review of Financial Studies 4: 597–622. [Google Scholar] [CrossRef]
- De Moor, Lieven, and Piet Sercu. 2013. The smallest firm effect: An international study. Journal of International Money and Finance 32: 129–55. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Dieobold, Francis X. 1986. Modeling The persistence of Conditional Variances: A Comment. Econometric Reviews 5: 51–56. [Google Scholar] [CrossRef]
- Dieobold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Drakos, Anastassios A. 2016. Does the relationship between small and large portfolios’ returns confirm the lead–lag effect? Evidence from the Athens Stock Exchange. Research in International Business and Finance 36: 546–61. [Google Scholar] [CrossRef]
- El Khoury, Rim, Nohade Nasrallah, Khaled Hussainey, and Rima Assaf. 2023. Spillover analysis across FinTech, ESG, and renewable energy indices before and during the Russia–Ukraine war: International evidence. Journal of International Financial Management & Accounting 34: 279–317. [Google Scholar] [CrossRef]
- Eleswarapu, Venkat R., and Marc R. Reinganum. 1993. The seasonal behavior of the liquidity premium in asset pricing. Journal of Financial Economics 34: 373–86. [Google Scholar] [CrossRef]
- Elsayed, Ahmed H., Nader Naifar, Gazi Salah Uddin, and Gang-Jin Wang. 2023. Multilayer information spillover networks between oil shocks and banking sectors: Evidence from oil-rich countries. International Review of Financial Analysis 87: 102602. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. Dynamic Conditional Correlation. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert F, and Kenneth F. Kroner. 1995. Multivariate Simultaneous Generalized Arch. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Engle, Robert F., and Victor K. Ng. 1993. Measuring and Testing the Impact of News on Volatility. The Journal of Finance 48: 1749–78. [Google Scholar] [CrossRef]
- Ewing, Bradley T., and Farooq Malik. 2005. Re-examining the asymmetric predictability of conditional variances: The role of sudden changes in variance. Journal of Banking & Finance 29: 2655–73. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Fiorentini, Gabriele, Enrique Sentana, and Giorgio Calzolari. 2003. Maximum Likelihood Estimation and Inference in Multivariate Conditionally Heteroscedastic Dynamic Regression Models With Student t Innovations. Journal of Business & Economic Statistics 21: 532–46. [Google Scholar] [CrossRef]
- Francis, Bill B., Mbodja Mougoué, and Valentyn Panchenko. 2010. Is there a symmetric nonlinear causal relationship between large and small firms? Journal of Empirical Finance 17: 23–38. [Google Scholar] [CrossRef]
- Giudici, Paolo, and Gloria Polinesi. 2021. Crypto price discovery through correlation networks. Annals of Operations Research 299: 443–57. [Google Scholar] [CrossRef]
- Halunga, Andreea G., and Christos S. Savva. 2019. Neglecting structural breaks when estimating and valuing dynamic correlations for asset allocation. Econometric Reviews 38: 660–78. [Google Scholar] [CrossRef]
- Hamao, Yasushi, Ronald W. Masulis, and Victor Ng. 1990. Correlations in Price Changes and Volatility across International Stock Markets. The Review of Financial Studies 3: 281–307. [Google Scholar] [CrossRef]
- Hamdi, Besma, Mouna Aloui, Faisal Alqahtani, and Aviral Tiwari. 2019. Relationship between the oil price volatility and sectoral stock markets in oil-exporting economies: Evidence from wavelet nonlinear denoised based quantile and Granger-causality analysis. Energy Economics 80: 536–52. [Google Scholar] [CrossRef]
- Hammoudeh, Shawkat M., Yuan Yuan, and Michael McAleer. 2009. Shock and volatility spillovers among equity sectors of the Gulf Arab stock markets. The Quarterly Review of Economics and Finance 49: 829–42. [Google Scholar] [CrossRef]
- Harris, Richard D. F., and Anirut Pisedtasalasai. 2006. Return and Volatility Spillovers Between Large and Small Stocks in the UK. Journal of Business Finance & Accounting 33: 1556–71. [Google Scholar] [CrossRef]
- Hasan, Iftekhar, and Bill B. Francis. 1998. Macroeconomic Factors and the Asymmetric Predictability of Conditional Variances. European Financial Management 4: 207–30. [Google Scholar] [CrossRef]
- Hassan, M. Kabir, Hadrian Geri Djajadikerta, Tonmoy Choudhury, and Muhammad Kamran. 2021. Safe havens in Islamic financial markets: COVID-19 versus GFC. Global Finance Journal 54: 100643. [Google Scholar] [CrossRef]
- Henry, Ólan T., and John Sharma. 1999. Asymmetric Conditional Volatility and Firm Size: Evidence from Australian Equity Portfolios. Australian Economic Papers 38: 393–406. [Google Scholar] [CrossRef]
- Hirshleifer, David. 2001. Investor Psychology and Asset Pricing. The Journal of Finance 56: 1533–97. [Google Scholar] [CrossRef]
- Huang, Wei. 2007. Financial integration and the price of world covariance risk: Large- vs. small-cap stocks. Journal of International Money and Finance 26: 1311–37. [Google Scholar] [CrossRef]
- James Chu, Chia Shang. 1995. Detecting parameter shift in garch models. Econometric Reviews 14: 241–66. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Jena, Sangram Keshari, Aviral Kumar Tiwari, Ashutosh Dash, and Emmanuel Joel Aikins Abakah. 2021. Volatility Spillover Dynamics between Large-, Mid-, and Small-Cap Stocks in the Time-Frequency Domain: Implications for Portfolio Management. Journal of Risk and Financial Management 14: 531. [Google Scholar] [CrossRef]
- Karmakar, Madhusudan. 2010. Information transmission between small and large stocks in the National Stock Exchange in India: An empirical study. The Quarterly Review of Economics and Finance 50: 110–20. [Google Scholar] [CrossRef]
- Katiyar, Saurabh, and Neeraj Dabake. 2019. Factor investing in Saudi Arabia: Size Matters. Available online: https://www.msci.com/www/blog-posts/factor-investing-in-saudi/01477760798 (accessed on 7 May 2022).
- Keim, Donald B. 1999. An analysis of mutual fund design: The case of investing in small-cap stocks. Journal of Financial Economics 51: 173–94. [Google Scholar] [CrossRef]
- Klein, Tony, Hien Pham Thu, and Thomas Walther. 2018. Bitcoin is not the New Gold—A comparison of volatility, correlation, and portfolio performance. International Review of Financial Analysis 59: 105–16. [Google Scholar] [CrossRef]
- Koulakiotis, Athanasios, Vassilios Babalos, and Nicholas Papasyriopoulos. 2016. Financial crisis, liquidity and dynamic linkages between large and small stocks: Evidence from the Athens Stock Exchange. Journal of International Financial Markets, Institutions and Money 40: 46–62. [Google Scholar] [CrossRef]
- Kroner, Kenneth F, and Jahangir Sultan. 1993. Time-Varying Distributions and Dynamic Hedging with Foreign Currency Futures. The Journal of Financial and Quantitative Analysis 28: 535–51. [Google Scholar] [CrossRef]
- Kroner, Kenneth F., and Victor K. Ng. 1998. Modeling asymmetric comovements of asset returns. Review of Financial Studies 11: 817–44. [Google Scholar] [CrossRef]
- Lamoureux, Christopher G., and William D. Lastrapes. 1990. Persistence in Variance, Structural Change, and the GARCH Model. Journal of Business & Economic Statistics 8: 225–34. [Google Scholar] [CrossRef]
- Lastrapes, William D. 1989. Exchange rate volatility and U.S. monetary policy: An ARCH application. Journal of Money, Credit and Banking 21: 66–77. [Google Scholar] [CrossRef]
- Lerner, Josh, Ann Leamon, and Steve Dew. 2017. The CMA and the Saudi Stock Market Crash of 2006. BELLA Research Group and Saudi Capital Market Authority (CMA). Available online: https://cma.org.sa/en/Market/Documents/CMA_Crash2006_en.pdf (accessed on 15 June 2022).
- Lo, Andrew W., and A. Craig MacKinlay. 1990a. An econometric analysis of nonsynchronous trading. Journal of Econometrics 45: 181–211. [Google Scholar] [CrossRef]
- Lo, Andrew W., and A. Craig MacKinlay. 1990b. When Are Contrarian Profits Due to Stock Market Overreaction? The Review of Financial Studies 3: 175–205. [Google Scholar] [CrossRef]
- Marcelo, José Luis M., José Luis Miralles Quirós, and María Mar Miralles Quirós. 2008. Asymmetric variance and spillover effects: Regime shifts in the Spanish Stock Market. Journal of International Financial Markets, Institutions and Money 18: 1–15. [Google Scholar] [CrossRef]
- Marshall, Pablo, and Eduardo Walker. 2002. Asymmetric Reaction to Information and Serial Dependence of Short-Run Returns. Journal of Applied Economics 5: 273–92. [Google Scholar] [CrossRef]
- McQueen, Grant, Michael Pinegar, and Steven Thorley. 1996. Delayed Reaction to Good News and the Cross-Autocorrelation of Portfolio Returns. The Journal of Finance 51: 889–919. [Google Scholar] [CrossRef]
- Mech, Timothy S. 1993. Portfolio return autocorrelation. Journal of Financial Economics 34: 307–44. [Google Scholar] [CrossRef]
- Mensi, Walid, Khamis Hamed Al-Yahyaee, Xuan Vinh Vo, and Sang Hoon Kang. 2021. Modeling the frequency dynamics of spillovers and connectedness between crude oil and MENA stock markets with portfolio implications. Economic Analysis and Policy 71: 397–419. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, and Aviral Kumar Tiwari. 2016. New evidence on hedges and safe havens for Gulf stock markets using the wavelet-based quantile. Emerging Markets Review 28: 155–83. [Google Scholar] [CrossRef]
- Mills, Terence C., and Jordan V. Jordanov. 2001. Lead-lag patterns between small and large size portfolios in the London stock exchange. Applied Financial Economics 11: 489–95. [Google Scholar] [CrossRef]
- Mohanty, Sunil K., Mohan Nandha, Abdullah Q. Turkistani, and Muhammed Y. Alaitani. 2011. Oil price movements and stock market returns: Evidence from Gulf Cooperation Council (GCC) countries. Global Finance Journal 22: 42–55. [Google Scholar] [CrossRef]
- Neaime, Simon. 2016. Financial crises and contagion vulnerability of MENA stock markets. Emerging Markets Review 27: 14–35. [Google Scholar] [CrossRef]
- Nyblom, Jukka. 1989. Testing for the Constancy of Parameters over Time. Journal of the American Statistical Association 84: 223–30. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Rahman, M. Arifur, Shah Saeed Hassan Chowdhury, and M. Shibley Sadique. 2015. Herding where retail investors dominate trading: The case of Saudi Arabia. The Quarterly Review of Economics and Finance 57: 46–60. [Google Scholar] [CrossRef]
- Reinganum, Marc R. 1983. Portfolio strategies based on market capitalization. The Journal of Portfolio Management 9: 29. [Google Scholar] [CrossRef]
- Reinganum, Marc R. 1999. The significance of market capitalization in portfolio management over time. The Journal of Portfolio Management 25: 39–50. [Google Scholar] [CrossRef]
- Reyes, Mario G. 2001. Asymmetric volatility spillover in the Tokyo Stock Exchange. Journal of Economics & Finance 25: 206–13. [Google Scholar] [CrossRef]
- Ross, Stephen A. 1989. Information and Volatility: The No-Arbitrage Martingale Approach to Timing and Resolution Irrelevancy. The Journal of Finance 44: 1–17. [Google Scholar] [CrossRef]
- Silvennoinen, Annastiina, and Timo Teräsvirta. 2009. Multivariate GARCH models. In Handbook of Financial Time Series. Edited by T. Mikosch, J. P. Kreiß, R. A. Davis and T. G. Andersen. Berlin/Heidelberg: Springer, pp. 201–29. [Google Scholar]
- van Dijk, Mathijs A. 2011. Is size dead? A review of the size effect in equity returns. Journal of Banking & Finance 35: 3263–74. [Google Scholar] [CrossRef]
- Wang, Jun, Robert Brooks, Xing Lu, and Hunter M. Holzhauer. 2014. Growth/Value, market cap, and momentum. The Journal of Investing 23: 33–42. [Google Scholar] [CrossRef]
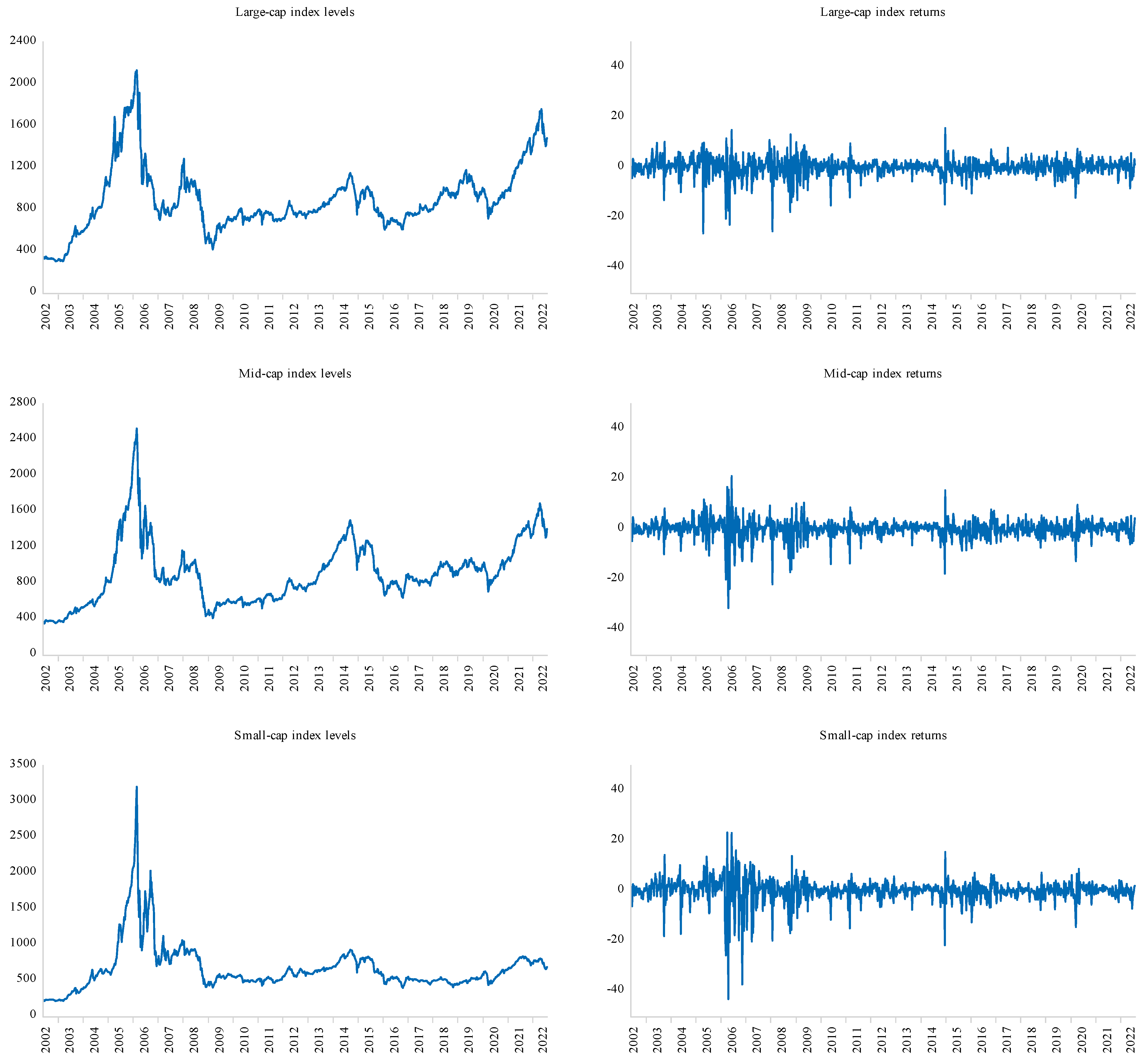
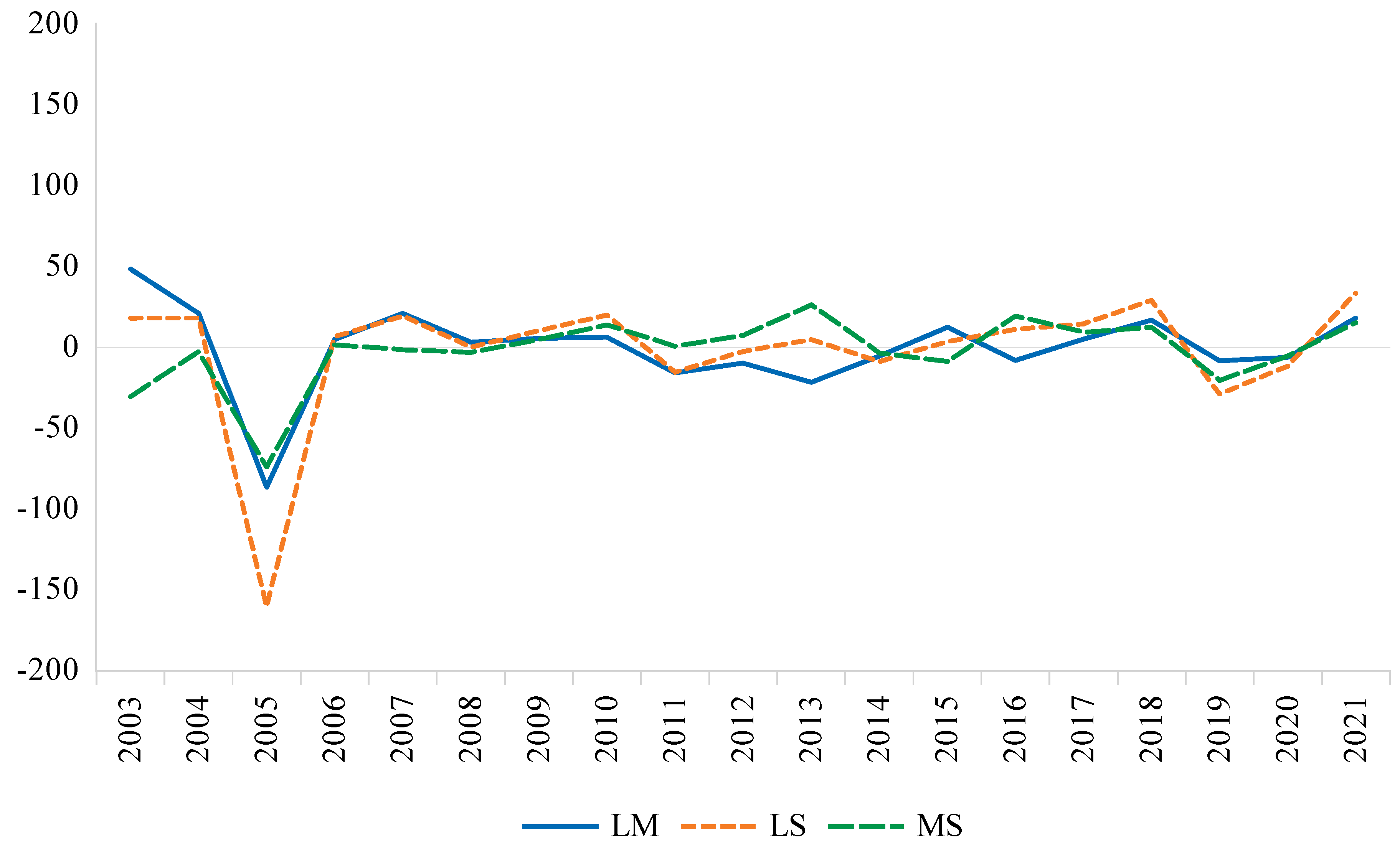
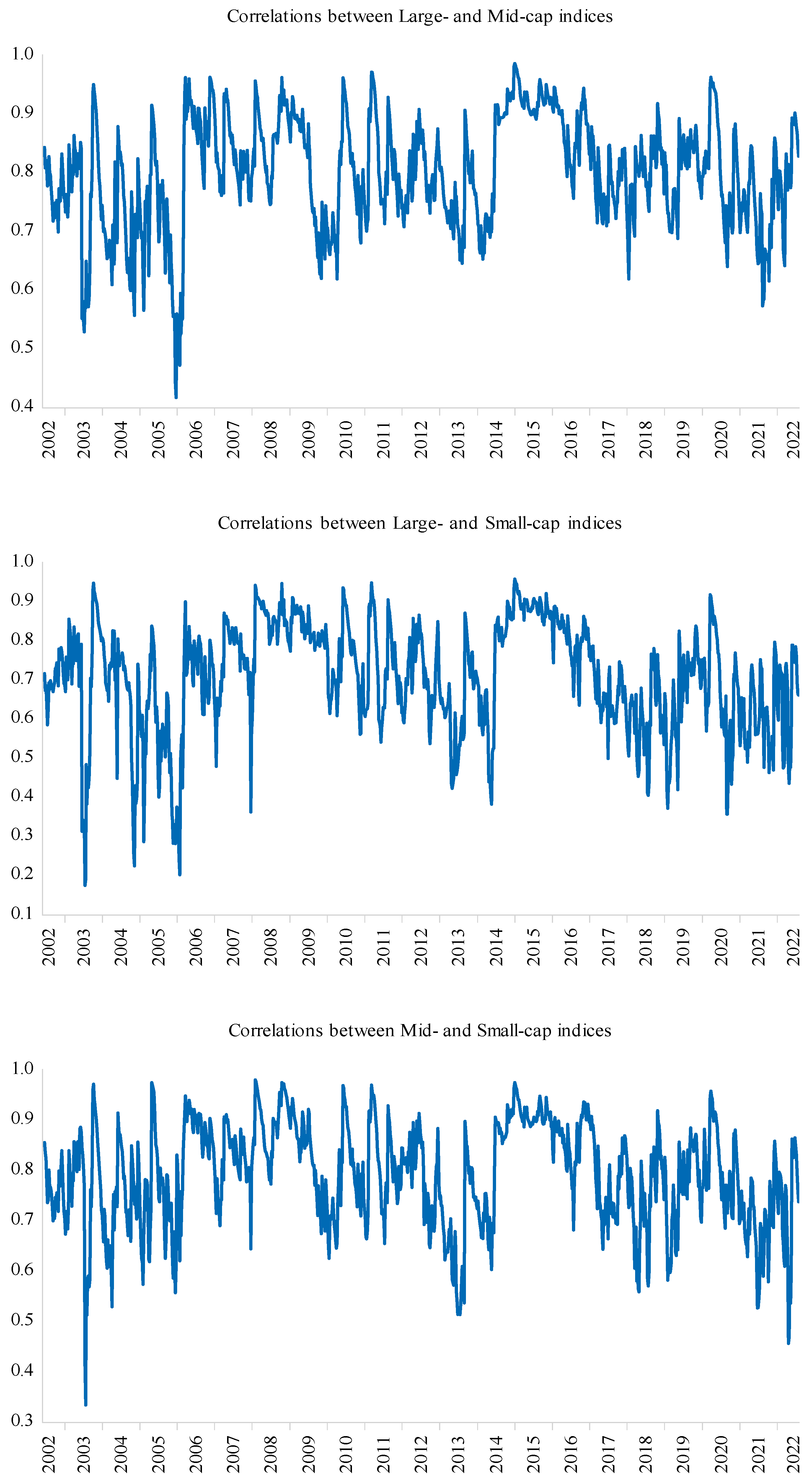
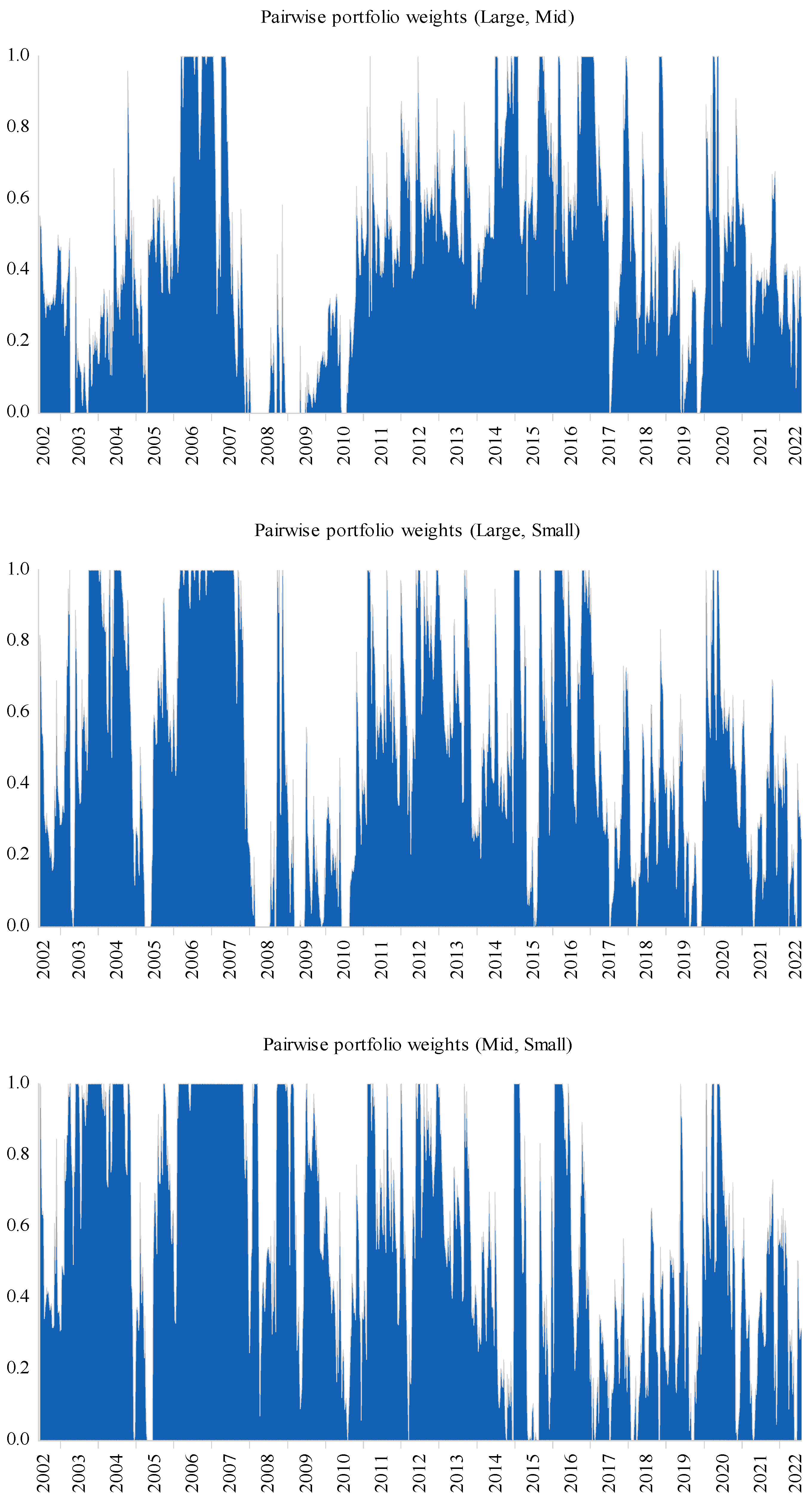
| Large | Mid | Small | |
|---|---|---|---|
| Mean | 0.14 | 0.13 | 0.10 |
| Median | 0.40 | 0.41 | 0.47 |
| Max | 15.79 | 21.29 | 23.39 |
| Min | −26.12 | −31.36 | −43.13 |
| Std. Dev. | 3.85 | 3.90 | 4.71 |
| Skewness | −1.30 | −1.31 | −1.92 |
| Kurtosis | 10.56 | 12.87 | 17.91 |
| Student t | 1.17 | 1.06 | 0.72 |
| Obs. | 1051 | 1051 | 1051 |
| J-B | 2798.92 *** | 4562.39 *** | 10383.45 *** |
| ADF | −32.03 *** | −11.65 *** | −15.54 *** |
| PP | −32.06 *** | −31.93 *** | −29.37 *** |
| Q(4) | 3.33 | 22.66 *** | 40.72 *** |
| ARCH–LM(4) | 108.43 *** | 233.38 *** | 135.15 *** |
| Large | Mid | Small | |
|---|---|---|---|
| 0.32 ** (2.41) | 0.19 (1.42) | 0.54 *** (5.43) | |
| −0.10 (−0.73) | −0.14 (−1.02) | −0.09 (−0.54) | |
| 0.08 (0.61) | −0.12 (−0.86) | −0.03 (−0.18) | |
| Joint test | 2.18 * | 1.26 | 3.61 ** |
| 0.19 (0.95) | −0.11 (−0.56) | 0.57 ** (2.40) | |
| −0.04 (−0.33) | −0.03 (−0.25) | 0.13 (0.95) | |
| −0.14 (−0.82) | −0.44 ** (−2.34) | −0.10 (−0.46) | |
| Joint test | 2.12 * | 2.49 * | 3.86 *** |
| Large | Mid | Small | |
|---|---|---|---|
| Large | 1.00 | ||
| Mid | 0.84 | 1.00 | |
| Small | 0.71 | 0.85 | 1.00 |
| BEKK | BEKK with Shift Dummies | |||||
|---|---|---|---|---|---|---|
| Coeff | t-Stat | p-Value | Coeff | t-Stat | p-Value | |
| Mean | ||||||
| 0.29 | 4.57 | 0.00 | 0.30 | 4.72 | 0.00 | |
| 0.02 | 0.44 | 0.66 | 0.01 | 0.31 | 0.76 | |
| 0.04 | 0.84 | 0.40 | 0.05 | 1.04 | 0.30 | |
| −0.03 | −1.08 | 0.28 | −0.04 | −1.17 | 0.24 | |
| 0.34 | 5.64 | 0.00 | 0.34 | 5.62 | 0.00 | |
| 0.04 | 1.07 | 0.29 | 0.04 | 1.10 | 0.27 | |
| 0.05 | 1.10 | 0.27 | 0.05 | 1.11 | 0.27 | |
| −0.03 | −1.02 | 0.31 | −0.04 | −1.15 | 0.25 | |
| 0.27 | 4.49 | 0.00 | 0.28 | 4.48 | 0.00 | |
| 0.00 | −0.03 | 0.98 | 0.00 | −0.04 | 0.96 | |
| 0.12 | 2.86 | 0.00 | 0.12 | 2.60 | 0.01 | |
| 0.01 | 0.15 | 0.88 | 0.00 | 0.01 | 1.00 | |
| Variance | ||||||
| 0.65 | 5.90 | 0.00 | 0.69 | 5.99 | 0.00 | |
| 0.79 | 7.61 | 0.00 | 0.69 | 4.92 | 0.00 | |
| 0.22 | 2.14 | 0.03 | 0.37 | 2.89 | 0.00 | |
| 0.52 | 5.09 | 0.00 | 0.49 | 4.46 | 0.00 | |
| 0.36 | 3.29 | 0.00 | 0.34 | 3.70 | 0.00 | |
| 0.18 | 0.79 | 0.43 | 0.27 | 2.63 | 0.01 | |
| 0.18 | 2.81 | 0.00 | 0.25 | 2.46 | 0.01 | |
| −0.03 | −0.65 | 0.52 | −0.01 | −0.07 | 0.94 | |
| −0.06 | −1.28 | 0.20 | −0.05 | −0.66 | 0.51 | |
| 0.22 | 5.39 | 0.00 | 0.12 | 0.91 | 0.36 | |
| 0.33 | 9.33 | 0.00 | 0.29 | 2.64 | 0.01 | |
| 0.06 | 1.09 | 0.28 | 0.05 | 0.54 | 0.59 | |
| 0.01 | 0.13 | 0.89 | 0.02 | 0.46 | 0.65 | |
| 0.12 | 2.89 | 0.00 | 0.12 | 2.62 | 0.01 | |
| 0.45 | 10.48 | 0.00 | 0.45 | 8.54 | 0.00 | |
| 0.97 | 74.75 | 0.00 | 0.94 | 24.20 | 0.00 | |
| 0.01 | 2.96 | 0.00 | 0.01 | 0.11 | 0.92 | |
| 0.03 | 2.61 | 0.01 | 0.04 | 0.93 | 0.35 | |
| −0.14 | −9.95 | 0.00 | −0.11 | −1.64 | 0.10 | |
| 0.84 | 40.15 | 0.00 | 0.84 | 11.89 | 0.00 | |
| −0.11 | −4.22 | 0.00 | −0.11 | −1.72 | 0.09 | |
| 0.03 | 2.73 | 0.01 | 0.02 | 0.67 | 0.50 | |
| −0.01 | −0.47 | 0.64 | −0.01 | −0.31 | 0.76 | |
| 0.92 | 51.13 | 0.00 | 0.91 | 26.18 | 0.00 | |
| 0.59 | 8.70 | 0.00 | 0.62 | 5.78 | 0.00 | |
| 0.61 | 8.66 | 0.00 | 0.67 | 5.84 | 0.00 | |
| 0.41 | 5.84 | 0.00 | 0.47 | 4.18 | 0.00 | |
| −0.23 | −4.06 | 0.00 | −0.37 | −1.61 | 0.11 | |
| −0.10 | −1.64 | 0.10 | −0.25 | −0.94 | 0.35 | |
| 0.14 | 2.76 | 0.01 | 0.01 | 0.03 | 0.98 | |
| −0.32 | −5.39 | 0.00 | −0.27 | −2.36 | 0.02 | |
| −0.41 | −6.74 | 0.00 | −0.39 | −3.32 | 0.00 | |
| −0.41 | −4.96 | 0.00 | −0.41 | −3.69 | 0.00 | |
| Shape (t degrees) | 4.83 | 12.88 | 0.00 | 4.97 | 13.20 | 0.00 |
| Log L | −6601.23 | −6591.54 | ||||
| AIC | 12.66 | 12.67 | ||||
| SC | 12.88 | 12.94 | ||||
| HQ | 12.66 | 12.67 | ||||
| BEKK | BEKK with Shift Dummies | |||||
|---|---|---|---|---|---|---|
| Large | Mid | Small | Large | Mid | Small | |
| Panel A: | ||||||
| 9.21 | 7.24 | 2.45 | 7.07 | 1.83 | 4.42 | |
| p-value | 0.06 | 0.12 | 0.65 | 0.13 | 0.77 | 0.35 |
| 1.07 | 1.59 | 8.98 | 1.28 | 1.00 | 31.14 | |
| p-value | 0.90 | 0.81 | 0.06 | 0.86 | 0.91 | 0.00 |
| Panel B: | ||||||
| Nyblom’s test | ||||||
| Joint test | Test Stat = 9.50 | p-value = 0.04 | Test Stat = 10.12 | p-value = 0.33 | ||
| The Portfolio of Interest | Mean Equation | Variance Equation |
|---|---|---|
| All portfolios | The null hypothesis of exogeneity , Test statistic: 2.17 ** Result: Reject | The null hypothesis of diagonal BEKK , Test statistic: 5.45 *** Result: Reject |
| Large | The null hypothesis of exogeneity Test statistic: 0.53 Result: Accept | The null hypothesis that shocks to the mid- and small portfolios do not affect the variance of interest: Test statistic: 6.03 *** Result: Reject |
| Mid | The null hypothesis of exogeneity , Test statistic: 0.81 Result: Accept | The null hypothesis that shocks to the large and small portfolios do not affect the variance of interest: Test statistic: 2.38 ** Result: Reject |
| Small | The null hypothesis of exogeneity , Test statistic: 4.30 ** Result: Reject | The null hypothesis that shocks to the large and mid-portfolios do not affect the variance of interest: Test statistic: 2.30 * Result: Reject |
| All portfolios | The null of symmetric behavior in variance , Test statistic: 10.12 *** Result: Reject |
| The Portfolio of Interest | Mean Equation | Variance Equation |
|---|---|---|
| All portfolios | The null hypothesis of exogeneity , Test statistic: 1.97 * Result: Reject | The null hypothesis of diagonal BEKK , Test statistic: 2.80 *** Result: Reject |
| Large | The null hypothesis of exogeneity Test statistic: 0.80 Result: Accept | The null hypothesis that shocks to the mid- and small portfolios do not affect the variance of interest: Test statistic: 1. Result: Accept |
| Mid | The null hypothesis of exogeneity , Test statistic: 1.05 Result: Accept | The null hypothesis that shocks to the large and small portfolios do not affect the variance of interest: Test statistic: 2.25 * Result: Reject |
| Small | The null hypothesis of exogeneity , Test statistic: 4.37 ** Result: Reject | The null hypothesis that shocks to the large and mid-portfolios do not affect the variance of interest: Test statistic: 1.03 Result: Accept |
| All portfolios | The null of symmetric behavior in variance , Test statistic: 10.09 *** Result: Reject |
| Mean | Std. Dev. | Min | Max | |
|---|---|---|---|---|
| Panel A: BEKK | ||||
| L/M | 0.46 | 0.29 | 0.00 | 1.00 |
| L/S | 0.51 | 0.33 | 0.00 | 1.00 |
| M/S | 0.57 | 0.32 | 0.00 | 1.00 |
| Panel B: BEKK with shift dummies | ||||
| L/M | 0.46 | 0.29 | 0.00 | 1.00 |
| L/S | 0.51 | 0.33 | 0.00 | 1.00 |
| M/S | 0.58 | 0.33 | 0.00 | 1.00 |
| Mean | Std. Dev. | Min | Max | |
|---|---|---|---|---|
| Panel A: BEKK | ||||
| L/M | 0.79 | 0.16 | 0.37 | 1.23 |
| L/S | 0.75 | 0.24 | 0.14 | 1.53 |
| M/S | 0.85 | 0.21 | 0.36 | 1.62 |
| Panel B: BEKK with shift dummies | ||||
| L/M | 0.78 | 0.16 | 0.35 | 1.28 |
| L/S | 0.74 | 0.24 | 0.13 | 1.50 |
| M/S | 0.85 | 0.21 | 0.34 | 1.54 |
| From | ||||
|---|---|---|---|---|
| To | Large | Mid | Small | Contribution from Others |
| Large | 49.52 | 27.57 | 22.91 | 50.48 |
| Mid | 26.92 | 46.91 | 26.17 | 53.09 |
| Small | 21.94 | 27.39 | 50.67 | 49.33 |
| Contribution to others | 48.86 | 54.96 | 49.08 | 152.89 |
| Contribution including own | 98.37 | 101.87 | 99.75 | Total connectedness index |
| Net volatility connectedness | −1.63 | 1.87 | −0.25 | 50.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Nassar, N.S. The Dynamic Return and Volatility Spillovers among Size-Based Stock Portfolios in the Saudi Market and Their Portfolio Management Implications during Different Crises. Int. J. Financial Stud. 2023, 11, 113. https://doi.org/10.3390/ijfs11030113
Al-Nassar NS. The Dynamic Return and Volatility Spillovers among Size-Based Stock Portfolios in the Saudi Market and Their Portfolio Management Implications during Different Crises. International Journal of Financial Studies. 2023; 11(3):113. https://doi.org/10.3390/ijfs11030113
Chicago/Turabian StyleAl-Nassar, Nassar S. 2023. "The Dynamic Return and Volatility Spillovers among Size-Based Stock Portfolios in the Saudi Market and Their Portfolio Management Implications during Different Crises" International Journal of Financial Studies 11, no. 3: 113. https://doi.org/10.3390/ijfs11030113
APA StyleAl-Nassar, N. S. (2023). The Dynamic Return and Volatility Spillovers among Size-Based Stock Portfolios in the Saudi Market and Their Portfolio Management Implications during Different Crises. International Journal of Financial Studies, 11(3), 113. https://doi.org/10.3390/ijfs11030113






