Abstract
In recent years, a great deal of attention has been devoted to the use of neural networks in portfolio management, particularly in the prediction of stock prices. Building a more profitable portfolio with less risk has always been a challenging task. In this study, we propose a model to build a portfolio according to an equity-market-neutral (EMN) investment strategy. In this portfolio, the selection of stocks comprises two steps: a prediction of the individual returns of stocks using LSTM neural network, followed by a ranking of these stocks according to their predicted returns. The stocks with the best predicted returns and those with the worst predicted returns constitute, respectively, the long side and the short side of the portfolio to be built. The proposed model has two key benefits. First, data from historical quotes and technical and fundamental indicators are used in the LSTM network to provide good predictions. Second, the EMN strategy allows for the funding of long-position stocks by short-sell-position stocks, thus hedging the market risk. The results show that the built portfolios performed better compared to the benchmarks. Nonetheless, performance slowed down during the COVID-19 pandemic.
1. Introduction
According to the market efficiency hypothesis developed by Fama (1970), it is impossible to make accurate predictions about stock prices in the future, because the current prices of financial assets reflect all the information that is available, and thus there is no such thing as an undervalued or overvalued stock. Nonetheless, many empirical studies have debunked this hypothesis, and have shown that, with some methods and techniques, it is possible to make good predictions about future stock prices. Most of these techniques use historical stock prices and/or financial information from the issuing companies, as part of two well-known types of stock analysis: fundamental analysis and technical analysis (Carhart 1997).
Since the foundational work of Markowitz (1952), which established the mathematical foundations of portfolio construction, many statistical and econometric models have been developed in order to predict the future prices and returns of financial assets, such as the Capital Asset Pricing Model (CAPM) in 1961, the Three Factor Model by Fama and French (1993), the Four Factor Model by Carhart (1997), the Autoregressive Model (AR) by Yule (1926), the Moving Average process (MA) by Wold in 1938 (Neyman 1939), the ARMA model by Box and Jenkins (1970), the ARIMA in 1976, the ARCH by Engle (1982), and the GARCH by Bollerslev (1986). All of these statistical models are based on assumptions relating to data, such as normality and stationarity.
With the technological and algorithmic evolution, rapid advances in artificial intelligence technologies, the development of processors with high computing capacity, large size disks, and digital platforms with high connectivity and automatic trading systems, portfolio managers are increasingly turning to automatic learning techniques, or machine learning (ML), in their investment decision. These techniques allow managers to benefit from opportunities by predicting future stock prices and increasing prediction accuracy. As a matter of fact, the techniques capture complex patterns in the data and provide quick executions, allowing for large-size data processing. Additionally, these technical solutions have revolutionized automatic trading and greatly reduced the impact of behavioral biases.
Many studies have used machine learning techniques to predict future stock prices/returns. Among these techniques are Logistic Regression (LR), the Support Vector Machine (SVM), Random Forest (RF), and Adaboost. Other studies have used neural networks to predict future stock prices and returns. Neural networks perform better than classic ML methods due to their ability to learn complex non-linear functions with significant accuracy, and to process a wide range of data (Nafia et al. 2022).
Since the appearance of the first Perceptron, made by Frank Rosenblatt, in 1957, the structure of neural networks has continued to evolve (Rosenblatt 1957). The Multilayer Perceptron (MLP) is an improved version of the Perceptron. It is considered the most simplified version of a deep neural network (DNN), and is composed of an input layer, several hidden layers, and an output layer. Other powerful and sophisticated DNN models have been developed over recent years, including Convolutional Neural Networks (CNN) that process visual data such as images and videos. Recurrent Neural Networks (RNN) have attracted a great deal of attention, especially in handling modeling problems related to time series, such as stock prices and returns, and sequential data in general, such as speech recognition, language modeling, and translation. Long Short-Term Memory (LSTM) neural networks have been devised to resolve the problem of the vanishing gradient, which is the problem encountered by RNNs when dealing with long-term data sequences. Gated Recurrent Unit (GRU) neural networks were introduced recently; they have a similar design to LTSMs, but with fewer parameters.
Designing a strategy to predict stock returns is nonetheless a demanding task that involves many challenges, since financial markets are complex, unstable, and evolving environments. Moreover, the portfolio manager not only needs to identify the model that best predicts stock returns, but also faces the challenge of building a high-performance portfolio by implementing a promising strategy.
Even if the stocks in a “Buy and Hold” portfolio are selected meticulously, the portfolio may still be exposed to high levels of systematic risk and be affected by market risk. Therefore, investment strategy is paramount when building a portfolio. The “Equity-Market-Neutral” strategy, designed and applied for the first time by Edward Thorp between 1979 and 1980, is widely used by hedge funds. It allows users to build a market-neutral portfolio with market exposure close to zero, while generating high returns. This strategy is an alternative to classic investment strategies that generate returns independent of market fluctuations. It essentially relies on the portfolio manager’s ability to pick stocks. In fact, when the market rises, the short positions’ losses are partially offset by the long positions’ gains, and when the market falls, the short positions provide a hedge against the long positions’ losses (Jacobs and Levy 2005; Ganchev 2022).
Thanks to their ability to accurately predict time series, LSTM neural networks are often used for stock price and return prediction. However, the utilization of LSTMs in constructing a profitable portfolio using the EMN strategy is a topic that has seldom been explored in the scientific literature. As a result of this gap, the following central research question emerges: “How can an EMN portfolio that outperforms the market be constructed using LSTM neural networks?” To answer this research question, this article proposes a portfolio construction model based on an Equity-Market-Neutral alternative investment strategy, where the stocks are selected according to their relative predicted performance. Stock selection is performed in two stages: in the first stage, stocks’ returns are predicted using LSTM neural networks with the same setting. Then, in the second stage, the stocks are ranked according to their predicted returns. Furthermore, since the stocks used in the model are part of the same business line and are thus structurally connected, and since the LSTM neural networks used to predict the future returns for these stocks have the same setting, we expect the model to perform well in the ranking of stocks. Moreover, with a strategy based on relative values, the accuracy of the predicted returns is not as important as the accuracy in ranking the stocks in the securities set.
The approach of the study involves building a portfolio with two sides (two portfolios), a long side and a short side each containing the same number of stocks, and with a net value of zero. The long side will contain the stocks that we expect to outperform the others. The other side, the short side, will contain the stocks expected to underperform compared to the others. The expected performance is measured with the future predicted returns by training the LTSM neural networks on the historical data of each stock, followed by cross-section classification operation at each rebalancing date. To enhance the robustness of this prediction/ranking process, we perform several iterations by changing one of the parameters that acts on the optimization of the LTSM networks (the seed). We create 15 different versions of this prediction/ranking, and the final stock selection is decided based on the “majority vote” principle.
This study displays robust features. First, it introduces a model using stock returns of the “S&P500 Consumer Staples” sector to build a market-neutral portfolio in two stages: prediction, and then selection. Second, the returns prediction is performed via LSTM neural networks that are demonstrably robust in short- and long-term time series predictions. Third, the model uses a decade’s worth of historical data (2010–2020): hundreds of explicative variables serve as the input, most of which are technical and fundamental indicators commonly used by portfolio management professionals. Other variables are also added using “feature engineering” techniques. These techniques consist of using subject matter knowledge to integrate relevant variables to input data. Fourth, the portfolio performance is measured during a test period with the most commonly utilized performance and risk metrics in the portfolio management domain. This study also presents a performance analysis of two periods: a pre-COVID-19 period and an including-COVID-19 period.
The major contributions of this paper are: First, it proposes a robust method that utilizes LSTM neural networks to build a portfolio according to EMN investment strategy that outperforms the market. In other words, how to harness the predictive power of the LSTM in a comprehensive framework, which encompasses the prediction and selection of stocks, to build an equal-weight EMN portfolio with a higher risk-adjusted return than benchmarks, namely, the sector index, and the market index. Second, this study demonstrates how feature engineering and enriching input data with technical and fundamental indicators, and features assessing the quality of the stocks can improve the performance of the constructed portfolio.
The remainder of this paper is structured as follows Section 2 provides a literature review and a brief discussion of certain related works. Section 3 offers detailed discussion of the data and the methodology used in this research. In Section 4, the detailed results of model performance are presented. Finally, Section 5 presents our conclusions.
2. Literature Review
Since machine learning (ML) was introduced to the finance world 40 years ago, neural networks in different form have risen to prominence in many research areas and fields of application, including portfolio management, scam detection, the evaluation of financial assets and derivatives, trading algorithms, studies of blockchains and cryptocurrency, feelings analysis and behavioral finance, and text-mining in finance. With the arrival of recurrent neuronal networks (RNN) and their improved version, long short-term memory (LSTM), which process time series and other sequential data, many studies have attempted to apply these techniques to portfolio management, particularly stock price predictions.
In their literature review of research related to the implementation of deep learning (DL) in finance during the last five years, Ozbayoglu et al. (2020) identified LSTM as the predominant process in the research in terms of the number of uses. The reason for this is that the LSTM structure is more able to adapt to financial time series. Jiang (2021) also conducted a literature review on the application of DL in stock prediction by studying more than 120 research papers from 2017, 2018, and 2019. He found that RNN models, including LSTM, are more commonly used than other models. Not only did he reveal that LSTM is popular in financial stock predictions, but he also demonstrated its predicting power. In their literature review of Forex and the prediction of stock prices, Hu et al. (2021) used data from the DBLP database and Microsoft Academic between 2015 and 2021, and found that all 27 papers that used LSTM agreed that LSTM neural networks outperform other models, or that it is at least capable of obtaining good prediction results.
Many research articles have used LSTM neural networks in applications related to stocks. Most of these studies apply LSTM to the prediction of stock prices with different study characteristics, such as the learning data period, the prediction horizon, the number of variables in the study, the frequency of the historical data used (intraday, daily, weekly, or monthly), the nature of the used variables (OCHLV prices (Open, Close, High, Low, and Volume), technical, fundamental, feeling analysis or macroeconomics), different hyperparameters, and different LSTM networks settings (Naik and Mohan 2019; Qiu et al. 2020; Ding and Qin 2020; Ghosh et al. 2019). Other research uses LSTM networks in the prediction of index prices, since they are less volatile than stocks and constitute a set of structurally linked stocks (in terms of sector, industry, size, etc.) (Michańków et al. 2022; Tfaily and Fouad 2022). The application of LSTM networks is not limited to the prediction of financial asset prices, but it is also used in the prediction of the direction of price trends. In fact, several studies have used LSTM to predict the rise or the fall of stock prices by transforming the regression problem to a classification problem with other metrics for performance measurement (Patel et al. 2015; Yao et al. 2018).
However, less research has focused on portfolio construction and asset allocation methods that use LSTM neural networks. Indeed, the real challenge for portfolio managers is to figure out the best investment strategy for building a profitable portfolio with less risk. The stocks need to be selected in such a way as to ensure optimal capital allocation. Managers not only strive for accuracy in their stock price predictions in order to build their portfolios, but also need to account for other considerations, such as the number of stocks their portfolios must contain to diversify away idiosyncratic risk, and questions such as how to hedge against systemic market risk, how to allocate capital among the stocks on the portfolio to maximize its profitability, and how to fund the acquisition of long positions.
Chaweewanchon and Chaysiri (2022) proposed a hybrid model, R-CNN-BiLSTM (BiLSTM is an improved version of LSTM), to build a mean-variance (MV) optimal portfolio containing stocks that obtained the best predicted returns. CNN networks are used to extract the data’s important characteristics and the BiLSTM networks are used to predict prices. The model these authors propose is compared to other reference models that use mean-variance optimization or equal weights to allocate capital on one side, and either LSTM or BiLSTM to select stocks on the other side. The authors used the following metrics to evaluate the portfolio performance: the mean return, the standard deviation, and the Sharpe ratio. Their experiments on the SET50 index of Thailand’s stock exchange between 2015 and 2020 demonstrate that BiLSTM outperforms other techniques. They also demonstrated that models that use “robust” inputs (i.e., those undergoing raw prices transformations) outperform those that directly use closing prices. This study also concluded that portfolios built with the support of LSTM or BiLSTM models outperform portfolios where stocks are randomly selected.
Sen et al. (2021) built portfolios containing five stocks each from the seven sectors that are part of the National Stock Exchange (NSE) in India. To achieve this, they used the OCHLV historical prices of the chosen stocks for the previous five years (from 2016 to 2020) to train the LSTM neural networks, and implemented a test period from 1 January to 1 June 2021. Two portfolios were built for each sector: a minimum risk portfolio and an optimal risk portfolio, according to Markowitz minimum variance optimization. LSTM networks were used to predict stock prices that were then used to calculate portfolios returns. The results demonstrated that LSTM performed well when the actual returns were compared to the predicted returns.
Zhang and Tan (2018) proposed a new model for stock selection, referred to as “Deep Stock Ranker”, to build a stock portfolio. Their model uses LSTM networks to predict future returns rankings based on the OCHLV historical daily raw prices of all the stocks listed in the Chinese market A-Share between 2006 and 2017. The authors built two portfolios: a portfolio with an equally weighted selection strategy of the top 100 stocks according to the obtained ranking, and another portfolio consisting of all the stocks in a score-weighted fashion, i.e., with the weight of each stock being proportional to a score given according to the stock’s position in the obtained ranking. The performance of these two portfolios was compared to the performance of other portfolios generated using other models and techniques. It was measured during a three-year test period (from 2015 to 2017) using the following metrics: the information coefficient (IC), active return (AR), and information ratio (IR). The authors found that the portfolio using the equally weighted selection with raw price data outperformed the other portfolios.
Touzani and Douzi (2021) proposed a trading strategy for some stocks in the Moroccan stock exchange using LSTM and GRU in the short term and the long term. To overcome the liquidity problem, the small number of listed stocks (76 stocks), and the low volume negotiated in the Moroccan market, the authors trained the model on data from the S&P500 index and the CAC40 index in the French stock exchange. Validation and other processes were performed on data from the Moroccan stock exchange. The trading strategy involved buying or selling a stock depending on how a function of the predicted price and the actual price compare to a certain calibrated threshold. Finally, two stocks were chosen to construct a portfolio and assess its performance during a test period from March 2019 to March 2021. Their results showed that the portfolio they built generated an annual return of 27.13%, and thus outperformed all the utilized benchmarks, except for the “Software and IT services” index, which achieved a high return during the COVID-19 period.
Liu et al. (2017) presented a trading strategy based on a hybrid model combining CNN and LSTM. CNN was used to select stocks and LSTM was used to manage the timing of opening or closing a position as part of a long-short strategy. To achieve this, the authors used OCHLV prices and returns data related to stocks in the Chinese Exchange. The training period ran from 2007 to 2013, and the test period from January 2014 to March 2017. They found that their strategy was more profitable than the benchmark and a simple momentum-based strategy (which stipulates that the stocks that performed best in the last three to twelve months will continue to perform well for the next few months, and that the reverse is also true).
Hou et al. (2020) proposed a hybrid LSTM-DNN model by integrating 18 monthly returns in LSTM and 19 fundamental variables in DNN to build a portfolio with a long–short strategy. The authors tested the model on 1398 stocks listed on NYSE, AMEX, and NASDAQ from 1977 to 2018. The portfolio was rebalanced in each period by buying the stocks with the highest predicted returns in the top decile and selling those in the lowest decile of the predicted returns ranking. To assess the model’s performance, two metrics were used: the average monthly return and the Sharpe ratio. The results demonstrated that this model outperformed other OLS and DNN reference models.
Cipiloglu Yildiz and Yildiz (2022) used LSTM to predict the prices of stocks in the Turkish BIST30 using monthly OCHLV data from May 2000 to June 2019. They calculated the predicted returns to infer price trends. Portfolios were built using stocks with predicted returns above a certain threshold. Among the five methods used for weighting, equal weighting and minimum variance were used. The metrics used to evaluate the portfolios’ performance were the Sharpe ratio, maximum drawdown, and conditional VaR. The results show that portfolios using LSTM outperformed the other portfolios and the benchmarks.
Yi et al. (2022) proposed a model named “IntelliPortfolio”, which is geared toward building a portfolio within the framework of Enhanced Index Tracking (EIT). The portfolio is constructed in two steps: the first step involves stock selection using principal component analysis (PCA) and the k-means clustering algorithm, and the second step comprises weight calculation using LSTM neural networks. Testing was performed on daily prices and some fundamental indicators of five stock exchange indexes from 2009 to 2018. The model was tested with four performance indicators (the tracking error, excess return, information ratio, and Sharpe Ratio) over the last 60 days of the sample. The model was compared to five existing models in the literature and the results show that it outperformed them.
This literature review can be summarized in the following Table 1:

Table 1.
Summary of the literature review.
The literature offers many studies focused on the prediction of prices and the direction of change or stocks returns, but the integration of predictions in portfolio construction is a research subject that has not yet been adequately explored. Furthermore, research that uses predictions as part of equity-market-neutral (EMN) alternative investment strategies is quite rare. Hence, it would be beneficial to have a comprehensive framework combining prediction, stock selection, and capital allocation to build a portfolio with an EMN strategy and offer a detailed performance analysis.
Based on the previous literature review, it is evident that LSTM neural networks outperform other methodologies in comparative model studies. Furthermore, in portfolio management research, portfolios constructed using LSTM networks outperform their benchmarks. Therefore, to answer the previously stated research question, the following research hypotheses are formulated:
Hypothesis 1.
A portfolio constructed based on the EMN investment strategy, which utilizes LSTM neural networks to forecast returns, outperforms both benchmarks: sector index and market index. The performance is measured in terms of risk-adjusted returns, expressed by metrics such as Sharpe ratio, Sortino ratio, Treynor ratio, Omega ratio, and Calmar Ratio.
Hypothesis 2.
Within a portfolio built according to an EMN investment strategy that utilizes LSTM neural networks, enriching input data enhances the portfolio’s performance in terms of risk-adjusted returns. The enrichment of input data is achieved by integrating fundamental indicator ratios of the stocks relative to those of their sector (stock to sector fundamental indicators) and by adding scoring variables (Scores and Piotroski) that assess the financial health of a stock by assigning a score to the company based on its fundamental indicators.
3. Data and Methodology
In this empirical study, we propose a stock prediction and selection model to construct an EMN portfolio. The model predicts the weekly returns of stocks in the “S&P 500 Consumer Staples” (CS) sector using LSTM neural networks to construct a robust portfolio that is rebalanced weekly in three distinct configurations. The literature boasts many models that predict stock price or the direction of its trend; however, in our model, we predict the stock return, not the stock price. This decision was made based on the fact that price series are not stationary, while returns are stationary.
For these purposes, ten years of historical data for all stocks in the CS sector were used to train and test the model. This dataset is composed of a set of OCHLV price variables, and a set of calculated technical and fundamental indicators. Each week, stocks were classified into five quintiles based on their predicted returns; the two extreme quintiles, quintile 1 and quintile 5, constituted candidate stocks for building the long and short portfolios, that is, the two sides of the robust EMN strategy portfolio. In such an alternative strategy, the accuracy of the predicted return value for the stock itself is not relevant. Rather, it is the accuracy of the stock’s ranking in the set of stocks composing the study universe at a given date (cross section) that matters most.
After generating the set of candidate stocks for each of the long and short sides of the portfolio through 15 different prediction repetitions, the final selection of the stocks of the robust portfolio was undertaken according to the majority voting technique, which was applied to the candidate stocks through all the repetitions performed.
To measure the model’s performance, two types of evaluations were undertaken: a first evaluation of the statistical model’s performance according to the errors in the prediction of future returns versus realized returns namely, MSE and MAE. Then, a second evaluation of the financial performance of the robust portfolios was performed.
A comparison of the model evaluations was made according to the following four levels (Figure 1):
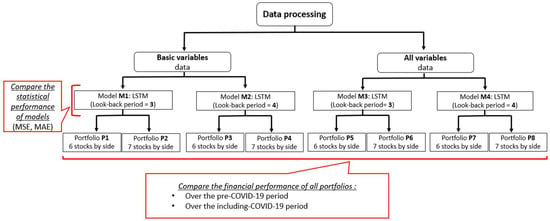
Figure 1.
Methodology overview.
- The category of explanatory variables introduced into the model, i.e., a basket of “basic variables” versus “all variables”.
- The size of the look-back period considered in LSTM to predict future weekly returns. Two sizes are to be compared: a window of the past three observations versus a window of the past four observations.
- The number of stocks selected for the two sides of the robust portfolio, i.e., six stocks in each side versus seven stocks.
- The financial performance during the test period, namely, the pre-COVID-19 period versus the whole period including the COVID-19 crisis period.
3.1. Data Preparation
3.1.1. Data Acquisition
Several research papers use historical market data of OCHLV stocks because they are more accessible than other stock data (Zhang and Tan 2018; Liu et al. 2017; Cipiloglu Yildiz and Yildiz 2022). Other research papers use technical indicators, such as simple moving averages, exponential moving averages, the relative strength index (RSI), daily, weekly, or monthly returns, and historical volatilities (Lanbouri and Achchab 2019). Other studies use fundamental indicators calculated based on financial statements, such as ratios of profitability, operational efficiency, solvency, growth, and debt (Yi et al. 2022).
This study combines different categories of data. Specifically, we used the stocks in the Consumer Staples (CS) sector of the US S&P 500 index according to the second level of the GICS classification (Global Industry Classification Standard). This sector index was chosen because it is part of a defensive sector, where firms produce or market basic goods and services that are always in demand. Theoretically, these stocks are more stable compared to stocks in other sectors, and they are equally impacted by financial or economic crises.
The basic data used in this study comprise stock and sector index market data and are taken directly from the Bloomberg data provider; meanwhile, the variables used are the result of calculations and transformations performed on these basic data.
To avoid survival bias, we listed all the stocks of the chosen sector index from January 2010 until December 2020. The number of active stocks at each time step during the study period varies between 30 and 45 stocks depending on the missing data (Table A1 in Appendix B). We then extracted the historical market data and the fundamental data generated during the whole study period. In addition, to avoid anachronistic bias and futuristic data use, and to ensure that the data reflected the true dates when the information was available, we associated the fundamental data with their release dates and not the dates recorded in the financial statement reports.
Given that financial statements are produced quarterly, and in order to be able to associate stock market data with fundamental data on a daily basis, we replicated the fundamental data for each stock over the entire period between two successive release dates. Furthermore, we combined by date the obtained data with the sector index data to obtain a mixture of three types of data: stock market data, stock fundamental data, and sector index data. From the daily data obtained, we calculated technical indicators, fundamental indicators, price multiples, stock-to-sector indicators, and sector indicators (Figure 2). Finally, we extracted weekly observations from this large daily database to form our final dataset. This approach had many upsides: we reduced redundancy and the computation time, and our data weekly frequency was in line with the portfolio rebalancing frequency.
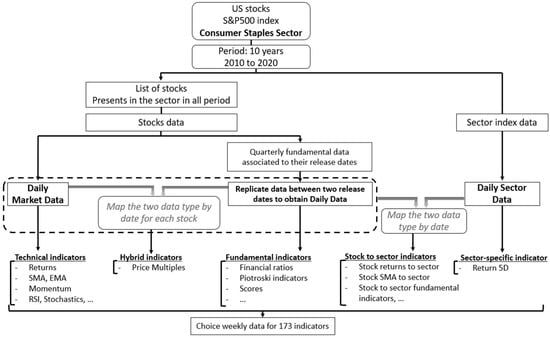
Figure 2.
Data process.
3.1.2. Calculating the Indicators
We applied “features engineering” to enrich our database with other derived variables that helped to improve the prediction process. With the raw data downloaded directly from the external data provider, we created new variables through performing some transformations. Furthermore, based on our experience and knowledge of the financial domain, we derived analytical representations by calculating a wide range of financial indicators (or approximations thereof) that are commonly used in the finance domain.
A major component of this study is to form a portfolio based on the EMN strategy by selecting the right stocks from the “S&P500 Consumer Staples” sector. It involved comparative selection between the stocks belonging to this sector in order to choose the best ones according to the selection criteria of the adopted strategy. Therefore, to capture the disparity of stocks and to be able to compare them within their sector, we calculated indicators relative to the sector (stock to sector indicators). To do this, we calculated the same indicators for both the stocks and the sector before calculating the ratio.
The process of preparing the explanatory variables taken from the model (Figure 3) begins with the direct download of the 57 “raw variables”: 34 stocks variables and 23 sector variables. These variables form the basis for the calculation of all other variables for both stocks (Table A2) and the sector (Table A3). After downloading the raw variables, a set of “intermediate indicators” was calculated both for the stocks (Table A4) and for the sector (Table A5), which were used in the calculation of our 173 final variables (Table A6).
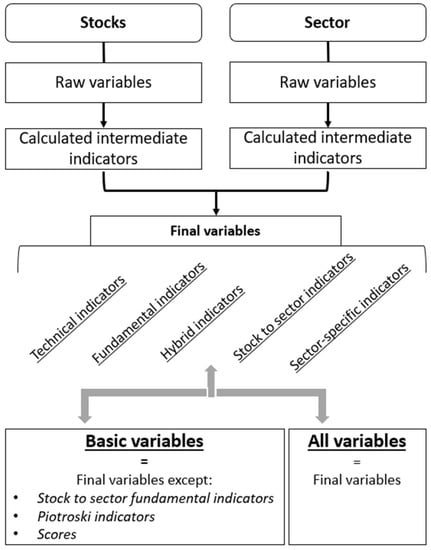
Figure 3.
Process for calculating the two variables’ baskets.
In order to compare the different models using different baskets of variables, and to study the impact of adding “stock to sector fundamental indicators”, “Piotroski indicators”, and “Scores” on the model’s performance, we generated two baskets of variables: the first basket contained all 173 of the final variables calculated, and the second basket contained 128 so-called “basic” variables, i.e., all the final variables except for those in the three categories of “stock to sector fundamental indicators”, “Piotroski Indicators”, and “Scores” (Figure 3). It should be noted that the number of variables varies from one stock to another, depending on the missing data.
The final variables taken from the model were classified into five categories:
- Technical indicators: this category of indicators includes stock market data without transformations, OCHLV and Market Capitalization, returns, volatilities, ratio of returns to volatilities, simple moving averages (SMA), exponential moving averages (EMA), prices relative to simple and exponential moving averages, momentum, the 14-day relative strength index (RSI), the 5-day RSI moving average, 14-day stochastic oscillators (slow and fast), the Williams 14-day indicator (%R), and On Balance Volume (OBV).
- Fundamental indicators: most of the fundamental indicators used in our model are ratios between the fundamental indicators of the stocks and the same indicators calculated on the sector data (“stock to sector fundamental indicators”). Other indicators are calculated differently, such as the “Piotroski indicators” and the “Scores”. The “Piotroski” indicators are binary indicators assigned to the stock at a given time if certain fundamental indicators satisfy certain criteria (0 if the criterion is satisfied, 1 otherwise). Thus, a total Piotroski score is the sum of all the calculated indicators (Piotroski 2000).Inspired by Piotroski’s indicators, we established “Scores” that can takes the values 0, 1, or 2, which are attributed to the stock at a given time according to the value of certain financial ratios. These ratios are compared to threshold set beforehand. For instance, if the value of the ratio is less than that of the small threshold, the score will be set at 0, and if the value of the ratio is situated between the small and the big thresholds, the score will equal 1. Otherwise, the score will take the value of 2. Thus, the total score of a group of financial ratios is the sum of the constituent scores.
- Hybrid indicators: these are indicators calculated based on both technical and fundamental indicators. This category of indicators consists mainly of price multiples (price-earnings ratio, price-to-book ratio, price-to-sales ratio, etc.)
- Stock to sector indicators: most of the final variables used in the model fall into this category of indicators. A stock-to-sector indicator is a ratio of a stock indicator and a sector indicator. For instance, close to sector, open to sector, price-to-sell to sector, price-to-book to sector, stock returns to sector, volatilities relative to sector, simple moving averages relative to sector, exponential moving averages relative to sector, momentum relative to sector, or price-to-moving average ratios relative to sector.
- Sector-specific indicators: in this category, we considered only the five-day sector return, since other indicators in the sector are already included in the calculation of the other variables.
3.1.3. Cleaning and Standardization of Data
After calculating all the indicators and building our final variables, we performed separate pre-processing of the weekly data of all variables of each stock (Figure 4). We removed the variables that had more than a third of their values missing, and we imputed the other missing values by the values that precede them according to their chronological order. When there was no doner (preceding value) for the imputation, the whole record was deleted. The deletion of data rows usually occurred at the beginning of the stock data histories that have no preceding values to be imputed. This situation mainly occurred with stocks that appeared during the study period and that have no previous history, as some indicators require a data history to calculate the early values. This explains the existence of empty observations at the beginning of the histories of certain stocks for some indicators, such as simple and exponential moving averages.

Figure 4.
Data processing steps.
Once the data for each stock were cleaned, they were standardized for all variables of the dataset of each stock separately. Standardization is a data normalization technique that allows for the direct comparison of scores by taking out the units of measurement. All the standardized explanatory variables are on the same measurement scale, which improves the performance and training stability of the model and ensures the rapid convergence of its parameters during the optimization operation.
3.2. LSTM Neural Networks
Long short-term memory (LSTM) neural networks are an improved version of recurrent neural networks (RNN). They are widely used in time series machine learning, and more specifically in the prediction of financial stock prices. They were initially proposed by Hochreiter and Schmidhuber (1997), and later improved by Gers et al. (2000). LSTM neural networks were introduced to solve the vanishing gradient problem, which RNN suffered with long term data sequences, by integrating a memory cell and other functions together in structures known as “gates”. LSTM networks can store a sequence of data via their memory cell, which stores the flow of information carried from one cell to another through the time sequence. Within each unit of the network, the “gates” control the information that is added to this memory.
As shown in Figure 5 and Figure 6, an LSTM unit is composed of a memory cell and three main gates: a forget gate, an input gate, and an output gate. These gates act as valves that control the information to be added to or ignored by the memory cell at each step of the sequence. Indeed, the “forgetting gate” receives the current value of the inputs x(t) combined with the output of the previous state of unit h(t − 1) and puts them into a sigmoid activation function, producing a value between 0 and 1 according to Formula (1), where and are the weights, and is the bias of the forgetting gate. The “forget gate” decides which information to keep and which to forget from the previous state. The extreme value 0 means “ignore everything” and the extreme value 1 means “keep everything”.
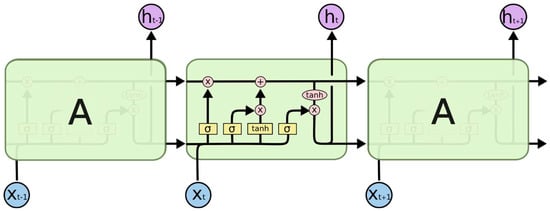
Figure 5.
Structure of long-short-term memory (LSTM) networks (Olah 2015).
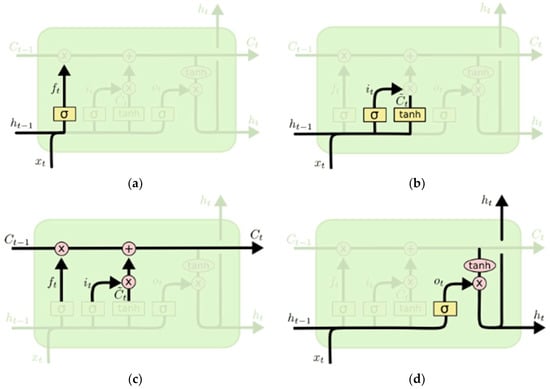
Figure 6.
The different steps in an LSTM unit (Olah 2015). (a) Forget gate. (b) Input gate. (c) Cell state. (d) Output gate.
Next, the input gate uses the combined input between x(t) and h(t − 1) to determine two components: what information to update in the memory cell and what new candidate information to add to it. The first component is computed via a sigmoid function according to Formula (2), and the second component is calculated via a hyperbolic tangent function according to Formula (3), where and are the weights and is the biases of the input gate and the memory cell.
Once the outputs of both the forget gate and input gate are calculated, the state of the memory cell is updated by multiplying the output value of the forget gate by the previous state of the memory itself . A decision is then made as to what information can be forgotten and what information needs to be updated or added via the multiplication of the result of the input gate and , according to Formula (4).
The output gate decides the amount of information to be fed to the output: first, it calculates this amount using the new inputs x(t) combined with the output of the previous state of unit h(t − 1), according to Formula (5). Second, it regulates this resulting amount using the current state of the memory cell according to Formula (6), where , , and are, respectively, the weights and bias of the output gate:
According to these formulas, the output of a state depends on the previous output of the unit and the current state of the memory cell, which in turn depends on the previous output of the unit and the previous state of the memory cell. This sequence makes LSTM networks powerful by providing them with the ability to hold information in a long-term memory (Qiu et al. 2020).
3.3. Prediction of Stock Returns
3.3.1. Training Set and Testing Set
To compare the predicted performance of the stocks in this study, we set the same training period and the same test period for all stocks. For this reason, we divided the study period into two segments: the first segment constituted the sample for training (60% of the period) and the second segment constituted the sample for testing (40% of the period). Thus, for each stock, we formed a training sample over the period from 8 January 2010 to 12 August 2016, totaling 330 weekly observations, and a test sample over the period from 19 August 2016 to 18 December 2020, totaling 222 weekly observations. However, some stocks did not cover the entirety of the training and testing periods. Furthermore, to avoid under-training the model, which can lead to bad predictions due to insufficient training data, we set up a filter that excludes stocks with a training sample size of less than 100 observations (about two years).
3.3.2. LSTM Structure and Setup
In the present work, we chose LSTM neural networks to predict the future return of each stock composing the studied sectorial index (S&P500 Consumer Staples index). We used the Python language for the scripts, and the Keras library with Tensorflow as the backend for the LSTM networks. Additionally, the SQL-Server was used for data organization and indicator calculations.
Before passing the processed data to the LSTM network, it was transformed into a supervised problem by associating each entry of the data with a target value equal to the future return (a later week’s return). Furthermore, the weekly return series serves both as an explanatory variable due to its historical values already observed at a given date “t”, and as a target variable when we consider the later values to be predicted at the same date “t”. Thus, we transformed the data to a three-dimensional format, adapted to the format expected by the multivariate LSTM input layer (in terms of the data sample size, the look-back period size, and the number of explanatory variables). We experimented with two types of LSTM network configurations: the first one had a look-back period w = 3 and, for the second, w = 4. For example, a size of w = 3 means that data from the first three weeks are used to predict the performance of the fourth week. This process was repeated by shifting the window one week in advance for all records, both for the training and testing datasets. During training and predicting, the data are not randomized, as the order of the time sequence is important in the case of time series.
As shown in Figure 7, the input layer passes data to the hidden LSTM layer consisting of 128 units with the Rectified Linear Unit (ReLu) activation function. The outputs of the LSTM layer are passed to a fully connected “Dense” layer that generates the output. When optimizing the model parameters, LSTM uses the mean square error (MSE) as the cost function and the Adam optimizer for stochastic gradient descent (SGD). The stochastic nature of the SGD changes the results obtained from the optimization depending on the series of random numbers generated during the optimization process. To obtain more robust results, we adopted an “iteration” technique for each stock that allowed for re-optimization by changing the “seed” of the random numbers used by the optimizer during the SGD. For each stock, we produced 15 iterations of predictions, which were stored for use in the selection of stocks by majority voting. Finally, for each stock, the model was trained for 300 epochs with a batch size of 16, as illustrated in Table 2. Since the choice of the lookback period (w) and the input data size (m) in LSTM networks is important for predictions, we studied the impact of two values of the first variable {w = 3, w = 4} and two values of the second {m = 173, m = 128} on the model’s performance. The other hyperparameters were set manually by measuring the error and choosing the best ones by applying the cross-validation detailed in the next section.

Figure 7.
LSTM model architecture.

Table 2.
Model hyperparameters.
3.3.3. Statistical Evaluation of the Model
To compare several model versions, we used cross-validation (CV): 70% of the training dataset is used to train the model and the remaining 30% is used for model validation while respecting the chronological order (Dangeti 2017; Kohavi 1995). For each version of the model, we calculated the statistical error of the prediction via two metrics: the mean square error (MSE) and the mean absolute error (MAE). The MSE metric is the average of the squares of the difference between the predicted and actual values (Formula (7)), while the MAE is the average of absolute difference between the predicted values and actual values (Formula (8)), where , , and T are the predicted value, the actual value, and the size of the prediction horizon, respectively. These metrics were calculated for the training dataset sample to estimate the training error, and on the validation sample to estimate the validation error (Val-Error). These measurements allowed us to choose the optimal configuration of the model hyperparameters in terms of batch size, the number of epochs, the number of units in the LSTM layer, etc.
Given that we made 15 different predictions per stock, corresponding to the 15 iterations made by changing the “seed” during the optimization of the model parameters, we calculated the average metrics per stock over all the iterations, namely, the average MSE of stock “i” according to Formula (9) and the average MAE of stock “i” according to Formula (10), where the number of repetitions R = 15:
Finally, the estimation of the model error was obtained by a simple average of the errors of all the stocks according to Formulas (11) and (12), where n is the number of stocks:
The final statistical performance of the different versions of the model was measured by the MSE and MAE errors calculated from the out-of-sample testing dataset. The diagram in Figure 8 shows the process of calculating the estimation of the training error (Train-MSE and Train-MAE), the validation error (Val-MSE and Val-MAE), and the test error (Test-MSE and Test-MAE).
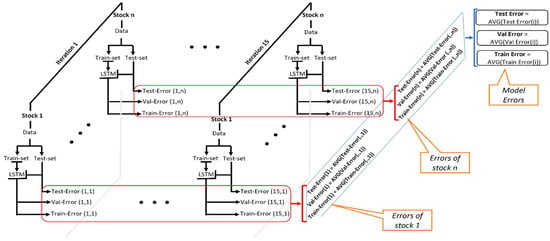
Figure 8.
Process for calculating the model’s statistical performance (where n indicates the number of stocks).
For the evaluation of models that make predictions in portfolio management, the statistical metrics commonly used in data mining, such as MSE or MAE, are not suitable measures for evaluating performance; instead, portfolio performance measures take precedence (Hou et al. 2020).
3.4. Portfolio Construction
In this study we construct an equally weighted portfolio according to an equity-market-neutral strategy. This type of strategy is used in alternative investment portfolios where the long position of the portfolio is covered by the short position composed of short-sold stocks. This strategy has two main advantages: financing, as the short position finances the long position, and hedging against market risk, i.e., if the market is falling, the strategy will lose on the long positions, but the loss will be compensated by the gains made from the short positions (Jacobs and Levy 2005).
Figure 9 shows the three steps of the portfolio construction process: first, the prediction of stock returns is performed in 15 iterations for each stock. The second step involves the selection of stocks, and the third step comprises the construction of the “robust” portfolio. The constructed portfolio consists of two sides, long and short, with the same number of stocks. Two portfolios are to be compared; the first one has 12 stocks, with 6 stocks in each side, and the second portfolio is composed of 14 stocks, with 7 stocks in each side. Moreover, the data used in the model have a weekly frequency, the same as the portfolio rebalancing frequency. Each week, the portfolio is reconstructed according to the results of the prediction, which leads to a new selection of stocks on both sides. In addition, the same market value (MV) is invested in each stock of the two sides of the portfolio, as illustrated in Formulas (13) and (14), where and are the market values of the “long” and “short” portfolios, respectively; and are the market values of stock “i” in the “long” portfolio and stock “j” in the “short” portfolio, respectively; and and are the number of stocks in the “long” and “short” portfolios, respectively. In effect, the market value of the long portfolio equals that of the short portfolio, resulting in a net market value of zero dollars.
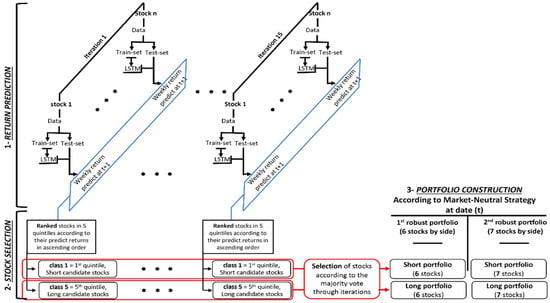
Figure 9.
Robust portfolio construction process.
For each date of the test period and for each iteration, the model predicts the next return (of the later week) for all stocks present at that date. The predicted returns obtained are ordered in ascending order and are ranked in five quintiles (five classes of stock). Only stocks belonging to the first and last quintiles are to be considered when forming the two classes of stocks, namely class “1” and class “5”. Class 1 corresponds to the first quintile, containing the stocks with the lowest predicted returns, and class 5 corresponds to the fifth quintile, containing the stocks with the highest predicted returns. The stocks in class 1, which are expected to perform poorly, are considered as candidate stocks in the “short” portfolio, while those in class 5, which are expected to perform well, form the candidate stocks in the “long” portfolio.
To build a robust portfolio, we ran the model 15 times (15 iterations) by changing the seed of the random numbers used by the LSTM neural network optimization algorithm to obtain 15 different classes of candidate stocks for the long and short portfolios. To construct the robust “short” portfolio, we applied the majority voting principle on the fifteen different “1” classes by counting the number of times the stock was classified as a candidate of the “short” portfolio. Thus, the stocks with the highest number of appearances formed the “short” portfolio (up to the number of stocks previously fixed in each of the two sides of the robust portfolio). We experimented with two types of robust portfolios: one with six stocks in each side, and a second with seven stocks in each side. The same method is applied to the different candidate stocks classified as “5” to construct the robust “long” portfolio. Note that the choice of the number of stocks in each side of the robust portfolio is justified by the average number of stocks that form the quintiles over the test-set period, which varies between six and eight stocks.
3.5. Evaluation of Portfolio Performance
In addition to the statistical evaluation of the model’s performance through the MAE and MSE error measures, we carried out an evaluation of the actual performance of the robust portfolios obtained by the different versions of the model on the test set. Several performance measures were used to evaluate the financial performance of the portfolios on the one hand, and, on the other, to compare them to benchmarks such as the S&P500 stock market index and the CS sector index. Indeed, eight portfolios were compared in terms of performance over two different periods (pre-COVID-19 and the period including the COVID-19 pandemic). Table 3 shows the eight portfolios that were constructed based on the four versions of the model by changing the following three hyperparameters:

Table 3.
Portfolios to measure performance.
- The type of basket of explanatory variables taken in the model, including a first basket of “basic variables” with 128 variables, and a second basket of “all variables” with 173 variables.
- The size of the look-back period used by the LSTM networks, which takes the following two values: w = 3 and w = 4.
- The number of stocks taken for each side of the robust portfolio, with the following two values: n = 6 and n = 7.
For this comparison, several performance measures were calculated, namely: return, volatility, downside volatility, Alpha, Beta, correlation, Sharpe ratio, Sortino ratio, Treynor ratio, Omega ratio, information ratio, capture ratio, and maximum drawdown. The benchmark and risk-free rate used to calculate these measures are, respectively, the S&P 500 Index and the three-month U.S. Treasury Bill (T-bills) rate.
3.5.1. Return
Since return is the main measure of portfolio performance, we calculated the entire series of actual weekly returns over the entire test period (222 weeks from 19 August 2016 to 18 December 2020) of the different portfolios to be compared. To do this, we first calculated the return series of the two portfolios, long and short, separately, and then deducted the return series of the net portfolio as the difference between the two returns series of the two portfolios at each date of the test period. The return of each of the long () and short () portfolios at date “t” was calculated by the arithmetic average of the return of stocks in the portfolio, according to Formulas (15) and (16) (Demonstration A1 in Appendix A). While the net return () of the portfolio at date “t” is the difference between the long portfolio return and the short portfolio return, as in Formula (17), where and are the number of stocks in the long and short portfolios, respectively; is the return of the stock “i” in the long portfolio at date “t” and is the return of the stock “j” in the short portfolio at date “t”.
From the series of net portfolio returns over the entire test period, we calculated all the performance indicators of the robust equity-market-neutral portfolio. The annualized average return is the most important indicator to consider. It does not give much detail on the behavior of the return series over time, but it nevertheless summarizes the realized performance of the portfolio over the whole test period. It is measured by the geometric mean of all weekly returns in the net portfolio series according to Formula (18), where is the weekly return of the net portfolio on date t and is the number of weeks in the test period.
3.5.2. NAV
The graphical representation of the evolution of the net asset value (NAV) of the net robust portfolio and the other portfolios (long and short) offers a highly relevant overview of the portfolio’s performance. It allows for a visual comparison of the performance of portfolios with each other and with the benchmarks. The NAV is calculated by accumulating returns from an initial NAV at the beginning of the period (USD 100, for example). The NAV at the end of the period is reinvested for the next period according to Formula (19), over the whole test period, where is the initial amount invested. is the portfolio NAV at date “t”, and is the weekly portfolio return in week “j”.
3.5.3. Volatility
Annualized volatility is the first indicator of risk to be seen in a portfolio, complementing the information provided by the first measure of performance: the annualized average return. It measures the degree to which the returns of the series deviate, on average, from the average return. It is calculated as the standard deviation of the series of weekly returns over the test period according to Formula (20), where is the weekly return of the portfolio in week t; is the arithmetic average of the weekly return series; and T is the number of weeks in the test period.
3.5.4. Sharpe Ratio
Developed by the economist Sharpe (1994), this ratio measures the risk-adjusted return of a portfolio. It is one of the best indicators for comparing the risk-adjusted performance of different portfolios, and for assessing a portfolio compared to benchmark portfolios. The higher the ratio, the better the portfolio. Thus, a value of this ratio greater than 1 means that the portfolio’s risk-taking is amply rewarded by an excess return of the portfolio over the risk-free return. This ratio is calculated by dividing the portfolio’s excess return by its volatility, according to Formula (21), where and are the annualized average returns of the portfolio and the risk-free rate, respectively, and is the annualized volatility of the portfolio.
3.5.5. Downside Volatility
Unlike volatility that considers both increases and decreases in returns relative to the mean, downside volatility is an additional risk measure that only takes into account bearish returns below the average. It is calculated according to Formula (22), where is the weekly portfolio return in week t; is the arithmetic average of the weekly return series; and T is the number of weeks in the test period.
3.5.6. Sortino Ratio
Developed by Frank A. Sortino, the Sortino ratio is an improved version of the Sharpe ratio (Bodson et al. 2010). Both ratios calculate a risk-adjusted performance measure. However, the Sortino ratio substitutes the volatility used in Sharpe’s ratio with the downside volatility, which only considers bearish returns. The rationale behind is that bullish returns are generally beneficial and should not be included in a risk measure, according to the author of the ratio. It calculated according to Formula (23), where and are the annualized average returns of the portfolio and the risk-free rate, respectively.
3.5.7. Beta
Beta measures the systematic risk of the portfolio; that is, the sensitivity of the portfolio to the market. It is always compared to the reference value 1. The portfolio fluctuates more than the market if the Beta value is higher than 1, and fluctuates less if its Beta value is lower than 1. Furthermore, a Beta-neutral portfolio is a portfolio with a Beta close to or equal to 0. It is calculated via Formula (24) as the ratio between the covariance of the portfolio’s return and the market’s return on the one hand, and the variance of the market’s return on the other hand, where and are the portfolio return and market return series, respectively. and are covariance and variance, respectively.
3.5.8. Alpha
Jensen’s Alpha, or simply the Alpha, is a performance metric that is widely used in active portfolio management strategies where managers use their skills to outperform the market. Proposed by Jensen (1968), it is extracted from the Capital Asset Pricing Model (CAPM) and measures how well the portfolio outperforms the market considering its systematic risk. The alpha is calculated as the difference between the excess return achieved by the portfolio and the expected return measured by the Beta weighted market excess return. It is calculated by Formula (25), where , , and are the average of the portfolio weekly returns, the average of weekly risk-free rates, and the average of weekly market returns, respectively. is the Beta of the portfolio and T is the number of weeks in the test period.
3.5.9. Correlation
Correlation measures the intensity of the linear relationship between two variables. If two variables move relatively and linearly in the same way, the correlation between them will be close to 1, and if they move relatively in the same way but in opposite directions, their correlation will be close to −1. A value of zero or close to zero for the correlation indicates that the two variables have no linear relationship or a very weak linear relationship. The correlation is calculated by Formula (26) as the ratio of the covariance of the portfolio return and the market return to the product of the standard deviations of the two series of portfolio and market returns. et are the portfolio and market return series, respectively, and refers to the standard deviation.
3.5.10. Treynor Ratio
Created by economist Treynor (1962), the Treynor ratio is similar to the Sharpe ratio, with both measuring the risk-adjusted return of a portfolio. However, the Sharpe ratio uses the risk of the portfolio represented by its volatility, whereas the Treynor ratio uses the systematic risk of the portfolio represented by the Beta value. The higher the ratio, the better the portfolio performs. It is calculated by dividing the excess return of the portfolio by its Beta according to the Formula (27), where and are the annualized portfolio average return and the risk-free rate, respectively:
3.5.11. Information Ratio
The information ratio measures how much the portfolio outperforms the benchmark, considering the risk of this benchmark. As shown in Formula (28), it is calculated as the ratio of the difference between the average return of the portfolio and the benchmark to the tracking error. The tracking error is calculated by the square root of variance of the series of differences between the portfolio returns and the benchmark returns, where and are the portfolio and benchmark annualized average returns, respectively. TE is the tracking error, and and are the portfolio and benchmark weekly return series, respectively, at date t (Bodson et al. 2010; Zhang and Tan 2018):
3.5.12. Capture Ratios
There are two capture ratios: the upside capture ratio and the downside capture ratio. The upside capture ratio calculates the performance of the portfolio compared to a benchmark if the benchmark is rising, whereas the downside capture ratio calculates the performance of the portfolio relative to a benchmark if the benchmark is falling. The upside capture ratio measures the extent to which the portfolio outperforms (or underperforms) the benchmark during periods of positive returns (bull market) and the downside capture ratio measures the extent to which the portfolio outperforms (or underperforms) the benchmark during periods of negative returns (bear market).
A value greater than one for the upside capture ratio means that the portfolio has performed better than the benchmark through periods when the benchmark is rising, whereas a value below one indicates that the portfolio has underperformed while the benchmark has risen. The analysis is reversed for the downside capture ratio, where a positive value less than one indicates that the portfolio has lost less than the index during periods when the index is falling. The difference between the value of this ratio and 1 measures the degree of resilience of the portfolio during periods when the market is falling. A negative downside capture value means that the portfolio has made a positive return when the benchmark has negative returns during its downside periods.
According to Formula (29), the upside capture ratio is calculated as the ratio of the annualized average return of the portfolio during periods when the benchmark has positive returns, to the annualized average return of the benchmark during the same periods. Similarly, the downside capture ratio is calculated over periods when the benchmark has a negative return according to Formula (30), where and are, respectively, the return of the portfolio and the return of the benchmark at date t. and are, respectively, the number of weeks when the benchmark returns are positive and the number of weeks when they are negative:
3.5.13. Omega Ratio
This ratio was developed by Keating and Shadwick (2002) and measures the risk-adjusted performance of the portfolio compared to a threshold or a benchmark. It identifies the chances of gain compared to loss. Omega captures all the moments of the portfolio return distribution and makes no assumptions about the distribution of returns. According to Formula (31), it is calculated as the ratio of total gains to total losses relative to an objective return (expected return) or a so-called “minimum accepted return” (MAR), which can be a risk-free rate or a benchmark portfolio. In the formula, is the portfolio return at date t; is the minimum accepted return, which may be a fixed threshold, a risk-free rate, or a benchmark return; and T is the number of weeks in the test period:
3.5.14. Maximum Drawdown
The maximum drawdown measures the widest loss in a portfolio that connects the highest peak and the next deepest trough. It measures the maximum loss over the history of a portfolio. A value of 100% for this metric means that the portfolio has lost all its value. It is a risk measure used to compare performances between portfolios and is also used as a risk measure in the Calmar ratio. It is calculated using Formula (32) as the accumulated return during the entire period of steep decline, where H is the highest portfolio value reached before the largest portfolio fall and L is the lowest value observed before a new H:
3.5.15. Calmar Ratio
Created by fund manager Terry Young in 1991, the Calmar ratio is a measure of risk-adjusted return similar to the Sharpe ratio, but it uses the maximum drawdown in its risk instead of volatility. It is calculated according to Formula (33) by the excess return divided by the maximum drawdown, where et are the portfolio annualized average return and the risk-free rate annualized average return, respectively:
4. Results and Discussion
4.1. Statistical Performance of the Model
During this study, several hyperparameters of the model were experimentally tested to select those that best fit the data. For these purposes, we used the cross-validation technique by calculating the two metrics MSE and MAE according to Formulas (11) and (12) detailed above in the section titled “Statistical evaluation of the model”. According to Figure 1, the performances of the four versions of the model were compared by changing the type of the basket of variables input to the model and the size of the look-back period used by the LSTM networks.
Table 4 presents the results of the statistical performance of the four model versions chosen for comparison by calculating the MSE and MAE for the training, validation, and test samples.

Table 4.
Statistical errors of the model. (The bold numbers indicate the best result).
With the same number of epochs (epoch = 300), the model versions have the same statistical error values for the training sample. Furthermore, the error generated by the cross validation (which is an estimate of the model error extracted from the training data) allowed us to calibrate the model hyperparameters. This error shows a minimal value for model M3, which uses “all variables”, and a size w = 3 of the look-back period. However, model M1, which uses the “basic variables” and a look-back period size w = 3, provides the best statistical performance (minimum error), measured from the unseen data of the test set.
Although they provide insights into the accuracy of the prediction, the errors used do not allow for an effective comparison of the different versions of the model because they only provide an estimate of the average of the errors over all the stocks and all the iterations used in the model. Moreover, they do not consider the selection process of the stocks in the portfolio, which is limited to only some of the stocks. For this reason, a financial performance evaluation of the portfolio is necessary.
4.2. Financial Performance of the Model
In addition to the statistical performance, we evaluated the financial performance of the eight robust portfolios from the different versions of the model, as shown in Table 3. For this purpose, we calculated the 15 performance and risk measures (detailed above in the “Evaluation of portfolio performance” section) for the different portfolios to be compared (P1, P2, …, P8) on the one hand, and for the benchmarks on the other hand. Recall that we used the “US three-month Treasury Bill” rate for the risk-free rate, and two benchmarks, the “S&P500 Consumer Staples” sector index from which we selected the stocks, and the “S&P 500” index, representing the market, which was also used in the calculation of the performance metrics.
To study the behavior of the different versions of the model in normal times and in highly volatile periods of crisis, we measured their performance over two periods: the pre-COVID-19 period and then the entire test period, including the period of the COVID-19 crisis. The frontier date separating the pre-COVID-19 period and the post-COVID-19 period was estimated by the effective start of the influence of the pandemic on the behavior of financial markets. In this study, we took the start date of the largest drop in the S&P500 index, 19 February 2020, as the frontier date.
According to the results of the financial performance of the portfolios represented by the NAV evolution graph (base USD 100) in Figure 10, Figure 11, Figure 12 and Figure 13, and summarized in Table 5a,b and Table 6a,b, we reached the following conclusions:
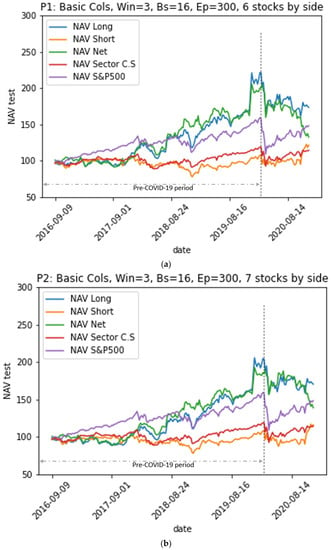
Figure 10.
Evolution of the net value of portfolios long, short, and net constructed based on Model M1 over the test period, versus the net value of the benchmarks. (a) Evolution of the net value of portfolios P1. (b) Evolution of the net value of portfolios P2.
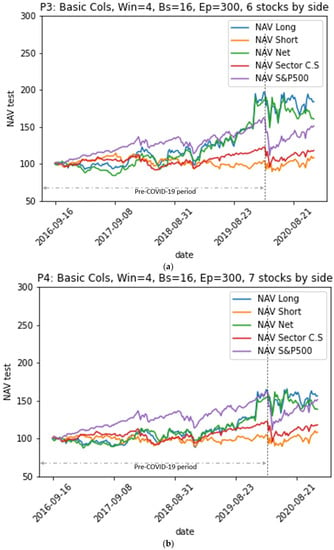
Figure 11.
Evolution of the net value of portfolios long, short, and net constructed based on Model M2 over the test period, versus the net value of the benchmarks. (a) Evolution of the net value of portfolios P3. (b) Evolution of the net value of portfolios P4.
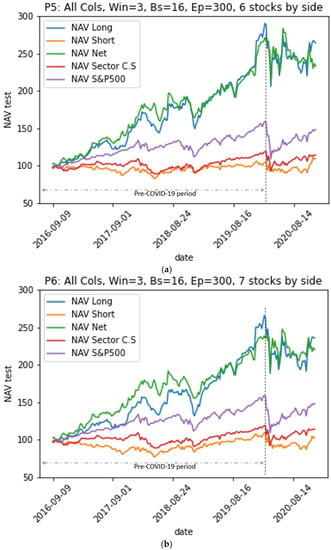
Figure 12.
Evolution of the net value of portfolios long, short, and net constructed based on Model M3 over the test period, versus the net value of the benchmarks. (a) Evolution of the net value of portfolios P5. (b) Evolution of the net value of portfolios P6.
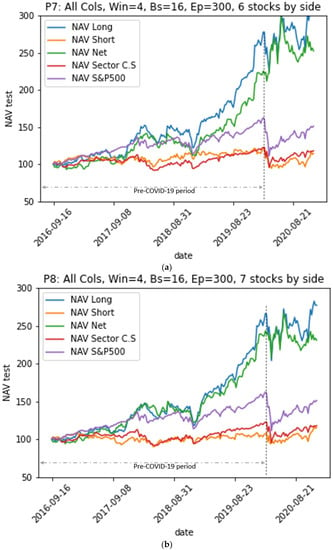
Figure 13.
Evolution of the net value of portfolios long, short, and net constructed based on Model M4 over the test period, versus the net value of the benchmarks. (a) Evolution of the net value of portfolios P7. (b) Evolution of the net value of portfolios P8.

Table 5.
(a) Pre-COVID-19 performance of the P1, P2, P3, and P4 portfolios constructed based on the M1 and M2 models versus the performance of the benchmarks. (b) Performance of the P1, P2, P3, and P4 portfolios constructed based on the M1 and M2 models versus the performance of the benchmarks during the COVID-19-inclusive period. (The bold numbers indicate the best result for each metric).

Table 6.
(a) Pre-COVID-19 performance of the P5, P6, P7, and P8 portfolios constructed based on the M3 and M4 models versus the performance of the benchmarks. (b) Performance of the P5, P6, P7, and P8 portfolios constructed based on the M3 and M4 models versus the performance of the benchmarks in the COVID-19-inclusive period. (The bold numbers indicate the best result for each metric).
- All portfolios outperformed their sector index in terms of risk-adjusted returns (Sharpe ratio, Sortino ratio, Treynor ratio, Omega ratio, Calmar ratio, and information ratio).
- Portfolios P5, P6, P7, and P8 from models M3 and M5, which use all of the explanatory variables, outperformed the sector index and the S&P500 index representing the market on the one hand; on the other hand, they largely outperformed portfolios P1, P2, P3, and P4 from models M1 and M2, which use “basic variables”.
- Portfolios from models where LSTM neural networks use a look-back period of size w = 4 to predict the stock’s future return outperformed the other models using w = 3 for the whole period including-COVID-19. However, portfolios from models using a look-back period with a size w = 3 outperformed the others during the pre-COVID-19 period.
- The P7 portfolio, which consists of six stocks in each of its long and short sides and which is generated by the model M4 (w = 4, all variables), provided the best performance both in the pre-COVID-19 period and in the period including COVID-19. It achieved an annualized average return of 25% over the entire test period compared to 27% over the pre-COVID-19 period, a decrease of 2%; meanwhile, the annualized average returns of the S&P 500 index and the sector index decreased from 15% to 10% and from 5% to 3%, respectively. However, the annualized volatility of the P7 portfolio increased from 19% pre-COVID-19 to 22% over the entire period (including COVID-19): an increase of 3%. Meanwhile, the annualized volatilities of the S&P500 index and the CS sector index increased from 12% to 18% and from 12% to 16%, increases of 6% and 4%, respectively.
- Over the entire period, the P7 portfolio achieved 1.04, 1.92, and 0.93 for the Sharpe, Sortino, and Treynor ratios, respectively, indicating that it achieved an acceptable risk-adjusted excess return. Indeed, the Sortino ratio is higher than the Sharpe ratio because it only takes into account the downside volatility, which is lower than volatility. In addition, its Sharpe, Sortino, and Treynor ratios are significantly higher than those of the benchmarks: the S&P500 market index had values of 0.48, 0.62, and 0.09 and the CS sector index had values of 0.12, 0.16, and 0.03 for the three ratios.
- The P7 portfolio has an Alpha of 23%, i.e., most of its returns are not made through systematic market risk taking, but are rather due to its own strategy. Its Beta and Correlation relative to the market are 0.25 and 0.20 over the whole test period, and 0.17 and 0.11 over the pre-COVID-19 period, respectively. This means that the portfolio has a very low correlation to the market, which is the goal of the EMN strategy.
- The P7 portfolio has an information ratio of 0.56, which means that it outperformed the benchmark, given its risk. Furthermore, its positive excess returns outperformed its negative excess returns over the entire period, which is reflected in its Omega ratio of 1.51. This is higher than the benchmarks S&P500 index and the CS sector index, which had values of 1.26 and 1.09, respectively.
- The Calmar ratio of the P7 portfolio reaches 1.11, compared to 0.27 for the S&P 500 index and 0.09 for the CS sector. This ratio measures the risk-adjusted return using the maximum drawdown in the denominator, which reached a value of −21% for this portfolio on 11 January 2019. This maximum loss is lower than the maximum drawdown of the benchmarks that took place simultaneously on 20 March 2020, with values of −32% for the S&P 500 index and −22% for the CS sector index.
- As for the upside capture and downside capture ratios, the P7 portfolio scored 0.42 and 0.09 for these two ratios, respectively, indicating that the P7 portfolio underperformed while the benchmark S&P 500 index was performing well; however, the portfolio was very resilient during periods when the benchmark S&P500 index declined. In addition, the CS Sector index had an upside capture value of 0.53, meaning that it also underperformed while the benchmark S&P500 index performed well, but with a downside capture of 0.79, showing little resilience to market downturns compared to the P7 portfolio.
- The risk-adjusted performance of all portfolios in the pre-COVID-19 period was better than that in the period including the COVID-19 pandemic. When the COVID-19 pandemic period was introduced to the test data, the returns experienced a decline ranging from 6% to 16% for the M1 and M2 model portfolios (using the basic variables). The level of decline ranged from 2% to 12% for the M3 and M4 model portfolios (using all variables). The pandemic caused the volatility of all portfolios to rise. The increase in volatility ranged from 3% to 6%. Similarly, the returns for the S&P500 benchmark and the CS sector index decreased by 5% and 2% and their volatilities increased by 6% and 4%, respectively. This means that the EMN strategy portfolios were more strongly impacted by the COVID-19 pandemic than the benchmarks were. Moreover, EMN was the strategy with the lowest performance according to a study conducted by Ganchev (2022) on the performance of hedge fund strategies before and after the COVID-19 crisis.
- Transitioning from the M1 and M2 models to the M4 and M5 models by introducing the three baskets of variables (“Piotroski”, “Scores”, and “stock to sector fundamental indicators”) greatly improved the performance of the EMN strategy portfolios. Indeed, for all of the portfolios, we saw an increase in the annualized average return, from 6% to 15%, with almost the same volatility.
- Portfolios from models M1 and M3 using a look-back period of size w = 3 performed well during the pre-COVID-19 period, while those from models M3 and M4 using w = 4 outperformed over the entire period, including the COVID-19 crisis period.
In summary, the portfolios obtained, on average, a pre-COVID-19 annualized average return of 30% compared to 5% and 15% for the CS sector index and the S&P500 index over the same period, respectively. Meanwhile, over the whole period, including the pandemic period, the portfolios of our model achieved an annualized average return of 22% compared to 3% and 10% for the same benchmarks, respectively.
As for the annualized volatility of the portfolios, it remains higher than that of the two benchmarks, reaching 18% on average, versus 12% for the two benchmarks during the pre-COVID-19 period, and 22% versus 16% and 18% for the CS sector index and the S&P500 index, respectively, during the period including COVID-19. However, despite the high volatility of the portfolios when compared against the benchmarks, the risk-adjusted return of the portfolios remains well above the benchmarks at, on average, 1.6 versus 0.3 and 1.05 in the pre-COVID-19 period, and 0.94 versus 0.48 and 0.12 in the COVID-19-inclusive period. Moreover, the Sortino ratio, which considers downside volatility, is significantly higher than that of the benchmark index, with an average value of 3.16 for all portfolios compared to 0.41 and 1.48 for the two indexes in the pre-COVID-19 period. The same ratio reached an average of 1.60 for all portfolios versus 0.16 and 0.62 for the benchmarks over the COVID-19-inclusive period.
Based on the results of this empirical study, we can conclude that portfolios constructed according to the EMN strategy and utilizing LSTM neural networks for return prediction outperformed the benchmarks (sector index and market index). This is due to the advantage of LSTM neural networks in predicting stock returns by effectively identifying sequential patterns in the data. LSTM is one of the most advanced techniques for capturing complex dependencies and relationships in financial time series data. This confirms the initially proposed hypothesis (1).
Furthermore, the results also show that the use of feature engineering and integration of new variable categories such as “Scores”, “Piotroski”, and “stock to sector fundamental indicators” enhance the portfolio’s performance. This is due to the fact that feature engineering enables the extraction of analytical representations from data, making them more relevant to the studied problem and easier to capture by the model. The categories of indicators, “Scores” and “Piotroski”, assess the financial quality of stocks in the medium and long term, whereas the “stock to sector fundamental indicators” category captures interactions by comparing the financial state of stocks to their sector based on financial statements information. This finding supports the previously stated hypothesis (2).
5. Conclusions
This study fills the existing gap in the literature regarding the construction of a profitable portfolio built according to an equity-market-neutral investment strategy using LSTM neural networks, which are widely used in portfolio management due to their strength in time series prediction. To achieve this purpose, this study proposed a new two-step portfolio construction approach according to the alternative equity-market-neutral investment strategy. The first step of our approach involved predicting stock returns using LSTM neural networks in 15 different iterations based on historical price data, technical indicators, fundamental indicators, and sector indicators. The second step consisted of selecting the stocks for the long and short sides of the portfolio by ranking the stocks according to their predicted returns. The long portfolio was made up of the stocks that we expected to perform the best, while the short portfolio was made up of the stocks that we expected to perform the worst. Thus, we constructed several portfolios by changing some of the hyperparameters of the model.
In the next stage of the research, we compared the performance of the constructed portfolios against each other and against two benchmarks, in periods exclusive and inclusive of the COVID-19 pandemic, using 15 performance and risk metrics that are commonly used in portfolio management. Our model was tested on the S&P500 Consumer Staples sector stocks with weekly portfolio rebalancing. By including all of the variables in the model, the portfolios experienced a change in their performance levels. Nonetheless, all of them outperformed the benchmarks.
The results show that integrating LSTM neural networks to predict returns and construct a portfolio based on the market-neutral strategy outperformed benchmarks. Moreover, incorporating all types of variables such as historical quotes, technical and fundamental indicators, stock-to-sector indicators, and indicators that assess the quality of stocks into the input data greatly improved the model’s performance. These results should give investors and managers more confidence in using alternative strategies that use LSTM neural networks in the process of developing investment strategies, stock selection and portfolio construction.
These findings support this research’s hypotheses: (1) Constructing a portfolio based on the EMN investment strategy, which utilizes LSTM neural networks to forecast returns, outperform both benchmarks: the sector index and the market index; and (2) enriching the input data by including features using feature engineering techniques enhances the portfolio’s performance.
Future work will focus on improving the predictive abilities of the model during crisis periods, such as the COVID-19 pandemic, in order to reduce the volatility of the portfolio returns. In fact, during the training period of the present model from 2010 to 2016, there was no sharp drop in the market such as that experienced during the COVID-19 crisis period. Whereas the test data used to measure the performance of the model from 2016 to 2020 included the COVID-19 crisis period.
One avenue to be explored in further research is the use of a rolling training period, i.e., using past data to predict later week’s return. Then, once the return is achieved, it can be incorporated into the model training data to predict the later week’s return, and so on. With this method, LSTM networks will adjust as they go along by using more and more recent data.
Finally, we intend to extend the scope of this approach to other sectors of activity, as well as to other alternative investment strategies.
Author Contributions
Conceptualization, A.N., A.Y. and A.E.; methodology, A.N., A.Y. and A.E.; software, A.N.; validation, A.N., A.Y. and A.E.; formal analysis, A.N.; investigation, A.N., A.Y. and A.E.; resources, A.N.; data curation, A.N.; writing—original draft preparation, A.N., A.Y. and A.E.; writing—review and editing, A.N., A.Y. and A.E.; visualization, A.N.; supervision, A.Y. and A.E.; project administration, A.N., A.Y. and A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to limitations in the use of the Bloomberg license.
Acknowledgments
We thank the portfolio managers of the Gestion Cristallin Inc. hedge fund for their support, and especially Papa Mamadou Bakayoko for his pertinent and informative comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Demonstration A1.
Hereafter, VM denotes the market value, L and S denote the long and short portfolios, respectively, denotes the number of stocks in the long portfolio, denotes the number of stocks in the short portfolio, and is the return of stock “i” which is part of the long portfolio at date “t”.
If the same market value is invested at date “t − 1” in both the long and short portfolios, whose stocks are equally weighted, the market value at date “t” of the long portfolio will be:
Similarly, the return of the short portfolio at date “t” is calculated as follows, where «» and «» are the returns at date “t” of the long and short portfolios, respectively. «» and «» are the number of stocks in the long and short portfolios, respectively:
Appendix B

Table A1.
List of stocks with their Bloomberg symbols and their start dates, end dates, and number of weeks in the data after imputation.
Table A1.
List of stocks with their Bloomberg symbols and their start dates, end dates, and number of weeks in the data after imputation.
| Symbol | Start Date | End Date | Number of Weeks | |
|---|---|---|---|---|
| 1 | ADM | 2010-01-08 | 2020-12-18 | 553 |
| 2 | AVP | 2010-01-08 | 2020-01-03 | 505 |
| 3 | BF/B | 2010-01-08 | 2020-12-18 | 553 |
| 4 | CAG | 2010-01-08 | 2020-12-18 | 553 |
| 5 | CCE | 2010-12-31 | 2018-11-02 | 396 |
| 6 | CHD | 2010-01-08 | 2020-12-18 | 553 |
| 7 | CL | 2010-01-08 | 2020-12-18 | 553 |
| 8 | CLX | 2010-01-08 | 2020-12-18 | 553 |
| 9 | COST | 2010-01-08 | 2020-12-04 | 551 |
| 10 | COTY | 2014-03-28 | 2020-12-18 | 338 |
| 11 | CPB | 2010-01-08 | 2020-12-18 | 553 |
| 12 | DPS | 2010-12-31 | 2018-07-06 | 379 |
| 13 | EL | 2010-01-08 | 2020-12-18 | 553 |
| 14 | GAPTQ | 2010-01-08 | 2012-03-09 | 111 |
| 15 | GIS | 2010-01-08 | 2020-12-18 | 553 |
| 16 | GMCR | 2010-01-08 | 2016-02-26 | 308 |
| 17 | HNZ | 2010-01-08 | 2013-06-07 | 174 |
| 18 | HRL | 2010-01-08 | 2020-12-18 | 553 |
| 19 | HSY | 2010-01-08 | 2020-12-18 | 553 |
| 20 | K | 2010-01-08 | 2020-12-18 | 553 |
| 21 | KHC | 2016-07-08 | 2020-12-18 | 228 |
| 22 | KMB | 2010-01-08 | 2020-12-18 | 553 |
| 23 | KO | 2010-01-08 | 2020-12-18 | 553 |
| 24 | KR | 2010-01-08 | 2020-12-18 | 553 |
| 25 | KRFT | 2013-07-12 | 2015-06-26 | 98 |
| 26 | LO | 2010-07-02 | 2015-06-05 | 249 |
| 27 | LW | 2017-08-25 | 2020-12-18 | 170 |
| 28 | MDLZ | 2010-01-08 | 2020-12-18 | 553 |
| 29 | MJN | 2010-03-12 | 2017-06-09 | 364 |
| 30 | MKC | 2010-01-08 | 2020-12-18 | 553 |
| 31 | MNST | 2010-01-08 | 2020-12-18 | 553 |
| 32 | MO | 2010-01-08 | 2020-12-18 | 553 |
| 33 | PEP | 2010-01-08 | 2020-12-18 | 553 |
| 34 | PG | 2010-01-08 | 2020-12-18 | 553 |
| 35 | PM | 2010-04-09 | 2020-12-18 | 541 |
| 36 | RAD | 2010-01-08 | 2020-12-18 | 553 |
| 37 | RAI | 2010-01-08 | 2017-07-21 | 379 |
| 38 | SJM | 2010-01-08 | 2020-12-18 | 553 |
| 39 | STZ | 2010-01-08 | 2020-12-18 | 553 |
| 40 | SVU | 2010-01-08 | 2018-10-19 | 443 |
| 41 | SWY | 2010-01-08 | 2015-01-23 | 255 |
| 42 | SYY | 2010-01-08 | 2020-12-18 | 553 |
| 43 | TAP | 2010-01-08 | 2020-12-18 | 553 |
| 44 | TSN | 2010-01-08 | 2020-12-18 | 553 |
| 45 | UN | 2010-01-08 | 2013-09-20 | 189 |
| 46 | WAG | 2010-12-31 | 2014-12-19 | 203 |
| 47 | WBA | 2010-01-08 | 2020-12-18 | 553 |
| 48 | WFM | 2010-01-08 | 2017-08-25 | 384 |
| 49 | WMT | 2010-01-08 | 2020-11-13 | 548 |

Table A2.
Raw variables of stocks directly downloaded from Bloomberg (BBG).
Table A2.
Raw variables of stocks directly downloaded from Bloomberg (BBG).
| Variable Name | Description | Bloomberg Field Name |
|---|---|---|
| Stock market data: BBG field (daily frequency) | ||
| curMrkCap | Current market capitalization | CUR_MKT_CAP |
| Open | Open price | OPEN |
| High | High price | HIGH |
| Low | Low price | LOW |
| Volume | Volume | PX_VOLUME |
| Close | Close price | PX_LAST |
| nbrShares | Total current number of shares outstanding | EQY_SH_OUT |
| indDivYld | Indicative dividend per share | EQY_IND_DPS_ANNUAL_GROSS |
| Fundamental data: BBG field (quarterly frequency) | ||
| _debt | Short-term and long-term debt | SHORT_AND_LONG_TERM_DEBT |
| _debtLT | Long term borrowing | BS_LT_BORROW, |
| _debtST | Short term borrowing | BS_ST_BORROW, |
| _marge1Y | Trailing 12-month gross margin | TRAIL_12M_GROSS_MARGIN |
| _cash | Cash | CASH_&_ST_INVESTMENTS |
| _cshMrkSecr | Cash and marketable securities | CASH_AND_MARKETABLE_SECURITIES |
| _Eqy | Total Equity | TOTAL_EQUITY |
| _sales1Y | Trailing 12-month sales | TRAIL_12M_NET_SALES |
| _CF1y | Trailing 12-month cash flow | TRAIL_12M_CASH_FROM_OPER |
| _FCF1y | Trailing 12-month free cash flow | TRAIL_12M_FREE_CASH_FLOW |
| _assets | Total assets | BS_TOT_ASSET |
| _divPerSh1y | Trailing 12-month dividend per share | TRAIL_12M_DVD_PER_SH |
| _Liab | Total liability | BS_TOT_LIAB2 |
| _earn1Y | Trailing 12-month earning | T12M_INC_BEF_XO_LESS_MIN_INT_PFD |
| _EPS1y | Trailing 12-month EPS | TRAIL_12M_EPS |
| _nbrShEps | Average number of shares for EPS | IS_AVG_NUM_SH_FOR_EPS |
| _nbrShDilEps | Average number of shares used for diluted Eps | IS_SH_FOR_DILUTED_EPS |
| _ROE | Return on common equity | RETURN_COM_EQY |
| _ebitda1Y | Trailing 12-month EBITDA | TRAIL_12M_EBITDA |
| _curAssets | Current assets | BS_CUR_ASSET_REPORT |
| _curLiab | Current liability | BS_CUR_LIAB |
| _inventori | Inventories | BS_INVENTORIES |
| _accReceiv | Receivable account | BS_ACCT_NOTE_RCV |
| _accPayble | Payable account | BS_ACCT_PAYABLE |
| _augCap | Trailing 12-month increase capital stock | TRAIL_12M_INCR_CAP_STOCK |
| _dimCap | Trailing 12-month decrease capital stock | TRAIL_12M_DECR_CAP_STOCK |

Table A3.
Raw variables of the sector index directly downloaded from Bloomberg (BBG).
Table A3.
Raw variables of the sector index directly downloaded from Bloomberg (BBG).
| Variable Name | Description | BBG Field |
|---|---|---|
| Sector data: BBG field (weekly frequency) | ||
| open_sec | Open price | OPEN |
| high_sec | High price | HIGH |
| low_sec | Low price | LOW |
| volume_sec | Volume | PX_VOLUME |
| close_sec | Close price | PX_LAST |
| curMrkCap_sec | Current market capitalization | CUR_MKT_CAP |
| rvnPerSh_sec | Revenue per share | REVENUE_PER_SH |
| divPerSh1Y_sec | Dividend per share last 12 months | DVD_SH_12M |
| Eps_sec | Trailing 12-month earnings per share | TRAIL_12M_EPS_BEF_XO_ITEM |
| assets_sec | Assets | BS_TOT_ASSET |
| EV_sec | Entreprise value | ENTERPRISE_VALUE |
| bkPerSh_sec | Book value per share | BOOK_VAL_PER_SH |
| cfPerSh_sec | Cash flow per share | CASH_FLOW_PER_SH |
| fcfPerSh_sec | Free cash flow per share | FREE_CASH_FLOW_PER_SH |
| ptMrg_sec | Trailing 12-month profit margin | TRAIL_12M_PROF_MARGIN |
| fcf2Pr_sec | Free cash flow to price | FREE_CASH_FLOW_YIELD |
| liab_sec | Total liability | BS_TOT_LIAB2 |
| ROE_sec | Return on equity | RETURN_COM_EQY |
| dbt2Eqy_sec | Debt to equity | TOT_DEBT_TO_TOT_EQY |
| salesPerSh1Y_sec | Sales per share last 12 months | TRAIL_12M_SALES_PER_SH |
| pr2CF_sec | Price to cash flow | PX_TO_CASH_FLOW |
| pr2Bk_sec | Price to book value | PX_TO_BOOK_RATIO |
| pr2Ern_sec | Price to earning | PE_RATIO |

Table A4.
Calculated intermediate stock indicators. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
Table A4.
Calculated intermediate stock indicators. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
| Variable Name | Description | Formula |
|---|---|---|
| _assetsTrnv | Asset turnover | _sales1Y/_assets |
| _debtSTminsCash | Short term debt minus cash | Max (_debtST − _cash, 0) |
| _debtMinsCash | Debt minus cash | _debtLT + _debtSTminsCash |
| _netIncome | Net income (NI) | _Eps1Y × _nbrShEps |
| Eps | Earnings per share (EPS) | earn1Y/nbShares |
| _ptMrg | Profit margin | earn1Y/sales1Y |
| _dbt2Eqy | Debt to Equity | _debt/_Eqy |
| _cfoMrg | Cash flow margin | _CF1y/_sales1Y |
| _yoyErnGr | Year to year earnings growth | _earn1Y(Q)/_earn1Y(Q-4) |
| _yoyErnGrRate | Year to year earnings growth rate | _yoyErnGr − 1 |
| yoyEpsGrRate | Year to year EPS growth rate | EPS(j)/EPS(j-252) − 1 |
| _yoyEbitdaGrRate | Year to year EBITDA growth rate | _ebitda1y(Q)/_ebitda1y(Q-4) − 1 |
| _yoySlGr | Year to year sales growth | _sales1Y(Q)/_sales1Y(Q-4) |
| _yoySlGrRate | Year to year sales growth rate | _yoySlGr − 1 |
| _netDebt | Net debt | _debt − _cshMrkSecur |
| EV | Enterprise value | curMrkCap + _debtMinsCash |
| _netDbtToEV | Net debt to EV | _netDebt/EV |
| _netDbt2Ebd | Net debt to EBITDA | _netDebt/_ebitda1Y |
| _curRatio | Current ratio | _curAssets/_curLiab |
| _ebitdaMrg | EBITDA margin | _ebitda1Y/_sales1Y |
| _inventryToSales | Inventories to sales | _inventori/_sales1y |
| _receivTurnover | Receivables turnover | _sales1y/_accReceiv |
| _operFin | Operations financing | (_accPayble − _accReceiv)/_sales1y |
| fcfPerSh | Free cash flow per share | _FCF1y/nbrShares |
| FcfDivCovRt | Free cash flow dividend coverage ratio | indDivYld/fcfPerSh |
| NiDivCovRt | Net income dividend coverage ratio | indDivYld/EPS |
| divPerShGr4Q | 4Q dividend per share growth | _divPerSh1y(Q)/_divPerSh1y(Q-4) |
| divPerShGr12Q | 12Q dividend per share growth | _divPerSh1y(Q)/_divPerSh1y(Q-12) |
| _netDebtIss | Net debt issuance | _debt(Q) − _debt(Q-4) |
| _netEqyIss | Net equity issuance | _augCap − _dimCap |
| _netFin | Net financing | _netEqyIss + _netDebtIss |
| _cfoToNiAcr | CFO to net income accrual | (_CF1y(Q) − _netIncome(Q))/assets(Q-4) |
| _ebidaToCfoAcr | EBITDA to CFO accrual | (_ebitda1Y(Q) − _CF1Y(Q))/assets(Q-4) |
| _acrEarn | Accrual earning | (_cshMrkSecr(Q) − _netEqyIss(Q)) − _cshMrkSecr(Q-4) |
| _3yAcrEarn | 3-year accrual earnings | _acrEarn(Q) + _acrEarn(Q-4) |
| _earn3Y | 3-year earnings | _earn1Y(Q) + _earn1Y(Q-4) + _earn1Y(Q-8) |
| _netAccrual | Net accrual | (_acrEarn − _earn1Y)/_Eqy |
| _3yNetAccrual | 3-year net accrual | (_3yAcrEarn(Q) − _earn3Y(Q))/_Eqy(Q-8) |
| _3yErnGrRate | 3-year earnings growth rate |
|
| _3ySlGrRate | 3-year sales growth rate |
|
| 3yEpsGrRate | 3-year EPS growth rate |
|
| _3yEbitdaGrRate | 3-year EBITDA growth rate |
|
| _pPsCurRtV | Piotroski positive current ratio variation indicator |
|
| _pNgEqyIss | Piotroski negative equity issuance indicator |
|
| _pPsGrsMrgV | Piotroski positive gross margin variation indicator |
|
| scNetDebtToEBITDA | Net debt to EBITDA score |
|
| scCurrentRatio | Current ratio score |
|
| scROE | Return on equity score |
|
| scEbidtaToSales | EBITDA to sales score |
|
| scInvtryToSales | Inventory to sales score |
|
| scReceivTurnover | Receivable turnover score |
|
| scOperFinancing | Operation financing score |
|
| scFcfDivCovRatio | FCF dividend coverage ratio score |
|
| scNiDivCovRatio | Net income dividend coverage ratio score |
|
| scDivShareGrowth4Q | 4Q dividend per share growth score |
|
| scDivShareGrowth12Q | 12Q dividend per share growth score |
|
| scNetEqyIssuance | Net equity issuance score |
|
| scNetFinancing | Net financing score |
|
| scEbitdaToCfoAccrual | EBITDA to CFO accrual score |
|
| scNetAccrual | Net accrual score |
|
| sc3yrNetAccrual | 3-year net accrual score |
|
| scYoyEbitdaGrowth | Year-on-year EBITDA growth score |
|
| sc3yrEbitdaGrowth | 3-year EBITDA growth score |
|

Table A5.
Calculated intermediate sector indicators. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
Table A5.
Calculated intermediate sector indicators. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
| Variable Name | Description | Formula |
|---|---|---|
| EV2Ass_sec | Enterprise value to total assets | EV_sec/assets_sec |
| debt_sec | Debt | bkPerSh_sec × dbt2Eqy_sec/100 |
| cfoMrg_sec | Cash flow margin | cfPerSh_sec/rvnPerSh_sec |
| yoyErnGr_sec | Year-to-year earning growth | Eps_sec/Eps_sec (j-252) |
| yoySlGr_sec | Year-to-year sales growth | rvnPerSh_sec/rvnPerSh_sec(j-252) |
| retD_sec | Daily return | (close_sec(j)/close_sec(j-1)) − 1 |
| ret5D_sec | 5-day return | (close_sec(j)/close_sec(j-5)) − 1 |
| ret9D_sec | 9-day return | (close_sec(j)/close_sec(j-9)) − 1 |
| ret22D_sec | 22-day return | (close_sec(j)/close_sec(j-22)) − 1 |
| ret50D_sec | 50-day return | (close_sec(j)/close_sec(j-50)) − 1 |
| ret130D_sec | 130-day return | (close_sec(j)/close_sec(j-130)) − 1 |
| ret200D_sec | 200-day return | (close_sec(j)/close_sec(j-200)) − 1 |
| ret252D_sec | 252-day return | (close_sec(j)/close_sec(j-252)) − 1 |
| RSI14D_sec | Sector 14-day Relative Strength Index (RSI) | 100 × SUM(UPs)/(SUM(UPs) + SUM(DOWNs)), Where, Ups = (px − px(j-1)) if px > px(j-1), DOWNs = (px(j-1) − px) if px < px(j-1) over 14 days, and px = Close_sec |
| MA5Rsi14D_sec | 5-day average 14-day RSI | AVG(RSI14D) over 5 days |
| stOscK14D_sec | 14-day Stochastic Oscillator (%k) | k = 100 × (close_sec − MIN(low_sec) over 14 days)/(MAX(high_sec) − MIN(low_sec) over 14 days) |
| fStOscK14D_sec | Fast 14-day Stochastic Oscillator | AVG(stOscK14D) over 3 days |
| sStOscK14D_sec | Slow 14-day Stochastic Oscillator | AVG(fStOscK14D) over 3 days |
| wliamR14D_sec | 14-day Williams percent range (%R) | 100 × (close_sec − MAX(high_sec) over 14 days)/(MAX(high_sec)−MIN(low_sec) over 14 days) |
| OBV_sec | On-balance-volume | OBV = SUM(sign(close_sec(j) − close_sec(j-1)) × Volume) over all historical data |
| volAn130D_sec | 130-day annualized volatility | sqrt(252) × std(retD_sec) over 130 days |
| volAn26W_sec | 26-week annualized volatility | sqrt(52) × std(ret5D) over 26 weeks |
| volAn52W_sec | 52-week annualized volatility | sqrt(52) × std(ret5D) over 52 weeks |
| volAn104W_sec | 104-week annualized volatility | sqrt(52) × std(ret5D) over 104 weeks |
| MA5D_sec | 5-day simple moving average | AVG(close_sec) over 5 days |
| MA20D_sec | 20-day simple moving average | AVG(close_sec) over 20 days |
| MA50D_sec | 50-day simple moving average | AVG(close_sec) over 50 days |
| MA130D_sec | 130-day simple moving average | AVG(close_sec) over 130 days |
| MA200D_sec | 200-day simple moving average | AVG(close_sec) over 200 days |
| MA252D_sec | 252-day simple moving average | AVG(close_sec) over 252 days |
| EMA5D_sec | 5-day exponential moving average | EMA5D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA5D_sec(j-1) Where, alpha = 2/(5 + 1) and EMA5D_sec(initial) = MA5D_sec |
| EMA20D_sec | 20-day exponential moving average | EMA20D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA20D_sec(j-1) Where, alpha = 2/(20 + 1) and EMA20D_sec(initial) = MA20D_sec |
| EMA50D_sec | 50-day exponential moving average | EMA50D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA50D_sec(j-1) Where, alpha = 2/(50 + 1) and EMA50D_sec(initial) = MA50_sec |
| EMA130D_sec | 130-day exponential moving average | EMA130D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA130D_sec(j-1) Where, alpha = 2/(130 + 1) and EMA130D_sec(initial) = MA130D_sec |
| EMA200D_sec | 200-day exponential moving average | EMA200D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA200D_sec (j-1) Where, alpha = 2/(200 + 1) and EMA200D_sec(initial) = MA200D_sec |
| EMA252D_sec | 252-day exponential moving average | EMA252D_sec(j) = alpha × close_sec(j) + (1 − alpha) × EMA252_sec (j-1) Where, alpha = 2/(252 + 1) and EMA252D_sec(initial) = MA252D_sec |
| momTCT_sec | Very short-term momentum | (close_sec/MA5D_sec) − 1 |
| momCT_sec | Short-term momentum | (MA5D_sec/MA20D_sec) − 1 |
| momMT_sec | Middle-term momentum | (MA20D_sec/MA50D_sec) − 1 |
| momLT_sec | Long-term momentum | MA50D_sec/MA200D_sec − 1 |
| momTLT_sec | Very long-term momentum | (MA200D_sec/MA252D_sec) − 1 |
| mmRt53Ex2w_sec | Momentum of weekly returns 1 year before 2 last weeks | mom53w_sec = AVG(rendW) over 52 weeks before 2 last weeks. Where, rendW is 5 days sector return weekly taken |
| pr2MA5D_sec | Price to 5-day simple moving average | close_sec/MA5D_sec |
| pr2MA20D_sec | Price to 20-day simple moving average | close_sec/MA20D_sec |
| pr2MA50D_sec | Price to 50-day simple moving average | close_sec/MA50D_sec |
| pr2MA130D_sec | Price to 130-day simple moving average | close_sec/MA130D_sec |
| pr2MA200D_sec | Price to 200-day simple moving average | close_sec/MA200D_sec |
| pr2MA252D_sec | Price to 252-day simple moving average | close_sec/MA252D_sec |
| pr2EMA5D_sec | Price to 5-day exponential moving average | close_sec/EMA5D_sec |
| pr2EMA20D_sec | Price to 20-day exponential moving average | close_sec/EMA20D_sec |
| pr2EMA50D_sec | Price to 50-day exponential moving average | close_sec/EMA50D_sec |
| pr2EMA130D_sec | Price to 130-day exponential moving average | close_sec/EMA130D_sec |
| pr2EMA200D_sec | Price to 200-day exponential moving average | close_sec/EMA200D_sec |
| pr2EMA252D_sec | Price to 252-day exponential moving average | close_sec/EMA252D_sec |

Table A6.
Final variables. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
Table A6.
Final variables. (Note that (j-n) means the end of the nth day before the day j, and (Q-n) means the nth quarter before the quarter Q).
| Variable Name | Description | Formula |
|---|---|---|
| Price | ||
| Open | Open price | |
| High | High price | |
| Low | Low price | |
| volume | Volume | |
| Close | Close price | |
| curMrkCap | Current market capitalization | |
| Stock price to sector | ||
| low2Sec | Low price to sector | low/low_sec |
| close2Sec | Close price to sector | close/close_sec |
| mrktCap2Sec | Market capitalisation price to sector | curMrkCap/curMrkCap_sec |
| open2Sec | Open price to sector | open/open_sec |
| high2Sec | High price to sector | high/high_se |
| Returns | ||
| retTD | Daily stock total return | (close(j) − close(j-1) + div)/close(j-1) |
| retT5D | 5-day stock total return | (close(j) − close(j-5) + div)/close(j-5) |
| retT9D | 9-day stock total return | (close(j) − close(j-9) + div)/close(j-9) |
| retT22D | 22-day stock total return | (close(j) − close(j-22) + div)/close(j-22) |
| retT50D | 50-day stock total return | (close(j) − close(j-50) + div)/close(j-50) |
| retT130D | 130-day stock total return | (close(j) − close(j-130) + div)/close(j-130) |
| retT200D | 200-day stock total return | (close(j) − close(j-200) + div)/close(j-200) |
| retT252D | 252-day stock total return | (close(j) − close(j-252) + div)/close(j-252) |
| Stock return to sector | ||
| retD2Sec | Daily return to sector | retTD/retD_sec |
| ret5D2Sec | 5-day return to sector | retT5D/ret5D_sec |
| ret9D2Sec | 9-day return to sector | retT9D/ret9D_sec |
| ret22D2Sec | 22-day return to sector | retT22D/ret22D_sec |
| ret50D2Sec | 50-day return to sector | retT50D/ret50D_sec |
| ret130D2Sec | 130-day return to sector | retT130D/ret30D_sec |
| ret200D2Sec | 200-day return to sector | retT200D/ret200D_sec |
| ret252D2Sec | 252-day return to sector | retT252D/ret252D_sec |
| Volatility | ||
| volAn130D | 130-day stock annualized volatility | sqrt(252) × std(retTD) over 130 days |
| volAn26W | 26-week stock annualized volatility | sqrt(52) × std(retT5D) over 26 weeks |
| volAn52W | 52-week stock annualized volatility | sqrt(52) × std(retT5D) over 52 weeks |
| volAn104W | 104-week stock annualized volatility | sqrt(52) × std(retT5D) over 104 weeks |
| Stock volatility to sector | ||
| volAn130D2Sec | 130-day annualized volatility to sector | volAn130D/volAn130D_sec |
| volAn26W2Sec | 26-week annualized volatility to sector | volAn26W/volAn26W_sec |
| volAn52W2Sec | 52-week annualized volatility to sector | volAn52W/volAn52W_sec |
| volAn104W2Sec | 104-weeksannualized volatility to sector | volAn104W/volAn104W_sec |
| Return to volatility | ||
| r5DToVol52W | 5-day return to 52-week volatility | retT5D/volAn52W |
| r5DToVol26W | 5-day return to 26-week volatility | retT5D/volAn26W |
| r5DToVol104W | 5-day return to 104-week volatility | retT5D/volAn104W |
| r5DToVol130D | 5-day return to 130-day volatility | retT5D/volAn130D |
| rDToVol130D | 1-day return to 130-day volatility | retTD/volAn130D |
| Simple moving average (SMA) | ||
| MA5D | 5-day SMA of stock Close | AVG(close) over 5 days |
| MA20D | 20-day SMA of stock Close | AVG(close) over 20 days |
| MA50D | 50-day SMA of stock Close | AVG(close) over 50 days |
| MA130D | 130-day SMA of stock Close | AVG(close) over 130 days |
| MA200D | 200-day SMA of stock Close | AVG(close) over 200 days |
| MA252D | 252-day SMA of stock Close | AVG(close) over 252 days |
| Stock SMA to Sector | ||
| MA5D2Sec | 5-day SMA to sector | MA5D/MA5D_sec |
| MA20D2Sec | 20-day SMA to sector | MA20D/MA20D_sec |
| MA50D2Sec | 50-day SMA to sector | MA50D/MA50D_sec |
| MA130D2Sec | 130-day SMA to sector | MA130D/MA130D_sec |
| MA200D2Sec | 200-day SMA to sector | MA200D/MA200D_sec |
| MA252D2Sec | 252-day SMA to sector | MA252D/MA252D_sec |
| Exponential moving average (EMA) | ||
| EMA5D | 5-day EMA of stock close | EMA5D(j) = alpha × close(j) + (1 − alpha) × EMA5D(j-1) Where, alpha = 2/(5 + 1) and EMA5D(initial) = MA5D |
| EMA20D | 20-day EMA of stock close | EMA20D(j) = alpha × close(j) + (1 − alpha) × EMA20D(j-1) Where, alpha = 2/(20 + 1) and EMA20D(initial) = MA20D |
| EMA50D | 50-day EMA of stock close | EMA50D(j) = alpha × close(j) + (1 − alpha) × EMA50D(j-1) Where, alpha = 2/(50 + 1) and EMA50D(initial) = MA50 |
| EMA130D | 130-day EMA of stock close | EMA130D(j) = alpha × close(j) + (1 − alpha) × EMA130D(j-1) Where, alpha = 2/(130 + 1) and EMA130D(initial) = MA130D |
| EMA200D | 200-day EMA of stock close | EMA200D(j) = alpha × close(j) + (1 − alpha) × EMA200D (j-1) Where, alpha = 2/(200 + 1) and EMA200D(initial) = MA200D |
| EMA252D | 252-day EMA of stock close | EMA252D(j) = alpha × close(j) + (1 − alpha) × EMA252 (j-1) Where, alpha = 2/(252 + 1) and EMA252D(initial) = MA252D |
| Stock EMA to Sector | ||
| EMA5D2Sec | 5-day EMA to sector | EMA5D/EMA5D_sec |
| EMA20D2Sec | 20-day EMA to sector | EMA20D/EMA20D_sec |
| EMA50D2Sec | 50-day EMA to sector | EMA50D/EMA50D_sec |
| EMA130D2Sec | 130-day EMA to sector | EMA130D/EMA130D_sec |
| EMA200D2Sec | 200-day EMA to sector | EMA200D/EMA200D_sec |
| EMA252D2Sec | 252-day EMA to sector | EMA252D/EMA252D_sec |
| Momentum | ||
| momTCT | Very short-term momentum | (close/MA5D) − 1 |
| momCT | Short-term momentum | (MA5D/MA20D) − 1 |
| momMT | Middle-term momentum | (MA20D/MA50D) − 1 |
| momLT | Long-term momentum | MA50D/MA200D − 1 |
| momTLT | Very long-term momentum | (MA200D/MA252D) − 1 |
| mmRt53Ex2w | Momentum of 1 year’s weekly returns before 2 last weeks | mom53w_sec = AVG(rendW) over 52 weeks before 2 last weeks. Where, rendW= rendT5D weekly taken |
| Stock Momentum to sector | ||
| momTCT2Sec | Very short-term momentum to sector | momTCT/momTCT_sec |
| momCT2Sec | Short-term momentum of sector | momCT/momCT_sec |
| momMT2Sec | Middle-term momentum of sector | momMT/momMT_sec |
| momLT2Sec | Long-term momentum of sector | momLT/momLT_sec |
| momTLT2Sec | Very long-term momentum of sector | momTLT/momTLT_sec |
| mmRet53Ex2w2Sec | Momentum of 1 year’s weekly returns before 2 last weeks to sector | mmRet53Ex2w/mmRet53Ex2w_sec |
| Price to SMA | ||
| pr2MA5D | Price to 5 days SMA ratio | close/MA5D |
| pr2MA20D | price to 20 days SMA ratio | close/MA20D |
| pr2MA50D | price to 50 days SMA ratio | close/MA50D |
| pr2MA130D | price to 130 days SMA ratio | close/MA130D |
| pr2MA200D | price to 200 days SMA ratio | close/MA200D |
| pr2MA252D | price to 252 days SMA ratio | close/MA252D |
| Price to SMA ratio to sector | ||
| pr2MA5D2Sec | Price to 5-day SMA ratio to sector | pr2MA5D/pr2MA5D_sec |
| pr2MA20D2Sec | price to 20-day SMA ratio to sector | pr2MA20D/pr2MA20D_sec |
| pr2MA50D2Sec | price to 50-day SMA ratio to sector | pr2MA50D/pr2MA50D_sec |
| pr2MA130D2Sec | price to 130-day SMA ratio to sector | pr2MA130D/pr2MA130D_sec |
| pr2MA200D2Sec | price to 200-day SMA ratio to sector | pr2MA200D/pr2MA200D_sec |
| pr2MA252D2Sec | price to 252-day SMA ratio to sector | pr2MA252D/pr2MA252D_sec |
| Price to EMA | ||
| pr2EMA5D | Price to 5-day EMA ratio | close/EMA5D |
| pr2EMA20D | price to 20-day EMA ratio | close/EMA20D |
| pr2EMA50D | price to 50-day EMA ratio | close/EMA50D |
| pr2EMA130D | price to 130-day EMA ratio | close/EMA130D |
| pr2EMA200D | price to 200-day EMA ratio | close/EMA200D |
| pr2EMA252D | price to 252-day EMA ratio | close/EMA252D |
| Price to EMA ratio to sector | ||
| pr2EMA5D2Sec | Price to 5-day EMA ratio to sector | pr2EMA5D/pr2EMA5D_sec |
| pr2EMA20D2Sec | price to 20-day EMA ratio to sector | pr2EMA20D/pr2EMA20D_sec |
| pr2EMA50D2Sec | price to 50-day EMA ratio to sector | pr2EMA50D/pr2EMA50D_sec |
| pr2EMA130D2Sec | price to 130-day EMA ratio to sector | pr2EMA130D/pr2EMA130D_sec |
| pr2EMA200D2Sec | price to 200-day EMA ratio to sector | pr2EMA200D/pr2EMA200D_sec |
| pr2EMA252D2Sec | price to 252-day EMA ratio to sector | pr2EMA252D/pr2EMA252D_sec |
| Other technical indicators | ||
| RSI14D | 14-day Relative Strength Index (RSI) | 100 × SUM(UPs)/(SUM(UPs) + SUM(DOWNs)), where, Ups = (px−px(j-1)) if px > px(j-1) and DOWNs = (px(j-1)-px) if px < px(j-1) over 14 days, and px = Close |
| MA5Rsi14D | 5-day average 14-day RSI | AVG(RSI14D) over 5 days |
| stOscK14D | 14-day stochastic oscillator (%k) | k = 100 × (close − MIN(low) over 14 days)/(MAX(high) − MIN(low) over 14 days) |
| fStOscK14D | Fast 14-day stochastic oscillator | AVG(stOscK14D) over 3 days |
| sStOscK14D | Slow 14-day stochastic oscillator | AVG(fStOscK14D) over 3 days |
| wliamR14D | 14-day Williams percent range (%R) | 100 × (close − MAX(high) over 14 days)/(MAX(high) − MIN(low) over 14 days) |
| OBV | On-Balance-Volume | OBV = SUM(sign(close(j) − close(j-1)) × Volume) over all historical data |
| Other stock to sector technical indicators | ||
| RSI14D2Sec | 14-day RSI to sector | RSI14D/RSI14D_sec |
| MA5Rsi14D2Sec | 5-day average 14-day RSI | MA5RSI14D/MA5RSI14D_sec |
| stOscK14D2Sec | 14-day stochastic oscillator to sector | stOscK14D/stOscK14D_sec |
| fStOscK14D2Sec | Fast 14-day stochastic oscillator to sector | fStOscK14D/fStOscK14D_sec |
| sStOscK14D2Sec | Slow 14-day stochastic oscillator to sector | sStOscK14D/sStOscK14D_sec |
| wliamR14D2Sec | 14-day Williams percent range to sector | wliamR14D/wliamR14D_sec |
| OBVlm2Sec | On-balance-volume to sector | OBV/OBV_sec |
| Price multiples | ||
| EV | Enterprise value | curMrkCap + _debtMinsCash |
| pr2Ern | Price to earning ratio | curMrkCap/_earn1Y |
| pr2ErnDil | Price to earning diluted ratio | close/_earn1Y/_nbrShDilEps |
| pr2Bk | Price to book ratio | curMrkCap/_Eqy |
| pr2Sl | Price to sales ratio | curMrkCap/_sales1Y |
| pr2CF | Price to cash flow ratio | curMrkCap/_CF1Y |
| pr2FCF | Price to free cash flow ratio | curMrkCap/_FCF1Y |
| Ev2As | Enterprise value to total assets ratio | EV/_assets |
| Stock price multiples to sector | ||
| pr2Sl2Sec | Price to sales to sector | pr2Sl/salesPerSh1Y_sec |
| pr2CF2Sec | Price to cash flow to sector | pr2CF/pr2CF_sec |
| pr2Bk2Sec | Price to free cash flow to sector | pr2Bk/pr2Bk_sec |
| pr2Ern2Sec | Price to book to sector | pr2Ern/pr2Ern_sec |
| Stock to sector fundamental indicators | ||
| dvPerSh1y2Sec | Dividend per share for 1 year to sector | _divPerSh1y/divPerSh1y_sec |
| eps2Sec | Earning per share to sector | EPS/Eps_sec |
| sl1y2Sec | Sales 4Q to sector | sales1Y/rvnPerSh_sec |
| assets2Sec | Assets to sector | _assets /assets_sec |
| ev2Sec | Enterprise value to sector | EV/EV_sec |
| eqy2Sec | Equity to sector | _Eqy/bkPerSh_sec |
| dbt2Eqy2Sec | Debt to equity to sector | _dbt2Eqy/dbt2Eqy_sec |
| cf1y2Sec | Cash flow to sector | (_CF1y/nbrShares)/cfPerSh_sec |
| fcf2Sec | Free cash flow to sector | (_FCF1y/nbrShares)/fcfPerSh_sec |
| ptMrg2Sec | Profit margin to sector | _ptMrg/ptMrg_sec |
| fcf2Pr2Sec | Free cash flow to price to sector | (1/pr2FCF)/fcf2Pr_sec |
| liab2Sec | Liability to sector | _liab/liab_sec |
| retOnEqy2Sec | Return on equity to sector | _ROE/ROE_sec |
| debts2Sec | Debt to sector | _debts/debts_sec |
| ev2Ass2Sec | Enterprise value to assets to sector | Ev2As/EV2Ass_sec |
| CfoMrg2Sec | Cash flow margin to sector | _cfoMrg/CfoMrg_sec |
| yoyErnGr2Sec | Year-to-year earning growth to sector | _yoyErnGr/yoyErnGr_sec |
| yoySlGr2Sec | year-to-year sales growth to sector | _yoySlGr/yoySlGr_sec |
| Piotroski indicators | ||
| _piotrROA | Piotroski return on assets (ROA) | _earn1Y/assets(Q-4) |
| _piotrCFO | Piotroski cash flow (CFO) | _CF1y/assets(Q-4) |
| _pPsRoa | Piotroski positive ROA indicator | If _piotrROA > 0: _pPsRoa = 1 Else _pPsRoa = 0 |
| _pPsCfo | Piotroski positive CFO indicator | If _piotrCFO > 0: _pPsCfo = 1 Else _pPsCfo = 0 |
| _pPsRoaV | Piotroski positive ROA variation indicator | If _piotrROA > _piotrROA(Q-4): _pPsRoaV = 1 Else: _pPsRoaV = 0 |
| _pPsCfoV | Piotroski positive CFO variation indicator | If _piotrCFO > _piotrCFO(Q-4): _pPsCfoV = 1 Else: _pPsCfoV = 0 |
| _pCfoS2Roa | Piotroski CFO greater than ROA indicator | IF _piotrCFO > _piotrROA: _pCfoS2Roa = 1 Else _pCfoS2Roa = 0 |
| _pNgDbtV | Piotroski negative debt variation indicator | if _debt > _debt(Q-4): _pNgDbtV = 0 Else _pNgDbtV = 1 |
| _pPsAsTrnV | Piotroski positive asset turnover variation indicator | If _assetsTrnv > _assetsTrnv(Q-4): _pPsAsTrnV = 1 Else _pPsAsTrnV = 0 |
| _piotrSc | Piotroski score | SUM (piotroski indicators) = _pPsRoa + _pPsRoaV + _pPsCfo + _pPsCfoV + _pCfoS2Roa + _pNgDbtV + _pPsAsTrnV + _pPsCurRtV + _pNgEqyIss + _pPsGrsMrgV |
| Scores | ||
| scNetDbt2EV | Net debt to enterprise value score | If _netDbtToEV < 0.25: score = 2 If 0.25 ≤ _netDbtToEV < 0.35: score = 1 If _netDbtToEV ≥ 0.35: score = 0 |
| scEty | Equity score | If _netDebt ≥ 0 and _Eqy > 0 and _Eqy ≥ (2 × _netDebt): score = 2 If _netDebt ≥ 0 and _Eqy > 0 and _Eqy < (2 × _netDebt): score = 1 If _netDebt ≥ 0 and _Eqy ≤ 0: score = 0 If _netDebt ≤ 0 and _Eqy > 0: score = 2 If _netDebt ≤ 0 and _Eqy ≤ 0: score = 0 |
| scBlncSht | Balance sheet score | score = scNetDebtToEBITDA + scNetDbt2EV + scCurrentRatio + scEty |
| scNi2Sl | Net income to sales score | If _ptMrg > 0.15: score = 2 If 0.1 < _ptMrg ≤ 0.15: score = 1 If _ptMrg ≤ 0.1: score = 0 |
| scOpEff | Operation efficiency score | score = (3 × scROE) + (3 × scEbidtaToSales) + (4 × scNiToSales) + (1 × scInvtryToSales) + (1 × scReceivTurnover) + (1 × scOperFinancing) |
| scDivQly | Dividend quality score | score = (2 × scFcfDivCovRatio) + (2 × scNiDivCovRatio) + (1 × scDivShareGrowth4Q) + (1 × scDivShareGrowth12Q) |
| scNetDbtIss | Net debt issuance score | If _netDebtIss < 0: score = 2 If _netDebtIss ≥ 0 and f_netDebtIss < (0.15 × curMrkCap): score = 1 If _netDebtIss ≥ (0.15 × curMrkCap): score = 0 |
| scFin | Financing score | scFin = (1 × scNetDebtIssuance) + (1 × scNetEqyIssuance) + (3 × scNetFinancing) |
| scCfo2NiAc | Cash flow to net income accrual score | If _cfoToNiAcr > −0.03: score = 2 If −0.07 < _cfoToNiAcr ≤ −0.03: score = 1 If _cfoToNiAcr ≤ −0.07: score = 0 |
| scErnQly | Earning quality score | score = (1 × scEbitdaToCfoAccrual) + (1 × scCfo2NiAc) + (1 × scNetAccrual) + (3 × sc3yrNetAccrual) |
| scYoyErnGrh | Year-to-year earning growth score | If _yoyErnGrRate > 0.15: score = 2 If 0.07 < _yoyErnGrRate ≤ 0.15: score = 1 If _yoyErnGrRate ≤ 0.07: score = 0 |
| sc3yrErnGr | 3-year earning growth score | If _3yErnGrRate > 0.15: score = 2 If _3yErnGrRate > 0.07 and _3yErnGrRate <= 0.15: score = 1 If _3yErnGrRate ≤ 0.07: score = 0 |
| scYoySlGr | Year-to-year sales growth score | If _yoySlGrRate > 0.10: score = 2 If 0.05 < _yoySlGrRate ≤ 0.10: score = 1 If _yoySlGrRate <= 0.05: score = 0 |
| sc3yrSlGr | 3-year sales growth score | If _3ySlGrRate > 0.10: score = 2 If 0.05 < _3ySlGrRate ≤ 0.10: score = 1 If _3ySlGrRate ≤ 0.05: score = 0 |
| scYoyEpsGr | Year-to-year earnings per share growth score | If yoyEpsGrRate > 0.15: score = 2 If 0.07 < yoyEpsGrRate ≤ 0.15: score = 1 If yoyEpsGrRate <= 0.07: score = 0 |
| sc3yrEpsGr | 3-year EPS growth score | If 3yEpsGrRate > 0.15: score = 2 If 0.07 < 3yEpsGrRate ≤ 0.15: score = 1 If 3yEpsGrRate ≤ 0.07: score = 0 |
| scGrowth | Growth score | scGrowth = (1 × scYoyEarnGrowth) + (3 × sc3yrEarnGrowth) + (1 × scYoyEbitdaGrowth) + (3 × sc3yrEbitdaGrowth) + (1 × scYoySalesGrowth) + (3 × sc3yrSalesGrowth) + (1 × scYoyEpsGrowth) + (3 × sc3yrEpsGrowth) |
| Other indicators | ||
| ret5D_sec | 5-day return of sector | [close_sec(j)/close_sec(j-5)) − 1 |
| sp | 5-day return spread between stock and sector | retT5D − ret5D_sec |
References
- Bodson, Laurent, Pascal Grandin, Georges Hübner, and Marie Lambert. 2010. Performance de Portefeuille. Paris: Pearson. [Google Scholar]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Box, George E. P., and Gwilym M. Jenkins. 1970. Time Series Analysis, Forecasting and Control. San Francisco: Holden-Day. [Google Scholar]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Chaweewanchon, Apichat, and Rujira Chaysiri. 2022. Markowitz Mean-Variance Portfolio Optimization with Predictive Stock Selection Using Machine Learning. International Journal of Financial Studies 10: 64. [Google Scholar] [CrossRef]
- Cipiloglu Yildiz, Zeynep, and Selim Baha Yildiz. 2022. A portfolio construction framework using LSTM-based stock markets forecasting. International Journal of Finance & Economics 27: 2356–66. [Google Scholar] [CrossRef]
- Dangeti, Pratap. 2017. Statistics for Machine Learning. Birmingham: Packt Publishing Ltd. [Google Scholar]
- Ding, Guangyu, and Liangxi Qin. 2020. Study on the prediction of stock price based on the associated network model of LSTM. International Journal of Machine Learning and Cybernetics 11: 1307–17. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Ganchev, Alexander. 2022. The Performance of Hedge Fund Industry during the COVID-19 Crisis—Theoretical Characteristics and Empirical Aspects. Economic Studies (Ikonomicheski Izsledvania) 31: 18–37. [Google Scholar]
- Gers, Felix A., Jürgen Schmidhuber, and Fred Cummins. 2000. Learning to Forget: Continual Prediction with LSTM. Neural Computation 12: 2451–71. [Google Scholar] [CrossRef]
- Ghosh, Achyut, Soumik Bose, Giridhar Maji, Narayan Debnath, and Soumya Sen. 2019. Stock price prediction using LSTM on Indian Share Market. Paper presented at the 32nd International Conference on Computer Applicationsin Industry and Engineering, San Diego, CA, USA, September 30–October 2, vol. 63, pp. 101–10. [Google Scholar]
- Hochreiter, Sepp, and Jürgen Schmidhuber. 1997. Long short-term memory. Neural Computation 9: 1735–80. [Google Scholar] [CrossRef]
- Hou, Xiurui, Kai Wang, Jie Zhang, and Zhi Wei. 2020. An enriched time-series forecasting framework for long-short portfolio strategy. IEEE Access 8: 31992–2002. [Google Scholar] [CrossRef]
- Hu, Zexin, Yiqi Zhao, and Matloob Khushi. 2021. A survey of forex and stock price prediction using deep learning. Applied System Innovation 4: 9. [Google Scholar] [CrossRef]
- Jacobs, Bruce I., and Kenneth N. Levy. 2005. Market Neutral Strategies, Frank J. Fabozzi Series. New York: John Wiley & Sons. [Google Scholar]
- Jensen, Michael C. 1968. The performance of mutual funds in the period 1945–1964. The Journal of Finance 23: 389–416. [Google Scholar] [CrossRef]
- Jiang, Weiwei. 2021. Applications of deep learning in stock market prediction: Recent progress. Expert Systems with Applications 184: 115537. [Google Scholar] [CrossRef]
- Keating, Con, and William F. Shadwick. 2002. An introduction to omega. AIMA Newsletter. Available online: https://scholar.google.ca/scholar?hl=fr&as_sdt=0%2C5&as_vis=1&q=%28Keating+and+Shadwick+2002%29+Keating%2C+Con%2C+and+William+F.+Shadwick.+2002.+An+introduction+to+omega.+AIMA+Newsletter.&btnG= (accessed on 20 January 2023).
- Kohavi, Ron. 1995. A study of cross-validation and bootstrap for accuracy estimation and model selection. International Joint Conferences on Artificial Intelligence 14: 1137–45. [Google Scholar]
- Lanbouri, Zineb, and Said Achchab. 2019. A new approach for Trading based on Long-Short Term memory Ensemble technique. International Journal of Computer Science Issues (IJCSI) 16: 27–31. [Google Scholar] [CrossRef]
- Liu, Shuanglong, Chao Zhang, and Jinwen Ma. 2017. CNN-LSTM neural network model for quantitative strategy analysis in stock markets. In International Conference on Neural Information Processing. Cham: Springer, pp. 198–206. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Michańków, Jakub, Paweł Sakowski, and Robert Ślepaczuk. 2022. LSTM in Algorithmic Investment Strategies on BTC and S&P500 Index. Sensors 22: 917. [Google Scholar] [CrossRef]
- Nafia, Abdellilah, Abdellah Youssefi, and Abdellah Echaoui. 2022. Modèles classiques et de datamining les plus utilisés en évaluation et en prédiction de la performance des actions. Revue des Etudes Multidisciplinaires en Sciences Economiques et Sociales 7: 231–68. [Google Scholar] [CrossRef]
- Naik, Nagaraj, and Biju R. Mohan. 2019. Study of stock return predictions using recurrent neural networks with LSTM. In International Conference on Engineering Applications of Neural Networks. Cham: Springer, pp. 453–59. [Google Scholar]
- Neyman, J. 1939. Review of A Study in Analysis of Stationary Time Series, by Herman Wold. Journal of the Royal Statistical Society 102: 295. [Google Scholar] [CrossRef]
- Olah, Christopher. 2015. Colah’s Blog: Understanding LSTM Networks. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs (accessed on 6 November 2022).
- Ozbayoglu, Ahmet Murat, Mehmet Ugur Gudelek, and Omer Berat Sezer. 2020. Deep learning for financial applications: A survey. Applied Soft Computing 93: 106384. [Google Scholar] [CrossRef]
- Patel, Jigar, Sahil Shah, Priyank Thakkar, and K Kotecha. 2015. Predicting stock and stock price index movement using trend deterministic data preparation and machine learning techniques. Expert Systems with Applications 42: 259–68. [Google Scholar] [CrossRef]
- Piotroski, Joseph D. 2000. Value investing: The use of historical financial statement information to separate winners from losers. Journal of Accounting Research 38: 1–41. [Google Scholar] [CrossRef]
- Qiu, Jiayu, Bin Wang, and Changjun Zhou. 2020. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS ONE 15: e0227222. [Google Scholar] [CrossRef]
- Rosenblatt, Frank. 1957. The Perceptron, a Perceiving and Recognizing Automaton. Buffalo: Cornell Aeronautical Laboratory. [Google Scholar]
- Sen, Jaydip, Sidra Mehtab, Abhishek Dutta, and Saikat Mondal. 2021. Precise Stock Price Prediction for Optimized Portfolio Design Using an LSTM Model. Paper presented at the 2021 19th OITS International Conference on Information Technology (OCIT), Bhubaneswar, India, December 16–18; pp. 210–15. [Google Scholar] [CrossRef]
- Sharpe, William F. 1994. The Sharpe Ratio. Journal of Portfolio Management 21: 49–58. [Google Scholar] [CrossRef]
- Tfaily, Fatima, and Mohamad M. Fouad. 2022. Multi-level stacking of LSTM recurrent models for predicting stock-market indices. Data Science in Finance and Economics 2: 147–62. [Google Scholar] [CrossRef]
- Touzani, Yassine, and Khadija Douzi. 2021. An LSTM and GRU based trading strategy adapted to the Moroccan market. Journal of Big Data 8: 126. [Google Scholar] [CrossRef]
- Treynor, Jack L. 1962. Toward a Theory of Market Value of Risky Assets. (SSRN Scholarly Paper Nᵒ 628187). Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=628187 (accessed on 22 March 2023). [CrossRef]
- Yao, Siyu, Linkai Luo, and Hong Peng. 2018. High-frequency stock trend forecast using lstm model. Paper presented at the 2018 13th International Conference on Computer Science & Education (ICCSE), Colombo, Sri Lanka, August 8–11; pp. 1–4. [Google Scholar]
- Yi, Kan, Jin Yang, Shuangling Wang, Zhengtong Zhang, Jing Zhang, Jinqiu Song, and Xiao Ren. 2022. IntelliPortfolio: Intelligent Portfolio for Enhanced Index Tracking Using Clustering and LSTM. Mathematical Problems in Engineering 2022: 3751452. [Google Scholar] [CrossRef]
- Yule, G. Udny. 1926. Why Do We Sometimes Get Nonsense-Correlations between Time-Series? A Study in Sampling and the Nature of Time-Series. Journal of the Royal Statistical Society 89: 1–63. [Google Scholar] [CrossRef]
- Zhang, Xiaolin, and Ying Tan. 2018. Deep stock ranker: A LSTM neural network model for stock selection. In International Conference on Data Mining and Big Data. Cham: Springer, pp. 614–23. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).