The Efficiency of Indonesian Pension Funds: A Two-Stage Additive Network DEA Approach

Abstract

Employer pension funds (EPFs) manage funds contributed by their members and sponsors with the ultimate goal of providing adequate pension benefits for beneficiaries upon retirement. The critical issue for EPFs is, therefore, their efficiency. This study aims to investigate Indonesian EPFs’ technical efficiency and its determinants using data from 38 EPFs actively operating in 2011–2017. By conceptualizing EPFs’ management processes as a network, this study employs the two-stage additive network data envelopment analysis (DEA) to measure the performance of EPFs based on their overall efficiency, operational efficiency, and investment efficiency. A regression analysis is then performed to examine the determinants of EPFs’ efficiency. The results reveal that investment efficiency is the main source of EPFs’ overall inefficiency, implying that more attention should be directed towards investment management when the EPFs seek to improve their overall performance. The regression analysis shows that size and ownership are the most significant factors that determine EPFs’ efficiency. Ownership positively correlates with both overall efficiency and investment efficiency, while size negatively affects investment efficiency. This study concludes that in order to improve their overall performance, EPFs need to make more efforts in investment management, while accounting for size and ownership as important determinants. This study provides a projection analysis model as a practical guidline for EPFs to improve their performance.

1. Introduction

Pension funds collect, pool, and invest funds contributed by the sponsors and their members to provide beneficiaries with an appropriate retirement income in the future (Davis 1995). As such, they are also financial intermediaries that convert household savings into investment. They allow households to smooth their consumption over very long periods (Barr and Diamond 2006; Kadarisman and Wahyuni 2010) and provide investment capital to the economy (Thomas and Spataro 2016; Bijlsma et al. 2018). The key issue for pension funds is, therefore, how efficiently they perform this intermediation function for both the providers (i.e., the pension funds’ participants) and users of capital. Pension funds’ inefficiency raises the costs of investments capital for firms; moreover, inefficiency in pension funds’ management reduces the retirement benefits of participants, increasing the amount that they need to save to provide for their retirement and, therefore, reducing their consumption.

In this respect, many developing countries have tried to reform their pension funds to increase the efficiency of their pension systems. For example, Indonesia started its reform by passing Act No. 11 of 1992 concerning Pension Funds. After the 2008 financial crisis, the Indonesian government gradually intensified its reform by stipulating the pension fund industry to adopt best and internationally standardized governance practices. Numerous crucial acts and regulations have been amended, including the Financial Services Authority or FSA (OJK—Otoritas Jasa Keuangan) (Act No. 21/2011); National Social Insurance Agency (BPJS—Badan Penyelenggara Jaminan Sosial) (Act No. 24/2011); pension fund administrators’ competence and integrity (FSA Regulation No. 4/2013); information transparency (FSA Regulation No. 7/2013); investment portfolio allocation (FSA Regulation No. 3/2015); and pension funds’ obligation to allocate their investments at least 30% to government securities (SBN—Surat Berharga Negara) (FSA Regulation No. 1/2016).

Despite the ongoing reform, the Indonesian pension fund industry demonstrates an alarming phenomenon.

Table 1. Pension fund dissolution (cumulative), 2011–2017.

Year		2011	2012	2013	2014	2015	2016	2017	Total
DB-EPFs	Active	204	201	198	194	190	180	169	169
	Disband	4	3	3	4	4	10	11	39
DC-EPFs	Active	41	43	43	48	45	44	44	44
	Disband	-	-	-	-	3	1	2	6
FIPF	Active	25	25	24	25	25	25	23	23
	Disband	-	-	1	-	-	-	2	3
All funds	Active	270	269	266	267	260	249	236	236
	Disband	4	3	4	4	7	11	15	48

Source: Author compilation based on statistics data from FSA. DB-EPFs: defined benefits EPFs; DC-EPFs: defined contribution EPFs; FIPF: financial institution pension funds.

presents the Indonesian pension fund industry’s current situation. In particular, employers freeze their employer pension funds or EPFs (DPPK—Dana Pensiun Pemberi Kerja), convert their defined benefit plans (PMP—Program Manfaat Pasti) into defined contribution plans (PIP—Program Iuran Pasti), and even dissolve their pension funds. Several factors explain these phenomena, including sponsors’ financial difficulties, the presence of mandatory pension fund programs from Employment BPJS, and more importantly, EPFs’ internal inefficiency and performance stagnation (Mangkoesoebroto 2017). Hence, it is crucial to empirically investigate the efficiency of Indonesian EPFs and their determinants to increase their efficiency, thereby optimizing their contribution to the economy.

Empirical references on pension funds’ efficiency remain relatively limited. Most prior studies have focused on developed countries, including the Netherlands (Alserda et al. 2018; Bikker 2017) and Australia (Bui et al. 2016; Galagedera 2017). Studies on developing countries still focus on European or Latin American countries, such as Poland (Karpio and Zebrowska-Suchodolska 2016), Turkey (Gokoz and Çandarli 2011), Croatia (Draženović et al. 2019), or Chile (Barrientos and Boussofiane 2005; Guillen 2008). Pension funds’ efficiency in Asia, especially in Indonesia, remains relatively understudied. For example, Asher and Bali (2015) conducted general assessments on ASEAN countries’ pension funds but did not focus on Indonesian pension funds’ efficiency. Similarly, Guerard (2012) only reviewed the Indonesian pension system reform but did not focus on efficiency in pension funds. Based on the recent phenomena of pension funds’ decreasing performance and prior efficiency research, this study seeks to evaluate and investigate the Indonesian EPFs’ technical efficiency and their determinants.

Methodologically, this study employs the non-parametric data envelopment analysis (DEA) method to measure the performance of pension funds. The DEA method has been widely used in studies on pension funds’ efficiency (Bui et al. 2016; Draženović et al. 2019). This method identifies a decision-making unit or DMU’s inefficiency by comparing it with other efficient DMUs (Coelli et al. 2005). A traditional DEA approach, however, considers the production process a ‘black box’ without sufficient details to identify sources of inefficiency (Färe and Grosskopf 2000; Cook et al. 2010). 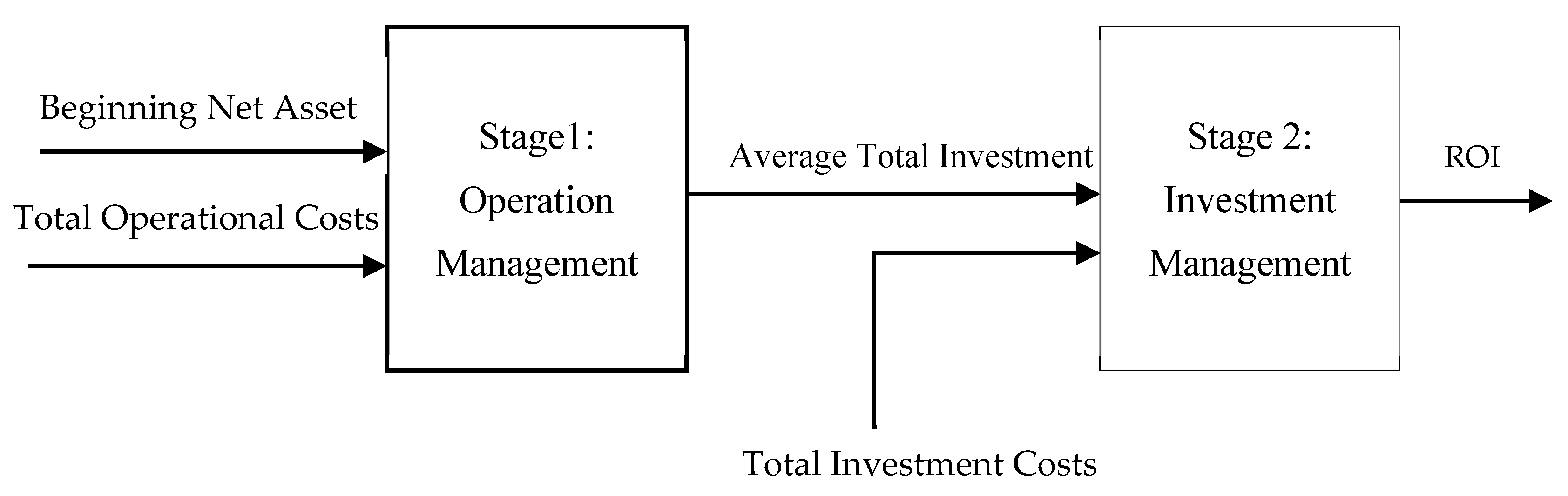New studies about pension fund performance consider the structure of pension funds as a network (Galagedera 2017; Lin et al. 2021); therefore, we chose to apply the two-stage additive network DEA in our study. In particular, in this research, we conceptualize the management function of employer pension funds (EPFs) as a serially linked dual sub-process, i.e., operational management and investment management (Galagedera 2017). This approach is beneficial because it allows us to evaluate not only the overall performance of the EPFs, but also the performance of their components, i.e., operation management and investment management.

We combine network DEA with a second stage regression analysis to determine factors explaining EPFs’ efficiency level, by adopting the technique used in Simar and Wilson (2007). Simar and Wilson (2007) proposed a bootstrap procedure coupled with truncated regression to mitigate the ambiguous data generating process and serial correlation problem in efficiency scores, thereby providing more statistically valid inference results.

This study has some contributions. First, in terms of method, this study is (to the best of our knowledge) the first to apply the two-stage additive network DEA to evaluate the EPFs industry. Previous studies have generally used traditional methods to assess EPFs’ performance, such as the risk-adjusted method (Hasanudin et al. 2017), ratio analysis (Sunaryo et al. 2020), or conventional DEA (Seran et al. 2022). Thus, this study extends the application of the method to EPFs, while at the same time, introducing the method as a useful alternative to the traditional method for measuring EPFs’ performance.

Second, using a two-stage additive network model, we are able to break down the EPFs management process into two stages, i.e., operations management and investment management, and evaluate them accordingly.

Third, this study proposes a projection analysis model that can be used as a practical guideline for EPFs to improve their performance.

Fourth, this study also conducts a regression analysis by adopting the procedure of Simar and Wilson (2007) to examine the correlation between pension funds’ efficiency and their specific characteristics (i.e., size, plan type, and ownership), finding that size and ownership are important characteristics that determine the performance of EPFs in Indonesia.

This article is organized as follows. Section 2 presents an overview of the Indonesian pension funds industry. Section 3 is the literature review. Section 4 discusses the methods. Section 5 presents the results, and Section 6 is the conclusion.

2. Overview of the Indonesian Pension Industry

The history of the Indonesian pension funds system can be traced back to the Dutch colonial era. Dutch colonial companies provided old age benefits (THT) for their employees based on the so-called Arbeiderfondsen Ordonnantie of 1926. Long after Indonesian independence in 1945, the provision of pensions for employees still referred to the same legal framework. It was only in 1992 that the government passed the Pension Fund Act (UU) (Number 11 of 1992) about Employer Pension Funds (EPFs) and Financial Institution Pension Funds (FIPFs). EPFs and FIPFs are voluntary pension funds. In 2004, Law No. 40 of the National Social Security System (SJSN) was passed, mandating the government to seek a mandatory basic pension for the general public. This was realized in 2011 with the establishment of the Badan Penyelenggara Jaminan Sosial—National Social Insurance Agency (BPJS) (Law Number 24 of 2011) as a government agency tasked with administering and managing the pension benefit program (JP) for the general public. The JP is a fully funded, defined benefit plan and is mandatory for the working population. The JP has been in effect since July 2015. Currently, the JP contribution is 3% of an employee’s monthly salary, of which 2% is borne by the employer and 1% is borne by the employee. In 2017, the number of JP participants was 10.63 million, and its assets amounted to IDR 25.67 trillion.

The presence of JP BPJS complements one of the important pillars in the Indonesian pension system. When viewed based on the “five pillars” model from the World Bank (Holzmann and Hinz 2005; Holzmann 2013), Indonesia’s current pension system consists of three pillars. “Pillar Zero”, consists of government subsidies or social assistance to the poor and elderly, according to the SJSN Law No. 40 of 2004. The “second pillar” includes the mandatory JP BPJS program and the pension for civil servants and military/police officers. The “third pillar” covers voluntary pension funds, as stipulated in Pension Law No. 11 of 1992, i.e., EPFs and FIPFs. Based on the World Bank’s “five pillars” model, the first pillar, i.e., a non-contributory mandatory defined benefit plan, is absent from the Indonesian pension system.

This study focuses on EPFs, which belong to the third pillar in the Indonesian pension system. In the context of Indonesian law, only pension funds on the third pillar, i.e., EPF and FIPF, are referred to as “Pension Funds”. EPF and FIPF are legal entities established with the sole objective of providing pensions benefits for their participants. In this respect, the JP from BPJS is not a “pension fund” but simply a pension benefit program administered by BPJS; BPJS is also not a “pension fund” because it administers not only a pension benefit program, but also other social security programs such as a health insurance program and other social security programs.

The EPF is established by an employer, whether in the form of a defined benefit or defined contribution plan. The membership is limited to the employees of the firm or the employees of its founding partners. Meanwhile, FIPF is an open membership, defined contribution plan established by a bank or an insurance company. EPF (also FIPF) is run based on the principles of freedom, funding, separation of wealth, postponed benefits, portability, vesting rights, and government supervision and guidance (Siswosudarmo 2010).

EPF management is carried out by a board of trustees appointed by the founder of the pension fund. The board members usually consist of senior employees who are competent in pension funds management. Pension benefits are only paid when a participant has reached retirement age. In the case of pension benefits from a defined contribution EPF, the payment of pension benefits is transferred to an insurance company through the purchase of an annuity. Pension benefits are tax protected. A participant can transfer to another pension fund (principle of portability).

In 2017, the total number of voluntary pension funds (third pillar) was 244, consisting of 220 EPFs and 24 FIPFs. FIPFs are much smaller in number than EPFs, but they have more participants. The total number of voluntary pension participants in 2017 was 4.46 million, of which 3.1 million were FIPFs’ participants, and only 1.4 million were EPFs’ participants. However, in terms of asset value, EPFs are still the largest with a total net asset value of 71.12% (IDR 185.5 trillion), compared to FIPFs, which only have a net asset value of IDR 75.4 trillion or (29%) IDR 260.83 trillion, i.e., the total net assets of all voluntary pension funds (EPFs + FIPFs). When compared to JP BPJS, the asset value of EPFs is greater than that of JP BPJS (IDR 185.5 versus 25.67 trillion), even though the number of JP BPJS participants was greater than EPF (10.63 million versus 1.4 million) participants in 2017. Thus, EPFs are still an important component of the Indonesian pension industry.

3. Literature Review

3.1. The Performance Measurement of Pension Funds Using Network DEA

Measuring the performance of pension funds can be achieved in various ways. Investment performance measurement generally uses risk-adjusted return models such as the Treynor ratio and Sharpe ratio (Hasanudin et al. 2017; Kompa and Witkowska 2016; Oran et al. 2017). The limitation of the risks-adjusted return models is that they cannot take into account the cost factor in their analysis (Gokoz and Çandarli 2011). Pension fund performance is usually also measured by financial ratios, such as the adequacy ratio of funds, return on assets (ROA), operating expense ratio (OER), etc. (Sunaryo et al. 2020). However, measurements using financial ratios generally do not provide accurate information when used to measure overall performance (Yang 2006).

The DEA measures pension fund performance from a different perspective. It is a performance measurement method with a structural approach based on theoretical models of company behavior, such as efforts to minimize costs or maximize profits (Psillaki and Mamatzakis 2017). Under the concept of the production frontier, the DEA measures the company’s efforts (management) to optimize all controllable factors (inputs) to achieve the desired level of output (Charnes et al. 1978). Different from the parametric measurement method, the DEA is a non-parametric method and does not require an explicit form of function that relates input and output variables (Cook and Seiford 2009). It does not enforce any functional form on the data or make distributional assumptions on the inefficiency term.

As a relative efficiency, the DEA identifies the inefficiency of a decision-making unit (DMU) by comparing it with other DMUs that are more efficient (Coelli et al. 2005). The advantage of the DEA compared to other performance measurements is that it can assess performance in a multi-dimensional framework by accommodating multiple inputs and outputs (Avkiran 1999). In measuring the performance of financial institutions, such as pension funds or insurance, the DEA can integrate production/operational and investment performance and even compromise these two aspects (Yang 2006).

Most studies on pension funds still use traditional DEA methods to evaluate pension fund performance (Bui et al. 2016; Draženović et al. 2019). However, performance measurement with traditional DEA treats a firm as a ‘black box’ and ignores the transformation processes inside it (Färe and Grosskopf 2000). However, in many situations, the transformation of inputs into outputs is not just a single stage process, but rather a series of connected stepwise processes. Therefore, recent studies have focused on DEA networks models that can take into account the complexity of the internal structure of a production process (Galagedera et al. 2018; Lin et al. 2021). The network DEA approach can provide more meaningful and informative results than the black box approach, which ignores the internal structure of the production process (Kao 2014).

In their research on Taiwanese non-life insurance companies, Kao and Hwang (2008) modified conventional DEA into a two-stage network DEA. The management process of Taiwanese non-life insurance companies is conceptualized as a series relationship of two processes within the whole process. With this framework, they could accurately identify sources of inefficiency in Taiwanese non-life insurance. In the Kao and Hwang (2008) model, all outputs from stage 1 are intermediate measures, which become inputs for the second stage to produce final outputs. Overall efficiency is the product of the efficiency of the two sub-processes. However, the limitation of this model is that it can only be applied under the constant return to scale (CRS) assumption.

To overcome the limitations in the model of Kao and Hwang (2008), Chen et al. (2009) developed a network DEA model called the additive efficiency decomposition (AED) approach. In this approach, overall efficiency is expressed as a weighted sum of the efficiencies of individual stages. The AED approach can convert non-linear models into models of a linear programming problem. Therefore, AED can be used to measure efficiency under the assumption of CRS and variable return to scale (VRS).

Based on AED, Cook et al. (2010) developed a more general and open network model, where each stage—apart from intermediate measures—can also have its own inputs and outputs. Some outputs can leave the network system, while other outputs become input for the next stage; likewise, new inputs can enter at any stage in the network system. This model can be applied to both CRS and VRS situations.

Many studies on the efficiency of pension funds and mutual funds have applied the AED approach. For example, Premachandra et al. (2012) extended the AED approach by adding an additional input in the second stage of the network and examined the performance of 66 large mutual funds families in the US over the period of 1993–2008. Galagedera et al. (2015) also extended the AED approach by proposing a two-stage leakage model and evaluating the performance of mutual funds families in the US in the 1999–2008 period. Lin et al. (2021) integrated the additive network DEA approach and trend analysis technique to evaluate and predict the performance of 34 investment trust companies (ITC) in Taiwan.

Galagedera (2017) conceptualized the pension fund management function as a two-stage process (i.e., operation management and portfolio management) and evaluated the overall and stage level performance of Australian superannuation funds in the years of 2008 and 2014. The results of the overall efficiency decomposition showed that public sector funds, on average, had the highest level of efficiency in terms of operation management. However, in terms of portfolio management, there was no dominant category in either 2008 or 2014.

The additive network DEA method enables the evaluation of pension funds from various aspects of management in a systematic and integrated manner, thus providing insight to managers. However, research on the efficiency of pension funds in the Indonesian context is still very rare. Moreover, to the best of the researcher’s knowledge, no studies have tried to evaluate the efficiency of pension funds in Indonesia using the DEA network method. Seran et al. (2022) evaluated the performance of 40 DPF for the 2011–2017 period using a conventional DEA approach.

3.2. The Determinants of Pension Funds’ Effiiciency

Many factors affect pension funds’ efficiency. However, prior studies have demonstrated that several variables, such as size, program type, ownership, interest rates, and regulation, consistently affect pension funds’ efficiency (Antolin et al. 2011; Bikker and Dreu 2009; Broeders et al. 2017; Mutula and Kagiri 2018; Stewart and Yermo 2008).

Related to the size effect, the economies of scale concept suggests that firms’ increased size is not proportionally followed by cost increases (Silberston 1972). Jang and Wu (2021) empirically observed pension funds’ economies of scale in administrative costs and net returns. Several studies have also reported that large pension funds perform better than smaller ones due to the economies of scale, i.e., they save costs by spreading fixed costs (Bikker and Dreu 2009), exploiting their negotiating powers with external stakeholders, organizing more efficient internal management, and exploiting alternative investments with higher returns (Cummings 2015; Dyck and Pomorsky 2011). Further, Sathye (2011) and Galagedera et al. (2015) documented a positive correlation between pension funds’ technical efficiency and size. Similarly, Alserda et al. (2018) revealed that size significantly affects pension funds’ x-efficiency.

EPFs (DPPK) offer defined benefit or defined contribution plans. Defined benefit plans offer pre-defined pension benefits to participants whose contributions are subject to change depending on actuarial calculations. In contrast, defined contribution plans require their participants to make certain contributions, while participants’ pension benefits vary depending on investment returns (Bodie et al. 1988). Under defined benefit plans, employers bear the investment risks/fund deficiency, while defined contribution plans’ participants bear the investment risks. Differences in the characteristics of these two types of pension plans may affect their efficiency levels. Defined contribution plans are arguably simpler and less costly than defined benefit plans (Bodie and Merton 1992). Bateman and Mitchell (2004) and Bikker and Dreu (2009) demonstrated that defined benefit plans exhibit greater operational costs than defined contribution plans. However, Munnell et al. (2015) found that defined contribution plans generate lower investment returns than defined benefit plans because of their higher investment costs. Moreover, several studies have documented that defined contribution plans exhibit lower investment performance due to their sponsors’ and participants’ lower financial literacy or agency problems (Andonov and Mao 2019; Clark et al. 2017).

Ownership is closely related to governance structure, which is crucial for firms’ performance (Giannetti and Laeven 2009). Stewart and Yermo (2008) emphasized that good governance, as operationalized with stakeholders’ balanced representations in top management, high managerial skills, and code of conduct implementation, likely affect pension funds’ performance and secured availability. However, empirical studies on the relationship between ownership and efficiency in banks and pension funds show different results. For example, Defung et al. (2016) reported that government-owned banks exhibit greater efficiency than private and other banks. Conversely, Shaban and James (2018) investigated the relationship between Indonesian banks’ ownership and efficiency in 2005–2012 and revealed that private banks are more efficient than government-owned banks. In the pension fund industry, several empirical studies have found that government-sponsored pension funds exhibit lower investment performance than private ones due to conflicts of interests, including political connections (Bradley et al. 2016; Coronado et al. 2003) or corruption (Zhang et al. 2018). In a similar vein, Pasqualeto et al. (2014) observed that SOE (state-owned enterprise)-sponsored pension funds incur greater administrative costs than private firm-sponsored pension funds. However, Siddiqui (2021), who examined pension funds in India, found that government-sponsored pension funds have a higher efficiency level than private pension funds. Meanwhile, Putri et al. (2020) did not find the significant role of ownership in moderating the effect of size on Indonesian EPFs’ investment performance and efficiency.

4. Methodology

4.1. Framework of the Performance Evaluation of EPFs

We aimed to evaluate the performance of Indonesian EPFs within the framework of the additive network DEA methodology (Cook et al. 2010; Chen et al. 2009). We viewed the overall EPF management process as comprising two serially linked sub-processes and use the additive network DEA method to evaluate the overall and sub-process performance of EPFs (Galagedera 2017). The first sub-process is operational management (OM), while the second sub-process is investment management (IM). In operation management, EPFs use their beginning net asset, with the addition of collected contributions, in order to pay pension benefits and financially support other administrative activities, while securing funds available for investments. Therefore, in this study, we consider net asset value at the beginning of each period and the total operational costs as inputs to the first stage (OM process) and funds available for investments (i.e., average total investment) as the output.

In the investment management process (second stage), the investment manager uses funds available for investment to generate returns (ROI). For the second stage (IM process), we consider two inputs and one output, i.e., funds available for investment (i.e., average total investment) and total investment costs (including compensation for investment managers and other investment costs) as inputs and return on investment (ROI) as the final output. Based on our conceptual framework, our study has one intermediate measure, i.e., funds available for investment (i.e., average total investment), which is an output of the first stage but becomes an input to the second stage. Our goal is to assess the overall efficiency and stage level efficiency (i.e., OM and IM) in a network DEA framework. Figure 1 presents the two-stage network DEA model for EPFs.

Our input and output variables are almost identical to Galagedera (2017). However, instead of using net asset value at the end of the period, we used total average investment as the intermediate variable (i.e., output of stage 1 and input to stage 2) (please see

Table 2. Descriptive statistics of input, intermediate, and output variables.

Variables	Obs.	Mean	SD	Min	Max
Inputs:
Net asset at start of period	266	1,840,000	2,930,000	10,200	16,300,000
Operational costs	266	10,000	16,400	263	91,700
Additional inputs:
Investment costs	266	8670	20,500	11	159,000
Intermediate:
Average total investment	266	1,840,000	2,950,000	9740	16,800,000
Outputs:
ROI (%)	266	10	6	7	41

Note: Input variables: net asset at start of period: the value of net asset at the beginning of each period. Operational costs: staff salaries and other expenses resulting from administrative activities. Additional inputs: total investment costs: compensation for investment managers and other investment expenses. Intermediate: total average investment: total investment at the beginning of the period + total investment at the end of the period divided by two. Outputs: return on investment (ROI): the ratio of total investment income to average total investment.

for the lists of the input and output variables and descriptive statistics).

4.2. Data

We manually collected EPFs’ 2011–2017 financial statements from ADPI and BKS Dapen-KI (Badan Kerja Sama Dana Pensiun Kristen Indonesia—Cooperating Agency of Indonesian Christian Pension Funds). After leaving out observations with incomplete data (or considered outliers), we obtained balanced model data of 2011–2017 from 38 EPFs, consisting of 29 pension funds with defined benefit plans and nine defined contribution plans, and 19 SOE-sponsored EPFs and 19 privately sponsored (non-SOE sponsored) EPFs.

DEA models assume input and output variables to satisfy “isotonicity” relations, i.e., an increase in any input should not result in a decrease in any output. In our case, there are some negative values in our data, i.e., the output variable ROI has some negative values. Thus, we have to transform the negative values to make them positive by adding a constant (Charnes et al. 1978). We conducted a Spearman correlation test to examine the “isotonicity” among the input and output variables. The results in

Table 3. The Spearman correlation coefficient of I/O variables.

	X1	X2	X3	Z	Y
X1	1
X2	0.9236 **	1
	(0.000)
X3	0.8612 **	0.8358 **	1
	(0.000)	(0.000)
Z	0.9989 **	0.9241 **	0.8613 **	1
	(0.000)	(0.000)	(0.000)
Y	0.2602 **	0.2672 **	0.1488 **	0.2759 **	1
	(0.000)	(0.000)	(0.0151)	(0.000)	(0.000)

Notes: T-statistics are given in parenthesis. **: passes the testing at level 0.05; X1 = net asset at the beginning of the period; X2 = total operational costs; X3 = total investment costs; Z = average total investment (intermediate); Y = ROI.

reveal that all variables including ROI satisfy the assumption of “isotonicity”; therefore, they can be included in the model.

4.3. The Approach Models

4.3.1. Two-Stage Additive Network DEA

In this research, we employ the two-stage network DEA approach to assess the overall and individual stage level (i.e., operational and investment management) performance of EPFs. Figure 1 shows the two-stage framework that we modeled to assess the performance of EPFs (as DMUs). Based on Figure 1, we assume each EPF $DM{U}_j \left(j=1,\dots , n\right)$. At each period, the EPFs use m inputs $x_{ij}^1$ (i = 1, …, m) to produce K outputs $z_{kj} \left(k=1,\dots , K\right)$ for the first stage. These outputs also function as intermediate measures that link stage 1 and stage 2 and become inputs for the second stage. The second stage also has additional C inputs $x_{cj}^2 \left(c=1,\dots C\right)$. The EPFs use K and C to generate S outputs $y_{rj}$ (r = 1, …, S) for the second stage. Using an input-oriented variable return to scale (VRS) model, we aimed to assess overall efficiency and estimate stage level efficiency through the decomposition of overall efficiency. The DEA requires all measures to be strictly positive. However, in our model, the output measures at the second stage could have negative values; therefore, we chose a DEA model that allowed us to modify (adding a positive constant to make them positive) the second output variables. The input-oriented VRS DEA model is translation invariant to output variable modification. We defined input oriented overall efficiency for the observed EPF (j0 = 1, …, n) by solving the program as follows:

$$max\left[w_1·\frac{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k Z_{kjo})-{\alpha }_1}{{{\displaystyle \sum }}_{i=1}^m{v}_i x_{ijo}^1}+w_2·\frac{({{\displaystyle \sum }}_{r=1}^S{\eta }_{r y_{rjo}})-{\alpha }_2}{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kjo}+{{\displaystyle \sum }}_{cjo}^C{\gamma }_c x_{cjo}^2)}\right]$$

(1)

$$s.t.\frac{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k Z_{kj})-\alpha }{{{\displaystyle \sum }}_{i=1}^m{v}_i x_{ij}^1}\le 1, \forall j$$

(2)

$$\frac{({{\displaystyle \sum }}_{r=1}^S{\eta }_{r y_{rj}})-{\alpha }_2}{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{cj}^C{\gamma }_c x_{cj}^2)}\le 1, \forall j$$

(3)

$${\zeta }_k, {\eta }_r, v_i, {\gamma }_c>0; {\alpha }_1, {\alpha }_2 free.$$

Based on the equations above, the multiplier for the input $x_{ij}^1$ in the stage 1 is v_i, while ${\eta }_r$ is the multiplier for the output component $y_{rj}$ flowing from stage 2. ${\zeta }_k$ is the weight and the multiplier for $Z_{kj}$ because $Z_{kj}$ is an intermediate measure, i.e., an output flowing from stage 1, and becomes an input for the second stage process; ${\gamma }_c$ is the weight for the additional input $x_{cj}^2$ of stage 2. The objective of Equation (1) is to obtain weights $({\zeta }_k, {\eta }_r, v_i, {\gamma }_c)$ and scalars $\left({\alpha }_{1, }{\alpha }_2\right)$ that maximize the ratio of observed DMU when evaluating DMU. The presence of constraints in (2) and (3) ensure that the obtained efficiency score of a DMU in both stages (i.e., operation management and investment management) is non-negative and should not exceed one.

In Equation (1), the total size of inputs consumed by the entire process is represented by ${{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1+{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c{x}_{cj}^2$, while the total inputs for the process of stage 1 and stage 2 are represented by ${{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1$ and ${{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{cj}^C{\gamma }_c x_{cj}^2$, respectively. Then, following Chen et al. (2009) and Cook et al. (2010), the component weights w₁ and w₂ can be expressed as the ratio of total inputs of stage 1 and stage 2 to the total inputs at both stages. Thus, we have Equation (4):

$$\begin{gathered} w_1=\frac{{{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1}{{{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1+{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c{x}_{cj}^2} \\ {w}_2=\frac{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{cj}^C{\gamma }_c x_{cj}^2}{{{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1+{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c{x}_{cj}^2} \end{gathered}$$

(4)

This approach allows the decision variables of the model to determine the weights objectively, thus avoiding the subjective weights specification by managers. The objective function of model (1) can now be written as Equation (5):

$${\theta }_{jo}=\max \left[\frac{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kjo})+({{\displaystyle \sum }}_{r=1}^s{\eta }_r{y}_{rjo})-{\alpha }_1-{\alpha }_2}{{{\displaystyle \sum }}_i^m{v}_i{x}_{ijo}^1+{{\displaystyle \sum }}_{k=1}^K{\zeta }_k Z_{kjo}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cjo}^1}\right]$$

(5)

By applying the Charnes and Cooper (1962) transformation, the fractional programming model of (1) to (3) can be rewritten in the following linear programming model:

$$\max \left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kjo}+{{\displaystyle \sum }}_{r=1}^S{\eta }_r{y}_{rjo}\right)-{\alpha }_1-{\alpha }_2$$

(6)

s.t.

$$\left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k Z_{kj}\right)-{\alpha }_1-\left({{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ij}^1\right) \le 0, \forall j$$

(7)

$$\left({{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rj}\right)-{\alpha }_2-\left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cj}^2\right) \le 0, \forall j$$

(8)

$${{\displaystyle \sum }}_{i=1}^m{v}_i{x}_{ijo}^1+{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kjo}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c{x}_{cjo}^2=1,$$

(9)

$${\eta }_{r , }{v}_i, {\zeta }_k,{\gamma }_c>0; {\alpha }_1, {\alpha }_2 \in free$$

The optimal solution of the model (6) accounting for (7) to (9) is the overall efficiency ${\theta }_{jo}^{*}$ of this two-stage process. Let ${\zeta }_k^{*}, {\eta }_r^{*}, v_i^{*}, {\gamma }_c^{*}, {\alpha }_1^{*}$ and ${\alpha }_2^{*}$ denote an optimal set of decision variable values and ${\theta }_{jo}^{*}$ denote the optimal overall efficiency in the solution of (6) subjected to (7) to (9). We then derive the overall efficiency (${\theta }_{jo}^{*}$), the efficiency scores for stage 1 (operating efficiency) (${\theta }_{1jo}^{*}$) and stage 2 (investment efficiency) (${\theta }_{2jo}^{*}$) from equations (10) to (12) for the observed EPFs as follows:

$${\theta }_{jo}^{*}=\left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k^{*} Z_{kjo}+{{\displaystyle \sum }}_{r=1}^S{\eta }_r^{*} y_{rjo} \right)-{\alpha }_1^{*}-{\alpha }_2^{*}$$

(10)

$${\theta }_{1jo}^{*}=\frac{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k^{*} Z_{kjo}-{\alpha }_1^{*} }{{{\displaystyle \sum }}_{i=1}^m{v}_i^{*} x_{ijo}^1}$$

(11)

$${\theta }_{2jo}^{*}=\frac{{{\displaystyle \sum }}_{r=1}^S{\eta }_r^{*} y_{rjo}-{\alpha }_2^{*}}{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{Z}_{kjo}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c{x}_{cjo}^2}$$

(12)

Equations (11) and (12) correspond to the sub-technologies ${\theta }_{1jo}^{*}$ and ${\theta }_{2jo}^{*}$, whose intercept multipliers are ${\alpha }_1^{*}$ and ${\alpha }_2^{*}$. The model (6) subjected to (7) to (9) may have alternative optimal solutions, implying that ${\theta }_{1jo}^{*}$ and ${\theta }_{2jo}^{*}$ obtained from Equations (11) and (12) are not unique. Kao and Hwang (2008) propose a procedure to overcome this problem by allowing one of the two stages (stage 1 or stage 2) to show its efficiency to itself in the best way, while keeping the overall efficiency (${\theta }_{jo}^{*})$ fixed. We prefer stage 1 (i.e., operational management) to be the first, and we determine the maximum value of ${\theta }_{1jo}^{*}$ in the solution of the model (13) while maintaining the overall efficiency estimated in (10) at ${\theta }_{jo}^{*}$.

$${\theta }_{1jo}^{*}=\max {{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kjo}-{\alpha }_1$$

s.t.

$$\begin{gathered} {{\displaystyle \sum }}_{i=1}^m{v}_i x_{ijo}^1=1 \\ \frac{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kj}-{\alpha }_1}{{{\displaystyle \sum }}_{i=1}^m{v}_i x_{ij}^1}\le 1, \forall j \\ \frac{{{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rj}-{\alpha }_2}{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cj}^2}\le 1, \forall j \\ {\theta }_{jo}^{*}=\left[\frac{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k z_{kjo }+{{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rjo})-{\alpha }_1-{\alpha }_2}{({{\displaystyle \sum }}_{i=1}^m{v}_i x_{ijo}^1)+\left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kjo}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cjo}^2\right)}\right] \\ {\zeta }_{k,} {\eta }_r, v_{i, } {\gamma }_c>0; {\alpha }_1{\alpha }_2 \in free \end{gathered}$$

(13)

Alternatively, we can also prioritize stage 2 (i.e., investment management) and determine the maximum value of ${\theta }_{2jo}^{*}$ using model (14), while keeping the overall efficiency at ${\theta }_{jo}^{*}$. We repeated this procedure for each DMU in the sample to obtain overall, stage 1 and stage 2 efficiency scores for each DMU.

$${\theta }_{2jo}^{*}=\max {{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rj}-{\alpha }_2$$

s.t.

$$\begin{gathered} {{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cj}^2=1 \\ \frac{{{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rj}-{\alpha }_2}{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kj}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cj}^2}\le 1, \forall j \\ {\theta }_{1jo}^{*}=\frac{{{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kjo}-{\alpha }_1}{{{\displaystyle \sum }}_{i=1}^m{v}_i x_{ijo}^1} \\ {\theta }_{jo}^{*}=\left[\frac{({{\displaystyle \sum }}_{k=1}^K{\zeta }_k z_{kjo }+{{\displaystyle \sum }}_{r=1}^S{\eta }_r y_{rjo})-{\alpha }_1-{\alpha }_2}{({{\displaystyle \sum }}_{i=1}^m{v}_i x_{ijo}^1)+\left({{\displaystyle \sum }}_{k=1}^K{\zeta }_k{z}_{kjo}+{{\displaystyle \sum }}_{c=1}^C{\gamma }_c x_{cjo}^2\right)}\right] \\ {\zeta }_{k,} {\eta }_r, v_{i, } {\gamma }_c>0; {\alpha }_1{\alpha }_2 \in free \end{gathered}$$

(14)

In their studies, Premachandra et al. (2012) and Lin et al. (2021) developed dual models (frontier projection model) as a practical guideline for the managers to improve the efficiency of their firms. We did the same by proposing a dual model (15) based on our models (6) to (9). Projection or target improvement analysis can be used as a guideline to improve the efficiency of EPFs.

$$Min{\theta }_{jo}$$

s.t.

$$\begin{gathered} {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^A x_{ij}^1 \le {\theta }_{jo} x_{ijo}^1, \left(i=1,\dots , m\right), \\ {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^A{z}_{kj} \le \theta z_{kjo}, \left(k=1, \dots , K\right), \\ {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^A=1, \\ {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^B{x}_{cj}^2 \le {\theta }_{jo}{x}_{cjo}^2, \left(c=1,\dots ,C\right), \\ {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^B y_{rj}\ge y_{rjo},(r=1,\dots ,S), \\ {{\displaystyle \sum }}_{j=1}^n{\lambda }_j^B=1, \\ 0\le {\lambda }_j^A, {\lambda }_j^B, \left(j=1,\dots ,n\right), {\theta }_{jo}\in free \end{gathered}$$

(15)

In model (15), ${\lambda }_j^A$ and ${\lambda }_j^B$ represent the intensity variables in stage 1 (operation management) and stage 2 (investment management) of the network processes. ${\theta }_{jo}$ is the overall efficiency applied to the target EPF $\left(j_o=1,\dots , n\right).$ Thus, we can improve the inefficient EPF_jo by referring the target input projection value $\left({\widehat{x}}_{ijo}^1 \mathrm{and} \widehat{x}{ }_{cjo}^2\right)$ for stage 1 and stage 2 as follows:

$$\begin{gathered} {\widehat{x}}_{ijo}^1={{\displaystyle \sum }}_{j=1}^n{\lambda }_j^{A*}{x}_{ij,}^1\left(i=1,\dots ,m\right), \\ \widehat{x}{}_{cjo}^2={{\displaystyle \sum }}_{j=1}^n{\lambda }_j^{B*}{x}_{cj,}\left(c=1,\dots ,C\right). \end{gathered}$$

(16)

4.3.2. Determinants Analysis

We also examined if there is relationship between the level of efficiency of EPFs and exogenous variables, such as size, type of pension plan, and ownership. To achieve this, we followed the procedure proposed by Simar and Wilson (2007).

According to Simar and Wilson (2007), the conventional technique, where the efficiency scores of the estimation results from the DEA in the first stage are directly regressed against exogenous variables, is not statistically valid due to an ambiguous data generating process (DGP) and serial correlation problems between the efficiency scores and estimation results. Therefore, Simar and Wilson (2007) apply a bootstrapping technique to obtain robust efficiency scores, while at the same time overcoming the problem of serial correlations on efficiency scores. Based on Simar and Wilson (2007), we view the efficiency of EPF as a result of the following equation:

$${\theta }_{it}=z_{it}\beta +{\epsilon }_{it}$$

(17)

where ${\theta }_{it}$ is the efficiency of EPF i at time t, which is expressed as a function of the exogenous vector variable $Z_{it}$ faced by each EPF; β is the estimated coefficient vector; and $\epsilon$ is an error term. In this study, we used three independent variables (i.e., size, type of plan, and ownership) to examine their relationship with EPF efficiency (please refer to

Table 4. Regression variables.

Variables	Symbol	Descriptions
Dependent variables: technical efficiency		Technical efficiency of EPFs for model 1 (overall efficiency), model 2 (operational efficiency), and model 3 (investment efficiency)
Independent variables:
EPFs’ size	Size	EPFs’ size measured by natural log of total assets
Pension plan’s type	Type	Dummy variable equal to 1 for DB and 0 for DC
Ownership	Ownership	Dummy variable equal to 1 for SOE EPFs and 0 for non-SOE EPFs

SOE/non-SOE: EPFs sponsored by State owned enterprises/non-state owned enterprises (private institutions).

for the details on our regression variables). We followed procedures suggested by Simar and Wilson (2007) and conducted our analysis as follows: We used the maximum likelihood method to obtain $\widehat{\beta }, \widehat{\sigma }$ from $\beta ,\sigma$ in a two-sided truncated regression based on model (17). Therefore, we carried out the following bootstrapping process:

• We repeated steps (a) to (c) B times (B = 2000) to obtain a set of bootstrapping estimates $A={\left\{{\widehat{\beta }}^b,{\widehat{\sigma }}^b\right\}}_{b=1}^B$.
  • For each DMU, i = 1, …, n, we randomly selected a dummy error term ${\tilde{\epsilon }}_{it}$ from the two-sided truncated normal distribution $N \left(0, \widehat{\sigma }\right)$ with the left-hand side at $–zit\widehat{\beta }$ and the right-hand side at $1-zit\widehat{\beta }$.
  • Once more for each EPF, i = 1, …, n we calculated a dummy efficiency score ${\tilde{\theta }}_{it}$ as ${\tilde{\theta }}_{it}=z_{it}\widehat{\beta }+{\tilde{\epsilon }}_{it}$.
  • We used the maximum likelihood method to estimate ${\tilde{\theta }}_{it}$ against $z_{it}$ in a truncated regression to obtain bootstrapping estimates $\left({\widehat{\beta }}^b, {\widehat{\sigma }}^b\right)$.
• We then used the bootstrapping estimates ${\left\{{\widehat{\beta }}^b,{\widehat{\sigma }}^b\right\}}_{b=1}^B$ and the original estimates $\widehat{\beta }, \widehat{\sigma }$ to calculate the confidence interval and standard error for each $\beta$ and $\sigma$.

5. Results and Discussion

5.1. Efficiency of Indonesian EPFs 2011–2017

By employing the additive network DEA approach, this study aims to measure the overall efficiency, operational efficiency, and investment efficiency of EPFs in the period of 2011–2017.

Table 5. Annual mean efficiency scores for Indonesian EPFs, 2011–2017.

Year	Scores/Number of Efficient Funds	Overall Technical Efficiency	Operational Efficiency	Investment Efficiency
2011	Scores	0.666	0.768	0.564
	Efficient funds	6	10	6
2012	Scores	0.679	0.779	0.579
	Efficient funds	9	12	10
2013	Scores	0.711	0.815	0.607
	Efficient funds	10	14	11
2014	Scores	0.663	0.808	0.518
	Efficient funds	7	11	7
2015	Scores	0.768	0.864	0.672
	Efficient funds	11	17	12
2016	Scores	0.754	0.834	0.673
	Efficient funds	11	14	12
2017	Scores	0.723	0.831	0.615
	Efficient funds	11	14	11
Mean	Scores	0.709	0.814	0.604
	Efficient funds	9	13	10

presents the efficiency scores and the number of efficient pension funds in 2011–2017. Table 5 shows that the average overall efficiency of EPFs in the observed period is only 70.9%. When decomposed into operations management and investment management, it is found that EPFs perform better in operations management (81.4%) but underperform in investment management (60.4%). These results suggest that investment management is a substantial source of the overall inefficiency of EPFs, implying that managers should put more effort into investment management when seeking to increase EPFs’ overall efficiency. In terms of the number of efficient EPFs, similar results are found, where on average more EPFs are efficient in operational management (13 EPFs) than in investment management (only 10 EPFs). On average, only nine EPFs were overall efficient during the observed period. Over the period of 2011–2017, the number of overall efficient EPFs increased, albeit inconsistently; for example, in 2013, 10 EPFs were overall efficient, but in 2014 the number of overall efficient funds dropped to only seven EPFs.

Table 5 also shows that in 2011–2017, the level of efficiency of Indonesian EPFs tended to fluctuate. The highest efficiency score for operational management was 86.4% in 2015, and the lowest efficiency score was 66.6% in 2011. Meanwhile, the highest efficiency score for investment management was 67.3% in 2016, and the lowest efficiency score was 51.8% in 2014. The variation in pension performance during the observed period might correlate with other factors such as a pension fund’s characteristics or other environmental variables. The next part of this paper examines the correlation between the specific characteristics of EPF and its efficiency levels.

Measuring and determining performance levels can generate useful information for managers to evaluate and improve their performance; however, managers often want detailed information about what should be improved and how it should be done. In this study, we propose a projection analysis model (15) that might be useful as a guideline for EPFs to improve their performance. We conducted a projection analysis based on model (15) using 16 selected inefficient EPFs (from our sample) in 2017 as examples. The results are presented in

Table 6. Projection analysis using 16 EPFs (from our sample) as examples for the performance in 2017.

EPFs	Operational Costs		Investment Costs
	Projection (IDR)	Differences (%)	Projection (IDR)	Differences (%)
EPF17	5,242,463,780	−9.5%	1,433,219,533	−10.6%
EPF26	1,398,902,108	−2.8%	66,153,104	−0.4%
EPF10	8,686,534,216	−23.1%	6,089,748,568	−251.8%
EPF13	14,950,051,860	−37.9%	1,742,876,172	−39.5%
EPF19	3,118,546,037	−4.0%	200,336,348	−0.6%
EPF38	500,839,838	−0.4%	13,189,180	−0.1%
EPF21	1,187,706,080	−17.1%	482,763,399	−9.0%
EPF25	1,405,704,697	−2.7%	67,333,213	−0.5%
EPF20	2,798,185,290	−3.1%	112,688,317	−0.8%
EPF7	23,724,250,331	−251.1%	20,094,920,536	−474.3%
EPF29	991,555,252	−2.5%	53,392,574	−1.3%
EPF37	460,358,655	−0.4%	16,933,580	−0.2%
EPF28	731,313,932	−2.2%	88,205,693	−6.6%
EPF11	4,917,560,501	−7.4%	2,921,284,709	−134.8%
EPF3	47,830,098,438	−0.8%	10,365,241,186	−177.7%
EPF34	580,853,957	−9.0%	31,332,720	−3.8%

Note: We do not have permission to reveal the real names of the EPFs. We present them by their code number in our sample.

. The projection analysis aims to provide information about the optimal input or output target level that can be achieved by an EPF in order to be efficient. For example, the results of the projection analysis for EPF17 in 2017 show that the optimal (efficient) targets for operational and investment costs are IDR 5.2 billion and IDR 1.4 billion, respectively. That target can be achieved by reducing operational costs and investment costs by 9.5% and 10.6%, respectively. This also applies to other inefficient EPFs, where they can increase their efficiency level and become efficient with reference to projected input targets.

5.2. Determinants of EPFs’ Efficiency

We performed a regression analysis by adopting the procedure proposed by Simar and Wilson (2007) to examine the correlation between the efficiency level of EPFs and their specific characteristics, namely size, type of pension plan, and ownership. The results are presented in

Table 7. Regression analysis results.

Variables	Overall Efficiency	Operational Efficiency	Investment Efficiency
Size	−0.0164	−0.0337	−0.0375 **
	(0.0114)	(0.0423)	(0.0154)
Type	0.0455	0.142	0.0108
	(0.0463)	(0.154)	(0.0637)
Ownership	0.109 **	0.102	0.232 ***
	(0.0465)	(0.162)	(0.0643)
Sigma	0.214 ***	0.346 ***	0.258 ***
	(0.0150)	(0.0774)	(0.0221)
Constant	0.977 ***	1.689	1.323 ***
	(0.299)	(1.175)	(0.400)

Standard errors in parenthesis; ***, **, denote significance at 1% level, 5% level.

.

As shown in Table 7 for overall efficiency, only ownership has a significant correlation (Coeff.: 0.109; p < 0.05). This result means that, on average, SOE-sponsored EPFs have a better overall performance than non-SOE EPFs. Size and type of plan do not show a significant correlation, which means that there are no significant differences between large vs. small, and defined benefits (DB) vs. defined contribution (DC) plans. In other words, the difference in size and plan type does not significantly affect the overall performance level of EPFs.

Regarding operational efficiency, size, ownership, and type do not show a significant correlation, which means that there are no differences in operational performance between large and small, DB and DC, or SOE-sponsored and private-sponsored EPFs. A difference in size, ownership, and type of pension plan seems to have no effect on the level of EPFs’ operational performance.

In terms of investment efficiency, the results show an estimated coefficient of −0.0375 (p < 0.05) for size, denoting a significant negative correlation. This means that the large EPFs have a significantly lower investment performance than the small ones. In contrast to size, the empirical results show an estimated coefficient of 0.232 (p < 0.01) for ownership, denoting a significant positive correlation, which implies that the SOE-sponsored EPFs have a higher investment performance than the private-sponsored EPFs.

Overall, this study concludes that size and ownership are the characteristics of pension funds that play a significant role in determining the level of EPFs’ performance. Large EPFs have a significantly lower investment performance than small ones, indicating diseconomies of scale in large EPFs. The return on investment obtained is not commensurate with the cost and the amount of investment funds used as inputs. Our findings contradict Dyck and Pomorsky (2011) but are in line with Mama et al. (2011), who found 25–30% unused scale economies in South African pension funds. Our results are especially similar to Bauer et al. (2010), who found that large pension funds of the United States of America cannot generate optimal investment returns due to a less-liquid domestic equity market. Meanwhile, the Indonesian authority imposes very strict regulations on pension funds’ investments, and the domestic capital market is limited. Consequently, pension funds with large asset values may not be able to generate optimal investment revenues commensurate with their size due to limited investment instruments (limited diversification options).

The SOE-sponsored EPFs performed better than private-sponsored ones, both in overall efficiency and investment efficiency. The results contradict Pasqualeto et al. (2014) and Zhang et al. (2018) but support Siddiqui (2021). SOE-sponsored EPFs are generally larger, sponsored by large state-owned firms/banks, and have sufficient skilled labor and better technology than non-SOE-sponsored EPFs, which are generally sponsored by smaller firms, foundations, or schools that invest conventionally with limited availability of skilled labor. These factors likely explain the performance difference in both types of employer pension funds.

6. Conclusions

Pension funds manage funds contributed by members and employers with the aim of providing sufficient benefits for each member upon retirement. In this respect, efficiency is an important issue for EPFs. This study measures and evaluates the performance of Indonesian EPFs within the framework of the two-stage additive network DEA method. Compared to the conventional DEA approach, which treats a firm as a black box so that it can only measure overall performance, the network DEA method enables us to measure the performance of Indonesian EPFs from various aspects of their management function, i.e., operational efficiency and investment efficiency. This is considered the strength of this methodology, namely, being able to measure the performance of pension funds based on the internal structure of the management processes. Thus, it can identify which management functions need to be given greater attention, in order to improve overall performance.

The results of this study can be summarized as follows. First, the average overall efficiency level of EPFs in the 2011–2017 period was 70.9%. When decomposed into operational efficiency and investment efficiency, it was found that EPFs perform better in operational management (81.4%) than in investment management (only 60.4%). Thus, it was identified that investment inefficiency is the main source of the overall inefficiency of EPFs. Therefore, to improve the overall performance of EPFs, greater attention needs to be directed to the efficiency of investment management.

Second, the efficiency of EPFs is certainly also influenced by external factors. The results of the empirical analysis of this study show that differences in size and ownership also determine the performance level of EPFs. In particular, management needs to be reminded that large size EPFs can perform negatively due to diseconomies of scale, or other factors, such as a small domestic capital market or overly tight investment regulations. In addition, this study shows that SOE-sponsored EPFs perform higher in both overall efficiency and investment efficiency. This implies that the privately sponsored EPFs (or other categories) can be modeled on SOE-sponsored EPFs. Specifically, the privately sponsored EPFs may refer to the SOE-sponsored EPFs in terms of technology deployment and improvements in participants’ and governing bodies’ financial and investments knowledge and skills.

Academically, this study broadens the literature on pension fund efficiency both in terms of performance measurement methods and results. In terms of methods, previous efficiency studies within the scope of pension funds have generally used traditional methods, such as the risk-adjusted method (Hasanudin et al. 2017), ratio analysis (Sunaryo et al. 2020), or conventional DEA (Seran et al. 2022). Efficiency studies using the additive network DEA method are still rare. Especially in the Indonesian context—to the best of our knowledge—this is the first study that applies network DEA to measure the performance of the pension funds industry. In terms of results, this study adds to the body of knowledge about the performance of pension funds from the perspective of developing countries such as Indonesia.

This study has some limitations. First, the results of this study indicate diseconomies of scale in EPFs but does not analyze them further to determine the optimal point size. Second, due to data unavailability, our study is less comprehensive in terms of the input and output variables included in the model. By including some considerably important input/output variables, such as the amount of participants’ contribution collected as an input to the first stage, benefits paid to members as a leaving output of the first stage, and total risk as an additional input to the second stage, the present model may give different results. Therefore, future studies can improve the model by including those variables to give a more comprehensive picture of EPFs’ performance.