Abstract
This study investigates return and asymmetric volatility spillovers and dynamic correlations between the main and small and medium-sized enterprise (SME) stock markets in Saudi Arabia and Egypt for the periods before and during the COVID-19 pandemic. Return and volatility spillovers are modelled using a VAR-asymmetric BEKK–GARCH (1,1) model, while a VAR-asymmetric DCC–GARCH (1,1) model is employed to model the dynamic conditional correlations between these markets, which are then used to determine and explore portfolio design and hedging implications. The results show that while bidirectional return spillovers between the main and SME stock markets are limited to Saudi Arabia, shock and volatility spillovers have different characteristics and dynamics in both main–SME market pairs. In addition, the dynamic correlations between the main and SME markets are mostly positive and have notably increased during the COVID-19 pandemic, particularly in Saudi Arabia, suggesting that adding SME stocks to a main stock portfolio enhances its risk-adjusted return, especially during tranquil market phases. One practical implication of our results is that the development of SME stock markets can indirectly contribute to economic development via the main market channel and provide an avenue for portfolio diversification and risk management.
Keywords:
MENA region; SME stock market; return and volatility spillovers; hedge ratios; optimal portfolio designs JEL Classifications:
C32; C58; D53; G11
1. Introduction
The interdependencies between financial markets, especially during turbulent times, have long attracted considerable interest among finance academics and practitioners. Changes in the dependence structure, particularly during periods of market turmoil, are of great concern to market participants and policymakers. During a crisis, the correlations between equity markets intensify due to spillover effects (see, e.g., Hwang 2014; Markwat et al. 2009; McIver and Kang 2020; Nikkinen et al. 2020; Rose and Spiegel 2010; Samarakoon 2011). In response, investors should adjust their portfolios taking cross-market spillovers into consideration to mitigate contagion risks. Financial market regulators, on the other hand, should take appropriate measures to maintain market stability during crisis episodes (Baumöhl and Lyócsa 2014; Hemche et al. 2016; Karanasos et al. 2014).
The COVID-19 crisis has sent shock waves through the global economy due to the stringent public health measures undertaken by governments around the world. Similar to the spread of the COVID-19 virus itself, the heightened volatility of asset prices during the pandemic was transmitted across markets through the mechanism of contagion, which is amplified by saturated media coverage (Akhtaruzzaman et al. 2021b). The sheer scale of the unfolding pandemic led to an unprecedented proliferation of studies on financial market dynamics, aimed particularly at understanding the linkages within and between financial markets, including stock, bond, foreign exchange, commodity, and cryptocurrency markets, during the COVID-19 crisis.
While a comprehensive review of the literature is beyond the scope of this paper, notable studies in this strand include those by Corbet et al. (2021), who examine volatility spillovers from Chinese financial markets to gold futures, oil futures, soybean futures, the US dollar/RMB spot exchange rate, and the Bitcoin price; Akhtaruzzaman et al. (2021a), who analyze financial contagion between China and the G7 countries via financial and nonfinancial companies; Gharib et al. (2021), who examine the contagion effects between oil and gold; Akhtaruzzaman et al. (2021c) who examine the hedging or safe-haven asset properties of gold during different stages of the COVID-19 pandemic; Papadamou et al. (2021), who investigate flight-to-quality episodes between 10 major stock and bond markets; and Umar et al. (2021), who explore the linkages between emerging markets and US bonds. Kinateder et al. (2021) examine the bivariate conditional correlations between sovereign bonds, commodities, and major exchange rates.
Despite the mushrooming literature on spillover dynamics between financial markets, the linkages between main and second-tier markets operating within the same stock exchange during the present pandemic represent an untapped area where research can further our understanding. The importance of this study stems from the role of second-tier markets in facilitating small and medium-sized enterprises’ (SMEs’) access to finance and reducing their reliance on debt1 by imposing less stringent listing requirements and serving as a steppingstone2 for aspiring SMEs to graduate to the main market. Moreover, second-tier markets (or SME exchanges, as the World Federation of Exchanges refers to them) have expanded globally, becoming an important part of the SME financing ecosystem (The World Federation of Exchanges 2015). According to The World Federation of Exchanges (2018), the number of listings on these markets has reached 6807 companies, with a total market capitalization of over USD 1.3 trillion across 33 markets spanning 29 exchanges around the world.
Given that the SME market serves as a pipeline to the main market, the extent of the linkages between these markets has important portfolio and risk management implications for investors. If the SME market is only weakly integrated with the main market, external shocks may have limited influence on the SME market, and then investors in the main market can benefit by including the stocks listed in the SME market in their portfolio, as this diversification should reduce risk. In contrast, if the SME market is fully integrated with the main market, volatility in the former may decrease, as it will primarily be determined by volatility in the main market, and investors in the SME market will benefit from a low cost of capital (Li 2007). However, this is not always the case, as volatility in the main market can also be affected by that in the SME market.
Despite the extensive body of evidence on the linkages between large and small stocks listed in the same main market (see, among others, Karmakar 2010; Koulakiotis et al. 2016; Lo and MacKinlay 1990), the potential linkages between SMEs and main stock markets have been investigated far less thoroughly. The few studies in this realm include those by Samitas et al. (2006) and Nguyen et al. (2020). Samitas et al. (2006) found unidirectional Granger causality running from the main index to the parallel (second-tier) index in the Greek stock exchange. Nguyen et al. (2020) examine both the return and volatility transmission between the main and second-tier markets in Hong Kong, Singapore, Thailand, and Malaysia. Their results show that significant unidirectional return transmission from the SME to the main market is present only in Hong Kong, while return transmission runs in the reverse direction in the remaining markets. Volatility spillovers, however, are relatively weak, with statistically significant asymmetric volatility transmission only apparent in the case of the Singaporean market and, to a lesser extent and in the opposite direction, in the Hong Kong market, while no trace of volatility transmission is found in the Thai and Malaysian markets.
While an asymmetric return and volatility transmission from large to small stock portfolios and from main to SME markets is documented in most cases, there exists contradictory evidence suggesting a bilateral return and volatility spillovers between large and small portfolios and, even more remarkably, transmission in the opposite direction from the SME to the main market, which has been interpreted as a potential indirect influence of the SME market on economic development through the main market channel (Nguyen et al. 2020). These mixed findings call for further research on the relation between main and SME markets in different contexts, especially during crisis periods, when diversification and hedging are highly sought after. To the best of the authors’ knowledge, no study has simultaneously examined return and volatility spillovers between main and SME stock markets during the COVID-19 pandemic crisis.
Therefore, we aim to extend the analysis of return and volatility spillovers to stock markets in the Middle East and North Africa (MENA) region during the COVID-19 pandemic.3 Our analysis covers the following two exchanges that have liquid SME markets in the region: the Egyptian Exchange and the Saudi stock exchange (Tadawul). Our choice of these markets for the study sample stems from the following considerations: First, the importance of this region in the world economy is growing. Several MENA countries have implemented structural economic reforms to diversify their economies and reduce their traditional reliance on oil and gas revenues (e.g., Saudi Arabia Vision 2030), and an important avenue to achieve this objective is to increase the contribution of SMEs to GDP. These reforms have helped the Saudi market rank among the top 10 largest exchanges globally in terms of market capitalization, accounting for approximately 76% of the market capitalization in the MENA region. Second, Saudi Arabia and Egypt are the largest economies in the MENA region.4 Third, Egypt has the largest SME market in the MENA region in terms of the number of listed companies, while Saudi Arabia is the largest in terms of market capitalization. Fourth, MENA markets represent a significant portion of existing shariah-compliant Islamic financial assets. Fifth, the MENA SME markets are in their early stage of development and have specific features that set them apart from their more established counterparts. Relative to the Asian SME markets examined by Nguyen et al. (2020), the SME markets in the MENA region are relatively smaller than their main board counterparts in terms of both market capitalization and number of listings. Thus, it is interesting to investigate the linkages between SME and main markets and determine how these markets have weathered the COVID-19 crisis.5
With the above in mind, we contribute to the literature in two ways. First, the return and volatility spillover effects between the main and SME stock markets are investigated over different time periods (the periods before and during the pandemic) to ascertain whether the relationship between these markets has been affected by the widespread pandemic. To this end, a disaggregated VAR-asymmetric BEKK–GARCH and an asymmetric DCC–GARCH approach are used, respectively, to examine return–risk spillovers and the time-varying dynamic correlations between the main and SME stock markets. Second, the results obtained from the asymmetric DCC–GARCH framework are used to build dynamic optimal portfolios and hedging strategies, taking the COVID-19 outbreak into consideration, which shed light on the potential of the SME portfolio in hedging the systematic risk of equity portfolios in the main market.
The empirical analysis reveals contrasting results between the Saudi and Egyptian main–SME market pairs. While significant return and volatility spillovers between the main and SME stocks are found in Saudi Arabia, only volatility spillovers are documented for Egypt. Indeed, the COVID-19 pandemic crisis has intensified the risk spillover among the Saudi main–SME market pairs, which, to our surprise, was not the case for the Egyptian pair. What is more remarkable is that the risk spillover between the Egyptian main and SME markets declined during the pandemic. The dynamic correlations between the main and SME markets are mostly positive and have notably increased during the COVID-19 pandemic, particularly in Saudi Arabia, suggesting that adding SME stocks to a main market stock portfolio can enhance its risk-adjusted return, especially during tranquil market phases.
The remainder of the paper is organized as follows. Section 2 presents the data and the preliminary analysis that justifies the specification of the econometric models that we use in our empirical analysis. Section 3 discusses the empirical methodology, while Section 4 presents and interprets the results from the asymmetric BEKK and asymmetric DCC models and portfolio management analysis. Section 5 provides concluding remarks along with policy implications, limitations, and future research avenues.
2. Data Definitions, Descriptive Statistics, and Preliminary Analysis
2.1. Data Definitions
The data set comprises the daily closing prices of the main and SME stock market indices in Saudi Arabia and Egypt. The indices used in this paper are the Tadawul All Share Index (TASI) and SME market index (NOMU) for the Saudi market and the Egyptian Exchange Price Index (EGX 30) and SME market index (NILEX) for Egypt. The daily data for the TASI, NOMU and EGX30 are taken from the Bloomberg database, whereas the NILEX data are pooled from the Egyptian Exchange website. The time span of the study runs from July 2013 to November 2020.6 To account for the COVID-19 pandemic effect, we have divided the sample into the following two subperiods: the period before the COVID-19 pandemic, which covers the period before the emergence of COVID-19, and the COVID-19 pandemic crisis period, which starts with the declaration of the identification of the virus and continues until the end of our sample period.7 Continuously compounded daily returns are calculated on the basis of the following logarithmic filter: , where and represent the percentage daily return and closing index price on day t, respectively.
2.2. Descriptive Statistics
Table 1 summarizes the descriptive statistics of the daily returns of the main and SME markets in Saudi Arabia and Egypt. Looking at Table 1, it seems that the data characteristics of the return series are considerably different across the full sample and subperiods for both the main and SME market indices. While the NOMU and NILEX saw highly positive returns during the COVID-19 pandemic, the EGX 30 returns experienced a sharp drop and were negative, on average, during the pandemic period. Similarly, the TASI returns witnessed an overall decline after the emergence of COVID-19, although the drop was less severe than that of the EGX30. The volatility (standard deviation) of the daily return was consistently higher across the board during the COVID-19 pandemic than before the pandemic crisis. The findings on skewness are mixed; however, for both the main and SME indices of the Saudi and Egyptian markets. For example, before the COVID-19 pandemic, the Saudi SME stock market, the NOMU, exhibited the most positively skewed returns, indicating that there was a higher probability that investors would earn positive rather than negative returns from the Saudi SME market. Excess kurtosis was found in all the market indices across the entire sample and in all the subperiods, indicating deviations from the normal distribution. These results confirm that the probability distribution of the sample return is asymmetric and leptokurtic, as normality is strongly rejected by the Jarque–Bera test. Furthermore, the ADF (Dickey and Fuller 1981) and PP (Phillips and Perron 1988) unit root tests were used to examine the stochastic properties of the return series. The null hypothesis of a unit root was rejected across the board, indicating that all the return series under study were stationary processes. The results that emerge from the Ljung–Box and tests for the serial correlation of residuals and squared residuals, respectively, as well as the ARCH effect in the return series from the application of the LM–ARCH (5) test highlight the presence of both serial correlation and ARCH effects in all the market indices for the full sample before and during the COVID-19 pandemic, which supports the use of GARCH-type models to investigate the dynamic correlation and volatility spillovers among the main and SME stock markets.

Table 1.
Descriptive statistics of daily stock market returns.
Moving to the bivariate correlations, we can see that the unconditional correlation coefficients between the main and SME stock markets were positive and clearly varied across the subperiods. This implies that there was a link between the main and SME stock markets and that both moved in the same direction. The NOMU showed the highest correlation with the TASI during the COVID-19 pandemic, while the NILEX exhibited the highest correlation with the EGX30 before the COVID-19 pandemic. On the other hand, the NILEX was found to be weakly correlated with the EGX30 during the COVID-19 pandemic. Hence, the main markets exhibited mixed correlations with the SME markets in both Saudi Arabia and Egypt, indicating potential short-run portfolio diversification benefits. However, these results should be cautiously interpreted, as linear correlations do not fully capture the time-varying linkages between these markets.
Figure 1 provides a plot of the main versus SME market indices for Saudi Arabia and Egypt. The figure shows evidence of positive co-movement between the main and SME indices in general. The strength of the co-movement, however, varies considerably across markets and subsamples. The NOMU tended to move more closely with the TASI during the pandemic than in the pre-pandemic period. However, the opposite is true for the co-movement between the NILEX and the EGX30, which weakened during the pandemic. The weak co-movement between the two Egyptian indices may be partially driven by the significant capital outflows of more than USD 15 billion that pulled out from the Egyptian market in a flight to safety.8 It is plausible to suggest that the sell-off has perhaps affected the main market index more severely compared to the SME market index. Naturally, SME markets are regulated to attract investors with longer horizons and are less prone to hot money flows. This is in line with the variation in correlation coefficients reported earlier in Table 1. In addition, during the COVID-19 pandemic (represented by the shaded area of the graph), we can see that the SME stock markets for both Saudi Arabia and Egypt enjoyed an upward trend, whereas the main stock markets suffered a massive decline in the same period. The apparent resilience of both SME markets, in the beginning of the pandemic, coincides with the reforms and development programs in the SME markets in Saudi and Egypt. The impact of these reforms is evident by the considerable increase in trading volume between 2019 and 2020 (see Table A1). Indeed, all the indices have rebounded during the later phases of the pandemic thanks to the economic stimulus measures taken by both the Saudi and Egyptian governments, which greatly alleviated the impact of the lockdown. Figure 2 depicts the squared return for the main and SME stock markets. Each series displays several periods of volatility clustering, particularly around the COVID-19 pandemic, with the effect being more pronounced for the SME indices (NILEX and NOMU).
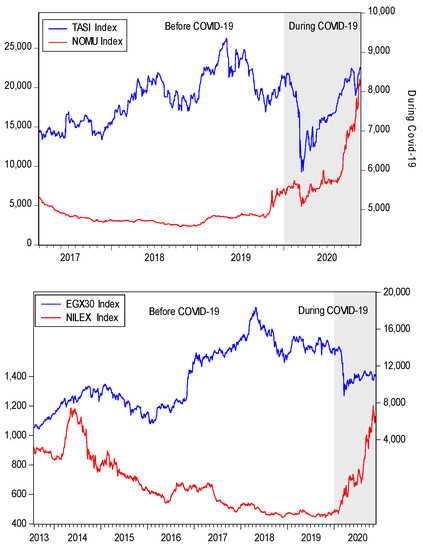
Figure 1.
Co-movements between the main and SME stock markets.
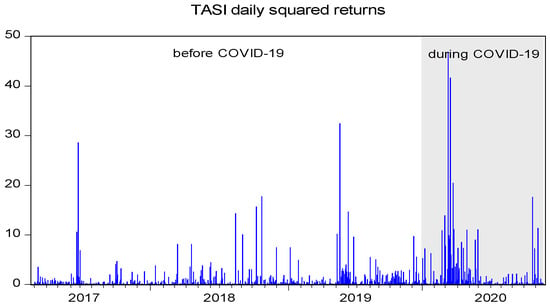
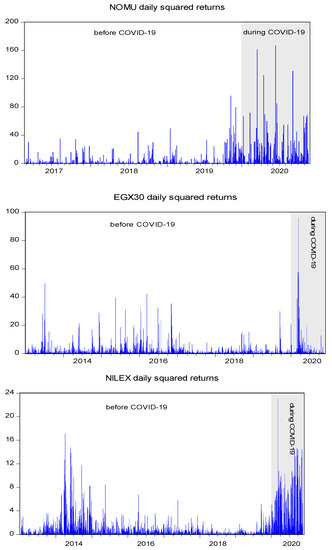
Figure 2.
Squared returns of the main and SME stock markets.
2.3. Preliminary Analysis
2.3.1. Asymmetric Causality Test between the Main and SME Stock Markets
We examine the possibility of asymmetric causality between each pair of main/SME stock indices for both Saudi Arabia and Egypt by using the cumulative sums of positive and negative shocks. The main desirable feature of the asymmetric causality test is its ability to distinguish the potential causal impacts of positive shocks from those of negative shocks, which provides insights for the portfolio selection based on different market phases (see, e.g., Jin et al. 2020; Nguyen et al. 2015; Tiwari and Albulescu 2016; Yarovaya and Lau 2016). To this end, we employ the asymmetric causality test proposed by Hatemi-J (2012), whereby the level price of each index is modelled as a driftless random walk process as follows:
where is the number of observations, and the constant is the initial price of the underlying index. is a white noise disturbance term of the underlying index. Positive and negative shocks to each index are first defined as . Then, the positive and negative shocks to each index are defined in a cumulative form as , . Next, the asymmetric causality effect between each pair of main/SME indices is calculated. For example, to determine the impact of decreases in the TASI return on decreases in the NOMU return, we test the hypothesis of Granger causality from the return of to the return of within the context of a bivariate VAR system.
Table 2 presents the results of the asymmetric causality test for the full sample, for the period before the COVID-19 pandemic and for the period during the COVID-19 pandemic. The results show that on the one hand, the transmission of both positive and negative shocks from the SME market to the main market is evident over the full sample period (except in the case of the hypothesis that , which cannot be rejected). The causality structure, in fact, changes across subsamples (the periods before and during the COVID-19 pandemic) and across markets. On the other hand, reverse information transmission, running from the main market to the SME market, is also evident for the same market phases. However, causality is more apparent during the COVID-19 pandemic crisis than before the outbreak of COVID-19, particularly for Saudi Arabia. For example, positive returns on the NOMU drove positive returns on the TASI during the COVID-19 pandemic, while negative returns on the TASI did not necessarily cause negative returns on the NOMU in the same period. Therefore, the negative changes in the NOMU caused a positive change in the TASI, while an effect in the reverse direction is not evident. The asymmetric causality test indicates no causal linkages between the NILEX and the EGX30 during the COVID-19 pandemic. As we mentioned earlier, the weak linkages may be due to the sell-off by investors predominantly in the main market while the SME market did not experience pull-outs of the same intensity. The overall evidence displays a pattern of rich asymmetric causality between the main and SME stock market returns and clearly suggests that ignoring the asymmetry in their relationships may lead to erroneous conclusions.

Table 2.
Asymmetric causality between the main and SME stock markets.
2.3.2. Directional Connectedness between the Main and SME Stock Markets
To examine the nature of the volatility connectedness between the main and SME stock markets, we use the spillover index approach developed by Diebold and Yılmaz (2014). This approach is based on forecast error variance decomposition, in which the forecast error variance of a variable is decomposed into parts attributed to the other variable in the VAR system. The main goal of this spillover index approach is to explore the total, directional, and net directional spillover effects for cross-stocks (see, e.g., Al-Yahyaee et al. 2019; Bahloul and Khemakhem 2021; Jin et al. 2020; Wu et al. 2019; Xu et al. 2019; Zhang and Hamori 2021). Following Diebold and Yılmaz (2014), we denote as the fraction of variable ’s H-step forecast error variance due to shocks in variable . The total directional connectedness from others to variable is , and the total directional connectedness from others to is The net total directional connectedness (NTDC)9 to others is obtained by taking the difference between the total directional connectedness to others and the total directional connectedness from others.
Table 3 reports the decomposition of the total volatility spillover index between the main and SME stock market volatilities for a forecast horizon of 10 days before and during the COVID-19 pandemic. Panel A of Table 3 shows that the volatility spillovers during the COVID-19 pandemic were significantly higher than those before the COVID-19 pandemic for Saudi Arabia. The total spillover index reached 12.7%, which indicates the importance of spillovers during the COVID-19 pandemic relative to those during the pre-COVID-19 period, when the total spillover index was only 1.6%. Conversely, panel B of Table 3 provides contrasting results for Egypt, as the total spillover index is found to be substantially higher before the pandemic (8% before the COVID-19 crisis and only 1% during the crisis). Overall, the main stock markets in both Saudi Arabia and Egypt are identified as net transmitters of volatility in the periods before and during the COVID-19 pandemic.

Table 3.
Total and directional spillovers between the main and SME markets.
Figure 3 displays the dynamics of the total spillover index and shows substantial fluctuations in the volatility spillovers between the main and SME markets in both Saudi Arabia and Egypt. Before the COVID-19 pandemic, the volatility spillovers between the TASI and NOMU moved relatively smoothly, fluctuating between 2 and 7%. However, with the onset of the pandemic, spillovers jumped to 12% at the beginning of March 2020 and steadily declined, hovering at approximately 7% until the end of the sample period, a result that is in line with previous studies, including those by Akhtaruzzaman et al. (2021a) and Elsayed and Yarovaya (2019). For Egypt, Figure 3 points to a different story, as the values of the total spillover index decreased sharply during the COVID-19 pandemic. The average volatility spillovers of the EGX30 and NILEX appear higher for the period before the COVID-19 crisis than the average spillovers for the COVID-19 pandemic period. Indeed, these findings are commensurate with results obtained from preliminary analyses. Among the possible explanations for this seemingly perplexing result is that the trading and investment strategies of market participants vary across the different time scales in association with different trading and investment horizons (Wang et al. 2016, 2017; Xu and Hamori 2012). This is evident with the benefit of hindsight as the Egyptian exchange experienced a huge sell-off during the early phases of the pandemic in the main rather than the SME market. Portfolio managers and speculators should, therefore, consider crisis periods when designing risk management portfolios.
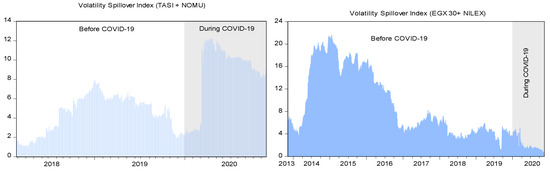
Figure 3.
Dynamic total volatility spillover indices based on the Diebold and Yılmaz (2014) framework. Notes: Dynamic spillover indices are calculated from the forecast error variance decompositions on 10-step-ahead forecasts. The total spillover indices are estimated by using 200-day rolling windows for the full sample period. TASI (NOMU) denotes the Saudi main stock market index (SME stock market index). EGX30 (NILEX) denotes the Egyptian main stock market index (SME stock market index).
3. Materials and Methods
To examine the features of risk and return transmission and the dynamic correlations between main and SME markets, we employed the VAR-asymmetric BEKK–GARCH model to examine the volatility spillover effect and asymmetries in the variance–covariance structure for main and SME returns. Additionally, the asymmetric DCC–GARCH model was employed in this paper with the aim of exploring the dynamic correlations that are used to compute optimal portfolio weights and hedge ratios.10
3.1. The Asymmetric BEKK–GARCH Model
The asymmetric version of the BEKK–GARCH model introduced by Engle and Kroner (1995) and later developed by Kroner and Ng (1998) was used in this study to examine shock and asymmetric volatility spillovers between markets. This version of the model has shown many advantages for investigations of volatility spillovers among two series (see, e.g., Boldanov et al. 2016; Majumder and Nag 2018; Vardar et al. 2018; Wen et al. 2014, 2020; Yu et al. 2020). In this paper, we used the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) model to examine the dynamic spillover effects between main and SME market stocks. Following Iglesias-Casal et al. (2020) and Asl et al. (2021), the conditional mean equations for the main and SME markets are represented by the following VAR(1) system:
with, , , and , and, where is a vector of constant terms; and are the returns of the main and SME stock markets at time t, respectively; and and represent the diagonal elements of the matrix , which captures a unidirectional causal relation between past returns and current returns in the same market, whereas the off-diagonal elements and measure the cross-mean spillovers between the main and SME stock markets. and are the residual terms for the main and SME stock markets’ conditional mean equations, respectively, such that .’ refers to the innovation (shock) term and is an . distributed random process: .
The time-varying conditional variance–covariance matrix is given by the following:
with , , , , ,
, and ,,
where matrix C is a lower triangular matrix of the constant term. Matrix A represents the ARCH coefficients of the model whose diagonal elements and capture the own ARCH effect of the fluctuations of the main and SME stock markets, whereas the off-diagonal elements and of matrix A represent the cross-shock spillover between the main and SME stock markets. Matrix B represents the GARCH coefficients of the model whose diagonal elements and capture the GARCH effect of the main and SME markets themselves, reflecting the persistence of volatilities in each market, while the off-diagonal elements and present the cross-volatility spillovers between the main and SME stock markets. is a matrix of coefficients that capture asymmetry in response to shocks whose diagonal elements and represent the own-asymmetric shock spillovers and capture the asymmetric response of the current conditional variance to own past negative shocks, whereas off-diagonal elements and represent the cross-asymmetric shock spillovers and capture the asymmetric response of the current conditional variance due to past negative shocks from another market.
We estimated the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) model by using the full information maximum-likelihood method (Engle and Kroner 1995; Kroner and Ng 1998). Under the normality assumption,11 the log-likelihood function, , can be written as follows:
where is the number of observations and indicates the vector of estimated coefficients. The BFGS algorithm was then used to obtain the final estimates of the variance-covariance matrix and the corresponding standard errors.
3.2. The Asymmetric DCC–GARCH Model
To further investigate the dynamics underlying dynamic volatilities and correlations, we employed an asymmetric DCC–GARCH (1,1) model developed by Cappiello et al. (2006) that is based on the DCC model of Engle (2002). The model takes into account conditional asymmetries in both volatilities and dynamic correlations, and it allows the modelling of time-varying correlations during a period of negative shocks in a multivariate setting (see, e.g., Basher and Sadorsky 2016; Hou and Li 2016). Indeed, it is necessary to take these asymmetric effects into consideration, especially in constructing portfolio weights and formulating hedging strategies (see, e.g., Jin et al. 2020). The conditional mean equations of the asymmetric DCC–GARCH (1,1) are represented by the following VAR (1) system:
where ,, and are defined in the mean equation of the asymmetric BEKK model. is the variance–covariance matrix defined as follows:
where represents a diagonal matrix of standard deviations obtained from the estimation of the univariate GARCH (1,1) model, which includes the leverage effect. For each pair of main/SME market indices, the equations for the conditional variance using GJR–GARCH (1,1) with spillovers (see Ling and McAleer (2003), McAleer et al. (2009), Salisu and Oloko (2015) and Singhal and Ghosh (2016)) are given by the following:
where is an indicator function that equals 1 if and 0 otherwise. Hence, in the asymmetric DCC model, the negative residuals increase the variance more than the positive residuals if the value for is positive. is a time-varying conditional correlation matrix given by the following:
Cappiello et al. (2006) define the correlation evolution as follows:
where and G are the unconditional correlation matrices and is equal to 1 and 0 otherwise. In the asymmetric DCC–GARCH (1,1) case, matrices A, B, and G are measured by scalars (a, b, g). To secure the positive definite constraint of , the intercept must be positive semidefinite, and the initial covariance matrix must be positive definite. This model is estimated by using the quasi-maximum likelihood (QML) technique based on the Berndt–Hall–Hall–Hausman (BHHH) optimization algorithm.
3.3. Optimal Portfolio Allocation and Risk Management
3.3.1. Optimal Portfolio Weights
The existence of risk spillovers between the two assets indicates that investors’ assets in both markets are more volatile and more susceptible to risk and uncertainty (Salisu et al. 2021). Indeed, investigating the optimal portfolio structure over the sample period could provide valuable insight as to what extent the COVID-19 pandemic has impacted the investors’ asset allocation decision. To this end, we employed the conditional variance and covariance estimated from the bivariate VAR (1)-asymmetric DCC–GARCH (1,1) model to compute portfolio weights. The approach outlined by Kroner and Ng (1998) was used to form a portfolio that minimizes risk without lowering expected returns. The optimal weight of SME stocks in a one-dollar portfolio of main/SME stocks at time t is given by the following:
As we assumed that portfolio holdings are fully invested with no short positions allowed, the portfolio weights are constrained to be nonnegative and to sum to one as follows:
where is the weight of SME stock in a one-dollar portfolio of the two assets (from the main and SME stock markets) at time and the term, represents the conditional variance of the main market index at time , represents the conditional covariance between the main and SME stock markets at time t while represents the conditional variance of the SME market index at time . The corresponding weight of the main index in this portfolio is .
3.3.2. Dynamic Optimal Hedge Ratios
Hedging is the best tool for mitigating the risks of investing in volatile assets. The optimal hedge ratio is defined according to Kroner and Sultan (1993), who consider a portfolio of two assets and argue that the risk of the investment portfolio is minimized when the acquisition of one dollar of the first asset is hedged by a short position of dollars in the second asset. The optimal hedge ratio between main/SME market stocks is given by the following:
Here, a long position of one dollar in the main market was hedged by shorting dollars in the SME market to minimize the portfolio risk. Then, following Ederington (1979), we computed the hedging effectiveness index (HEI) to gauge the performance of the optimal hedging strategies. The hedging effectiveness index, which represents the gain or loss in the variance of the hedged portfolio in comparison to that of the unhedged portfolio, is defined as follows:
where variance unhedged represents the variance in the main stock market return and variance hedged represents the variance in the return on the main/SME stock market portfolios. A higher HEI value indicates greater risk reduction, which implies that the investment method can be considered a superior hedging strategy. More interestingly, when the HEI is close to one, it means that the hedge strategy is perfect.
3.3.3. Hedging Effectiveness during the COVID-19 Pandemic
Risk management and asset portfolio allocation emerge as important issues during crisis periods. In this sense, Junttila et al. (2018) emphasize the importance of examining hedging performance during market turmoil as the demand for hedging instruments generally increases.12 To ascertain whether SME stocks are a suitable hedging instrument for main stocks in both the Saudi and Egyptian markets, particularly for the COVID-19 pandemic period, we compared the HEI values during the COVID-19 pandemic with the HEI values before the pandemic (see, e.g., Jin et al. 2020). Thus, we calculated in the following manner:
A positive value of indicates a better hedging performance during the COVID-19 pandemic.
4. Empirical Results and Discussion
In this section, we first present the results obtained from estimating the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) and the bivariate VAR (1)-asymmetric DCC–GARCH (1,1) models in Section 4.1 and Section 4.2, respectively.13 Then, we discuss portfolio weight analysis as well as hedging strategies and their hedging effectiveness, particularly during the COVID-19 pandemic, in Section 4.3.
4.1. Returns and Risk Spillovers between the Main and SME Stock Markets
Table 4 reports the estimation results of the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) model for the Saudi and Egyptian main and SME stock markets for the full sample period, the period before the COVID-19 pandemic and the period during the COVID-19 pandemic. Panel A of Table 4 shows that the returns on the main market indices (TASI and EGX30) are strongly affected by their own lagged values, as the estimates of the diagonal element () are found to be statistically significant over the entire sample and the two subsamples at the 5% level at least. These effects are positive in the returns on the TASI and EGX30 for the full sample period and for the period before the COVID-19 pandemic, indicating persistence, but negative in the TASI returns for the COVID-19 pandemic period, indicating a downward drift in the TASI. Similarly, the estimates of the other diagonal element () indicate that the SME markets (NOMU and NILEX) display significant initial lag dependence across the board at the 5% level at least. While the NILEX is positively affected by its own lagged values, the impact of the NOMU’s own lagged value is found to be persistently negative. Thus, we can see that both the main and SME markets in Saudi Arabia and Egypt show short-term predictability, which casts doubt on the efficient market hypothesis in its weak form for both the main and SME markets.

Table 4.
Estimation results of the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) model.
Moving to the off-diagonal elements of matrix , we can see that there are significant positive mean spillovers from the SME to the main market but only for Saudi Arabia, i.e., from NOMU stocks to TASI stocks (), reaching statistical significance for the full sample period and the period before the COVID-19 pandemic (), which indicates that information in the NOMU is transmitted into the pricing process of the TASI. The estimates of the other diagonal element () are substantially higher and are statistically significant, indicating that the return spillovers from the returns on the TASI to the returns on the NOMU are stronger and apparent for the full sample ) and the period before the COVID-19 pandemic ), which indicates in turn that an increase in the returns of the TASI positively influences the returns of the NOMU. In contrast, we find no traces of a mean spillover effect from the main to the SME stock market or vice versa in Egypt for any of the three subsample periods.
The linkages between the NOMU and the TASI are partially consistent with those documented by Nguyen et al. (2020), who find evidence for a unidirectional return transmission running from the SME to the main market in Hong Kong only, while the other markets (Thailand, Singapore and Malaysia) display return transmission but in the opposite direction, that is, from the main to the SME market. A plausible explanation for this finding might be the importance of the NOMU market relative to that of the NILEX market (see Table A1 in the Appendix A) in terms of size with respect to the main market. In addition, the NOMU has thus far successfully fulfilled its role as a steppingstone for aspiring SMEs, with more than half of its listed companies graduating to the main market. Therefore, we can think of the NOMU as an indirect contributor to economic growth via the main market channel.14 This is not the case for the Nile Exchange, however, as only one company has been able to move to the main board since the exchange’s inception (Enterprise 2020b), which may also explain the lack of integration between the SME and main markets in Egypt in addition to the thin trading and minute size of the Egyptian SME market.
Panel B of Table 4 presents the estimated coefficients for the ARCH and GARCH terms, where the former captures the short-run persistence of volatility shocks while the latter measures the long-run persistence. The estimates of the diagonal elements of matrix , i.e., and , and matrix , i.e., and , which measure the effects of the own past shock (past volatility) of the main and SME stock markets on conditional present volatility, are statistically significant at least at the 5% level across the board for the full sample and both subsample periods. This shows that the main stock markets (TASI and EGX30) and the SME stock markets (NOMU and NILEX) have strong short-run (ARCH) and long-run (GARCH) persistence. For each index, we note that the estimated and values are smaller than their respective estimated and values, indicating that past volatilities are more important than shocks or news in predicting future volatility, consistent with results reported elsewhere.
We now examine how shocks and volatility spillovers are transmitted between the main and SME stock markets. Here, our focus is directed toward the estimates of the off-diagonal elements of matrix , i.e., and , and matrix , i.e., and , which measure the interdependencies between the main and SME stock markets that manifest in the form of shock and volatility spillovers between these markets. Panel B of Table 4 reveals some instances where spillovers are found to be bidirectional or absent depending on the subperiod and the market under consideration. The short-term persistence coefficients are found to be negative and statistically significant for the periods before and during the COVID-19 pandemic for Saudi Arabia, indicating that short-term shocks originating in the main market have a calming effect on volatility in the SME market in the short run. Similarly, shocks originating from returns on the NOMU stocks measured by affect the variability of returns on the TASI for the three sample periods. However, only for the COVID-19 pandemic period do the signs of the shock spillover from the NOMU to the TASI become negative. On the other hand, a bidirectional shock between the variability of returns of the EGX30 and NILEX stocks is documented but only for the pre-COVID-19 pandemic period.
For the long-term volatility spillovers ( and coefficients), the results show the presence of bidirectional volatility spillovers but with different signs for the full period and the pandemic period, whereas significant spillovers are absent for the pre-pandemic period. For the full sample period, the past volatility of the TASI positively affects the current volatility of the NOMU, whereas the past volatility of the NOMU negatively affects the current volatility of the TASI; however, the role of the TASI is much greater than that of the NOMU, which is a qualitatively similar finding to the results obtained using the Diebold and Yılmaz approach. The COVID-19 pandemic period, however, witnessed positive bidirectional volatility spillovers between the two markets. Likewise, the main and SME markets in Egypt exhibit bidirectional volatility spillovers with different signs and in opposite directions; that is, past volatility on the EGX30 negatively affects current volatility on the NILEX, whereas past volatility on the NILEX positively affects current volatility on the EGX30, which implies a calming effect, mainly from the SME market, in the long run. However, no volatility spillovers between the Egyptian markets are detected for the COVID-19 pandemic period, indicating that neither market was affected by the riskiness of the other. These results are inconsistent with those of Nguyen et al. (2020), who fail to find strong evidence for either shock or volatility spillovers between the main and SME markets in any of the countries that they examine. That said, volatility linkages between markets can arise from the following two different sources: (i) common information that affects more than one market concurrently and (ii) informational spillovers attributable to cross-market hedging (Fleming et al. 1998, p. 112). This could reconcile our findings with others in the literature; for example, Karmakar (2010), Koulakiotis et al. (2016) and Kyrkilis et al. (2018) find strong evidence for feedback in conditional variance between portfolios of small stocks and of large stocks in the Indian and Greek markets, respectively.
Panel C of Table 4 presents the asymmetric volatility spillover effects.15 The estimates of the diagonal elements of matrix measuring the asymmetric own shocks to returns given by and are mixed. On the one hand, the estimates of pertaining to the main markets are found to be positive and strongly significant at the 1% level for both markets and for the entire period and both subsamples, which indicates that negative news from the TASI (EGX30 index) amplifies the volatility of the TASI (EGX30 index) to a greater extent than positive news does. Shocks in the TASI show the largest asymmetric effect on its own conditional volatility. On the other hand, the results pertaining to the SME markets show little evidence for an asymmetric own shock to returns as measured by , which is limited to the NILEX for the full sample period only.
Looking at the estimates of the off-diagonal elements of matrix , we find significant asymmetric shock spillover effects between the main and SME markets in both Saudi Arabia and Egypt. Negative shocks from the NILEX index affect the EGX30 index more than positive shocks for the full sample period and the period during the COVID-19 pandemic. The effect is positive, implying that a negative shock from the NILEX index increases the variability of EGX30 index returns. In contrast, negative shocks from the EGX30 stocks exert a positive asymmetric effect on the variability of NILEX stock returns for the full sample period and the period before the COVID-19 pandemic. In addition, asymmetric volatility spillover effects from the TASI to the NOMU index are found to be significant and positive for the COVID-19 pandemic period only. In contrast, there is no asymmetric volatility spillover from the NOMU to the TASI during any of the three periods.
The major findings of this study are as follows: First, the return transmission from the SME to the main market in Saudi Arabia supports the potential role of the SME market as a contributor to economic growth by operating as a pipeline for the main market, which has a direct impact on economic growth. Therefore, all the policies and initiatives that facilitate the functioning of the SME market are essential for sustaining economic growth.16 Second, the volatility spillovers documented in both markets can be attributed to common information (macroeconomic information). As the main and SME markets are hosted under the same exchange, they are conducive to cross-market hedging, which in turn enhances volatility linkages. Finally, the results are not universal, as they vary not only between markets but also across different subsample periods (especially for the COVID-19 crisis period). These findings carry important implications for asset allocation and risk management strategies.
4.2. Dynamic Conditional Correlations between the Main and SME Stock Markets
This section reports the empirical results obtained from estimating a bivariate VAR (1)-asymmetric DCC–GARCH (1,1) model for the main–SME stock market pairs in Saudi Arabia and Egypt. In panel C of Table 5, the estimated coefficients for the correlation equation show that , , and are significantly different from zero and vary for the periods both before and during the COVID-19 crisis. The significance of and indicates short- and long-term persistence in the correlation. For each pair of main and SME markets in a country, the dynamic conditional correlation of the pair’s returns exhibits significant reversion, as the sum of and is less than 1, consistent with the findings of Tiwari et al. (2019), Alexakis and Pappas (2018) and Jin et al. (2020). The significance of indicates that positive and negative shocks tend to induce different correlations between stock markets. As shown in panel C of Table 5, is significant and positive for the TASI/NOMU for the full sample period (5.4%). Hence, asymmetry exists in the correlation between the TASI and NOMU markets for the COVID-19 pandemic period (12%). This suggests that the correlation between the main and SME market stocks in Saudi Arabia is greater when markets are falling than when they are rising, in line with the findings of Campbell et al. (2002).17 For Egypt’s main and SME markets, is not significant for the COVID-19 pandemic period, reinforcing the results obtained using the Diebold and Yılmaz approach.

Table 5.
Estimation results of the bivariate VAR (1)-asymmetric DCC–GARCH (1,1) model.
The movements of the dynamic conditional correlations are depicted in Figure 4, which shows that the correlations between each pair of main–SME market indices are quite volatile and vary over time. Noticeably, negative correlations are occasionally observed for both Saudi Arabia and Egypt when main stocks are paired with SME stocks. We can also see that the dynamic conditional correlations exhibit higher positive co-movement between the TASI and the NOMU, particularly for the COVID-19 pandemic period. In contrast, the dynamic conditional correlations between the EGX30 and the NILEX declined considerably during the outbreak. The documented instability in the dynamic correlation between the main and SME market stocks is indicative of the changing preferences of investors over the sample period, dictating frequent portfolio rebalancing. Methodologically, these findings confirm the inadequacy of relying solely on unconditional correlations and carry important implications for investors making hedging and asset allocation decisions, as discussed in the following section.
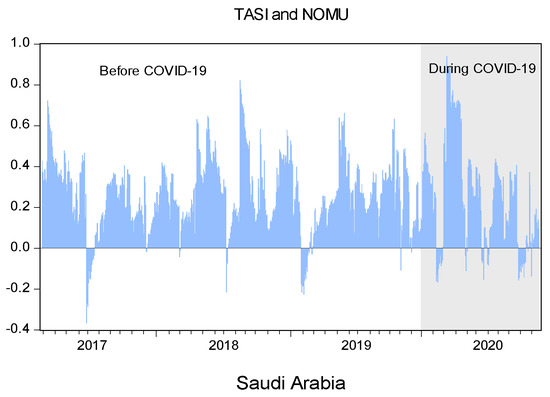
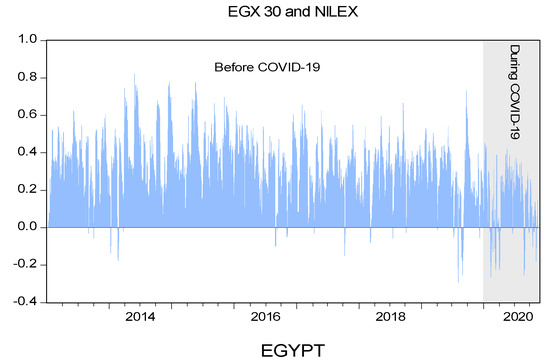
Figure 4.
Dynamic conditional correlations between main and SME stock markets estimated from the asymmetric DCC–GARCH (1,1) model.
4.3. Portfolio Weights, Hedge Ratios, and Hedging Effectiveness
The results obtained from the VAR (1)-asymmetric DCC–GARCH (1,1) model are used to compute the optimal weights of the stock portfolios for the main–SME markets. Table 6 reports the averages of the dynamic conditional correlations, optimal weights, and hedge ratios for the full sample and the periods before and during the COVID-19 pandemic. The findings reveal that the weights allocated to SME stocks are substantially lower for both markets for the COVID-19 pandemic period than for the period before the pandemic. This suggests that investors are inclined to hold more SME stocks during stable periods, especially in the Egyptian market, where the weight of SMEs constituted four-fifths of the main–SME stock portfolio before the pandemic. Figure 5 illustrates the dynamics of optimal portfolio weights for each pair of main–SME stock portfolios. The shaded area in Figure 5 shows the same story, as we can clearly see a dramatic decrease in the weight attributed to SME stocks during the COVID-19 pandemic.

Table 6.
Dynamic conditional correlations, optimal portfolio weights, hedge ratios and hedging effectiveness (%) for main–SME stock pairs.
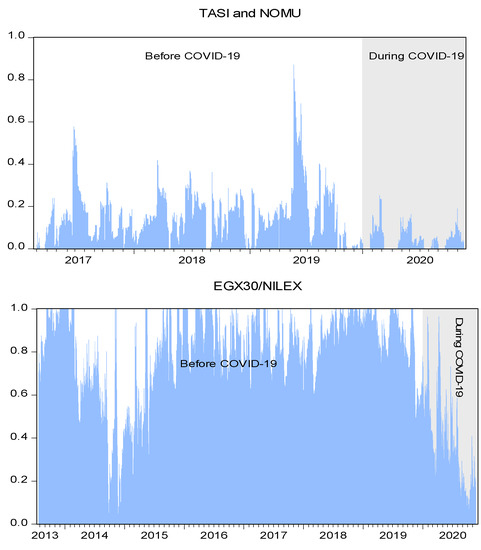
Figure 5.
Time-varying portfolio weights computed from the VAR (1)-asymmetric DCC–GARCH (1,1) model.
The results pertaining to the optimal hedge ratios and their effectiveness based on Table 6 are mixed not only across markets but also across phases in the same market. On the one hand, we find that the optimal hedge ratio is relatively high, reaching 0.614 for the EGX30/NILEX for the pre-COVID-19 pandemic period, which means that a USD 1 long position in the EGX30 can be hedged by taking a short position of 61.4 cents in the NILEX. On the other hand, during the COVID-19 pandemic, the optimal hedge ratios witnessed a drastic decline for the EGX30/NILEX. The optimal hedge ratios are considerably lower for the Saudi portfolio; however, they show less variation over the sample period. Figure 6 shows the time-varying hedge ratios for each short-hedged main market portfolio. Notably, the hedge ratios fluctuate significantly over time and are generally lower for the COVID-19 pandemic period than for the period before the pandemic. The decline in hedge ratios implies lower hedging costs during the COVID-19 pandemic period due to the lower number of stocks required to short the SME market. However, to judge the hedging effectiveness, the hedging effectiveness index is calculated for each main–SME stock market pair and is reported in Table 6.
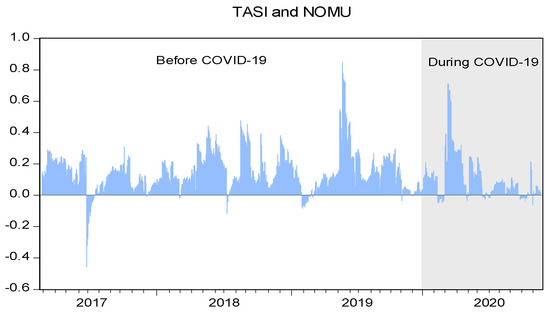
Figure 6.
Time-varying hedge ratios computed from the VAR (1)-asymmetric DCC–GARCH (1,1) model.
From Table 6, we can see that when investors include SME stock as part of their hedging strategy, portfolio risk decreases significantly, but only for the Egyptian market. The hedging effectiveness index is higher for the period before the COVID-19 pandemic for the EGX30/NILEX (62.95%), which indicates that shorting the NILEX stocks to hedge the EGX30 significantly reduces the portfolio risk by 62.95% from the level of the unhedged portfolio. For the Saudi Arabian main market (TASI), the SME stock market (NOMU) persistently offers poor hedging performance. Looking at the last column of Table 6, which compares the HEI values for the COVID-19 pandemic and pre-pandemic periods, we find that hedging effectiveness has improved marginally during the pandemic for Saudi Arabia. On the other hand, the values of are negative for the main–SME Egyptian markets, suggesting a less effective hedging performance during the pandemic period. One important takeaway from the results presented in this section is that investors should change their portfolio structure and hedging strategy in accordance with different market conditions (see, e.g., Jiang et al. 2019).
5. Conclusions and Policy Implications
This paper analyzed how return and volatility spillovers arise within the main and SME markets in Saudi Arabia and Egypt, the two largest economies in the MENA region, and explored the availability of portfolio diversification and hedging opportunities in the periods before and during the COVID-19 pandemic. The equity markets within this region constitute an interesting case due to the growth potential in these economies and the importance of SMEs for achieving ambitious visions for these economies.
A bivariate asymmetric BEKK–GARCH model was employed to estimate the return and volatility spillovers, while a bivariate asymmetric DCC–GARCH model was used to estimate dynamic correlations on the basis of which optimal portfolio weight hedge ratios are computed. The results of the VAR (1) estimation provide evidence of bidirectional return spillovers between the main and SME stock markets only in Saudi Arabia, and these spillovers diminished during the COVID-19 pandemic. The results of the estimation of the MGARCH (1,1) in the asymmetric BEKK formulation provide evidence of shock and volatility spillovers with different characteristics and dynamics between each of the main–SME stock market pairs. The shock and volatility transmission effect has strengthened during the COVID-19 pandemic for the Saudi pair while weakening between the Egyptian main and SME markets, suggesting that the interlinkages between the main and SME stocks in Saudi Arabia are stronger during turbulent periods than those of the Egyptian market, where no shock or volatility spillovers are detected for the COVID-19 pandemic period. The result of the estimation of the asymmetric DCC–GARCH (1,1) model reveals that the time-varying conditional correlations between the main and SME markets are mostly positive and have notably increased during the COVID-19 pandemic, but only in Saudi Arabia. The optimal portfolio weights allocated to SME stocks fluctuated considerably over the sample period, decreasing substantially for both markets during the COVID-19 pandemic period. The hedge ratio also exhibits a similar pattern, failing to provide meaningful risk reduction during the pandemic.
Policy implications follow naturally from the aforementioned conclusions. First, the documented return spillovers from the SME to the main market in Saudi Arabia support the notion that the SME market, while acting as a pipeline for the main market, indirectly promotes economic growth in Saudi Arabia through its transmission mechanism via the main market. Second, the bidirectional volatility spillovers highlight cross-market hedging and portfolio rebalancing in response to common information that affects the entire economy. Third, the absence of spillovers within the Egyptian markets during the pandemic can be attributed to the sell-offs experienced majorly by the Egyptian main rather SME market as a part of flight-to-safety episode triggered by concerns about the future prospects of emerging markets during the pandemic. Fourth, the results from the portfolio design and hedging analysis suggest that adding SME stocks to a main market stock portfolio enhances the risk-adjusted return, particularly during tranquil market phases when investors adjust their portfolio weight allocations and hedging positions based on different market conditions. Overall, it is imperative for policymakers to take all the necessary measures to attract more listings in addition to promoting the SME market to fund managers who ultimately enhance the liquidity of SME markets and increase investors’ confidence in those markets.
A caveat of this study is the narrow sample, which considers the interdependencies between the main and second-tier markets within just two countries. This limitation can be addressed in future work by examining a large sample of countries to explore the potential factors that affect the interdependencies between main and second-tier markets, which may assist in accounting for the heterogeneity of results across countries. Another potentially viable extension of this work is to compare the linkages between large- and small-sized portfolios within the main market against the results obtained by portfolios of companies of a similar size but listed in the second-tier market to explore whether differences in the rules and regulations of the main and second-tier markets impact the nature of the linkages between these portfolios.
Author Contributions
Conceptualization, N.S.A.-N. and B.M.; methodology, N.S.A.-N. and B.M.; software, N.S.A.-N. and B.M.; validation, N.S.A.-N. and B.M.; formal analysis, N.S.A.-N. and B.M.; investigation, N.S.A.-N. and B.M.; resources, N.S.A.-N. and B.M.; data curation, N.S.A.-N. and B.M.; writing—original draft preparation, N.S.A.-N. and B.M.; writing—review and editing, N.S.A.-N. and B.M.; visualization, N.S.A.-N. and B.M.; supervision, N.S.A.-N. and B.M.; project administration, N.S.A.-N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data were obtained from the Bloomberg Terminal and Egyptian Exchange websites and will be made available upon request.
Acknowledgments
We are grateful to the editor-in-chief, Sabri Boubaker, for his constructive comments and valuable insights that helped us to bring the paper to its present form. In addition, we would like to thank two anonymous referees for many helpful comments. All remaining errors are our own.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Stock market characteristics.
Table A1.
Stock market characteristics.
| Saudi Arabia | Egypt | |||||||
|---|---|---|---|---|---|---|---|---|
| Main Market | SME Market | Main Market | SME Market | |||||
| Years | 2019 | 2020 | 2019 | 2020 | 2019 | 2020 | 2019 | 2020 |
| Inception a | 1985 | 2017 | 1998 | 2012 | ||||
| No. of listed companies | 199 | 203 | 5 d | 4 | 210 | 209 | 27 e | 27 |
| Representative index | TASI | NOMU | EGX 30 | NILEX | ||||
| Market capitalization b | 2406.73 | 2427.15 | 0.68 | 3.25 | 44.13 | 41.35 | 0.07 | 0.06 |
| Percentage of GDP | 303.51% | 347% | 0.09% | 0.46% | 14.56% | 11% | 0.02% | 0.02% |
| Percentage of main index | - | - | 0.03% | 0.13% | - | - | 0.16% | 0.15% |
| Trading value b | 234.7 | 556.75 | 0.61 | 1.90 | 11.28 | 16.14 | 0.016 | 0.083 |
| Percentage of main index | - | - | 0.26% | 0.34% | - | - | 0.14% | 0.51% |
| Trading volume c | 33.06 | 79.32 | 0.08 | 0.11 | 43.74 | 87.10 | 0.77 | 1.58 |
| Percentage of main index | - | - | 0.24% | 0.14% | - | - | 1.8% | 1.8% |
Source: Annual Statistical Report (2019) published by the Saudi stock exchange (Tadawul), annual and quarterly reports from the Egyptian Exchange and the World Federation of Exchanges’ (WFE) statistics portal. Notes: a Inception refers to the year in which the respective index was first developed with its base level regardless of subsequent restructurings; b in USD billion; c in billion shares; d the NOMU started 2019 with 10 companies, 5 of which transitioned their shares from the SME (parallel) market to the main market by the end of the year; e the NILEX started 2019 with 29 companies; one company was newly listed in the market, and three companies were delisted by the end of the year.

Table A2.
Diagnostic tests on standardized residuals.
Table A2.
Diagnostic tests on standardized residuals.
| Full Sample Period | Before the COVID-19 Crisis | During the COVID-19 Crisis | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TASI | NOMU | EGX30 | NILEX | TASI | NOMU | EGX30 | NILEX | TASI | NOMU | EGX30 | NILEX | |
| Panel A: VAR (1)-asymmetric BEKK–GARCH (1,1) model | ||||||||||||
| ARCH–LM(5) | 8.8641 (0.1146) | 4.4711 (0.4834) | 6.4930 (0.2612) | 3.6942 (0.5942) | 11.9986 (0.3485) | 7.2395 (0.1601) | 7.0067 (0.2201) | 7.4165 (0.2209) | 5.400 (0.6678) | 7.9289 (0.1602) | 3.2929 (0.8073) | 6.1898. (0.8221) |
| 9.0712 (0.6312) | 5.5485 (0.3214) | 6.2715 (0.1800) | 4.7411 (0.3151) | 5.7916 (0.2154) | 5.3610 (0.2529) | 3.5884 (0.5464) | 4.5581 (0.3367) | 3.723 (0.4343) | 4.091 (0.3993) | 5.1287 (0.2742) | 6.7398 (0.2046) | |
| 9.0953 (0.1053) | 4.4905 (0.4812) | 6.6196 (0.2516) | 3.7643 (0.584) | 12.5598 (0.3520) | 8.2212 (0.1445) | 7.0025 (0.2221) | 7.4870 (0.1879) | 5.655 (0.6819) | 8.2819 (0.1415) | 3.3292 (0.8871) | 6.3895 (0.2934) | |
| Panel B: VAR (1)-asymmetric DCC–GARCH (1,1) model | ||||||||||||
| ARCH–LM(5) | 3.7645 (0.5834) | 2.9368 (0.7079) | 3.573 (0.6123) | 6.7855 (0.2371) | 10.5801 (0.6042) | 5.2708 (0.3837) | 6.8975 (0.2284) | 7.4975 (0.18625) | 0.8181 (0.9759) | 5.8824 (0.3178) | 2.2472 (0.8140) | 9.9312 (0.7106) |
| 12.007 (0.1754) | 4.9998 (0.2872) | 5.2439 (0.2630) | 6.0145 (0.1980) | 7.6671 (0.1066) | 3.4814 (0.1482) | 4.0498 (0.3991) | 4.4744 (0.3468) | 5.0911 (0.1650) | 3.3827 (0.4963) | 5.7879 (0.435) | 6.4391 (0.1693) | |
| 3.9104 (0.5620) | 2.9740 (0.7040) | 3.5939 (0.6090) | 6.9802 (0.2225) | 10.3100 (0.6315) | 5.9150 (0.3562) | 6.8068 (0.2351) | 7.6227 (0.1783) | 0.8712 (0.9720) | 6.1399 (0.2939) | 2.2021 (0.8214) | 9.0987 (0.6859) | |
Notes: and represent the Ljung–Box Q-statistics on the order of 10 for the standardized residuals and squared standardized residuals, respectively, along with their corresponding p-values in parentheses. LM–ARCH(10) refers to the Engle (1982) test statistics along with their corresponding p-values in parentheses. TASI (NOMU) denotes the Saudi main stock market index (SME stock market index). EGX30 (NILEX) denotes the Egyptian main stock market index (SME stock market index).
Notes
| 1 | Several financing sources exist for SMEs, including venture capital, private equity, private debt, trade credit, initial public offerings (IPOs), business angel finance, and crowdfunding, as well as grants, funding from incubators or accelerators, and support from family and friends (Cumming et al. 2019); however, bank loans remain their main source of funding (Beck et al. 2008; The World Federation of Exchanges 2015). Nonetheless, Cosh et al. (2009) find that SMEs are less likely than larger firms to receive the desired amount of funding from banks. This is primarily due to information asymmetries, a lack of brick-and-mortar collateral, a lack of positive and regular cash flows, and the need for longer maturities to finance capital expenditure (Berger and Udell 2006; Jaffee and Russell 1976; Nassr and Wehinger 2016; Stiglitz and Weiss 1981). Moreover, SMEs are found to be more vulnerable in financial crises, as several studies have shown that the global financial crisis (GFC) exacerbated credit rationing, thereby undermining SMEs’ business and investment activities (see Cowling et al. 2016; D’Amato 2019; Ferrando and Ruggieri 2018). |
| 2 | Other models of second-tier market segmentation include sectoral and demand-side models (see Vismara et al. 2012). However, the sequential segmentation (steppingstone) model is recommended by international bodies (Nassr and Wehinger 2016, p. 70). Under the sequential segmentation (steppingstone) model, second-tier markets are expected to screen small companies in the ‘seasoning’ market, and if a company is successful, it graduates to the main market. |
| 3 | For more on the specificities of emerging markets, including the MENA region and their intraction with the global economy, see Arouri et al. (2013), while Boubaker et al. (2016) focus on risk management practices in emerging markets. |
| 4 | Based on GDP, PPP (current international USD); see https://data.worldbank.org/indicator/NY.GDP.MKTP.PP.CD (accessed on 15 June 2021). |
| 5 | The Nile Exchange (NILEX) was launched under the Egyptian Exchange in 2007, whereas the NOMU—Parallel Market was initiated in 2017 under Tadawul. While both markets had a slow start at the outset, interest has noticeably grown in the past few years (see Table A1 in the Appendix A). |
| 6 | An unbalanced sample is used, where the starting date is selected based on the following two considerations: the first is data availability for the corresponding SME market index, and the second is the desire to avoid any overlap with previous crises, including the European sovereign debt crisis (2010–2012) and the 2013 Egyptian coup d’état. Accordingly, the sample starting date was 24 July 2013, for Egypt, and 27 February 2017, for Saudi Arabia, and the sample ended on 20 November 2020, for both markets. |
| 7 | The starting date of the COVID-19 subsample was 31 December 2019, according to the World Health Organization (WHO) (see WHO 2020). |
| 8 | https://www.imf.org/en/News/Articles/2021/07/14/na070621-egypt-overcoming-the-COVID-shock-and-maintaining-growth (accessed on 15 June 2021). |
| 9 | , which denotes how shocks in the main stock market are transmitted to the SME stock market and how the main stock market receives shocks from the SME stock market . |
| 10 | The models’ specification is chosen on the basis of a two-step procedure to select the optimal lag structure (according to the AIC). Vrieze (2012) has argued in favour of the superiority of the AIC for model selection. |
| 11 | The normality assumption produces the highest value of the log-likelihood; see, e.g., Liu et al. (2017). |
| 12 | Jin et al. (2020) also examine hedging performance. |
| 13 | Table A2 in the Appendix A displays the postestimation diagnostics for the bivariate VAR (1)-asymmetric BEKK–GARCH (1,1) and VAR (1)-asymmetric DCC–GARCH (1,1) models. The Ljung–Box and Engle ARCH–LM tests at five lags are used to test for the presence of serial correlation and heteroskedasticity in the standardized residuals, respectively. All the models pass the diagnostic tests, suggesting that they are well specified. |
| 14 | Al Rasasi et al. (2019) examine the stock market and economic growth nexus in Saudi Arabia. They find a significant long-run relationship between the real price level of the main market index and real economic activity, indicating that stock prices have a significant impact on real economic growth. |
| 15 | A major advantage of the model is its capacity to account for cross-market asymmetric shock spillovers, which capture whether a positive or a negative shock in one market translates to either a positive or negative shock in another market. |
| 16 | The Egyptian Exchange is embarking on a restructuring plan for the Nile Exchange with the European Bank for Reconstruction and Development (Enterprise 2020a). |
| 17 | Campbell et al. (2002) show that during periods of heightened volatility, stocks tend to become more correlated. This finding has important implications for portfolio and risk management because it means that the benefits of diversification are somewhat undermined just when investors have the greatest need for them. |
References
- Akhtaruzzaman, Md, Sabri Boubaker, and Ahmet Sensoy. 2021a. Financial Contagion during COVID-19 Crisis. Finance Research Letters 38: 101604. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, and Zaghum Umar. 2021b. COVID-19 media coverage and ESG leader indices. Finance Research Letters, 102170. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, Brian M. Lucey, and Ahmet Sensoy. 2021c. Is gold a hedge or a safe-haven asset in the COVID–19 crisis? Economic Modelling 102: 105588. [Google Scholar] [CrossRef]
- Al Rasasi, Moayad H., Soleman O. Alsabban, and Omar A. Alarfaj. 2019. Does Stock Market Performance Affect Economic Growth? Empirical Evidence from Saudi Arabia. International Journal of Economics and Finance 11: 1–21. [Google Scholar] [CrossRef] [Green Version]
- Alexakis, Christos, and Vasileios Pappas. 2018. Sectoral dynamics of financial contagion in Europe—The cases of the recent crises episodes. Economic Modelling 73: 222–39. [Google Scholar] [CrossRef]
- Al-Yahyaee, Khamis Hamed, Walid Mensi, Ahmet Sensoy, and Sang Hoon Kang. 2019. Energy, precious metals, and GCC stock markets: Is there any risk spillover? Pacific-Basin Finance Journal 56: 45–70. [Google Scholar] [CrossRef]
- Arouri, Mohammed El Hedi, Sabri Boubaker, and Duc Khuong Nguyen. 2013. Emerging Markets and the Global Economy: A Handbook. Cambridge: Academic Press. [Google Scholar]
- Asl, Mahdi Ghaemi, Giorgio Canarella, and Stephen M. Miller. 2021. Dynamic asymmetric optimal portfolio allocation between energy stocks and energy commodities: Evidence from clean energy and oil and gas companies. Resources Policy 71: 101982. [Google Scholar] [CrossRef]
- Bahloul, Slah, and Imen Khemakhem. 2021. Dynamic return and volatility connectedness between commodities and Islamic stock market indices. Resources Policy 71: 101993. [Google Scholar] [CrossRef]
- Basher, Syed Abul, and Perry Sadorsky. 2016. Hedging emerging market stock prices with oil, gold, VIX, and bonds: A comparison between DCC, ADCC and GO-GARCH. Energy Economics 54: 235–47. [Google Scholar] [CrossRef] [Green Version]
- Baumöhl, Eduard, and Štefan Lyócsa. 2014. Volatility and dynamic conditional correlations of worldwide emerging and frontier markets. Economic Modelling 38: 175–83. [Google Scholar] [CrossRef]
- Beck, Thorsten, Asli Demirguc-Kunt, and Vojislav Maksimovic. 2008. Financing Patterns around the World: Are Small Firms Different? Journal of Financial Economics 89: 467–87. [Google Scholar] [CrossRef] [Green Version]
- Berger, Allen N., and Gregory F. Udell. 2006. A more complete conceptual framework for SME finance. Journal of Banking & Finance 30: 2945–66. [Google Scholar] [CrossRef]
- Boldanov, Rustam, Stavros Degiannakis, and George Filis. 2016. Time-varying correlation between oil and stock market volatilities: Evidence from oil-importing and oil-exporting countries. International Review of Financial Analysis 48: 209–20. [Google Scholar] [CrossRef] [Green Version]
- Boubaker, Sabri, Bonnie Buchanan, and Duc Khuong Nguyen. 2016. Risk Management in Emerging Markets: Issues, Framework, and Modeling. Bingley: Emerald Group Publishing. [Google Scholar]
- Campbell, Rachel, Kees Koedijk, and Paul Kofman. 2002. Increased Correlation in Bear Markets. Financial Analysts Journal 58: 87–94. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Corbet, Shaen, Yang Hou, Yang Hu, Les Oxley, and Danyang Xu. 2021. Pandemic-related financial market volatility spillovers: Evidence from the Chinese COVID-19 epicentre. International Review of Economics & Finance 71: 55–81. [Google Scholar] [CrossRef]
- Cosh, Andy, Douglas Cumming, and Alan Hughes. 2009. Outside Enterpreneurial Capital. The Economic Journal 119: 1494–533. [Google Scholar] [CrossRef]
- Cowling, Marc, Weixi Liu, and Ning Zhang. 2016. Access to bank finance for UK SMEs in the wake of the recent financial crisis. International Journal of Entrepreneurial Behavior & Research 22: 903–32. [Google Scholar] [CrossRef] [Green Version]
- Cumming, Douglas, Marc Deloof, Sophie Manigart, and Mike Wright. 2019. New directions in entrepreneurial finance. Journal of Banking & Finance 100: 252–60. [Google Scholar] [CrossRef]
- D’Amato, Antonio. 2019. Capital Structure, Debt Maturity, and Financial Crisis: Empirical Evidence from SMEs. Small Business Economics 55: 919–41. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yılmaz. 2014. On the network topology of variance decompositions: Measuring the connectedness of financial firms. Journal of Econometrics 182: 119–34. [Google Scholar] [CrossRef] [Green Version]
- Ederington, Louis H. 1979. The Hedging Performance of the New Futures Markets. The Journal of Finance 34: 157–70. [Google Scholar] [CrossRef]
- Elsayed, Ahmed H., and Larisa Yarovaya. 2019. Financial stress dynamics in the MENA region: Evidence from the Arab Spring. Journal of International Financial Markets, Institutions and Money 62: 20–34. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. Dynamic Conditional Correlation. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate Simultaneous Generalized ARCH. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Enterprise. 2020a. EBRD Could Support Small-Caps Facing New Sponsor Regs. Available online: https://enterprise.press/stories/2020/09/08/ebrd-could-support-small-caps-facing-new-sponsor-regs-21459/ (accessed on 15 June 2021).
- Enterprise. 2020b. Speed Medical to be the First Jump from Nilex to the EGX. Available online: https://enterprise.press/stories/2020/12/03/speed-medical-to-be-the-first-jump-from-nilex-to-the-egx-26032/ (accessed on 15 June 2021).
- Ferrando, Annalisa, and Alessandro Ruggieri. 2018. Financial constraints and productivity: Evidence from euro area companies. International Journal of Finance & Economics 23: 257–82. [Google Scholar] [CrossRef]
- Fleming, Jeff, Chris Kirby, and Barbara Ostdiek. 1998. Information and volatility linkages in the stock, bond, and money markets. Journal of Financial Economics 49: 111–37. [Google Scholar] [CrossRef]
- Gharib, C., S. Mefteh-Wali, and S. B. Jabeur. 2021. The Bubble Contagion Effect of COVID-19 Outbreak: Evidence from Crude Oil and Gold Markets. Finance Research Letters 38: 101703. [Google Scholar] [CrossRef]
- Glosten, Lawrence R, Ravi Jagannathan, and David E Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. J. Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Hatemi-J, Abdulnasser. 2012. Asymmetric causality tests with an application. Empirical Economics 43: 447–56. [Google Scholar] [CrossRef]
- Hemche, Omar, Fredj Jawadi, Samir B. Maliki, and Abdoulkarim Idi Cheffou. 2016. On the study of contagion in the context of the subprime crisis: A dynamic conditional correlation–multivariate GARCH approach. Economic Modelling 52: 292–99. [Google Scholar] [CrossRef]
- Hou, Yang, and Steven Li. 2016. Information transmission between U.S. and China index futures markets: An asymmetric DCC GARCH approach. Economic Modelling 52: 884–97. [Google Scholar] [CrossRef]
- Hwang, Jae-Kwang. 2014. Spillover effects of the 2008 financial crisis in Latin America stock markets. International Advances in Economic Research 20: 311–24. [Google Scholar] [CrossRef]
- Iglesias-Casal, Ana, María Celia López-Penabad, Carmen López-Andión, and José Manuel Maside-Sanfiz. 2020. Diversification and Optimal Hedges for Socially Responsible Investment in Brazil. Economic Modelling 85: 106–18. [Google Scholar] [CrossRef]
- Jaffee, Dwight M., and Thomas Russell. 1976. Imperfect Information, Uncertainty, and Credit Rationing. The Quarterly Journal of Economics 90: 651–66. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Jiang, Yonghong, Yuyuan Fu, and Weihua Ruan. 2019. Risk Spillovers and Portfolio Management between Precious Metal and BRICS Stock Markets. Physica A: Statistical Mechanics and its Applications 534: 120993. [Google Scholar] [CrossRef]
- Jin, Jiayu, Liyan Han, Lei Wu, and Hongchao Zeng. 2020. The hedging effectiveness of global sectors in emerging and developed stock markets. International Review of Economics & Finance 66: 92–117. [Google Scholar] [CrossRef]
- Junttila, Juha, Juho Pesonen, and Juhani Raatikainen. 2018. Commodity market based hedging against stock market risk in times of financial crisis: The case of crude oil and gold. Journal of International Financial Markets, Institutions and Money 56: 255–80. [Google Scholar] [CrossRef]
- Karanasos, Menelaos, Alexandros G. Paraskevopoulos, Faek Menla Ali, Michail Karoglou, and Stavroula Yfanti. 2014. Modelling stock volatilities during financial crises: A time varying coefficient approach. Journal of Empirical Finance 29: 113–28. [Google Scholar] [CrossRef] [Green Version]
- Karmakar, Madhusudan. 2010. Information transmission between small and large stocks in the National Stock Exchange in India: An empirical study. The Quarterly Review of Economics and Finance 50: 110–20. [Google Scholar] [CrossRef]
- Kinateder, Harald, Ross Campbell, and Tonmoy Choudhury. 2021. Safe haven in GFC versus COVID-19: 100 turbulent days in the financial markets. Finance Research Letters 43: 101951. [Google Scholar] [CrossRef]
- Koulakiotis, Athanasios, Vassilios Babalos, and Nicholas Papasyriopoulos. 2016. Financial crisis, liquidity and dynamic linkages between large and small stocks: Evidence from the Athens Stock Exchange. Journal of International Financial Markets, Institutions and Money 40: 46–62. [Google Scholar] [CrossRef]
- Kroner, Kenneth F., and Victor K. Ng. 1998. Modeling Asymmetric Comovements of Asset Returns. Review of Financial Studies 11: 817–44. [Google Scholar] [CrossRef]
- Kroner, Kenneth F., and Jahangir Sultan. 1993. Time-Varying Distributions and Dynamic Hedging with Foreign Currency Futures. The Journal of Financial and Quantitative Analysis 28: 535–51. [Google Scholar] [CrossRef]
- Kyrkilis, Dimitrios, Athanasios Koulakiotis, Vassilios Babalos, and Maria Kyriakou. 2018. Feedback Trading and Short-Term Return Dynamics in Athens Stock Exchange. International Journal of Managerial Finance 14: 574–90. [Google Scholar] [CrossRef]
- Li, Hong. 2007. International linkages of the Chinese stock exchanges: A multivariate GARCH analysis. Applied Financial Economics 17: 285–97. [Google Scholar] [CrossRef]
- Ling, Shiqing, and Michael McAleer. 2003. Asymptotic Theory for a Vector ARMA-GARCH Model. Econometric Theory 19: 280–310. [Google Scholar] [CrossRef] [Green Version]
- Liu, Xueyong, Haizhong An, Shupei Huang, and Shaobo Wen. 2017. The evolution of spillover effects between oil and stock markets across multi-scales using a wavelet-based GARCH–BEKK model. Physica A: Statistical Mechanics and its Applications 465: 374–83. [Google Scholar] [CrossRef] [Green Version]
- Lo, Andrew W., and A. Craig MacKinlay. 1990. When Are Contrarian Profits Due to Stock Market Overreaction? Review of Financial Studies 3: 175–205. [Google Scholar] [CrossRef]
- Majumder, Sayantan Bandhu, and Ranjanendra Narayan Nag. 2018. Shock and volatility spillovers among equity sectors of the national stock exchange in India. Global Business Review 19: 227–40. [Google Scholar] [CrossRef]
- Markwat, Thijs, Erik Kole, and Dick van Dijk. 2009. Contagion as a domino effect in global stock markets. Journal of Banking & Finance 33: 1996–2012. [Google Scholar] [CrossRef] [Green Version]
- McAleer, Michael, Suhejla Hoti, and Felix Chan. 2009. Structure and Asymptotic Theory for Multivariate Asymmetric Conditional Volatility. Econometric Reviews 28: 422–40. [Google Scholar] [CrossRef]
- McIver, Ron P., and Sang Hoon Kang. 2020. Financial crises and the dynamics of the spillovers between the U.S. and BRICS stock markets. Research in International Business and Finance 54: 101276. [Google Scholar] [CrossRef]
- Nassr, Iota Kaousar, and Gert Wehinger. 2016. Opportunities and limitations of public equity markets for SMEs. OECD Journal: Financial Market Trends 2015: 49–84. [Google Scholar]
- Nguyen, Duc Khuong, Ricardo M. Sousa, and Gazi Salah Uddin. 2015. Testing for asymmetric causality between U.S. equity returns and commodity futures returns. Finance Research Letters 12: 38–47. [Google Scholar] [CrossRef]
- Nguyen, Trang, Taha Chaiechi, Lynne Eagle, and David Low. 2020. Dynamic transmissions between main stock markets and SME stock markets: Evidence from tropical economies. The Quarterly Review of Economics and Finance 75: 308–24. [Google Scholar] [CrossRef]
- Nikkinen, Jussi, Vanja Piljak, and Timo Rothovius. 2020. Impact of the 2008–2009 financial crisis on the external and internal linkages of European frontier stock markets. Global Finance Journal 46: 100481. [Google Scholar] [CrossRef]
- Papadamou, Stephanos, Athanasios P. Fassas, Dimitris Kenourgios, and Dimitrios Dimitriou. 2021. Flight-to-quality between global stock and bond markets in the COVID era. Finance Research Letters 38: 101852. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a Unit Root in Time Series Regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Rose, Andrew K., and Mark M. Spiegel. 2010. Cross-country causes and consequences of the 2008 crisis: International linkages and American exposure. Pacific Economic Review 15: 340–63. [Google Scholar] [CrossRef] [Green Version]
- Salisu, Afees A., and Tirimisiyu F. Oloko. 2015. Modeling oil price–US stock nexus: A VARMA–BEKK–AGARCH approach. Energy Economics 50: 1–12. [Google Scholar] [CrossRef]
- Salisu, Afees, Xuan Vinh Vo, and Adedoyin Isola Lawal. 2021. Hedging Oil Price Risk with Gold during COVID-19 Pandemic. Resources Policy 70: 101897. [Google Scholar] [CrossRef]
- Samarakoon, Lalith P. 2011. Stock market interdependence, contagion, and the U.S. financial crisis: The case of emerging and frontier markets. Journal of International Financial Markets, Institutions and Money 21: 724–42. [Google Scholar] [CrossRef]
- Samitas, Aristeidis, Dimitris Kenourgios, and Nick Konstantopoulos. 2006. The small business capital market behavior in Athens Stock Exchange. Small Business Economics 27: 409–17. [Google Scholar] [CrossRef]
- Singhal, Shelly, and Sajal Ghosh. 2016. Returns and volatility linkages between international crude oil price, metal and other stock indices in India: Evidence from VAR-DCC-GARCH models. Resources Policy 50: 276–88. [Google Scholar] [CrossRef]
- Stiglitz, Joseph E., and Andrew Weiss. 1981. Credit Rationing in Markets with Imperfect Information. The American Economic Review 71: 393–410. [Google Scholar]
- The World Federation of Exchanges. 2015. WFE Report on SME Exchanges. Available online: https://www.world-exchanges.org/storage/app/media/research/Studies_Reports/WFE%20Report%20on%20SME%20Exchanges.pdf (accessed on 27 February 2021).
- The World Federation of Exchanges. 2018. An Overview of WFE SME Markets. Available online: https://www.world-exchanges.org/news/articles/world-federation-exchanges-publishes-report-global-sme-markets (accessed on 27 February 2021).
- Tiwari, Aviral Kumar, and Claudiu Tiberiu Albulescu. 2016. Oil price and exchange rate in India: Fresh evidence from continuous wavelet approach and asymmetric, multi-horizon Granger-causality tests. Applied Energy 179: 272–83. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Ibrahim Dolapo Raheem, and Sang Hoon Kang. 2019. Time-varying dynamic conditional correlation between stock and cryptocurrency markets using the copula-ADCC-EGARCH model. Physica A: Statistical Mechanics and its Applications 535: 122295. [Google Scholar] [CrossRef]
- Umar, Zaghum, Youssef Manel, Yasir Riaz, and Mariya Gubareva. 2021. Return and volatility transmission between emerging markets and US debt throughout the pandemic crisis. Pacific-Basin Finance Journal 67: 101563. [Google Scholar] [CrossRef]
- Vardar, Gülin, Yener Coşkun, and Tezer Yelkenci. 2018. Shock transmission and volatility spillover in stock and commodity markets: Evidence from advanced and emerging markets. Eurasian Economic Review 8: 231–88. [Google Scholar] [CrossRef]
- Vismara, Silvio, Stefano Paleari, and Jay R. Ritter. 2012. Europe’s Second Markets for Small Companies. European Financial Management 18: 352–88. [Google Scholar] [CrossRef]
- Vrieze, Scott I. 2012. Model Selection and Psychological Theory: A Discussion of the Differences between the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Psychol Methods 17: 228–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Gang Jin, Chi Xie, Zhi Qiang Jiang, and H. Eugene Stanley. 2016. Extreme Risk Spillover Effects in World Gold Markets and The Global Financial Crisis. International Review of Economics & Finance 46: 55–77. [Google Scholar] [CrossRef]
- Wang, Gang Jin, Chi Xie, Min Lin, and H. Eugene Stanley. 2017. Stock Market Contagion during the Global Financial Crisis: A Multiscale Approach. Finance Research Letters 22: 163–68. [Google Scholar] [CrossRef]
- Wen, Xiaoqian, Yanfeng Guo, Yu Wei, and Dengshi Huang. 2014. How do the stock prices of new energy and fossil fuel companies correlate? Evidence from China. Energy Economics 41: 63–75. [Google Scholar] [CrossRef]
- Wen, Danyan, Yudong Wang, Chaoqun Ma, and Yaojie Zhang. 2020. Information transmission between gold and financial assets: Mean, volatility, or risk spillovers? Resources Policy 69: 101871. [Google Scholar] [CrossRef]
- WHO. 2020. Novel Coronavirus (2019-nCOV) Situation Report-1. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200121-sitrep-1-2019-ncov.pdf?sfvrsn=20a99c10_4 (accessed on 10 March 2021).
- Wu, Fei, Dayong Zhang, and Zhiwei Zhang. 2019. Connectedness and risk spillovers in China’s stock market: A sectoral analysis. Economic Systems 43: 100718. [Google Scholar] [CrossRef]
- Xu, Haifeng, and Shigeyuki Hamori. 2012. Dynamic Linkages of Stock Prices between the BRICs and the United States: Effects of the 2008–09 Financial Crisis. Journal of Asian Economics 23: 344–52. [Google Scholar] [CrossRef]
- Xu, Weiju, Feng Ma, Wang Chen, and Bing Zhang. 2019. Asymmetric volatility spillovers between oil and stock markets: Evidence from China and the United States. Energy Economics 80: 310–20. [Google Scholar] [CrossRef]
- Yarovaya, Larisa, and Marco Chi Keung Lau. 2016. Stock market comovements around the Global Financial Crisis: Evidence from the UK, BRICS and MIST markets. Research in International Business and Finance 37: 605–19. [Google Scholar] [CrossRef]
- Yu, Lean, Rui Zha, Dimitrios Stafylas, Kaijian He, and Jia Liu. 2020. Dependences and volatility spillovers between the oil and stock markets: New evidence from the copula and VAR-BEKK-GARCH models. International Review of Financial Analysis 68: 101280. [Google Scholar] [CrossRef]
- Zhang, Wenting, and Shigeyuki Hamori. 2021. Crude oil market and stock markets during the COVID-19 pandemic: Evidence from the US, Japan, and Germany. International Review of Financial Analysis 74: 101702. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).