Numerical Modeling of the Walls Perforation Influence on the Accuracy of Wind Tunnel Experiments Using Two-Dimensional Computational Fluid Dynamics Model

Abstract

The presented work is dedicated to the development of the mathematical model of a closed-type wind tunnel (WT) in a two-dimensional (2D) formulation based on the computational fluid dynamics (CFD) Unsteady Reynolds Averaged Navier Strokes Equations (URANS) method. The influence of the WT walls perforation percentage on the aerodynamic characteristics of the SC1095 (SC is an abbreviation for “supercritical”) airfoil in a wide range of pitch angles from 0 to 28 degrees has been studied. The obtained data are compared with the aerodynamic characteristics of the airfoil in free flow conditions. It is shown that the use of perforation makes it possible to significantly reduce the influence of the wind tunnel walls on the obtained aerodynamic characteristics of the airfoil bringing them closer to the airfoil characteristics under free flow conditions. The developed low resource-intensive 2D CFD WT model can be used to determine the optimal ratio between the walls perforation percentage, the WT test section dimensions, and the experimental model dimensions for various test modes. Support of WT experiments with the help of preliminary parametric studies based on the 2D CFD model could significantly reduce material costs and increase the accuracy of the obtained results.

1. Introduction

When conducting experiments in closed-type WT, some phenomena can be often noticed that affect the aerodynamic characteristics of the experimental models. One of them is the “blockage” effect, which can significantly complicate the study of the aerodynamic characteristics of airfoils performed on the basis of WT tests of the wing section model. The occurrence of blockage effect is possible at trans and supersonic flow, when the shock waves overlap the working section of WT. As a result, a further increase in flow speed becomes impossible, even with an increase in pressure in front of a model. Also, the blockage effect is observed when the working section of WT is significantly overlapped by the studied wing section model. This is due to the fact that at large pitch angles (α), the area of increased pressure overlaps the working section of the WT, distorting the flow. To avoid the blockage effect, perforation of the walls of the WT working section is usually used, reaching a perforation percentage value of up to 20%. At the same time, an actual problem is the study of the influence of the WT walls perforation on the accuracy of obtained results, depending on the conditions and tasks of a particular experiment.

To study the effect of wall perforation on the flow in the WTs working section and on the aerodynamic characteristics of the model, both an experimental approach [1] and mathematical modeling can be used [2]. Nowadays, CFD methods based on the solution of the Navier-Stokes equations by the finite volume method have become the most widespread.

Currently, CFD methods allow supplementing experimental studies of aerodynamics with numerical modeling using mathematical CFD models of WTs [2]. CFD methods are successfully applied for modeling the flow in subsonic [3,4] and supersonic WTs [5,6]. This direction is widely used in the development of aircraft [7,8], in the industrial aerodynamics [9], and in the design of the WTs [10,11]. With the help of CFD, WTs equipment devices are designed with minimal influence on the studied model’s aerodynamic characteristics [12]. The influence of WT walls on the characteristics of propellers has been determined [13,14]. The influence of slot perforation on the aerodynamic characteristics of a cars model have been studied [15,16]. CFD methods based on the URANS approach with various turbulence models have been used the most widely in WTs modeling [17,18].

The use of CFD methods allows for the determination of special corrections to clarify the WTs aerodynamic experiment. CFD methods make it possible to implement parametric studies to find the optimal configuration of the experimental rig. CFD methods also allow evaluating various physical effects that cannot be studied on existing experimental stands [19].

Kirillov et al. [20] used a three-dimensional (3D) CFD model of a WT with a special experimental rig that had been previously been developed to study the unsteady aerodynamic characteristics of a wing section with a helicopter blade airfoil. This model has shown its effectiveness, but 3D formulation requires significant computing resources (the model consisted of approximately 23 billion cells), as well as a lot of time to create a computational mesh in the event of a change in the experimental rig configuration. At the same time, a number of tasks (for example, the study of WT walls perforation effect on the accuracy of the experiment) in this scenario can be effectively solved using a simplified 2D CFD WT model. Such a model makes it possible to conduct massive parametric studies with significantly less computational and time costs. In the future, the results of such studies can be taken into account in a full 3D CFD model for further research and can be implemented in a real experiment.

In the presented work, the steady aerodynamic characteristics of the SC1095 (SC is an abbreviation for “supercritical”) airfoil are studied in a wide range of pitch angles, using the developed 2D CFD WT model based on the URANS method. Three variants of WT walls perforation have been considered: 0% (solid walls without perforation), 7.5% and 15%.

2. Materials and Methods

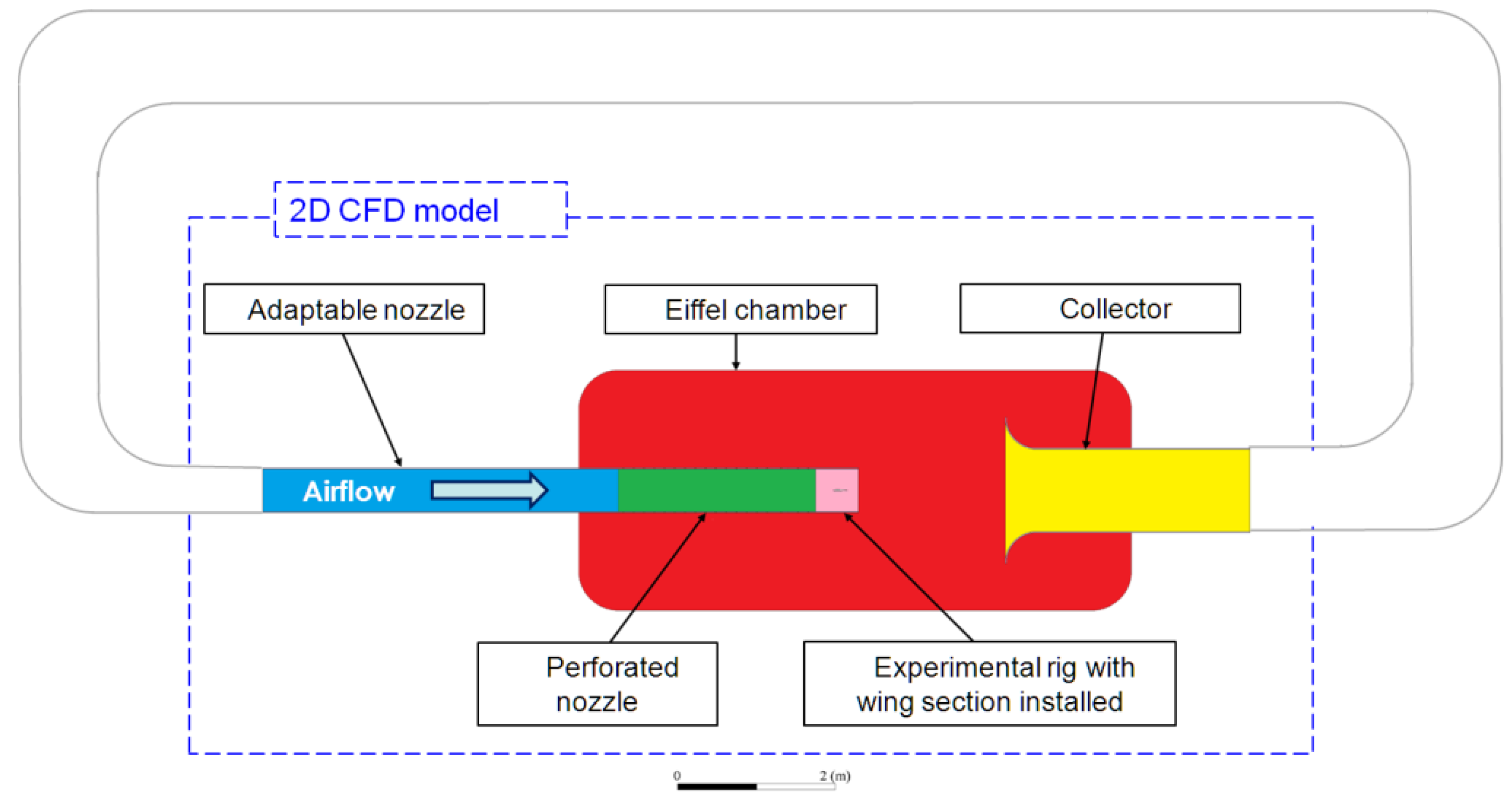
The configuration of the 3D CFD WT model is taken as the basis for the created 2D CFD model [20]. The principal scheme of the WT is shown in Figure 1, and includes an adaptable nozzle (at M < 0.9, the upper and lower walls are straight), an Eiffel chamber, an output collector, a working section with a perforation, and an experimental rig with wing section model. Three variants of the WT walls perforation are considered. In the first, the working section is represented by solid walls (0% perforation). In the second, the walls are 7.5% perforated, the holes have a diameter of 10 mm and are arranged in 110 mm increments. In the third configuration, the walls of the working section have a 15% perforation made of 10 mm holes arranged in 55 mm increments. The experimental rig is made with solid walls. Inside the rig there is an aerodynamic airfoil SC1095 with a chord of 180 mm.

The ANSYS ICEM CFD (version 14.5, ANSYS, Inc., Canonsburg, PA, USA) software package has been used for making the computational mesh. The overall computational mesh (Figure 2) has been divided into four areas. Area 1 is the main area with an adaptable nozzle, an Eiffel chamber and an output collector (Figure 2a). Area 2 is the area of the working section with perforation (Figure 2a,d). Area 3 is the area of the experimental rig. Area 4 is the area of the model (aerodynamic airfoil) (Figure 2a,e). Studies of the effect of perforation have been carried out by replacing Area 2 with variants with different wall perforations.

A feature of the considered WT is the boundary layer, reaching 70–100 mm. For correct modeling of the boundary layer, a long adjustable nozzle has been created in the 2D model.

A hybrid mesh was used for constructing the computational mesh, combining structured (Area 1 in Figure 2a,b) and unstructured mesh (Areas 2, 3 and 4 in Figure 2a,c). This approach was chosen because creating an array of perforation holes makes it extremely time-consuming to also make an optimized structured mesh with minimal computational time costs. For this reason, the WT working section with perforation is made in the form of unstructured mesh. The unstructured mesh of the WT working section (Area 2) was interfaced with the unstructured mesh of the experimental rig (Area 3) to avoid distortion when switching between meshes with different structures. In order to consider the WT walls boundary layer, while not increasing the number of cells, prismatic cells have been used. This approach to creating a computational grid was verified by the authors in [21]. In all areas, the same height was selected for the prismatic cells to reduce the conversion time during the transition between areas (Figure 2d,e). The prismatic layer on the airfoil is of particular importance as it affects the accuracy of drag force calculating. On the airfoil, the prismatic layer consisted of 23 cells with an initial cell height of 0.005 mm and a total height of 1.3 mm (Figure 2e). To improve the mesh quality, the geometry of the calculated area has been optimized in the zones of sharp and blunt angles (Figure 2e). The unstructured grid cells range in size from 0.25 mm (close to the airfoil) to 2 mm at the maximum distance in Area 4. Such a breakdown of the computational grid was verified by the authors in [22].

Thus, the computational mesh of the WT has been created with a relatively small total number of cells (about 900,000) with rather high quality. By using a prismatic layer on the airfoil surface, the Y+ coefficient was confirmed to be less than 1, and the minimum quality of the mesh according to the Quality criterion was 0.5.

Numerical simulation has been carried out in the ANSYS Fluent software (version 2021 R1, ANSYS, Inc., Canonsburg, PA, USA) package using the URANS method and the k-ω SST turbulence model [23]. The fluid flow is compressible with the calculation of viscosity according to the Sutherland law. The initial turbulence parameters have been selected based on the conditions of low intensity of the turbulent flow. The value of the relative turbulent viscosity has been assumed to be μ_t/μ = 1, and the turbulence intensity I = 1%. The simulation was performed with the second order of accuracy according to the Coupled scheme.

Verification of the CFD method used to calculate the aerodynamic characteristics of the SC1095 airfoil has been performed in [20] by comparing with experimental data. These results are shown in Figure 3 [20]. The obtained dependences of the aerodynamic characteristics are: the dependence of the drag force coefficient on the Mach number (for zero lift C_L = 0) (Figure 3a); the dependences of the lift C_L (Figure 3b) and drag C_D (Figure 3c) force coefficients on the pitch angles; the dependence of the drag force coefficient on the Mach number (for zero lift C_L = 0). Here there is a satisfactory coincidence of the calculation results with the experimental data [24].

An additional study was conducted to analyze the mesh convergence. The simulation of the airfoil in a free flow with a high resolution mesh was performed. The high resolution mesh had double number of cells compared to the basic mesh. The maximum cell size on the airfoil surface was halved (from 2 to 1 mm), the number of prismatic layers was increased to 40, and the height of the first cell on the airfoil surface was reduced to 0.001 mm. The data obtained is shown in

Table 1. Obtained mesh convergence analysis data.

Pitch Angle, α	8°	13°	18°
CL, basic mesh	0.9442	1.3041	0.7879
CL, high resolution mesh	0.9471	1.3116	0.7933
CD, basic mesh	0.0137	0.0312	0.2084
CD, high resolution mesh	0.0138	0.0310	0.2069

.

The analysis of the obtained data showed that the difference in the results obtained between the basic mesh and the high resolution mesh does not exceed 0.75%. This indicates sufficient resolution of the basic mesh.

3. Results and Discussion

To study the effect of WT walls interference on the SC1095 airfoil aerodynamic characteristics, four calculation series were performed. One series of calculations was performed for free flow conditions, and the other three series of calculations were for the 2D CFD WT model with different wall perforation percentage values: 0% (without perforation), 7.5% and 15%. Calculations were performed for the pitch angles α = 0°, 3°, 5°, 8°, 9°, 10°, 13°, 14°, 15°, 16°, 17°, 18°, 20°, 24°, 28°. The flow rate was set at the beginning of the adaptable WT nozzle at M = 0.4. All calculations were performed at a temperature of 15 °C and an air density of 1.225 kg/m³. In addition to calculating the aerodynamic loads on the airfoil model, CFD methods provide extensive opportunities for visualizing the flow inside the WT. Visualization of the flow in the WT and especially around of the airfoil model provides additional information important for the interpretation of experimental studies’ results.

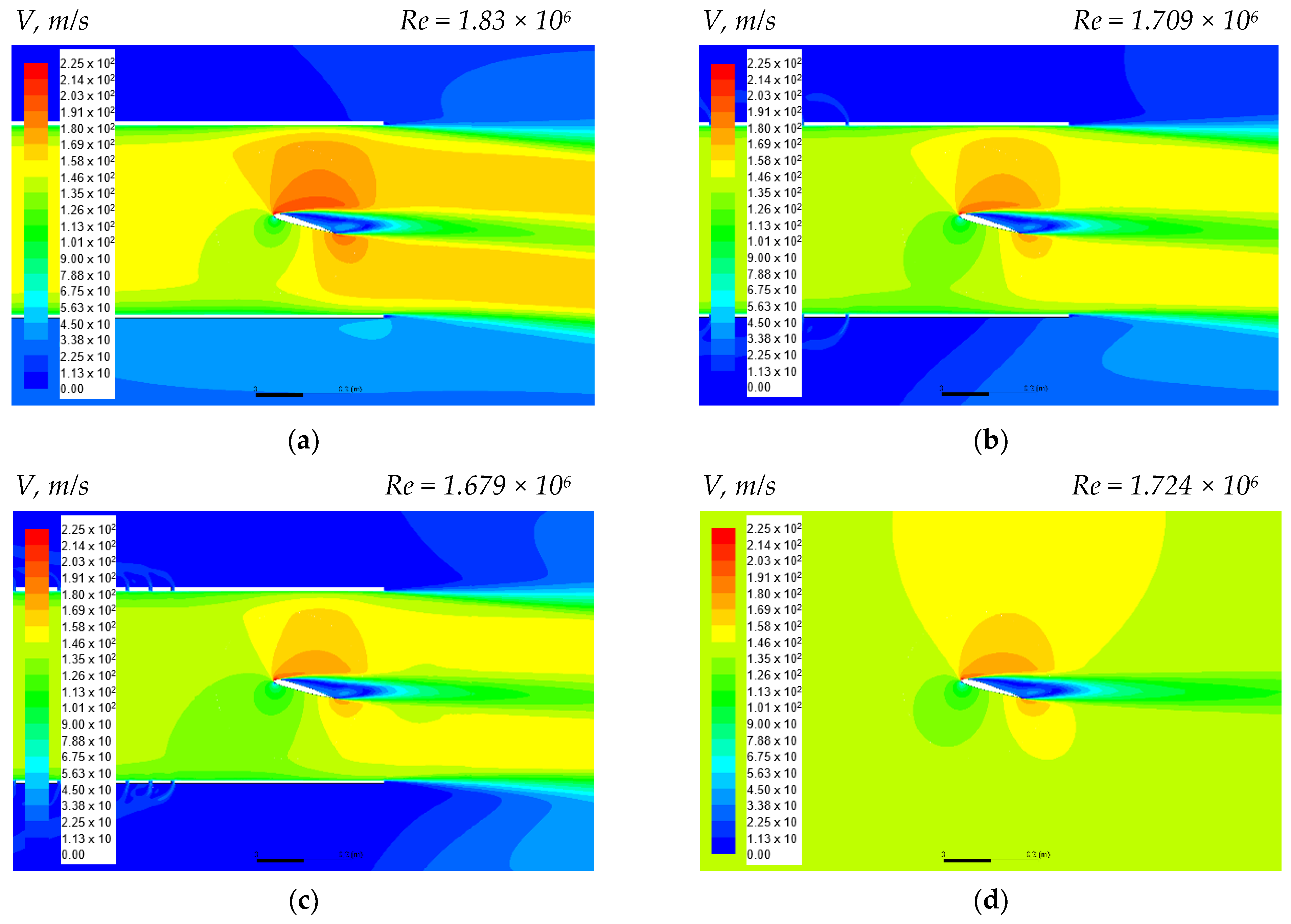
Figure 4 shows the visualization of velocity fields in the working section of the WT and in close to the airfoil for the three perforation percentage values: 0%, 7.5%, and 15%. The presented results are for the pitch angle α = 16°, when the WT blockage effect was at its greatest extent. In addition, Figure 4d shows a visualization of the velocity field around the airfoil for the case of free flow. It can be seen that for 0% perforation (solid walls) (Figure 4a), there is a significant difference in the obtained velocity field than in the case of free flow (Figure 4d). Figure 4b,c show that increasing the percentage of perforations brings the velocity field around the airfoil closer to the free flow conditions. Thus, in the working section of the WT, the flow conditions around the airfoil became close to the real full-scale ones, therefore, minimizing the influence of WT on the experimental results.

Figure 5 shows the visualization of static pressure fields for the three variants of perforation (0%, 7.5%, 15%; Figure 5a–c) and for free flow conditions (Figure 5d) with the pitch angle α = 16° (Figure 5a–c). It can be seen here that the use of WT walls perforation makes it possible to obtain a pressure distribution in the vicinity of the airfoil close to the free flow conditions. It can be seen that a perforation of 7.5% (Figure 5b) is insufficient, and it is necessary to use a perforation of 15% (Figure 5c).

Figure 6 shows the dependences of the pressure coefficient (C_p for the angle of the airfoil (α = 16°) for the three perforation options and for free flow around the airfoil.

It can be seen from the graphs presented in Figure 6 that, despite the close Reynolds numbers (Re), the perforation dependences of 7.5% and 15% differ from the profile in the free flow. These dependencies have been moved up “in parallel”. This is probably due to the influence of the upper and lower solid walls of the experimental stand. This issue requires additional research.

Figure 7 shows the aerodynamic forces’ coefficients obtained using the 2D CFD WT model with various perforation percentage values and for the free flow conditions. The diagrams presented in Figure 6 demonstrate the difference between aerodynamic characteristics of the airfoil obtained for the free flow and for WT with solid walls (perforation 0%). These differences are related to the influence of WT walls, which can be reduced by the use of WT walls perforation.

The dependences of the aerodynamic forces coefficients C_L = f(α) and C_D = f(α) presented in Figure 6 can be divided into three parts: the zone of attached flow and initial stall development with small flow separation area (α = 0–13°); the zone of deep stall development with large flow separation area (α = 14–16°) and the zone of fully developed stall (α = 17–28°). For the first zone (α = 0–13°) the obtained airfoil’s aerodynamic characteristics slightly differ from the characteristics of free flow. That is, they practically do not depend on the WT walls perforation. The deviation of the obtained characteristics does not exceed 2–3%. This is due to the fact that at small pitch angles that match the attached flow regime, the effect of WT blockage does not appear. The second zone (α = 14–16°) is characterized by the separation of the flow over most of the airfoil upper surface. In this zone, the aerodynamic characteristics of the airfoil obtained for WT with solid walls (0% perforation) have significant differences from the case of free flow, reaching values up to 25%. The use of 7.5% perforation reduces the deviation of aerodynamic characteristics, but even in this case the deviations still reach 16%. An increase in the perforation to 15% practically does not change this picture: the differences in the airfoil characteristics from the characteristics in the free flow remain at 16%. This confirms the assumption that solid walls of the experimental stand have a significant influence on these angles of attack. For the third zone (α = 17–28°), the smallest differences in the airfoil characteristics in the WT from the airfoil characteristics in the free flow are achieved when the WT walls are perforated for 15%. In this case, the aerodynamic coefficients C_L and C_D differ by no more than 1.5%. At the same time, in the case of the WT configuration with solid walls (0% perforation), there are differences in the characteristics obtained for free flow in the range of 8–10%. Starting from the pitch angle α = 20° and up to α = 28°, there is an increase in the deviations of the airfoil’s aerodynamic characteristics for both WT with a 7.5% perforation and with solid walls (0% perforation). Here, the differences in the aerodynamic characteristics for the 0% perforation reach 37%. The deviation for the 7.5% perforation does not exceed 12.5%, and for the 15% perforation does not exceed 4% of the free flow case.

4. Conclusions

The developed 2D CFD model of WT has low requirements for computing resources and does not require specialized supercomputer clusters. The 2D CFD model allows for the determination of the aerodynamic characteristics of airfoils in a wide range of operating modes, taking into account the influence of the working section of the WT. The block structure of the developed 2D CFD model allows for changes to the configuration of the WT working section and the models under study, providing the possibility of conducting parametric studies with minimal time costs.

The studies of the aerodynamic characteristics of the SC1095 profile conducted using the developed 2D CFD WT model for three variants of WT walls perforation (0% (solid walls), 7.5% and 15%) generated the following conclusions. In the area of attached flow regimes (pitch angles in the range of α = 0–13°), the aerodynamic characteristics of the airfoil obtained using the 2D CFD WT model coincide well with the airfoil aerodynamic characteristics in free flow. Various variants of WT walls perforation percentage had limited effect on the obtained results, with the differences in the aerodynamic coefficients never exceeding 2–4%. The use of 7.5% perforation in the area of the stall development regime (pitch angles in the range of α = 14–16°) slightly improves the accuracy of obtained aerodynamic characteristics. Meanwhile, a further increase in the perforation to 15% does not improve the accuracy of calculations. In this area, additional studies of the impact of the experimental stand are required, possibly using other CFD approaches. In the area of fully stalled regimes (pitch angles in the range of α = 17–28°), it is recommended to use WT walls perforation. The best match with the case of free flow has been obtained with a perforation percentage of 15%. In this case errors do not exceed 4%.

Thus, the developed 2D CFD model makes it possible to provide parametric studies with minimal computational and time resource costs. The model may help to determine the optimal ratios between walls perforation percentage values, WT cross-section size and the dimensions of the model for various test modes. The results obtained in the course of such studies could be used in the future when creating a 3D CFD WT model and conducting further research with its implementation in a real experiment.