Research on Mechanical Properties of V-Type Folded Core Sandwich Structures
Abstract
:1. Introduction
2. Research Methodology
3. Analysis of Mechanical Properties of VFC
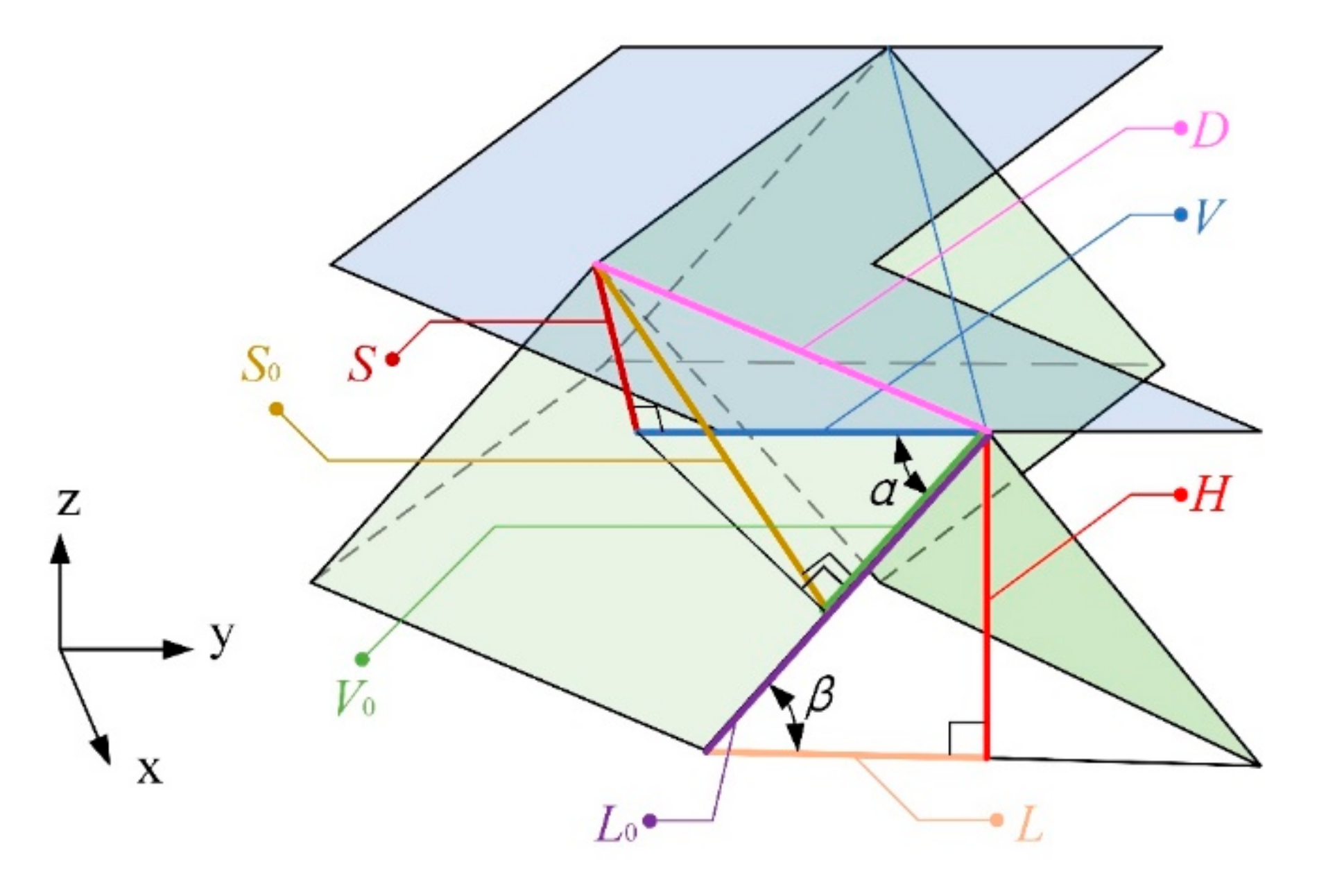
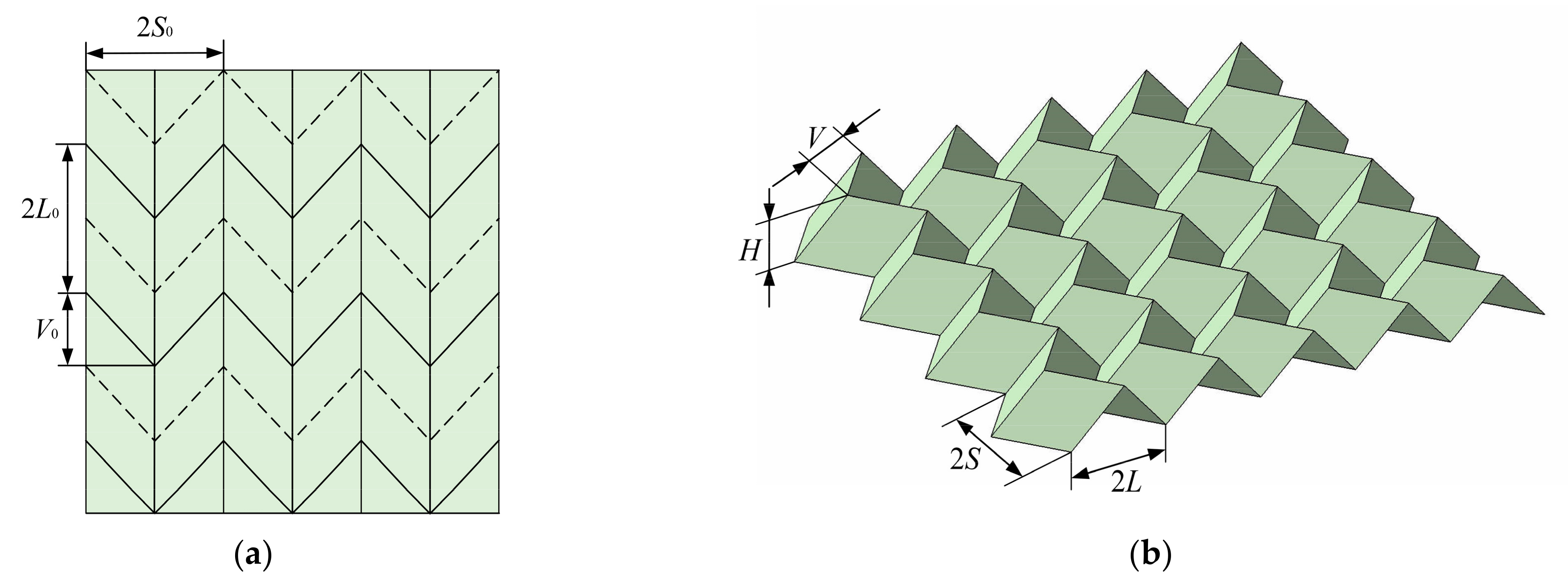
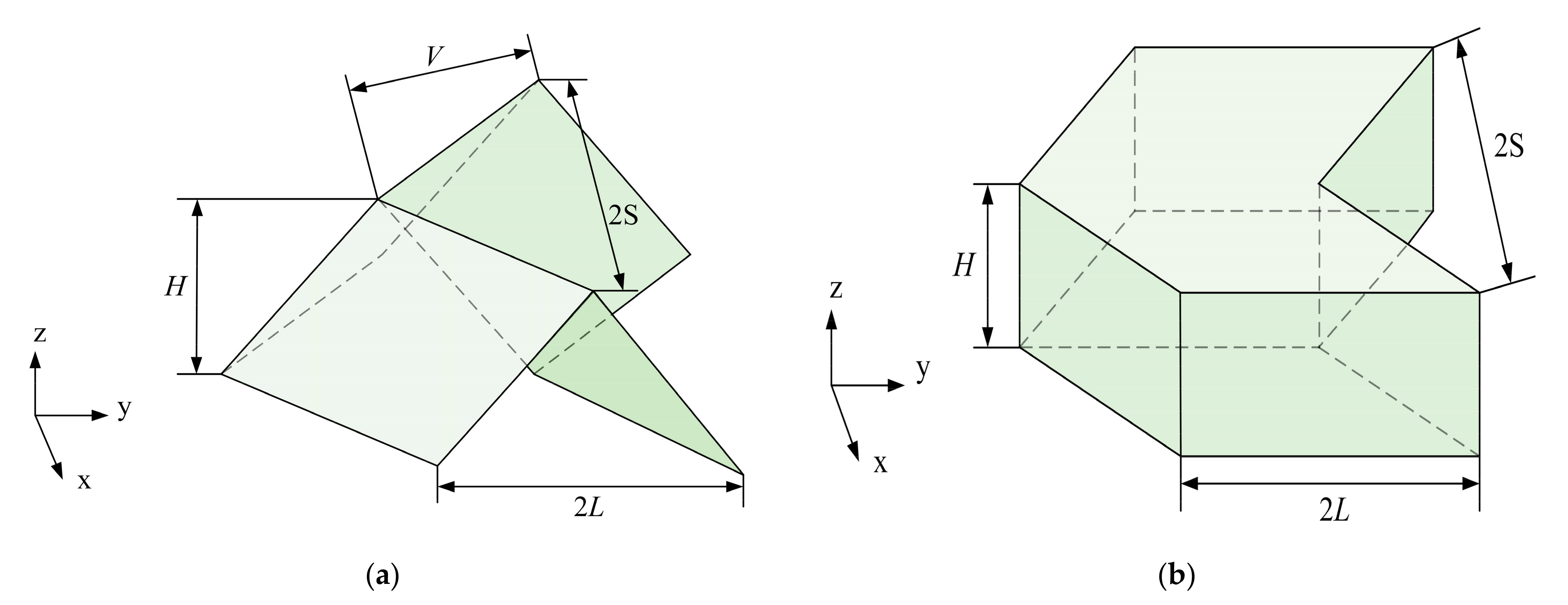
3.1. Geometric Properties of VFC
3.2. Equivalent Density ρ
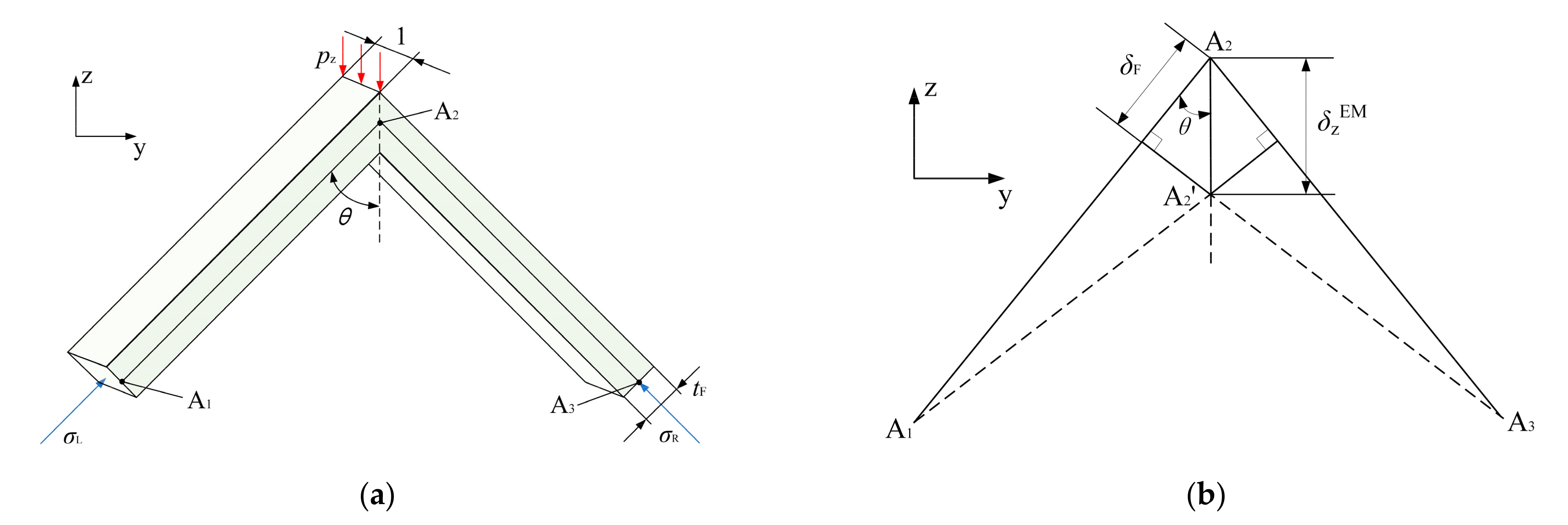
3.3. Equivalent Elastic Modulus in Direction z Ez
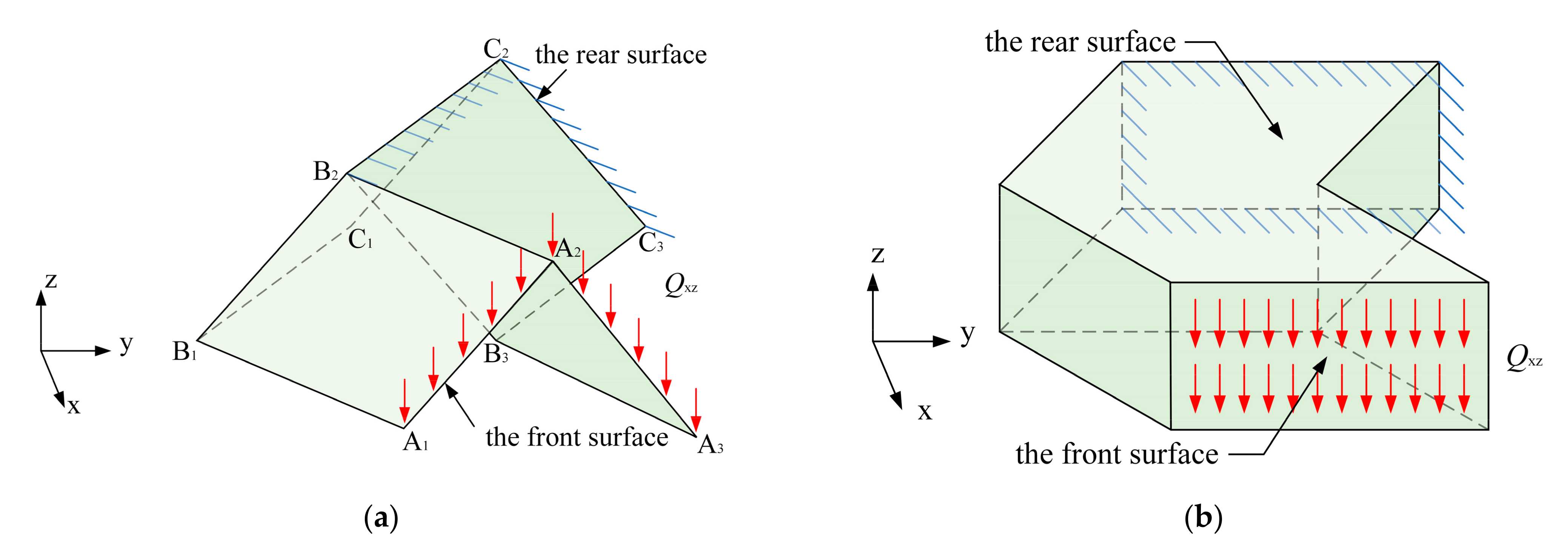
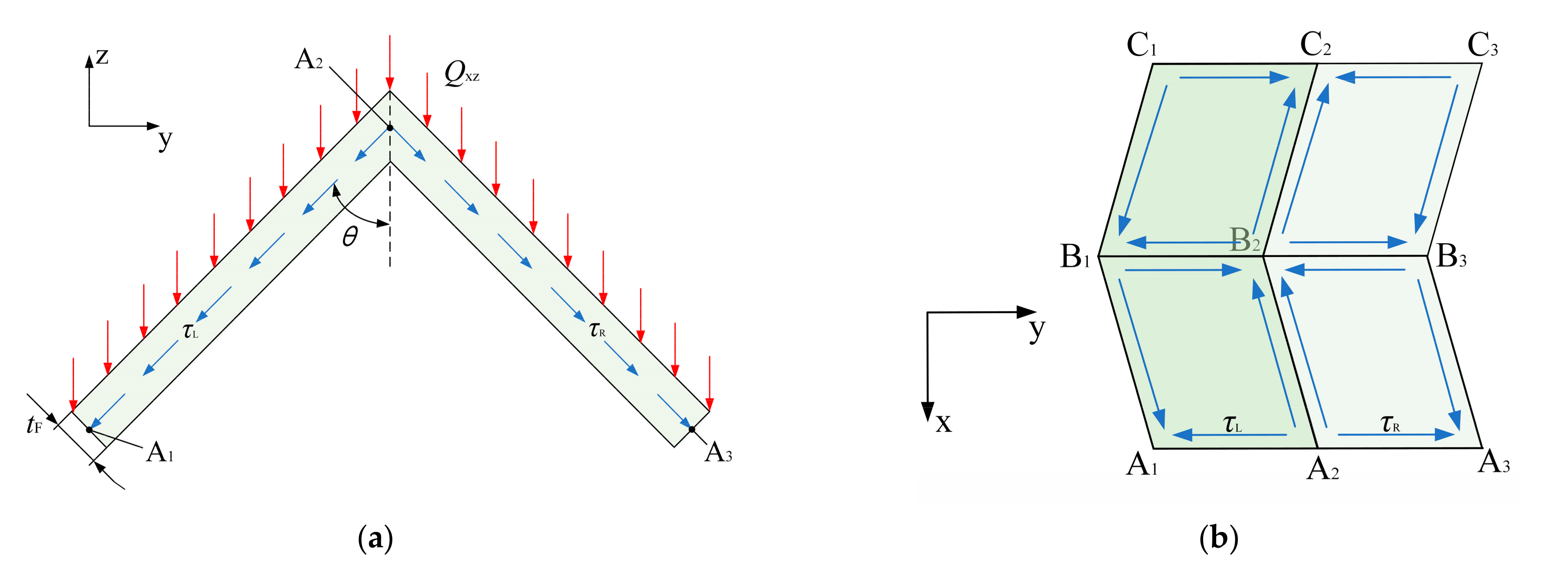
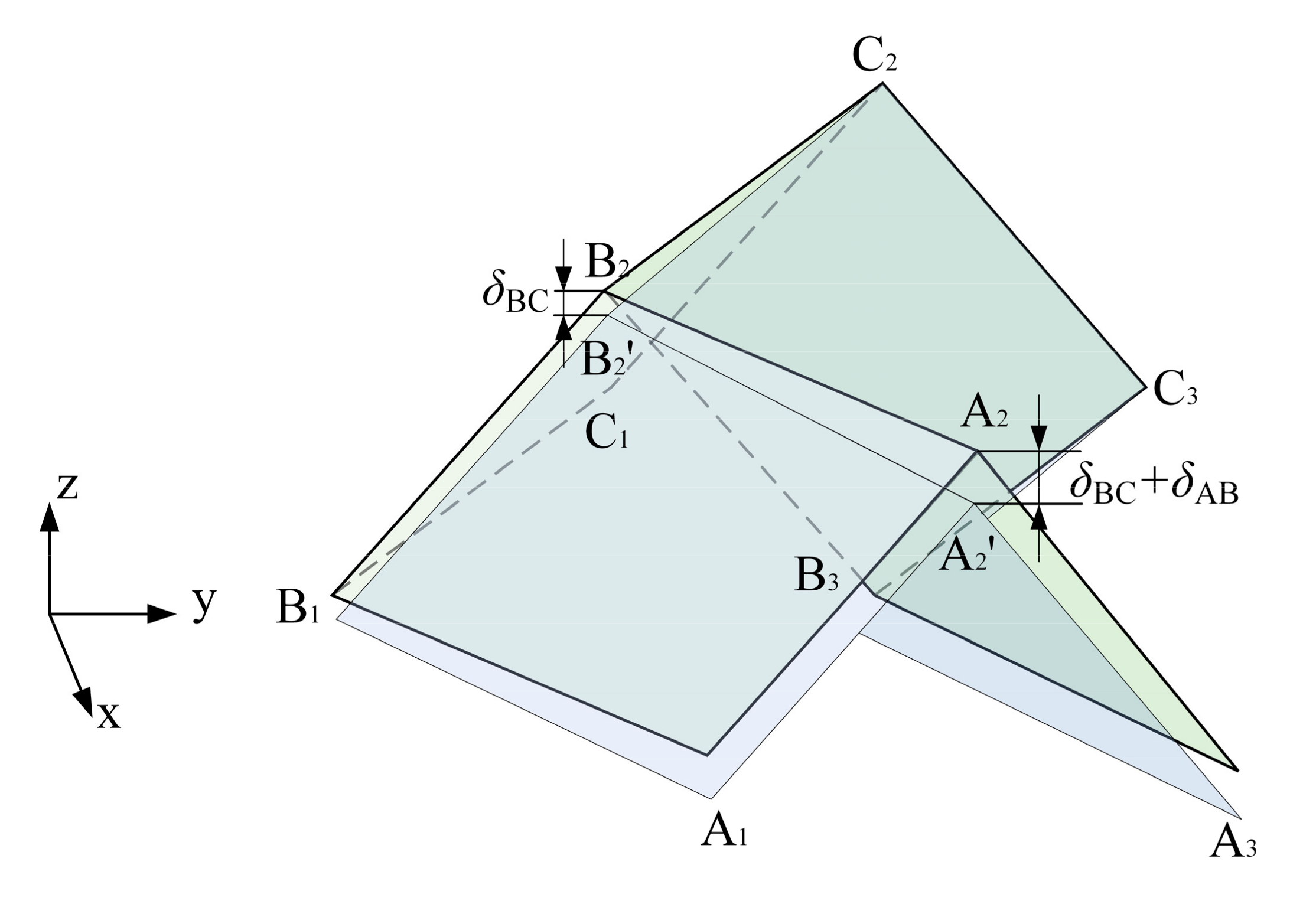
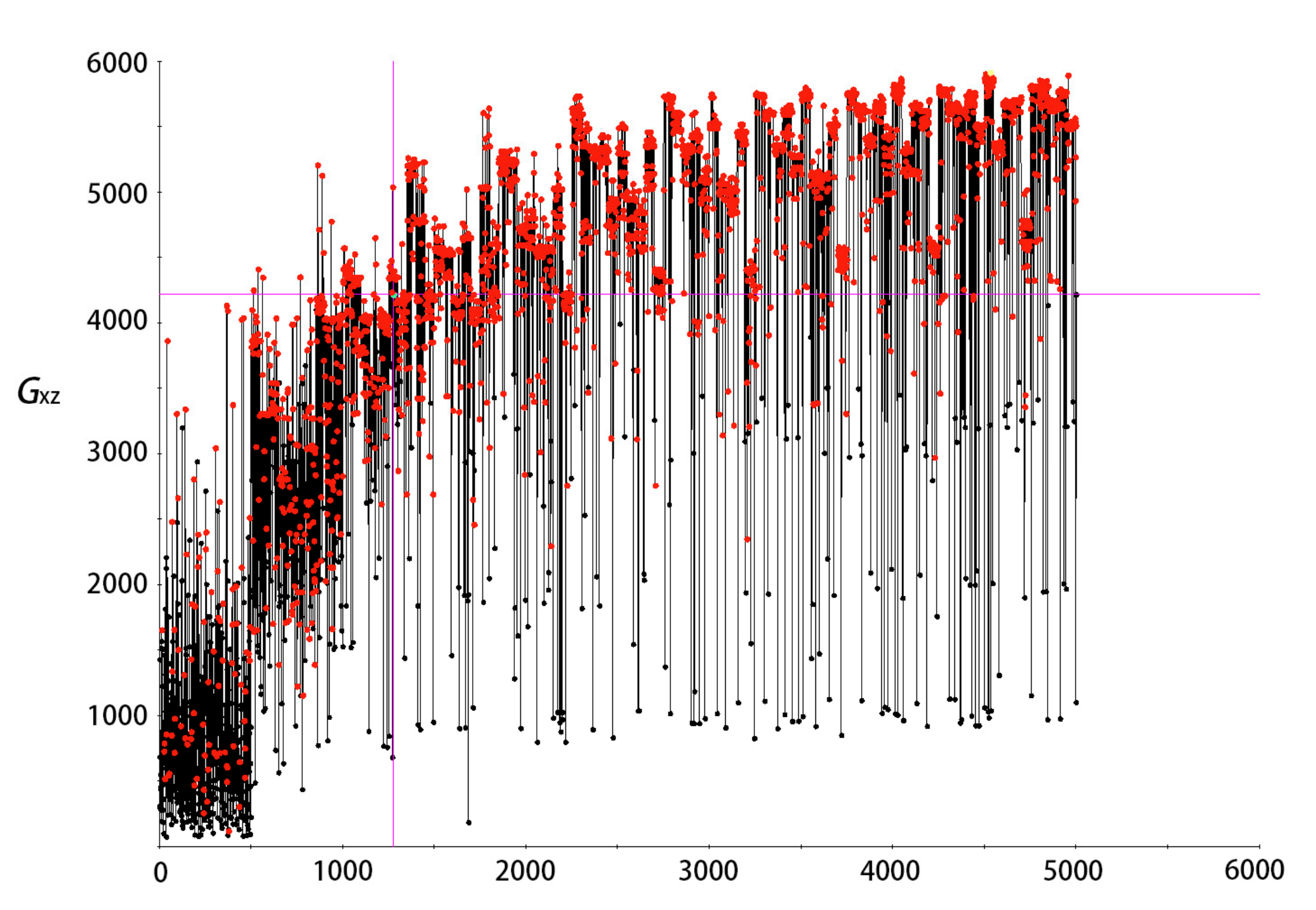
3.4. Equivalent Shear Modulus in Plane xz Gxz
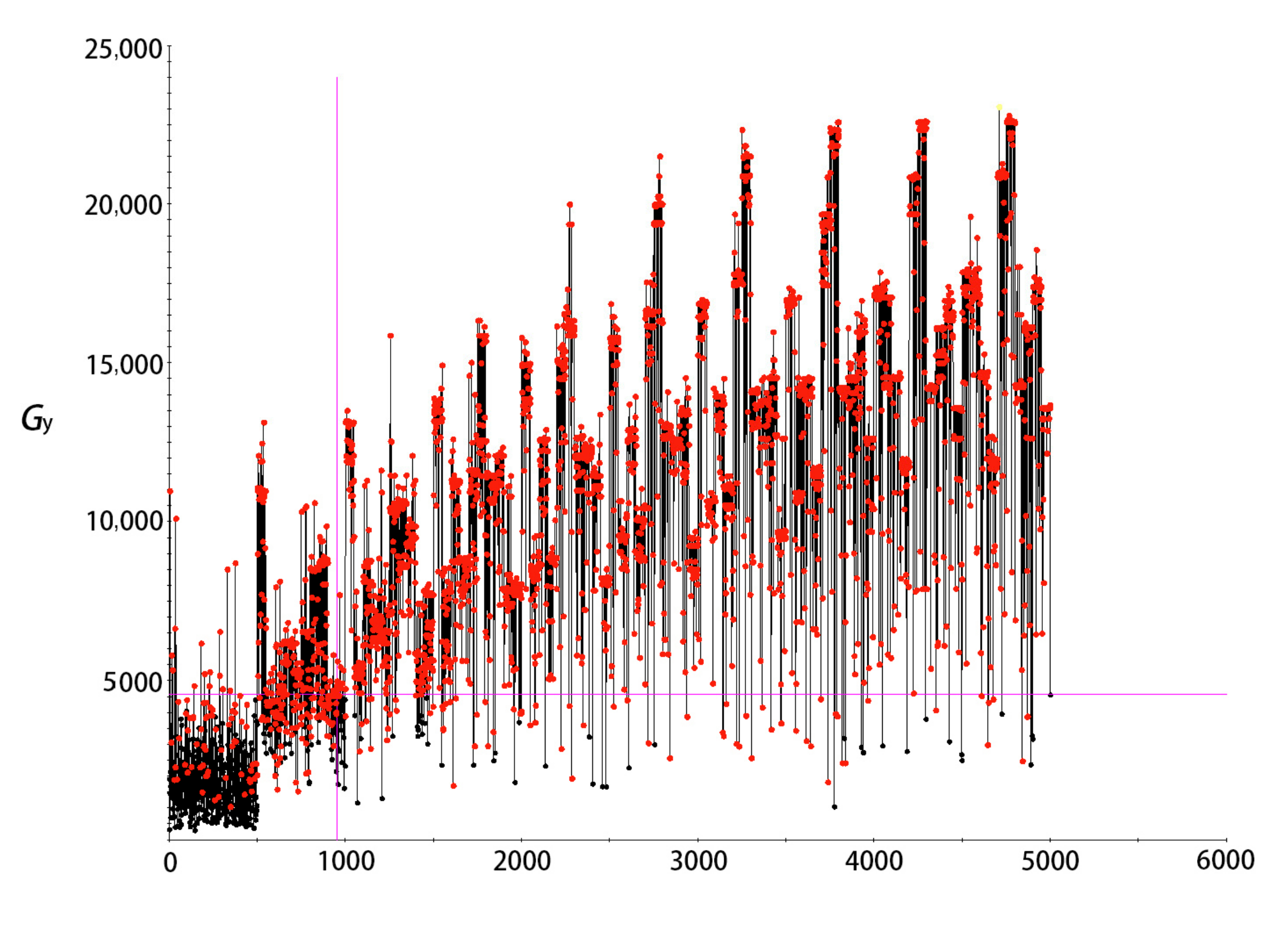
3.5. Equivalent Shear Modulus in Plane yz Gyz
3.6. Mechanical Properties of VFC
4. Verification by Numerical Simulation
4.1. Selection of Configuration Parameters
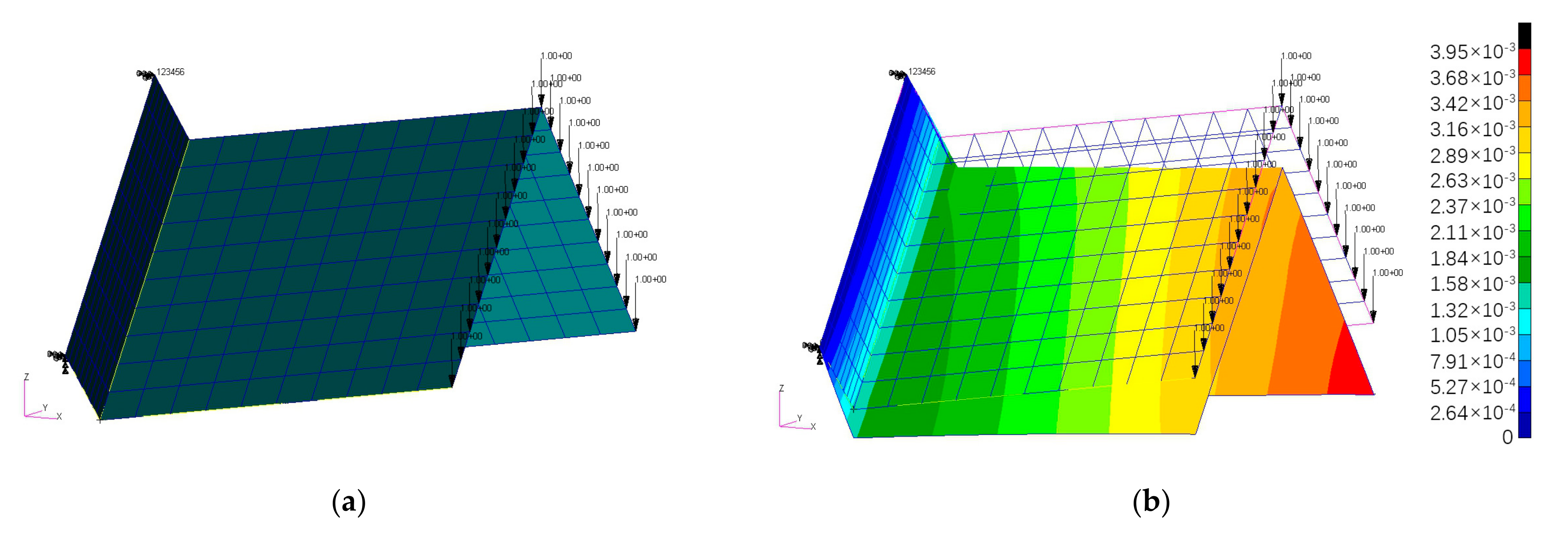
4.2. Verification of Ez
4.3. Verification of Gxz
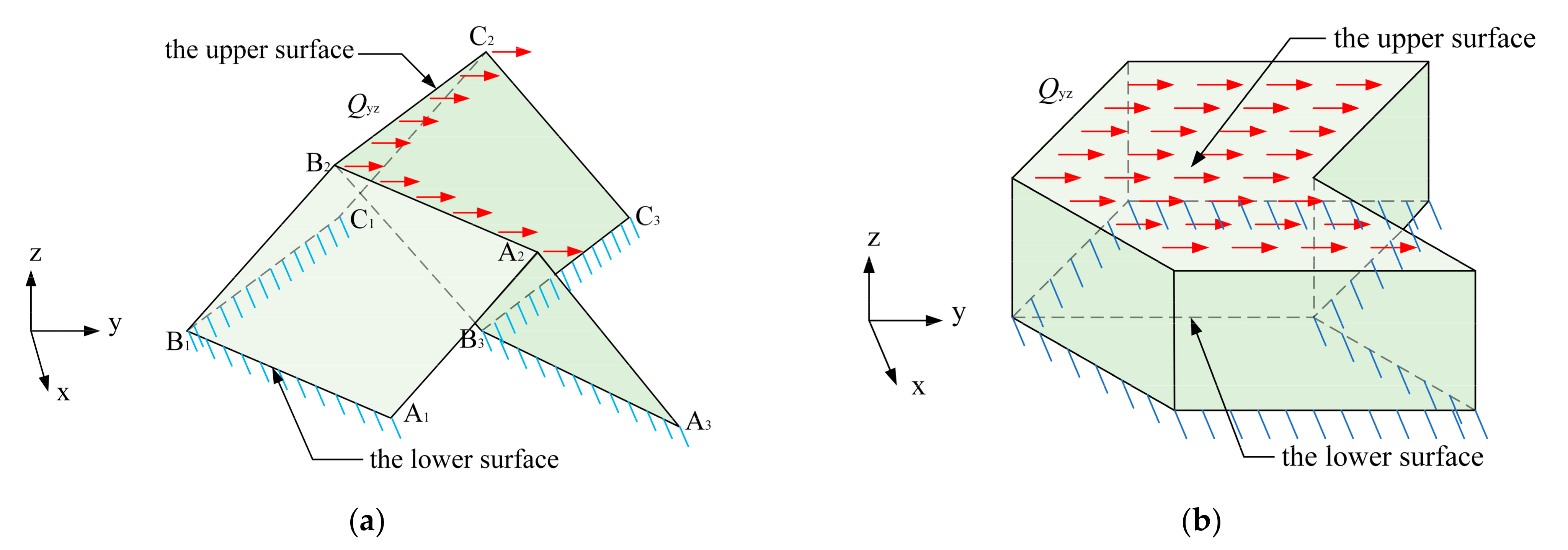
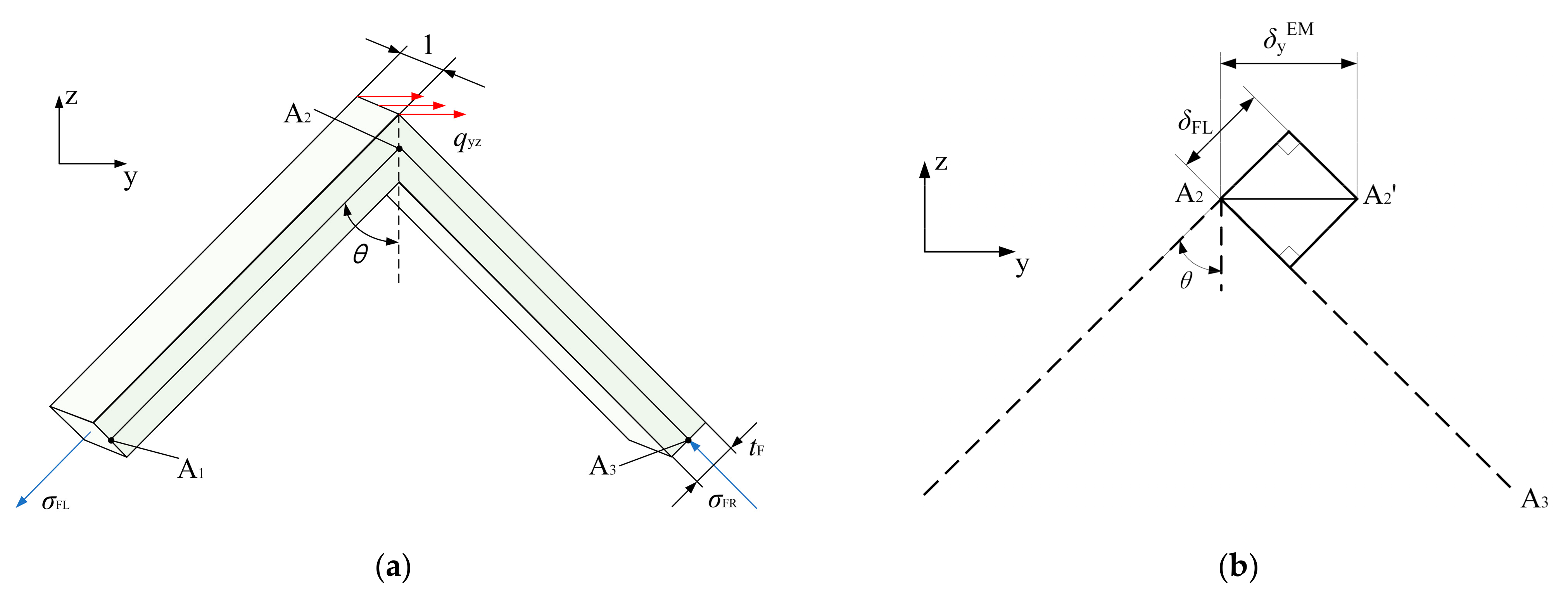
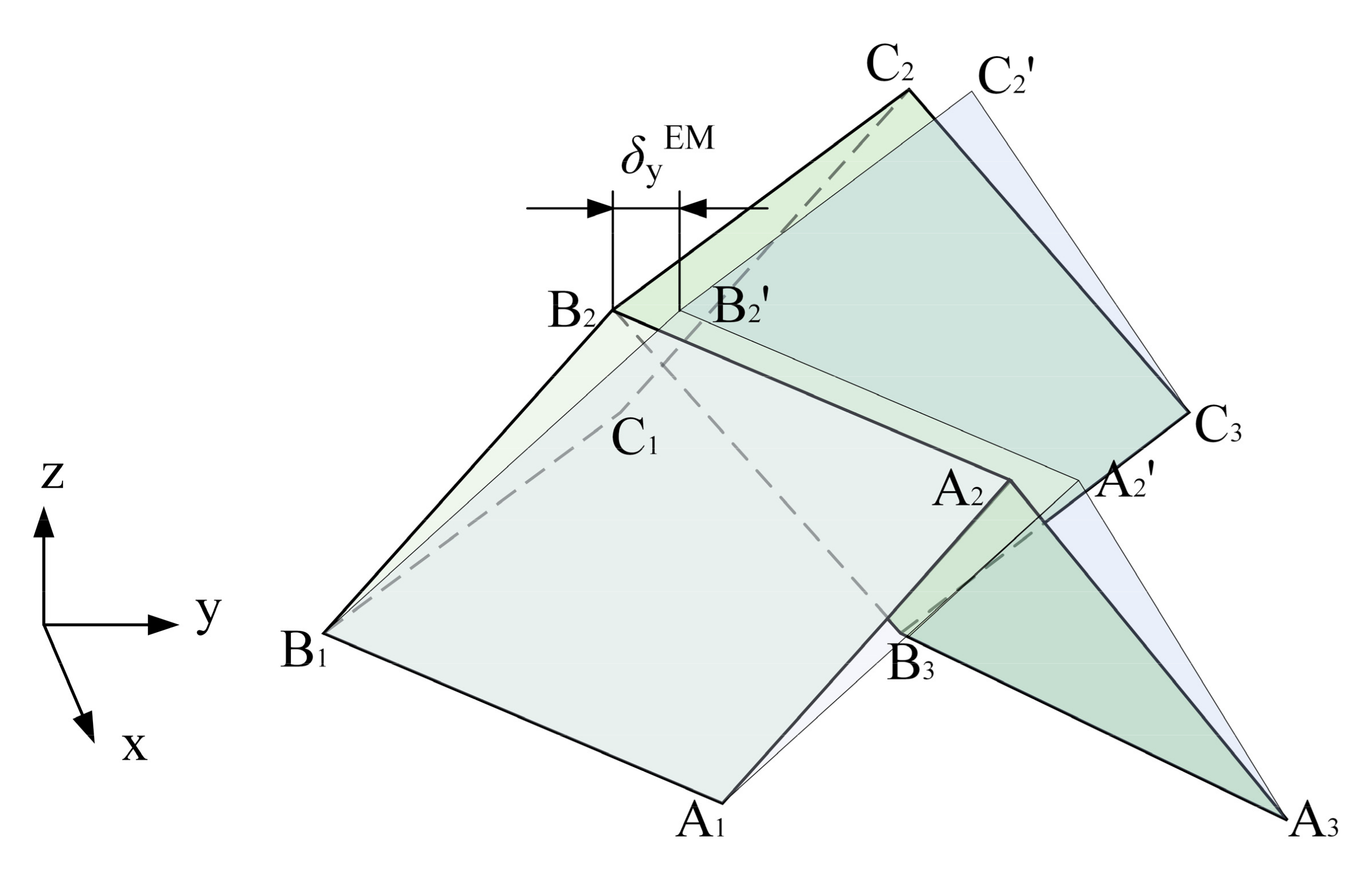
4.4. Verification of Gyz
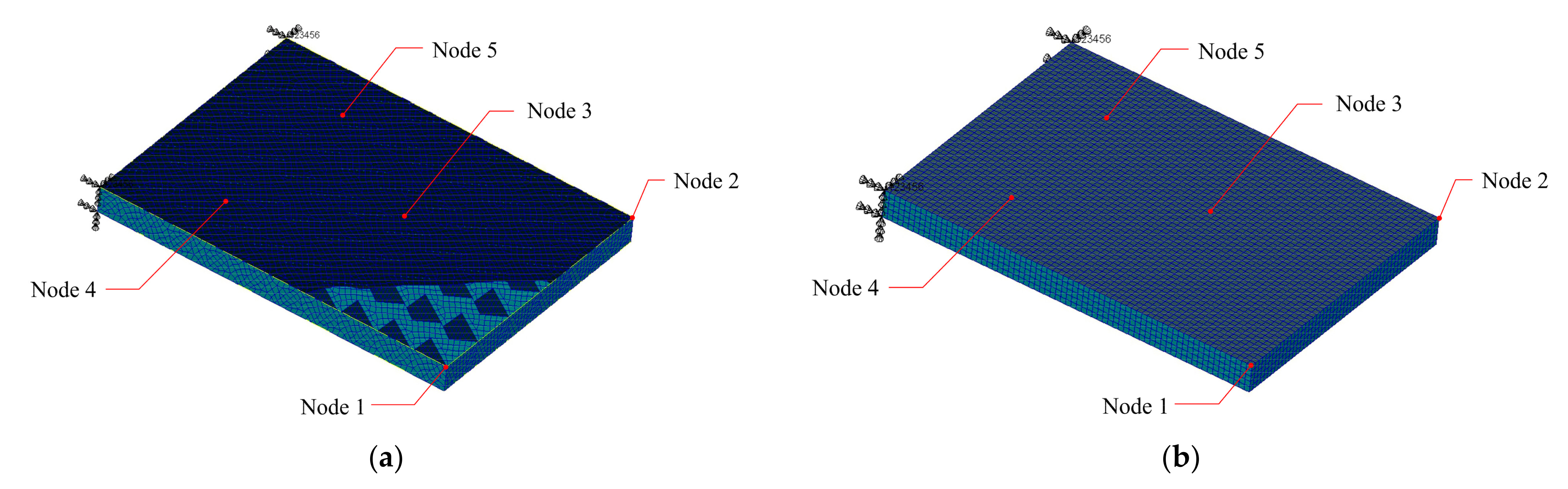
5. Case Study
6. Optimization for Structural Stiffness
6.1. Optimization Goals
6.2. Optimization Program
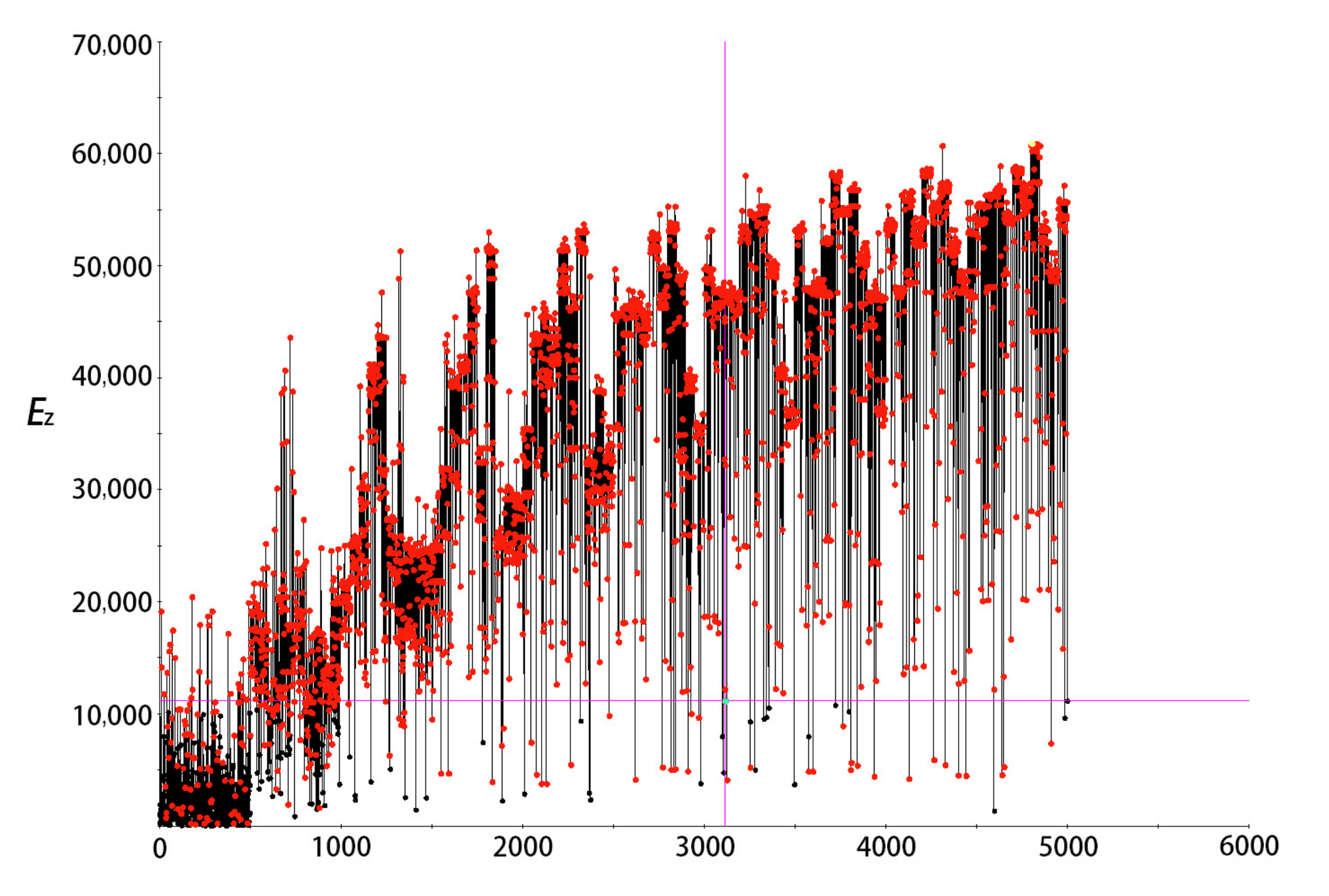
6.3. Optimization Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ez | Equivalent elastic modulus in Direction z of VFC. |
| Gxz | Equivalent shear modulus in Plane xz of VFC. |
| Gyz | Equivalent shear modulus in Plane yz of VFC. |
| ρ | Equivalent density of VFC. |
| 2S0 | Zigzag line step length in line drawing template. |
| 2L0 | Serrated line step length in line drawing template. |
| V0 | Fold width of zigzag line in line drawing template. |
| 2S | Zigzag line step length. |
| 2L | Serrated line step length. |
| V | Fold width of zigzag line. |
| H | Height of VFC. |
| EF | Elastic modulus of the foil material forming the core. |
| GF | Shear modulus of the foil material forming the core. |
| tF | The thickness of the foil material forming the core. |
| v | Poisson’s ratio of the foil material forming the core. |
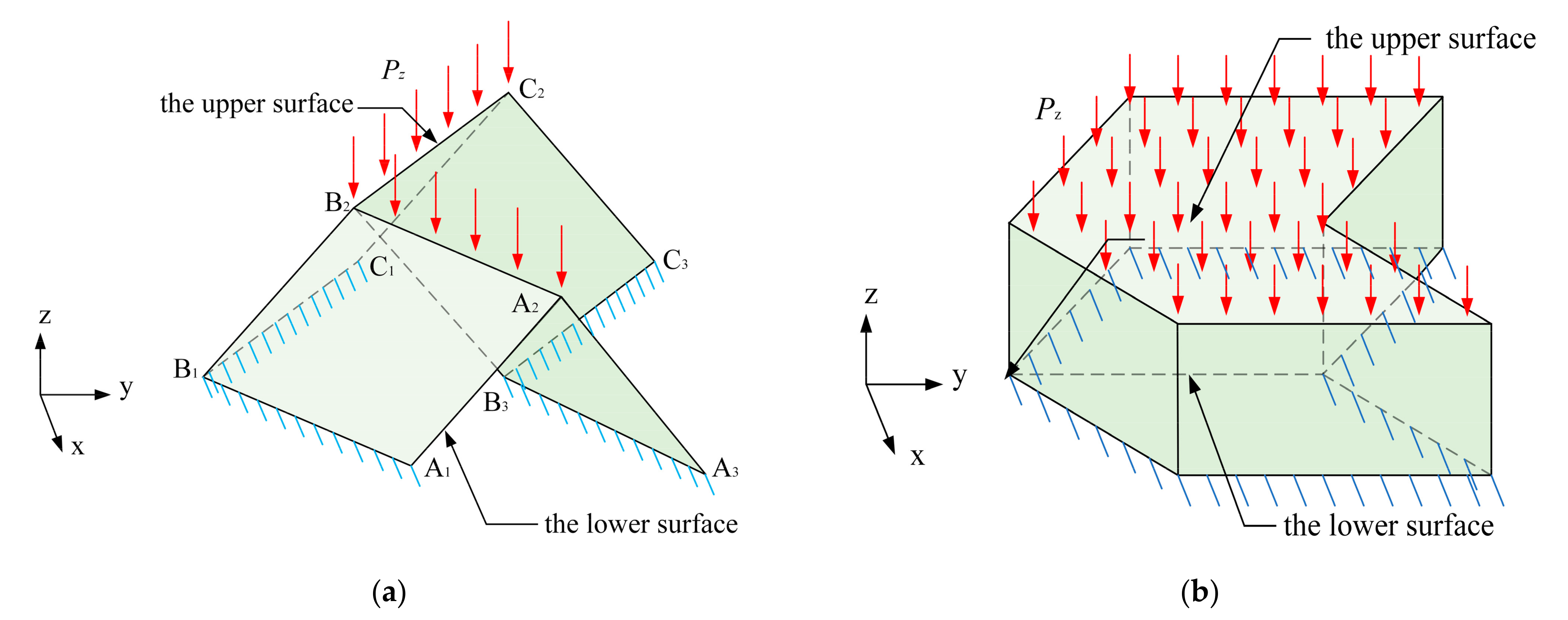
| Pz | Loads on the upper surface of EM and ESE in Direction z. |
| pz | Load per unit length on the upper edge of EM under the action of Pz. |
| σL | Stress at the left panel of EM under the action of Pz. |
| σR | Stress at the right panel of EM under the action of Pz. |
| θ | The angle between the left and right panels of EM and the vertical direction. |
| δF | Deformation of the left and right panels under the action of Pz. |
| δzEM | Displacement of the upper edge of EM in Direction z under the action of Pz. |
| σzESE | The stress of ESE in Direction z under the action of Pz. |
| δzESE | Displacement of the upper surface of ESE in Direction z under the action of Pz. |
| Qxz | Shear forces on the front surface of EM and ESE in Plane xz. |
| τL | Shear stress at the left panel of EM under the action of Qxz. |
| τR | Shear stress at the right panel of EM under the action of Qxz. |
| δABP | Displacement of Point A2 with respect to Point B2 in Panel A1A2B2B1. |
| δAB | Displacement of Point A2 with respect to Point B2 in Direction z. |
| δBC | Displacement of Point B2 with respect to Point C2 in Direction z. |
| γxzEM | Shearing angle of Point A2 on EM under the Qxz. |
| τxzESE | Shear stress of ESE in Plane xz under the action of Qxz. |
| γxzESE | Shearing angle of the front surface on ESE under the action of Qxz. |
| Qyz | Shear forces on the upper surface of EM and ESE in Plane yz. |
| qyz | Load per unit length on the upper edge of EM under the action of Qyz. |
| σFL | Stress at the left panel of EM under the action of Qyz. |
| σFR | Stress at the right panel of EM under the action of Qyz. |
| δFL | Deformation of the left panel under the action of Qyz. |
| δFR | Deformation of the right panel under the action of Qyz. |
| δyEM | Displacement of the upper edge of EM in Direction y under the action of Qyz. |
| γyzEM | Shearing angle of the upper edge of EM under the Qxz. |
| τyzESE | Shear stress of ESE in Plane yz under the action of Qyz. |
| γyzESE | Shearing angle of the upper surface on ESE under the action of Qyz. |
| Ez-Num | Numerical solution of equivalent elastic modulus in Direction z of VFC. |
| Ez-Ana | Analytical solution of equivalent elastic modulus in Direction z of VFC. |
| Gxz-Num | Numerical solution of equivalent shear modulus in Plane xz of VFC. |
| Gxz-Ana | Analytical solution of equivalent shear modulus in Plane xz of VFC. |
| Gyz-Num | Numerical solution of equivalent shear modulus in Plane yz of VFC. |
| Gyz-Ana | Analytical solution of equivalent shear modulus in Plane yz of VFC. |
Appendix A
References
- Huang, W.J.; He, Z.P.; Cheng, X.Q. Development and application analysis of high modulus glass fiber for helicopter blade. High-Tech Fibers Appl. 2016, 41, 7–14. [Google Scholar]
- Dou, R.L.; Hu, P. Application of composite foam sandwich structure in civil aircraft. Civ. Aircr. Des. Res. 2004, 3, 42–45. [Google Scholar]
- Hu, P. Design of Aerospace Foam Sandwich Structure. Aviat. Manuf. Technol. 2012, 414, 99–104. [Google Scholar]
- Zhang, B.B.; Guo, E.Y.; Lv, B.Q.; Gao, X.B. Application of composite materials in helicopters. Technol. Innov. Appl. 2013, 33, 55. [Google Scholar]
- Chen, J.; Qiu, Q.Y. Application and development of honeycomb sandwich structures in aircraft. New Mater. Ind. 2018, 7, 63–67. [Google Scholar]
- Li, S.F.; Wang, Z.J.; Zhou, C. Forced Convection Heat Transfer in V-Pattern Folded Core Sandwich Structures. Int. J. Aerosp. Eng. 2022, 2022, 8926764. [Google Scholar] [CrossRef]
- Chambers, A.T.; Manimala, J.M.; Jones, M.G. Design and optimization of 3D folded-core acoustic liners for enhanced low-frequency performance. AIAA J. 2019, 58, 1–13. [Google Scholar] [CrossRef]
- Zhou, H.Z.; Wang, Z.J. The Influence of Geometric Characteristics on Energy Absorption of M-Type Folded Core. In Proceedings of the 7th International Conference on Mechatronics, Control and Materials, Changsha, China, 29–30 October 2016; Available online: https://perma.cc/PP5U-6GT3 (accessed on 15 June 2022).
- Khaliulin, V.I. Classification of Regular Row-arranged Folded Structures. Izv. Vyss. Uchebnykh Zaved. Aviat. Tekh. 2003, 2, 7–13. [Google Scholar]
- Li, W.; Zheng, Q.; Fan, H.; Ji, B. Fabrication and mechanical testing of ultralight folded lattice-core sandwich cylinders. Engineering 2020, 6, 196–204. [Google Scholar] [CrossRef]
- Magliozzi, L.; Micheletti, A.; Pizzigoni, A. On the design of origami structures with a continuum of equilibrium shapes. Compos. Part B Eng. 2016, 115, 144–150. [Google Scholar] [CrossRef]
- Alekseev, K.A.; Zakirov, I.M.; Karimova, G.G. Geometrical model of creasing roll for manufacturing line of the wedge-shaped folded cores production. Russ. Aeronaut. 2011, 54, 104–107. [Google Scholar] [CrossRef]
- Zakirov, I.M.; Alekseev, K.A. Design of a wedge-shaped folded structure. J. Mach. Manuf. Reliab. 2010, 39, 412–417. [Google Scholar] [CrossRef]
- Cai, K.Q.; Jin, M.S.; Jiang, K.Y. Review of Progress in Materials for Sandwich Structure with Folded Core. Mater. Rev. 2015, 29, 129–133. [Google Scholar]
- Wang, Z.J.; Khaliulin, V.I.; Skripkin, E. Geometry design method of folded structure. J. Nanjing Univ. Aeronaut. Astronaut. 2002, 34, 6–11. [Google Scholar]
- Zhou, X.; Wang, H.; You, Z. Mechanical properties of Miura-based folded cores under quasi-static loads. Thin-Walled Struct. 2014, 82, 296–310. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhou, C.; Khaliulin, V.; Shabalov, A. An Experimental study on the Radar Absorbing Characteristics of Folded Core Structures. Compos. Struct. 2018, 194, 199–207. [Google Scholar] [CrossRef]
- Duan, C.Z.; Xu, Z. Stamping process of aluminum alloy folded core structure. Forg. Stamp. Technol. 2015, 40, 21–26. [Google Scholar]
- Heimbs, S.; Middendorf, P.; Kilchert, S.; Johnson, A.F.; Maier, M. Experimental and numerical analysis of composite folded sandwich core structures under compression. Appl. Compos. Mater. 2007, 14, 363–377. [Google Scholar] [CrossRef]
- Heimbs, S.; Cichosz, J.; Klaus, M.; Kilchert, S.; Johnson, A.F. Sandwich structures with textile-reinforced composite foldcores under impact loads. Compos. Struct. 2010, 92, 1485–1497. [Google Scholar] [CrossRef]
- Kong, X.H.; Wang, Z.J. Design and optimization of V-type folded structure. Comput. Appl. Softw. 2014, 31, 38–42. [Google Scholar]
- Cong, L.X.; Sun, Y.G.; Gao, L.; Chen, P. Preparation and compression performance of an improved V-type folded GERP sandwich structure. Acta Mater. Compos. Sin. 2014, 31, 456–464. [Google Scholar]
- Ren, Y.F. Study on Basic Mechanical Properties of Foldcore Sandwich Structures. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. Available online: https://perma.cc/R4DA-FH3B (accessed on 15 June 2022).
- Kayumov, R.A.; Zakirov, I.M.; Alekseev, K.P.; Alekseev, K.A.; Zinnurov, R.A. Determination of load-carrying capacity in panels with chevron-type cores. Russ. Aeronaut. 2007, 50, 357–361. [Google Scholar] [CrossRef]
- Kintscher, M.; Kärger, L.; Wetzel, A.; Hartung, D. Stiffness and failure behaviour of folded sandwich cores under combined transverse shear and compression. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1288–1295. [Google Scholar] [CrossRef] [Green Version]
- Fischer, S.; Heimbs, S.; Kilchert, S.; Klaus, M.; Cluzel, C. Sandwich structures with folded core: Manufacturing and mechanical behaviour. In Proceedings of the Sampe Europe International Conference, Paris, France, 23–25 March 2009; Available online: https://perma.cc/5Q9Z-7JCX (accessed on 15 June 2022).
- Fischer, S. Aluminium foldcores for sandwich structure application: Mechanical properties and FE-simulation. Thin-Walled Struct. 2015, 90, 31–41. [Google Scholar] [CrossRef]
- Minh, D.P.T. Numerical Simulation for the Folded Core Sandwich Plates under Torsion by Homogenization Method. Am. J. Eng. Res. 2017, 6, 149–155. [Google Scholar]
- Xiang, X.M.; You, Z.; Lu, G. Rectangular sandwich plates with miura-ori folded core under quasi-static loadings. Compos. Struct. 2018, 195, 359–374. [Google Scholar] [CrossRef]
- Sun, Y.G.; Li, Y.X. Prediction and experiment on the compressive property of the sandwich structure with a chevron carbon-fibre-reinforced composite folded core. Compos. Sci. Technol. 2017, 150, 95–101. [Google Scholar] [CrossRef]



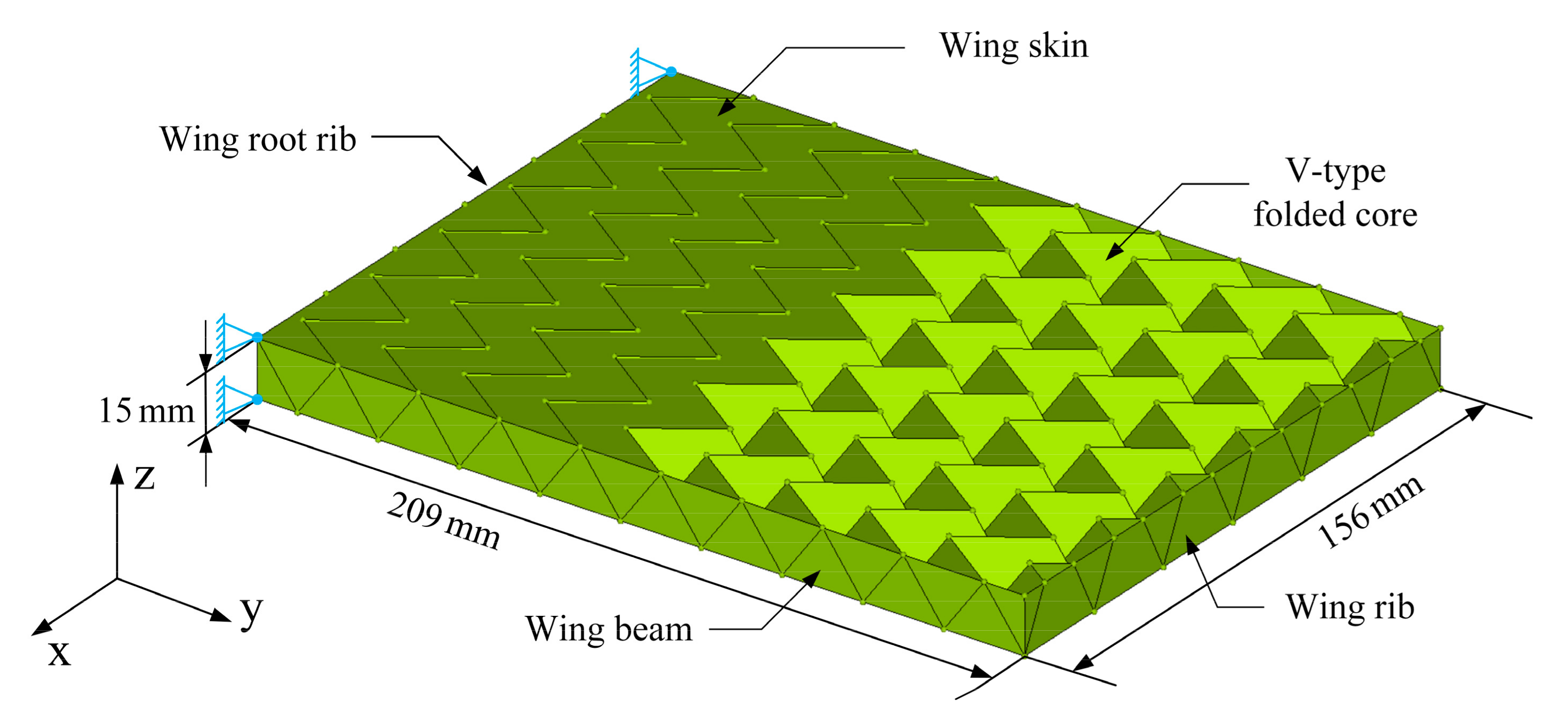

| No. | H (mm) | L (mm) | S (mm) | V (mm) | EF (MPa) | v | tF (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 12.0 | 10.0 | 11.0 | 17.0 | 70 × 103 | 0.3 | 0.2 |
| 2 | 14.0 | 17.0 | 16.0 | 13.0 | 70 × 103 | 0.3 | 0.4 |
| 3 | 15.0 | 11.0 | 13.0 | 19.0 | 70 × 103 | 0.3 | 0.5 |
| 4 | 16.0 | 13.0 | 15.0 | 11.0 | 70 × 103 | 0.3 | 0.4 |
| 5 | 14.0 | 11.0 | 12.0 | 18.0 | 70 × 103 | 0.3 | 0.3 |
| 6 | 18.0 | 16.0 | 18.0 | 10.0 | 70 × 103 | 0.3 | 0.4 |
| 7 | 19.0 | 18.0 | 14.0 | 12.0 | 70 × 103 | 0.3 | 0.2 |
| 8 | 15.0 | 10.0 | 10.0 | 20.0 | 70 × 103 | 0.3 | 0.5 |
| 9 | 15.0 | 12.0 | 12.0 | 20.0 | 70 × 103 | 0.3 | 0.3 |
| 10 | 16.0 | 10.0 | 14.0 | 18.0 | 70 × 103 | 0.3 | 0.4 |
| No. | Displacement (mm) | Ez-Ana (MPa) | Ez-Num (MPa) | Error Percentage |
|---|---|---|---|---|
| 1 | 4.86 × 10−4 | 1168.22 | 1180.74 | −1.06% |
| 2 | 4.76 × 10−4 | 545.20 | 567.38 | −3.91% |
| 3 | 1.95 × 10−4 | 2954.81 | 2824.10 | 4.63% |
| 4 | 3.65 × 10−4 | 1248.64 | 1180.19 | 5.8% |
| 5 | 3.45 × 10−4 | 1673.26 | 1614.03 | 3.67% |
| 6 | 4.18 × 10−4 | 835.84 | 784.99 | 6.48% |
| 7 | 10.32 × 10−4 | 391.91 | 383.36 | 2.23% |
| 8 | 1.78 × 10−4 | 4508.19 | 4424.13 | 1.90% |
| 9 | 3.43 × 10−4 | 1619.54 | 1592.78 | 1.68% |
| 10 | 2.33 × 10−4 | 2781.10 | 2575.11 | 8.00% |
| No. | Displacement (mm) | Gxz-Ana (MPa) | Gxz-Num (MPa) | Error Percentage |
|---|---|---|---|---|
| 1 | 7.83 × 10−3 | 224.72 | 245.85 | −8.59% |
| 2 | 4.02 × 10−3 | 312.55 | 351.19 | −11.00% |
| 3 | 3.20 × 10−3 | 557.26 | 517.05 | 7.78% |
| 4 | 3.24 × 10−3 | 518.46 | 467.41 | 10.92% |
| 5 | 5.82 × 10−3 | 320.27 | 281.16 | 13.91% |
| 6 | 3.25 × 10−3 | 439.76 | 403.85 | 8.89% |
| 7 | 5.91 × 10−3 | 164.88 | 145.46 | 13.36% |
| 8 | 3.14 × 10−3 | 500.91 | 445.86 | 12.35% |
| 9 | 5.78 × 10−3 | 270.41 | 242.21 | 11.64% |
| 10 | 3.50 × 10−3 | 560.67 | 525.00 | 6.79% |
| No. | Displacement (mm) | Gyz-Ana (MPa) | Gyz-Num (MPa) | Error Percentage |
|---|---|---|---|---|
| 1 | 8.03 × 10−4 | 811.38 | 713.23 | 13.76% |
| 2 | 3.56 × 10−4 | 803.89 | 759.05 | 5.91% |
| 3 | 3.84 × 10−4 | 1589.03 | 1434.11 | 10.80% |
| 4 | 5.37 × 10−4 | 824.30 | 802.18 | 2.76% |
| 5 | 6.18 × 10−4 | 1032.98 | 901.00 | 14.65% |
| 6 | 5.09 × 10−4 | 660.42 | 644.65 | 2.45% |
| 7 | 9.81 × 10−4 | 351.75 | 403.50 | −12.83% |
| 8 | 4.19 × 10−4 | 2003.64 | 1879.47 | 6.61% |
| 9 | 5.89 × 10−4 | 1036.50 | 928.48 | 11.63% |
| 10 | 6.12 × 10−4 | 1086.37 | 980.39 | 10.81% |
| Load Case No. | Load (N) | Maximum Displacement (mm) | Error (mm) | Error Percentage | |||||
|---|---|---|---|---|---|---|---|---|---|
| Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | VFC | Equivalent Solid | |||
| 1 | 200 | 0 | 0 | 0 | 0 | 1.86 | 1.94 | 0.08 | 4.10% |
| 2 | 200 | 100 | 0 | 0 | 0 | 2.56 | 2.66 | 0.10 | 3.76% |
| 3 | 0 | 100 | 0 | 100 | 0 | 1.09 | 1.13 | 0.04 | 3.54% |
| 4 | 0 | 50 | 100 | 0 | 100 | 1.10 | 1.13 | 0.03 | 2.65% |
| 5 | 100 | 0 | 100 | 0 | 0 | 1.38 | 1.44 | 0.06 | 4.17% |
| 6 | 50 | 50 | 200 | 0 | 0 | 1.71 | 1.77 | 0.06 | 3.39% |
| 7 | 50 | 0 | 0 | 200 | 0 | 0.84 | 0.87 | 0.02 | 3.23% |
| 8 | 0 | 0 | 50 | 0 | 200 | 0.59 | 0.61 | 0.02 | 3.27% |
| 9 | 50 | 100 | 100 | 0 | 50 | 1.82 | 1.88 | 0.06 | 3.19% |
| 10 | 0 | 50 | 0 | 100 | 100 | 0.81 | 0.84 | 0.03 | 2.99% |
| Optimization Objectives | Design Variables | Binding Conditions |
|---|---|---|
| Ez → Max Gxz → Max Gyz → Max | H: 5~20 mm | ρ ≤ 0.5 g/cm3 |
| L: 5~20 mm | ||
| S: 5~20 mm | ||
| V: 5~20 mm | ||
| tF: 0.2~1.2 mm |
| No. | Optimization Objectives | H (mm) | L (mm) | S (mm) | V (mm) | tF (mm) |
|---|---|---|---|---|---|---|
| 1 | Ez = 11,162.36 MPa | 17.78 | 5.16 | 5.89 | 19.64 | 0.267 |
| 2 | Gxz = 4215.02 MPa | 19.40 | 5.65 | 19.66 | 5.12 | 0.952 |
| 3 | Gyz = 4562.34 MPa | 14.95 | 19.20 | 5.34 | 17.00 | 0.981 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Wang, Z.; Cao, F. Research on Mechanical Properties of V-Type Folded Core Sandwich Structures. Aerospace 2022, 9, 398. https://doi.org/10.3390/aerospace9080398
Cui Z, Wang Z, Cao F. Research on Mechanical Properties of V-Type Folded Core Sandwich Structures. Aerospace. 2022; 9(8):398. https://doi.org/10.3390/aerospace9080398
Chicago/Turabian StyleCui, Zehao, Zhijin Wang, and Feng Cao. 2022. "Research on Mechanical Properties of V-Type Folded Core Sandwich Structures" Aerospace 9, no. 8: 398. https://doi.org/10.3390/aerospace9080398
APA StyleCui, Z., Wang, Z., & Cao, F. (2022). Research on Mechanical Properties of V-Type Folded Core Sandwich Structures. Aerospace, 9(8), 398. https://doi.org/10.3390/aerospace9080398






