Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles
Abstract
:1. Introduction
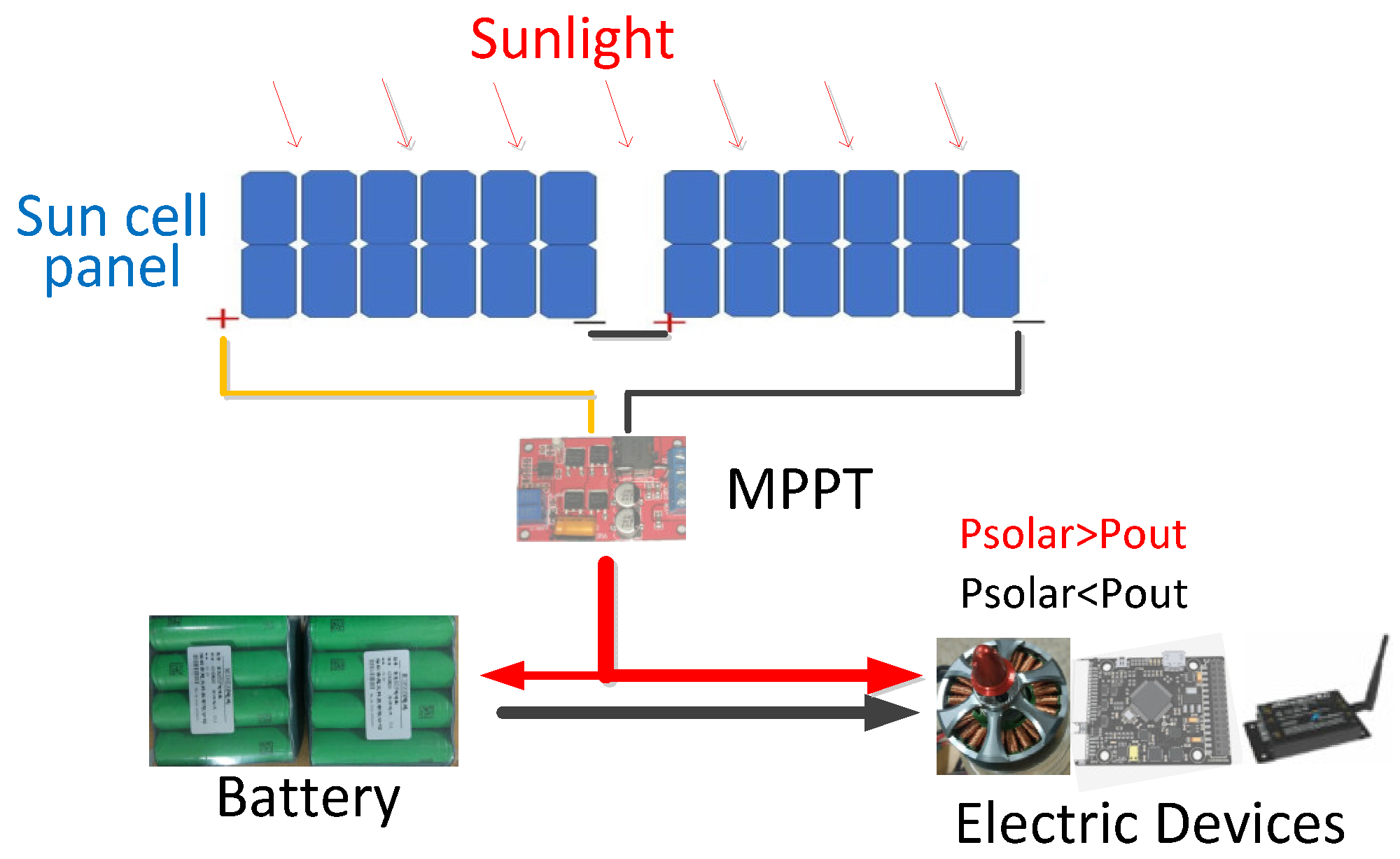
2. Solar UAV’s Energy System Composition
3. Energy System Management Method
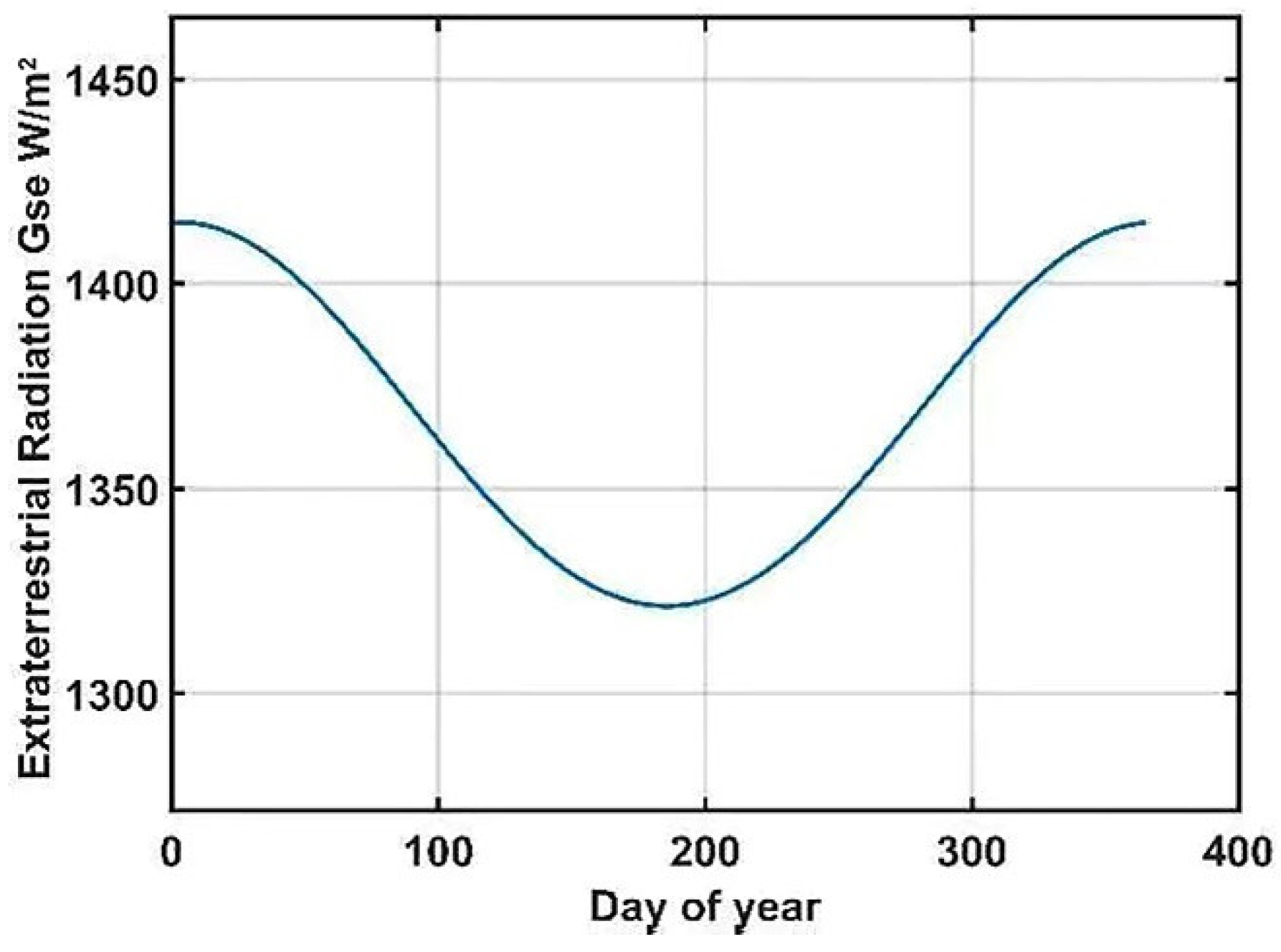
3.1. Solar Radiation Power of UAV
3.2. UAV Energy Output
3.3. Criteria of Method Extended
- Determine the local geographical latitude , the date Date of the aircraft flight, and the date window Date [min, max] for continuous flight.
- Calculate the length of the night , according to the date window Date [min, max] of the flight.
- Earnings time calculation:
- Change in night time caused by date change:
- Estimate the influence of meteorological factors such as clouds and water fog in the early morning and evening . The impact of rainfall is fatal for solar-powered aircraft; thus, the selection date of flight should, as far as possible, avoid local rainy days.
- The addition time because of the night flight environment effects on the aircraft, such as gusts, vertical turbulence, etc., causes additional power consumption of the aircraft.
- (1)
- The battery capacity required for the surplus period:
- (2)
- Maximum battery capacity required for night flight:
- (3)
- Battery design minimum state value SOCmin.
- (4)
- The required minimum battery capacity:
4. UAV Platform Parameter Design Method
5. The Method Simulation Results
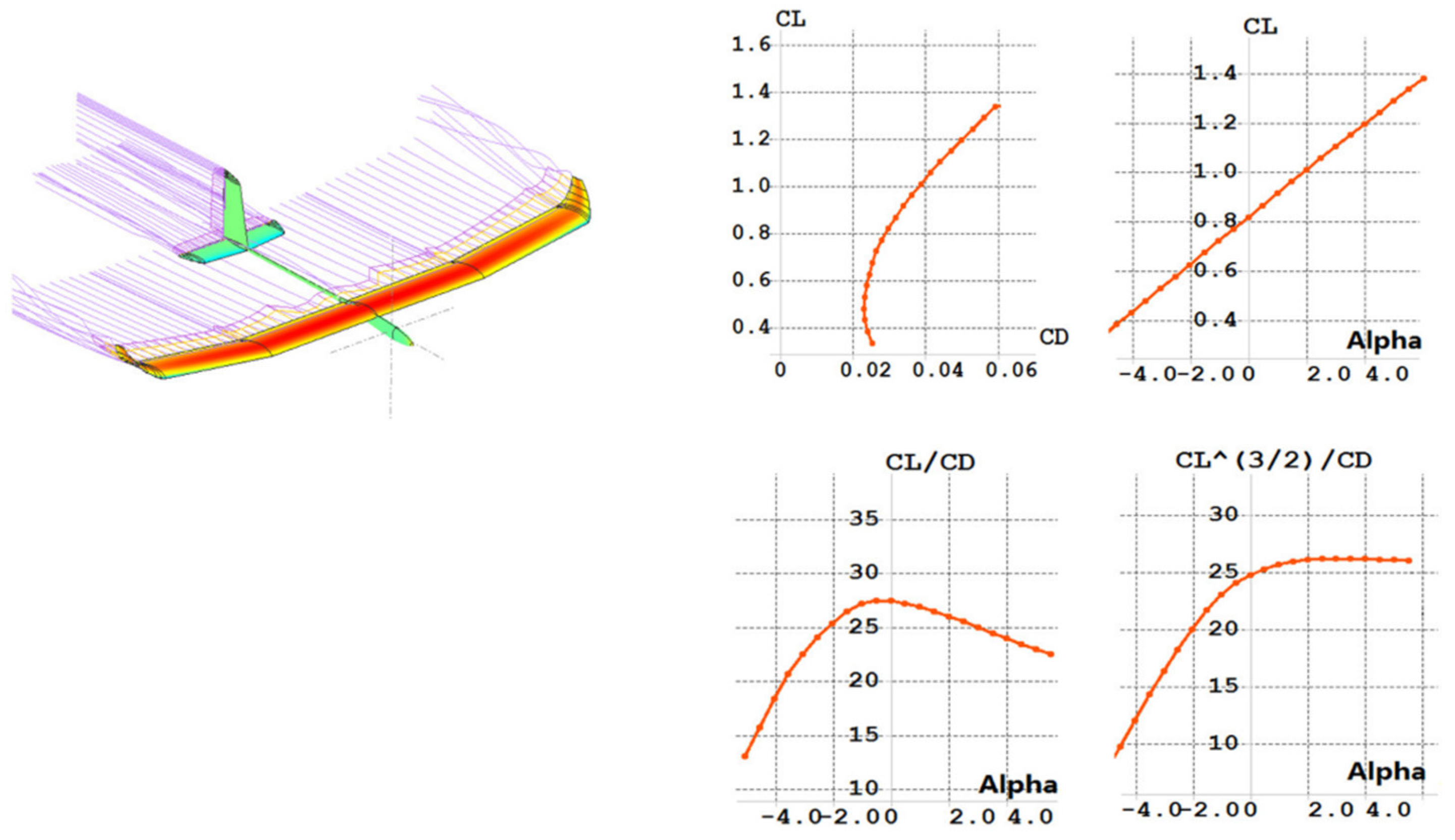
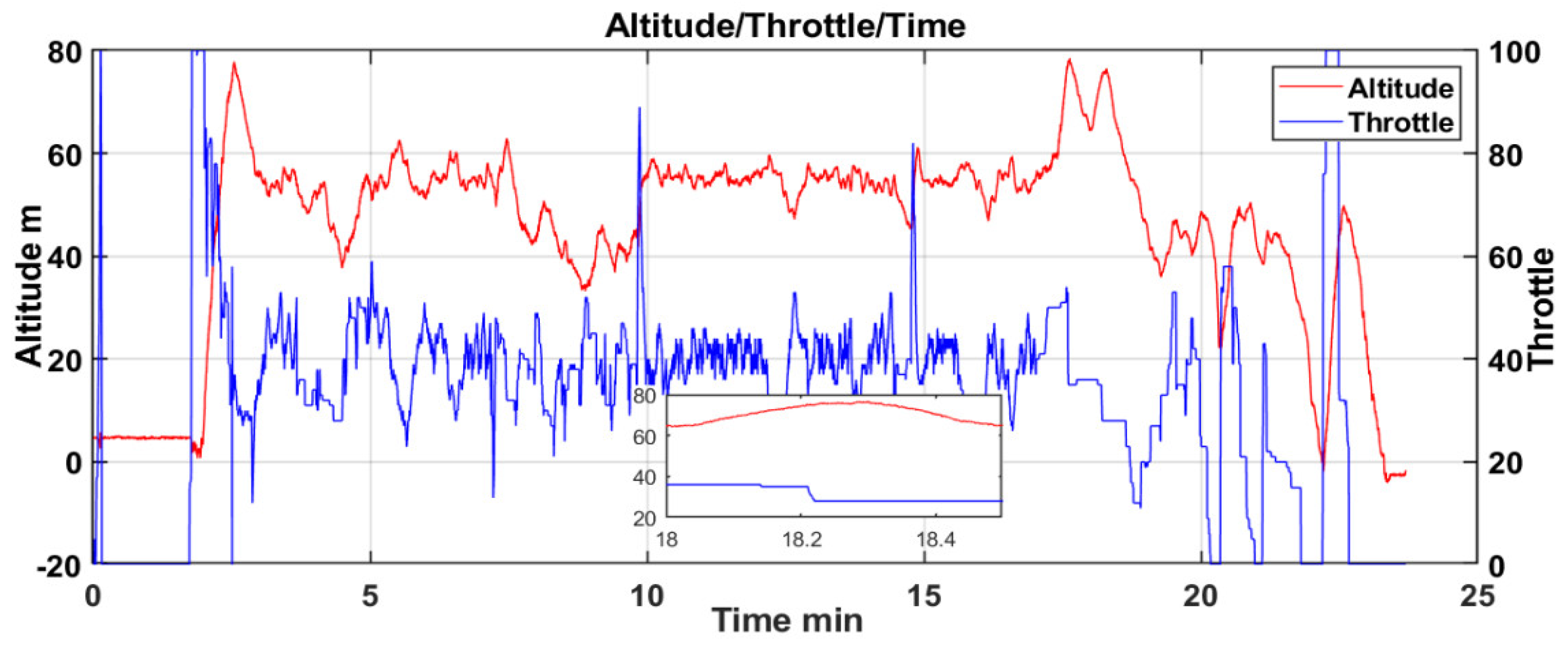
5.1. UAV Input/Output Power
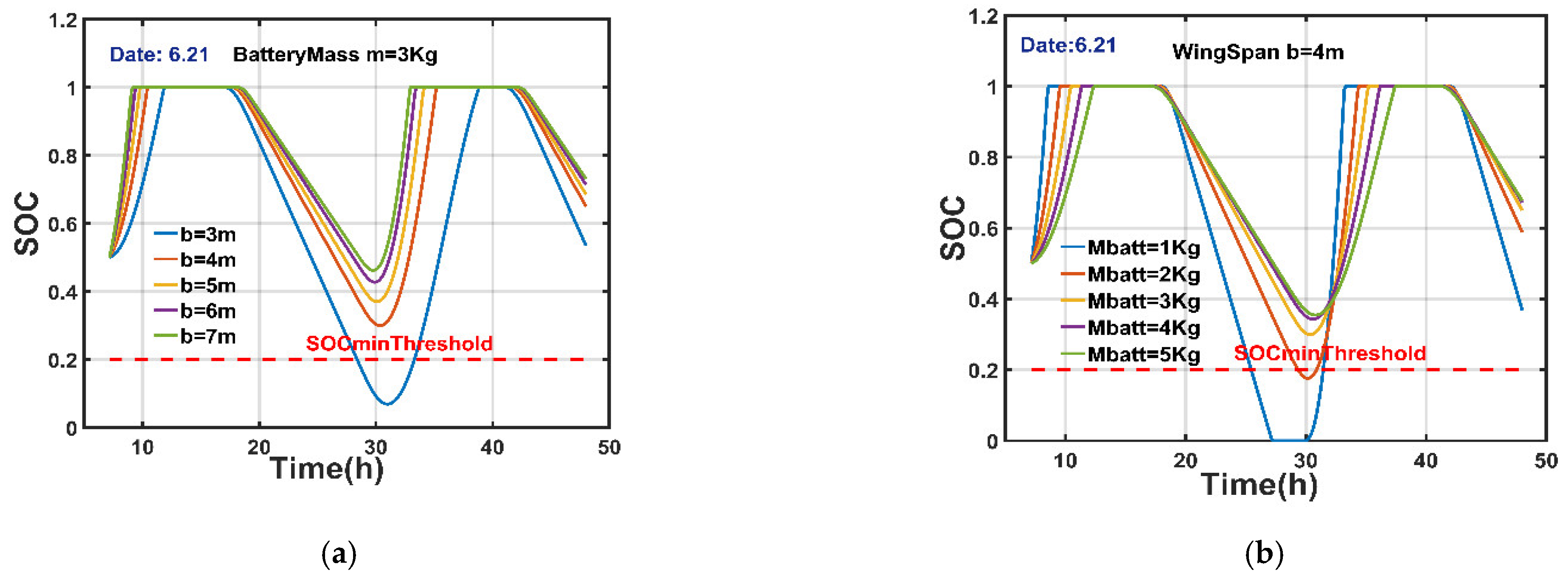
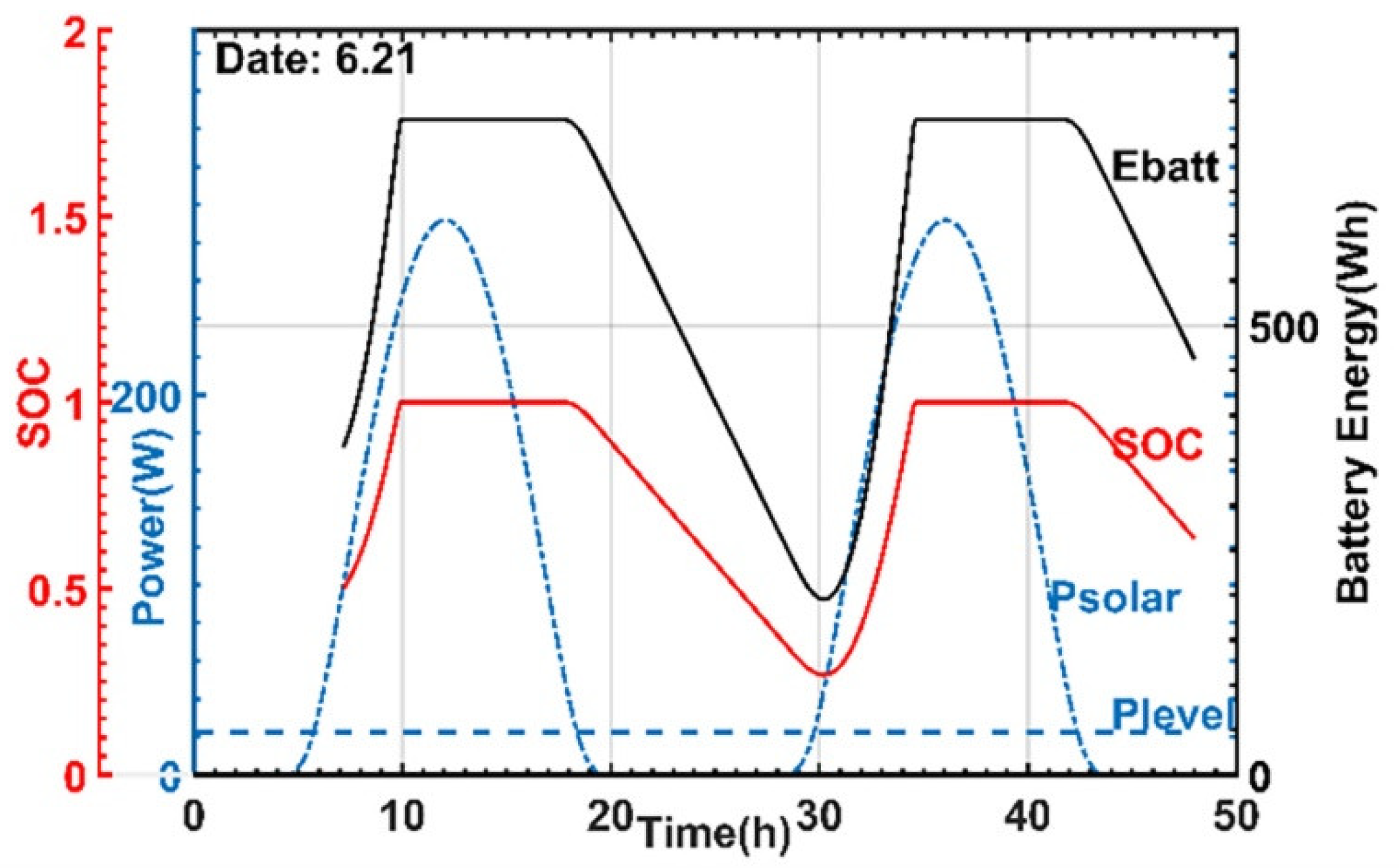
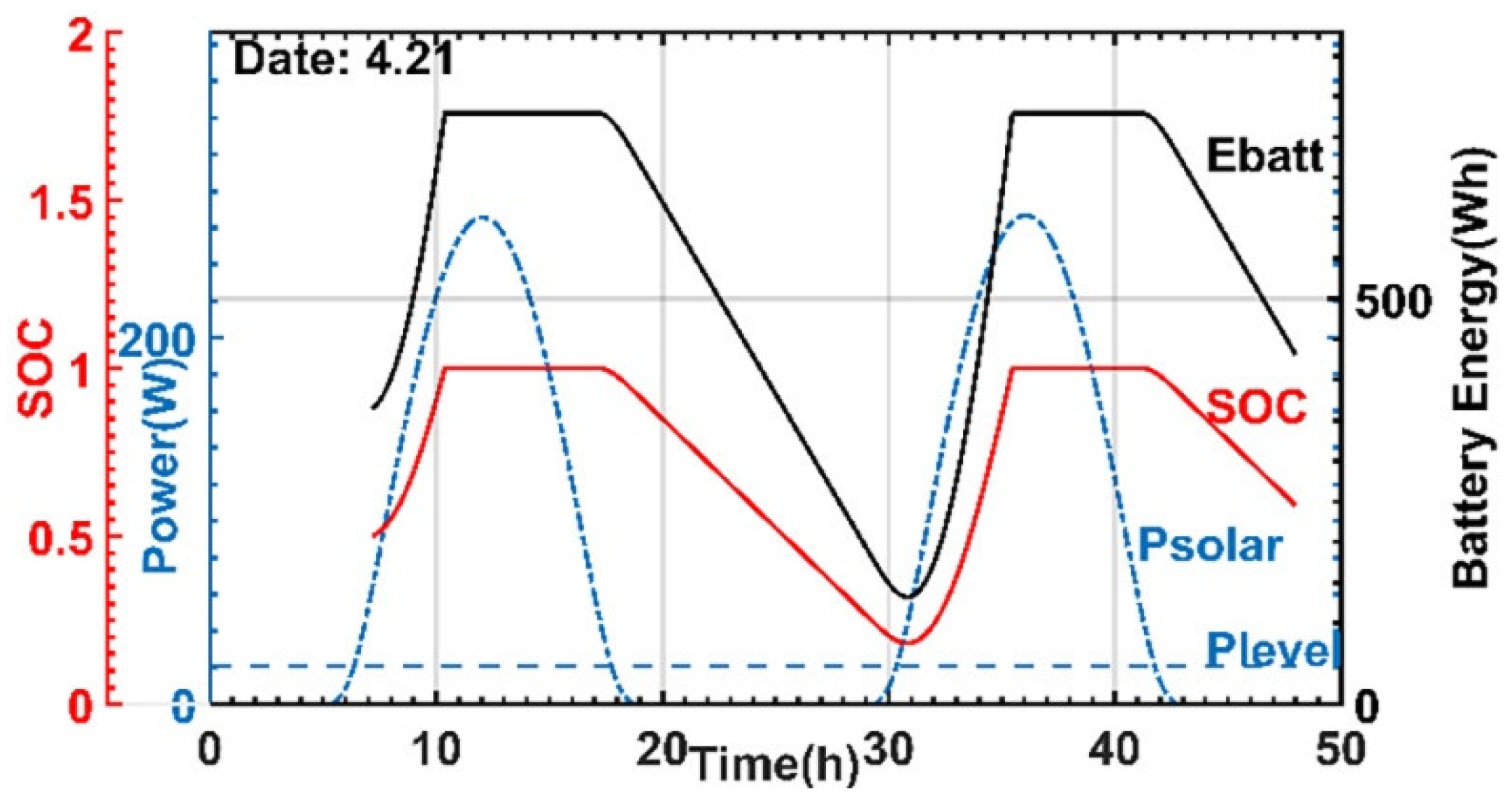
5.2. Power Balance Simulation Test of System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hening, S.; Baumgartner, J.; Teodorescu, M.; Nguyen, N.T.; Ippolito, C.A. Distributed sampling using small unmanned aerial vehicles (UAVs) for scientific missions. In Proceedings of the AIAA InfoTech and Aerospace Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Malaver, A.; Motta, N.; Corke, P.; Gonzalez, F. Development and Integration of a Solar Powered Unmanned Aerial Vehicle and a Wireless Sensor Network to Monitor Greenhouse Gases. Sensors 2015, 15, 4072–4096. [Google Scholar] [CrossRef] [PubMed]
- Jiang, R.; Wang, P.; Xu, Y.; Zhou, Z.Y.; Luo, X.W.; Lan, Y.B.; Zhao, G.P.; Sanchez-Azofeifa, A.; Laakso, K. Assessing the Operation Parameters of a Low-altitude UAV for the Collection of NDVI Values Over a Paddy Rice Field. Remote Sens. 2020, 12, 1850. [Google Scholar] [CrossRef]
- Wu, J.F.; Wang, H.L.; Li, N.; Yao, P.; Huang, Y.; Su, Z.K.; Yu, Y. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Ackerman, E. Giant Solar-Powered UAVs are Atmospheric Satellites. IEEE Spectrum 2013. Available online: https://spectrum.ieee.org/giant-solar-powered-uavs-are-atmospheric-satellites (accessed on 21 August 2013).
- Noth, A. Design of Solar Powered Airplanes for Continuous Flight. Ph.D. Thesis, ETH, Zurich, Switzerland, 2008. [Google Scholar]
- Cocconi, A. AC Propulsion’s Solar Electric Powered SoLong UAV; AC Propulsion: San Dimas, CA, USA, 2005; Available online: https://xpda.com/junkmail/junk173/ACP_SoLong_Solar_UAV_2005-06-05.pdf (accessed on 5 June 2005).
- Laurenzo, R. Soaring on a Solar Impulse. Aerosp. Am. 2009, 5, 32–36. [Google Scholar]
- Cheng, K.; Wang, Z.; Zhou, Z. Exploring Effects of Solar-Powered Airplane Operating Conditions on Solar Cell Performance. J. Northwest. Polytech. Univ. 2012, 4, 535–540. [Google Scholar]
- Lee, J.S.; Yu, K.H. Optimal Path Planning of Solar-Powered UAV Using Gravitational Potential Energy. IEEE Trans. Aerosp. Electron. Syst. 2017, 52, 1442–1451. [Google Scholar] [CrossRef]
- Al-rabghi, O.M.; Akyurt, M.M. A survey of energy efficient strategies for effective air conditioning. Energy Convers. Manag. 2004, 45, 1643–1654. [Google Scholar] [CrossRef]
- Ipsakis, D.; Voutetakis, S.; Seferlis, P.; Stergiopoulos, F.; Elmasides, C. Power management strategies for a stand-alone power system using renewable energy sources and hydrogen storage. Int. J. Hydrogen Energy 2009, 34, 7081–7095. [Google Scholar] [CrossRef]
- Abbe, G.; Smith, H. Technological development trends in Solar-powered Aircraft Systems. Renew. Sustain. Energy Rev. 2016, 60, 770–783. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhang, C.M.; Li, L.Y.; Guo, Q.B. Parameter analysis of power system for solar-powered unmanned aerial vehicle. Appl. Energy 2021, 295, 117031. [Google Scholar] [CrossRef]
- Panagiotou, P.; Tsavlidis, I.; Yakinthos, K. Conceptual design of a hybrid solar MALE UAV. Aerosp. Sci. Technol. 2016, 53, 207–219. [Google Scholar] [CrossRef]
- Dwivedi, V.S.; Kumar, P.; Ghosh, A.K.; Kamath, G.M. Selection of size of battery for solar powered aircraft. In Proceedings of the 11th IFAC Conference on Control Applications in Marine Systems, Robotics, and Vehicles, Opatija, Croatia, 10–12 September 2018. [Google Scholar]
- Soon, T.K.; Mekhilef, S.; Safari, A. Simple and low cost incremental conductance maximum power point tracking using buck-boost converter. J. Renew. Sustain. Energy 2013, 5, 1777–1790. [Google Scholar]
- Miles, R.W.; Hynes, K.M.; Forbes, I. Photovoltaic Solar Cells: An Overview of State-of-the-Art Cell Development and Environmental Issues. Prog. Cryst. Growth Charact. Mater. 2005, 51, 1–42. [Google Scholar] [CrossRef]
- McEvoy, A.; Markvart, T.; Castaner, L. Practical Handbook of Photovoltaics: Fundamentals and Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2012; ISBN 978-0-12-385934-1. [Google Scholar]
- Markvart, T. Solar Electricity; John Wiley: New York, NY, USA, 1994; ISBN 9780471941613. [Google Scholar]
- Xiao, W.; Elnosh, A.; Khadkikar, V.; Zeineldin, H. Overview of maximum power point tracking technologies for photovoltaic power systems. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, Optimal, Intelligent and Classical PV MPPT Techniques: A Review. CSEE J. Power Energy 2021, 7, 9–33. [Google Scholar]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO) based MPPT for PV with reduced steady state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Implementation of incremental conductance method with direct control. In Proceedings of the 2011 IEEE Region 10 Conference, Bali, Indonesia, 21–24 November 2011. [Google Scholar]
- Green, M.A.; Blakers, A.W.; Shi, J.; Keller, E.M.; Wenham, S.R. 22.6% efficient silicon solar cells. In Proceedings of the 4th International Photovoltaic Science and Engineering Conference, Sydney, Australia, 14–17 February 1989. [Google Scholar]
- De Brito, M.; Sampaio, L.; Luigi, G.; Melo, G.; Canesin, C. Comparative analysis of MPPT techniques for PV applications. In Proceedings of the 2011 International Conference on Clean Electrical Power, Ischia, Italy, 14–16 June 2011. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 3rd ed.; John Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-69867-8. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley: Hoboken, NJ, USA, 2013; ISBN 978-0-470-87366-3. [Google Scholar]
- Klesh, A.T.; Kabamba, P.T. Solar-Powered Aircraft: Energy-Optimal Path Planning and Perpetual Endurance. J. Guid. Control Dyn. 2009, 32, 1320–1329. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.; Dai, R.; Mesbahi, M. Optimal path planning and power allocation for a long endurance solar-powered UAV. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Mark, D. XFOIL 6.9 User Primer; MIT Aero & Astro: Cleveland, OH, USA, 2001; Available online: http://web.mit.edu/aeroutil_v1.0/xfoil_doc.txt (accessed on 30 November 2001).
- Moura, S.J.; Callaway, D.S.; Fathy, H.K.; Stein, J.L. Tradeoffs between battery energy capacity and stochastic optimal power management in plug-in hybrid electric vehicles. J. Power Source 2010, 195, 2979–2988. [Google Scholar] [CrossRef]
- Wirth, L.; Oettershagen, P.; Ambuhl, J.; Siegwart, R. Meteorological path planning using dynamic programming for a solar-powered UAV. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Oettershagen, P.; Melzer, A.; Mantel, T.; Rudin, K.; Lotz, R.; Siebenmann, D.; Leutenegger, S.; Alexis, K.; Siegwart, R. A solar-powered hand-launchable UAV for low-altitude multi-day continuous flight. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Leutenegger, S.; Jabas, M.; Siegwart, R.Y. Solar airplane conceptual design and performance estimation. J. Intell. Robot. Syst. 2010, 61, 545–561. [Google Scholar] [CrossRef]
- Rajendran, P.; Smith, H. Development of Design Methodology for a Small Solar-Powered Unmanned Aerial Vehicle. Int. J. Aerospace Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Overview of Lithium Ion Batteries. Available online: https://www.epectec.com/downloads/Panasonic-Lithium-Ion-Battery-Overview.pdf (accessed on 1 January 2007).
- Kimura, K.; Stephenson, D. Solar radiation on cloudy days. ASHRAE J. 1969, 75. [Google Scholar]
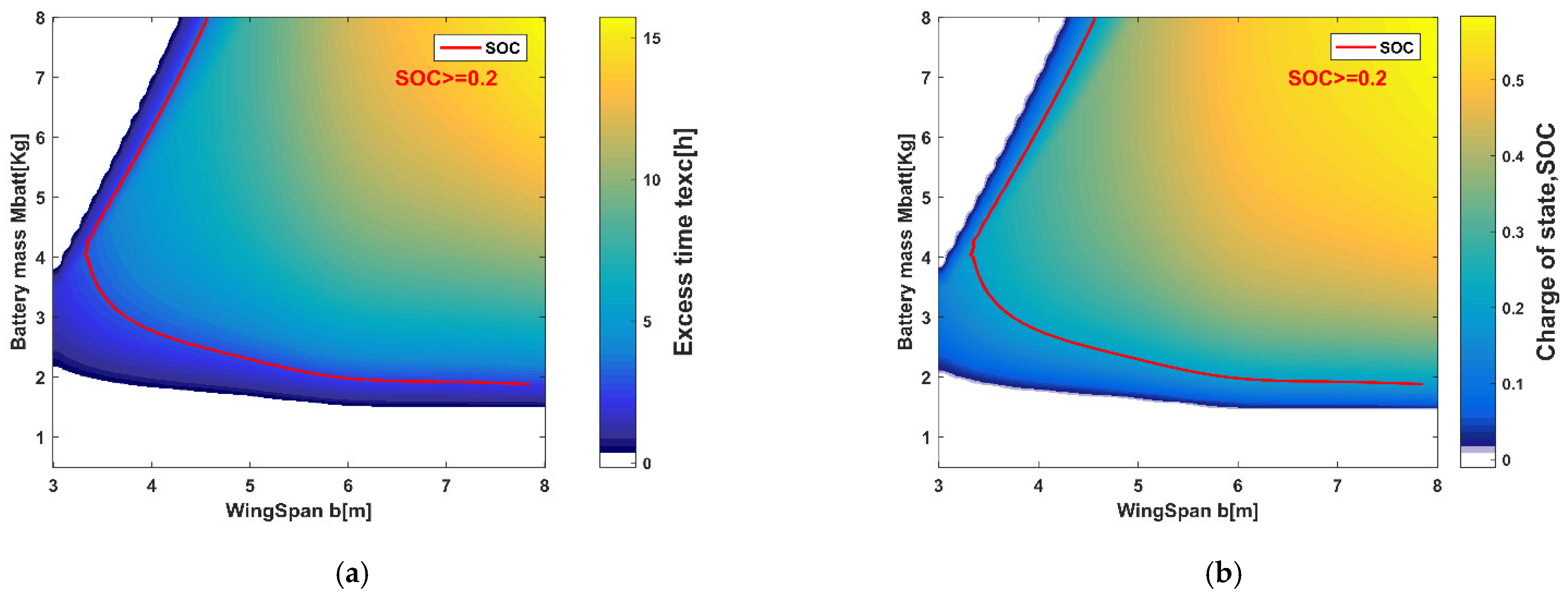
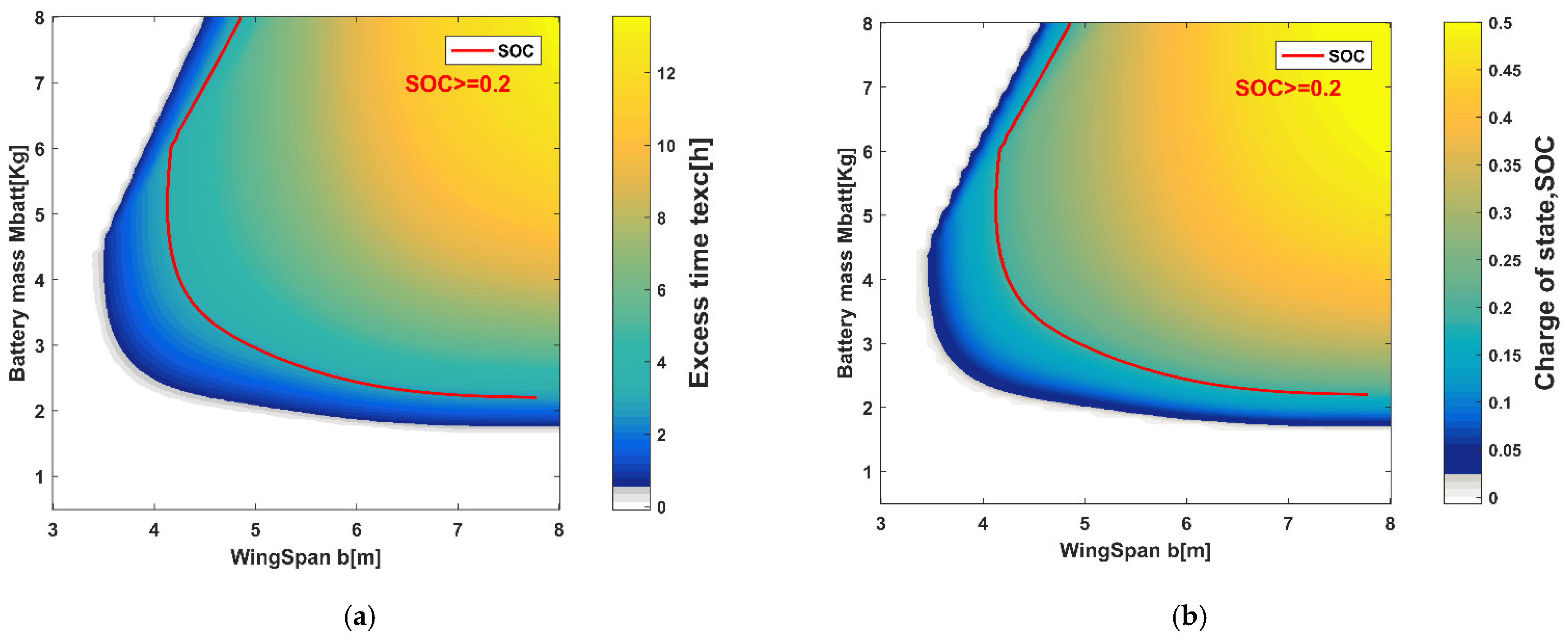

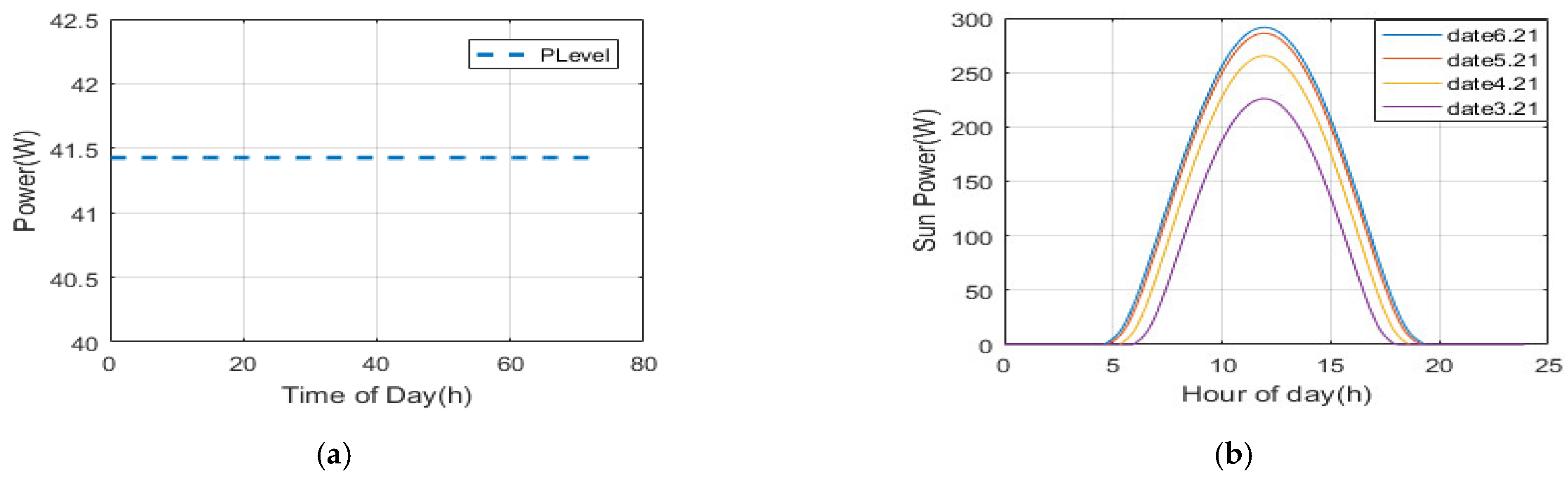
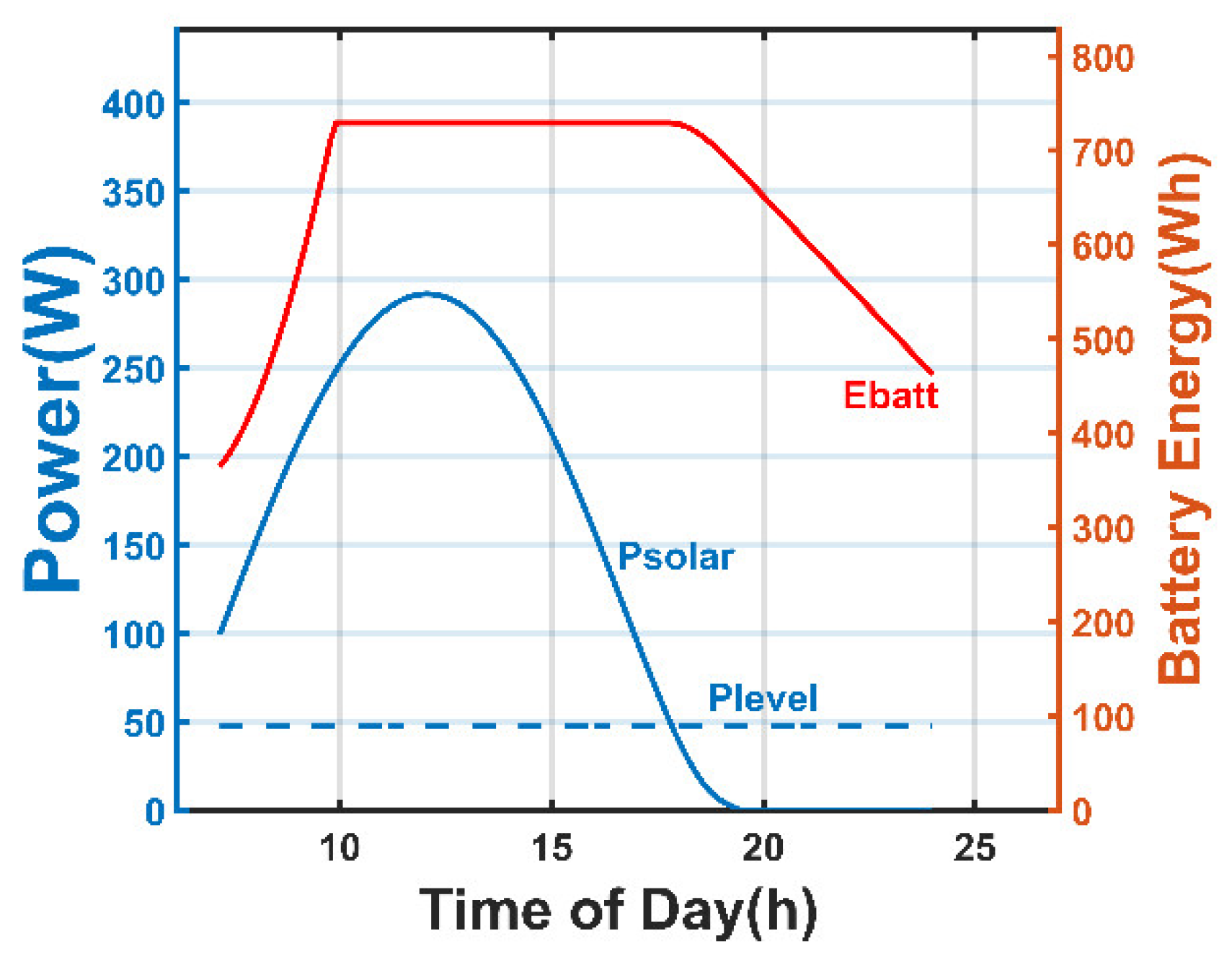

| Parameter | Latitude | Altitude | Visibility | Weather | Wind | Precipitation |
|---|---|---|---|---|---|---|
| Value | 40° (N) | 200 m | 23 Km “transparent” sky | Sunny (almost no clouds) | Level 3 below | No |
| Parameter | ηprop | Pav | Ppld | Cl | Cd | A |
|---|---|---|---|---|---|---|
| Value | 0.7 | 10 W | 0 W | 0.883 | 0.041 | 200 m |
| Parameter | Value |
|---|---|
| Wingspan | 5 m |
| Aspect ratio | 13.3 |
| Wing area | 1.875 m2 |
| Total mass | 6.8 kg |
| Battery mass | 3 kg |
| Level velocity | 8 m/s |
| Solar cell area | 1.688 m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Wu, Y.; Bakar, A.; Wang, S.; Li, Y.; Wen, D. Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles. Aerospace 2022, 9, 331. https://doi.org/10.3390/aerospace9060331
Li K, Wu Y, Bakar A, Wang S, Li Y, Wen D. Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles. Aerospace. 2022; 9(6):331. https://doi.org/10.3390/aerospace9060331
Chicago/Turabian StyleLi, Ke, Yansen Wu, Abu Bakar, Shaofan Wang, Yuangan Li, and Dongsheng Wen. 2022. "Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles" Aerospace 9, no. 6: 331. https://doi.org/10.3390/aerospace9060331
APA StyleLi, K., Wu, Y., Bakar, A., Wang, S., Li, Y., & Wen, D. (2022). Energy System Optimization and Simulation for Low-Altitude Solar-Powered Unmanned Aerial Vehicles. Aerospace, 9(6), 331. https://doi.org/10.3390/aerospace9060331








