Midcourse Iterative Guidance Method for the Impact Time and Angle Control of Two-Pulse Interceptors

Abstract

To address the need for flexible energy management and impact angle control in the midcourse guidance of modern long-range antiballistic interceptors, an impact time and angle guidance law is designed for the exoatmospheric midcourse flight of antiballistic interceptors, which covers two pulse sections and two coast sections. The problem is described as an optimal control model with discontinuities in the system equations at interior points, and an iterative guidance method is used to efficiently solve the two-point boundary value problem. Simulation results demonstrate the effectiveness of the proposed guidance law; the obtained miss distance accuracy has an order of magnitude of 1 m, and the impact angle accuracy has a 1° order of magnitude while the angle can be achieved.

1. Introduction

In the context of modern aerospace vehicle guidance, the search for a larger interception range is the development direction of interceptors. With increasing ranges and flight times, the structures and flight procedures of interceptors are becoming increasingly complex, and flexible energy management is also required. For example, to support the extended range of an exoatmospheric interceptor, additional thrust is provided in a new third stage for the SM-3 vehicle, which contains a dual-pulse rocket motor. Upon separation (the second stage), the first pulse burn of the third-stage rocket motor provides an axial thrust to maintain the vehicle’s trajectory into the exoatmosphere. Upon entering the exoatmosphere, the third stage coasts. If the third stage requires a course correction for an interceptor, the rocket motor begins burning the second pulse. On the other hand, impact angle constraints are widely used in modern guidance law investigations due to their advantages, such as exploiting the weak points of a target, avoiding directional defense mechanisms, addressing seeker positioning and orientation requirements, and pincer attacking [1,2,3,4,5,6,7]. For antiballistic interceptors, it is suitable to carry out impact angle control during midcourse guidance because terminal guidance is realized by a kill vehicle (whose main task is to hit the target) with limited acceleration. Thus, for modern long-range antiballistic interceptors, due to the needs of flexible energy management and impact angle control, higher requirements for midcourse guidance algorithms are proposed.

To the best of the authors’ knowledge, no existing impact angle guidance methods address the multipulse guidance problem with coast sections. Most methods require continuous control and no great changes in speed. Limited published works have addressed the 2D impact angle control guidance problem for an interceptor with a booster [8,9], while research on a 3D multipulse guidance method for an interceptor has yet to be conducted. This paper focuses on the design of impact time and angle guidance laws for an antiballistic interceptor’s exoatmospheric midcourse flight. During this phase, the interceptor flies towards a predicted intercept point (PIP), with strict arrival time requirements and relatively loose impact direction requirements, and all those parameters are given by the command system. Based on iterative guidance methods (IGM), which are under the framework of optimal control and have been successfully applied in real space missions [10], a midcourse guidance law is derived for a two-pulse interceptor against a stationary PIP with impact time and impact angle constraints in this paper. In addition, the proposed iterative guidance method can also be used independently in missions such as multi-interceptor pincer attacks.

The remainder of this paper is organized as follows. In Section 2, the IGM is presented. In Section 3, the simulation results are presented and discussed. Finally, in Section 4, the conclusions are presented.

2. Iterative Guidance Method

2.1. Motion Model

The motion equations of the interceptor are modeled in an earth-centered inertial frame (J2000). $r$ and $v$ are defined as the position and the velocity vectors of the interceptor, respectively. Then, the motion equations of the pulse section can be written as

$$\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{v}=\frac{T}{m_0-m_{d}t}\mathit{l}+\mathit{g}\end{array}$$

(1)

where $m_0$ is the mass of the interceptor when the pulse starts; $T$ is the constant thrust magnitude; $m_d$ is the fuel consumption rate; $\mathit{l}$ is the direction vector of the thrust, which satisfies $\Vert \mathit{l}\Vert =1$; and $\mathit{g}$ is the gravity acceleration vector. The motion equations of the coast section can be written as

$$\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{\mathit{v}}=-\mu \mathit{r}/{\Vert \mathit{r}\Vert }^3\end{array}$$

(2)

The general flight procedure of a two-pulse interceptor in the midcourse guidance phase can be described as “first pulse section + first coast section + second pulse section + second coast section”. Thus, an integrated motion model can be described as

$$\begin{array}{l}\{\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{\mathit{v}}=\frac{T_1}{m_{10}-m_{d1}t}\mathit{l}+\mathit{g}\end{array} ,0<t<t_1\\ \{\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{\mathit{v}}=-\mu \mathit{r}/{\Vert \mathit{r}\Vert }^3\end{array} ,t_1<t<t_2\\ \{\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{\mathit{v}}=\frac{T_2}{m_{20}-m_{d2}t}\mathit{l}+\mathit{g}\end{array} ,t_2<t<t_3\\ \{\begin{array}{l}\dot{\mathit{r}}=\mathit{v}\\ \dot{\mathit{v}}=-\mu \mathit{r}/{\Vert \mathit{r}\Vert }^3\end{array} ,t_3<t<t_{PIP}\end{array}$$

(3)

where $t_1,t_2,t_3$ denote the start or end time of each section and $t_{PIP}$ is the required arrival time.

2.2. Optimization Model

The state variable vector and control variable vector are defined as

$$\mathit{x}=\left[\begin{array}{c}\mathit{r}\\ \mathit{v}\end{array}\right],\mathit{u}=\left[\mathit{l}\right]$$

(4)

The motion equations of the two coast sections can be replaced with algebra equations for the two-body solution, i.e.,

$${\mathit{x}}_t=\mathit{\Phi }\left(\mathit{x},\mathit{t}\right)$$

(5)

where the detailed expressions of the function $\mathit{\Phi }$ and its partial derivative can be found in Appendix A. Thus, the state equations can be written as two pulse section equations with discontinuities in the state variables at interior points, i.e.,

$$\dot{\mathit{x}}=\left[\begin{array}{c}\dot{\mathit{r}}\\ \dot{\mathit{v}}\end{array}\right]=\{\begin{array}{l}{\mathit{f}}^{\prime }=\left[\begin{array}{c}\mathit{v}\\ \frac{T_1}{m_{10}-m_{d1}t}\mathit{l}+\overline{\mathit{g}}\end{array}\right],0<t<t_s\\ {\mathit{f}}^{″}=\left[\begin{array}{c}\mathit{v}\\ \frac{T_2}{m_{20}-m_{d2}t}\mathit{l}+\overline{\mathit{g}}\end{array}\right],t_s<t<t_f\end{array}$$

(6)

$$\begin{array}{l}{\mathit{x}}_{s+}=\mathit{\Phi }\left({\mathit{x}}_{s-},{\delta }^2\right)\\ {\mathit{x}}_{f+}=\mathit{\Phi }\left({\mathit{x}}_{f-},t_{PIP}-{\delta }^2-t_f\right)\end{array}$$

(7)

where $t_s=t_1$ and $t_f=t_1+t_3-t_2$ are specified, while ${\delta }^2=t_2-t_1$ is free. In this paper, we use the subscripts $0,s,f$ to signify variables at the initial, discontinuous, and final points, respectively, and the subscripts + and – signify the variables just before and after discontinuities, respectively. Realistic position-dependent gravity can be approximated as the mean of the gravitation vectors at the initial point ${\mathit{r}}_0$ of the interceptor and at the PIP ${\mathit{r}}_{PIP}$ [10], i.e.,

$$\overline{\mathit{g}}=-\frac{1}{2}\left(\mu {\mathit{r}}_0/{\Vert {\mathit{r}}_0\Vert }^3+\mu {\mathit{r}}_{PIP}/{\Vert {\mathit{r}}_{PIP}\Vert }^3\right)$$

(8)

The optimization goal is to achieve both a zero miss distance and impact angle constraints at a specified terminal time. The impact angle is considered a cost function instead of a terminal constraint in case the expected impact angle cannot be essentially achieved. Thus, the cost function can be written as

$$\max J=\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{\Vert {\mathit{v}}_{f+}\Vert }$$

(9)

where ${\mathit{e}}_d$ represents the desired velocity direction of the interceptor, and the terminal constraint can be written as

$${\mathit{r}}_{f+}-{\mathit{r}}_{PIP}=0$$

(10)

Thus, the optimal control problem with discontinuities in the state variables at interior points can be modeled as

$$\begin{array}{l}\min J=-\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{\Vert {\mathit{v}}_{f+}\Vert }\\ s.t.\dot{\mathit{x}}=\left[\begin{array}{c}\dot{\mathit{r}}\\ \dot{\mathit{v}}\end{array}\right]=\{\begin{array}{l}{\mathit{f}}^{\prime }=\left[\begin{array}{c}\mathit{v}\\ \frac{T_1}{m_{10}-m_{d1}t}\mathit{l}+\overline{\mathit{g}}\end{array}\right],t<t_s\\ {\mathit{f}}^{″}=\left[\begin{array}{c}\mathit{v}\\ \frac{T_2}{m_{20}-m_{d2}\left(t-t_s\right)}\mathit{l}+\overline{\mathit{g}}\end{array}\right],t_s<t<t_f\end{array}\\ \{\begin{array}{l}\Vert \mathit{l}\Vert =1\\ \mathit{\Phi }\left({\mathit{x}}_{s-},{\delta }^2\right)-{\mathit{x}}_{s+}=0\\ {\mathit{x}}_{f+}=\mathit{\Phi }\left({\mathit{x}}_{f-},t_{PIP}-{\delta }^2-t_f\right)\\ {\mathit{r}}_{f+}-{\mathit{r}}_{PIP}=0\end{array}\end{array}$$

(11)

The optimization model needs to be nondimensionalized for numerical computation purposes. The reference variables are chosen as follows:

$$\begin{array}{l}{R}_{ref}=R_e,V_{ref}=\frac{\mu }{R_e{}^2},a_{ref}=\frac{V_{ref}{}^2}{R_{ref}},\\ t_{ref}=\frac{R_{ref}}{V_{ref}},m_{ref}=\frac{m_{10}+m_{20}}{2},T_{ref}=m_{ref}{a}_{ref}\end{array}$$

(12)

Accordingly, the dimensionless variables can be written as

$$\begin{array}{l}\tilde{\mathit{r}}=\frac{\mathit{r}}{R_{ref}},\tilde{\mathit{v}}=\frac{\mathit{v}}{V_{ref}},\tilde{\mathit{t}}=\frac{\mathit{t}}{t_{ref}},\tilde{\mathit{a}}=\frac{\mathit{a}}{a_{ref}},\\ \Delta \widetilde{\overline{\mathit{g}}}=\frac{\Delta \overline{\mathit{g}}}{a_{ref}},{\tilde{m}}_d=\frac{m_d}{m_{ref}/t_{ref}},\tilde{T}=\frac{T}{T_{ref}}\end{array}$$

(13)

Thus, the dimensionless optimization model can be rewritten, and the wavy lines on the variables can be ignored for convenience. Thus, the dimensionless model has the same form as Equation (11).

2.3. Optimal Solution

The optimization model in Equation (11) is solved by applying optimal control theory [11,12], where the concept of a Hamiltonian function and Lagrange multipliers are used to carry out a calculus of variations-based local optimization. Let

$$\phi =-\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{\Vert {\mathit{v}}_{f+}\Vert }+{\xi }^T\left({\mathit{r}}_{f+}-{\mathit{r}}_{PIP}\right)+{\xi }_s{}^T\left[\mathit{\Phi }\left({\mathit{x}}_{s-},{\delta }^2\right)-{\mathit{x}}_{s+}\right]$$

(14)

The Hamiltonian function can be written as

$$\begin{array}{l}{H}^{\prime }={{\lambda }^{\prime }}^T{\mathit{f}}^{\prime }={{\lambda }^{\prime }}_r{}^T\mathit{v}+\frac{T_1}{m_{10}-m_{d1}\left(t-t_s\right)}{{\lambda }^{\prime }}_v{}^T\mathit{l}+{{\lambda }^{\prime }}_v{}^T\overline{\mathit{g}}\\ H^{″}={{\lambda }^{″}}^T{\mathit{f}}^{″}={{\lambda }^{″}}_r{}^T\mathit{v}+\frac{T_2}{m_{20}-m_{d2}\left(t-t_s\right)}{{\lambda }^{″}}_v{}^T\mathit{l}+{{\lambda }^{″}}_v{}^T\overline{\mathit{g}}\end{array}$$

(15)

where ${\lambda }^{\prime }={\left[\begin{array}{cc}{{\lambda }^{\prime }}_r{}^T& {{\lambda }^{\prime }}_v{}^T\end{array}\right]}^T$ and ${\lambda }^{″}={\left[\begin{array}{cc}{{\lambda }^{″}}_r{}^T& {{\lambda }^{″}}_v{}^T\end{array}\right]}^T$ are the adjoint variables. The optimal conditions can be written as

$${{\dot{\lambda }}^{\prime }}^T=-\frac{\partial H^{\prime }}{\partial \mathit{x}},{{\dot{\lambda }}^{″}}^T=-\frac{\partial H^{″}}{\partial \mathit{x}}$$

(16)

$${{\lambda }^{\prime }}_{s-}{}^T=\frac{\partial \phi }{\partial {\mathit{x}}_{s-}},{{\lambda }^{″}}_{s+}{}^T=-\frac{\partial \phi }{\partial {\mathit{x}}_{s+}},{{\lambda }^{″}}_{f-}{}^T=\frac{\partial \phi }{\partial {\mathit{x}}_{f-}}$$

(17)

and

$$\frac{\partial \phi }{\partial \delta }=0$$

(18)

$$\min H^{\prime }\left(\mathit{l}\right),\min H^{″}\left(\mathit{l}\right)$$

(19)

From Equation (16), it can be derived that

$$\{\begin{array}{l}{{\lambda }^{\prime }}_r={{\lambda }^{\prime }}_{r0}\\ {{\lambda }^{\prime }}_v={{\lambda }^{\prime }}_{v0}-{{\lambda }^{\prime }}_{r0}t\end{array},\{\begin{array}{l}{{\lambda }^{″}}_r={{\lambda }^{″}}_{r0}\\ {{\lambda }^{″}}_v={{\lambda }^{″}}_{v0}-{{\lambda }^{″}}_{r0}t\end{array}$$

(20)

From Equation (17), it can be derived that

$$\begin{array}{ccc}{{\lambda }^{\prime }}_{s-}{}^T& =\frac{\partial \phi }{\partial {\mathit{x}}_{s-}}& ={\xi }_s{}^T\frac{\partial \mathit{\Phi }\left({\mathit{x}}_{s-},{\delta }^2\right)}{\partial {\mathit{x}}_{s-}}\\ {{\lambda }^{″}}_{s+}{}^T& =-\frac{\partial \phi }{\partial {\mathit{x}}_{s+}}& ={\xi }_s{}^T\\ {{\lambda }^{″}}_{f-}{}^T& =\frac{\partial \phi }{\partial {\mathit{x}}_{f-}}& =\left(-\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d{}^T+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}{}^T\right)\frac{\partial {\mathit{v}}_{f+}}{\partial {\mathit{x}}_{f-}}+{\xi }^T\frac{\partial r_{f+}}{\partial {\mathit{x}}_{f-}}\\ & & =\left[\begin{array}{cc}{\xi }^T& -\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d{}^T+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}{}^T\end{array}\right]\frac{\partial {\mathit{x}}_{f+}}{\partial {\mathit{x}}_{f-}}\end{array}$$

(21)

From Equation (18), it can be derived that

$$\left[\begin{array}{cc}{\xi }^T& -\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d{}^T+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}{}^T\end{array}\right]\frac{\partial {\mathit{x}}_{f+}}{\partial \delta }+{\xi }_s{}^T\frac{\partial {\mathit{x}}_{s+}}{\partial \delta }=0$$

(22)

From Equation (19), it can be derived that

$$\mathit{l}=-\frac{{\lambda }_{\mathit{v}}}{\Vert {\lambda }_{\mathit{v}}\Vert },{\lambda }_{\mathit{v}}\ne 0$$

(23)

The Jacobian matrixes (detailed expressions can be found in Appendix A) are denoted as

$$\begin{array}{l}{\mathit{J}}_s=\frac{\partial \mathit{\Phi }\left({\mathit{x}}_{s-},{\delta }^2\right)}{\partial {\mathit{x}}_{s-}}\\ {\mathit{J}}_f=\frac{\partial \mathit{\Phi }\left({\mathit{x}}_f,t_{PIP}-{\delta }^2-t_f\right)}{\partial {\mathit{x}}_f}\end{array}$$

(24)

Thus, from Equation (21) we have

$$\begin{array}{l}{\mathit{J}}_s{}^{-T}{{\lambda }^{\prime }}_{s-}={{\lambda }^{″}}_{s+}={\xi }_s\\ {\mathit{J}}_f{}^{-T}{{\lambda }^{″}}_{f-}=\left[\begin{array}{c}\xi \\ -\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}\end{array}\right]\end{array}$$

(25)

By substituting Equation (21) into (20) and denoting ${{\lambda }^{″}}_{f+}={\mathit{J}}_f{}^{-T}{{\lambda }^{\prime }}_{f-}$, the adjoint variables can be expressed as

$$\begin{array}{l}\{\begin{array}{l}{{\lambda }^{\prime }}_r={\lambda }_{r0}\\ {{\lambda }^{\prime }}_{\mathit{v}}={\lambda }_{\mathit{v}0}-{\lambda }_{r0}t\end{array},{{\lambda }^{\prime }}_{s-}=\left[\begin{array}{c}{\lambda }_{r0}\\ {\lambda }_{\mathit{v}0}-{\lambda }_{r0}{t}_s\end{array}\right]\\ {{\lambda }^{″}}_{s+}={\mathit{J}}_s{}^{-T}{{\lambda }^{\prime }}_{s-}\\ \{\begin{array}{l}{{\lambda }^{″}}_r={{\lambda }^{″}}_{rs+}\\ {{\lambda }^{″}}_{\mathit{v}}={{\lambda }^{″}}_{\mathit{v}s+}-{{\lambda }^{″}}_{rs+}\left(t-t_s\right)\end{array},{{\lambda }^{″}}_{f-}=\left[\begin{array}{c}{{\lambda }^{″}}_{rs+}\\ {{\lambda }^{″}}_{\mathit{v}s+}-{{\lambda }^{″}}_{rs+}\left(t_f-t_s\right)\end{array}\right]\\ {{\lambda }^{″}}_{f+}={\mathit{J}}_f{}^{-T}{{\lambda }^{″}}_{f-}\end{array}$$

(26)

Thus, the optimal control expression (23) can be rewritten as

$$\mathit{l}=\{\begin{array}{l}-\frac{{\lambda }_{\mathit{v}0}-{\lambda }_{r0}t}{\Vert {\lambda }_{\mathit{v}0}-{\lambda }_{r0}t\Vert },t<t_s\\ -\frac{{{\lambda }^{″}}_{\mathit{v}s+}-{{\lambda }^{″}}_{rs+}\left(t-t_s\right)}{\Vert {{\lambda }^{″}}_{\mathit{v}s+}-{{\lambda }^{″}}_{rs+}\left(t-t_s\right)\Vert },t_s<t<t_f\end{array}$$

(27)

The state variables can be integrated (by using the expression in Appendix B) as

$$\begin{array}{cc}{\mathit{v}}_{s-}& ={\mathit{v}}_0+{\displaystyle {\int }_0^{t_s}\left(-\frac{T_1}{m_{10}-m_{d1}t}\frac{{\lambda }_{\mathit{v}0}-{\lambda }_{\mathit{r}0}t}{\Vert {\lambda }_{\mathit{v}0}-{\lambda }_{\mathit{r}0}t\Vert }+\overline{g}\right)\mathrm{d}t}\\ & ={\mathit{v}}_0+\overline{g}{t}_s-{\mathit{v}}_T\left(0,t_s,{\lambda }_{\mathit{r}0},{\lambda }_{\mathit{v}0},T_1,m_{10},m_{d1}\right)\\ {\mathit{r}}_{s-}& ={\mathit{r}}_0+{\displaystyle {\int }_0^{t_s}\left({\mathit{v}}_0+\overline{g}\tau +{\displaystyle {\int }_0^{\tau }-\frac{T_1}{m_{10}-m_{d1}t}\frac{{\lambda }_{\mathit{v}0}-{\lambda }_{\mathit{r}0}t}{\Vert {\lambda }_{\mathit{v}0}-{\lambda }_{\mathit{r}0}t\Vert }\mathrm{d}t}\right)\mathrm{d}\tau }\\ & ={\mathit{r}}_0+{\mathit{v}}_0{t}_s+\frac{1}{2}\overline{g}{t}_s{}^2-r_T\left(0,t_s,{\lambda }_{\mathit{r}0},{\lambda }_{\mathit{v}0},T_1,m_{10},m_{d1}\right)\end{array}$$

(28)

$$\begin{array}{cc}{\mathit{v}}_{f-}& ={\mathit{v}}_{s+}+{\displaystyle {\int }_{t_s}^{t_f}\left(-\frac{T_2}{m_{20}+m_{d2}{t}_s-m_{d2}t}\frac{\left({{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{rs+}{t}_s\right)-{{\lambda }^{″}}_{\mathit{r}s+}t}{\Vert \left({{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{\mathit{r}s+}{t}_s\right)-{{\lambda }^{″}}_{\mathit{r}s+}t\Vert }+\overline{g}\right)\mathrm{d}t}\\ & ={\mathit{v}}_{s+}+\overline{g}\left(t_f-t_s\right)\\ & \hspace{0.17em}\hspace{0.17em}-{\mathit{v}}_T\left(t_s,t_f,{{\lambda }^{″}}_{\mathit{r}s+},{{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{\mathit{r}s+}{t}_s,T_2,m_{20},m_{d2}\right)\\ r_{f-}& ={\mathit{r}}_{s+}+{\displaystyle {\int }_{t_s}^{t_f}\left(\begin{array}{l}{\mathit{v}}_{s+}+\overline{g}\left(\tau -t_s\right)\\ +{\displaystyle {\int }_{t_s}^{\tau }-\frac{T_2}{m_{20}+m_{d2}{t}_s-m_{d2}t}\frac{\left({{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{\mathit{r}s+}{t}_s\right)-{{\lambda }^{″}}_{\mathit{r}s+}t}{\Vert \left({{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{\mathit{r}s+}{t}_s\right)-{{\lambda }^{″}}_{\mathit{r}s+}t\Vert }\mathrm{d}t}\end{array}\right)\mathrm{d}\tau }\\ & =r_{s+}+{\mathit{v}}_{s+}\left(t_f-t_s\right)+\frac{1}{2}\overline{g}{\left(t_f-t_s\right)}^2\\ & \hspace{0.17em}\hspace{0.17em}-r_T\left(t_s,t_f,{{\lambda }^{″}}_{\mathit{r}s+},{{\lambda }^{″}}_{\mathit{v}s+}+{{\lambda }^{″}}_{\mathit{r}s+}{t}_s,T_2,m_{20}+m_{d2}{t}_s,m_{d2}\right)\end{array}$$

(29)

It can be derived from Equation (25) that

$${{\lambda }^{″}}_{\mathit{v}f+}=-\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}$$

(30)

Note that $\frac{\partial {\mathit{x}}_t}{\partial t}={\dot{\mathit{x}}}_t$; then, it can be derived from Equation (22) that

$$\delta \left({{\lambda }^{″}}_{s+}{}^T{\dot{\mathit{x}}}_{s+}-{{\lambda }^{″}}_{f+}{}^T{\dot{\mathit{x}}}_{f+}\right)=0$$

(31)

Thus, the optimal condition can be expressed as a function of ${\lambda }_{r0},{\lambda }_{\mathit{v}0},\delta$, i.e.,

$$\{\begin{array}{l}{r}_{f+}-r_{PIP}=0\\ {{\lambda }^{″}}_{\mathit{v}f+}=-\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}\\ \delta \left({{\lambda }^{″}}_{s+}{}^T{\dot{\mathit{x}}}_{s+}-{{\lambda }^{″}}_{f+}{}^T{\dot{\mathit{x}}}_{f+}\right)=0\end{array}$$

(32)

Hence, Equation (32) can be solved for ${\lambda }_{r0},{\lambda }_{\mathit{v}0},\delta$ during each guidance cycle by using algorithms for solving nonlinear equations (a Levenberg–Marquardt algorithm is used in this paper), and the current guidance command can be written as

$$\mathit{l}=-\frac{{\lambda }_{\mathit{v}0}}{\Vert {\lambda }_{\mathit{v}0}\Vert }$$

(33)

It is worth mentioning that all the expressions in Equation (32) are derived analytically following the calculus of variations method, although the equations need to be solved using numerical algorithms.

2.4. The IGM in the Second Pulse Section

After completing the first pulse section, the vehicle coasts until the second pulse is on. The prerequisites for starting the second pulse can be derived using the IGM in the previous section by setting $t_s=0$ in the model. Specifically, the optimal condition can be expressed as a function of ${\lambda }_{r0},{\lambda }_{\mathit{v}0},\delta$, i.e.,

$$\{\begin{array}{l}{r}_{f+}-r_{PIP}=0\\ {\lambda }_{\mathit{v}f+}=-\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}\\ \delta \left({\lambda }_{s+}{}^T{\dot{\mathit{x}}}_{s+}-{\lambda }_{f+}{}^T{\dot{\mathit{x}}}_{f+}\right)=0\end{array}$$

(34)

where

$$\begin{array}{l}{\mathit{x}}_{s+}=\mathit{\Phi }\left(\left[\begin{array}{c}{r}_0\\ {\mathit{v}}_0\end{array}\right]{\mathit{x}}_{s-},{\delta }^2\right)\\ {\mathit{v}}_{f-}={\mathit{v}}_{s+}+\overline{g}{t}_f-{\mathit{v}}_T\left(0,t_f,{\lambda }_{rs+},{\lambda }_{\mathit{v}s+},T_2,m_{20},m_{d2}\right)\\ r_{f-}=r_{s+}+{\mathit{v}}_{s+}{t}_f+\frac{1}{2}\overline{g}{t}_f-r_T\left(0,t_f,{\lambda }_{rs+},{\lambda }_{\mathit{v}s+},T_2,m_{20},m_{d2}\right)\end{array}$$

(35)

$$\begin{array}{l}{\lambda }_{s+}={\mathit{J}}_s{}^{-T}\left[\begin{array}{c}{\lambda }_{r0}\\ {\lambda }_{\mathit{v}0}\end{array}\right]\\ {\lambda }_{f-}=\left[\begin{array}{c}{\lambda }_{rs+}\\ {\lambda }_{\mathit{v}s+}-{\lambda }_{rs+}{t}_f\end{array}\right]\\ {\lambda }_{f+}={\mathit{J}}_f{}^{-T}{\lambda }_{f-}\end{array}$$

(36)

After the solution is obtained, the prerequisites for starting the second pulse can be written as

$$\delta \le 0$$

(37)

Then, we present the IGM for the second pulse section. The optimization model in this section can be rewritten as

$$\begin{array}{l}\min \mathit{J}=-\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{\Vert {\mathit{v}}_{f+}\Vert }\\ s.t.\dot{\mathit{x}}=\left[\begin{array}{c}\dot{r}\\ \dot{\mathit{v}}\end{array}\right]=\mathit{f}=\left[\begin{array}{c}\mathit{v}\\ \frac{T_2}{m_{20}-m_{d2}t}\mathit{l}+\overline{\mathit{g}}\end{array}\right]\\ \{\begin{array}{l}\Vert \mathit{l}\Vert =1\\ {\mathit{x}}_{f+}=\mathit{\Phi }\left({\mathit{x}}_f,t_{PIP}-t_f\right)\\ {\mathit{r}}_{f+}-{\mathit{r}}_{PIP}=0\end{array}\end{array}$$

(38)

where the approximation of gravity is modeled as $\overline{\mathit{g}}=-\mu {\mathit{r}}_0/{\Vert {\mathit{r}}_0\Vert }^3$ for accuracy purposes in this section.

With a derivation similar to that in the previous section, the optimal condition can be expressed as a function of ${\lambda }_{\mathit{r}0},{\lambda }_{\mathit{v}0}$, i.e.,

$$\begin{array}{l}{\mathit{r}}_{f+}-{\mathit{r}}_{PIP}=0\\ {\lambda }_{\mathit{v}f+}=-\frac{1}{\Vert {\mathit{v}}_{f+}\Vert }{\mathit{e}}_d+\frac{{\mathit{e}}_d{}^T{\mathit{v}}_{f+}}{{\Vert {\mathit{v}}_{f+}\Vert }^3}{\mathit{v}}_{f+}\end{array}$$

(39)

where

$$\begin{array}{l}{\mathit{v}}_f={\mathit{v}}_0+\overline{\mathit{g}}{t}_f-{\mathit{v}}_T\left(0,t_f,{\lambda }_{\mathit{r}0},{\lambda }_{\mathit{v}0},T_2,m_{20},m_{d2}\right)\\ {\mathit{r}}_f={\mathit{r}}_0+{\mathit{v}}_0{t}_f+\frac{1}{2}\overline{\mathit{g}}{t}_f{}^2-{\mathit{r}}_T\left(0,t_f,{\lambda }_{\mathit{r}0},{\lambda }_{\mathit{v}0},T_2,m_{20},m_{d2}\right)\end{array}$$

(40)

$$\begin{array}{l}{\lambda }_f=\left[\begin{array}{c}{\lambda }_{\mathit{r}0}\\ {\lambda }_{\mathit{v}0}-{\lambda }_{\mathit{r}0}{t}_f\end{array}\right]\\ {\lambda }_{f+}={\left[\frac{\partial \mathit{\Phi }\left({\mathit{x}}_f,t_{PIP}-t_f\right)}{\partial {\mathit{x}}_f}\right]}^{-T}{\lambda }_f\end{array}$$

(41)

and the current guidance command can be written as

$$\mathit{l}=-\frac{{\lambda }_{\mathit{v}0}}{\Vert {\lambda }_{\mathit{v}0}\Vert }$$

(42)

2.5. The Complete IGM Procedure

The procedure for calculating the guidance command during each guidance cycle is summarized as in Figure 1.

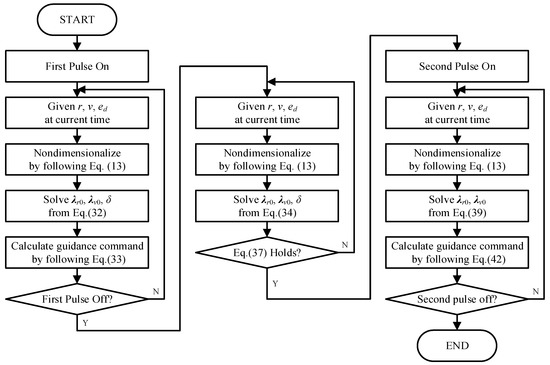
Figure 1. The complete IGM procedure.

3. Simulation Results

In this section, two simulations are carried out to verify the effectiveness of the proposed IGM. The basic performance of the IGM is shown in the first scenario without course correction, while in the second scenario, a course correction is added in the coast section immediately after the first pulse. A square-inverse gravity model is used in the simulation. The state variables of the interceptor can be obtained from its own inertial navigation system, and information regarding the PIP is calculated and provided by the ground system. It is assumed that all information required for the implementation of the proposed guidance law is obtained without noise during the simulations. The update rate of the guidance command is 10 Hz.

3.1. Simulation Conditions

The initial conditions of the simulation are listed in Table 1 and shown in Figure 2.

Table 1. Initial conditions of engagement.

Parameters		Symbol (Unit)	Value
Initial	Position	r0/km	[Re + 65, 0, 0]T
	Velocity	v0/m/s	2500 × [1/√2, 1/√2, 0]T
	Mass	m/kg	125
Pulse 1	Thrust	T1/N	7000
	Specific impulse	Isp1/m/s	2800
	duration	t1/s	7.5
Pulse 2	Thrust	T2/N	7000
	Specific impulse	Isp2/m/s	2800
	duration	(t2 − t1)/s	7.5
PIP	Time	tpip/s	215
	Position	rpip/km	[Re + 300, 0, 500]T
	Desired direction	ed	[0, 0, 1]T
PIP (correction)	Time	tpip/s	215
	Position	rpip1/km	[Re + 320, 20, 520]T
	Desired direction	ed	[0, 0, 1]T

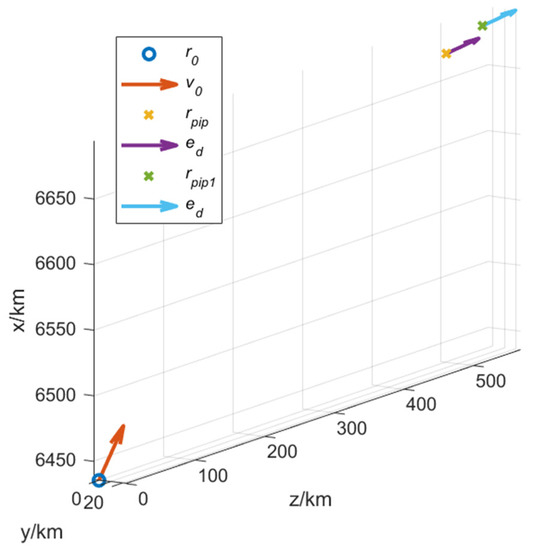
Figure 2. Initial states of the interceptor and the PIP.

3.2. Scenario 1

In this scenario, a normal IGM guidance procedure is performed, where the guidance command in each guidance cycle is calculated during the whole two pulse sections and the first coast section. The simulation results are shown in Figure 3 and Table 2, where the relative position is defined as $\mathit{r}-{\mathit{r}}_{PIP}$. The final position error at the predicted interception time is less than 1 m (measured by distance), and the impact angle error is approximately 1°. The time cost for computing the guidance command in each guidance period is less than 10 ms using a 2.8 GHz CPU.

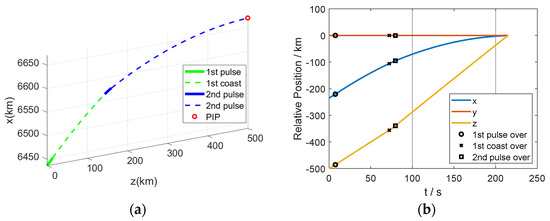
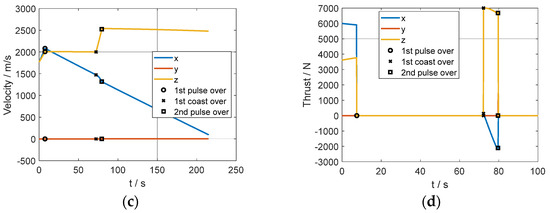
Figure 3. Curves of the state and control variables of the interceptor in scenario 1: (a) trajectory, (b) relative position, (c) velocity, and (d) thrust.

Table 2. Results of the proposed method in scenarios 1 and 2.

Scenario	Duration of the First Coast/s	Position Error/m	Miss Distance/m	Impact Angle Error/deg
1	62.4	[0.2, 0, −0.4]T	0.4	1.2
2	0	[1.2, 0.8, 0.3]T	1.5	5.9

3.3. Scenario 2

In this scenario, the simulation condition and the IGM guidance procedure in the first pulse section are the same as those in scenario 1, while a corrected PIP information is obtained at the beginning of the first coast section. Hence, a course correction is implemented by using the IGM in this simulation. The simulation results are shown in Figure 4 and Table 2. Compared to the results in scenario 1, the start time of the second pulse is modified (immediately after the first pulse) because of the change in the PIP. The final position error at the predicted interception time is approximately 1 m (measured by distance), and the impact angle error is approximately 6 degrees because the speed increment offered by the second pulse is used for PIP correction rather than impact angle control.

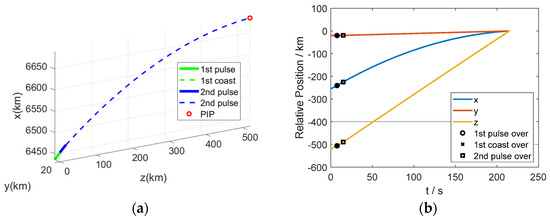
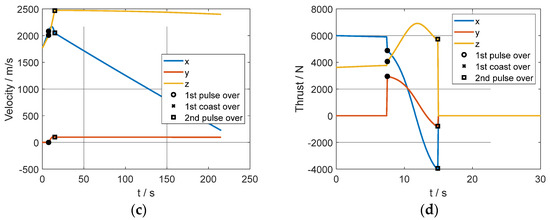
Figure 4. Curves of the state and control variables of the interceptor in scenario 2: (a) trajectory, (b) relative position, (c) velocity, and (d) thrust.

4. Conclusions

An impact time and angle guidance law is designed for the exoatmospheric midcourse flight of antiballistic interceptors; it covers two pulse sections and two coast sections. The problem is described as an optimal control model with discontinuities in the system equations at interior points, and an IGM is used to efficiently solve the two-point boundary value problem. Simulation results demonstrate the effectiveness of the proposed guidance law; the obtained miss distance accuracy has an order of magnitude of 1 m (i.e., the impact time accuracy has an order of magnitude of 1 ms for a 1 km/s speed target), and the impact angle accuracy has a 1° order of magnitude while the angle can be achieved.