Identification Strategy Design with the Solution of Wavelet Singular Spectral Entropy Algorithm for the Aerodynamic System Instability

Abstract

In order to effectively identify the signs of instability in the aerodynamic system of an axial compressor, a wavelet singular spectral entropy algorithm incorporated within the wavelet transform, singular value decomposition and information entropy is proposed to describe the distribution complexity of the spatial modalities in the flow field. This kind of identification design can accurately distinguish the boundary between the stable and unstable states of the internal flow field from the view of a dynamic system. On the basis of the information entropy algorithm, the wavelet singular spectral entropy algorithm is designed to integrate with the advantages of wavelet transform analysis on the time-frequency localization and singular value decomposition for signal processing and data mining together. So that the quantitative analysis of the definition of rebuilding a system image can be achieved by the solution of wavelet singular spectral entropy. This method can automatically extract the transient information of the space mode in the time-frequency domain. It effectively avoids the shortcoming that the feature extraction on spatial information cannot be accomplished from multiple angles with the single information entropy algorithm. In the data processing of instability signals under different speeds, the wavelet singular spectral entropy algorithm shows a greater advantage in the early warning for compressor stall. The result shows that the value of the wavelet singular spectral shows an obvious mutation when the aerodynamic system approaches the instability boundary. According to the threshold set, the identification hybrid algorithm can detect the stall precursor about 23~96 r in advance. Compared to the single information entropy algorithm, the hybrid wavelet singular spectral entropy algorithm is able to shift to an earlier precursor identification by about 11~82 r. This established hybrid identification algorithm accounts for the nonlinearity of the aerodynamic system, providing a new perspective for the nonlinear system instability identification.

1. Introduction

The aerodynamic instability in a compressor is an extremely dangerous operating condition that happens in aircraft engines during operation. When approaching the limitation line of surge or stall in the compressor characteristic line [1], the compressor may lose aerodynamic stability. This kind of destabilization phenomenon can impose a significant mechanical burden on the structure, and lead to the engine becoming out of control, severely limiting the operation safety of the aircraft. Therefore, the identification of the aerodynamic instability of the operating system is of great significance for the normal operation of aircraft. So far, the research in this area has been carried out for years; it is still a challenge to study the essential mechanism of this complex flow phenomenon.

A major breakthrough in the field was the introduction of the concept of active control on surge and stall by Epsein [2]. Rotating stall is a major factor in the entry of the unstable operation, and the investigation has shown that there are two main types of rotating stall [3,4]: modal wave type and spike type. Then, a great deal of research has been carried out to detect stall precursors as early as possible. The most common methods used for detection are correlation analysis, variance analysis, harmonic Fourier transform, wavelet analysis, etc. A discrete form of autocorrelation analysis was applied by Chritensen et al. [5] in the technique of control on a rotating stall in a compressor. Qiu et al. [6] used a combination method of spatial fast Fourier transform and multi-statistical parameters for the analysis. The results showed that a stall precursor was detected about 0.04–0.137 s before stalling in the compressor. The harmonic Fourier mean amplitude method and heterotopic variance analysis were used by Tu et al. [7] to achieve the early detection of a rotating stall in a two-stage axial compressor at low and high speeds. Liu et al. [8] used a fast wavelet analysis to identify spike stall and modal wave stall, obtaining a warning of instability in an axial flow compressor. The wavelet method was adopted by Salunkhe et al. [9] to analyze the mechanism of stall precursors under distortion conditions in a compressor. It was found that the rotating stall inception can be detected 200 revolutions in advance. Although the successes have been achieved by these methods on the identification of a stall precursor, there are still many challenges and difficulties that need to be solved urgently for the diagnosis and prediction of stall inception identification at present. Methods such as correlation analysis and variance analysis mainly consider the information in the time domain. The harmonic Fourier transform method is used to analyze the frequency domain of the signal, while ignoring the relevant information in the time series. Although the wavelet analysis method overcomes the shortcomings of the above methods, the direct filtering provided by the wavelet analysis cannot be obtained from the filtered data to obtain objective information.

Entropy as an effective information feature extraction expression has been widely used in the field of fault identification. It can be measured by entropy for the complexity and uncertainty of a certain state of the system’s signal. It is a useful tool for dealing with compressor instability signals. Anand et al. [10] used the information entropy measurement to quantify the complexity of network system in the physics field. Altaher et al. [11] proposed a real-time anomaly detection system based on the relative entropy. By using the relative entropy and adaptive filter, the dynamical changes can be determined, and the anomaly detection can be achieved in the network. Zhang et al. [12] introduced the sample entropy to investigate the identification method for stall inception. It is proven that, based on the principle of a sample entropy algorithm, the nonlinear characteristic of the rotating stall can be well described. The inception can be suggested by about 12–68 revolutions before the stall arrival. On this basis, a hybrid neural fusion network was proposed by Zhang to represent the properties of a compressor system by artificial intelligence learning [13]. By taking the identification strategy with sample entropy and a difference quotient criterion, an inception warning can be suggested in advance with a multi-step prediction of a neural network. Although the entropy algorithm can reflect a better effect on the expression of the system nonlinearity, it is difficult to cope with the uncertainty of the instability signal by only depending on a single entropy algorithm for the feature extraction, due to the complexity of the internal flow field of the compressor. This kind of shortcoming easily leads to problems such as the slow computation efficiency, thus failing to guarantee the accuracy and effectiveness of the precursor identification in the compressor, particularly for the spike type stall.

In reference [14], wavelet transform was performed with a local analysis without losing the time-frequency information in the signal. Chen [15] used wavelet transform to decompose the data signal to obtain necessary frequency details, improving the accuracy of classification and detection for fault. Because of its time-frequency function and refinement capability, the wavelet transform is widely used in the analysis of non-stationary signals and processing with its nature of being adaptive to the signal [16,17,18]. However, under the only consideration with the wavelet transform, it may cause the problem of overlapping information features. Singular value decomposition (SVD) can exploit the signal characteristic with time-frequency information, showing a good denoise effect. A multi-resolution algorithm was presented by Xie et al. [19] with a combination of singular spectrum analysis and information entropy. Through the processing of a mechanical vibration signal, it was found that the algorithm could effectively characterize the internal information of the system, and could be used as the basis for identifying the operating state of the equipment. Aiming at the deficiency of information entropy, He et al. [20] integrated the wavelet transform with singular value decomposition to address the shortcoming. By proposing indexes of wavelet transform and singular value decomposition to reflect different characteristics of information [21,22], it provides a technique for the detection and classification of faults in the analysis of transient signal.

Therefore, from the perspective of the energy variation of the traveling wave in the system, in this paper the dynamic pressure signal in the circumference is converted into the spatial mode of the dynamic system in the flow field. Although the time domain information of the spatial mode is analyzed by the information entropy algorithm, the characteristic information may be ignored, which is contained in the frequency domain. Because of this weakness, the information entropy algorithm may not accurately achieve the nonlinear information at the short length scale. As the continuation and deepening of previous research [12], the main purpose of this paper is to seek a more reliable entropy algorithm to identify compressor stall precursors. In order to capture the sensitive instability signal more effectively, a mixed information entropy methodology is proposed and subsequently combined with wavelet transform and singular value decomposition, namely as wavelet singular spectral entropy (WSE). The wavelet time-frequency diagram of the spatial mode can be obtained by using wavelet transform to reflect the process of the occurrence of a rotating stall in the system of the compressor. By observing the transformation of a time-frequency diagram in the state space, the omen of system instability could be tracked in recognition of the entropy algorithm and identification strategy.

The organization of this paper can be described as follows. Firstly, an introduction of the basic theory of wavelet singular spectral entropy algorithm is described. Then, the spatial mode acquisition process is introduced during the rotating stall in the experiment. Next, the wavelet singular spectral entropy analysis is carried out on the detection of stall inception. As to prove the superiority of the WSE algorithm, it is compared with the single information entropy algorithm for the detection of rotating stall inception. The simulation experiments verify that the mixed WSE algorithm can identify the stall precursor of the compressor more effectively at different speeds. Finally, the discussion and conclusion on the identification of stall inception with the mixed WSE algorithm are presented.

2. Definition of Information Entropy Algorithm

Information entropy (IEn) is a measurement algorithm of the uncertainty of state information in a system by using the probability distribution. It is a concept derived from thermodynamics. Aiming to solve the problem of measuring the uncertainty state in a time series, it is suitable for the state recognition of a time series.

The information entropy algorithm is defined as follows:

Let A = {a₁, a₂,⋯, a_m} be the m dimensional sampled random signal, in which each a_j (j = 1, 2,⋯, m) can treated as a state mode. Thus, it may contain m sorts of possible state modes in set A. Appropriately, define the dataset P = {p₁, p₂,⋯, p_m}, where p_j (j = 1, 2,⋯, m) denotes the variable of probability distribution corresponding to these state modes. The probability distribution value p_j (j = 1, 2,⋯, m) must satisfy the condition with $0\le p_j\le 1\cup {\displaystyle \mathit{\sum }_{i=1}^n{p}_j}$. Then the information contained in the possible state patterns in set A is noted as, I(a_i) = −ln p_j, j = 1, 2, …, m.

In general, the amount of uncertain information contained in the random variable A is referred to as the self-information I(A). It is denoted by I(A) as the magnitude of the amount of information occurring in a given random event. In order to make the analyzed signal sequence more statistical, the expression of the information entropy algorithm [23] is given as:

$$H(A)=-{\displaystyle \mathit{\sum }{p}_j}\ln p_j,j=1,2,\cdots ,m.$$

(1)

According to the expression of the information entropy algorithm, it can be seen that the smaller the information entropy, the greater the uncertainty of the information contained in the signal of the system. Therefore, the method of information entropy can characterize the uncertainty of the global distribution as a quantitative index of the information content of the system. If the amount of information being analyzed is more homogeneous, and the layout is more regular, then the corresponding information entropy will be computed to be larger. On the contrary, the more uneven the amount of information analyzed, the smaller the information entropy. Therefore, the information entropy algorithm is used in this paper to describe the amount of information reflected by the spatial mode of the flow field. The detection on the stall inception would be achieved with the observation of information entropy variation.

3. Methodology of Wavelet Singular Spectral Entropy Algorithm

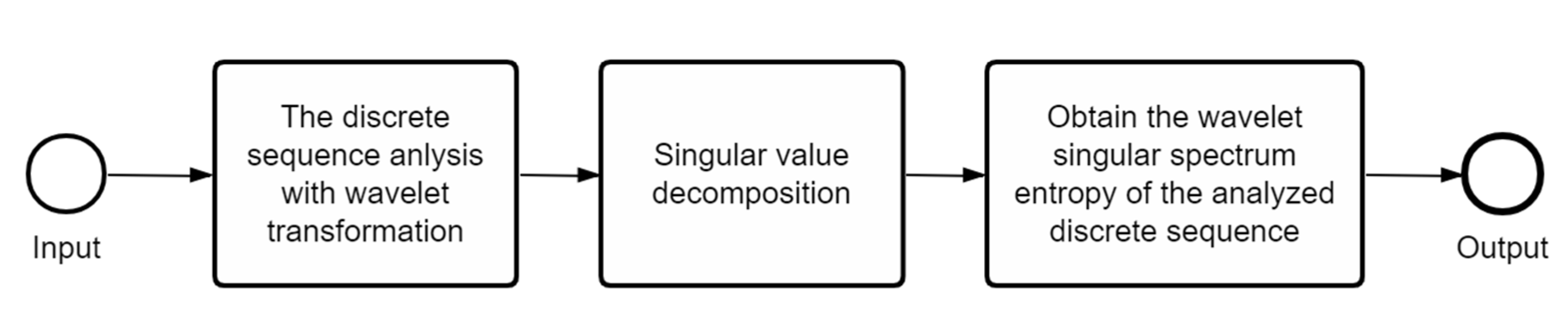
Wavelet singular spectral entropy (WSE) is an algorithm combining wavelet transform and singular value decomposition with the information entropy. Its main idea is to transform the coefficient matrix of wavelet transform into a series of probability distributions, then decompose the sequence of probability distributions into a set of singular values which can reflect the basic characteristic of the original signal through singular value decomposition. Finally, the uncertainty of the singular values of this dataset is simulated with the algorithm of the information entropy, which behaves with a degree of complexity in the time sequence of system. The procedure of data processing is expressed in the following description.

3.1. The Wavelet Transform

The wavelet transform (WT) is a technique for time-frequency localization analysis of signals. It decomposes the signal on multiple scales by means of translation and scaling operation, achieving frequency subdivision at a low frequency and time subdivision at a high frequency. It can be adaptively adjusted to the requirement of time-frequency analysis of the signal.

Suppose the system signal in the time series to be x(1), x(2), …, x(n), the continuous wavelet transformation [24] of the basic wavelet function $\psi (t)$ is defined as:

$$W_x(a,b)=<x,{\psi }_{a,b}(t)>={\displaystyle \underset{t\in R}{\int }x(t)\psi }(t)dt,$$

(2)

where ${\psi }_{a,b}(t)$ denotes the function family formed by the basic wavelet $\psi (t)$ through the scale factor a and the translation factor, the symbol < > indicates the sign of the inner product, $\overline{\psi }\left(t\right)$ is the complex conjugate function of $\psi \left(t\right)$ which is expressed as:

$$\psi (t)={\left|a\right|}^{-\frac{1}{2}}\psi (\frac{t-b}{a})dt.$$

(3)

The discrete wavelet transformation is obtained by discretizing the continuous wavelet transform as follows:

$$D_x(i,j)=<x,{\psi }_{i,j}(t)>={\displaystyle \underset{t\in R}{\int }x(t){\overline{\psi }}_{i,j}}(t)dt,$$

(4)

where ${\psi }_{i,j}\left(t\right)$ is the discrete wavelet and ${\overline{\psi }}_{i,j}\left(t\right)$ is the complex conjugate function of ${\psi }_{i,j}\left(t\right)$. Generally,

$${\psi }_{i,j}(t)=a_0^{-\frac{i}{2}}\psi (a_0^{-i}t-j{b}_0), a_0,b_0>0; i,j\in Z.$$

(5)

The discrete wavelet transform is used for multi-scale analysis of the signal x(n), and the signal is decomposed on the k-scale to obtain the low-frequency part A_i and the high-frequency part D_i. If required for a further solution, a further effort can be made to decompose the low-frequency part of the previous into the low and high parts. With the procedure repeated, the wavelet coefficient reconstruction matrix needed can be constituted by the low-frequency parts and the high-frequency parts. Then, the decomposition relation of the system signal is obtained with x(n) = D₁ + D₂ + … + D_k + A_k. The m-order wavelet coefficient reconstruction matrix is obtained under the k-scale.

3.2. Singular Value Decomposition

According to the singular value decomposition theorem [25], for any matrix W with n × m order where the elements belong to the real or complex field, there must exist a kind of decomposition so that the matrix can be decomposed into the formula [26] as:

$$W=E\Sigma F^T,$$

(6)

where the matrix Σ is the h × h order diagonal matrix, E is the n × h order orthogonal matrix, and F^T is the transpose of the h × m orthogonal matrix. The elements λ_j (λ_j ≥ 0, j = 1, 2,⋯, h) in the main diagonal of the matrix Σ are called the singular eigenvalues of the matrix W. This kind of solution is named the singular value decomposition of the matrix.

3.3. Wavelet Singular Spectral Entropy

Combined with the wavelet transform and singular value decomposition, the mixing information entropy is represented in this part. For the discrete sequence, the corresponding calculation steps of the wavelet singular spectral entropy algorithm are suggested as follows:

(1)

The processing of the signal sequence x(1), x(2), …, x(n) is conducted by wavelet transform. The wavelet basis function is selected for scale decomposition to obtain the wavelet coefficient reconstruction matrix W_(k+1),n;

(2)

The singular eigenvalue matrix Σ is achieved by the use of singular value decomposition theory with the wavelet coefficient reconstruction matrix. Then the elements λ_j (λ_j ≥ 0, j = 1, 2, …, h) are obtained on the main diagonal of matrix Σ;

(3)

Normalize the singular eigenvalues obtained in step (2), which is defined as Equation (7):

$$p_m=\frac{{\lambda }_m}{{\displaystyle \mathit{\sum }_{i=1}^r{\lambda }_i}}\left(r\le h\right),$$

(7)

where r denotes the rank of matrix Σ;

(4)

Finally, the wavelet singular spectral entropy of the discrete sequence x(1), x(2), …, x(n) is calculated, as shown in Equation (8):

$$WS{E}_r={\displaystyle \mathit{\sum }_{m=1}^r{p}_m}\ln p_m\left(r\le h\right),$$

(8)

where p_m satisfies the condition of $0\le p_m\le 1$, ${\displaystyle \mathit{\sum }_{m=1}^r{p}_m}=1$.

In summary, the procedure diagram of the calculation based on the wavelet singular spectral entropy algorithm is described in Figure 1.

In the analysis of signals in the time and frequency domains, the wavelet transform has an excellent localized analysis ability for the processing of unsteady time-frequency signals. The time-frequency window can be adjusted to decompose the analyzed signal into different frequency bands, so as to obtain the dynamic information that changes with time. By reflecting the basic characteristic of the mode of time-frequency signal by singular value decomposition, information entropy has the property of providing a statistical analysis of the overall distribution of the signal. Therefore, the wavelet singular spectral entropy can better portray the complexity of discrete signals under singular spectral division. The more complex the mode of the signal is, the more dispersed the energy distribution is, and the larger the corresponding wavelet singular spectral entropy is. On the contrary, the more concentrated the energy distribution of the signal, the smaller the corresponding wavelet singular spectral entropy.

Compared with the single information entropy algorithm, the mixed wavelet singular fusion entropy is a statistical information analysis of the exploitation of the instability of information in discrete signals. Through subsequent investigation of the spatial modes of flow field in the compressor, it is found that the wavelet singular spectral entropy mixture algorithm is more suitable for the identification of the internal instability sign of the compressor system.

4. Data Acquisition Introduction in Experiment

The subject of this paper is a low-speed axial compressor, which is adopted in the literature [27] as the same test rig. It consists of a single stage with 19 rotor blades and 13 stator blades with a design speed of 3000 rpm. The rotor diameter is 450 mm with the hub-tip ratio to be 0.75. The Reynolds number is about 2 × 10⁵ in the rotor tip chord. A detailed description of the test rig is introduced in the literature [27]. The relevant geometric parameters of the research object are listed in

Table 1. Brief introduction of the geometric parameters.

Parameter	Value
Design speed n (rpm)	3000
Outer diameter D (mm)	450
Blade height h (mm)	56
Tip speed (m/s)	70.7
Hub-tip ratio	0.75
Rotor blade number	19
Stator blade number	13

for a brief introduction.

The acquisition points are uniformly located at circumferential positions on the casing with five Kulite dynamic pressure sensors to measure the dynamic pressure. In order to sensitively detect the variation of pressure, the acquisition locations of the signal are placed at the leading edge of the rotor tip. With the establishment of a high-speed data acquisition system in the compressor, the pressure data in the process of rotating stall are recorded at different working rotating speeds. A large amount of noise information may be mixed in the process of experimental data collection, and it needs to be filtered out by low-pass filtering to remove high frequency noise. As to preserve the instability information, the low-pass filtering is selected to be 200 Hz as the cut-off frequency. Based on the pressure data collected by five monitoring points in the circumference, the pretreatment is conducted in data fusion of a traveling wave extracted by discrete Fourier transform (DFT). The mentioned high Reynolds number means the turbulence in the flow field of the tip. This requires an efficient method with processing for the nonlinear data. The evolution of the compressor system is portrayed to reveal the occurrence process of stall inception from the perspective of modal wave energy, which is described subsequently in next section.

5. Analysis on the Spatial Mode of Flow Field

In this section, the pressure signals from the above experiment are converted into the spatial mode in the form of a traveling wave. The amplitude of the first-order spatial mode is analyzed in the time and frequency domains to reflect the occurrence process of the stall inception from the perspective of modal wave energy in the system. It provides a prerequisite for the identification of rotating stall precursors.

5.1. Feature Extraction of Spatial Mode in Time-Domain

The theory of spatial mode given by Longly [28] provides an effective way to analyze the stall microcells which can be expanded into a superposition of multiple harmonics during instability development. The spatial mode amplitude of each order of traveling waves is extracted through the discrete Fourier transform after filtering the multiple signals accordingly. Then a measurement for the spatial mode can be obtained to reflect the state of the compressor system, with its mathematical expression indicated in Equation (9):

$$a_m=\frac{1}{N}{\displaystyle \mathit{\sum }_{j=1}^N{\Phi }_j}{e}^{-\frac{i2\pi mj}{N}},$$

(9)

where am denotes the m-order spatial mode amplitude, N is the number of dynamic pressure sensors (N = 5), and Φ_j indicates the flow coefficient computed from the signal of the j-th dynamic pressure sensor.

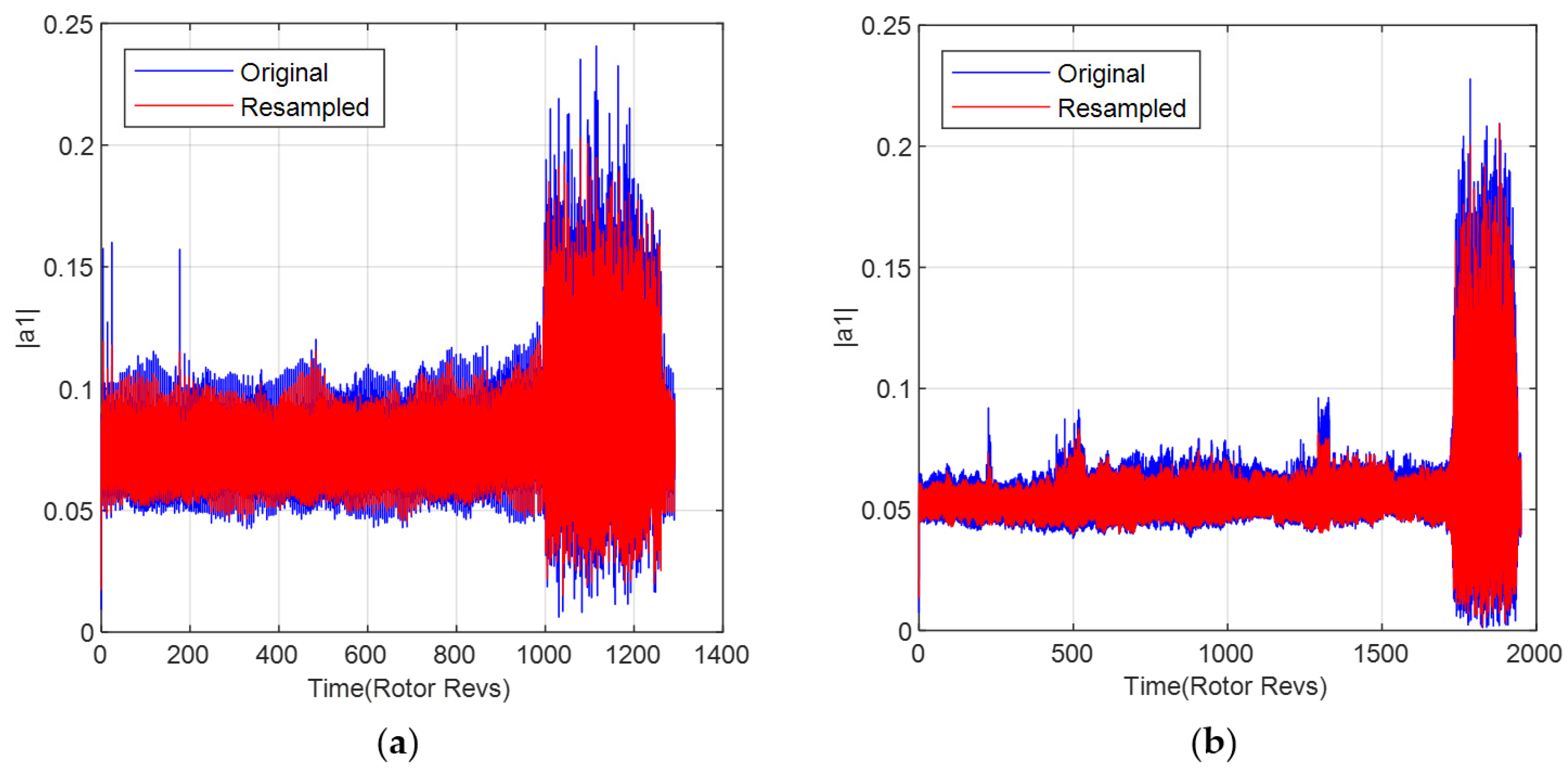
According to Equation (9), the first several orders of space mode can be theoretically obtained. Due to the symmetry of discrete Fourier transform, and the mapping effect from high-order modal energy to low-order modal energy, the follow-up discussion is mainly focused on the variation of first-order spatial mode within the system at various speeds based on the previous investigation [12]. In order to speed up the calculation speed of the input and output of the sampling data, the amplitude of the first-order spatial mode is resampled, and the sampling frequency is set to 500 Hz. Taking the results of two rotation speeds as an example, the amplitude $\left|a_1\right|$ of the first-order spatial mode in time-domain is revealed in Figure 2. It can be observed from the figures that the wave pulsation begins to appear in the flow field, when the compressor system approaches the instability boundary from the normal working state. With the appearance of the stall traveling wave propagating along the circumferential direction of the compressor, an obvious rise of the amplitude is observed for the modal energy. From Figure 2a, before 998.75 r of the experiment, the compressor was in normal operation. It exhibits smooth fluctuations during the transition from normal operating conditions to a rotating stall. When entering the rotating stall stage, the modal amplitude starts to fluctuate greatly. The same analysis is also confirmed in the literature [13], showing the repeatability of the reported results. It is concluded that the essential characteristic of the compressor system is captured by the increment in amplitude of modal energy in the gradual process of stall development. Therefore, the information of spatial modal amplitude in the time-domain can be used as a key parameter for the identification of the occurrence of compressor system instability. The energy of spatial mode exceeds a certain value with a large pulsation, corresponding to the boundary of flow instability.

5.2. Feature Analysis of Spatial Mode with Time-Frequency Information Extraction

The mechanism of the stall inception is more complicated and more difficult to assess quantitatively. It is composed of a short length scale vortex, especially for the spike type which is a local disturbance traveling at a higher speed. The characteristic in the time-domain of the first-order spatial mode is discussed above, but it may likely ignore the more valuable information feature in the frequency domain if only depending on the time-domain analysis. In order to obtain the time-frequency characteristic of the spatial mode, the time-frequency analysis of the first-order spatial mode is carried out by using wavelet transform.

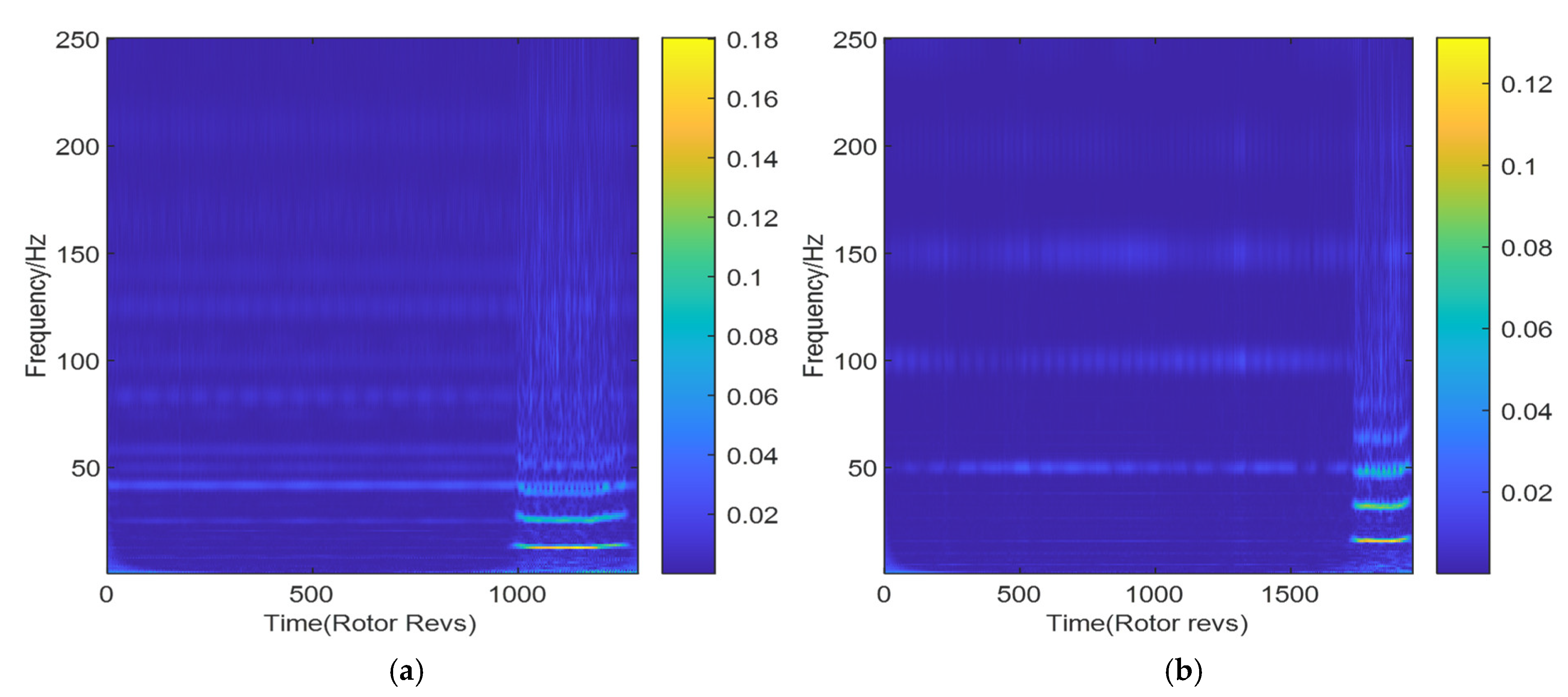
Taking the first-order modal measurement at a speed of 2500 rpm as the research object, the time-frequency diagram of the first-order spatial mode is obtained as shown in Figure 3a. The time-frequency diagram shows that the stall frequency and its multiplier components can be clearly achieved. A characteristic frequency with 15 Hz appeared around 998.75 r, which is consistent with the results in the analysis of the time domain. Combined with the analysis of the time and frequency domains, it can be judged that the instability boundary of the compressor is located at the time of 998.75 r at the speed of 2500 rpm. It indicates that the traveling wave propagates along the circumferential direction of the compressor with the 15 Hz, corresponding to the rotation of the stall cell. Simultaneously, the time-frequency diagram of the first-order spatial mode is exhibited in Figure 3b with a rotation speed of 3000 rpm. When the compressor system enters into the stability, the interference components of amplitude and frequency are significantly enhanced. It is concluded that the location of flow losing its stability is recognized at the beginning of 1732 r.

On the basis of the results of the time-frequency analysis of the first-order spatial mode, the regular pattern can be well reflected during the occurrence of the rotating stall in the aerodynamic system. It is relatively easy to extract features directly from the first-order mode in the time domain; meanwhile, the correspondence between time series and mode features can be obtained. Furthermore, the initiation point of each frequency component of the first-order mode can be directly and quantitatively evaluated in the operation of the time-frequency domain. The energy reflections in the time-frequency domain do not overlap and interfere with each other, and contain more intuitive information. In order to capture the sensitive instability signal more effectively, this paper will contrast the effects of wavelet singular spectral entropy based on time-frequency analysis and information entropy based on time domain analysis on the identification of stall inception in subsequent chapters.

6. Identification Strategy Design with Recognition Algorithms

So as to achieve a more effective method of identification of instability precursors, the information entropy algorithm and wavelet singular entropy algorithm are used to realize recognition based on the analysis of the first-order spatial mode in the time and time-frequency domains. From different perspectives of energy, the goal of this paper is to provide a more accurate algorithm for realizing the stall precursor of the compressor system. Therefore, a mixed information entropy methodology is proposed combined with wavelet transform and singular value decomposition. For the sake of proving the superiority of the wavelet singular entropy algorithm, it is compared with the single information entropy algorithm for the detection of rotating stall inception.

6.1. Parameter Selection on Wavelet Singular Spectral Entropy

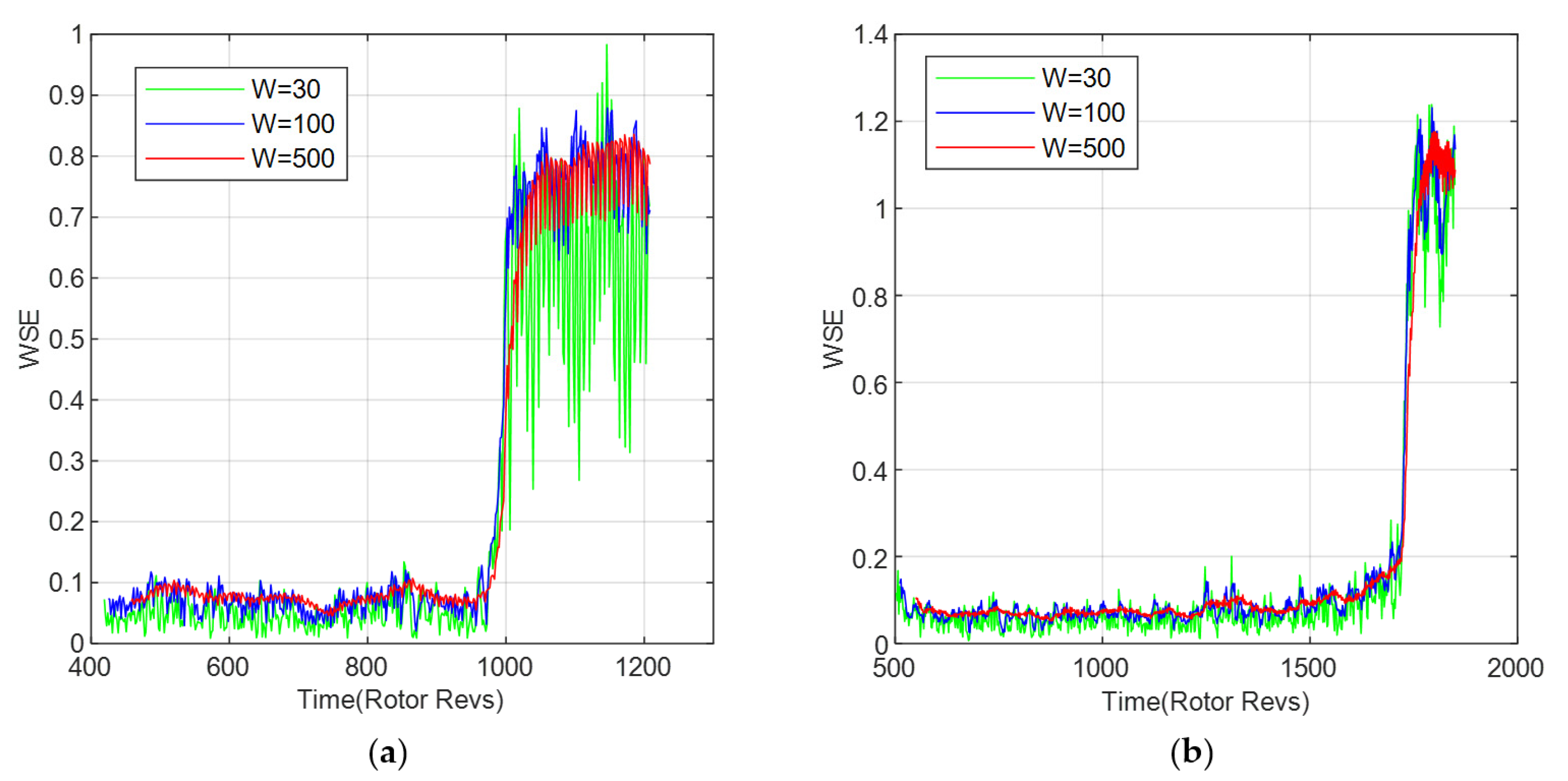
In the process of calculation on the first-order spatial mode with the wavelet singular spectral entropy, a sliding window needs to be set, and the wavelet singular spectral entropy is calculated for each small window. The variation of wavelet singular spectral entropy can be observed by moving the sliding window. Considering that the width of the sliding window may affect the performance of wavelet singular spectral entropy on identification, the selection of the window parameter should be conducted first. Therefore, the procedures of wavelet singular spectral entropy analysis with parameter selection are performed below by changing the width of the window at 2500 rpm and 3000 rmp. Figure 4 shows the results with sliding window widths of 30, 100, and 500, respectively.

As can be seen from the figures, when the width of the sliding window increases, the range of fluctuation in entropy decreases accordingly. In summary, the more periodic cycles contained in width of the sliding window, the less influence can be obtained on the singular characteristic, resulting in a reduction of entropy fluctuation naturally. However, the selection with an oversize width of the sliding window is not necessary for the variable detection. For instance, when the width of the sliding window is chosen as 500, the curve of entropy becomes smooth, thus reducing the recognition sensitivity. Contrarily, if the window width is too small, the entropy value may fluctuate greatly. This will easily weaken the recognition accuracy on the instability boundary. Therefore, with an overall consideration, the window width of 100 is selected in this paper to perform wavelet singular spectral entropy analysis in spatial mode.

6.2. Wavelet Singular Mixed Entropy Identification Algorithm

On the basis of the theoretical analysis in the previous description, the wavelet singular spectral entropy algorithm is adopted in this this section to effectively identify the compressor instability signal based on the characteristic of the first-order spatial pattern in the time-frequency domain. In order to improve the accuracy of the recognition resolution, the first-order modality includes a noise reduction. The width of the sliding window is set to be 100 with a sliding step of 20. 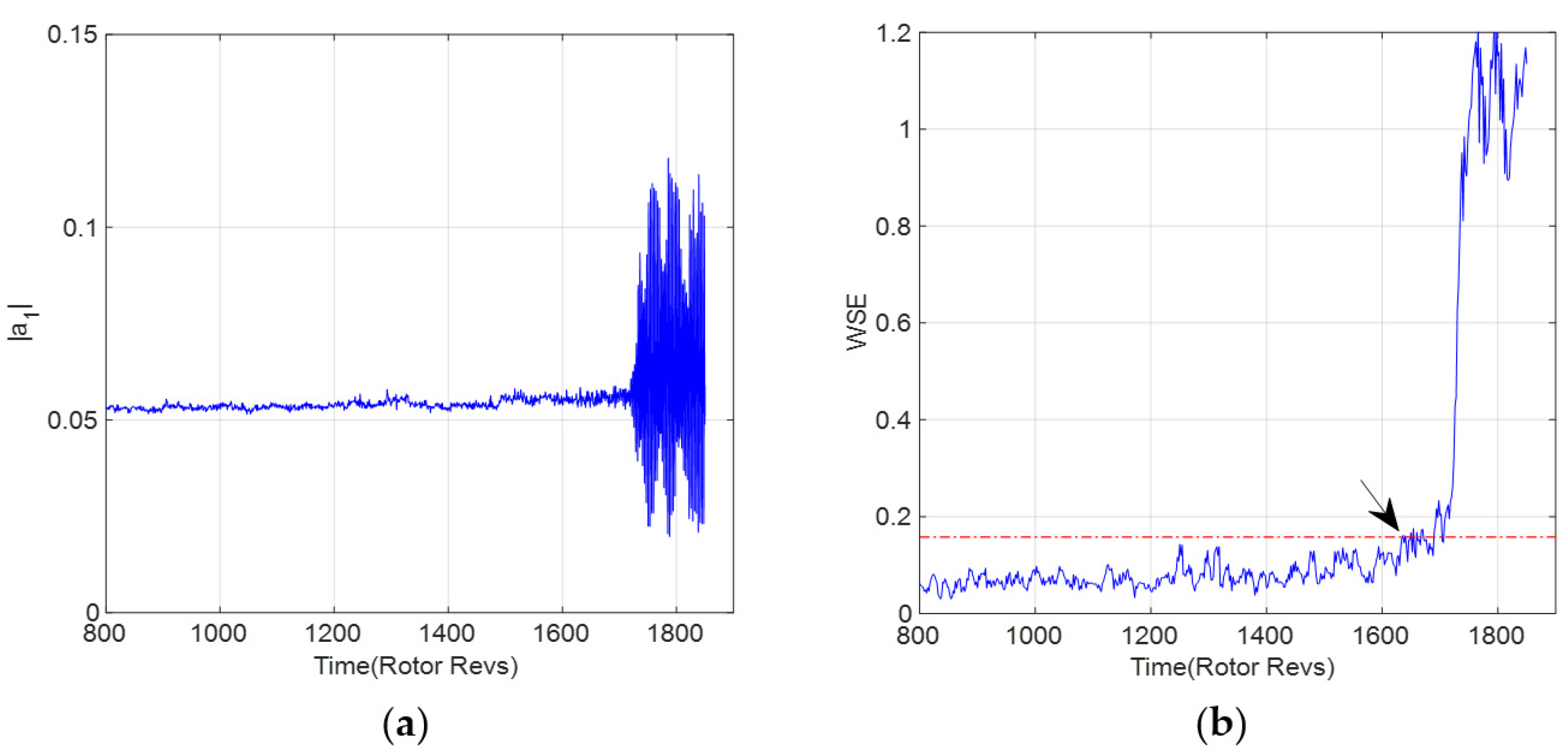The singular eigenvalues in each window are obtained as shown in Figure 5. It can be seen that when the compressor system steps into the unstable state, the singular value increases obviously. Therefore, the singular value can be effectively extracted as the characteristic of the instability signal and it can be used to quantitatively distinguish the instability state. By a combination with wavelet transform and information entropy, the evolution processes of WSE under different rotational speeds are computed, as shown in Figure 6 and Figure 7. The boundary is then distinguished between the stable and unstable states of the internal flow field from the view of a dynamic system.

The energy distributions of wavelet singular spectrum entropy are indicated above under different rotational speeds. It can be seen from the figures that when the compressor system is in a normal state, the first-order spatial mode is relatively stable. The difference between the wavelet singular spectral entropy values in each window is very small, so the energy distribution of the flow field is almost in equality. It can be reflected by a small oscillation on the amplitude of the wavelet singular spectral entropy, remaining in a relatively stable level through time variation. When the aerodynamic system is close to the stall boundary, the time-frequency distribution of the spatial mode is more complex than that of the normal state. The entropy increases obviously, corresponding to the wavelet singular spectrum. By observing the change of the wavelet singular entropy, the previous theoretical analysis is verified exactly. This kind of phenomenon with mutation can better distinguish the initial disturbance of instability from the normal state in general.

In order to realize the identification of compressor rotating stall inception, it is necessary to set a threshold for the identification strategy with wavelet singular spectral entropy. According to the $3\sigma$ principle, the recognition threshold ε is set as the mean value plus three times the standard deviation, and the WSE under normal conditions is taken as the benchmark. The calculation formula is indicated as:

$$\epsilon =(3\sigma +\overline{w}),$$

(10)

where $\sigma$ expresses the standard deviation, and $\overline{w}$ represents the mean value of the WSE in normal conditions. The location where WSE is greater than the set threshold is considered the stall precursor of the compressor system, as indicated by the arrows in Figure 6b and Figure 7b.

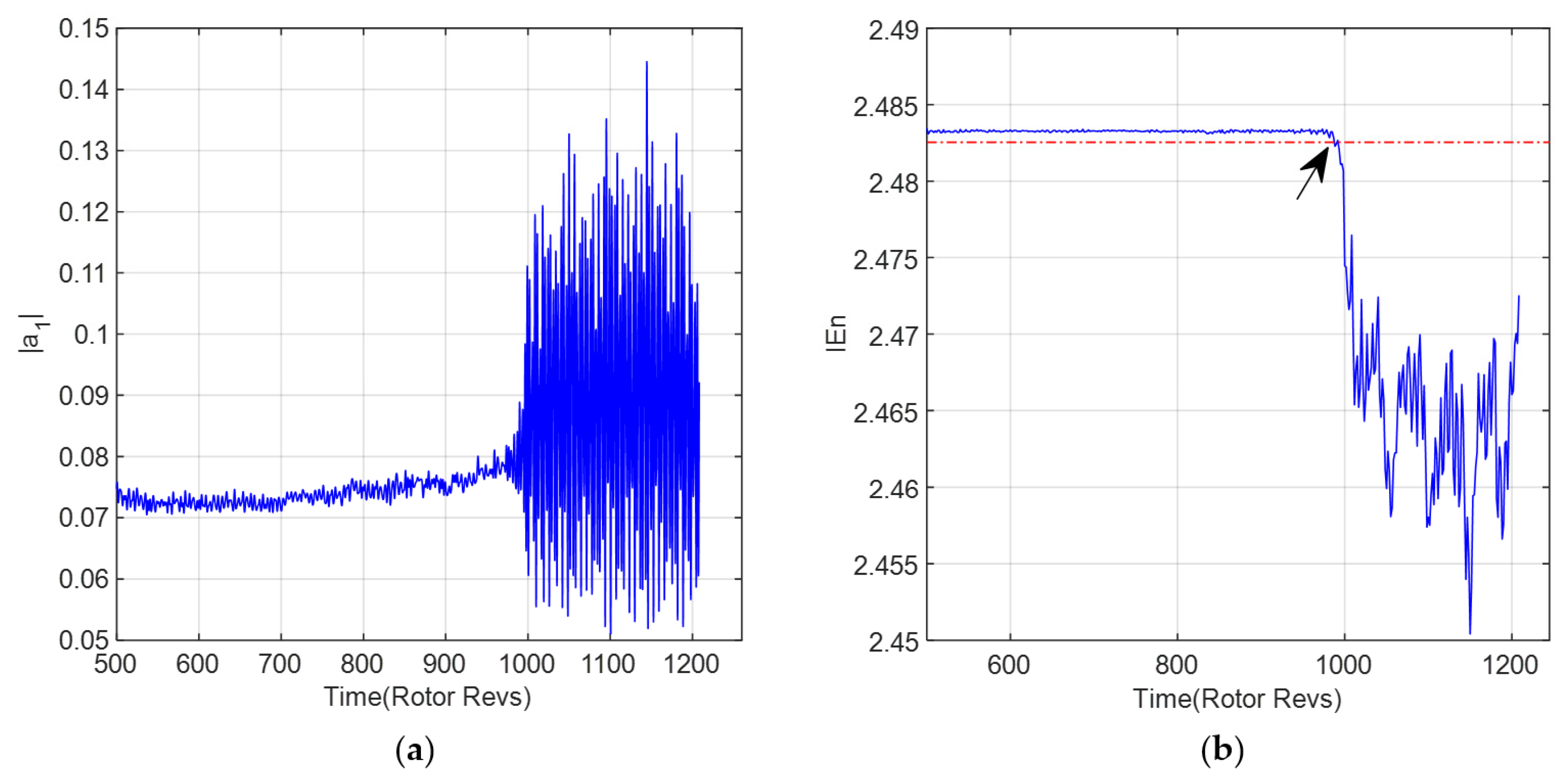
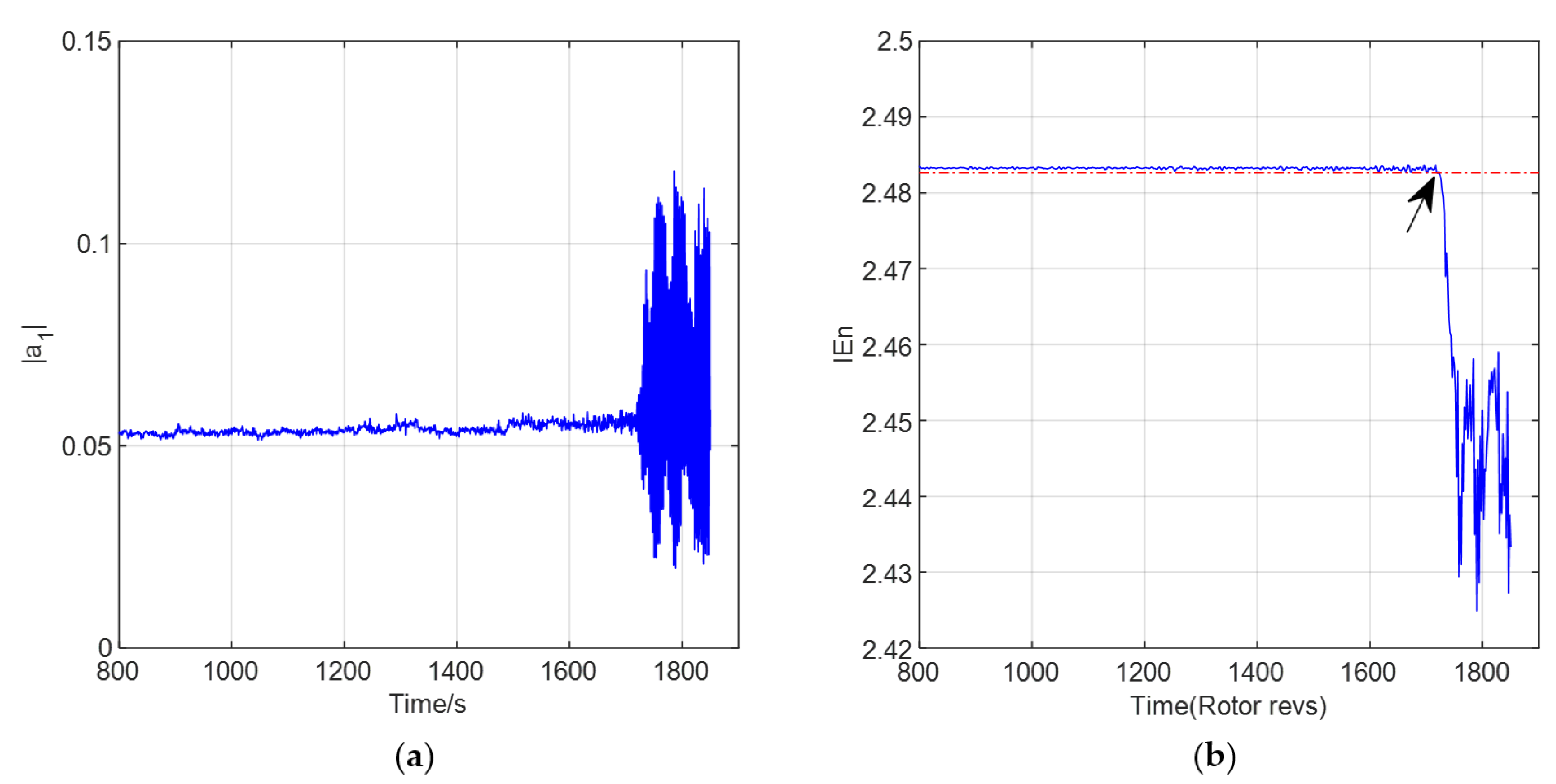
As to verify the superiority of WSE in identifying stall precursors, it is compared with the single information entropy algorithm, for which the same parameters are set as for WSE. Similarly, according to the $3\sigma$ principle, the recognition threshold ε is set to be the value of three times the standard deviation minus its average, with the information entropy under normal conditions takens as the benchmark. The calculation formula is shown as:

$$\epsilon =(3\sigma -\overline{i}),$$

(11)

where $\sigma$ indicates the standard deviation, and $\overline{i}$ represents the average of the information entropy under normal conditions. When the information entropy is less than the threshold set up, this point in time is regarded as the stall precursor of the compressor system, as indicated by the arrows in Figure 8 and Figure 9.

When the working state of the compressor approaches the stall point from the normal state, the pressure wave pulsation of the stall precursor appears in the flow field. The flow field energy distribution of the instable situation is no more uniform in each window. It is accompanied by large fluctuations, resulting in a significant drop in the information entropy value. This is consistent with the theoretical analysis of information entropy described previously with a reduction of the uncertainty of information. For this kind of mutation phenomenon, the information entropy algorithm can also be used as the basic basis for identifying stall precursors.

The comparison of the prediction results with IEn and WSE algorithms is listed in

Table 2. The pre-stall time of IEn and WSE.

Speed	2500 rpm	3000 rpm
Stall revolution	998.75 r	1732 r
IEn pre-stall revolution	986.67 r	1718 r
WSE pre-stall revolution	975 r	1636 r
REV before stall in IEn	12.08 r	14 r
REV before stall in WSE	23.75 r	96 r

for identifying the system instability with different operating states. It can be seen that WSE can detect the stall precursor about 23~96 r in advance at different speeds. Compared to the single IEn algorithm, the early warning time of 11~82 r can be shifted forward by the WSE algorithm. The identification strategy proposed improves the timeliness and adaptability of the recognition algorithm. In the data processing of instability signals under different speeds, the wavelet singular mixed entropy algorithm shows a greater advantage in the early warning for stall inception in comparison with the single information entropy algorithm.

7. Discussion

This paper explores the effects of information entropy and wavelet singular mixed entropy, which are based on the time-domain and time-frequency analyses of first-order spatial mode, respectively. Both algorithms are able to identify differences in the system between the normal and stall states. However, from the view of efficiency and accuracy, the wavelet singular entropy algorithm is superior in identifying signs of instability. The information entropy algorithm considers the information expression of the first-order spatial mode varying with time, but ignores the part of the information that changes with the frequency. Based on the information entropy algorithm, the wavelet singular mixed entropy algorithm can be used to accurately reconstruct a space mode with the solution of wavelet transform, which provides a non-interfering time and frequency energy distribution for the identification of stall precursors. The time-frequency information of the reconstruction matrix is mined by singular value decomposition to obtain more valuable statistical information about the first-order space mode.

In order to examine the effectiveness of the wavelet singular spectrum entropy algorithm proposed in this paper, a comparison is concluded in

Table 3. The comparison of the proposed method and related work.

Work	Approach	Method	Pre-Stall REV at 2500 rpm	Pre-Stall REV at 3000 rpm
[12]	Sample Entropy	Time Domain Analysis	12.083 r	60 r
	Global-Sample Entropy		12.083 r	68 r
Proposed Work	Wavelet Singular Entropy	Frequency-Time Domain Analysis	23.75 r	96 r

along with similar related work [12]. It can be seen from the comparison shown in Table 3 that the proposed wavelet singular spectrum entropy algorithm has certain advantages in identifying the origin of stall precursors.

In the description of the flow field, there are dimensionless parameters that can be considered including Reynolds number, Mach number, flow coefficient, pressure coefficient, hub ratio, etc. According to the requirement of data processing under the condition of high Reynolds number, the wavelet singular spectrum entropy method is adopted in this paper for nonlinear data treatment. Through simulation experiments, it is verified that the wavelet singular entropy with multi-information combination plays a more effective role in the identification of system instability. Due to the complex structure of the compressor system, it contains multi-dimensional and multi-category mode information in the internal flow field, as well as the other dimensionless parameters. However, in the application of these two algorithms, this paper mainly focuses on the information expression of the internal structure of the first-order spatial mode. Further in-depth research is needed on the diagnosis of compressor stall inception, such as a statistical analysis with fuzzy logic classifier [29].

8. Conclusions

In this paper, a low-speed axial compressor test rig is adopted as the research object for stall inception identification. After the first-order spatial mode reconfiguration by feature transformation of the dynamic pressure signals, the wavelet singular mixed entropy algorithm is introduced to quantify the development of the stall signal. By designing the strategy of identification, a warning of instability inception can be suggested in advance of the stall arrival under different operating conditions. The main conclusions of this study are listed as follows:

(1)

On the basis of time-frequency analysis of the first-order spatial mode, it is concluded that the essential characteristic of the system is well reflected during the gradual process of stall development. The information of spatial modal amplitude can be used as a key parameter for the identification of the occurrence of compressor system instability. By extending the information entropy algorithm, the wavelet singular spectral mixed entropy algorithm is proposed to integrate wavelet transform analysis into the time-frequency localization with singular value decomposition. The results show that the wavelet singular algorithm is very sensitive to small disturbances during the rise of amplitude;

(2)

The WSE represents the complexity of the spatial mode of the flow field in the time-frequency domain framework. Combined with the description of spatial mode, the recognition capacity of the WSE is displayed well for the detection of stall inception in a compressor. Compared with the single information entropy algorithm, the wavelet singular mixed entropy algorithm can better extract the uncertain information contained in the system during the instability process. The wavelet singular spectral indicates an obvious mutation when the system approaches the instability boundary;

(3)

In the data processing of instability signals under different speeds, the wavelet singular spectral entropy algorithm shows the ability for early warning of stall inception. According to the threshold set for identification, the wavelet singular mixed entropy algorithm can detect the stall precursor about 23~96 r in advance, which verifies its validity and feasibility for the identification of system instability. Compared to the single information entropy algorithm and related work, the hybrid entropy algorithm is able to shift to an earlier precursor identification by about 11~82 r.