Fault-Tolerant Control for Hexacopter UAV Using Adaptive Algorithm with Severe Faults
Abstract
:1. Introduction
- The combination of adaptive SMC and online control allocation can provide good tracking performance in the presence of actuator faults and model uncertainties in the hexacopter model;
- The adaptive law is developed to overcome fault estimation error;
- The stability of the system is validated using Lyapunov theory;
- The proposed method is validated by simulation and is compared with a recent method [18]. The advantage of the proposed method is handling unknown complete faults in one motor. Moreover, the proposed method in this article considers the input saturation in controller design and self-reconfiguration through control allocation by using virtual control.
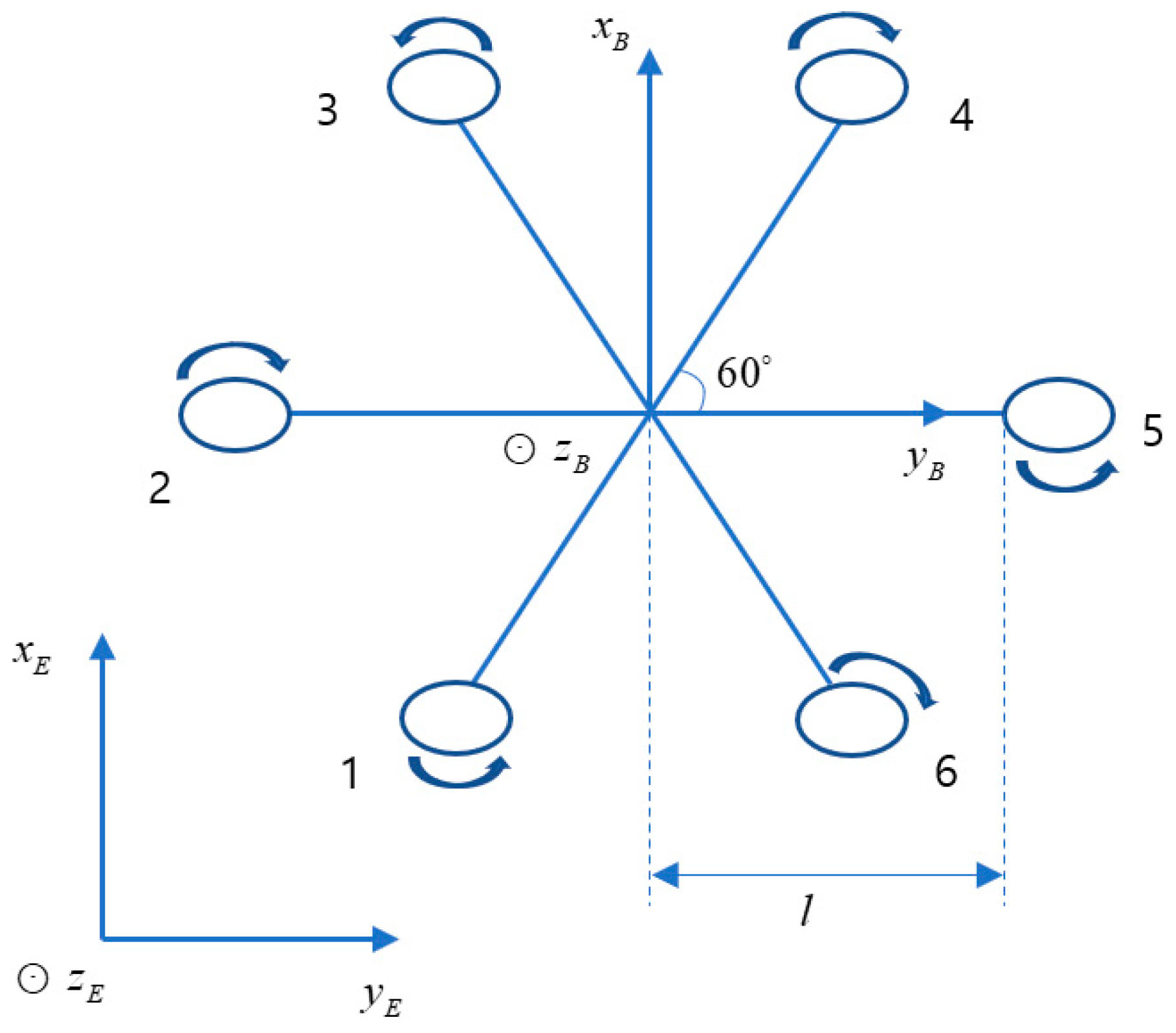
2. Mathematical Model of Hexacopter
3. Design of Attitude Fault-Tolerant Control
3.1. Model of Attitude System in Fault-Free Case
3.2. Design of Adaptive Fault-Tolerant Control Allocation
3.2.1. Control Allocation
3.2.2. Adaptive Fault-Tolerant Control Allocation
3.3. Fault-Tolerant Control with Input Saturation
4. Design of Position Control
5. Simulation Results
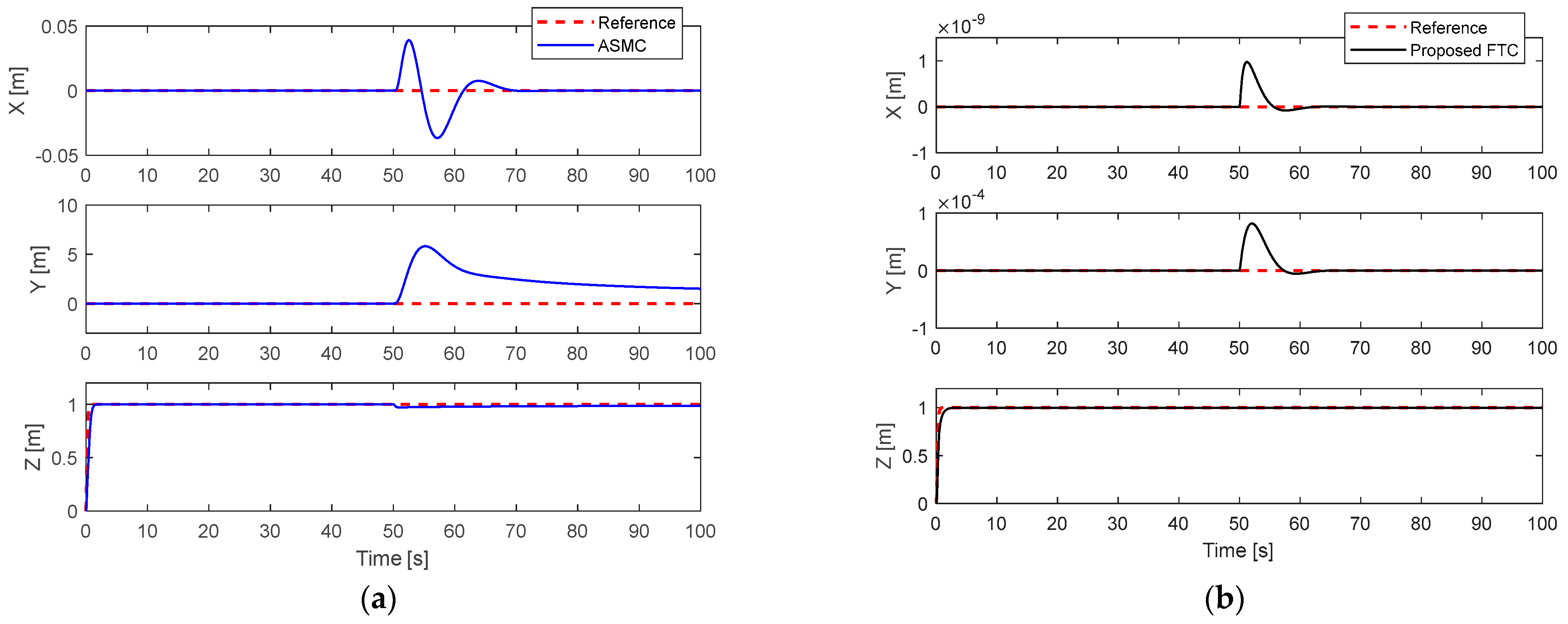
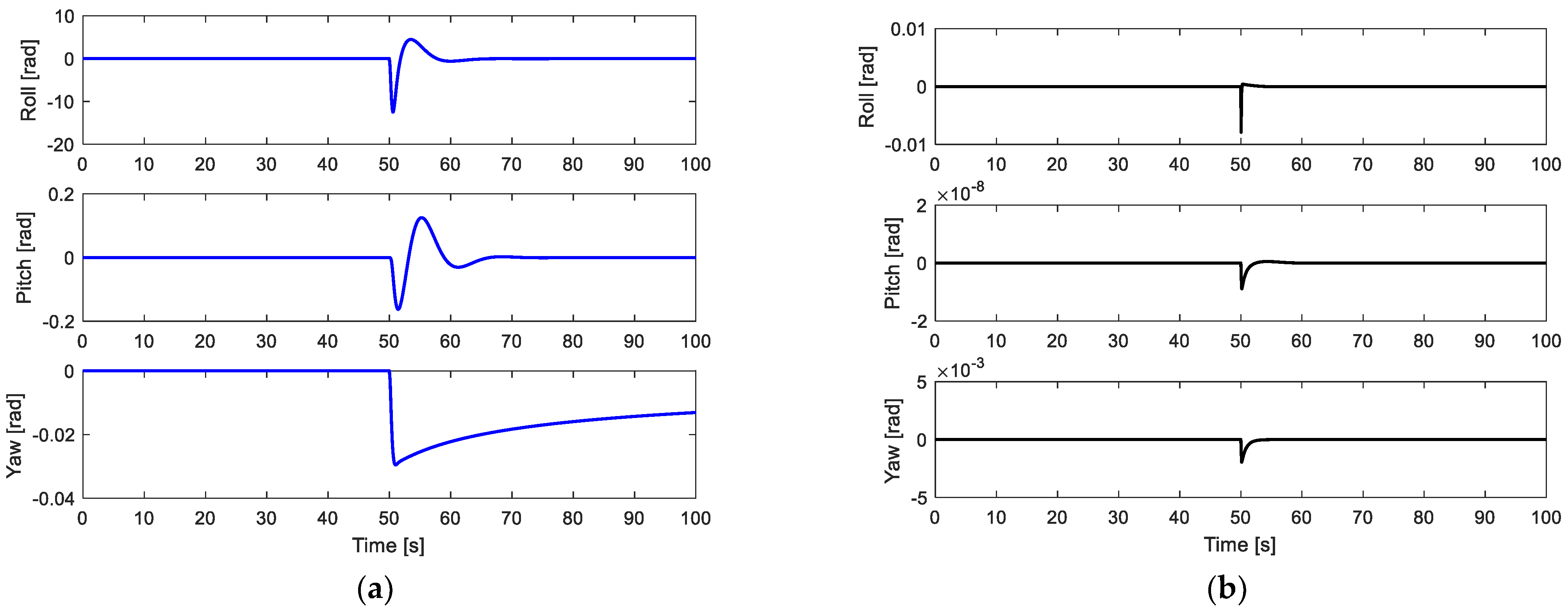
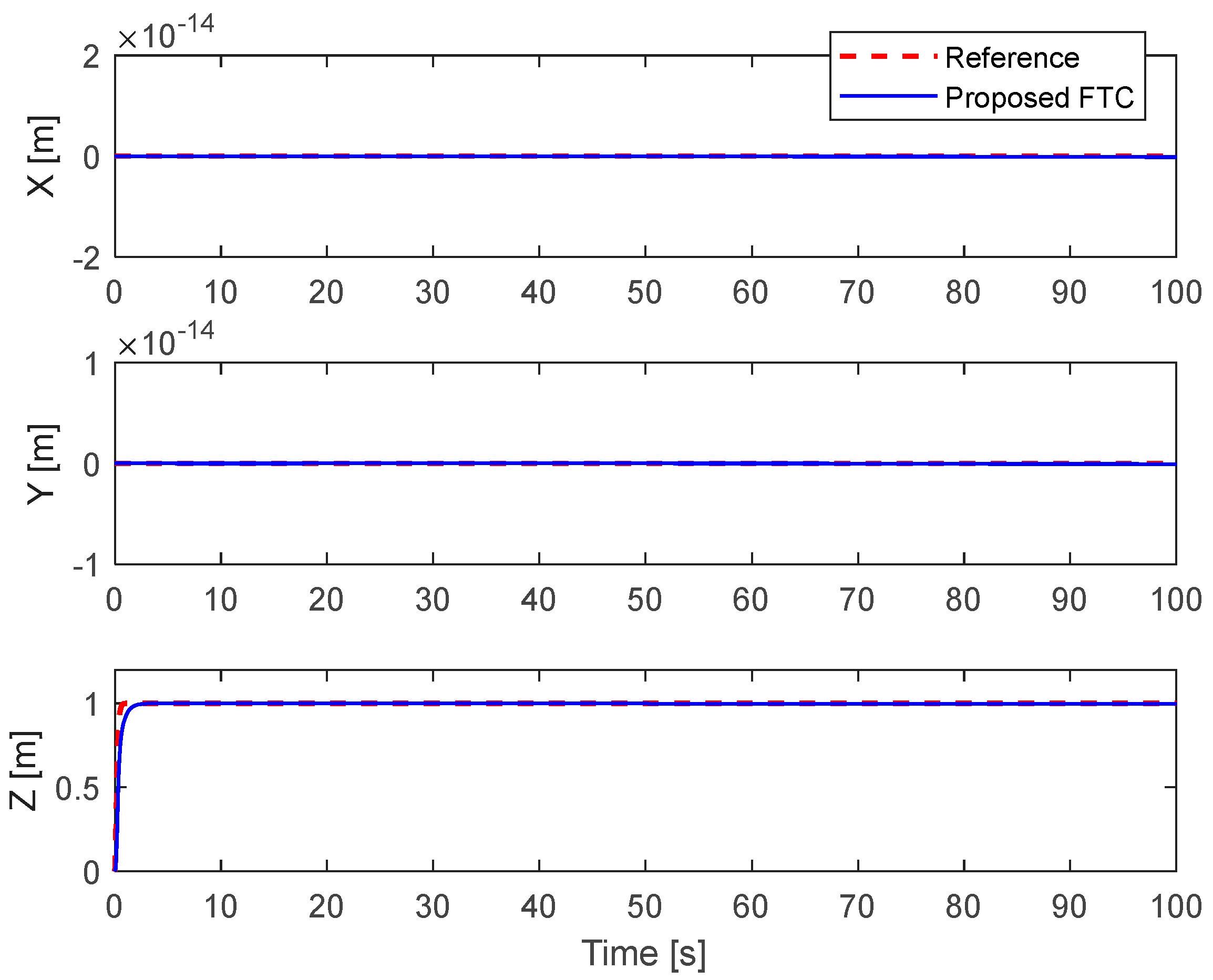
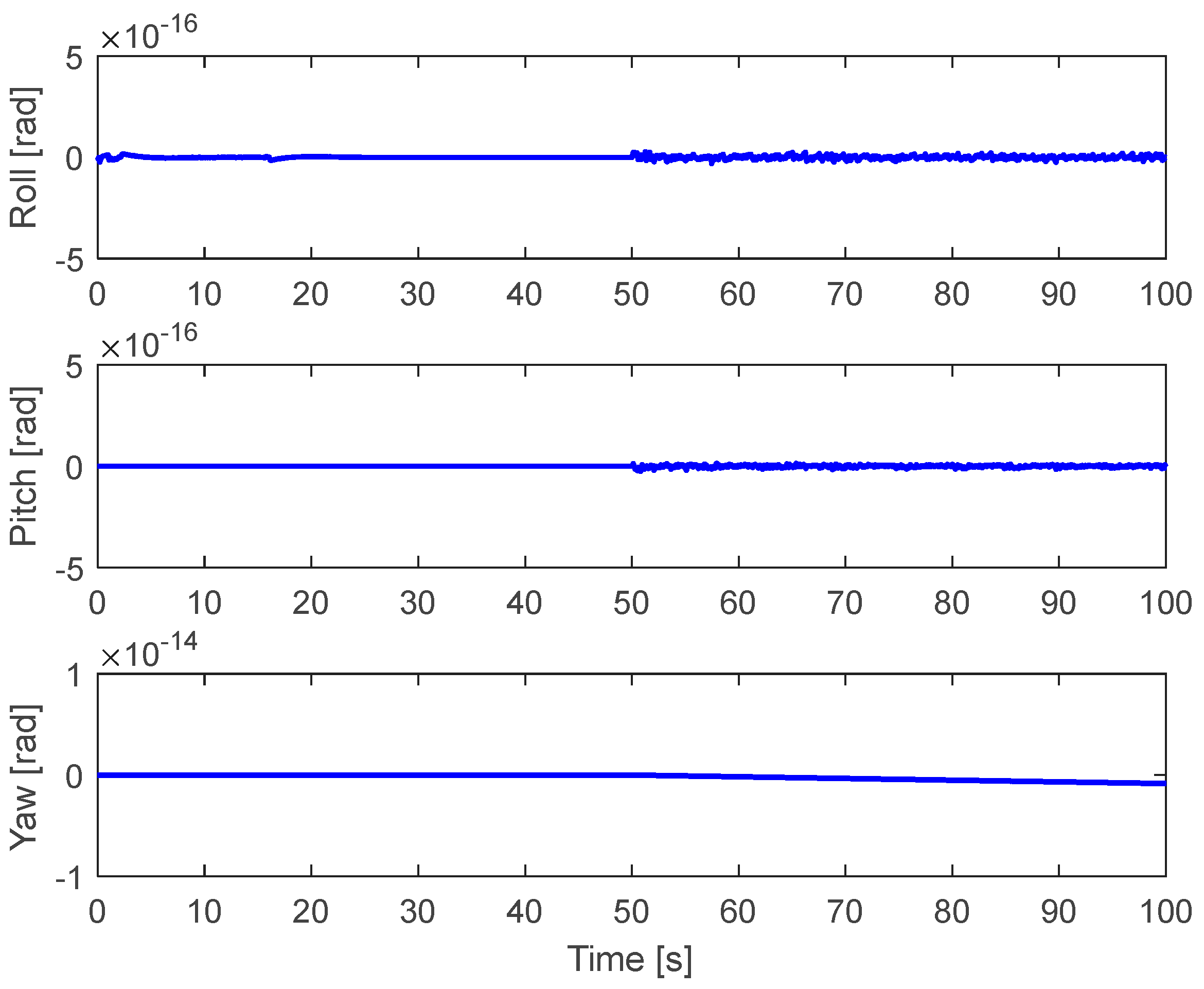
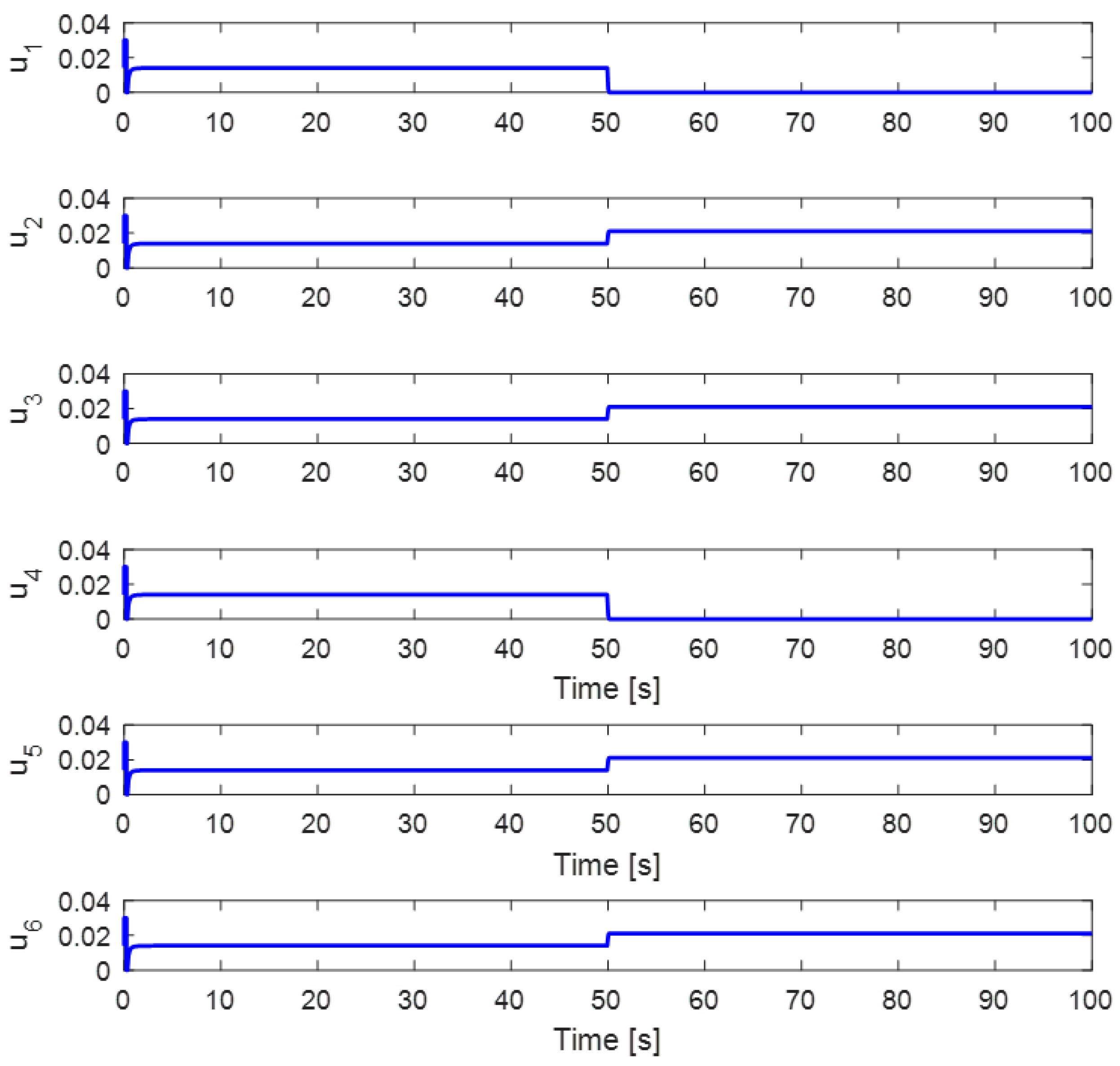
5.1. 50% Loss of Control Effectiveness in Actuator #2
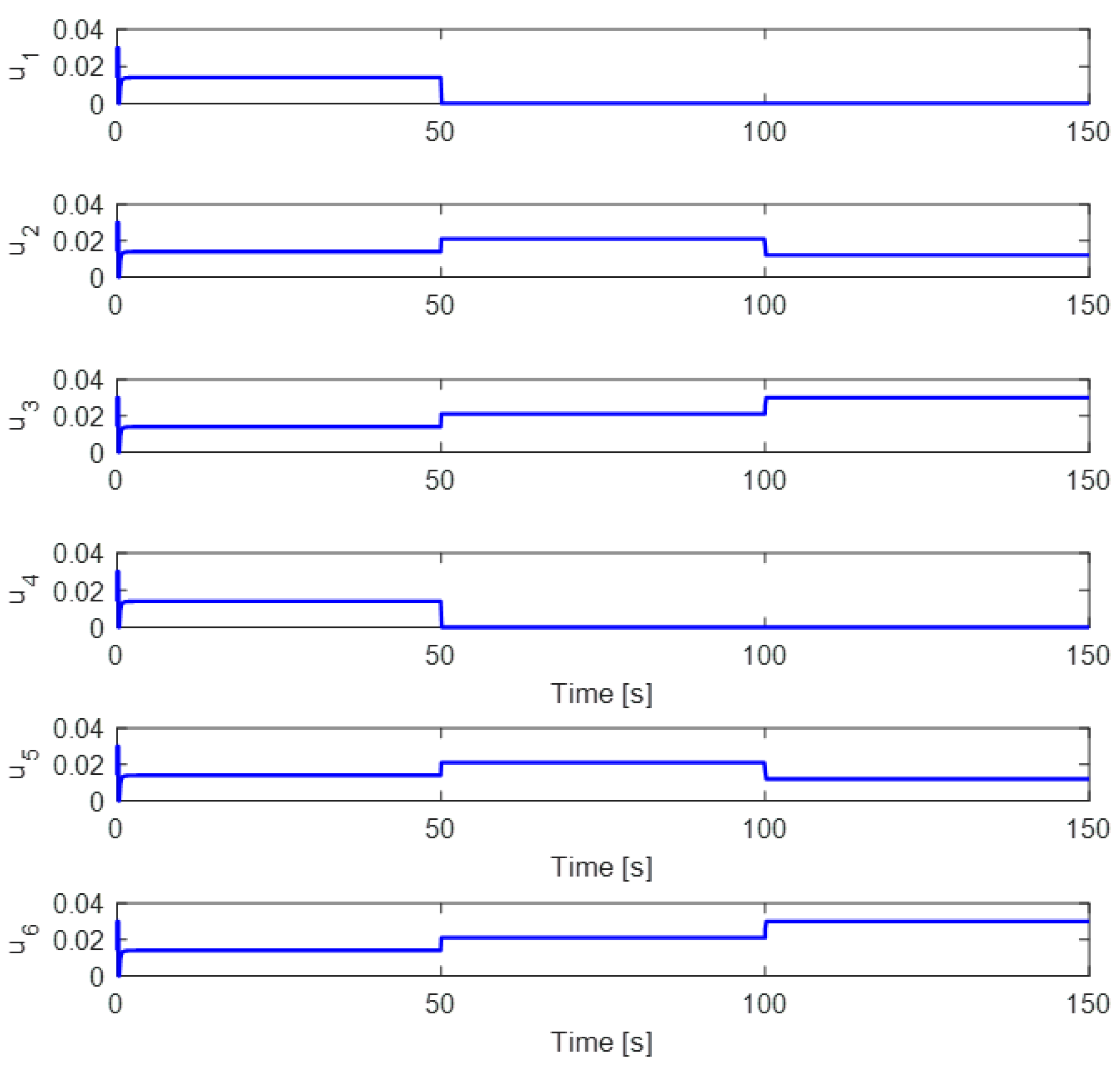
5.2. Complete Fault in Actuator 1 and Partial Fault in Actuator 2
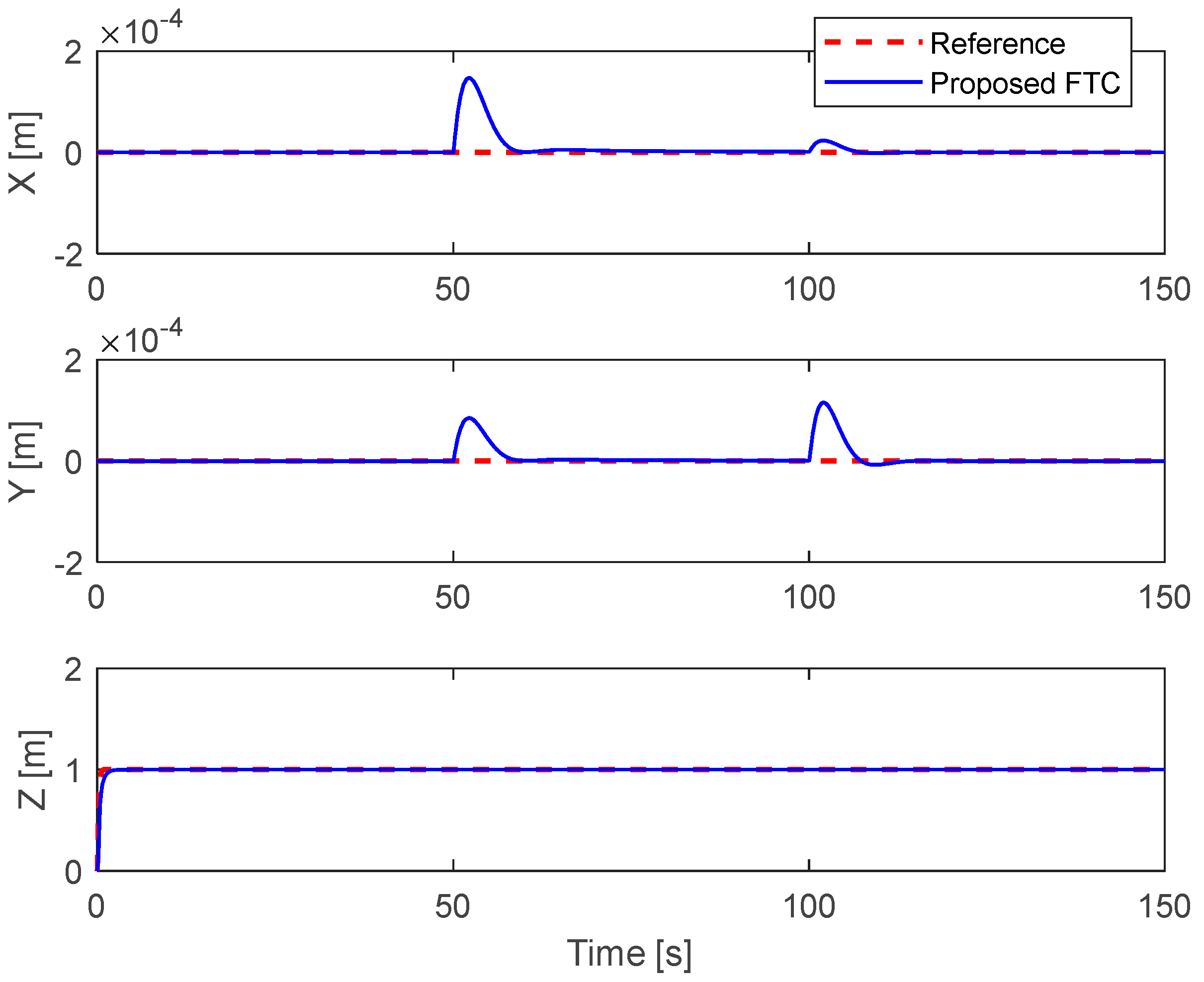
5.3. Simultaneous Fault in Actuator 1 and Actuator 4
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.M.; Chamseddine, A.; Gordon, B.W.; Su, C.-Y.; Rakheja, S.; Fulford, C.; Apkarian, J.; Gosselin, P. Development of advanced FDD and FTC techniques with application to an unmanned quadrotor helicopter testbed. J. Frankl. Inst. 2013, 350, 2396–2422. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, C.; Zhang, Y. Active fault-tolerant control of unmanned quadrotor helicopter using linear parameter varying technique. J. Intell. Robot. Syst. 2017, 88, 415–436. [Google Scholar] [CrossRef]
- Cen, Z.; Noura, H.; Susilo Younes, Y.A. Robust fault diagnosis for quadrotor UAVs using adaptive Thau observer. J. Intell. Robot. Syst. 2014, 73, 573–588. [Google Scholar] [CrossRef]
- Cen, Z.; Noura, H. An Adaptive Thau Observer for estimating the time-varying LOE fault of quadrotor actuators. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013. [Google Scholar]
- Lee, C.H.; Park, M.K. Actuator Fault Estimation Method using Hexacopter Symmetry. J. Inst. Control Robot. Syst. 2016, 22, 519–523. [Google Scholar] [CrossRef]
- Antonio, G.R.; Agus, H.; Poramate, M. Robust actuator fault diagnosis algorithm for autonomous UAVs. IFAC-Pap. 2020, 52, 682–687. [Google Scholar]
- Alwi, H.; Edwards, C. Fault tolerant control using sliding modes with on-line control allocation. Automatica 2008, 44, 1859–1866. [Google Scholar] [CrossRef] [Green Version]
- Ban, W.; Youmin, Z. An adaptive fault-tolerant sliding mode control allocation scheme for multirotor hexacopter subject to simultaneous actuator faults. IEEE Trans. Ind. Electron. 2018, 65, 4227–4236. [Google Scholar]
- Halim, A.; Christopher, E. Sliding mode FTC with on-line control allocation. In Proceedings of the 45th IEEE Conference on Decision & Control, San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Salman, L.; Fuyang, C.; Mirza, T.H.; Lin, Y.; Cun, S. An adaptive integral sliding mode FTC scheme for dissimilar redundant actuation system of civil aircraft. Int. J. Syst. Sci. 2019, 50, 2687–2702. [Google Scholar]
- Saied, M.; Lussier, B.; Fantoni, I.; Francis, C.; Shraim, H.; Sanahuja, G. Fault diagnosis and fault-tolerant control strategy for rotor failure in an octorotor. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 2 July 2015. [Google Scholar]
- Alwi, H.; Hamayun, M.T.; Edwards, C. An integral sliding mode fault tolerant control scheme for an octorotor using fixed control allocation. In Proceedings of the 13th International Workshop on Variable Structure Systems (VSS), Nantes, France, 29 June–2 July 2014. [Google Scholar]
- Samir, Z.; Hemza, M.; Abderrahmen, B.; Ali, D. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV. ISA Trans. 2018, 80, 267–278. [Google Scholar]
- Hussein, M.; Majd, S.; Hassan, S.; Clovis, F. Fault-tolerant control of an hexacopter unmanned aerial vehicle applying outdoor tests and experiments. IAFC-Pap. 2018, 51, 312–317. [Google Scholar]
- Nguyen, D.-T.; Saussié, D.; Saydy, L. Fault-Tolerant Control of a Hexacopter UAV based on Self-Scheduled Control Allocation. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018. [Google Scholar]
- Nguyen, D.-T.; Saussie, D.; Saydy, L. Design and Experimental Validation of Robust Self-Scheduled Fault-Tolerant Control Laws for a Multicopter UAV. IEEE/ASME Trans. Mechatron. 2021, 26, 2548–2557. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Xuan Mung, N.; Hong, S.K. Actuator Fault Detection and Fault-Tolerant Control for Hexacopter. Sensors 2019, 19, 4721. [Google Scholar] [CrossRef] [Green Version]
- Sudhir, N.; Swarup, A. On adaptive sliding mode control for improved quadrotor tracking. J. Vib. Control 2017, 24, 3219–3230. [Google Scholar]
- Asadi, D.; Ahmadi, K.; Nabavi, S.Y. Fault-tolerant trajectory tracking control of a quadcopter in presence of a motor fault. Int. J. Aeronaut. Space Sci. 2022, 23, 129–142. [Google Scholar]
- Ljaz, S.; Fuyang, C.; Hamayun, M.T. Adaptive non-linear integral sliding mode fault-tolerant control allocation scheme for octorotor UAV system. IET Control Theory Appl. 2020, 14, 3139–3156. [Google Scholar]


| Parameter | Description | Value |
|---|---|---|
| Arm length | ||
| Thrust coefficient | ||
| Drag coefficient | ||
| Total mass | ||
| Drag coefficient | 0.01; 0.01; 0.01; 0.01; 0.01 | |
| Motor frequency | 15 rad/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, N.P.; Xuan Mung, N.; Ha, L.N.N.T.; Hong, S.K. Fault-Tolerant Control for Hexacopter UAV Using Adaptive Algorithm with Severe Faults. Aerospace 2022, 9, 304. https://doi.org/10.3390/aerospace9060304
Nguyen NP, Xuan Mung N, Ha LNNT, Hong SK. Fault-Tolerant Control for Hexacopter UAV Using Adaptive Algorithm with Severe Faults. Aerospace. 2022; 9(6):304. https://doi.org/10.3390/aerospace9060304
Chicago/Turabian StyleNguyen, Ngoc Phi, Nguyen Xuan Mung, Le Nhu Ngoc Thanh Ha, and Sung Kyung Hong. 2022. "Fault-Tolerant Control for Hexacopter UAV Using Adaptive Algorithm with Severe Faults" Aerospace 9, no. 6: 304. https://doi.org/10.3390/aerospace9060304
APA StyleNguyen, N. P., Xuan Mung, N., Ha, L. N. N. T., & Hong, S. K. (2022). Fault-Tolerant Control for Hexacopter UAV Using Adaptive Algorithm with Severe Faults. Aerospace, 9(6), 304. https://doi.org/10.3390/aerospace9060304









