Micro Coaxial Drone: Flight Dynamics, Simulation and Ground Testing
Abstract
:1. Introduction
1.1. State of the Art
1.2. Problem Statement
1.3. Previous Work
- 1.
- A design methodology is proposed based on conceptual design, flight dynamics, CFD simulation and ground testing of a micro coaxial unmanned aerial vehicle.
- 2.
- The CFD simulation is obtained for later transient and stationary modes.
- 3.
- The ground testing results are analyzed to validate the proposed computational methodology.
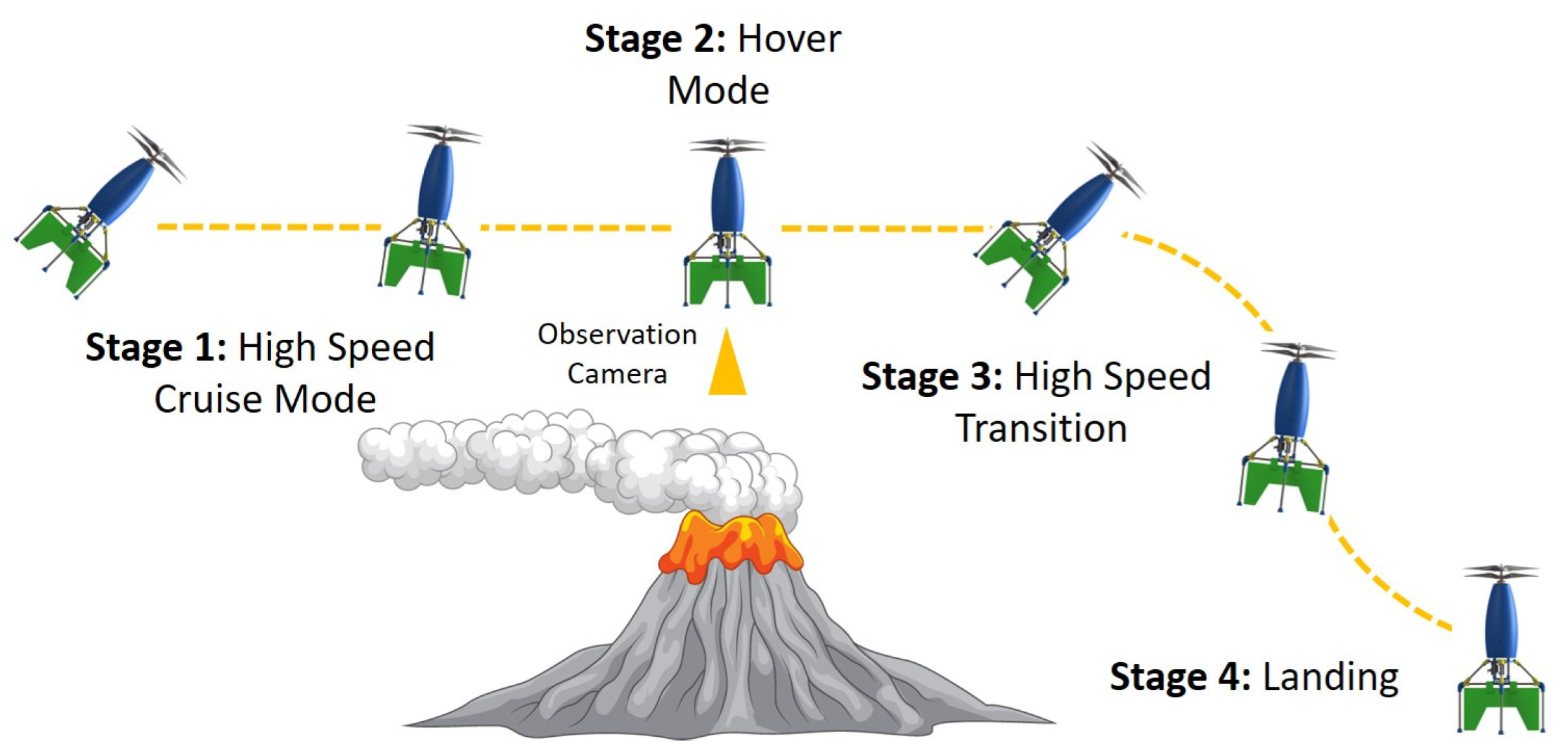
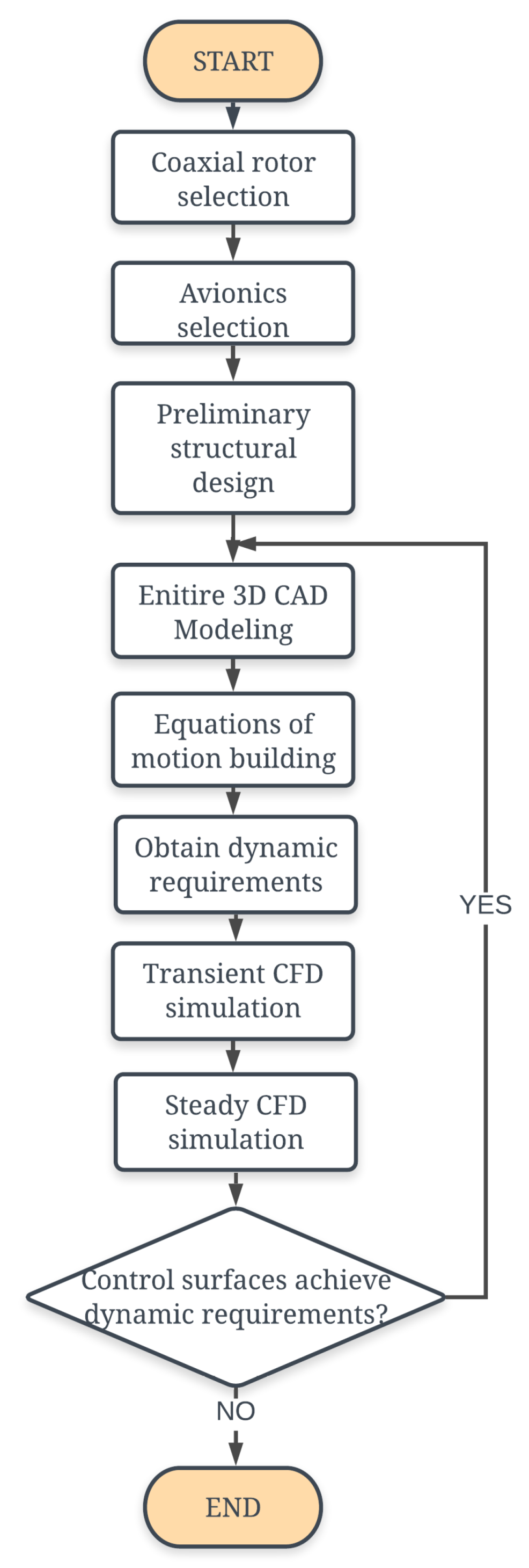
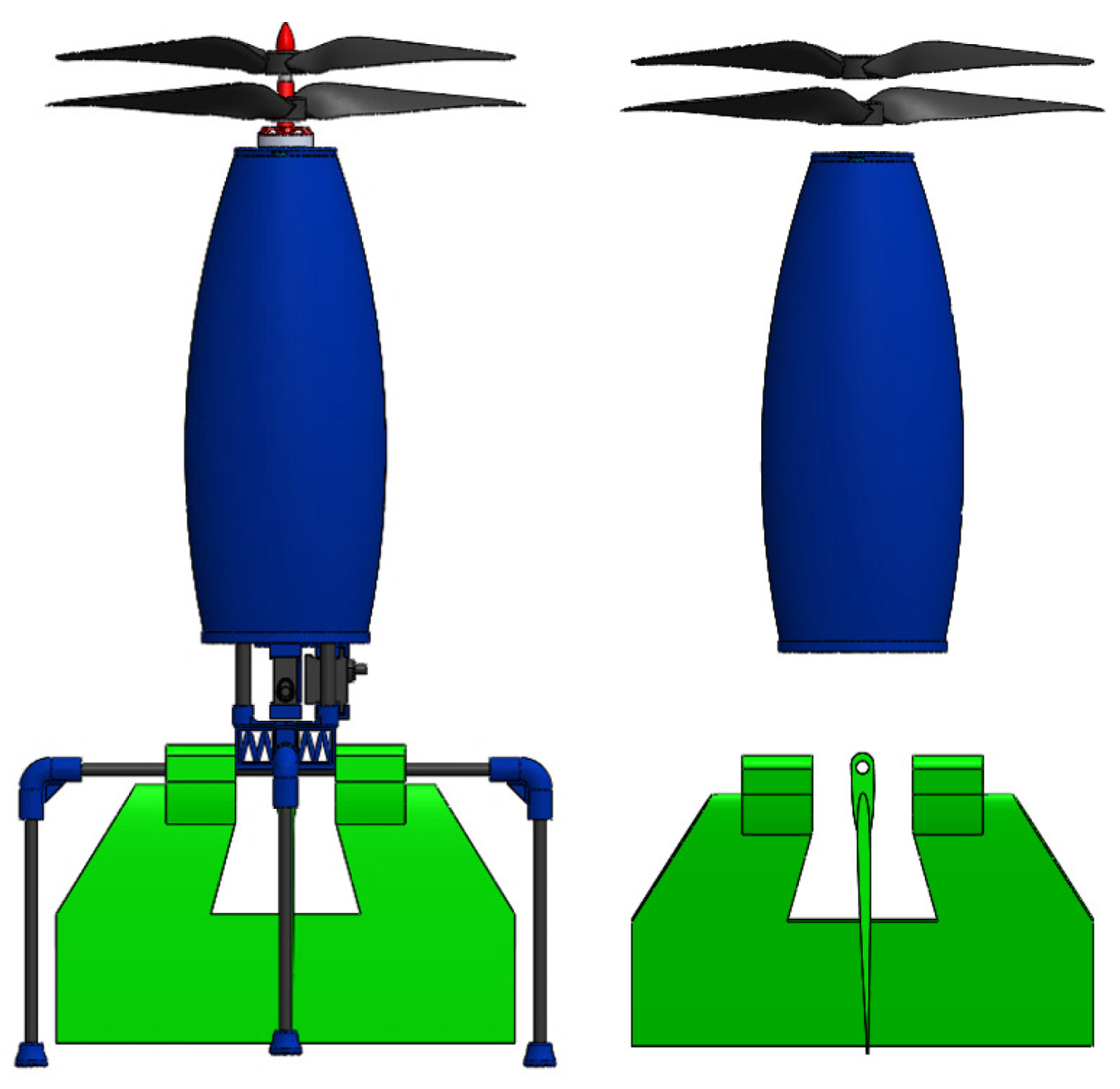
2. Conceptual Design of Micro Coaxial Rocket UAV (MCR UAV v3.0)
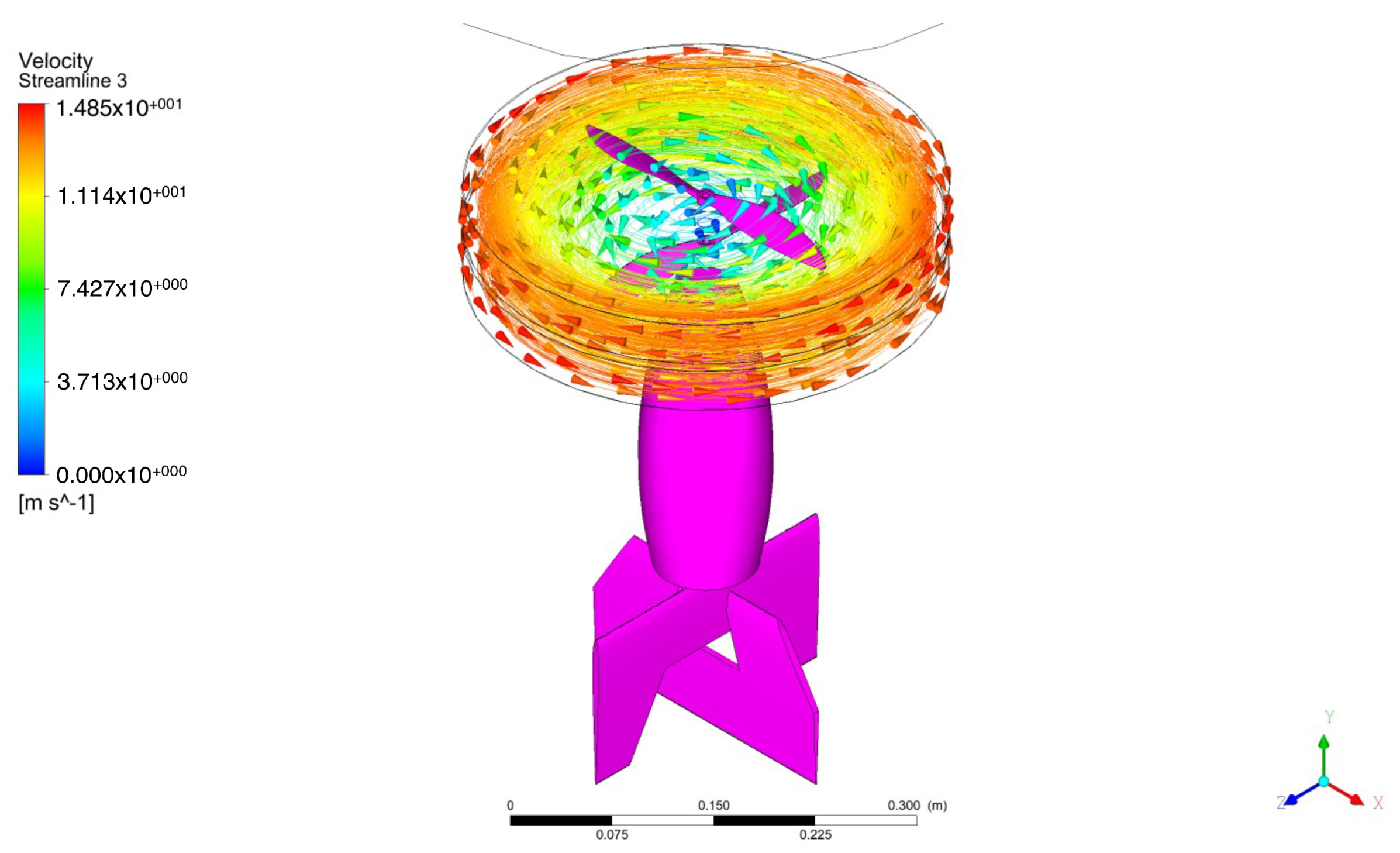
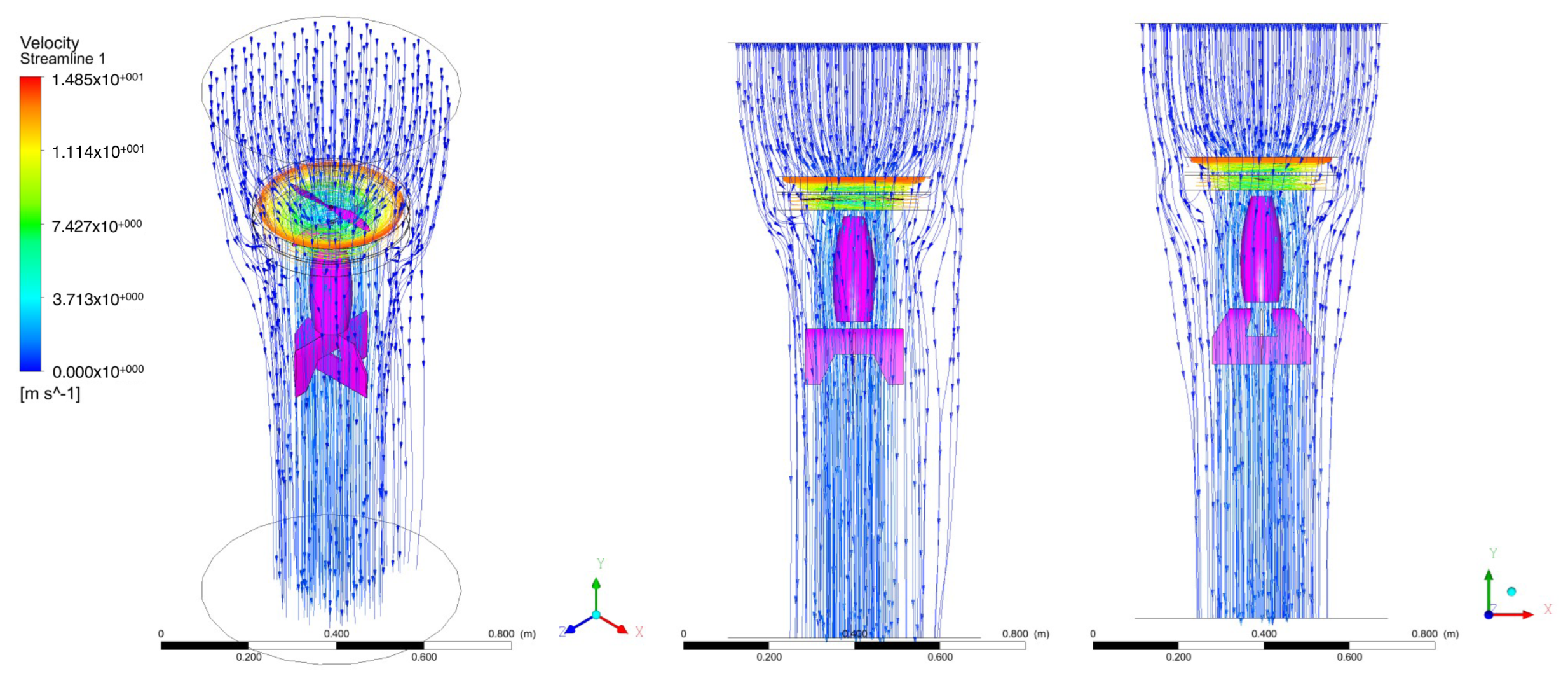
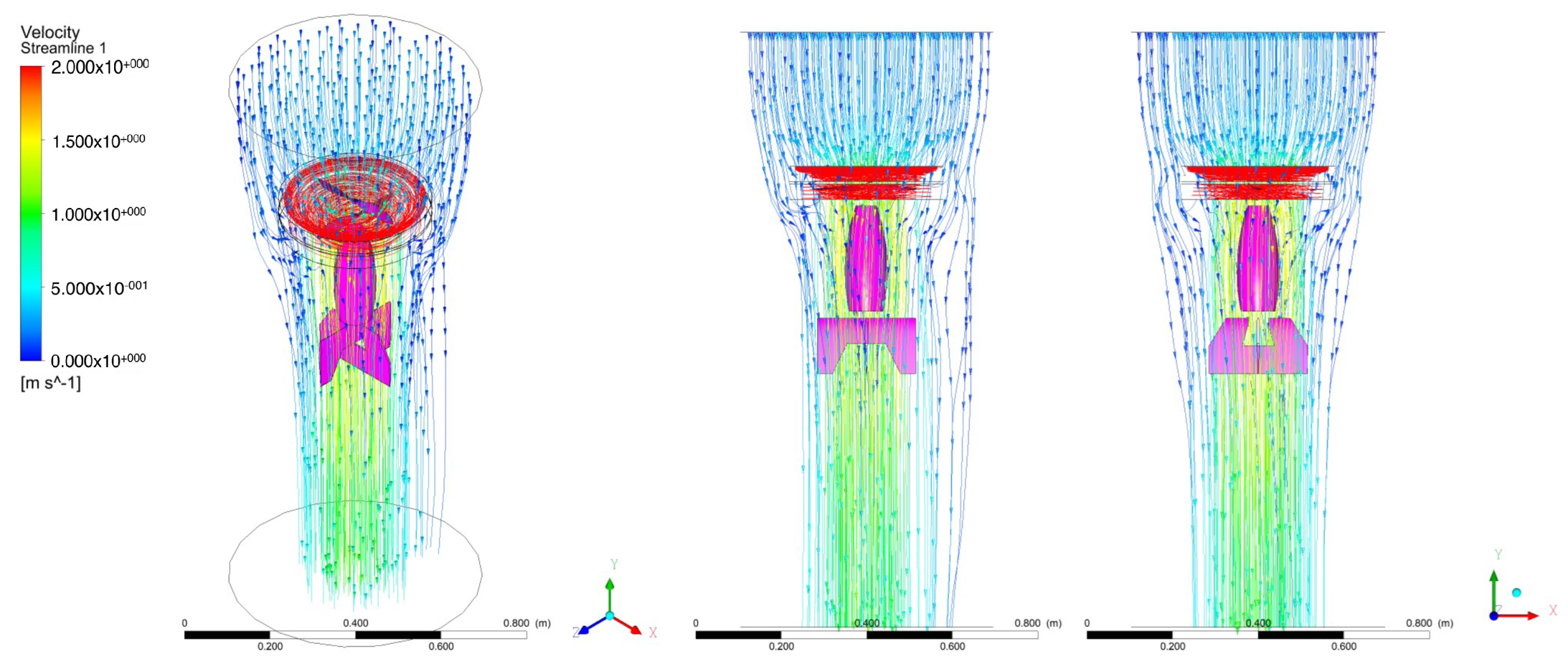
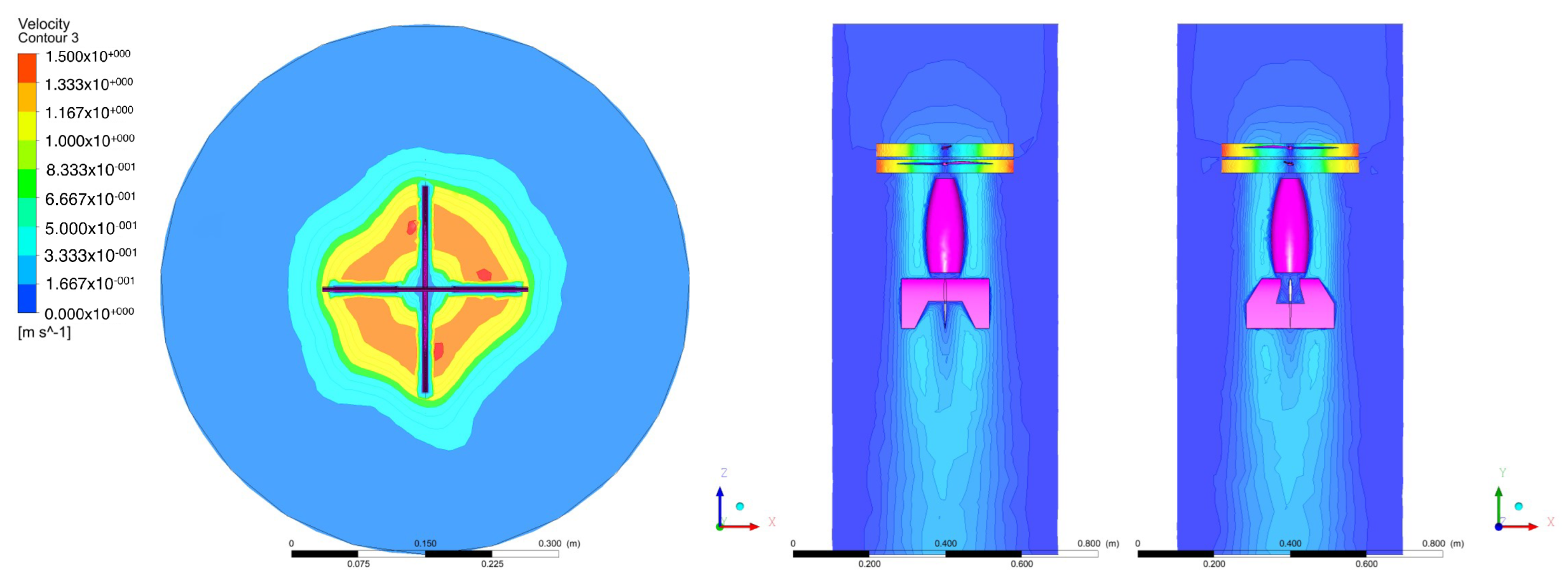
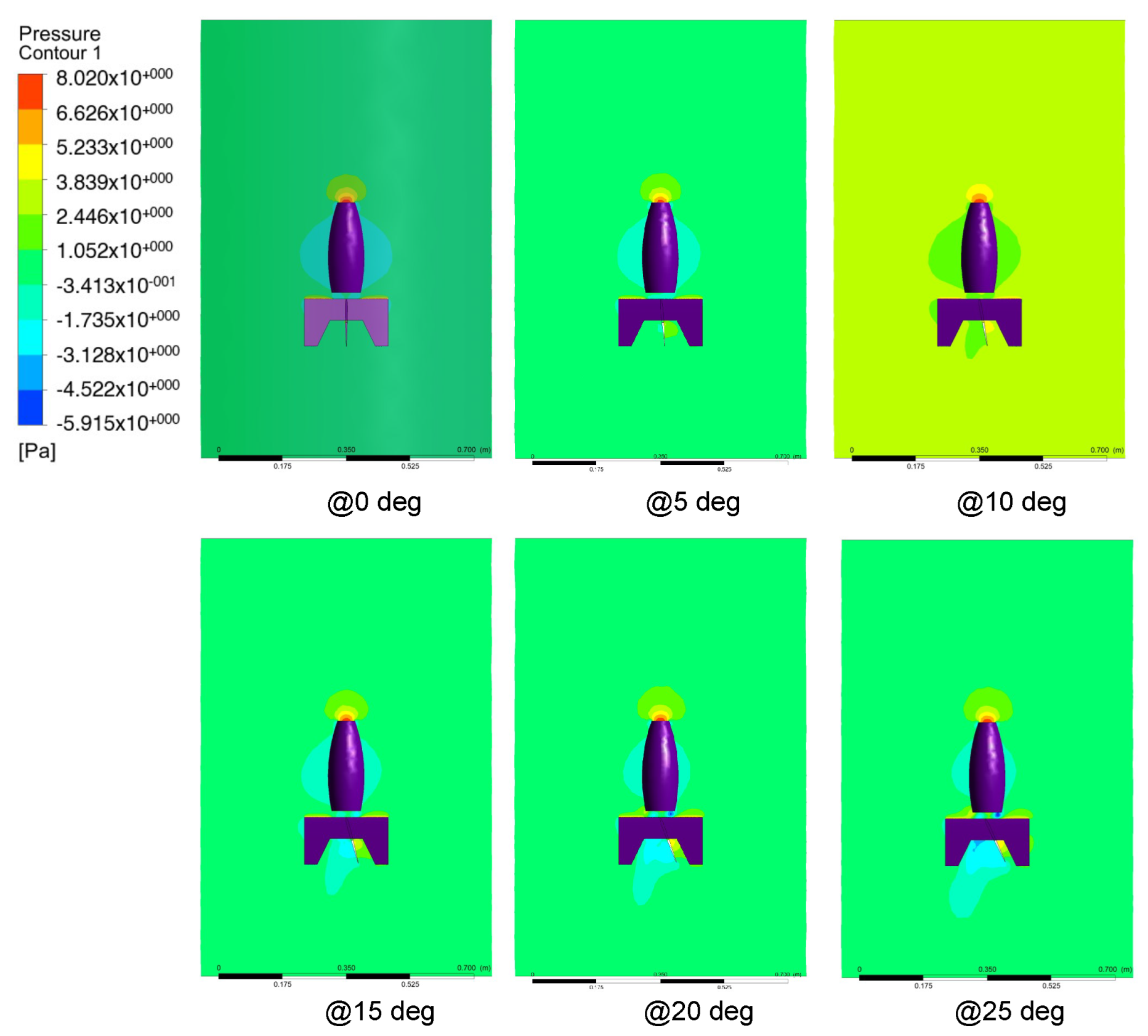
3. CFD Analysis
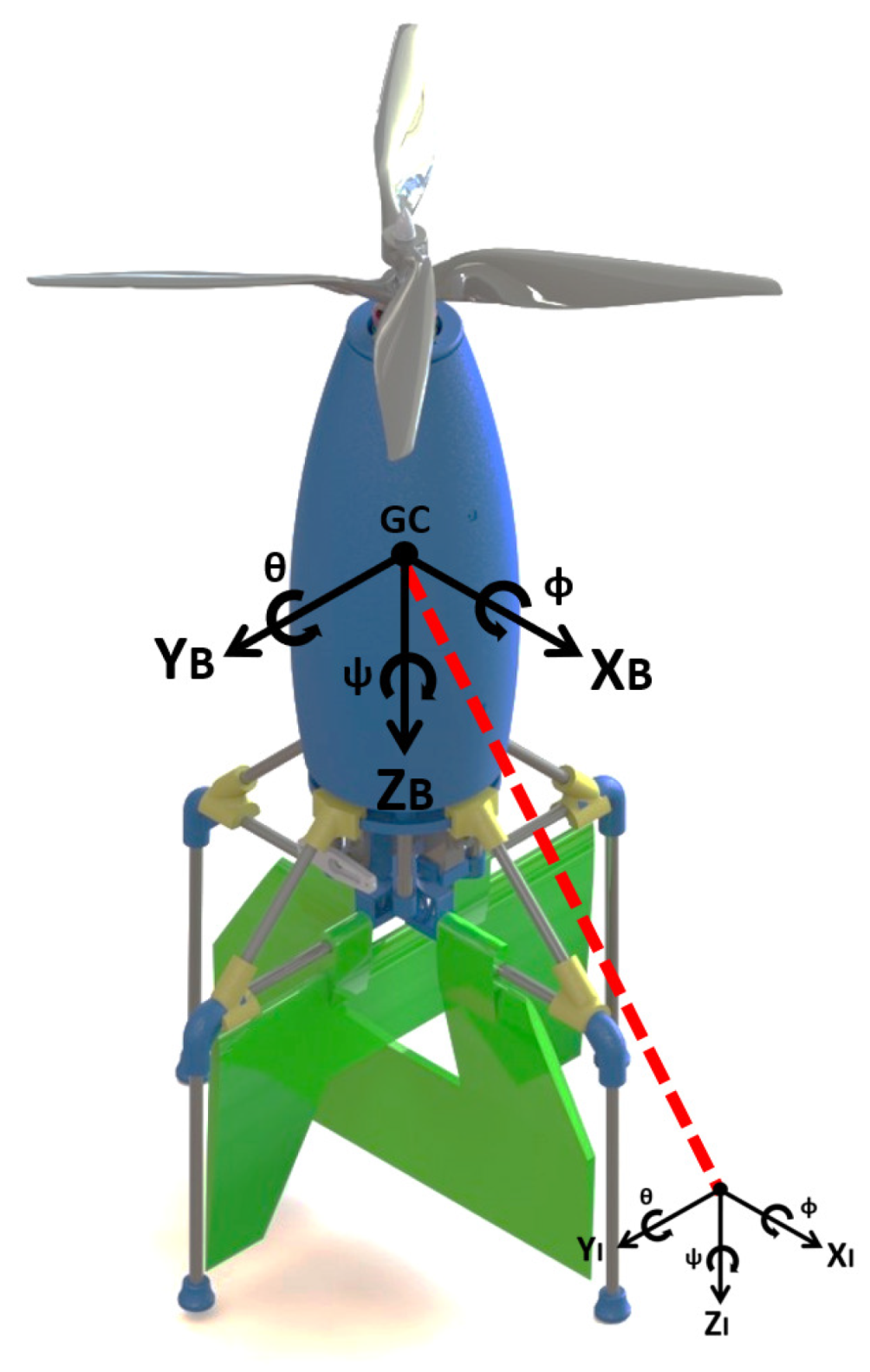
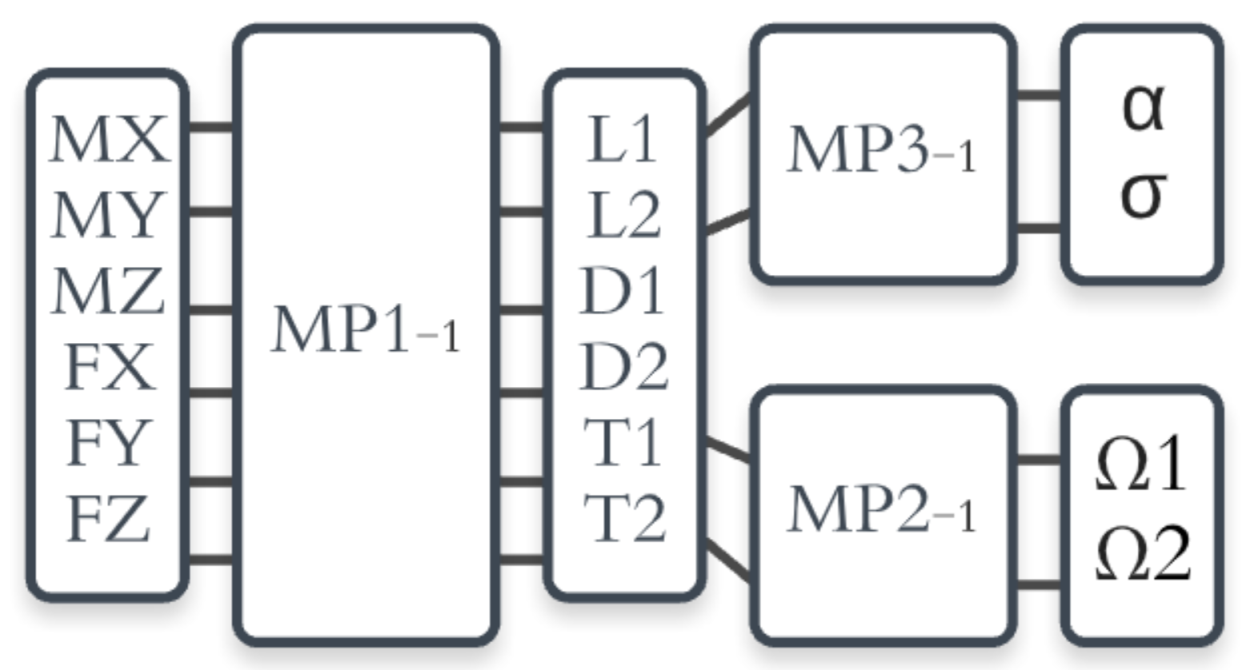
4. Mathematical Model
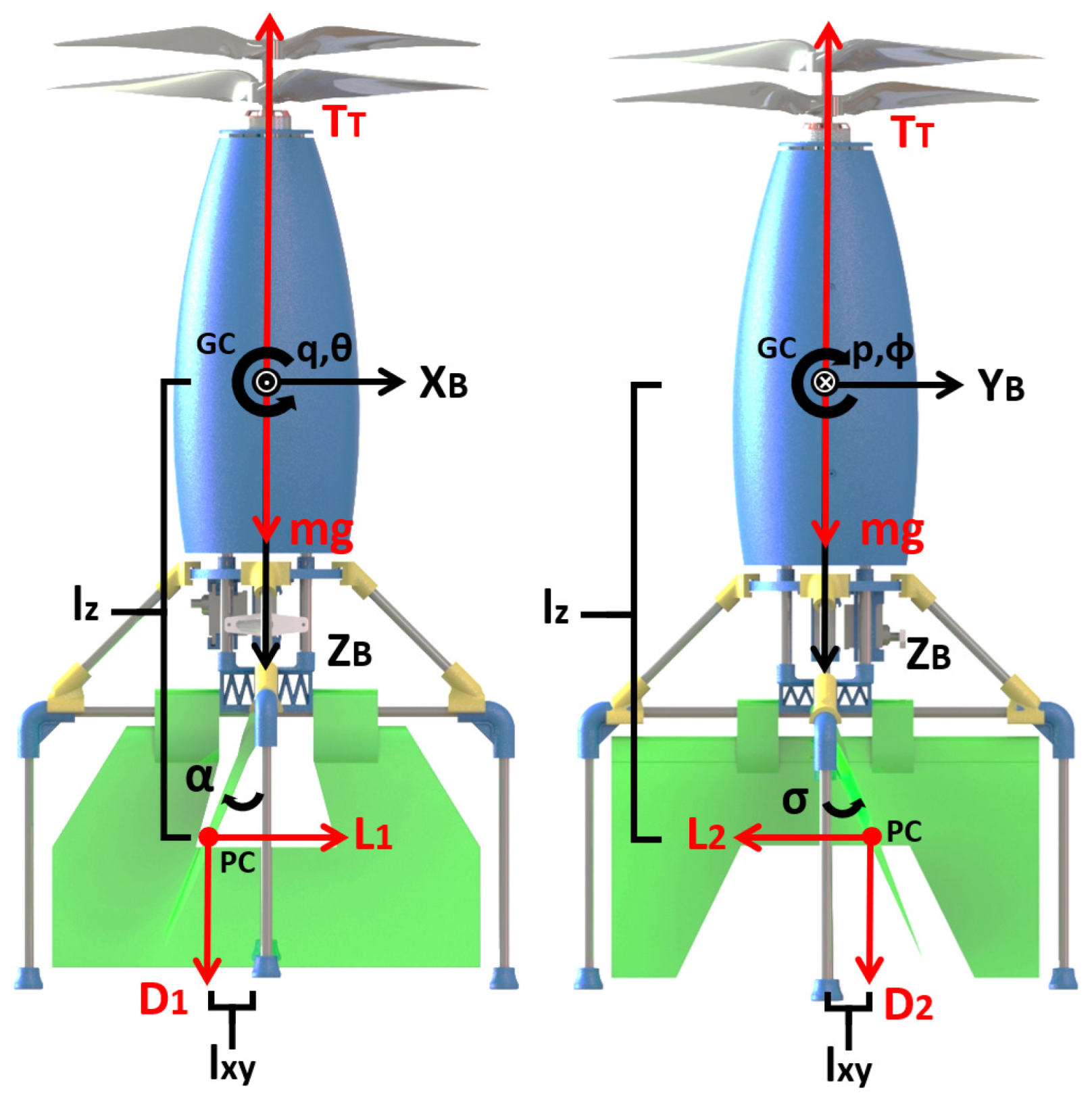
4.1. Forces
4.2. Moments
4.3. Equations of Motion
4.4. Stability Analysis
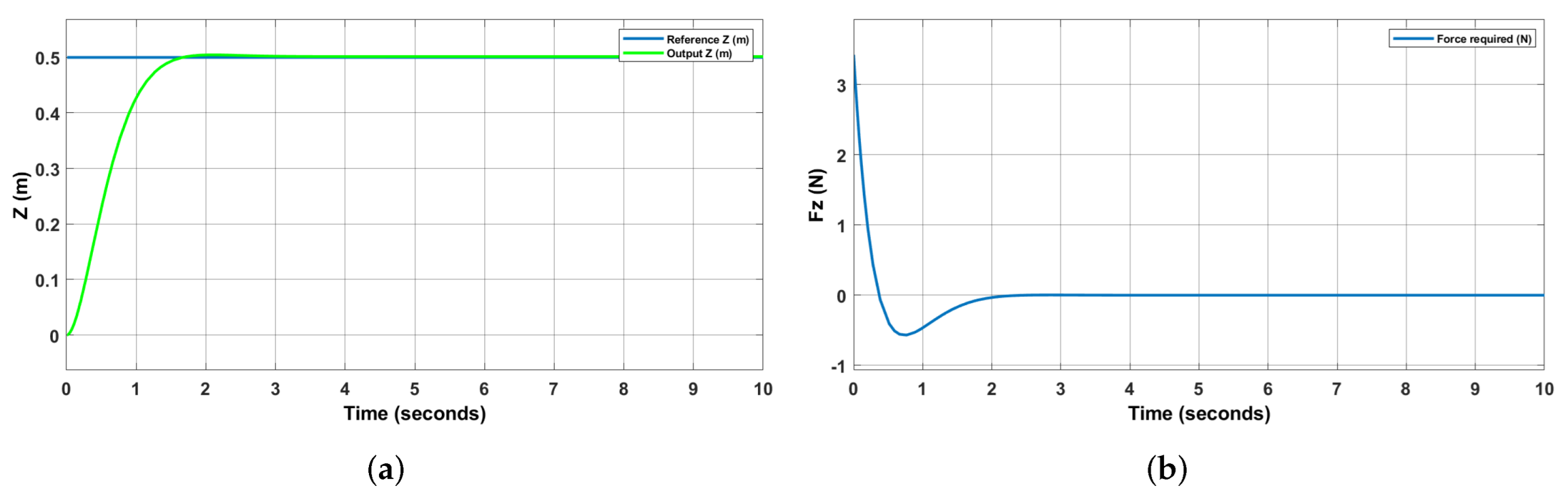
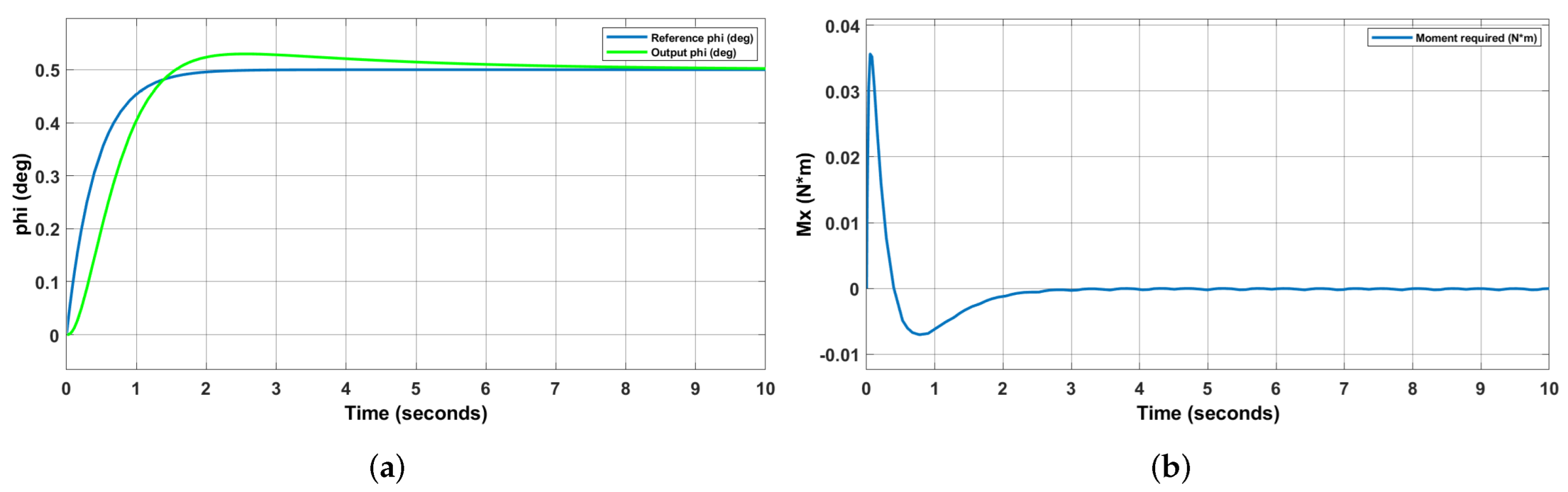
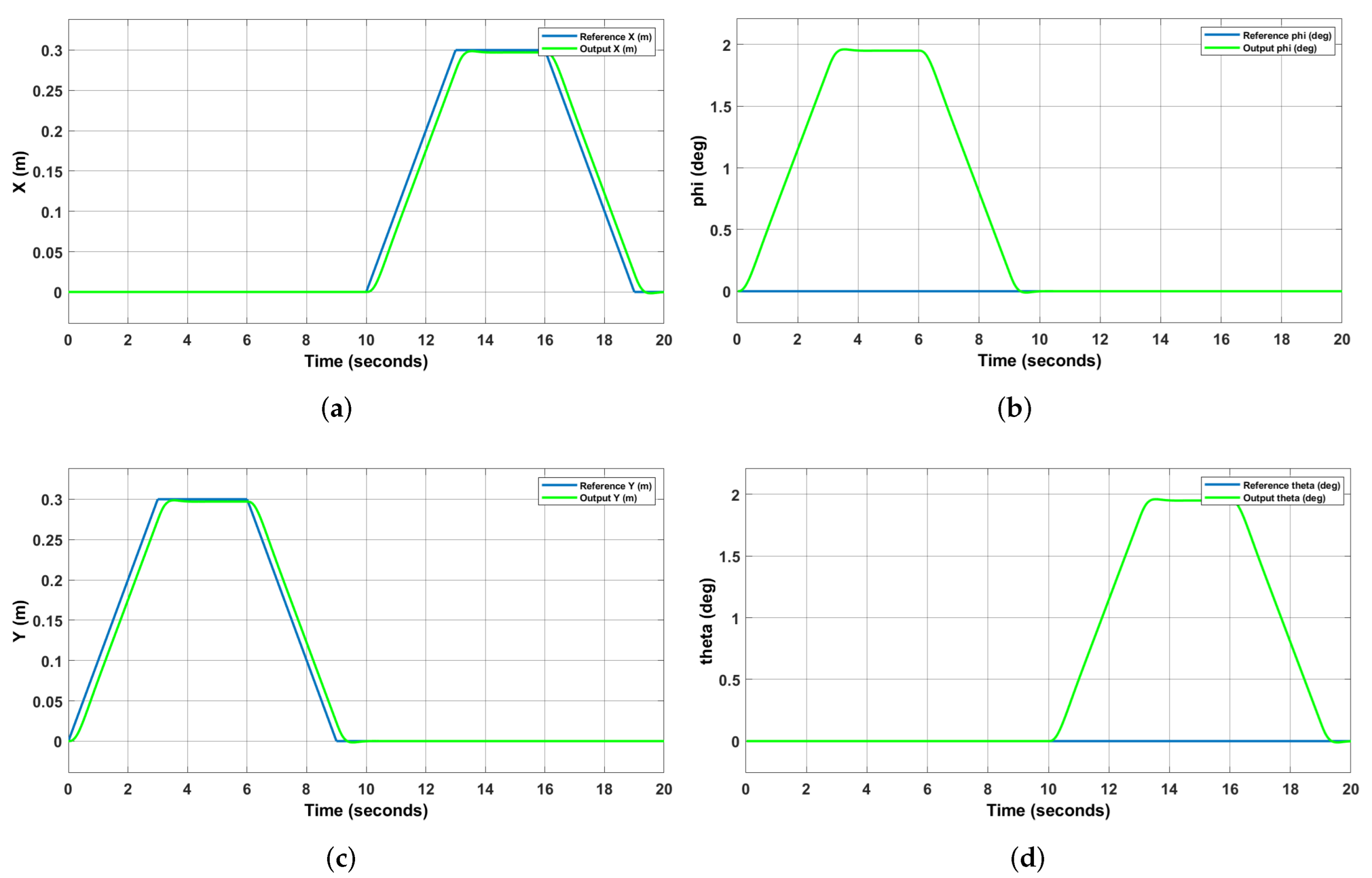
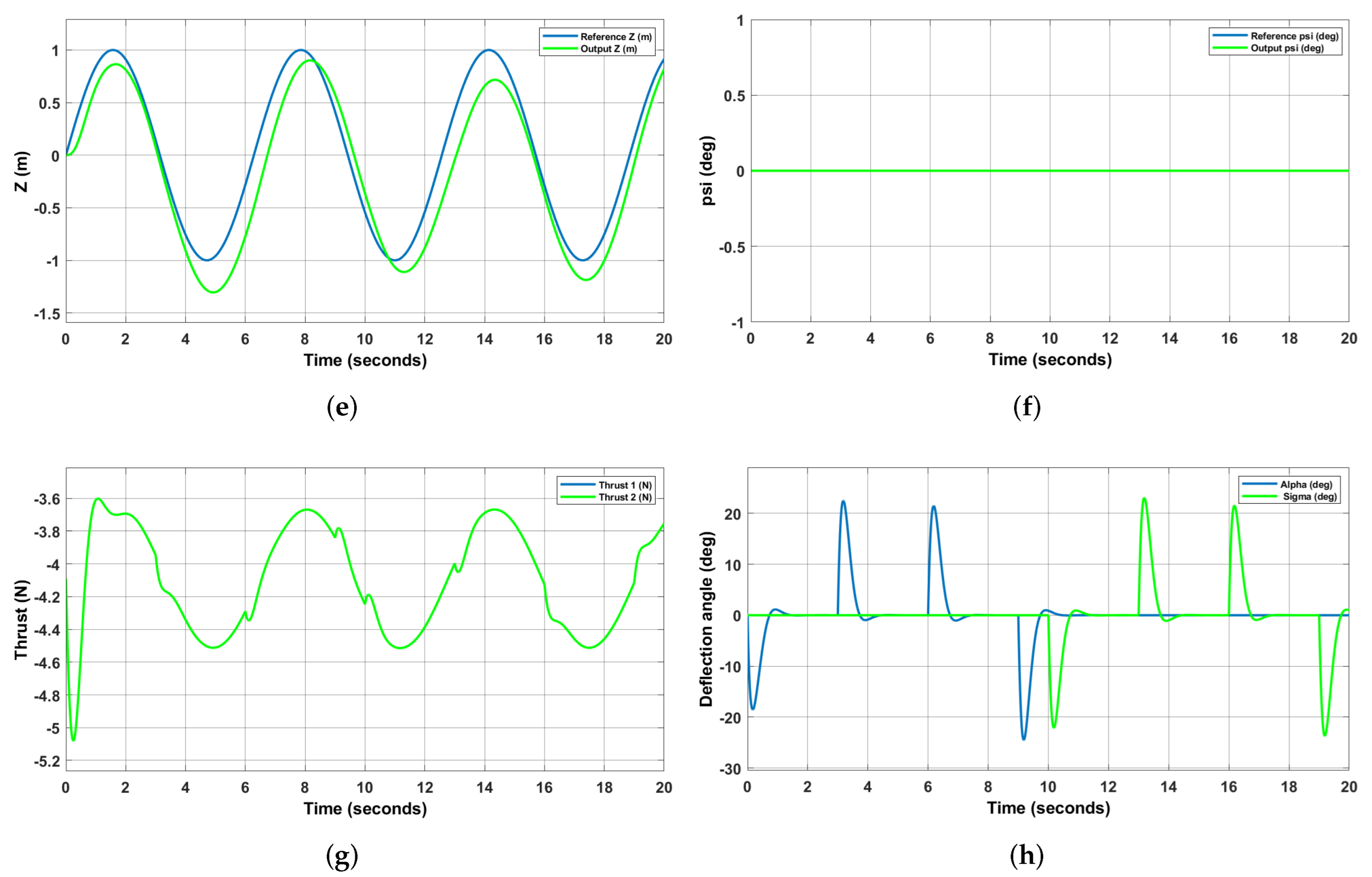
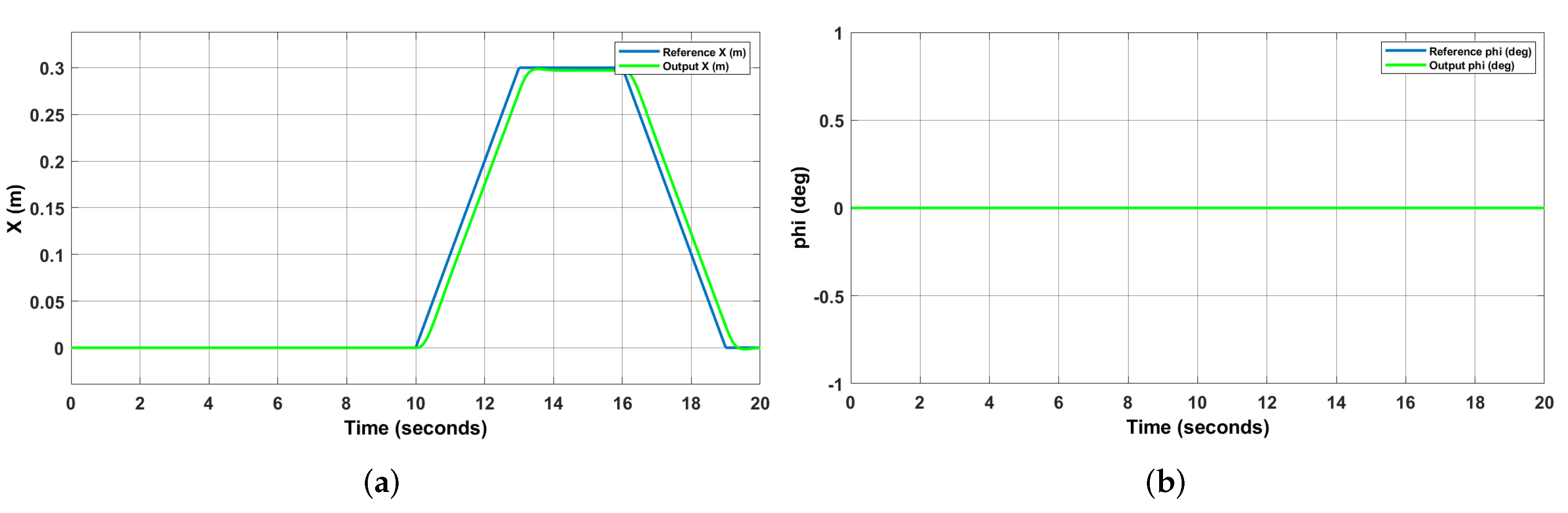
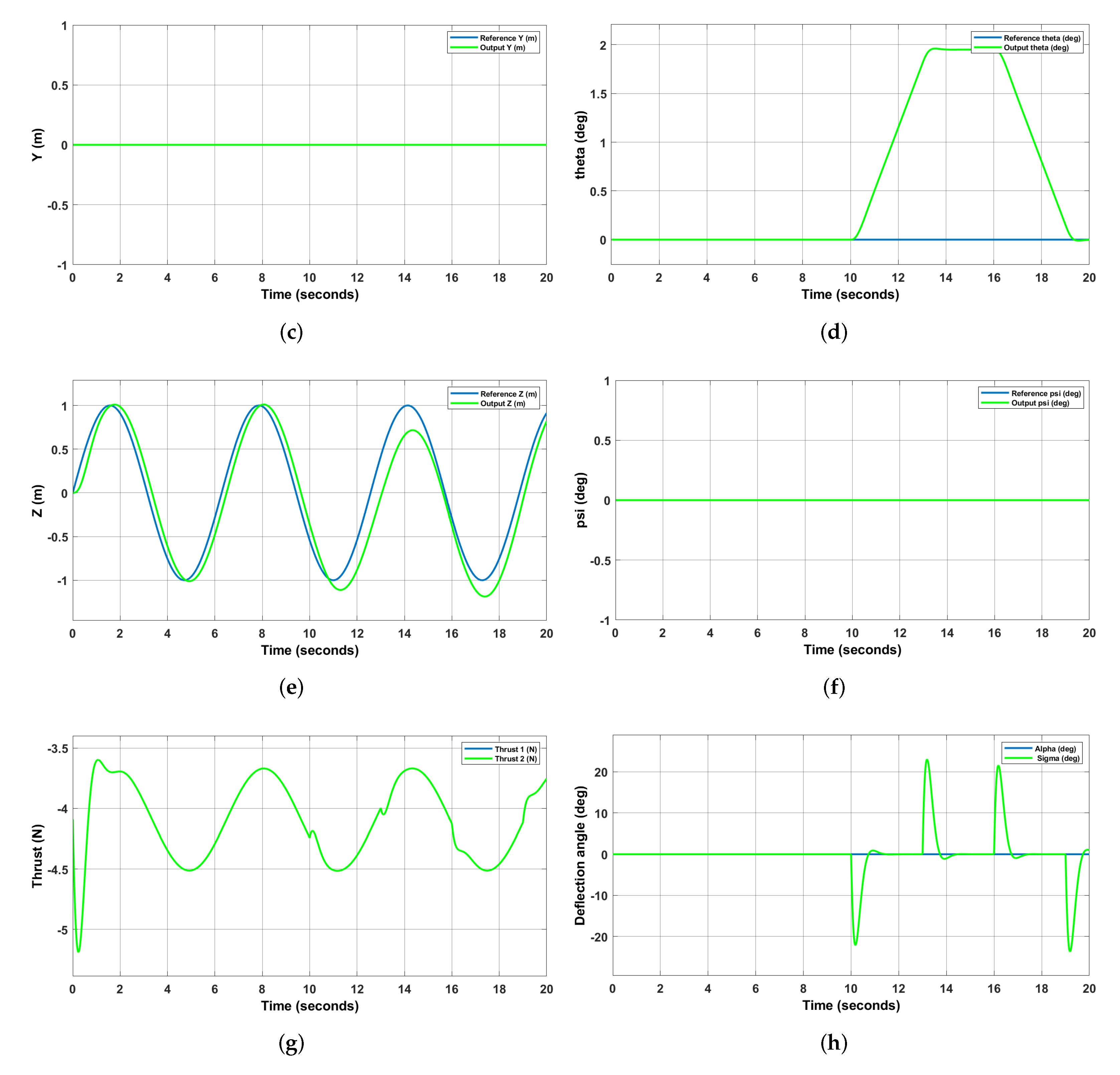
4.5. Simulation Results
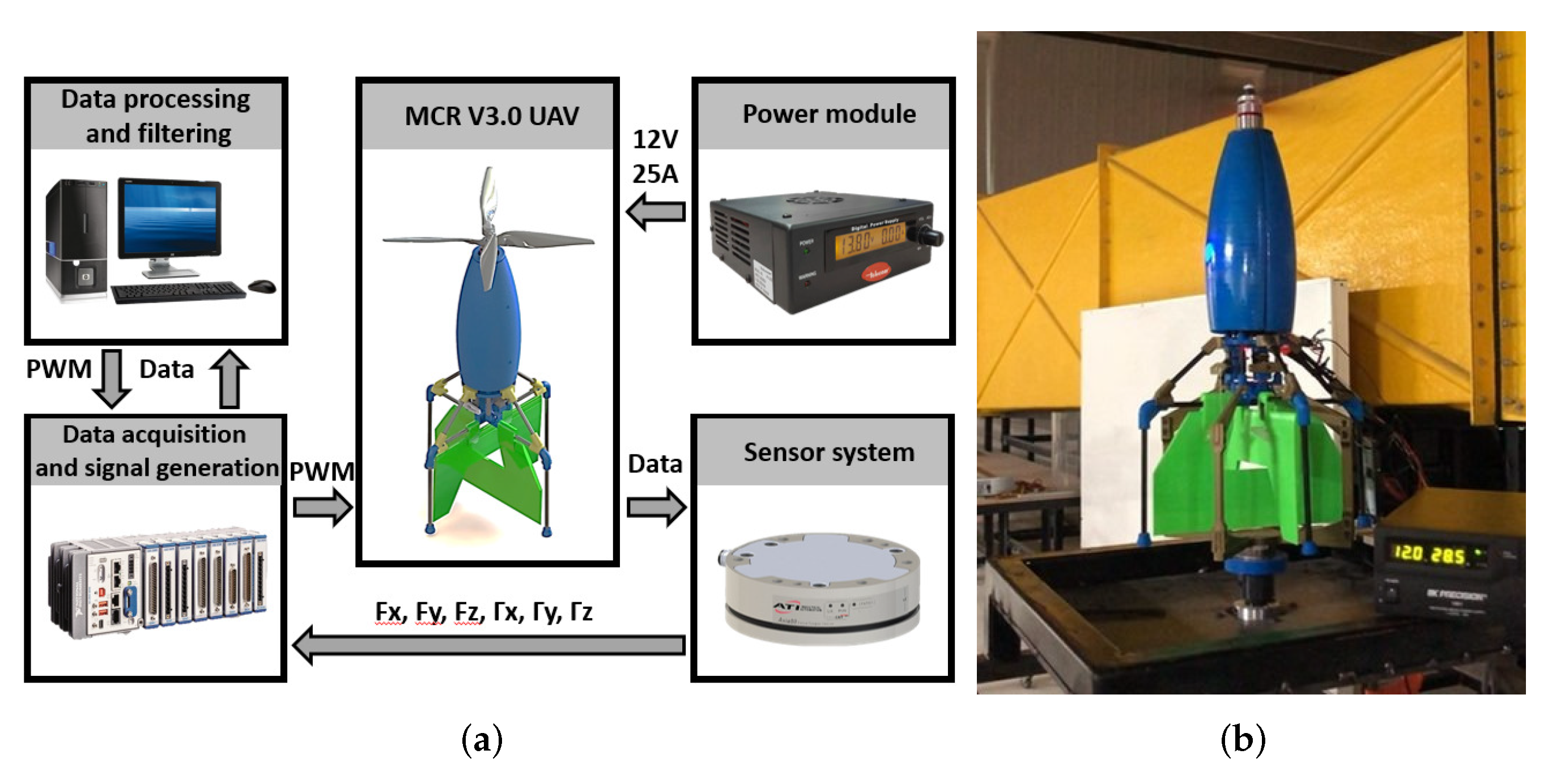
5. Ground Testing
5.1. Test Bench
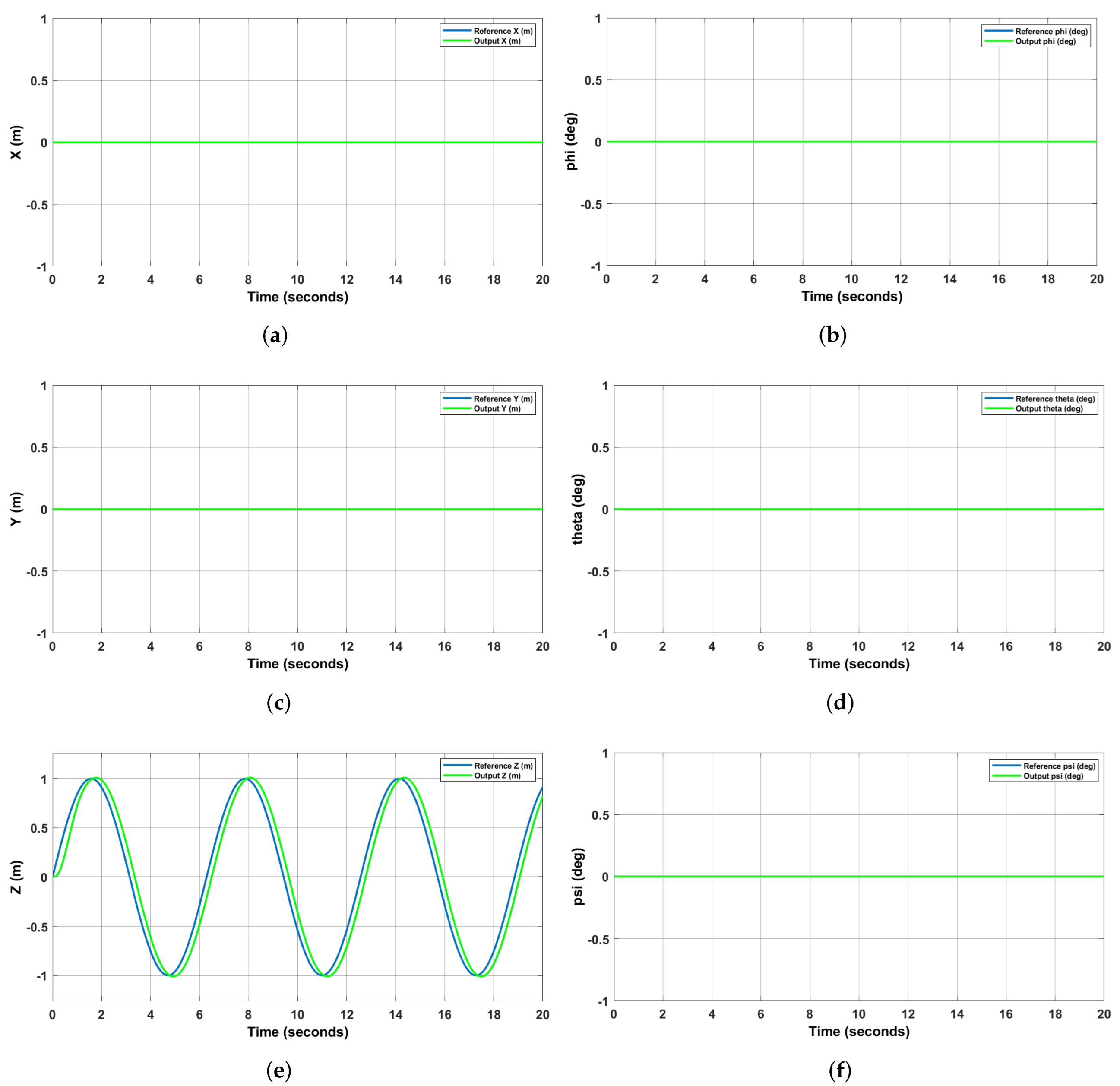
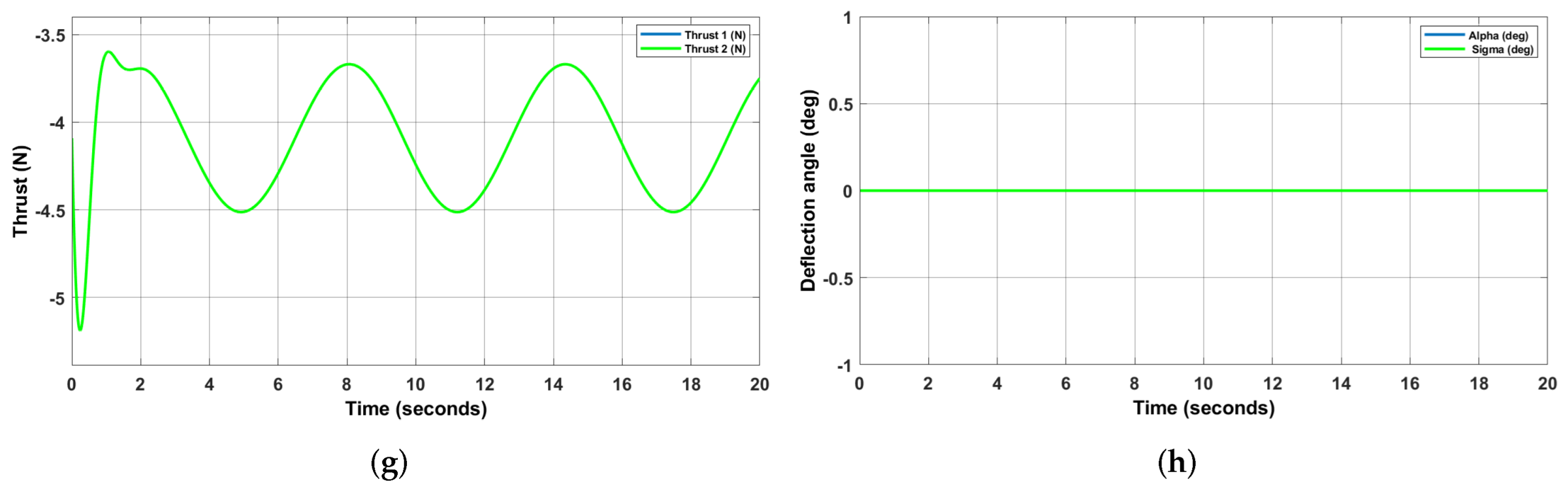
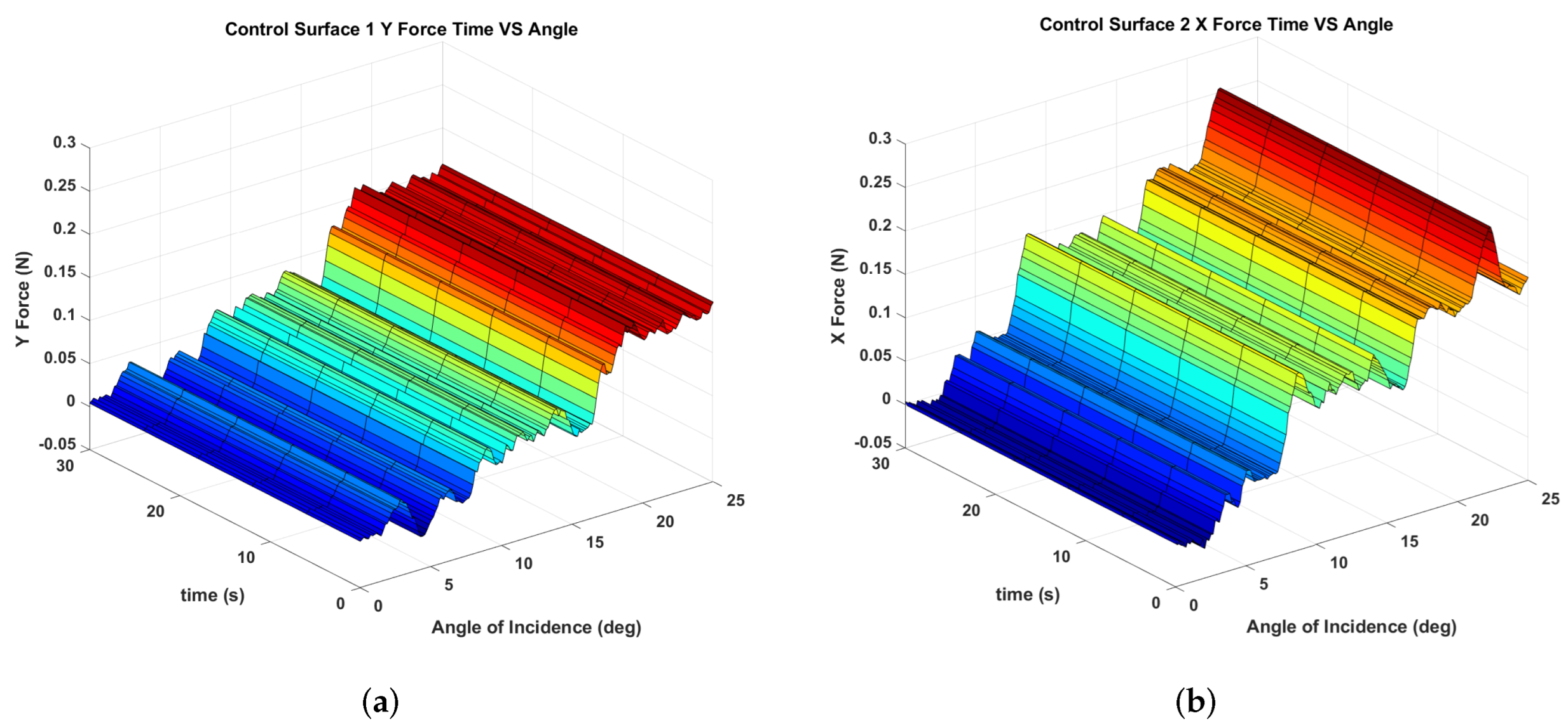
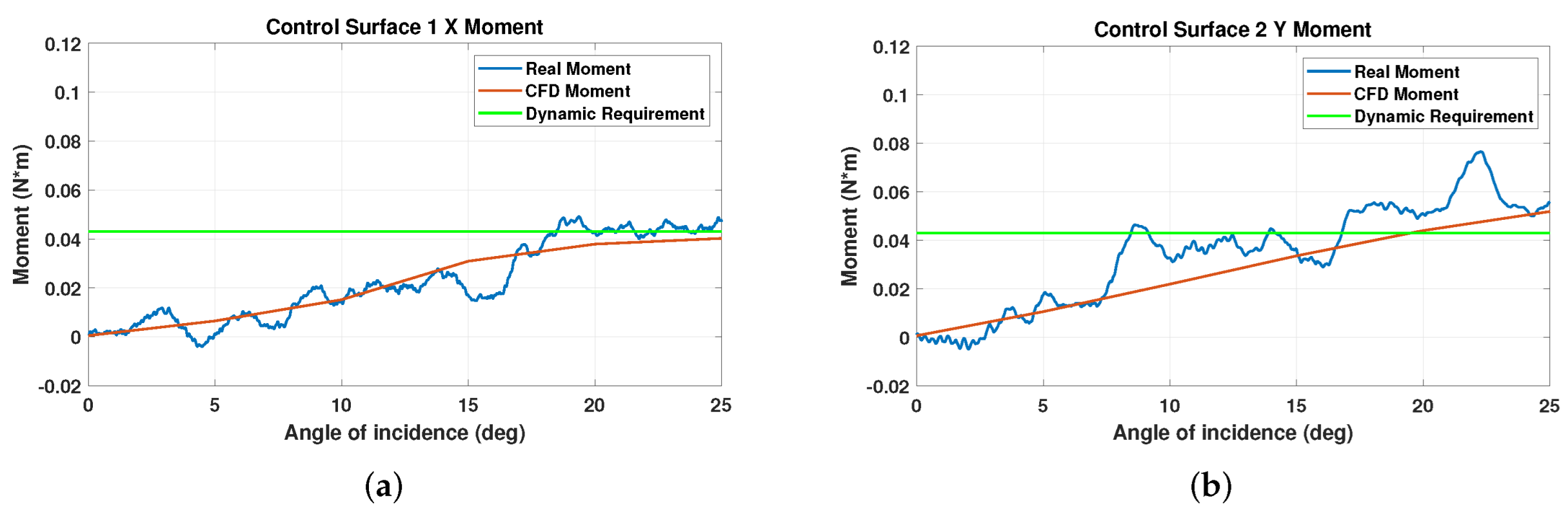
5.2. Comparison of Results
6. Conclusions
Author Contributions
Funding
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paulos, J.; Yim, M. Flight performance of a swashplateless micro air vehicle. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5284–5289. [Google Scholar]
- Carholt, O.C.; Fresk, E.; Andrikopoulos, G.; Nikolakopoulos, G. Design, modelling and control of a single rotor UAV. In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 840–845. [Google Scholar]
- Joel, N.C.; Djalo, H.; Aurelien, K.J. Robust control of UAV coaxial rotor by using exact feedback linearization and PI-observer. Int. J. Dyn. Control 2019, 7, 201–208. [Google Scholar] [CrossRef]
- Malandrakis, K.; Dixon, R.; Savvaris, A.; Tsourdos, A. Design and Development of a Novel Spherical UAV. IFAC-PapersOnLine 2016, 49, 320–325. [Google Scholar] [CrossRef]
- Lee, S.J. Modeling of real-time flight control system for small coaxial helicopter. In Proceedings of the 2014 IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2014. [Google Scholar]
- Drouot, A.; Richard, E.; Boutayeb, M. Hierarchical backstepping-based control of a Gun Launched MAV in crosswinds: Theory and experiment. Control Eng. Pract. 2014, 25, 16–25. [Google Scholar] [CrossRef]
- Mokhtari, M.R.; Cherki, B.; Braham, A.C. Disturbance observer based hierarchical control of coaxial-rotor UAV. ISA Trans. 2017, 67, 466–475. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Sun, K. Adaptive fault tolerant control for a small coaxial rotor unmanned aerial vehicles with partial loss of actuator effectiveness. Aerosp. Sci. Technol. 2019, 88, 362–379. [Google Scholar] [CrossRef]
- Fan, W.; Xiang, C.; Najjaran, H.; Wang, X.; Xu, B. Mixed adaptive control architecture for a novel coaxial-ducted-fan aircraft under time-varying uncertainties. Aerosp. Sci. Technol. 2018, 76, 141–154. [Google Scholar] [CrossRef]
- Wang, Y.; Song, H.; Li, Q.; Zhang, H. Research on a full envelop controller for an unmanned ducted-fan helicopter based on switching control theory. Sci. Technol. 2019, 62, 1837–1844. [Google Scholar] [CrossRef]
- Li, J.; Yang, Q.; Sun, Y. Robust State and Output Feedback Control of Launched MAVs with Unknown Varying External Loads. J. Intell. Robot. Syst. 2018, 92, 671–684. [Google Scholar] [CrossRef]
- Koehl, A.; Rafaralahy, H.; Boutayeb, M.; Martinez, B. Aerodynamic modelling and experimental identification of a coaxial-rotor uav. J. Intell. Robot. Syst. 2012, 68, 53–68. [Google Scholar] [CrossRef]
- Vogeltanz, T. Conceptual design and control of twin-propeller tail-sitter mini-UAV. CEAS Aeronaut. J. 2019, 10, 937–954. [Google Scholar] [CrossRef]
- Kim, Y.T.; Park, C.H.; Kim, H.Y. Three-dimensional CFD investigation of performance and interference effect of coaxial propellers. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 376–383. [Google Scholar]
- Wei, Y.; Deng, H.; Li, K.; Xiong, H.; Jiang, M. Experimental investigation of aerodynamic characteristic for a coaxial rotor aircraft. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 251–257. [Google Scholar]
- Lei, Y.; Ye, Y. Aerodynamic Characteristics of a Hex-Rotor MAV With Three Coaxial Rotors in Hover. IEEE Access 2020, 8, 221312–221319. [Google Scholar] [CrossRef]
- Xu, H.; Ye, Z. Numerical Simulation of Unsteady Flow Around Forward Flight Helicopter with Coaxial Rotors. Chin. J. Aeronaut. 2011, 24, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Fan, F.; Liu, P.; Huang, S.; Lin, Y. Aerodynamic characteristics of rigid coaxial rotor by wind tunnel test and numerical calculation. Chin. J. Aeronaut. 2019, 32, 568–576. [Google Scholar] [CrossRef]
- Han, H.; Xiang, C.; Xu, B.; Yu, Y. Experimental and computational analysis of microscale shrouded coaxial rotor in hover. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1092–1100. [Google Scholar]
- Bondyra, A.; Gardecki, S.; Gasior, P.; Giernack, W. Performance of coaxial propulsion in design of multi-rotor UAVs. In Challenges in Automation, Robotics and Measurement Techniques; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 440. [Google Scholar]
- Wang, F.; Jinqiang, J.; Chen, B.M.; Lee, T.H. Flight dynamics modeling of coaxial rotorcraft UAVs. In Handbook of Unmanned Aerial Vehicles; Valavanis, K., Vachtsevanos, G., Eds.; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Espinoza, E.S.; Garcia, O.; Lugo, I.; Ordaz, P.; Lozano, R.; Malo, A. Micro-Helicopter for Long-Distance Missions: Description and Attitude Stabilization. J. Intell. Robot. Syst. 2012, 70, 151–163. [Google Scholar] [CrossRef]
- Chauffaut, C.; Escareno, J.; Lozano, R. The Transition Phase of a Gun Launched Micro Air Vehicle. J. Intell. Robot. Syst. 2013, 70, 119–131. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill Co.: New York, NY, USA, 2010. [Google Scholar]
- Stengel, R.F. Flight Dynamics; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation; John Wiley and Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Kermode, A.C. Mechanics of Flight, 11th ed.; Pearson Prentice-Hall: Harlow, UK, 2006. [Google Scholar]
- Chen, C.-H. Linear System Theory and Design, 3rd ed.; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Cook, M.V. Flight Dynamics Principles; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar]
- You, W. Pixhawk Users Manual; Getech Ltd.: Ipswich, UK, 2015. [Google Scholar]
- Pecho, P.; Ažaltovič, V.; Kandera, B.; Bugaj, M. Introduction study of design and layout of UAVs 3D printed wings in relation to optimal lightweight and load distribution. Transp. Res. Procedia 2019, 40, 861–868. [Google Scholar] [CrossRef]






| MCR UAV v3.0 AVIONICS | |
|---|---|
| Motor | CR23L KV1100 |
| ESC | (2×) AEO E-Power 30A |
| Propeller | CR/CCR 9047 |
| Flight Controller | Pixhawk 1 |
| CPU | CPU: 180 MHz ARM® Cortex |
| IMU | MPU6000 |
| Barometer | ST Micro 16-bit |
| Magnetometer | ST Micro 14-bit |
| GPS | U-Blox 6 (3D Robotics) |
| Servo | Hitec HS65-MG |
| Radio | Spektrum DX8 |
| Mass | 0.843 Kg |
| CFD Simulation Parameters | ||
|---|---|---|
| Time | Steady-state model | Transient model |
| Solver | Pressure-based | Pressure-based |
| Viscous model | k- Realizable | k- Realizable Cell zone conditions |
| Default conditions | Propeller enclosure, vehicle enclosure | |
| Boundary conditions | Velocity inlet, pressure outlet | Velocity inlet, pressure outlet |
| Methods | Coupled default equations | Simple default equation |
| Solution initialization | Standard initialization coupled from inlet | Hybrid initialization |
| Solution | Iterations: 1000 | Time step size: 0.1 s Number of time steps: 800 Max. iterations: 50 |
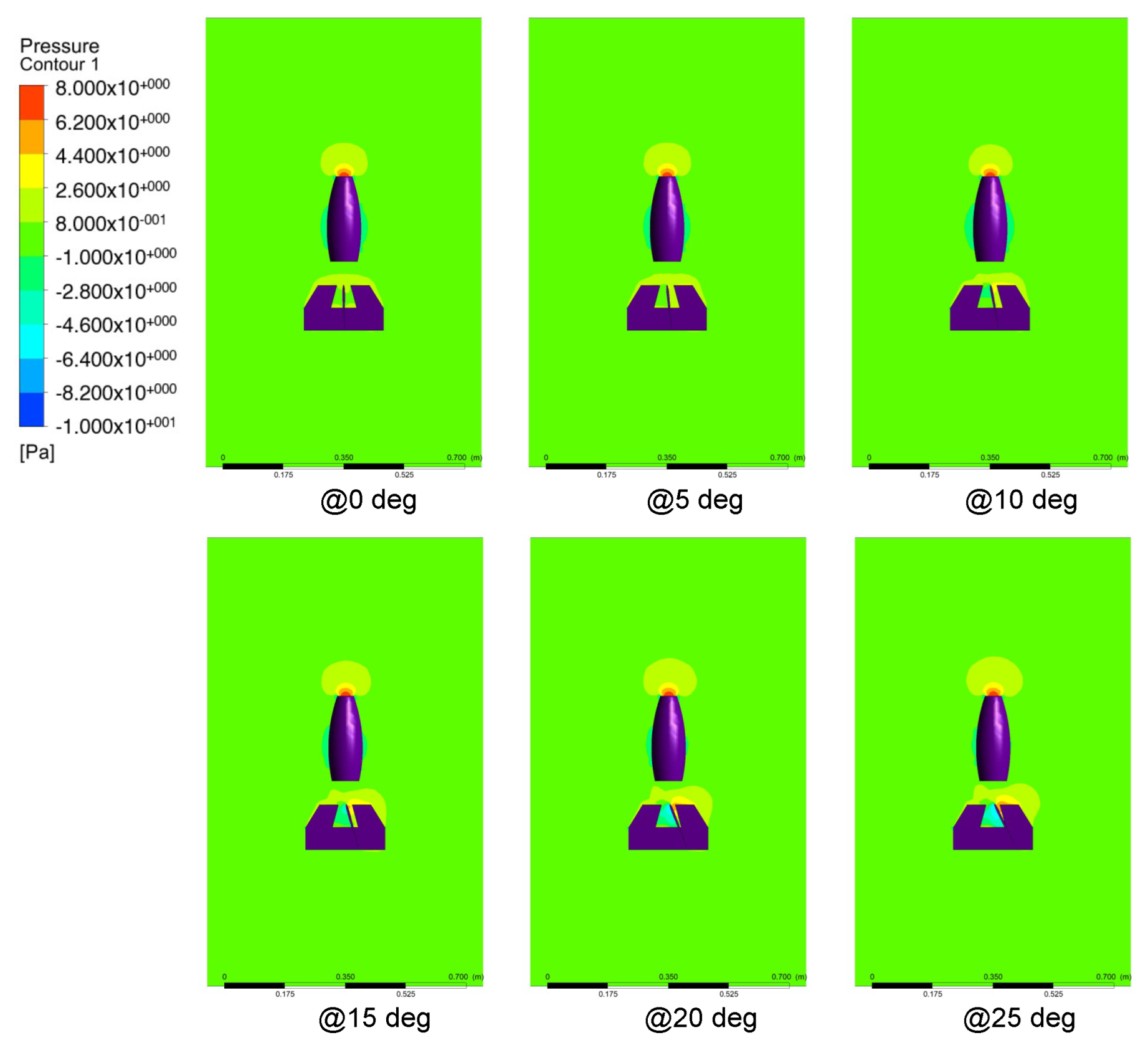
| Control Surface 1 forces | |||||||
|---|---|---|---|---|---|---|---|
| Angle (deg) | 0 | 5 | 10 | 15 | 20 | 25 | Deviation |
| CFD Y Axis (N) | 0.0016 | 0.021 | 0.050 | 0.103 | 0.126 | 0.134 | 5.6% |
| Real Y Axis (N) | 0.0043 | 0.029 | 0.035 | 0.081 | 0.125 | 0.149 | 5.8% |
| CFD Z Axis (N) | 0.003 | 0.004 | 0.009 | 0.024 | 0.045 | 0.061 | 2.4% |
| Cal. Z Axis (N) | 8.276 | 8.275 | 8.27 | 8.255 | 8.234 | 8.218 | 2.4% |
| Real Z Axis (N) | 8.46 | 8.56 | 8.47 | 8.52 | 8.39 | 8.38 | 7.1% |
| Control Surface 2 forces | |||||||
|---|---|---|---|---|---|---|---|
| Angle (deg) | 0 | 5 | 10 | 15 | 20 | 25 | Deviation |
| CFD X Axis (N) | 0.0023 | 0.035 | 0.073 | 0.111 | 0.146 | 0.172 | 6.6% |
| Real X Axis (N) | 0.0029 | 0.027 | 0.068 | 0.106 | 0.139 | 0.161 | 6.2% |
| CFD Z Axis (N) | 3.7 | 0.005 | 0.015 | 0.031 | 0.052 | 0.078 | 3.0% |
| Cal. Z Axis (N) | 8.279 | 8.274 | 8.264 | 8.248 | 8.227 | 8.201 | 3.0% |
| Real Z Axis (N) | 8.47 | 8.6 | 8.43 | 8.42 | 8.57 | 8.49 | 7.0% |
| Control Surface 1 Moments | |||||||
|---|---|---|---|---|---|---|---|
| Angle (deg) | 0 | 5 | 10 | 15 | 20 | 25 | Deviation |
| CFD X Axis (N·m) | 0.0005 | 0.006 | 0.015 | 0.030 | 0.037 | 0.040 | 1.7 |
| Real X Axis (N·m) | 0.001 | 0.008 | 0.010 | 0.024 | 0.037 | 0.040 | 1.7 |
| Control Surface 2 Moments | |||||||
|---|---|---|---|---|---|---|---|
| Angle (deg) | 0 | 5 | 10 | 15 | 20 | 25 | Deviation |
| CFD Y Axis (N·m) | 0.0006 | 0.010 | 0.021 | 0.033 | 0.044 | 0.051 | 2.0 |
| Real Y Axis (N·m) | 0.0008 | 0.008 | 0.020 | 0.031 | 0.041 | 0.048 | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dominguez, V.H.; Garcia-Salazar, O.; Amezquita-Brooks, L.; Reyes-Osorio, L.A.; Santana-Delgado, C.; Rojo-Rodriguez, E.G. Micro Coaxial Drone: Flight Dynamics, Simulation and Ground Testing. Aerospace 2022, 9, 245. https://doi.org/10.3390/aerospace9050245
Dominguez VH, Garcia-Salazar O, Amezquita-Brooks L, Reyes-Osorio LA, Santana-Delgado C, Rojo-Rodriguez EG. Micro Coaxial Drone: Flight Dynamics, Simulation and Ground Testing. Aerospace. 2022; 9(5):245. https://doi.org/10.3390/aerospace9050245
Chicago/Turabian StyleDominguez, Victor H., Octavio Garcia-Salazar, Luis Amezquita-Brooks, Luis A. Reyes-Osorio, Carlos Santana-Delgado, and Erik G. Rojo-Rodriguez. 2022. "Micro Coaxial Drone: Flight Dynamics, Simulation and Ground Testing" Aerospace 9, no. 5: 245. https://doi.org/10.3390/aerospace9050245
APA StyleDominguez, V. H., Garcia-Salazar, O., Amezquita-Brooks, L., Reyes-Osorio, L. A., Santana-Delgado, C., & Rojo-Rodriguez, E. G. (2022). Micro Coaxial Drone: Flight Dynamics, Simulation and Ground Testing. Aerospace, 9(5), 245. https://doi.org/10.3390/aerospace9050245






