Simulation of Unsteady Flows of Oil/Gas in the Ventless Bearing Chamber of an Aero-Engine

Abstract

The unsteady motion behavior of oil/gas two-phase flow in a novel ventless bearing chamber has significant impacts on the lubrication and heat transfer efficiency of bearings due to the various advantages of lower pressure levels and weaker rotating airflow effects. In this paper, the unsteady motion behavior of oil/gas two-phase flow in a ventless aero-engine bearing chamber is investigated by three-dimensional numerical simulation through the volume of fluid (VOF) method, and the numerical method is verified using published experimental data. The flow characteristics of oil/gas two-phase in the secondary flow and three-dimensional flow are investigated. The results show the evolution of vortices and the transition of the driving mode in the unsteady motion of oil/gas two-phase flow, and a criterion for the shift of the driving mode at different rotor speeds is proposed. As the rotation speed increases, the variation trend of the velocity field and pressure field of oil/gas two-phase flow is consistent, and the accumulation region of oil becomes inconspicuous. The results indicate a reference for enhancing the performance of lubrication systems for aero-engines.

1. Introduction

Oil/gas two-phase flow in the bearing chamber of the aero-engine lubrication system can provide lubrication to avoid material deterioration by reducing friction, and it is crucial to avoid heat accumulation, which can further degrade the oil properties and overall deterioration in heat transfer functionality [1,2]. For the process from engine startup to steady operation, the unsteady motion behavior of oil/gas two-phase will directly affect the performance of the bearing. Thus, the related knowledge is essential for improving the lubrication and heat transfer performance of the bearing chamber, and reducing the maintenance cost of aero-engines.

The flow behavior of oil/gas two-phase in the chamber is mainly affected by the internal pressure, chamber structures and size, rotor speed and flow rates of oil/gas. Therein, chamber structures such as geometry and oil return design have important influences on lubricating oil distribution [3,4,5]. At present, there are three bearing chambers in an aero-engine: the bearings (No. 1–3) located in the compressor uses the front bearing chamber together, the bearing (No. 4) near the combustion chamber uses the centre bearing chamber alone, and the bearing (No. 5) located at the nozzle uses the rear bearing chamber alone. The position of the aero-engine bearing chamber and structural diagrams are shown in Figure 1. There are two main types of chamber structures of aero-engines: one is a vented bearing chamber with vent and scavenge offtake [6,7], and the other is the novel ventless bearing chamber with only a single outlet for air and lubricating oil to flow out together [3]. As far as the vented bearing chamber is concerned, air easily entraps lubricating oil from the vent offtake under high rotor speeds, resulting in a decrease in the lubricating oil to the oil/gas separator and the maldistribution of the oil phase. The superheating in areas of missing lubricating oil may lead to coked oil fragments and subsequent combustion [8,9]. The better sealing performance of the ventless bearing chamber eliminates the leakage of oil from the vent offtake, and due to the small pressure drop gradient in the ventless bearing chamber, the flow rate of air in the chamber and the influence of rotating airflow on the distribution of oil are reduced, increasing the gravity of the lubricating oil itself and causing the lubricating oil to flow out from the scavenge off take at the bottom [10,11,12]. However, most of the studies are on the steady motion of oil/gas two-phase in vented bearing chambers, and the studies of unsteady motion in the ventless bearing chambers are scarce. In view of this, it is necessary and important to study the unsteady motion characteristics of oil/gas two-phase in a ventless bearing chamber.

In the present work, the unsteady motion behavior of oil/gas two-phase in a ventless bearing chamber is investigated by three-dimensional simulation through the volume of fluid (VOF) method, and the numerical method is verified using published experimental data in the literature. The velocity fields and pressure fields of oil/gas two-phase in the chamber at different rotor speeds are observed, and the evolution of twin vortices and a single vortex in the secondary flow is clearly defined. The shift from the rotational speed driving mode to the lubricating oil driving mode and the distribution of lubricating oil at different rotational speeds are analyzed, and the dimensionless correlation of the shift criteria is proposed. Thus, the study of the unsteady motion behavior of oil/gas two-phase in the ventless bearing chamber could provide a reference for improving the performance of lubrication systems for aero-engines.

2. Model and Solution Method

2.1. Mathematical Model

CFD software (ANSYS CFX was developed by AEA Technology company in the UK, version 15.0) is used to simulate the three-dimensional flow field of the ventless bearing chamber, and the interlacing of static and dynamic grids are solved by the construction of two pairs of interfaces. The interface of oil/gas two-phase is tracked by the volume of fluid method (VOF). In this method, a particular phase is identified by its volume fraction in a computational cell, where ${\alpha }_{\mathrm{l}}$ = 1 means the oil phase, ${\alpha }_{\mathrm{g}}$ = 1 means the gas phase, and 0 < ${\alpha }_{\mathrm{g}}$ < 1 means the interface of oil and gas, which is constrained simultaneously by ${\alpha }_{\mathrm{g}}{+\alpha }_{\mathrm{l}}=1$ [13]. For the oil phase, the volume fraction equation is as follows:

$$\frac{1}{{\rho }_{\mathrm{l}}}\frac{\partial \left({\alpha }_{\mathrm{l}}{\rho }_{\mathrm{l}}\right)}{\partial t}+\frac{1}{{\rho }_{\mathrm{l}}}·\nabla \left({\alpha }_{\mathrm{l}}{\rho }_{\mathrm{l}}{\overrightarrow{\nu }}_{\mathrm{l}}\right)=\frac{S_{{\mathsf{\alpha }}_{\mathrm{l}}}}{{\rho }_{\mathrm{l}}}+\frac{1}{{\rho }_{\mathrm{l}}}\sum ({\stackrel{·}{m}}_{\mathrm{gl}}-{\stackrel{·}{m}}_{\lg }),$$

(1)

where ${\alpha }_{\mathrm{l}}$ is the volume fraction of oil phase, ${\overrightarrow{\nu }}_{\mathrm{l}}$ is the velocity vector of oil phase, ${\rho }_{\mathrm{l}}$ is the density of oil phase, $S_{{\mathsf{\alpha }}_{\mathrm{l}}}$ is the mass source of oil phase, ${\stackrel{·}{m}}_{\mathrm{gl}}$ is the mass transfer from gas to oil, and ${\stackrel{·}{m}}_{\lg }$ is the mass transfer from oil to gas. The momentum equation is shared for oil/gas two-phase flow, and the momentum equation for each phase in the whole bearing chamber can be expressed as follows:

$$\frac{\partial \left(\rho \overrightarrow{\nu }\right)}{\partial \mathrm{t}}+\nabla \left(\rho \overrightarrow{\nu }\overrightarrow{\nu }\right)=-\nabla P+\nabla ·\left[\mu \left(\nabla \overrightarrow{\nu }+\nabla {\overrightarrow{\nu }}^T\right)\right]+\rho \overrightarrow{g}+{\overrightarrow{F}}_{\mathrm{s}},$$

(2)

where P is pressure, $\mu$ is dynamic viscosity, and $\overrightarrow{g}$ is the acceleration of gravity. The average density and average viscosity of the oil/gas two-phases can be obtained by the following formulas:

$${\rho =\alpha }_{\mathrm{g}}{\rho }_{\mathrm{g}}{+\alpha }_{\mathrm{l}}{\rho }_{\mathrm{l}},$$

(3)

$${\mu =\alpha }_{\mathrm{g}}{\mu }_{\mathrm{g}}{+\alpha }_{\mathrm{l}}{\mu }_{\mathrm{l}}.$$

(4)

$F_{\mathrm{s}}$ is a body force due to surface tension, which can be calculated by the continuous surface force (CSF) model:

$$F_{\mathrm{s}}{=\mathsf{\sigma }}_{\lg }\frac{{2\rho \kappa }_{\mathrm{l}}\nabla {\alpha }_{\mathrm{l}}}{{\rho }_{\mathrm{l}}{+\rho }_{\mathrm{g}}},$$

(5)

where σ is the surface tension, and κ is the interface curvature of oil/gas, which can be obtained by Equation (6):

$$\kappa =\nabla \frac{\mathrm{n}}{\left|\mathrm{n}\right|},$$

(6)

where, n is the surface normal.

The lubricating oil attached to the wall produces a contact angle with the wall, which will affect the interface curvature of oil phase, as seen in Figure 2. Thus, the actual unit normal vector $\overrightarrow{n}$ can be obtained as follows:

$$\overrightarrow{n}={\overrightarrow{ n}}_{\mathrm{w}}{\cos \theta }_{\mathrm{w}}+{\overrightarrow{t}}_{\mathrm{w}}{\sin \theta }_{\mathrm{w}},$$

(7)

where ${\overrightarrow{n}}_{\mathrm{w}}$ is the unit normal vector at the wall, ${\overrightarrow{t}}_{\mathrm{w}}$ is the unit tangent vector at the wall, and ${\theta }_{\mathrm{w}}$ is the contact angle between the oil phase and the wall.

2.2. Geometric Model

The geometric model of the ventless bearing chamber is shown in Figure 3, which is consistent with that adopted in the experiment by Kurz et al. [3]. It is noted that the circumferential angle is defined as follows: the angle of scavenge offtake is 180°, and the angle is increased in clockwise direction. Air and lubricating oil enter the bearing chamber from the air inlet and oil inlet respectively, and flow out from the scavenge offtake. The inner wall is a slip wall in counterclockwise rotation, and the other walls are fixed non-slip walls. In different directions, positive radial velocities point radially outward from the rotation Z axis, the positive axial velocities are in the direction of the rotation Z axis vector, and positive tangential velocities are based on the right-hand rule using the positive rotation Z axis.

The dimensions and boundary conditions of the bearing chamber are shown in

Table 1. Geometric dimensions and boundary conditions.

Geometry Structure	Dimension (mm)	Boundary	Condition Setting	Values
Shaft radius	64	Shaft wall	Rotating wall	5000/10,000/15,000 rpm
Outer (rim) wall radius	111	Outer wall	Constant high temperature wall	393 K
Chamber axial width	66
Scavenge pipe radius/length	5/60	Scavenge vent	Pressure outlet	1.7 bar
Air inlet channel thickness/length	0.7/12	Air inlet	Mass flow of inlet	0.2 g/s, 333 K
Oil inlet channel thickness	2	Oil inlet	Mass flow of inlet	100 L/h, 333 K

. The radial height (h) and axial width (b) are the important dimensions of the bearing chamber. The relative size of the bearing chamber is defined by the aspect ratio A to characterize the flow characteristics of oil/gas two-phase under this size of the ventless bearing chamber. The aspect ratio of the ventless bearing chamber is 0.712, and its formula is as follows:

$$A=\frac{h}{b}.$$

(8)

The scavenge ratio (SR = 4) was adopted for the mass flow of the inlet, which is consistent with the experimental literature [3]. The initial pressure P_ch of the computational domain is 2.7 bar and the initial temperature T_ch is 393 K. In the VOF model, air is the dominant phase with a density of 2.52 kg/m³ and a viscosity of 2.21 × 10⁻⁵ kg/m∙s. The lubricating oil is the secondary phase, and the surface tension coefficient between the primary and secondary phases is 0.036 N/m. The angle between the incident direction of lubricating oil entering the chamber and the rotor wall is 45°. The physical properties of the oil phase refer to the 4109-type aviation lubricating oil, the formulae are listed below [14].

$${\rho }_{\mathrm{l}}=1080.482-0.753T,$$

(9)

$${\lambda }_{\mathrm{l}}=0.180915-0.0001T,$$

(10)

$${Cp}_{\mathrm{l}}=1015.8+2.8T,$$

(11)

$$\mathrm{InIn}\left({\upsilon }_{\mathrm{l}}+0.8\right)=21.171-3.538\mathrm{In}T,$$

(12)

where ${\rho }_{\mathrm{l}}$ is the density of oil phase, ${\lambda }_{\mathrm{l}}$ is the thermal conductivity of oil phase, ${Cp}_{\mathrm{l}}$ is the specific heat at constant pressure, ${\upsilon }_{\mathrm{l}}$ is the kinematic viscosity of oil phase.

Fluent 15.0 software (One of ANSYS CFX’s software modules) was used to solve the flow characteristics of oil/gas two-phase flow in the ventless bearing chamber. The pressure implicit with splitting of operator (PISO) algorithm was employed to solve the coupling of pressure and velocity in transient flow. The momentum equation was solved by the second-order upwind equation with double precision. The step size was adjusted to ensure that the Courant value was between 0.01 and 2 to meeting the accuracy and stability of the calculated results.

2.3. Grid Independence Verification and Simulation Method Verification

Hexahedral structured grids are generated by ICEM 15.0 software (One of ANSYS CFX’s software modules) in the whole chamber. The overall ventless bearing chamber is cleaved into different basins to construct the grids. The lubricating oil film is attached to the outer wall of the bearing chamber, and the velocity gradient is very large, which is in the viscous bottom layer and the vorticity is not zero. The flow characteristics of the oil film must be solved with high precision. The wall function method was adopted for the solving process. The thickness of the first layer of wall grids is calculated by the dimensionless number Y⁺. After solving and modifying, the value of Y⁺ is determined to be 5. The dimensionless number Y⁺ is defined as follows:

$${\tau }_{\mathrm{w}}=\mu {\left(\frac{\partial u}{\partial y}\right)}_{y=0},$$

(13)

$$u^{*}=\sqrt{\frac{{\tau }_w}{\rho }},$$

(14)

$$Y^{+}=\frac{u^{*}y}{\upsilon },$$

(15)

where ${\tau }_{\mathrm{w}}$ is the shear stress of the wall, u is the characteristic velocity of the fluid, y is the normal distance of the first-layer mesh nodes, u* is the friction velocity of the wall, and υ is the viscosity of fluid movement.

The quality of the minimum grid in the whole chamber is 0.75, and the overall grids and the cross-section of grids of 90° are shown in Figure 4. The interface is set to complete the transmission of watershed information at the intersection of the grids. The slip-mesh is set as the motion block to complete the rotating motion of the shaft wall.

For the grid independence verification, Figure 5a shows the independence verification result of grids. The inlet flow rate of air is 10 g/s, the rotation speed is 15,000 rpm, and the number of grids is 430,000, 620,000, 680,000, 730,000, and 820,000. Figure 5a shows that the variation of air velocity is small when the number of grids reaches a certain extent. Thus, the adopted number of grids is 680,000, considering the factors of calculation accuracy and computing time.

Figure 5b shows the comparison of the steady-state oil film thickness between the simulated value and the experimental value in the literature at a shaft speed of 15,000 rpm, the oil inlet flow rate of 100 L/h and the air inlet flow rate of 0.2 g/s. It can be seen that the simulated value is in good agreement with the experimental value, but the simulated value is slightly lower than the experimental value at a circumferential angle of 45~135°, which may be caused by the high airtightness and the low influence of the rotating air flow of the simulated process. Thus, the numerical method is capable of predicting the film thickness with fairly good accuracy.

3. Results

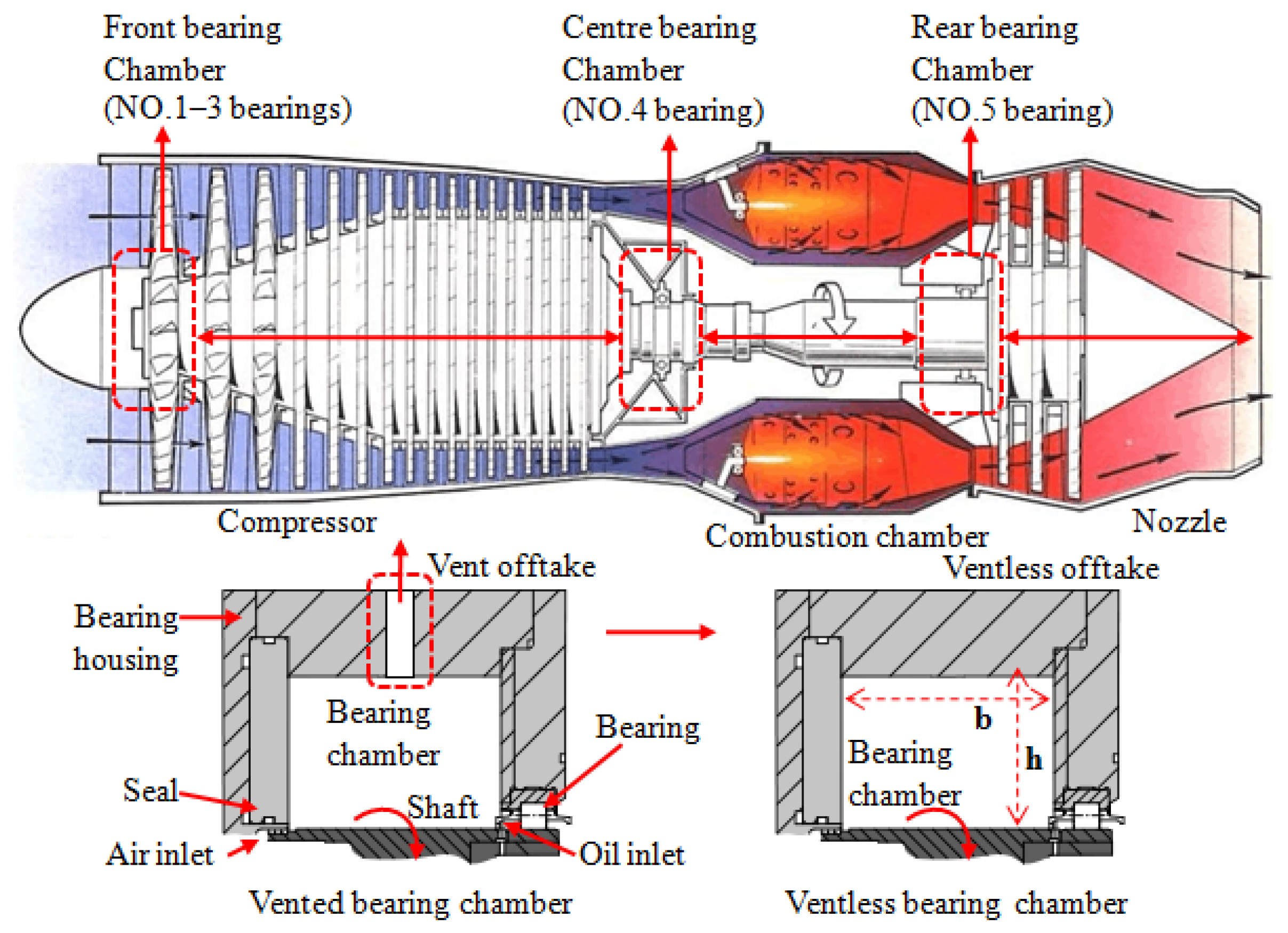
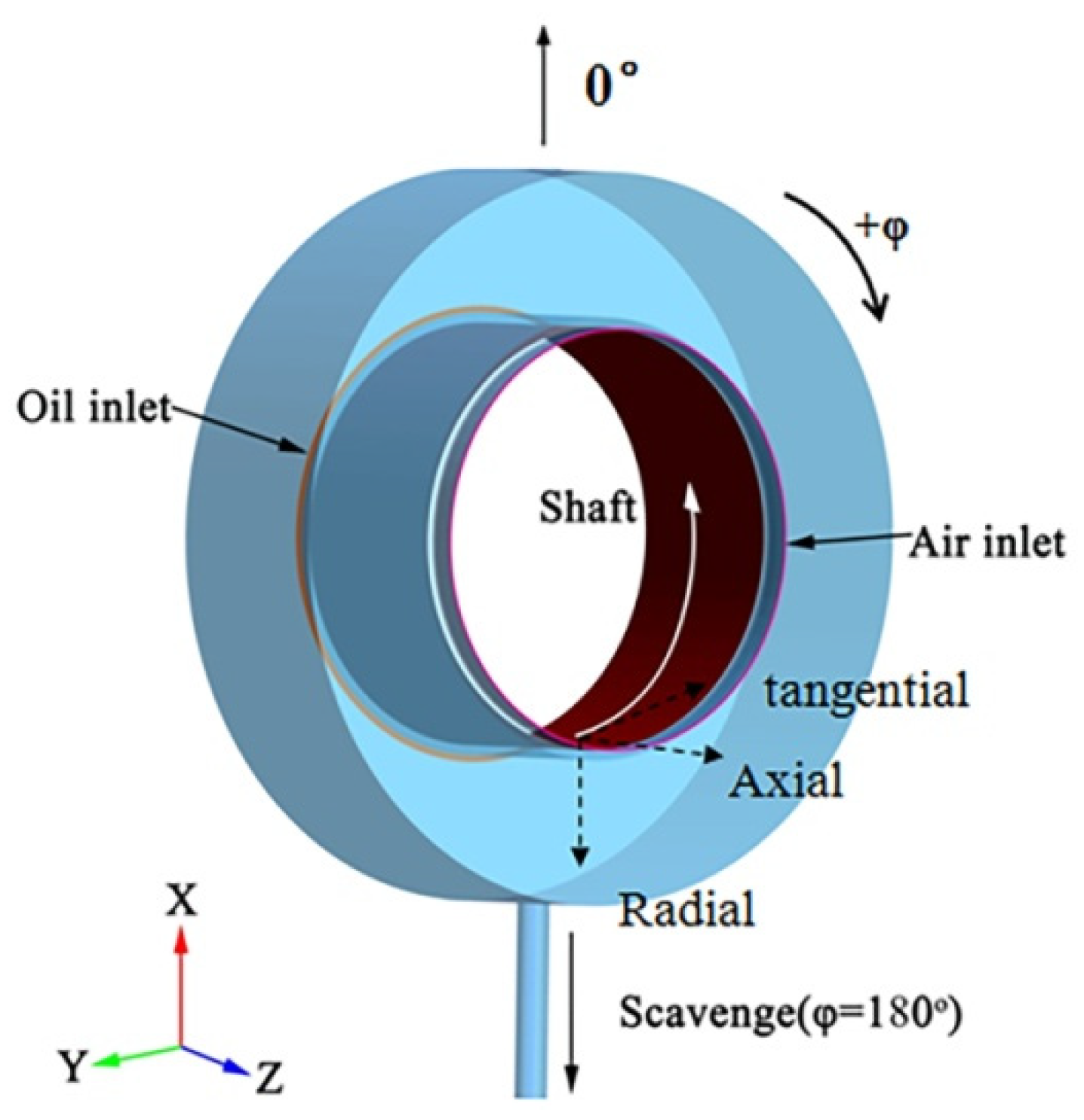
3.1. Secondary Flow of Two-Phase Flow

Gorse et al. [15] studied the airflow characteristics in a vented bearing chamber using a 3D Laser Doppler Anemometry (LDA) system, and proposed the criterion for the transition between the rotational speed drive mode (RSDM) and the sealing air driven mode (SADM) by the velocity ratio ($R_{\mathsf{\nu }}$), which is defined as follows:

$$R_{\mathsf{\nu }}=\frac{u_{\mathrm{s}}}{u_{\mathrm{in}}}=\frac{{\mathit{Re}}_{\mathrm{s}}}{{\mathit{Re}}_{\mathrm{g}}},$$

(16)

where $u_{\mathrm{s}}$ is the rotational speed of the shaft, $u_{\mathrm{in}}$ is the air inlet velocity; ${Re}_{\mathrm{s}}$ is the Reynolds number of the rotor, and ${Re}_{\mathrm{g}}$ is the Reynolds number of air. For $R_{\mathsf{\nu }}\ge$ 4.2, it is the rotational speed driving mode with twin vortices in the chamber. For $R_{\mathsf{\nu }}<$ 4.2, it is the sealed air drive mode with only a single vortex.

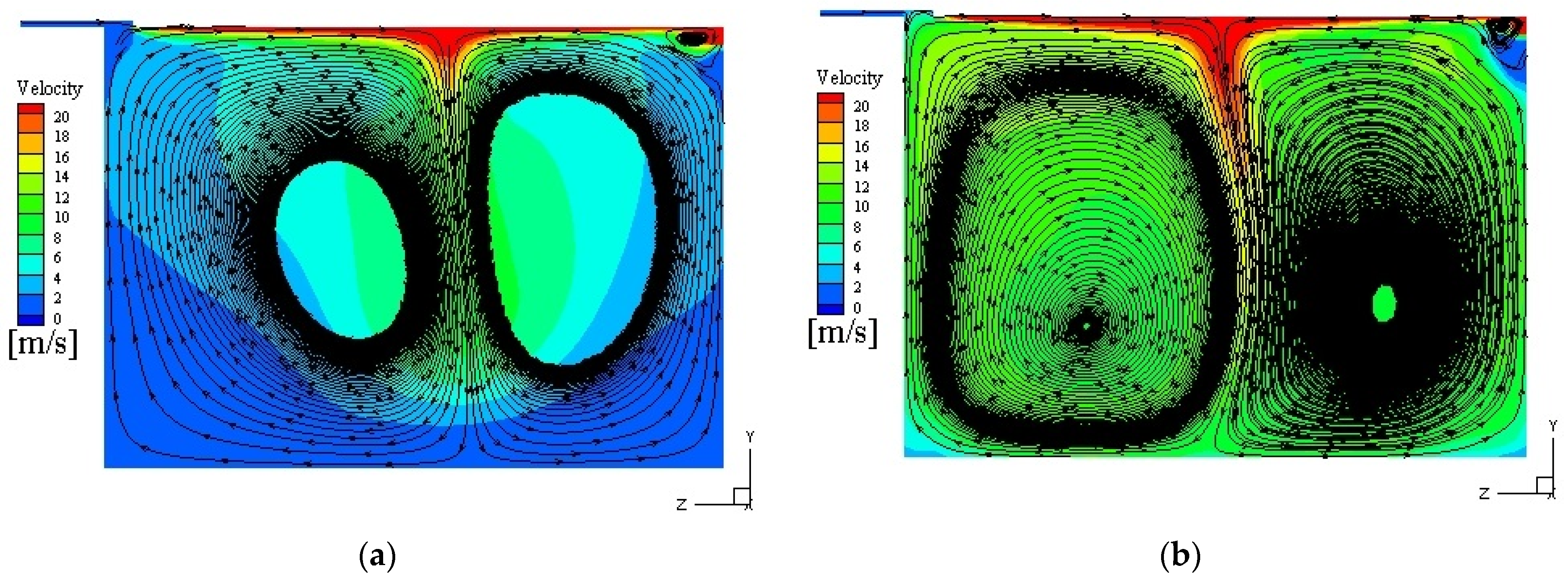
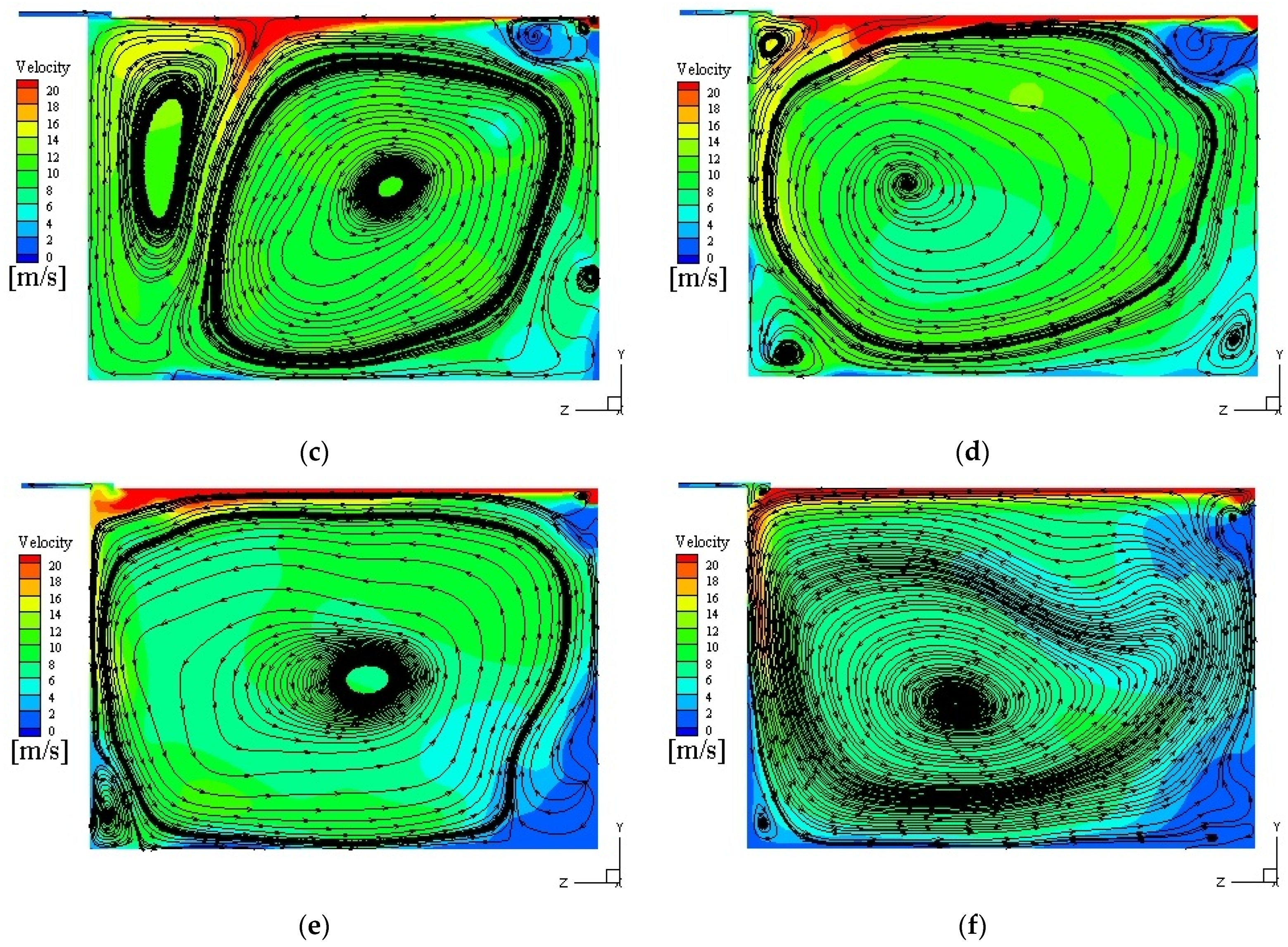
Figure 6 shows the secondary flow field at 10,000 rpm in the 90° cross section. It can be seen that there exists a transition of twin vortices to a single vortex for the unsteady process in the ventless bearing chamber under the aspect ratio of 0.712. At 0.027 s, there are twin hollow vortices with similar sizes and opposite directions, the velocity decreases gradually from the vortex center to the outside except at the inlet, and the velocity near the rotor gradually decreases from the center to both sides and the radial direction. The circulations of twin vortices collide at 1/2b in the axial direction. At this point, the actual vorticity value obtained by selecting a vorticity level of 0.05 is 4670.6 s⁻¹. Figure 6b shows that the vortex of the air inlet side begins to disperse, the vortex core becomes larger, the vortex intensity decreases, and the vortex intensity at the oil inlet side increases. The average vorticity value in the bearing chamber is 4889.2 s⁻¹. At 0.363 s, the vortex of the oil inlet side gradually merges with the vortex of the air inlet side, and the vortex core shifts to a higher velocity region. The motion of vortices is related to the dominant role of the rotor shear force, which is consistent with the evolution of the rotational speed driving mode into transition mode (TM) in the literature [15]. Then, the twin vortices merge into a single vortex with the vortex core at the air inlet side, and there are several low-velocity eddies at the corner of the chamber (Figure 6d). At 0.528 s, the small eddies in the corner are swallowed up by a single vortex. Finally, the vortex core is located in the center of the chamber, and the motion of oil/gas two-phase in the bearing chamber tends to be stable (Figure 6f). In this state, the tangential velocity direction of the vortex is consistent with the oil inlet direction, which is defined as the lubricating oil drive mode (ODM). The numerical simulation results of Singh et al. [16] at 10,000 rpm and an air flow rate of 10 g/s also show a similar result.

Gorse et al. [15] characterized the drive mode using the ratio of rotational speed to air velocity. However, the influence of oil flow on the drive mode cannot be ignored due to the simultaneous existence of oil/gas two-phase in the chamber. Therefore, the modified Reynolds number involving the gas/oil two-phase is adopted according to the literature [17], which is shown as follows:

$${Re}_{\mathrm{g}}=\frac{{\overline{c}}_{\mathrm{g}}·D_{\mathrm{h}}}{{\upsilon }_{\mathrm{g}}}\approx \frac{0.0004·{\stackrel{·}{m}}_{\mathrm{g}}}{{\overline{\mu }}_{\mathrm{g}-T}{D}_{\mathrm{h}}},$$

(17)

$${Re}_{\mathrm{l}}=\frac{{\overline{c}}_{\mathrm{l}}·D_{\mathrm{h}}}{{\upsilon }_{\mathrm{l}}}\approx \frac{0.0004·{\stackrel{·}{V}}_{\mathrm{l}}}{3600{\overline{\upsilon }}_{\mathrm{l}-T}{D}_{\mathrm{h}}},$$

(18)

$$D_{\mathrm{h}}=\frac{2·b·h}{b+h},$$

(19)

where ${Re}_{\mathrm{l}}$ is the Reynolds number of lubricating oil, $\overline{c}$ is the average velocity of oil/gas two-phase flow; D_h is the hydraulic diameter of chamber, and υ is the kinematic viscosity; ${\stackrel{·}{m}}_{\mathrm{g}}$ is the mass flow of air; ${\overline{\mu }}_{\mathrm{g}-\mathrm{T}}$ is the average dynamic viscosity of air at the average temperature of bearing chamber; ${\stackrel{·}{V}}_{\mathrm{l}}$ is the volume flow of oil; and ${\overline{v}}_{\mathrm{l}-\mathrm{T}}$ is the average kinematic viscosity of oil at the average temperature of the bearing chamber. b is the chamber axial length, and h is the chamber radial height.

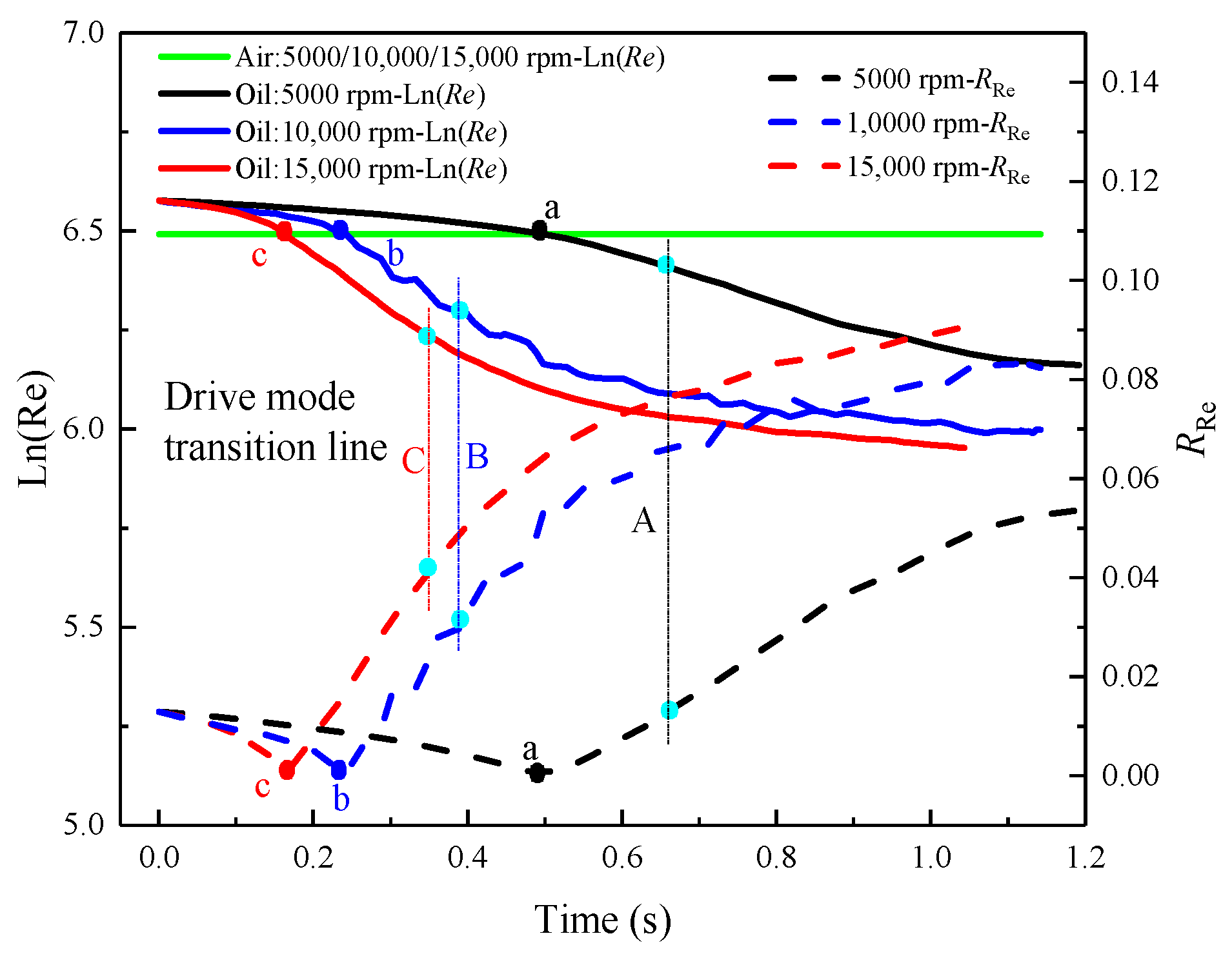
The evolution of the Reynolds number over time is shown in Figure 7. It can be seen from Figure 7 that the oil Reynolds number decreases over time and then levels off under the aspect ratio of 0.712. At the initial stage, the viscosity of lubricating oil after heat transfer is small and the Reynolds number is large due to the high temperature of the chamber. The flow of oil/gas two-phase is mainly affected by the rotor speed, which is called the rotational speed driving mode [15]. Thus, the Reynolds numbers of air and oil are equal for three rotor speeds owing to the shear force of the rotor. Moreover, the variation range of the natural log-Reynolds number of oil is symmetrically up and down based on the natural log-Reynolds number of air before the driving mode transition points (A, B, and C). Then, the natural log-Reynolds number of oil decreases over time after points A, B, and C. The viscosity of oil increases with decreasing average temperature in the chamber. Therefore, it is more susceptible to the impact of the rotor shear force compared with air and forms a single vortex dominated by lubricating oil. Here, the Reynolds ratio of two phases can be used as the criterion of the driving mode, which is as follows:

$$R_{\mathrm{Re}}=\frac{\left|\ln \left({Re}_{\mathrm{l}}\right){-\ln (Re}_{\mathrm{g}})\right|}{{\ln (\mathit{Re}}_{\mathrm{g}})}.$$

(20)

The dotted line in Figure 7 shows the Reynolds ratio ($R_{\mathrm{Re}}$) over time under the aspect ratio of 0.712. At 5000 rpm, 0 $\le R_{\mathrm{Re}}\le$ 0.01373 and 0.01373 $<R_{\mathrm{Re}}$ are the rotational speed driving mode and the lubricating oil drive mode, respectively. At 10,000 rpm, 0 $\le R_{\mathrm{Re}}\le$ 0.02963 is the rotational speed driving mode, and 0.02963 $<R_{\mathrm{Re}}$ is the lubricating oil drive mode. At 15,000 rpm, 0 $\le R_{\mathrm{Re}}\le$ 0.03965 is the rotational speed driving mode, and 0.03965 $<R_{\mathrm{Re}}$ is the lubricating oil drive mode.

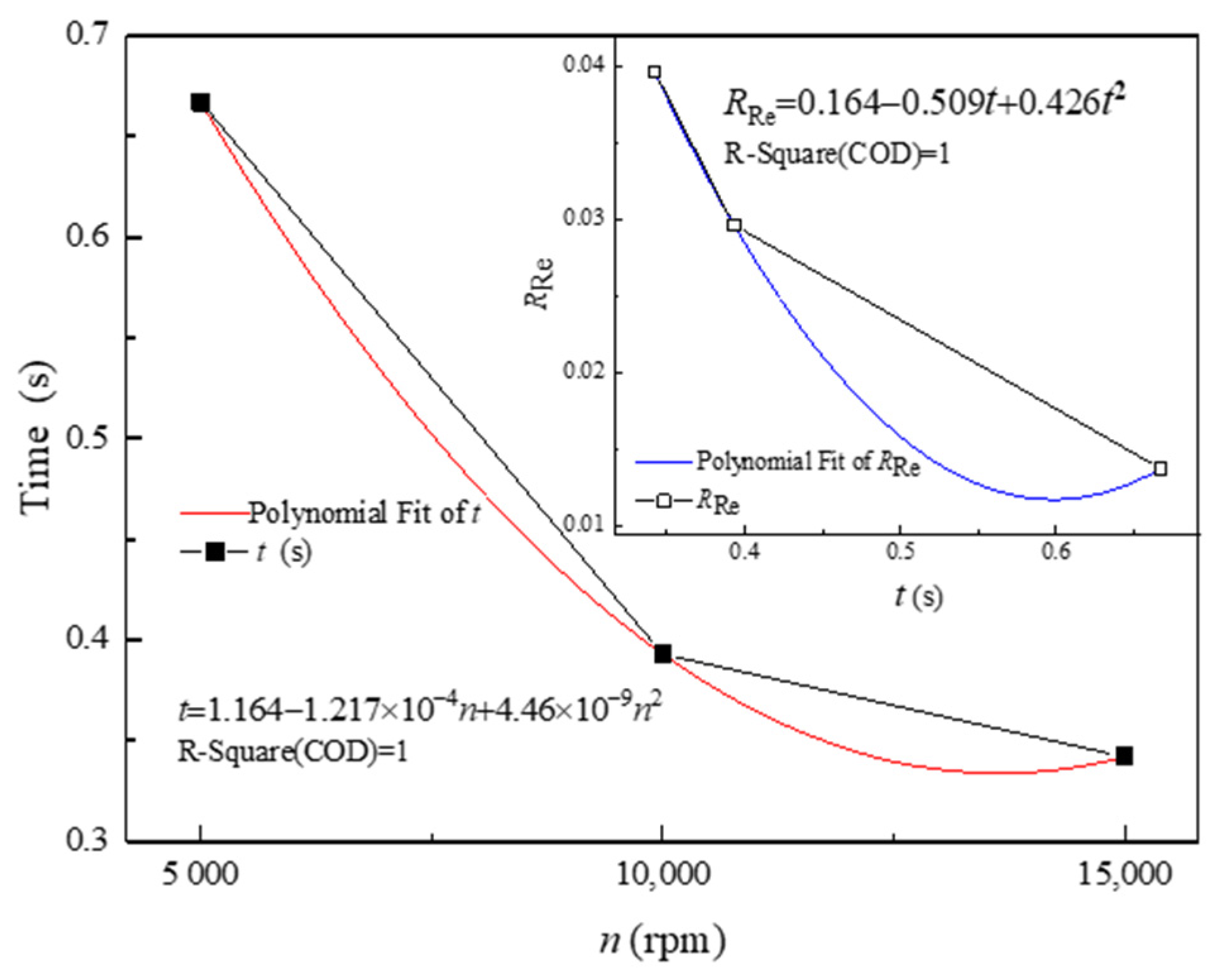
As shown in Figure 7, the higher the rotational speed is, the higher the $R_{\mathrm{Re}}$ is, and the shorter the time reaches the mode transition point. However, it is not convenient to use $R_{\mathrm{Re}}$ as a criterion of the driving mode transition since it varies with the rotor speed. As shown in Figure 8, the correlation between rotor speeds (n) and $R_{\mathrm{Re}}$ is proposed according to the simulation results, which is as follows:

$$t=1.164-n·1.217\times {10}^{-4}+n^2·4.46\times {10}^{-9}.$$

(21)

Meanwhile, time (t) and $R_{\mathrm{Re}}$ obtained at different speeds are also fitted as follows:

$$R_{\mathrm{Re}}=0.164-t·0.509+{\mathrm{t}}^2·0.426.$$

(22)

Substituting Equation (21) into Equation (22), the correlation equation can be obtained as follows:

$$R_{\mathrm{Re}}=0.1487-n·5.875\times {10}^{-5}+n^2·8.463\times {10}^{-9}-n^3·4.6245\times {10}^{-13}+n^4·8.4738\times {10}^{-18}.$$

(23)

Table 2. Comparison between the simulated results and calculated values of Equation (23).

n (rpm)	t (s)	Simulated Values-${\mathit{R}}_{\mathbf{Re}}$	Fit Values- ${\mathit{R}}_{\mathbf{Re}}$	Relative Error
5000	0.667	0.01373	0.01404	2.258%
10,000	0.393	0.02963	0.02978	0.506%
15,000	0.342	0.03965	0.03979	0.014%

shows the comparison between the simulated results and the calculated values of Equation (23), and it can be seen that the error is small. Thus, the driving mode criterion of the ventless bearing chamber at 5000 rpm ≤ n ≤ 15,000 rpm is as follows:

$0\le R_{\mathrm{Re}}\le 0.1487-n·5.875\times {10}^{-5}+n^2·8.463\times {10}^{-9}-n^3·4.6245\times {10}^{-13}+n^4·8.4738\times {10}^{-18}$ is the rotational speed driving mode with twin vortices and $R_{\mathrm{Re}}\ge 0.1487-n·5.875\times {10}^{-5}+n^2·8.463\times {10}^{-9}-n^3·4.6245\times {10}^{-13}+n^4·8.4738\times {10}^{-13}$ is the lubricating oil drive mode with a single vortex.

3.2. Three-Dimensional Flow Characteristics of Oil/Gas Two-Phase

The density of streamlines in the three-dimensional flow field within the same benchmark can reflect the velocity of air and lubricating oil at this moment. The fluid velocity in the dense area is large, and vice versa. At the same time, according to the turbulence intensity in the ventless bearing chamber, the intensity of the developed turbulence and the disturbance in the oil/gas two-phase flow in the bearing chamber can be characterized. At different times, when the turbulence intensity of oil/gas two-phase is small, there is a small trend of turbulence development. Because the Reynolds number of oil/gas in the chamber is inversely proportional to the turbulence intensity, compared with the viscous force, the inertia force has a larger effect, and the trend of turbulence developing in the flow field decreases, and the degree of disturbance of oil/gas two-phase reaches a larger value. For the turbulence intensity (I) of oil/gas two-phase in the bearing chamber, the formula is as follows:

$$I=\frac{V^{\prime }}{V_{avg}}=0.16 ·{ (Re}_{{\mathrm{D}}_{\mathrm{h}}}{)}^{-\frac{1}{8}}.$$

(24)

The turbulence intensity (I) is defined as the ratio of the root-mean-square of the velocity fluctuations ($V^{\prime }$) to the mean flow velocity of oil/gas two-phase ($V_{avg}$), and ${Re}_{{\mathrm{D}}_{\mathrm{h}}}$ is the Reynolds number of oil/gas two-phase flow under the hydraulic diameter in the bearing chamber. The turbulence intensity is determined by calculating the Reynolds number of the hydraulic diameter in the bearing chamber. The Reynolds number can be calculated as follows:

$${Re}_{{\mathrm{D}}_{\mathrm{h}}}=\frac{V_{avg}·{\rho }_{avg}·D_{\mathrm{h}}}{{\mu }_{avg}},$$

(25)

where, ${\rho }_{avg}$ is the average density of the oil/gas two-phase in the bearing chamber, and ${\mu }_{avg}$ is the average dynamic viscosity of the oil/gas two-phase. The three-dimensional flow of oil/gas two-phase in the ventless bearing chamber is characterized by the velocity value and turbulence intensity.

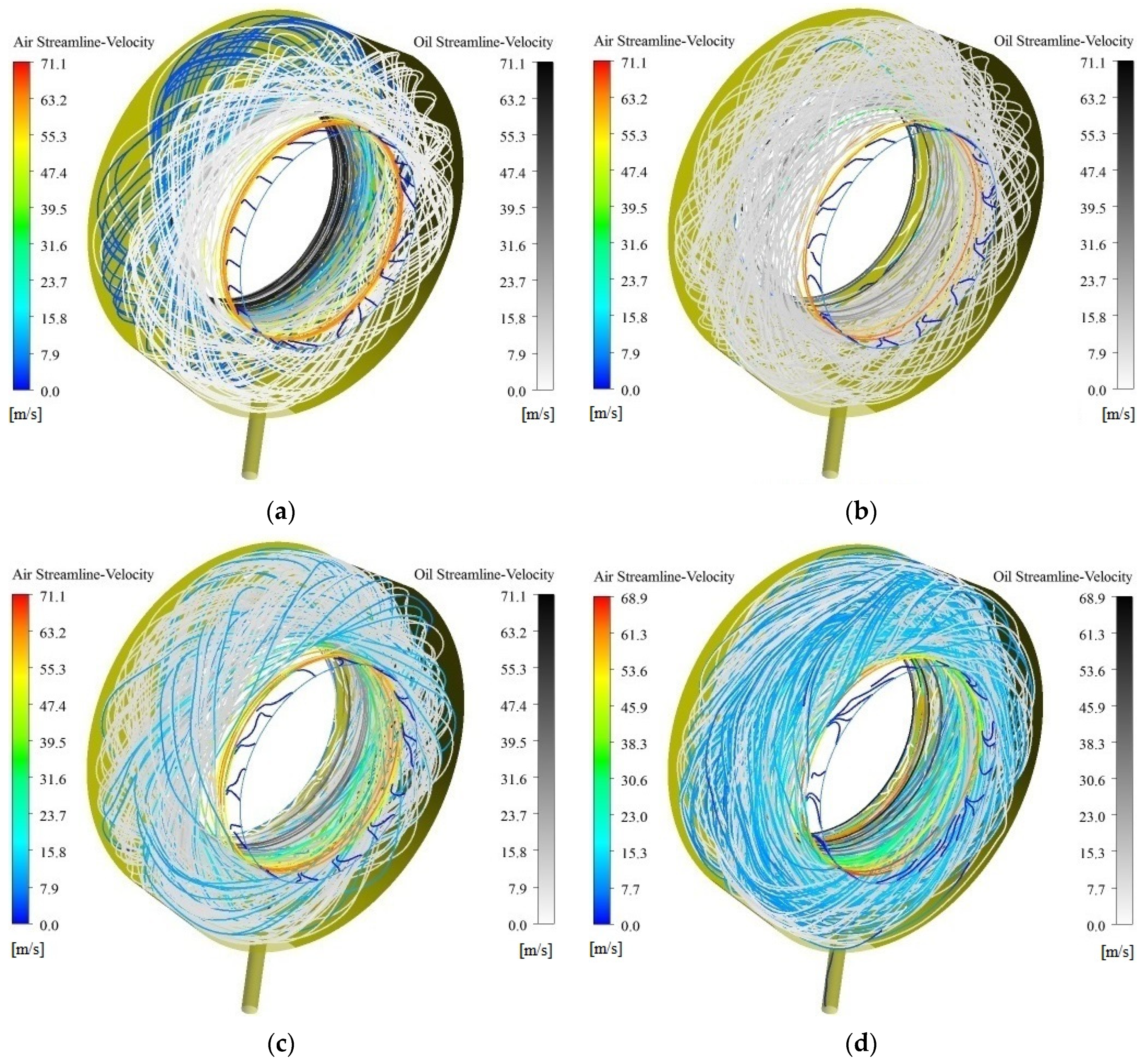
Figure 9 shows the shows the oil/gas streamlines of the rotational speed driving mode at 10,000 rpm. Twenty-five equidistant streamlines at the interface between the air inlet and oil inlet are selected, respectively, where the colored lines are the air streamlines and the gray lines are the oil streamlines. These are the streamlines of the oil/gas two-phase in the unsteady process, and also represent the evolution of the twin-vortex circulations in the three-dimensional chamber. As it can be seen, when the aspect ratio of the bearing chamber is 0.712, oil and air have low velocities at 0.056 s, and the streamlines of oil and air are interleaved with each other. The velocity of oil/gas two-phase is 5.08 m/s by monitoring the velocity change of oil/gas two-phase, and the turbulence intensity of the flow in the chamber is 8.69%. The actual vorticity value at the same vorticity level can indicate the vortex intensity in the flow field. At this point, the actual value of vorticity obtained by selecting a vorticity level of 0.05 is 4708.8 s⁻¹.Then, the oil gradually dominates and fills the whole bearing chamber at 0.198 s, while the air streamline is almost non-existent in the chamber and only serves as a sealing role, and the pitch of the twin-vortex circulations decreases. The streamlines of oil/gas two-phase become dense, the average velocity of oil/gas two-phase increases to 10.70 m/s, the turbulence intensity of the flow in the chamber is 7.89%, and the average value of vortex in the bearing chamber is 4889.2 s⁻¹. The vorticity value and the intensity of the vortex increases. In addition, the air streamlines become more in the chamber and the oil/gas velocities reach a maximum under the disturbance at 0.213 s and 11.13 m/s. The streamlines are the densest. At this point, the turbulence intensity of oil/gas two-phase flow in the ventless bearing chamber reaches the minimum value, which is 7.86%. In the unsteady process, the trend of turbulence development decreases from large to small, and the resistance of turbulence development increases. At this moment, the disturbance in the bearing chamber reaches the maximum and the value of vorticity reaches the maximum of 4966.5 s⁻¹. Then, the value of vorticity begins to decrease. At 0.303 s, the air streamlines increase in the chamber and are comparable to oil streamlines. At this time, the velocity of oil/gas two-phase decreases to 10.29 m/s, and the turbulence intensity in the chamber gradually increases to 7.87%. The pitch of the twin-vortex circulations in opposite spiral directions gradually increases, and the average value of vorticity in the bearing chamber is 4925.4 s⁻¹, reducing the vortex intensity. This is because the increase of air and lubricating oil retention increases the pressure in the chamber and reduces the velocity of the oil/gas two-phase, and the scrambled air streamlines appear on the air inlet side to prevent the leakage of lubricating oil from the air inlet to the other parts of the engine [18].

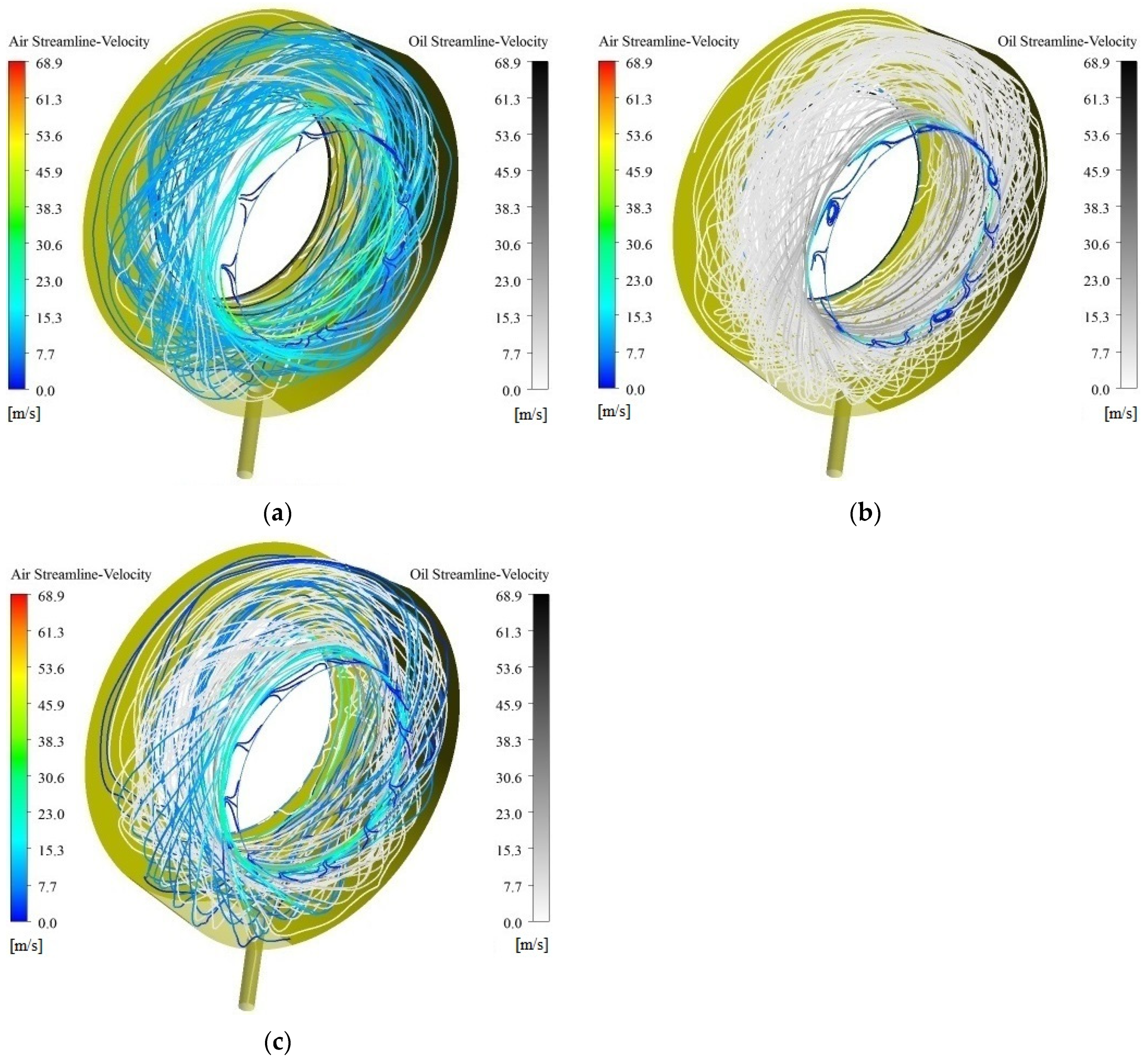
Figure 10 shows the oil/gas streamlines of the oil driving mode at 10,000 rpm under the aspect ratio of 0.712. The streamlines of the oil/gas two-phase flow decrease in the chamber, and there are almost no streamlines at the angle between the two sides, and a single vortex is formed in Figure 10a. At this point, the average velocity of the oil/gas two-phase in the bearing chamber is 9.03 m/s, which further decreases, and the turbulence intensity of the oil/gas two-phase is 7.93%, indicating an increasing trend of turbulence development. Combined with the single vortex in Figure 6d, there are small eddies at the four corners of chamber, and the tangential velocity of small eddies is low, which is not conducive to heat transfer. This shows that the flow characteristics of the oil/gas two-phase are the key factor for heat transfer between lubricating oil and the outer wall [13,19,20]. At 0.588 s, air streamlines disappear, and the oil streamlines dominate the circumferential motion in the bearing chamber. At this time, the average velocity of the oil/gas two-phase in the bearing chamber is 6.9 m/s, and the turbulence intensity of the oil/gas two-phase is 8.12%. The trend of turbulence development further increases. Then, air and lubricating oil streamlines are mixed and the motion of oil/gas two-phase flow in the bearing chamber tend to be stable at 1.137 s, the average velocity of oil/gas two-phase in the bearing chamber is basically maintained at 5.7 m/s, and the turbulence intensity also reaches a constant value, basically at 8.2%. The average value of the vorticity in the bearing chamber is 4868.5 s⁻¹.

For the unsteady flow process at 5000 rpm and 15,000 rpm under the aspect ratio of 0.712, the process is basically consistent with 10,000 rpm, but the higher the speed, the shorter the time for the oil/gas two-phase to reach the mode transition point (twin vortices and a single vortex). The velocity of oil/gas two-phase and the turbulence intensity of oil/gas two-phase in the bearing chamber also changes. The higher the rotational speed is, the greater the value of the average velocity of oil/gas two-phase is in the bearing chamber, while the value of the turbulence intensity is relatively small. At 5000 rpm and 15,000 rpm, the average velocity of oil/gas two-phase reaches maximum values at 0.492 s and 0.162 s, which are 5.78 m/s and 15.96 m/s respectively. Meanwhile, there are increasingly dense streamlines of oil/gas two-phase in the bearing chamber. At 0.667 s and 0.342 s, the phenomenon of twin vortices changes to a single vortex at 5000 rpm and 15,000 rpm respectively, and the speed at this time is 5.22 m/s and 12.67 m/s, respectively. At high speeds, the number of streamlines of oil/as two-phase in the chamber at 10,000 rpm and 15,000 rpm decreases and then increases in the unsteady process, while 5000 rpm basically remains unchanged, which may be related to the change of pressure in the chamber. At 1.192 s of 5000 rpm and at 1.003 s of 15,000 rpm, the velocity is reduced to 3.47 m/s and 8.6 m/s respectively, and the turbulence intensity is 8.87% and 7.83% respectively, which gradually tends to be a steady state with running time. In the flow process of oil/gas two-phase, with increasing rotor speed, the streamlines at the included angle around the bearing chamber decrease. This is due to the shear force on the rotor wall, which leads to the tangential velocity of the oil and gas two phases increasing, and the radial velocity and axial velocity components being small. As a result, the turbulence intensity decreases when the rotational speed increases, the streamlines near the shaft wall are dense, and the streamlines move close to the rotor wall. The higher the rotational speed is, the more obvious this phenomenon is. Apart from the above factors, the increase in rotational speed leads to an increase in oil film thickness on the outer wall and the accumulation of lubricating oil in the chamber [3], which reduces the flow volume of oil/gas two-phase.

3.3. Average Pressure and Velocity of Oil/Gas Two-Phase

In the transformation of driving mode, the average velocity and the average pressure values of oil/gas two-phase obviously change. Figure 11 shows the relationship between average pressure (a) and average velocity (b) of oil/gas two-phase at different rotor speeds.

As shown in Figure 11a, the average pressure of oil/gas two-phase under the aspect ratio of 0.712 at different rotor speeds first decreases and then increases before the points of a single vortex (A, B, and C), and finally tends to be stable. The average pressure of 15,000 rpm drops sooner and the decrease magnitudes are greater than 5000 rpm and 10,000 rpm, with the lowest value being 169.72 kPa at 0.147 s. The lowest values of 5000 rpm and 10,000 rpm are 169.98 kPa at 0.492 s and 169.86 kPa at 0.198 s, respectively. Since the oil and air flow into the bearing chamber at high-pressure values from the narrow oil inlet and air inlet, respectively, the volume of the two phases then expands, resulting in a decrease in the average pressure. After reaching the lowest value, the average pressure begins to increase owing to the retention of lubricating oil in the bearing chamber and tends to be stable after the single vortex point (A, B, and C), fluctuating at approximately 170 kPa, which may be the reason for the alternating phenomenon of the existence and disappearance of air streamlines in the chamber.

As shown in Figure 11b, the average velocity under the aspect ratio of 0.712 first increases, then decreases and finally tends to be stable at different rotational speeds. The maximum velocities of 15,000 rpm and 10,000 rpm are 15.96 m/s and 11.13 m/s at 0.162 s and 0.213 s respectively, while the maximum velocity of 5000 rpm is 5.78 m/s at 0.492 s. However, because of the compressibility of air, the change of average velocity in the chamber lags behind the change in the average pressure. The lower the rotor speed is, the more moderate the changes of pressure and velocity in chamber are, indicating that the flow of air/oil tends to be stable faster at low speed.

3.4. Radial and Axial Flow of Oil/Gas Two-Phase

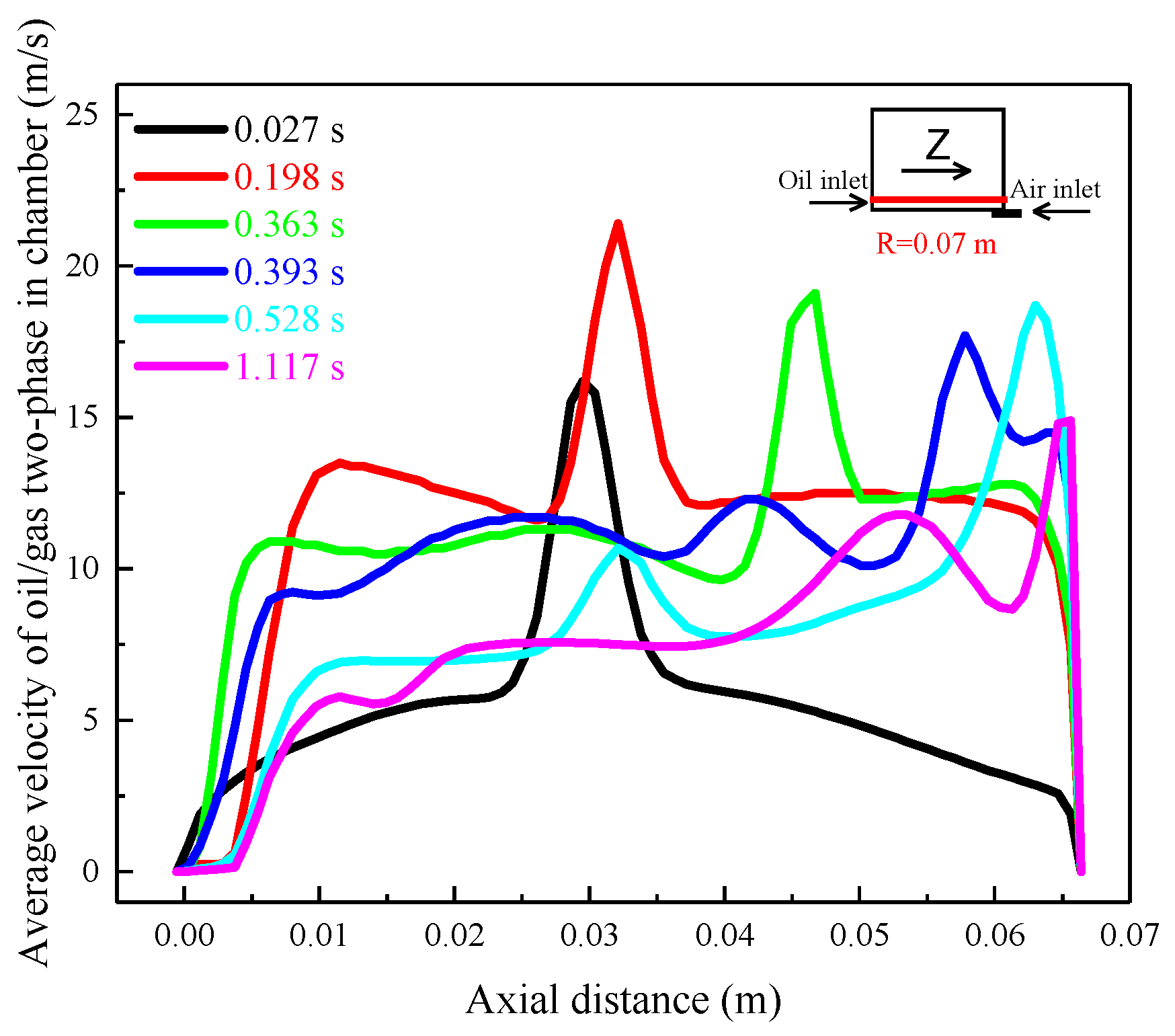
Figure 12 shows the axial variation of average velocity of oil/gas two-phase on the 0.07 m radius section at 10,000 rpm. The radius is 0.07 m, and it is close to the rotor wall under the aspect ratio of 0.712. As time goes on, the region with relatively large velocity of oil/gas two-phase at the section tends to the air inlet side. As shown in Figure 12, the average velocity presents asymmetrical distribution of high in the middle and low on both sides at time ranges from 0.027 to 0.198 s, which is consistent with the distribution of the twin vortices in Figure 6b. At the beginning, the velocity of the oil/gas is larger at 1/2b in the axial direction. The peak of velocity shifts to the air inlet side over time and gradually forms a single vortex, which is consistent with the evolution from the rotational speed driving mode to the oil driving mode. The peak of the velocity also firstly increases, then decreases, and then stabilizes. After reaching 0.393 s, the peak is at the inlet side, and the motion of oil/gas two-phase in the bearing chamber is integrated into a single vortex circulation.

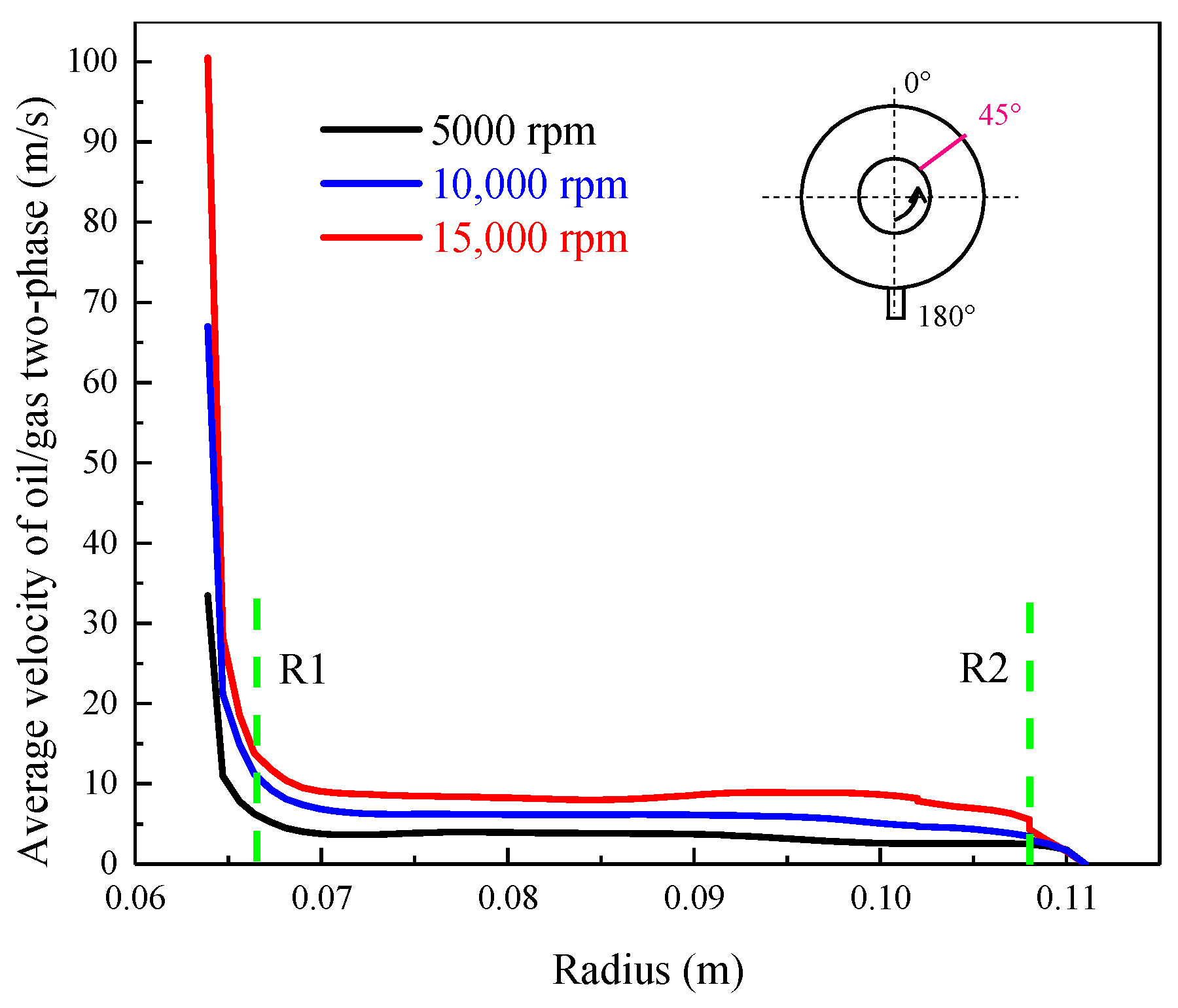
Figure 13 shows the variation of the oil/gas average velocity at 45° cross section for different rotor speeds along with the aspect ratio of the bearing chamber. The velocity distribution is similar at different rotational speeds under the aspect ratio of 0.712, which can be partitioned into three zones: a severe drop zone from the inner wall of the rotor to A1 (0~0.003), a steady zone from A1 to A2 (0.03~0.667), and a fast drop zone from A2 to the outer wall of the chamber (0.667~0.712). Here, the average velocity of the oil/gas two-phase close to the inner wall of the rotor is large in the severe drop zone, and the velocity decreases sharply with the increasing radius. The thickness layer of the severe drop zone is small, mainly close to the rotor wall, and the cross-sectional area of the thickness layer accounts for 4.25% of the cross-sectional area. The average velocity in the steady zone is basically unchanged. This is mainly the flow domain of the vortex, where the oil/gas two-phase moves circumferentially in the form of a single-vortex circulation, spirally, with a large range, accounting for 89.36% of the cross-sectional areas. In the fast drop zone, the average velocity near the outer wall drops to zero under the action of the outerwall shear force, and this velocity change layer accounts for 6.39%.

3.5. Flow Characteristics of Lubricating Oil

Figure 14 shows the evolution of the oil distribution (α = 0.25) and velocity fields at 10,000 rpm. As shown in Figure 14, the oil is sprayed at an incident angle of 45° at 0.243 s, and some larger oil drops fall off and are thrown to the outer wall under the shear force on the rotor wall at 0.448 s. Then, the number of oil drops on the outer wall increases with the decrease of the oil drop volume, resulting in a gradually uniform circumferential distribution at 0.648 s, accompanied by a small amount of lubricating oil flowing out of the scavenging offtake at the bottom of the bearing chamber. The volume of oil drops becomes larger and the contact area with the outer wall increases with the accumulation of oil. Large drops gather at the bottom of the chamber since the shear force cannot offset the effect of gravity at 0.847 s. When the time is 1.057 s, the aggregation area is mainly located in the circumferential range of 135~180°. At t = 1.142 s, an increasing number of oil drops adhere to the top of the outer wall and gradually stretch, showing a trend of forming an oil film. However, the tangential velocity of oil is small, and it is difficult to form a uniform oil film due to the influence of gravity.

The distributions of lubricating oil are mainly affected by the rotor shear force and oil phase gravity [21,22]. Figure 15 shows the distributions (α = 0.25) and velocity fields of oil at different rotational speeds in the steady state. The oil drops mostly appear in blocks for 5000 rpm. There is a significant slipping of oil on the sidewall of oil inlet, and a large amount of lubricating oil accumulates at the bottom of the chamber in the circumferential range of 165~225°, with a symmetrical distribution, indicating that gravity plays a leading role. At 10,000 rpm, oil drops in the chamber are large in number and small in volume, and most of them are attached to the outer wall in flat spheres. The accumulation area at the bottom shifts circumferentially along the outer wall under the action of shear force. At 15,000 rpm, the oil drops are thrown to the outer wall at high velocity under the action of shear force, and the impact of airflow vertically entering the bearing chamber accentuates the oil drop ruptures. Therefore, a large number of thin-sheet oil drops are formed on the outer wall, the circumferential distributions of oil are more uniform, and the accumulation area at the bottom of the chamber disappears.

The Weber (We) number is an important dimensionless parameter to characterize the droplet shape and is the ratio of inertia force to the surface tension. For oil drops in the bearing chamber, the We is as follows:

$$We=\frac{{\rho }_{\mathrm{l}}{u}_{\mathrm{g}}^2{D}_{\mathrm{h}}}{{\sigma }_{\mathrm{g}}},$$

(26)

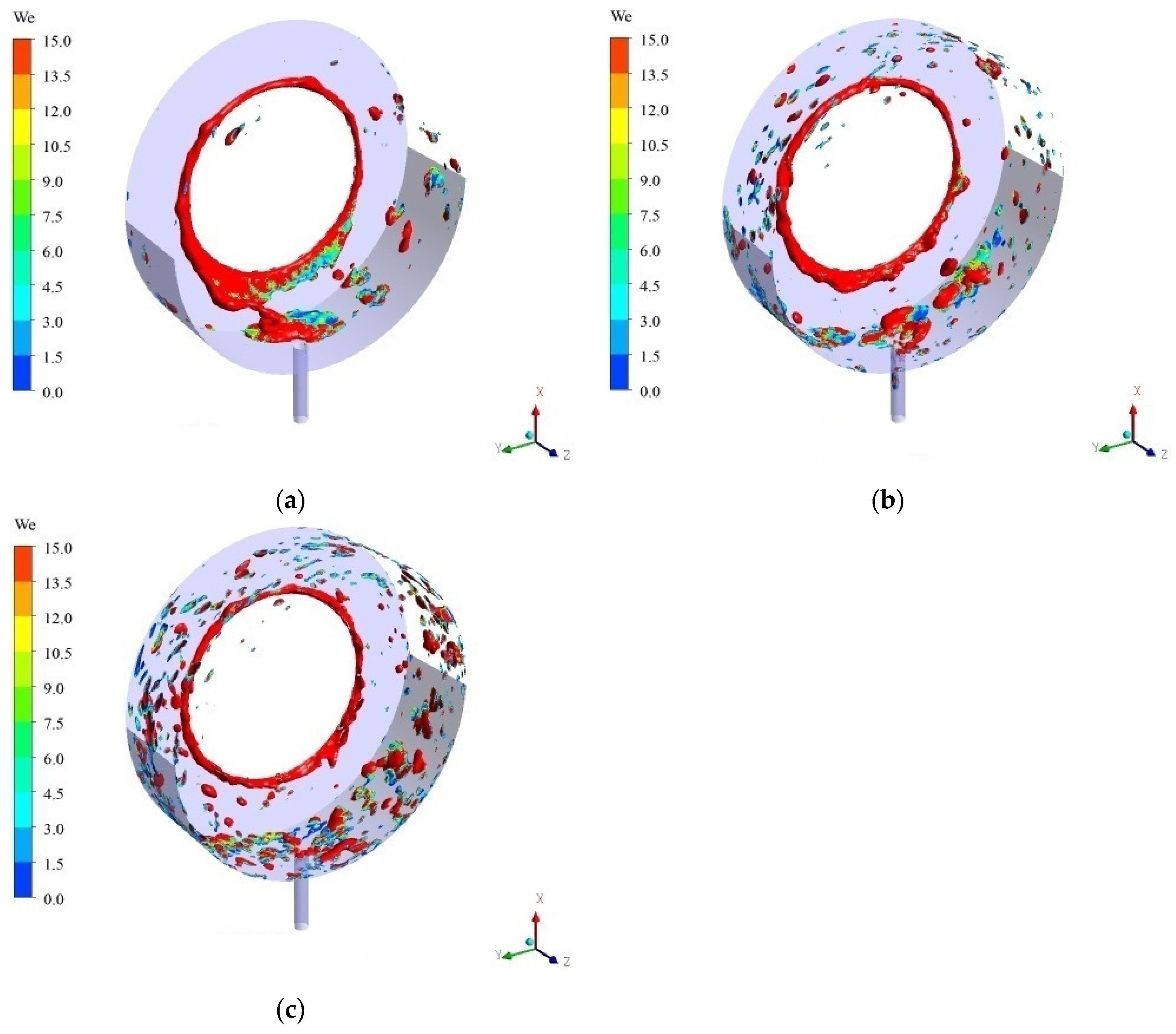
where, u_g is the average velocity at the interface of oil/gas; and σ_g is the surface tension coefficient of oil/gas. Figure 16 shows the contour of the Weber number (α = 0.25) at different rotor speeds in the steady state. The Weber number near the rotor is greater than 1, indicating that the inertia force is greater than the surface tension, and oil drops break soon after entering the bearing chamber. For 5000 rpm, the Weber number near the outlet of the bearing chamber is small, showing that the volume of oil drops is larger and that accumulation occurs. The Weber number on the outer wall of the chamber decreases with increasing rotor speed, and the oil forms a uniform oil film. The number of Weber at the corner of the outer wall of the bearing chamber is small, and lubricating oil easily accumulates. Attention should be given to oil deterioration or coked oil caused by poor heat transfer at this position [13]. The circumferential distribution of oil becomes more uniform with the increasing rotor speed under the aspect ratio of 0.712. Therefore, the increase of speed is beneficial to the heat transfer of the bearing chamber [23].

4. Conclusions

In this paper, the unsteady motion of gas/oil in a novel ventless bearing chamber under the aspect ratio of 0.712 was investigated numerically using the VOF model. The secondary flow, three-dimensional distribution of oil/gas, the velocity field and pressure field of oil/gas two-phase were analyzed in detail through three different rotational speeds. The main conclusions are as follows:

(1) In the secondary flow, the circulations of the twin vortices collide at 1/2b in the axial direction and then shift. The twin vortices gradually change to a single vortex. Meanwhile, the driving mode also changes from rotational speed driving mode to lubricating oil driving mode, as the higher the rotational speed, the shorter the time from the twin vortices to the single vortex;

(2) The criterion of the driving mode transition under the aspect ratio of 0.712 in the unsteady process of the ventless bearing chamber at different speeds is established;

(3) In the unsteady motion of oil/gas two-phase flow, the streamlines of air and oil are entangled with the velocity increasing and the pressure decreasing in the rotational speed drive mode, forming the twin-vortex circulations with opposite directions. The average velocity first increases, then decreases, and finally tends to be stable at different rotational speeds, as the variation of pressure is opposite to that of the velocity. The twin-vortex circulations evolve into a single vortex circulation, which is also the transformation from the driving mode evolving into the lubricating oil driving mode in the process. In the lubricating oil driving mode, the intensity of the average pressure oscillation and the average velocity oscillation of oil/gas two-phase increases with the increasing rotor speed;

(4) The average velocity of oil/gas shows three zones along with the aspect ratio of the bearing chamber: a severe drop zone, a steady zone, and a fast drop zone;

(5) The oil shape on the outer wall changes from block to flat-spheres to thin-sheets and the circumferential distribution of oil becomes more uniform with increasing rotor speed.