Adaptive Backstepping Nonsingular Terminal Sliding-Mode Attitude Control of Flexible Airships with Actuator Faults

Abstract

This paper studies the attitude tracking control of a flexible airship subjected to wind disturbances, actuator saturation and control surface faults. Efficient flexible airship models, including elastic deformation, rigid body motions, and their coupling, are established via Lagrange theory. A fast-nonsingular terminal sliding-mode (NTSM) combined with a backstepping control is proposed for the problem. The benefits of this approach are NTSM merits of high robustness, fast transient response, and finite time convergence, as well as the backstepping control in terms of globally asymptotic stability. However, the major limitation of the backstepping NTSM is that its design procedure is dependent on the prior knowledge of the bound values of the disturbance and faults. To overcome this limitation, a wind observer is designed to compensate for the effect of the wind disturbances, an anti-windup compensator is designed to compensate for actuator saturation, and an adaptive fault estimator is designed to estimate the faults of the control surfaces. Globally exponential stability of the closed-loop control system is guaranteed by using the Lyapunov stability theory. Finally, simulation results demonstrate effectiveness and advantages of the proposed control for the Skyship-500 flexible airship, even in the presence of unknown wind disturbances, control surface faults, and different stiffness variants.

1. Introduction

Airships have many potential applications for transport, environment surveillance, communication relay, and aerial photography, etc. These applications have attracted much research interest [1]. As one of the lighter-than-air unmanned vehicles, reliable autonomous control is highly desired for different airship missions. Thus, the key objective is to realize accurate trajectory-tracking control for the unmanned airship. However, due to the inherent system nonlinearity and underactuation of the airship under diverse environment disturbances, this makes the trajectory-tracking control of the airship quite challenging and difficult.

To achieve high-precision tracking performance, many control schemes of the airship have been proposed to solve the trajectory tracking problem, which includes gain scheduling control [2], backstepping design [3,4], sliding-mode control [5,6], neural network control [7,8], and fuzzy control [9]. Among these methods, the sliding-mode control and backstepping design are potentially useful approaches to overcome disturbance and faults of the airship. The backstepping approach has been proposed for the robust control of nonlinear systems in a strict feedback form through the construction of control Lyapunov functions (CLFs) [10]. The nonlinear backstepping design has been widely studied for various aerospace and underwater vehicle control problems [11,12]. Meanwhile, the sliding-mode control, due to its insensitivity to disturbances and model uncertainties, has been applied to the trajectory-tracking control for the airship with unknown disturbances and winds [5]. To make the output response quickly converge to the desired values, the terminal sliding-mode control (SMC) is proposed for robust control within a finite time [7,13]. Mofid et al. proposed a super-twisting terminal SMC and barrier function terminal SMC to deal with the quad-rotor unmanned aerial vehicles (UAVs) with delay input [14] and drive the error dynamics to converge on a region near the origin within a finite time [15]. The event-triggered fractional-order SMC technique was proposed to stabilize the quadrotor UAV with external random/time-varying disturbances [16]. In addition, recently, some researchers developed the backstepping sliding-mode control design to use combination merits of SMC and the backstepping design [17,18].

On the other hand, the system faults and disturbances of the airship are unknown and nonlinear. Thus, it is necessary for disturbance rejection and fault compensation to achieve the desired robust performance. Guo et al. [19] investigated a distributed fault-tolerant sliding-mode control for 2-D plane vehicular platoon systems, where a neuro-adaptive fault-tolerant control scheme was implemented by combining a sliding-mode control technique with a radial basis function neural network (RBFNN) to guarantee the finite-time stability. Xiao et al. [20] proposed an adaptive integral sliding-mode approach to realize fault-tolerant tracking control for a multi-vectored thrust ellipsoidal airship. Liu and Whidborne [8] proposed a neural network adaptive backstepping fault tolerant control for the unmanned airship with multi-vectored thrusters. These methods not only guarantee the system with faults of robust stability, but also tolerate the unknown actuator faults, even in the disturbance environment.

However, all the above nonlinear designs are focused on rigid-body airship models, which cannot guarantee the performance for flexible cases. To realize high altitude and long endurance missions, the stratospheric airship often uses the flexible inflated membrane material as the airship hull; thus, the weight is lighter and endurance is longer. Unlike conventional rigid airships, the mutual interaction between flexibility, aerodynamics, and flight dynamics of flexible airships should be modeled [21,22], because this interaction will improve the model precision and control performance [23]. For the trajectory-tracking control of the flexible airship, Li et al. [21] proposed an integrated model, including the flight dynamics, structural dynamics, aerostatics, and aerodynamics, but they only analyzed the linear mode characteristics of the flexible airship without consideration of nonlinear control problems. The main difficulties for the flexible airship are nonlinear and coupling control between the rigid and flexible body. Bennaceur and Azouz [24] proposed a Lagrangian method to build up an efficient model of flexible airships. In addition, Han et al. [25] proposed a command filtered backstepping approach to design the trajectory controller for a flexible airship. However, they did not consider disturbances and fault effects on the flexible airship, both of which can result in system instability. In fact, from long endurance-hovering in the air and working in diverse environments day and night, the sensors and actuators of the flexible stratospheric airship are easily impaired. Thus, fault tolerant control of the airship with actuator faults is studied here.

Motivated by Li’s [21] and Han’s work [25], the main work in this paper is a novel backstepping nonsingular terminal sliding-mode (BNTSM) control scheme proposed for attitude tracking of the airship with unknown faults, disturbances, and actuator saturation. In the proposed BNTSM control scheme, the nonsingular terminal sliding-mode technique and backstepping technique are integrated. The proposed BNTSM control has advantages of high robustness, fast transient response, and finite time convergence, and the globally asymptotic stability of the closed-loop system can be guaranteed. Furthermore, a wind observer and an adaptive fault estimator are designed to observe the wind disturbances and estimate the control surface faults; thus, the limitation of the BNTSM control dependent on prior knowledge is overcome. The main contributions of the proposed scheme are summarized as follows.

• A backstepping nonsingular terminal sliding-mode control scheme is proposed for attitude tracking control of the flexible airship with actuator faults, actuator saturation, and uncertainties of stiffness.
• A wind observer with an adaptive disturbance observer is designed to reject variable external bounded disturbances and cope with model parameter uncertainties.
• An anti-windup compensator based on proportion to saturation errors is used to compensate actuator saturation.
• An adaptive fault estimator is incorporated into the BNTSM control to implement fault estimation and fault tolerant control.

This paper is organized as follows. The nonlinear dynamics-modeling of the flexible airship and the robust control problem are described in Section 2. The BNTSM control is proposed in Section 3, and stability is proven for the corresponding closed-loop tracking system. In Section 4, three scenarios are simulated to demonstrate the BNTSM control performance. Section 5 gives the conclusions.

2. Airship Modeling and Problem Formulation

The structure of the flexible airship is shown in Figure 1. There are four control surfaces, including two rudders and two elevators on the tail fins, and two propellers are set up on each side of the hull. The gondola under the airship envelope houses the avionics system and the flight control system and other payloads.

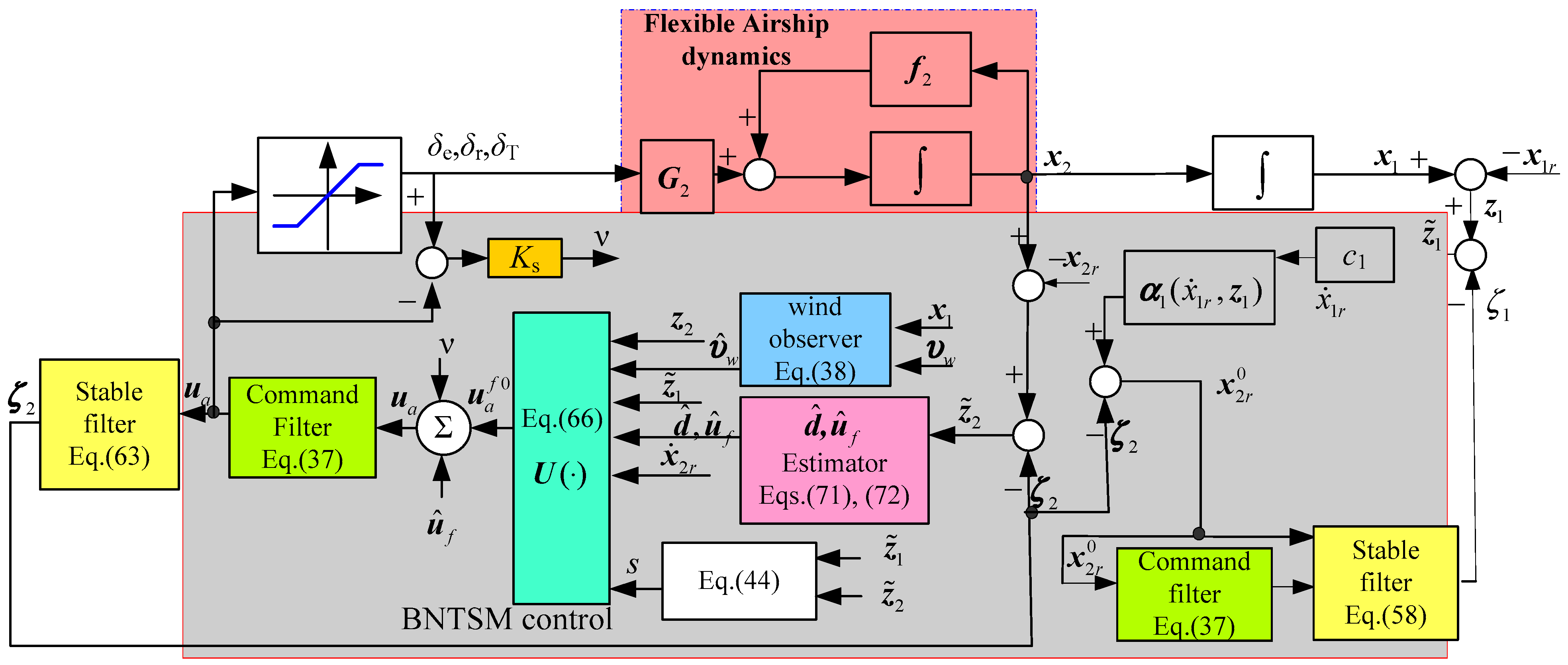
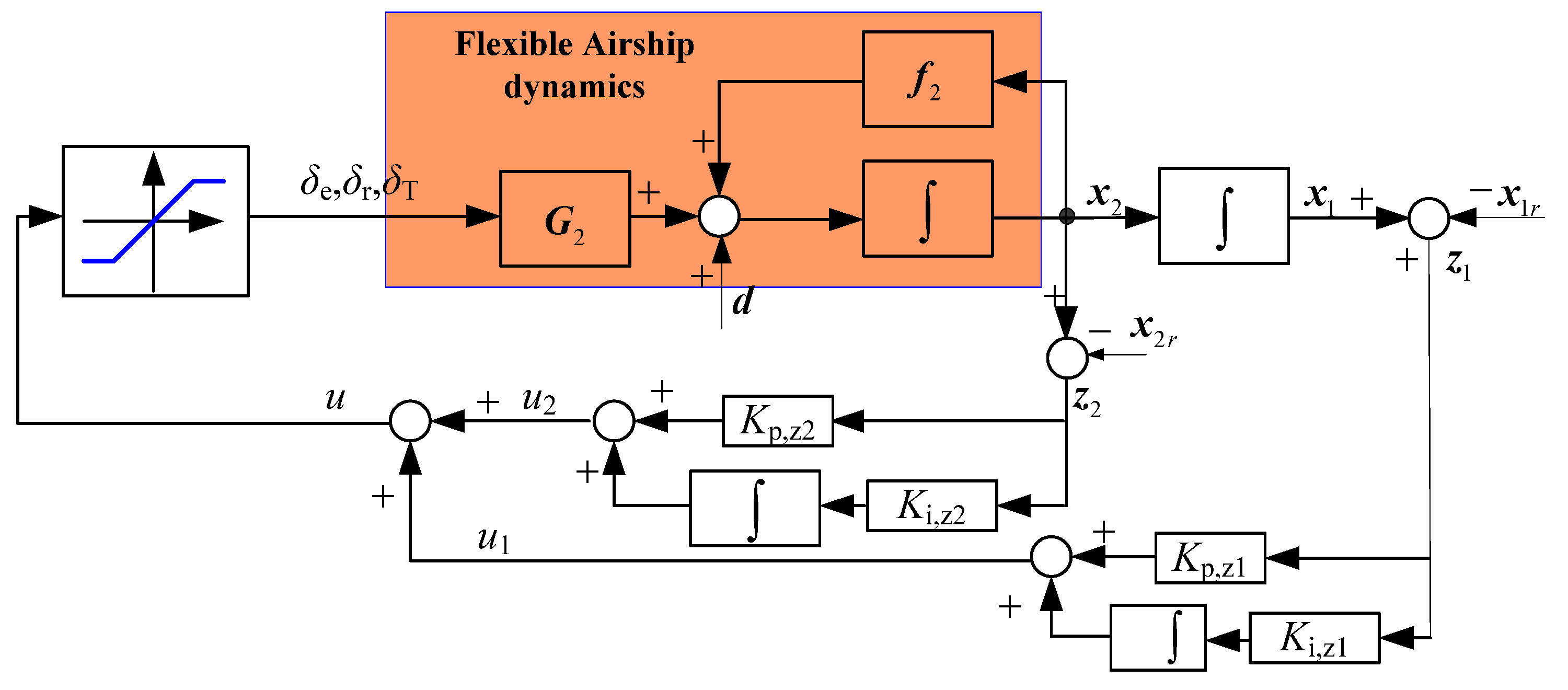
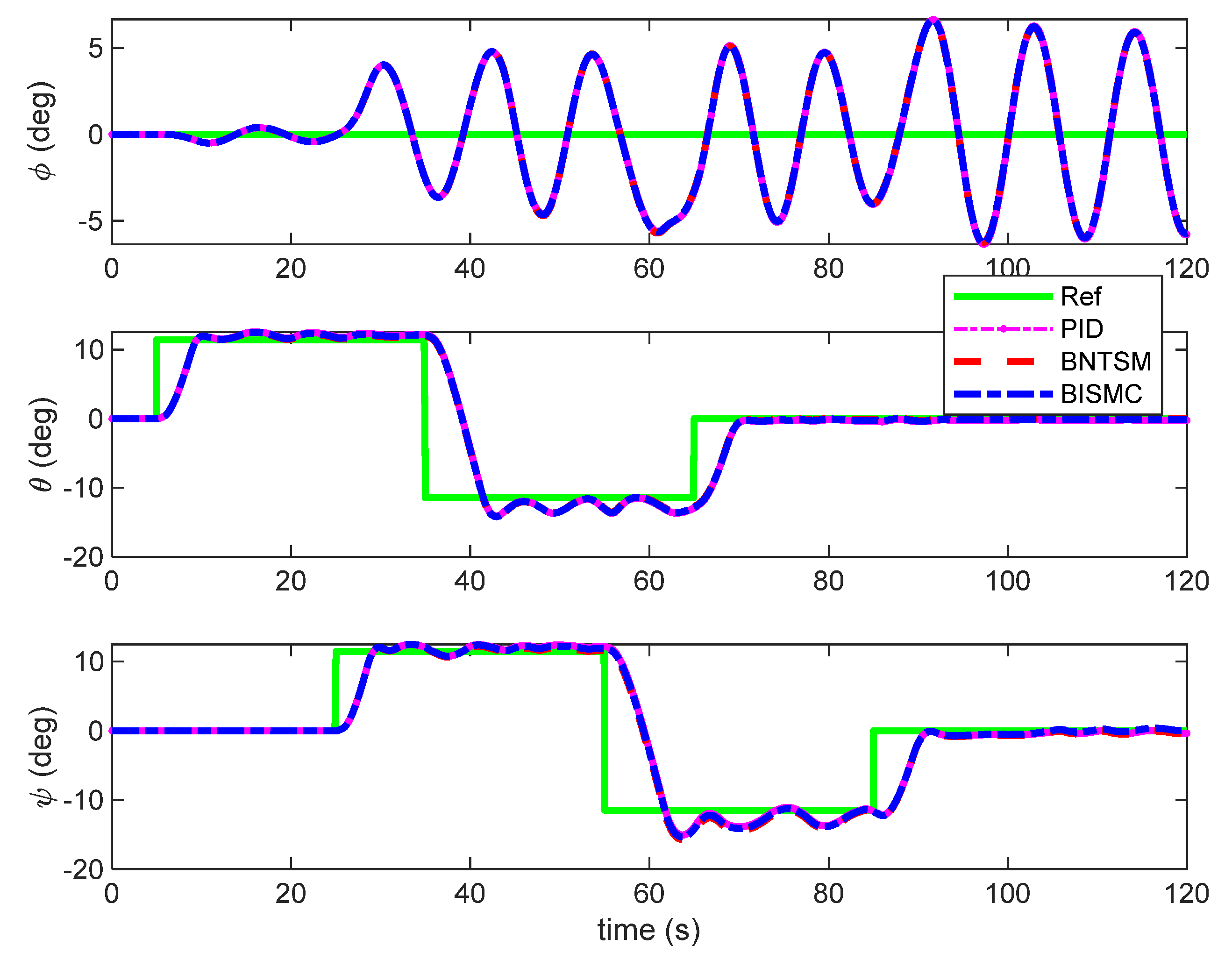
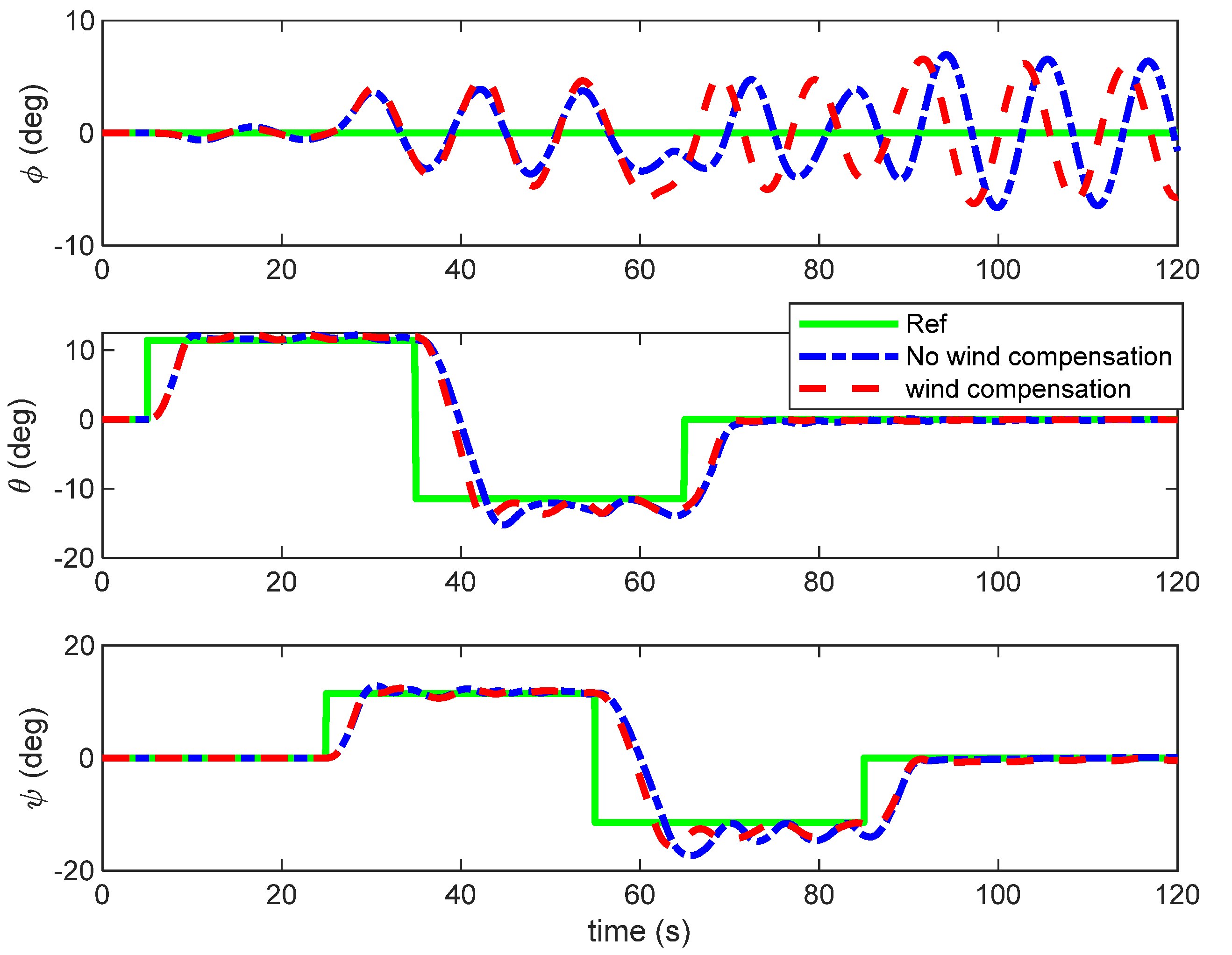
2.1. Airship Kinematics Model

The equations of motion of a flexible airship are expressed in a body frame F_b{O_bx_by_bz_b} fixed on the undeformed airship with its origin, O_b, at the center of volume (CV), see Figure 1. The motion of the airship is described as the translation and rotation of this body frame with respect to the inertial frame F_I{O_Ix_Iy_Iz_I}, plus the deformation of the material points on the body relative to the body frame [21]. A centerline frame F_p{O_px_py_pz_p} is introduced to calculate the aerodynamics forces of the flexible airship. The elastic displacement u of a material point on the airship can be written by a summation of the shape functions, as

$$\mathit{u}={\displaystyle \sum }{q}_i\left(t\right){\Phi }_i\left(\mathit{r}\right), (i=1, 2, \dots N)$$

(1)

where $q_i$ are the time-dependent generalized coordinates, ${\Phi }_i={\left[\begin{array}{ccc}{\mathsf{\Phi }}_{xi}& {\mathsf{\Phi }}_{yi}& {\mathsf{\Phi }}_{zi}\end{array}\right]}^T$ are the structural mode shape vector, and r is the position vector of the material point from the origin, O_b. The associated velocity distribution over the elastic body is:

$$v={\mathbf{\upsilon }}_a+\Omega \times r+\Omega \times u+\dot{u}$$

(2)

where ${\mathbf{\upsilon }}_a$ = [u, v, w]^T is the translational velocity vector in F_b, $\mathsf{\Omega }={\left[\begin{array}{ccc}p& q& r\end{array}\right]}^T$ is the angular rate vector, and the × denotes cross-product operation. The first two terms of Equation (2) are related to the rigid body translation and rotation, while the last two terms reflect the influence of the elasticity on the local velocity.

Assume the airship is modeled as a free-free Euler–Bernoulli beam only undergoing bending deformation; hence, if the internal pressure is high enough to prevent wrinkling, then the hull bending can be described as the fundamental mode shape of the airship. The shape functions $\Phi$ are chosen as the natural vibration mode shapes of the beam, and 2N shape functions are employed to describe the airship’s deflection, that is,

$$\{\begin{array}{c}{\Phi }_i={\left[\begin{array}{ccc}0& {\Phi }_i& 0\end{array}\right]}^T, \mathrm{the} \mathrm{bending} \mathrm{in} \mathrm{the} \mathrm{Oxy} \mathrm{plane} \\ {\Phi }_{\mathrm{N}+i}={\left[\begin{array}{ccc}0& 0& {\Phi }_i\end{array}\right]}^T, \mathrm{the} \mathrm{bending} \mathrm{in} \mathrm{the} \mathrm{Oxz} \mathrm{plane}\end{array}(i=1, 2, \dots N)$$

(3)

where ${\Phi }_i$ is the ith natural mode shape of the free-free Euler–Bernoulli beam. The kinematics equations of the position and attitude of the airship are [3]:

$$\{\begin{array}{l}\dot{\xi }=\mathit{R}\left(\mathbf{\eta }\right){\mathbf{\upsilon }}_a+{\mathbf{\upsilon }}_w\\ \dot{\mathbf{\eta }}=\mathit{J}\left(\mathbf{\eta }\right)\Omega \end{array}$$

(4)

where ξ = [x, y, z]^T is the position vector, $\eta ={\left[\begin{array}{ccc}\varphi & \theta & \psi \end{array}\right]}^T$ is the attitude vector, ${\upsilon }_a$ = [u, v, w]^T is the translational velocity vector in F_b, and ${\mathbf{\upsilon }}_w$ is the wind velocity in fixed frame. From Equation (4), it can be obtained that the local velocity is:

$$\upsilon ={\upsilon }_a+R^T\left(\eta \right)\cdot {\upsilon }_w$$

(5)

where R(η) denotes the direction cosine matrix [3], and the transformation matrix J is:

$$J(\eta )=\left(\begin{array}{ccc}1& s(\varphi )\tan \theta & c(\varphi )\tan \theta \\ 0& c(\varphi )& -s(\varphi )\\ 0& s(\varphi )\sec \theta & c(\varphi )\sec \theta \end{array}\right)$$

(6)

where |θ| < π/2 is assumed to avoid the matrix singularity, and s(·) and c(·) denote sine and cosine functions, respectively.

The motions of the flexible airship are described as Lagrange equations [24], and the flexible dynamics model is obtained as follows [21]:

$$M_{sys}\left[\begin{array}{c}{\dot{\mathsf{\upsilon }}}_a\\ \dot{\Omega }\\ \ddot{\mathrm{q}}\end{array}\right]=-\left[\begin{array}{c}0\\ 0\\ S_E\end{array}\right]+\left[\begin{array}{c}{F}_I\\ M_I\\ Q_I\end{array}\right]+\left[\begin{array}{c}{F}_G\\ M_G\\ Q_G\end{array}\right]+\left[\begin{array}{c}{F}_{AS}\\ M_{AS}\\ Q_{AS}\end{array}\right]+\left[\begin{array}{c}{F}_{AD}\\ M_{AD}\\ Q_{AD}\end{array}\right]+\left[\begin{array}{c}{F}_C\\ M_C\\ Q_C\end{array}\right]$$

(7)

where $M_{sys}=\left[\begin{array}{ccc}{M}_{11}& M_{12}& M_{13}\\ M_{21}& M_{22}& M_{23}\\ M_{31}& M_{32}& M_{33}\end{array}\right]$ is the airship total mass, the virtual mass terms are included, F_I denotes the inertia force vector, F_G denotes the gravity vector, F_AS denotes the aerostatic force vector, F_AD denotes the aerodynamics force vector, and F_C denotes the control force vector; $M_i$ and $Q_i$ denote the associated moments and general elastic forces of the flexible airship, i = I, G, AS, AD and C. The local velocity is as Equation (5); $\mathit{q}={[q_1,q_2,\cdots ,q_{2N}]}^T$ denotes the generalized elastic coordinate vector. $S_E$ denotes the internal elastic force vector,

$$S_E=\mathit{K}\mathit{q}$$

(8)

where the stiffness matrix K meets

$$K_{i,j}=K_{N+i,N+j}={\displaystyle \underset{L}{\int }EI\cdot {\Phi }_i^{″}{\Phi }_j^{″}dx,}(i,j=1,2\cdots ,N)$$

(9)

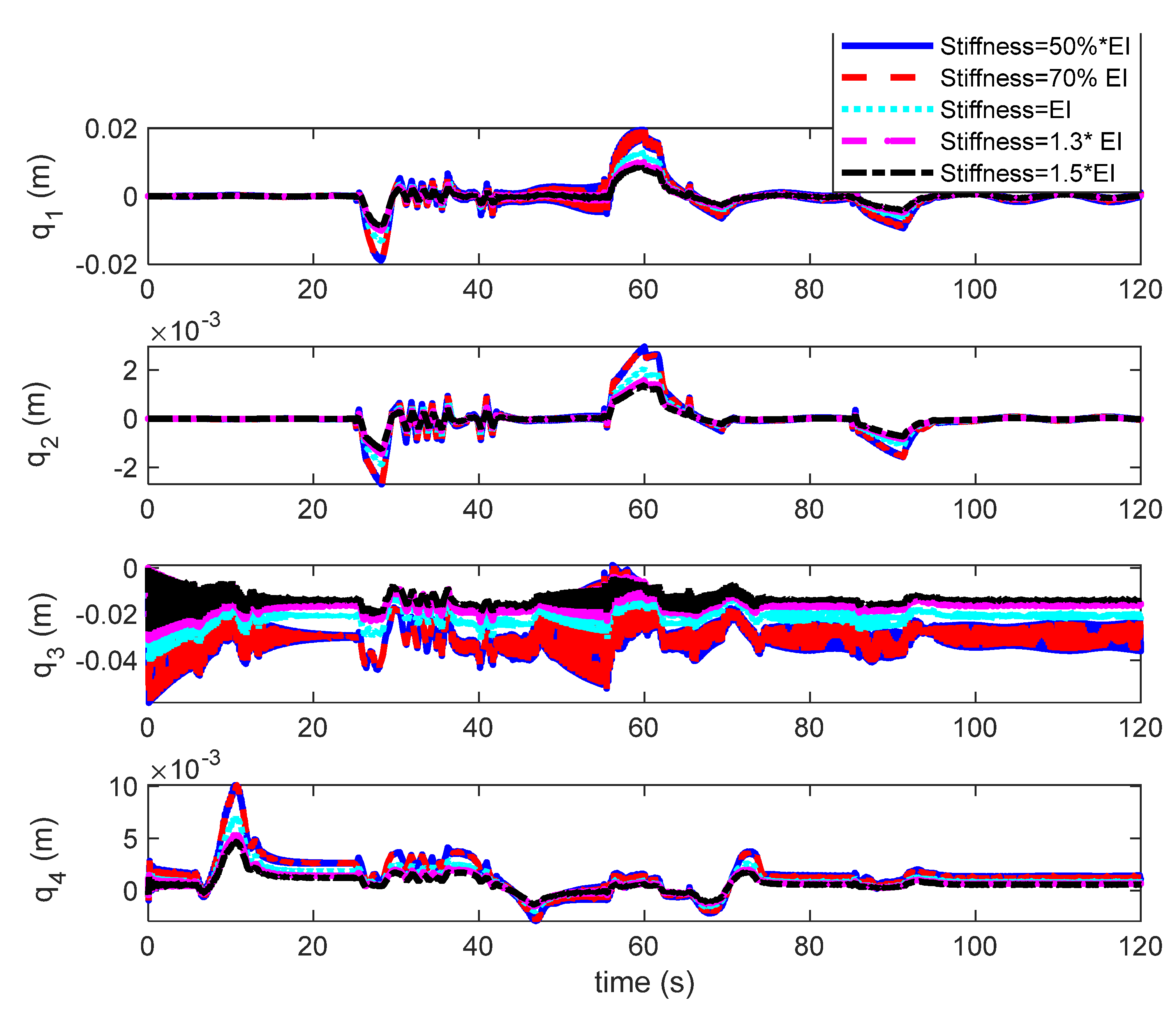
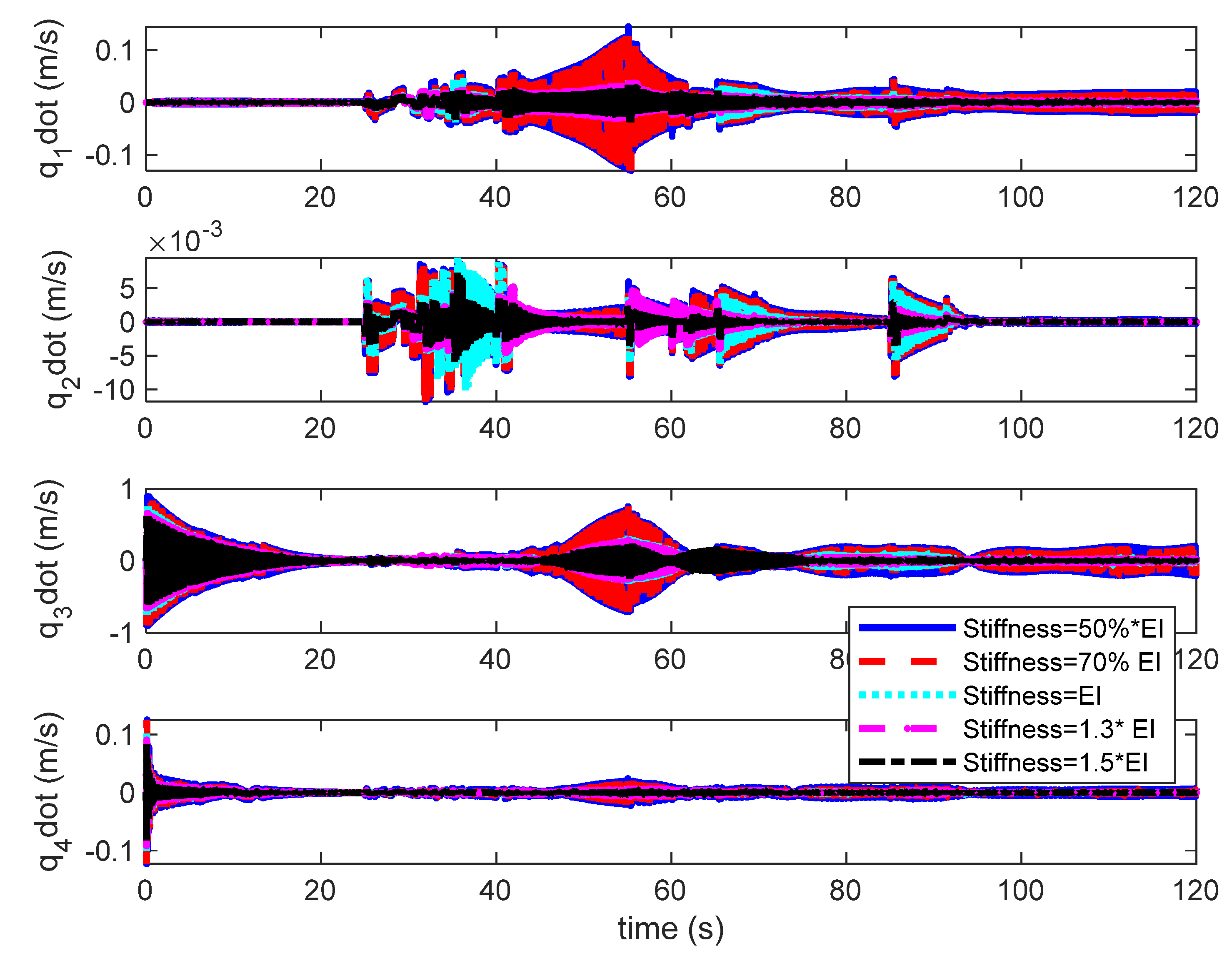
where ${\Phi }_i^{″}=\frac{d^2{\Phi }_i}{d{x}^2}$. EI denotes bending stiffness with EI = πR³ ET₀, E is the elastic modulus of the hull envelope, T₀ is its thickness, and R is the hull radius. Equation (7) can be rewritten as

$$\dot{\mathit{X}}(t)=f(X)+g(X)u(t)$$

(10)

where $X={\left[\begin{array}{ccc}{\upsilon }_a^T& {\Omega }^T& {\dot{\mathit{q}}}^T\end{array}\right]}^T$ is the augmented state vector, $u={\left[\begin{array}{ccc}{\delta }_T& {\delta }_{\mathrm{e}}& {\delta }_{\mathrm{r}}\end{array}\right]}^{\mathrm{T}}$ denote control inputs of the thruster, elevator, and rudder, and

$$f=\frac{1}{{\mathit{M}}_{sys}}\left(-\left[\begin{array}{c}0\\ 0\\ S_E\end{array}\right]+\left[\begin{array}{c}{F}_I\\ M_I\\ Q_I\end{array}\right]+\left[\begin{array}{c}{F}_G\\ M_G\\ Q_G\end{array}\right]+\left[\begin{array}{c}{F}_{AS}\\ M_{AS}\\ Q_{AS}\end{array}\right]+\left[\begin{array}{c}{F}_{AD}\\ M_{AD}\\ Q_{AD}\end{array}\right]\right)$$

(11)

$$g={\left[\begin{array}{ccc}{g}_1& g_2& g_3\end{array}\right]}_{9\times 3}$$

(12)

$$g_1=\frac{1}{{\mathit{M}}_{sys}}{\left[\begin{array}{c}{\overline{F}}_{kT}\\ \left(S_T+{\displaystyle \sum _{i=1}^{2N}{q}_i{S}_{\Phi i}}\right){\overline{F}}_{kT}\\ {\overline{F}}_{kT}^T{\left[\begin{array}{ccc}{\Phi }_{xi}& {\Phi }_{yi}& {\Phi }_{\mathrm{z}i}\end{array}\right]}^T\end{array}\right]}_{9\times 1},g_2=\frac{1}{{\mathit{M}}_{sys}}{\left[\begin{array}{c}{\overline{F}}_{{\delta }_e}\\ \left(S_f+{\displaystyle \sum _{i=1}^{2N}{q}_i{S}_{\Phi i}}\right){\overline{F}}_{{\delta }_e}\\ {\overline{F}}_{{\delta }_e}^{\mathrm{T}}{\left[\begin{array}{ccc}{\Phi }_{xi}& {\Phi }_{yi}& {\Phi }_{\mathrm{z}i}\end{array}\right]}^T\end{array}\right]}_{9\times 1}, g_3=\frac{1}{{\mathit{M}}_{sys}}{\left[\begin{array}{c}{\overline{F}}_{{\delta }_{\mathrm{r}}}\\ \left(S_f+{\displaystyle \sum _{i=1}^{2N}{q}_i{S}_{\Phi i}}\right){\overline{F}}_{{\delta }_{\mathrm{r}}}\\ {\overline{F}}_{{\delta }_{\mathrm{r}}}^{\mathrm{T}}{\left[\begin{array}{ccc}{\Phi }_{xi}& {\Phi }_{yi}& {\Phi }_{\mathrm{z}i}\end{array}\right]}^T\end{array}\right]}_{9\times 1},$$

(13)

$$S_T=\left[\begin{array}{ccc}0& -z_T& y_T\\ z_T& 0& -x_T\\ -y_T& x_T& 0\end{array}\right],S_{\Phi i}=\left[\begin{array}{ccc}0& -{\Phi }_{\mathrm{z}i}& {\Phi }_{yi}\\ {\Phi }_{\mathrm{z}i}& 0& -{\Phi }_{xi}\\ -{\Phi }_{yi}& {\Phi }_{xi}& 0\end{array}\right],S_f=\left[\begin{array}{ccc}0& -z_r& y_r\\ z_r& 0& x_r-x_m\\ -y_r& -x_r+x_m& 0\end{array}\right],$$

(14)

$${\overline{F}}_{kT}={\left[\begin{array}{ccc}{k}_T& 0& 0\end{array}\right]}^T,{\overline{F}}_{{\delta }_e}=\overline{q}{S}_{ref}{\left[\begin{array}{ccc}0& 0& C_{z{\delta }_e}\end{array}\right]}^T,{\overline{F}}_{{\delta }_{\mathrm{r}}}=\overline{q}{S}_{ref}{\left[\begin{array}{ccc}0& C_{y{\delta }_r}& 0\end{array}\right]}^T,$$

(15)

where (x_T, y_T, z_T) and (x_r, y_r, z_r) denote positions of the thrust and control surface in the body frame, F_b, respectively; x_m is the position of the aerostatic center along the x-axis, k_T is control gain for thruster. $C_{z{\delta }_e}$ and $C_{y{\delta }_r}$ denote the aerodynamic derivative coefficients of the elevator and rudder, respectively, $\overline{q}=\frac{1}{2}\rho V^2$ denotes the dynamic pressure, V is the airspeed, and ρ is the air density.

Next, we detailed and present each force and moment on the right-hand side of Equation (11). The inertia force and moment vector of the flexible airship in Equation (11) is [21]:

$$\left[\begin{array}{c}{F}_I\\ M_I\\ Q_I\end{array}\right]=-\left[\begin{array}{ccc}m{\Omega }^{\times }& -{\Omega }^{\times }{c}_{total}^{\times }& 2P_{\dot{q}}\\ c_{total}^{\times }{\Omega }^{\times }& {\Omega }^{\times }{J}_{total}& 2H_{\dot{q},total}\\ -P_{\dot{q}}^T& -H_{\dot{q},total}^T& 2M_{e\dot{q}}\end{array}\right]\left[\begin{array}{c}{\upsilon }_a\\ \Omega \\ \dot{q}\end{array}\right]$$

(16)

where

$$\begin{array}{c}{c}_{total}^{\times }=M_{21}={\left({\displaystyle \underset{m}{\int }(r+u)dm}\right)}^{\times }={\left(m{r}_G+{\displaystyle \underset{m}{\int }\left({\displaystyle \sum q_i(t){\Phi }_i(r)}\right)dm}\right)}^{\times },J_{total}=M_{22}=-{\displaystyle \underset{m}{\int }{(r+u)}^{\times }{(r+u)}^{\times }dm},P_{\dot{q}}={\Omega }^{\times }P={\Omega }^{\times }{M}_{13},\hfill \\ H_{\dot{q}}=\left[\begin{array}{cccc}{J^{\prime }}_{ru,1}\Omega & {J^{\prime }}_{ru,2}\Omega & \cdots & {J^{\prime }}_{ru,2N}\Omega \end{array}\right],{J^{\prime }}_{ru,i}={\displaystyle \underset{m}{\int }{r}^{\times }{\Phi }_i^{\times }dm},H_{\dot{q},total}=H_{\dot{q}}+H_{\dot{q}u},\hfill \\ \hfill H_{\dot{q}u}=\left[\begin{array}{cccc}{\displaystyle \sum q_j(t){J^{″}}_{uu,1j}\Omega }& {\displaystyle \sum q_j(t){J^{″}}_{uu,2j}\Omega }& \cdots & {\displaystyle \sum q_j(t){J^{″}}_{uu,2Nj}\Omega }\end{array}\right](i, j=1, 2, \dots , 2N), M_{e\dot{q}}={\displaystyle \underset{m}{\int }{\Phi }^T{\Omega }^{\times }\Phi dm}.\hfill \end{array}$$

(17)

The superscript denotes the skew-symmetric matrix form of a vector (corresponding to a cross-product operation). Consider the gravity, aerostatic force, and moment vector of the flexible airship in Equation (11). Gravity, the resulted moment, and its generalized one are described as follows:

$$F_G=mg\widehat{g}$$

(18)

$$M_G=(r_G+u_G)\times F_G=r_G\times F_G+\frac{1}{m}{\displaystyle \sum _{i=1}^{2N}{q}_i(t)p_i\times F_G}$$

(19)

$$Q_{Gi}={\displaystyle \underset{m}{\int }g{\widehat{g}}^T{\Phi }_{i}dm=}g{\widehat{g}}^T{p}_i,i=1,2,\cdots ,2N$$

(20)

where g denotes that the acceleration of gravity and unit direction vector of gravity is:

$$\widehat{g}={\left[\begin{array}{ccc}-\sin \theta & \cos \theta \sin \varphi & \cos \theta \cos \varphi \end{array}\right]}^T$$

(21)

$$u_G={\displaystyle \underset{m}{\int }udm/m}=\frac{1}{m}{\displaystyle \sum _{i=1}^{2N}{q}_i(t)p_i},p_i={\displaystyle \underset{m}{\int }{\Phi }_{i}dm}$$

(22)

The aerostatic force in the body frame in Equation (11) is:

$$F_{AS}=-\rho g{V}_B\widehat{g}$$

(23)

The resulted moment and its generalized moment are presented as follows:

$$M_{AS}=u_V\times F_{AS}=\left({\displaystyle \underset{V_B}{\int }u\mathrm{d}V/V_B}\right)\times F_{AS}={\displaystyle \sum q_i(t)I_{AS,i}^{\times }{F}_{AS}}$$

(24)

$$Q_{AS,i}=-{\displaystyle \underset{L}{\int }\rho {\widehat{g}}^T{\Phi }_{i}Sdx=}{F}_{AS}^T{I}_{AS,i},i=1,2,\cdots ,2N$$

(25)

where V_B denotes the volume of the airship hull and S is the hull cross-sectional area:

$$u_{\mathrm{V}}=\frac{1}{V_B}{\displaystyle \underset{V_B}{\int }udV},I_{AS,i}^{\times }=\frac{1}{V_B}{\displaystyle \underset{V_B}{\int }{\Phi }_{i}dV}=\frac{1}{V_B}{\displaystyle \underset{L}{\int }{\Phi }_{i}S(x)dx}$$

(26)

The aerodynamics force and moment vector of the flexible airship in Equation (11) is:

$$\left[\begin{array}{c}{F}_{AD}\\ M_{AD}\\ Q_{AD}\end{array}\right]=\left[\begin{array}{c}{F}_p\\ M_p\\ Q_p\end{array}\right]+\left[\begin{array}{c}{F}_v\\ M_v\\ Q_v\end{array}\right]+\left[\begin{array}{c}{F}_F\\ M_F\\ Q_F\end{array}\right]+\left[\begin{array}{c}{F}_{\mathbf{H}(\mathbf{F})}\\ M_{\mathbf{H}(\mathbf{F})}\\ Q_{\mathbf{H}(\mathbf{F})}\end{array}\right]+\left[\begin{array}{c}{F}_{\mathrm{axial}}\\ M_{\mathrm{axial}}\\ Q_{\mathrm{axial}}\end{array}\right]$$

(27)

where subscripts p, v, F, H(F), and the axial on the right-hand side of Equation (27) denote the forces and moments due to the potential-flow (related to the added mass), viscous effect on the hull, aerodynamic force acting on fins and acting on the hull due to the fins, and axial drag, respectively. The calculation of the aerodynamics forces is the same as in [21].

The control force and moment vector $F_C,M_C,Q_C$ of the flexible airship includes those of propellers and control surface deflections. The thrust in the body frame is $F_T={\left[\begin{array}{ccc}{\mathrm{F}}_{Tx}& {\mathrm{F}}_{Ty}& {\mathrm{F}}_{Tz}\end{array}\right]}^T$; the corresponding moment and generalized moment are as follows:

$$M_T=r_T\times F_T+{\displaystyle \sum q_i(t){\Phi }_i(r_T)\times F_T}$$

(28)

$$Q_{Ti}=F_T{\Phi }_i(r_T)$$

(29)

where ${\Phi }_i(r_T)$ is the mode shape function at the propeller-mounted position $r_T$. Forces due to the control surface deflection are presented in the body frame, as

$$F_{\delta }^T=\left[\begin{array}{c}\Delta C_D\\ \Delta C_L({\delta }_r)\\ \Delta C_L({\delta }_e)\end{array}\right]\cdot \overline{q}\cdot S_f$$

(30)

where $S_f$ denotes the area of control surface, and $\Delta C_L$ and $\Delta C_D$ are the lift and drag resulted from the control surface deflection. The corresponding moment and generalized moment are:

$$M_{\delta }=r_{\delta }\times F_{\delta }+{\displaystyle \sum q_i(t){\Phi }_i(r_{\delta })\times }{F}_{\delta }$$

(31)

$$Q_{\delta ,i}=F_{\delta }^T{\Phi }_i(r_{\delta })$$

(32)

where ${\Phi }_i(r_{\delta })$ is the shape function at the control surface-mounted position of $r_{\delta }$.

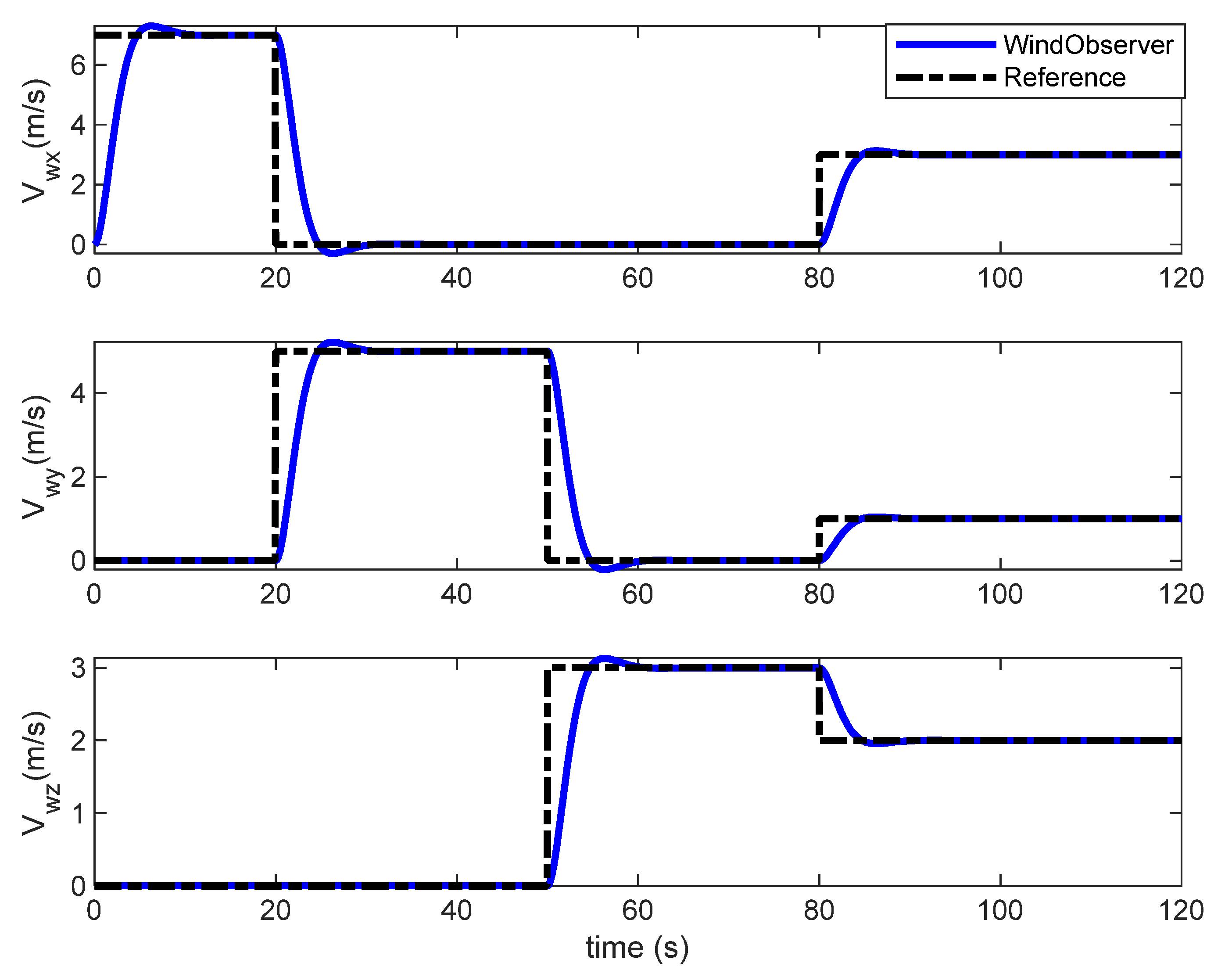
Considering the model uncertainties or disturbances often occurring in the dynamics system of Equation (10), assume the atmospheric parameters are stable and disturbances are bounded; thus, a model uncertainty, d, and the actuator saturation are introduced, thus the system (10) can be modified, as

$$\dot{\mathit{X}}(t)=\mathit{f}(\mathit{X})+\mathit{g}(\mathit{X})\mathrm{sat}({\mathit{u}}_a(t))+\Gamma d(t)$$

(33)

where d denotes disturbances except for winds and model uncertainties, such as aerodynamic coefficients and structural stiffness; $\mathrm{sat}(\cdot )$ denotes saturation function. As the airship has a large inertia and its motion is slow and sedate, d can be assumed to be a slow-varying disturbance, which can be estimated on-line by using an adaptive law. Let $\widehat{\mathit{d}}$ be the estimated value of the uncertain parameter d; $\tilde{\mathit{d}}=\widehat{\mathit{d}}-\mathit{d}$ is the associated estimated error. 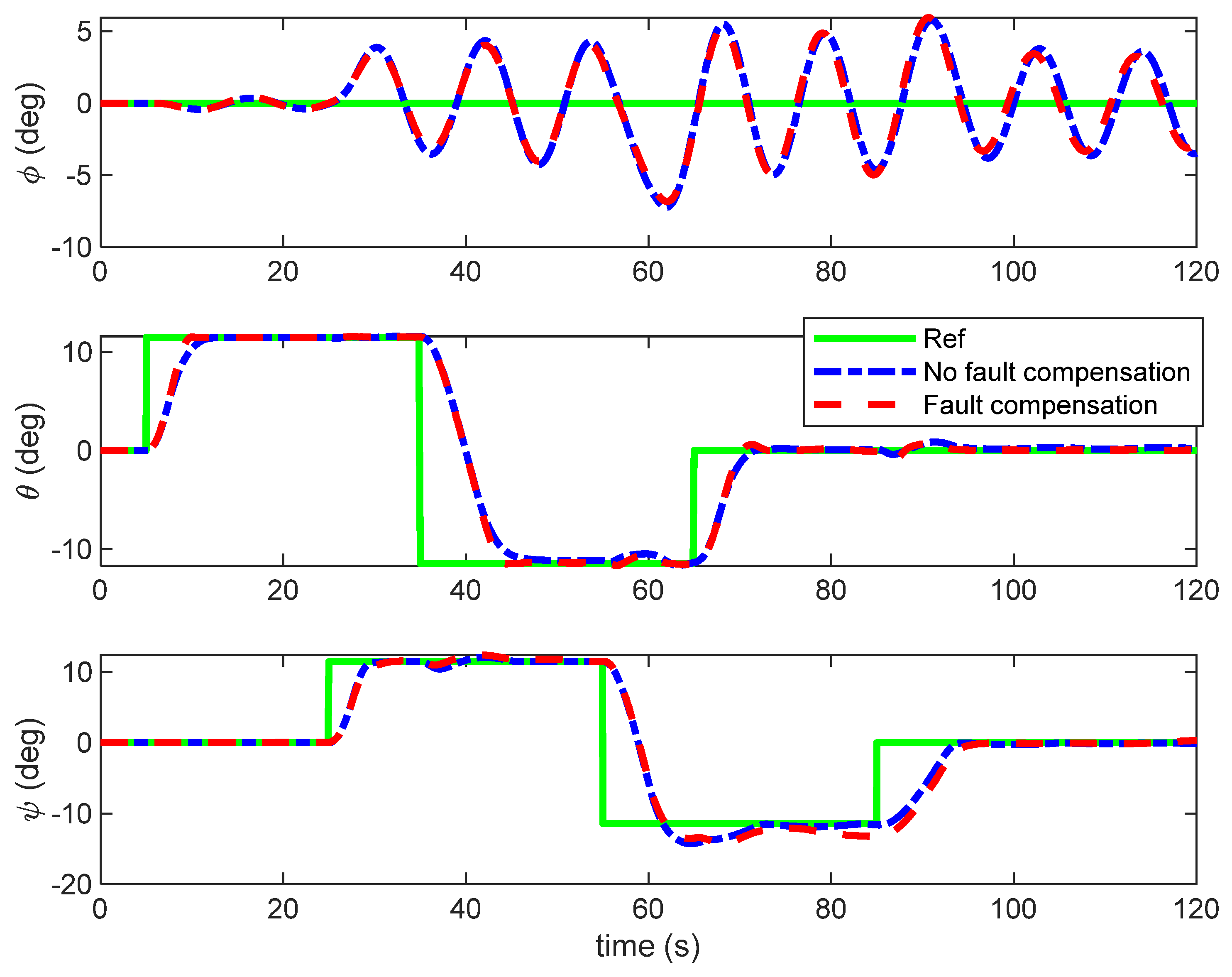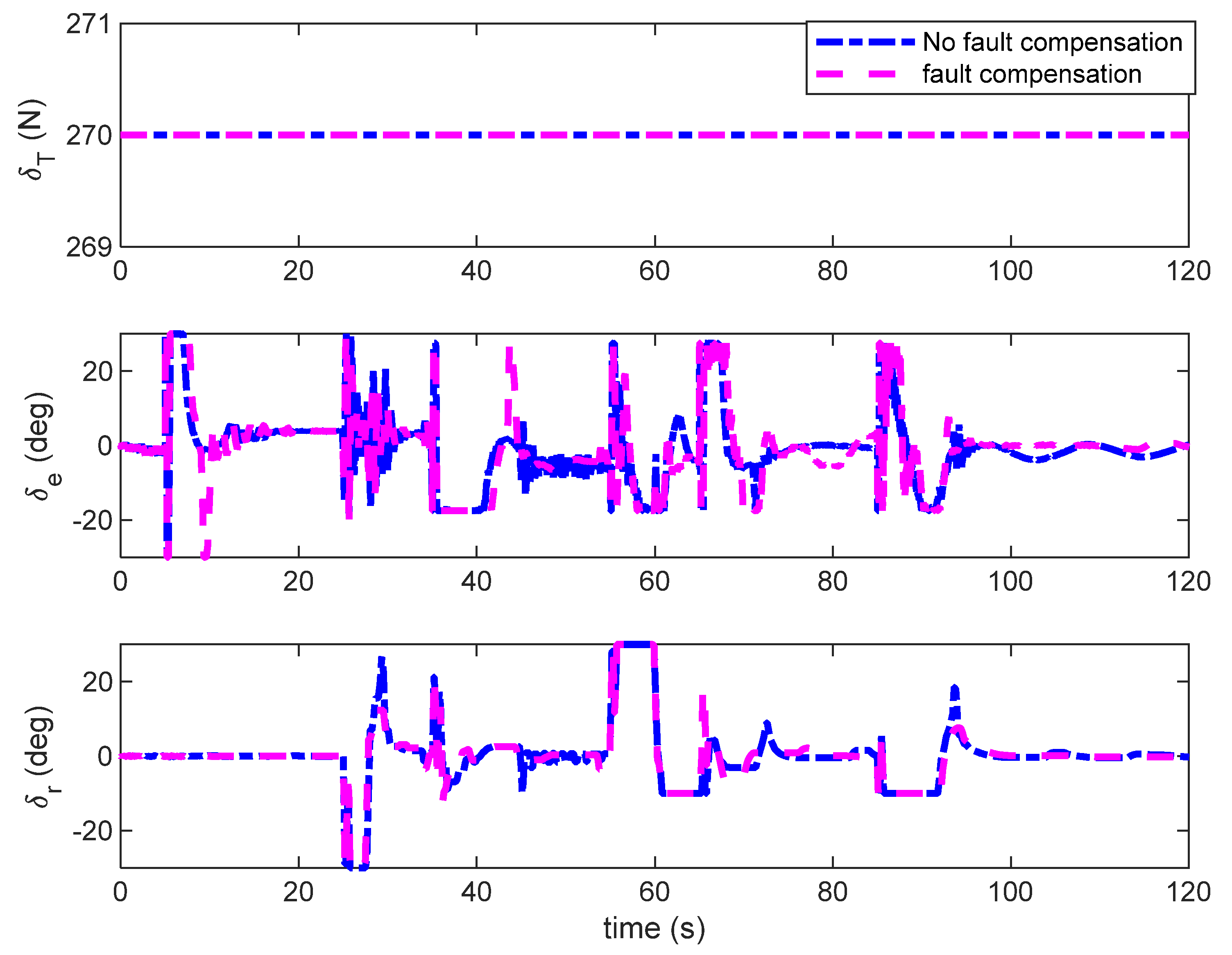Finally, Г denotes the disturbance coefficient matrix. The faults can be modeled as abrupt changes of the nominal control action from ${\mathit{u}}_a$ [26,27],

$${\mathit{u}}_a^f(t)={\mathit{u}}_a(t)+(\mathit{I}-{\overline{\rho }}_a(t))\left({\mathit{f}}_a(t)-{\mathit{u}}_a(t)\right)$$

(34)

that is,

$${\mathit{u}}_a^f(t)={\mathit{u}}_h+{\mathit{u}}_f=\underset{{\mathit{u}}_h}{\underbrace{{\overline{\rho }}_a{\mathit{u}}_a(t)}}+\underset{{\mathit{u}}_f}{\underbrace{(\mathit{I}-{\overline{\rho }}_a(t)){\mathit{f}}_a(t)}}$$

(35)

where ${\mathit{u}}_a=\left[u_{a,1},u_{a,2},\cdots ,u_{a,m}\right]\in R^m$ is the actual control output; the diagonal matrix ${\overline{\rho }}_a=\mathrm{diag}\left\{{\rho }_{a,1},{\rho }_{a,2},\cdots ,{\rho }_{a,m}\right\}$ denotes the operational effectiveness of the actuators; I is the m×m identity matrix; the fault vector ${\mathit{f}}_a=\left[f_{a,1},f_{a,2},\cdots ,f_{a,m}\right]\in R^m$ denotes the control action from the failed or un-manipulated actuators; $u_h={\overline{\rho }}_a{\mathit{u}}_a(t)$ denotes the remaining control of the health actuators; ${\mathit{u}}_f=(\mathit{I}-{\overline{\rho }}_a(t)){\mathit{f}}_a(t)$ 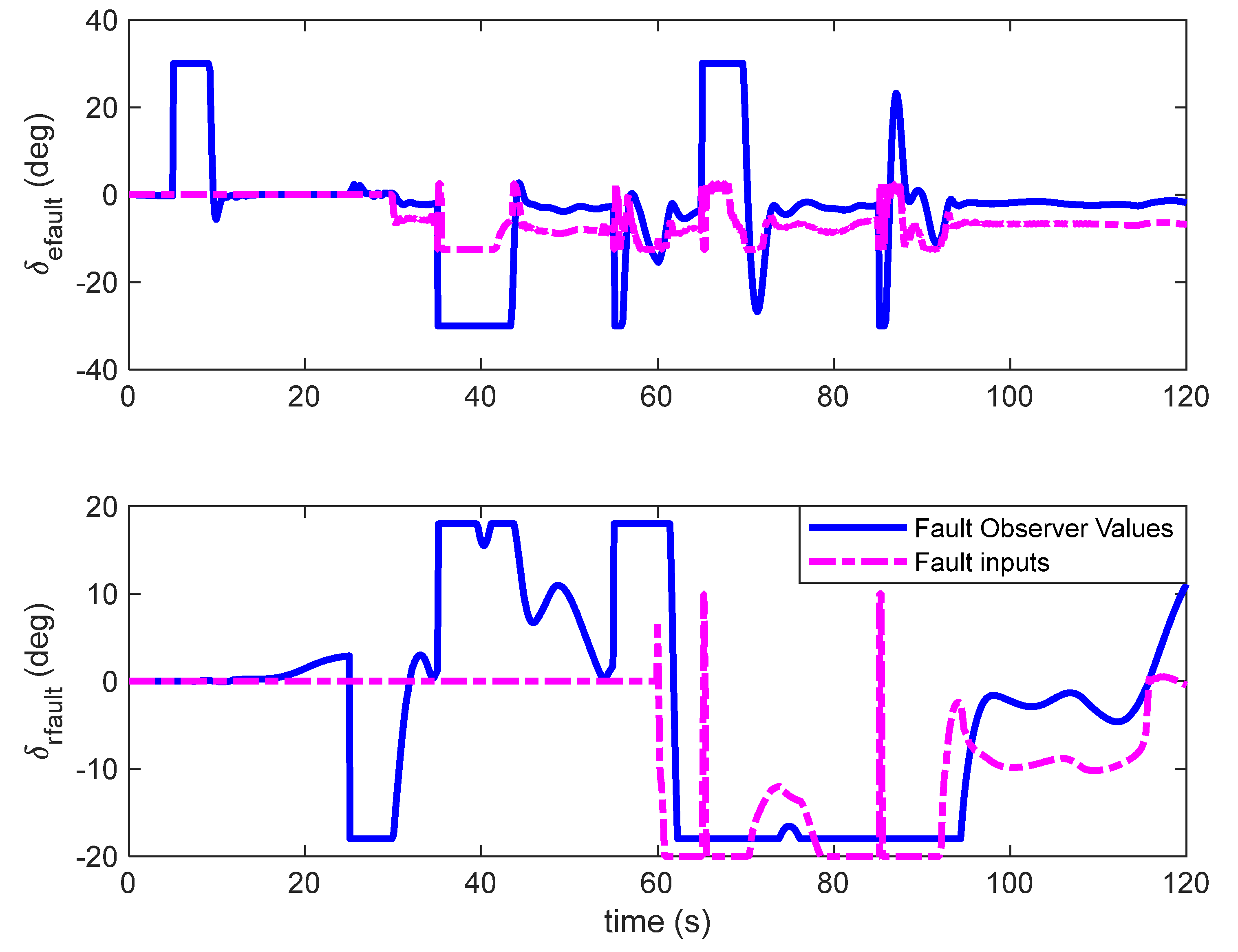denotes the fault of the inputs.

Assumption 1.

In Equation (34), for the multiplicative and additive actuator faults,${\rho }_{a,i}$and$f_{a,i}$are all bounded. In addition,${\dot{\rho }}_{a,i}$and${\dot{f}}_{a,i}$exist and are bounded, i = 1, 2, …, m.

Substituting Equation (35) into Equation (33) yields:

$$\dot{\mathit{X}}(t)=\mathit{f}(\mathit{X})+\mathit{g}(\mathit{X}){\overline{\rho }}_a\mathrm{sat}({\mathit{u}}_a(t))+\mathit{g}(\mathit{X})(\mathit{I}-{\overline{\rho }}_a(t)){\mathit{f}}_a(t)+\Gamma d$$

(36)

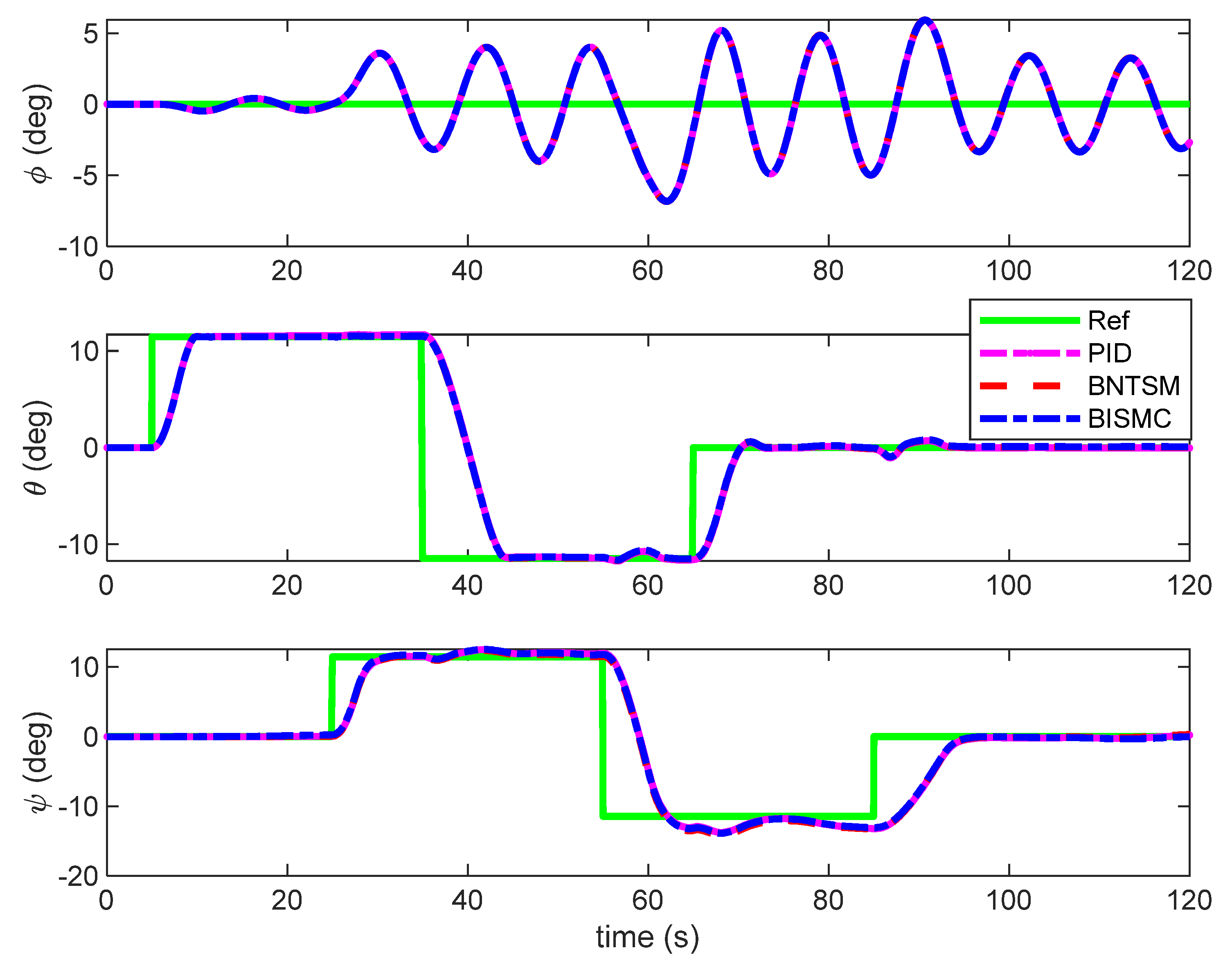
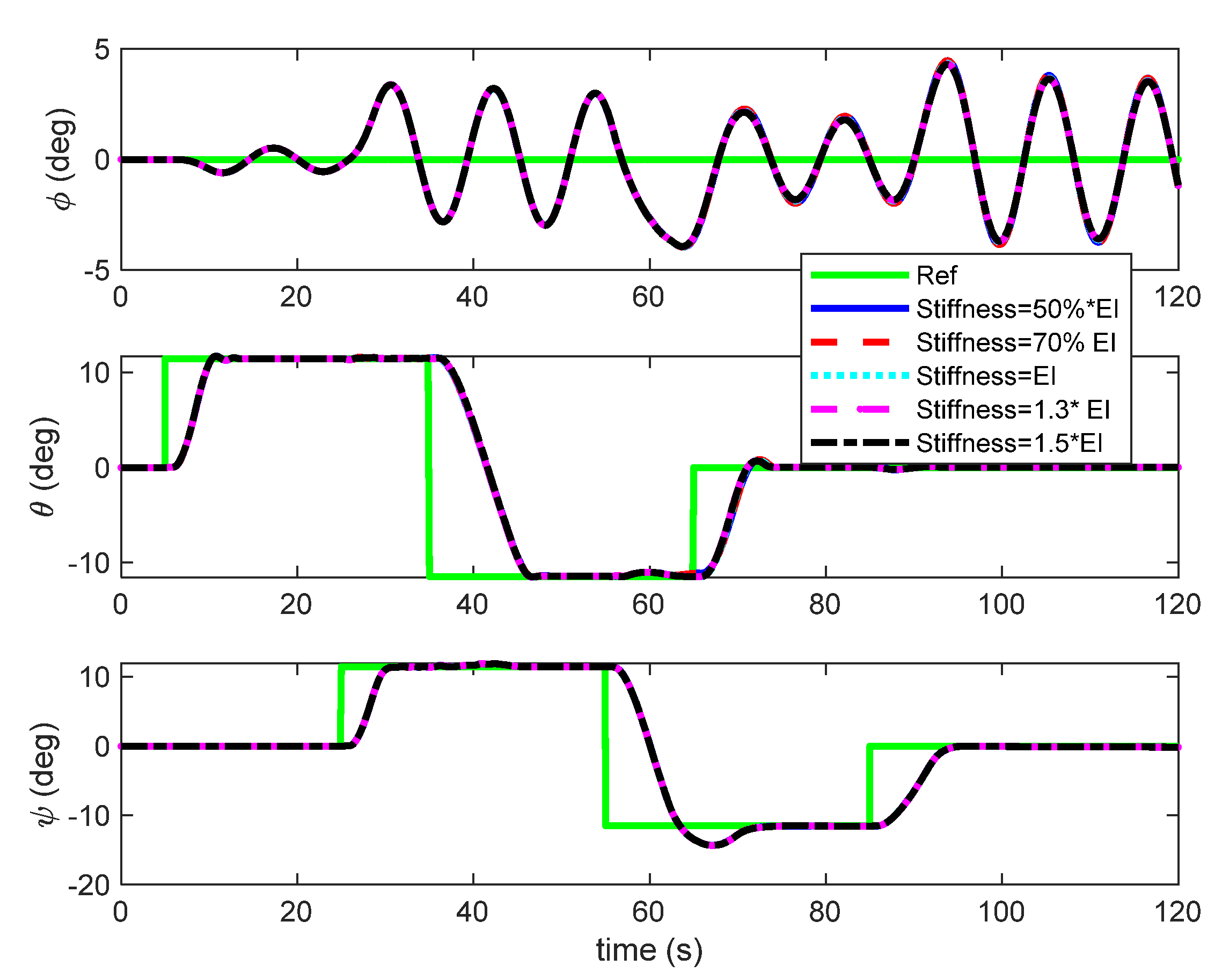
Remark 1.

There are two underactuated cases for the flexible airship. Case 1. The airship without a lateral tilt angle of the propellers (i.e., the thrust direction is fixed) is underactuated in the y-direction (that is, the lateral control force, T_sy = 0); thus, the sway velocity, v, cannot be directly controlled. If the wind is in the presence in this case, then the airship can align against the wind through the yaw motion, reducing the lateral forces requirement to a low and acceptable value; thus, the lateral force input can vanish in stationary conditions. Case 2. The airship works in Case 1 without ailerons or differential actuators (i.e., δ_eL = δ_eR, δr_U = δ_rB, and the roll control moment, M_Tx ≈ 0). Sway velocity, v, and bank angle, φ, cannot be directly controlled. In this case, the disturbance of the roll moment resulting from the wind can be attenuated by the airship roll damp; thus, the roll moment input can vanish in stationary conditions.

2.2. Fault Tolerant Trajectory Tracking Problem

The fault-tolerant trajectory tracking problem is a challenge for the flexible stratospheric airship because it is a hard task to achieve precise trajectory tracking under the actuator faults; the main reason is that the interaction between fluid and structure should be considered. Presently, consider the system of Equations (10) and (36)—the control task is to design a fault-tolerant trajectory-tracking controller, such that the closed-loop system is globally asymptotically stable and the output trajectory, η, is steered towards a given reference trajectory, η_r, with $\underset{t\to \infty }{\lim }{\Vert e(t)\Vert }_2<{\epsilon }_0$, even in a specified model parameter uncertainty, unknown wind disturbances, and control surface faults; where the tracking error is $\mathit{e}(t)=\eta (t)-{\eta }_r(t)$, ε₀ is a prescribed constant, and 2-norm is ${\Vert \mathit{e}(t)\Vert }_2=\sqrt{{\mathit{e}}^T\mathit{e}}$.

3. BNTSM-Based Trajectory Tracking Design

In this section, the robust BNTSM controller is designed to solve the problem in Section 2.2. Firstly, a command filter is used to meet the magnitude and rate constraints of the input signal. The command filter can be obtained by using a second-order lower pass filter, as follows:

$$G_r(s)=\frac{X_r(s)}{X_r^0(s)}=\frac{{\omega }_n^2}{s^2+2{\zeta }_n{\omega }_{n}s+{\omega }_n^2}$$

(37)

where ${\zeta }_n$ denotes the filter-damping ratio and ω_n denotes the undamped nature frequency of the filter. To reduce the filter error $e=x_r^0-x_r$, the filter frequency, ω_n, is the bandwidth of $X_r^0(s)$, which is generally less than that of G_r(s), and then ω_n can be selected.

Secondly, for the system (4), the wind field is assumed as a constant, due to the stable meteorological condition in the stratosphere [28]. Some people regarded wind speed as one kind of external disturbance, but it is hard to separate wind and model uncertainty and they are not easily handled. Here, a wind observer is introduced to improve tracking performances. A wind observer state is defined, ${\left[\begin{array}{cc}{\widehat{\mathit{\xi }}}^T& {\widehat{\mathit{\upsilon }}}_w^T\end{array}\right]}^T$, where $\widehat{\mathit{\xi }}$ and ${\widehat{\mathit{\upsilon }}}_w$ denote estimates of $\mathit{\xi }$ and ${\mathit{\upsilon }}_w$. The wind can be sensed by the wind speed sensors in the fixed frame, and the observer dynamics are designed, as follows [4]:

$$\left[\begin{array}{c}\dot{\widehat{\mathit{\xi }}}\\ {\dot{\widehat{\mathit{\upsilon }}}}_w\end{array}\right]=\left[\begin{array}{c}R(\mathit{\eta }){\mathit{\upsilon }}_a\\ 0\end{array}\right]+\left[\begin{array}{cc}{\mathit{L}}_{\xi }& {\mathit{I}}_3\\ {\mathit{L}}_w& 0\end{array}\right]\left[\begin{array}{c}\xi -\widehat{\xi }\\ {\widehat{\upsilon }}_w\end{array}\right]$$

(38)

The estimation error of the position and wind speed are defined as ${\mathit{e}}_4=\left[\begin{array}{c}\mathit{\xi }-\widehat{\mathit{\xi }}\\ {\mathit{\upsilon }}_w-{\widehat{\mathit{\upsilon }}}_w\end{array}\right]$, and the estimation error e₄ can be obtained as

$${\dot{\mathit{e}}}_4=\left[\begin{array}{c}\mathit{\xi }-\widehat{\mathit{\xi }}\\ {\mathit{\upsilon }}_w-{\widehat{\mathit{\upsilon }}}_w\end{array}\right]=\left[\begin{array}{cc}-{\mathit{L}}_{\xi }& {\mathit{I}}_3\\ -{\mathit{L}}_w& 0\end{array}\right]{\mathit{e}}_4={\tilde{\mathit{A}}}_e{\mathit{e}}_4$$

(39)

where ${\mathit{L}}_{\xi }$, ${\mathit{L}}_w$ are gain matrices such that ${\tilde{\mathit{A}}}_e=\left[\begin{array}{cc}-{\mathit{L}}_{\xi }& {\mathit{I}}_3\\ -{\mathit{L}}_w& 0\end{array}\right]$ be Hurwitz; I₃ is the unit matrix with a dimension of 3 × 3. Thus, there exists a positive definite symmetrical matrix, ${\mathit{P}}_e$, such that

$$\frac{d}{dt}\left({\mathit{e}}_4^T{\mathit{P}}_e{\mathit{e}}_4\right)=-{\mathit{e}}_4^T{\mathit{Q}}_e{\mathit{e}}_4$$

(40)

where ${\mathit{Q}}_e=\mathrm{diag}({\mathit{Q}}_{\xi },{\mathit{Q}}_{{\upsilon }_w})$, ${\mathit{Q}}_{\xi }$, and $Q_{{\upsilon }_w}$ are symmetric positive definite matrices and the weight matrix, ${\mathit{P}}_e$, meets the following Lyapunov equation,

$${\tilde{\mathit{A}}}_e^T{\mathit{P}}_e+{\mathit{P}}_e{\tilde{\mathit{A}}}_e=-{\mathit{Q}}_e$$

(41)

Thirdly, consider the kinematics in Equation (4) and dynamics in Equation (36). The control objective is to track a reference signal, $x_{1r}={\eta }_{\mathrm{r}}$, with the derivative ${\dot{x}}_{1r}$ under unknown disturbances and faults. The tracking error vectors of the attitudes are defined as

$${\mathit{z}}_1={\mathit{x}}_1-{\mathit{x}}_{1r}$$

(42)

$${\mathit{z}}_2={\mathit{x}}_2-{\mathit{x}}_{2r}$$

(43)

where $x_1=\eta$$x_2={\dot{x}}_1=\dot{\eta }$,${\mathit{x}}_{1r}$ is the reference or desired attitude angle, and ${\mathit{x}}_{2r}$ is the output of a command filter.

Presently, the BNTSM controller is designed, and the kinematics Equation (4) and dynamics Equation (33) are considered. To obtain a fast and transient response and finite time convergence without a singular problem, a non-singular terminal sliding-mode (NTSM) surface or manifold is designed by using the fractional order derivative, as follows [29,30:

$$\mathit{s}={\tilde{\mathit{z}}}_1+{\alpha }_{\gamma }{\tilde{\mathit{z}}}_1^{\lambda }+\frac{1}{\beta }{\tilde{\mathit{z}}}_2{}^{p/q}={\tilde{\mathit{z}}}_1+{\alpha }_{\gamma }|{\tilde{\mathit{z}}}_1{|}^{\lambda }\mathrm{sgn}({\tilde{\mathit{z}}}_1)+\frac{1}{\beta }|{\tilde{\mathit{z}}}_2{|}^{p/q}\mathrm{sgn}({\tilde{\mathit{z}}}_2)$$

(44)

where ${\tilde{\mathit{z}}}_1$ and ${\tilde{\mathit{z}}}_2$ are defined in (A6), the SMC parameter λ > p/q, ${\alpha }_{\gamma }>0$, $\mathit{s}={\left[\begin{array}{ccc}{s}_1& s_2& s_3\end{array}\right]}^T\in R^3$ denotes the sliding-mode surface, i.e., s₁ = s(φ), s₂ = s(θ), s₃ = s(ψ) and 1 < p/q < 2, β > 0; sgn(·) is the sign function. In addition, the derivative of the sliding-mode surface, s, is

$$\dot{\mathit{s}}={\dot{\tilde{\mathit{z}}}}_1+{\alpha }_{\gamma }\lambda |{\tilde{\mathit{z}}}_1{|}^{\lambda -1}\cdot {\dot{\tilde{\mathit{z}}}}_1+\frac{1}{\beta }\cdot \frac{p}{q}|{\tilde{\mathit{z}}}_2{|}^{(p/q-1)}\cdot {\dot{\tilde{\mathit{z}}}}_2$$

(45)

Using an extended CLF, a control law will be designed to drive the virtual angular rate error, ${\tilde{\mathit{z}}}_2$, to zero, while ensuring that the current attitude vector, η, will converge to the desired value of η_r. The attitude controller is derived in two steps, and the detailed design is presented in Appendix A.

Presently, we consider the input saturation problem, in order to analyze the effect of the actuator saturation on the closed-loop dynamics; the actuator output is

$$\mathrm{sa}t({\mathit{u}}_a)=\{\begin{array}{l}{\mathit{u}}_a^{f0}+{\widehat{\mathit{u}}}_f \mathrm{for} \left|{\mathit{u}}_a^{f0}+{\widehat{\mathit{u}}}_f \right|<U_{\lim }\\ U_{\lim } \mathrm{for} {\mathit{u}}_a^{f0}+{\widehat{\mathit{u}}}_f>U_{\lim }\\ -U_{\lim } \mathrm{for} {\mathit{u}}_a^{f0}+{\widehat{\mathit{u}}}_f<-U_{\lim }\end{array}$$

(46)

where ${\mathit{u}}_a^{f0}$ is the input of the BNTSM controller as Equation (A13), and ${\widehat{\mathit{u}}}_f$ is the fault estimator as Equation (A19).

Furthermore, defining ∆u as the difference between the desired control input u and the actuator output, i.e., ∆u = u_a − sat(u_a), an anti-windup compensator is designed to compensate for the actuator saturation, as follows:

$$\mathit{v}=K_s\left({\mathit{u}}_a-\mathrm{sat}({\mathit{u}}_a)\right)$$

(47)

where $K_s$ is the control gain of the saturation compensator, and then the total control is

$${\mathit{u}}_a={\mathit{u}}_a^{f0}+{\widehat{\mathit{u}}}_f+\mathit{v}$$

(48)

Remark 2.

For the fault estimator (A19) (in Appendix A), if ${\tilde{\mathit{z}}}_2$ converges to zero, then ${\dot{\widehat{\mathit{u}}}}_f$ will converge to zero, and the fault becomes constant; a disturbance observer method [31] can be used to estimate ${\widehat{\mathit{u}}}_f=const$.

Note that the operational effectiveness, ${\overline{\rho }}_a$, (or the multiplicative fault) of the actuators in Equation (34) can also be estimated by using a similar method as Equation (A19) [32]; thus, there is no more detail.

The BNTSM controller for the trajectory-tracking control is designed as Figure 2, which includes the flexible airship dynamics and a BNTSM control module. The BNTSM controller is designed based on the above steps. The disturbance estimator and the fault estimator are governed by Equations (A18) and (A19). A wind observer is also used according to Equation (38). The control output is filtered by the command filter (37).

4. Simulation and Analysis

The considered model is the flexible Skyship-500 airship, and the structure parameters are listed in

Table 1. Structure parameters for the studied airship.

Parameter	Value	Parameter	Value (kg)
Ix	1.0834 × 105 (kg·m2)	m	2.682 × 103
Iy	2.8819 × 105 (kg·m2)	m11	5.0575 × 102
Iz	2.1722 × 105 (kg·m2)	m22	5.0737 × 103
Ixz	0	m33	5.0737 × 103
L	50 (m)	m44	6.8879 × 104
(xG, yG, zG)	(0, 0, 3.605) (m)	m55	5.8540 × 105
VB	5.131 × 103 (m3)	m66	5.8540 × 105
ET0	433,440 (N/m)

; the aerodynamic coefficients are as in [21].

The initial position in F_g of the airship is ${\xi }_0$ = [0, 0, 0 m]^T, the initial velocity in F_b is υ₀ = [8.42 m/s, 0, 0]^T, the initial attitude is η₀ = [0, 0, 0]^T, and the initial angular velocity is ω₀ = [0, 0, 0]^T. The position constraints for the elevator and rudder are [−30°, 30°]. Three scenarios of bounded wind disturbances, control surface faults, and the variable stiffness of the flexible airship envelope are simulated to illustrate the BNTSM controller performances. The software of MATLAB and Simulink are employed to solve the problems.

Scenario 1.

Attitude tracking control under unknown winds.

This scenario will demonstrate the attitude-tracking performance by using the proposed BNTSM controller and the wind observer. The wind vector is initially set as

$${\mathit{\upsilon }}_w=\{\begin{array}{l}{[7,0,0]}^T(\mathrm{m}/\mathrm{s}),t\le 20\mathrm{s}\\ {[0,5,0]}^T(\mathrm{m}/\mathrm{s}), 20\mathrm{s}<t\le 50\mathrm{s}\\ {[0,0,3]}^T(\mathrm{m}/\mathrm{s}), 50\mathrm{s}<t\le 80\mathrm{s}\\ {[3,1,2]}^T(\mathrm{m}/\mathrm{s}),t>80\mathrm{s}\end{array}$$

(49)

Wind parameters in (38) and (39) are chosen as ${\mathit{L}}_{\xi }=diag(1,1,1)$, ${\mathit{L}}_w=\mathrm{diag}(2.5,2.5,2.5)$, and ${\mathit{Q}}_{\xi }={\mathit{I}}_3$, ${\mathit{Q}}_{{\upsilon }_w}={\mathit{I}}_3$. To illustrate the proposed performances, a backstepping integral sliding-mode control (BISMC) [3,4] and a PID controller are employed for comparison. The sliding surface s of the BISMC is defined as follows: $s={\lambda }_1{z}_1+{\lambda }_2{\displaystyle {\int }_0^t{z}_1\mathrm{d}(t)}+z_2$. In addition, the PID controller structure is as in Figure 3.

The controller parameters are designed as shown in

Table 2. Selected parameters of the controller.

Controller	Parameters	Value
PID	kp,zj, ki,zj (j = 1, 2)	2, 0.04
BNTSM	c1, c2	diag(2, 2, 2), diag(0.2, 0.2, 0.2)
	h, ς, φs	0.01 * diag(1,1,1), 0.01 * diag(1, 1.2, 1), 0.4
	p, q, β	5, 3, 0.1 * diag(1, 1, 1)
	αr, γd, λ	5, 1, 1. 8 * diag(1, 1, 1)
BISMC	c1, c2	0.1 * diag(1, 1, 1), 0.01 * diag(1, 1, 1)
	h, ς	0.1 * diag(1, 1, 1), diag(1, 1.2, 1)
	λ1,λ2	0.5 * diag(1, 1, 1),0.05 * diag(1, 1, 1)
	φs, ki,smc	0.4, 0.1

.

The parameters are selected to satisfy the requirements in Section 3 after several design iterations. The damping ratio and undamped nature frequency of the command filter are selected as ζ_n = 0.9, ω_n = 20 rad/s. The mode number, N, selects N = 2, P_e = 0.1, $\mathit{\Gamma }=1$. The gain of the actuator saturation compensator is K_s = 1, and control gain for thruster k_T = 90,000. A doublet command is predefined as the desired attitude.

For an easier comparison, the averaged tracking error is defined as

$$E=\sqrt{\frac{1}{N}{\displaystyle \sum _{k=1}^N\left({\Vert e(k)\Vert }^2\right)}}$$

(50)

where N is the number of simulation steps, and the elapsed time (ET) is the time that MATLAB has used to complete the 10-s simulation time. This may not reflect the true computational burden of the controllers, but it can be used to provide a general idea about the comparison in computational time among the controllers. The simulation results are shown, as follows.

It can be observed from Figure 4 and

Table 3. Tracking errors and ET of the airship under the input of the controller without wind compensation.

Controller Error	Eφ (rad)	Eθ (rad)	Eψ (rad)	ET (s)
PID	0.0532	0.0843	0.0893 × 10−3	2153.6
BNTSM	0.0525	0.0834	0.0887 × 10−3	2367.2
BISMC	0.0528	0.0839	0.0890 × 10−3	2226.2

that the reference signals of pitch and yaw angles are precisely tracked, but the averaged tracking errors of the BNTSM controller are smallest, and then those by the BISMC design are smaller, and the PID controller provides worse tracking performances comparing with the BNTSM control and the BISMC. In view of the computational burden, the BNTSM controller is time consuming, while the cost of the PID controller is the cheapest. The roll motion response is free oscillating and has not been controlled due to the absence of the direct roll moment under the underactuated Case 2.

It also can be observed from Figure 5 and Table 3 and

Table 4. Tracking errors and ET of the airship under the input of the controller with wind compensation.

Controller Error	Eφ (rad)	Eθ (rad)	Eψ (rad)	ET (s)
PID	0.0577	0.0786	0.0817 × 10−3	1993.2
BNTSM	0.0574	0.0774	0.0805 × 10−3	2050.4
BISMC	0.0575	0.0780	0.0811 × 10−3	2048.9

that the responses have smaller overshoots and shorter transient times by using the BNTSM controller with wind observer compensation versus those without wind compensation. The wind speeds are precisely estimated by the proposed wind observer, as shown in Figure 6. Figure 7 demonstrates the structure mode shapes in the Oxy and Oxz planes; that is, according to (3), the 1st and 2nd bending mode in the Oxy plane are ${\Phi }_1={\left[\begin{array}{ccc}0& {\varphi }_1& 0\end{array}\right]}^T$ and ${\Phi }_2={\left[\begin{array}{ccc}0& {\varphi }_2& 0\end{array}\right]}^T$; the 1st and 2nd bending mode in the Oxz plane are ${\Phi }_3={\left[\begin{array}{ccc}0& 0& {\varphi }_1\end{array}\right]}^T$ and ${\Phi }_4={\left[\begin{array}{ccc}0& 0& {\varphi }_2\end{array}\right]}^T$; the associated nature frequency of the 1st and 2nd bending modes can be obtained by the modal rigidness and mass, i.e., ${\omega }_{n1}=22.8\mathrm{rad}/\mathrm{s}$ and ${\omega }_{n2}=64.2\mathrm{rad}/\mathrm{s}$, respectively, and it can be observed from Figure 7 that the rigidness is bigger and the elastic displacement is smaller in the middle airship than those on the two sides of the airship.

Scenario 2.

Trajectory-tracking control under actuator faults with unknown winds.

This scenario will demonstrate fault-tolerant tracking performance by using the proposed BNTSM controller and the fault observer. The faults of actuator bias forces with wind are studied here. The faults are set as follows: Fault 1, the bias from the nominal value is 5 deg and the loss of effectiveness is 25% for the elevator in t > 30 s; Fault 2, the bias from the nominal value is 5 deg and the loss of effectiveness is 50% for the rudder in t > 60 s. The faults are simulated by setting bias values of each actuator at the triggering time. The wind disturbances are set as Equation (49) in Scenario 1. A doublet attitude is predefined as the desired attitudes to verify the tracking performance of the BNTSM control. The controller parameters are the same as Table 2, except for

$$\{\begin{array}{l}{c}_2=\mathrm{diag}\left(\begin{array}{ccc}0.2,& 20,& 0.2\end{array}\right),\beta =\mathrm{diag}(0.1, 0.002, 0.2), \mathrm{for} \mathrm{BNTSM}\\ c_1=c_2=\mathrm{diag}\left(\begin{array}{ccc}2,& 2,& 2\end{array}\right), \mathrm{for} \mathrm{BISMC}\end{array},$$

(51)

In addition, the fault observer parameters are designed as

$${{\mathsf{\gamma }}_f}_{ }=3, P_f=\mathrm{3,000,000}\times \mathrm{diag}(0,1,-1).$$

(52)

By using the above design, the simulation results are demonstrated as follows.

Figure 8 and Figure 9 shows the pitch step input of 0.2, the rad shows at 5 s, and the tracking response converges the desired value at 10 s (within 10 s). Because the doublet command is a changing signal, the steady value of the tracking response also changes; thus, the overall tracking process is dynamically varying, but the response will quickly converge when the command is fixed. It can be observed from Figure 8 and

Table 5. Tracking errors and ET of the airship under the input of the controller without fault compensation.

Controller Error	Eφ (rad)	Eθ (rad)	Eψ (rad)	ET (s)
PID	0.0510	0.0810	0.0788 × 10−3	2171.4
BNTSM	0.0511	0.0803	0.0775 × 10−3	2354.3
BISMC	0.0510	0.0805	0.0780 × 10−3	2193.0

that the reference inputs of pitch and yaw angles are well tracked, even with control surface faults and unknown winds. Comparing with the PID controller and the BISMC, the BNTSM controller has smaller averaged tracking errors. In the view of elapsed time, the PID controller is the least, with the BISMC next, while the BNTSM control will cost more time. The roll motion is not controlled due to the underactuated character of the flexible airship. It also can be observed from Figure 9 and Table 5 and

Table 6. Tracking errors and ET of the airship under the input of the controller with fault compensation.

Controller Error	Eφ (rad)	Eθ (rad)	Eψ (rad)	ET (s)
PID	0.0488	0.0804	0.0829 × 10−3	1821.0
BNTSM	0.0490	0.0797	0.0817 × 10−3	2114.1
BISMC	0.0489	0.0798	0.0819 × 10−3	2016.2

that the responses have shorter transient times by using the fault observer compensation and the BNTSM controller than those without fault compensation. This demonstrates the fault tolerant control capability of the BNTSM controller. The control inputs are shown in Figure 10 and Figure 11. Figure 11 shows that the control surface faults are estimated by using the proposed estimator of (A19) (in Appendix A). There are some differences initially because the corresponding tracking errors ${\tilde{z}}_2$ are affected by the variable reference signals. The fault estimations are gradually close to the true values. Figure 12 shows the response of the sliding-mode variable, s, which asymptotically approach zero except for s(φ), due to the underactuated roll motion.

Scenario 3.

Trajectory-tracking control under variable stiffness and unknown faults and winds.

In this scenario, we investigate the significance envelope flexibility has on the effect of rigid-body dynamics of the airship. What effect does the hull stiffness of the airship have on the structure modes? Four hull stiffness variants, plus the baseline stiffness case, are compared. The bending stiffness of the envelope is scaled for the model variants by ±30% and ±50%, respectively. The model was trimmed in steady level flight at 9 m/s and sea level. Winds and faults are also considered as Scenario 2. The controller parameters are the same as Scenario 2 except for

$$\{\begin{array}{l}{c}_2=\mathrm{diag}(0.2, 0.2, 0.4),\beta =\mathrm{diag}(0.1, 0.1, 0.2), \mathrm{for} \mathrm{BNTSM}\\ c_1=c_2=\mathrm{diag}(2, 2, 2), \mathrm{for} \mathrm{BISMC}\end{array},$$

(53)

By using the BNTSM control design, the simulation results are shown in Figure 13, Figure 14, Figure 15 and Figure 16.

From Figure 13, it can be observed that the variable stiffness of the airship envelope has a small effect on the rigid-body attitude and the position motions. However, the stiffness variation has a great effect on the structure modes, as shown in Figure 14 and Figure 15, where it can be found that the bending mode responses of q_i will become a smaller and smaller amplitude of oscillation with the increasing stiffness. The general coordinate, q₁, for the first bending mode, is increased in amplitude by 30% for the −50% stiffness variant, and the general coordinate, q₁, reduced in amplitude by 8.3% for the +30% stiffness case. The same case happens for the generalized coordinate velocity responses. This demonstrates that stiffness can suppress structural mode oscillation. Figure 16 shows that the control inputs change little when the stiffness of the flexible airship is variable, where * denotes multiplication sign.

5. Conclusions

This paper proposes a nonlinear attitude tracking control approach for the flexible airship. A nonlinear backstepping nonsingular terminal sliding-mode control method is used to design the controller to track desired attitudes and stabilize structural modes of the flexible airship. Meanwhile, a wind observer is designed to estimate variable wind speeds. An adaptive fault estimator is designed to deal with nominal offset and loss of effectiveness faults of the control surfaces. Saturation compensator is designed to reduce effect of the actuator saturation. The stability analysis demonstrates that the closed-loop attitude tracking error dynamics are globally exponentially stable. Simulation results demonstrate that the BNTSM control designed for three scenarios of the flexible airship can achieve better attitude tracking performances by using the corresponding compensation controller, even though the airship is affected by unknown winds, control surface faults, and variable stiffness of the airship envelope. Therefore, the effectiveness and availability of the BNTSM control design are verified.

6. Future Recommendation

The future work is to expand the control strategy into a position control loop and velocity control loop for the flexible airship.