Sensitivity Analysis of Geometrical Parameters to the Flow of Pre-swirl System after Turbine Blade Fracture
Abstract
:1. Introduction
2. Computational Method
2.1. Computational Model
2.2. Computational Validation
2.3. Definition of Parameters
3. Results and Discussion
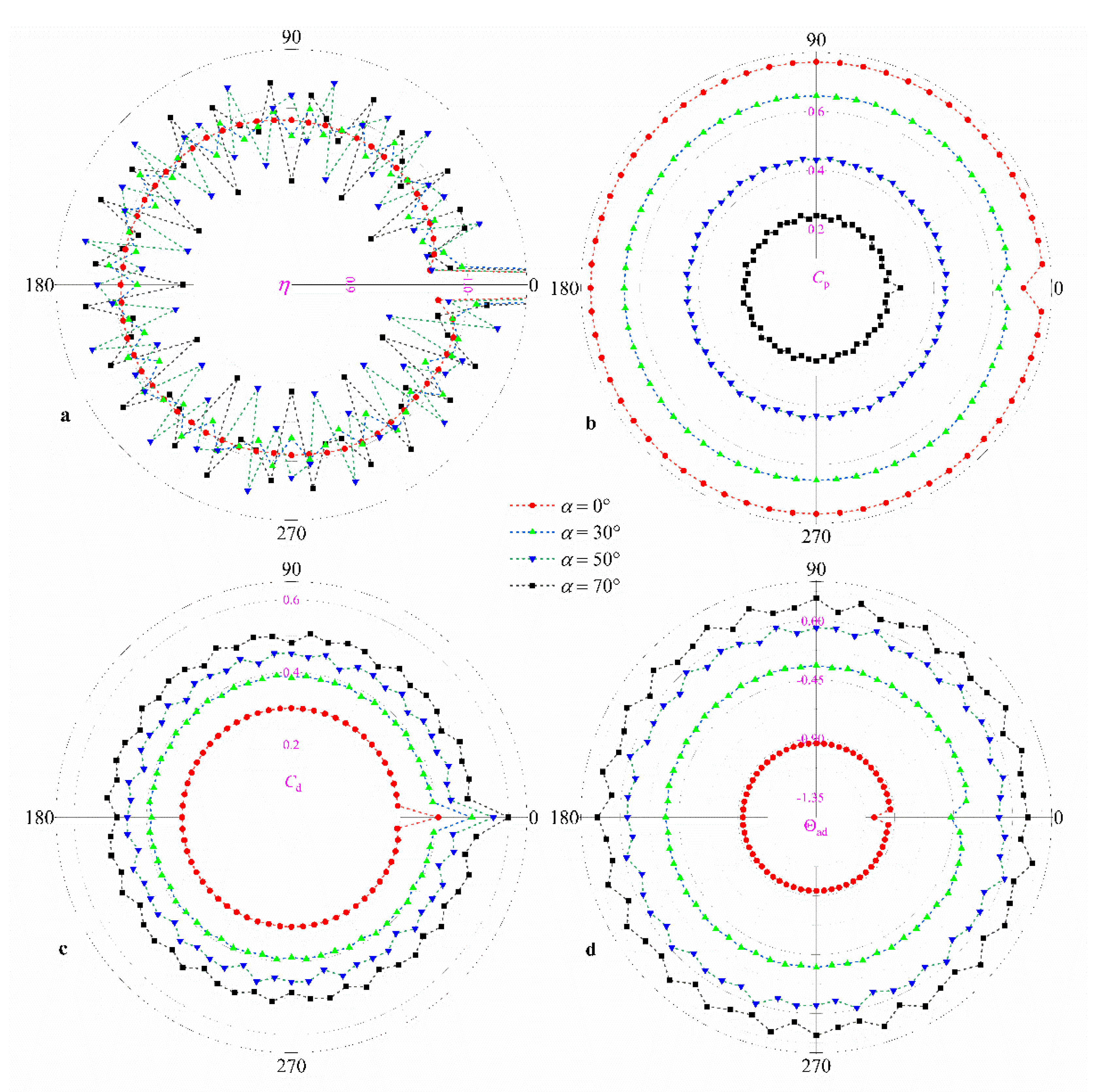
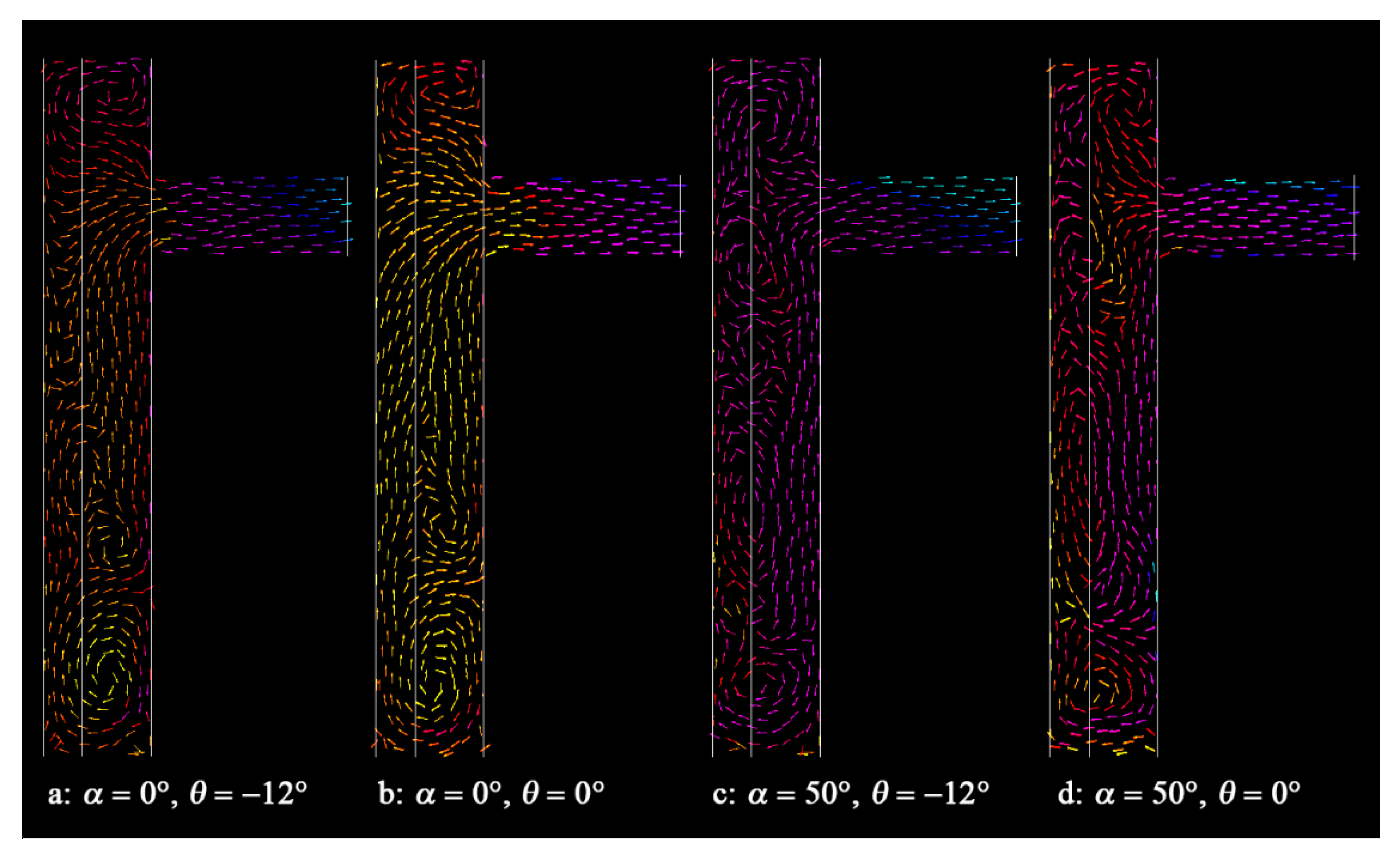
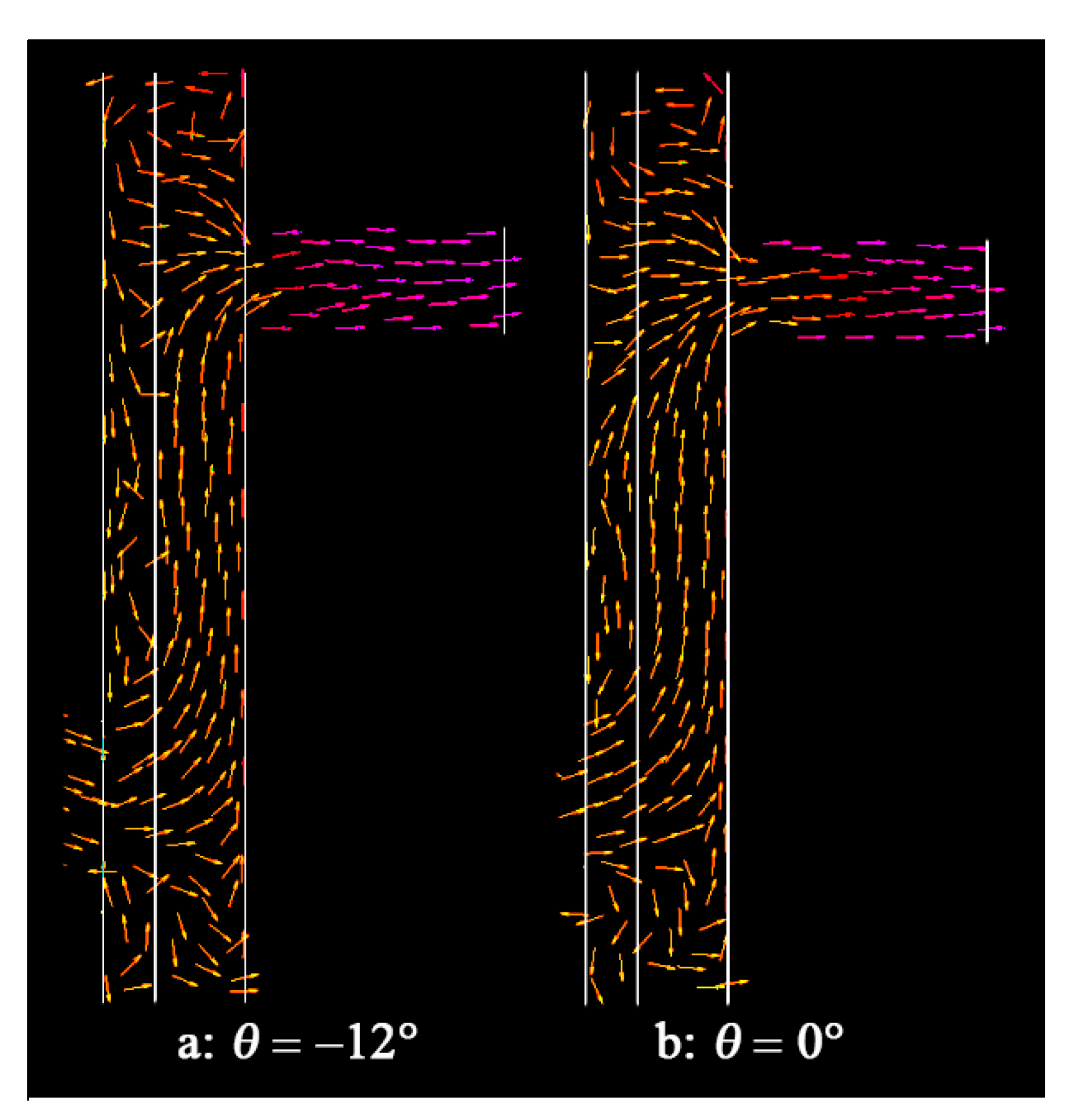
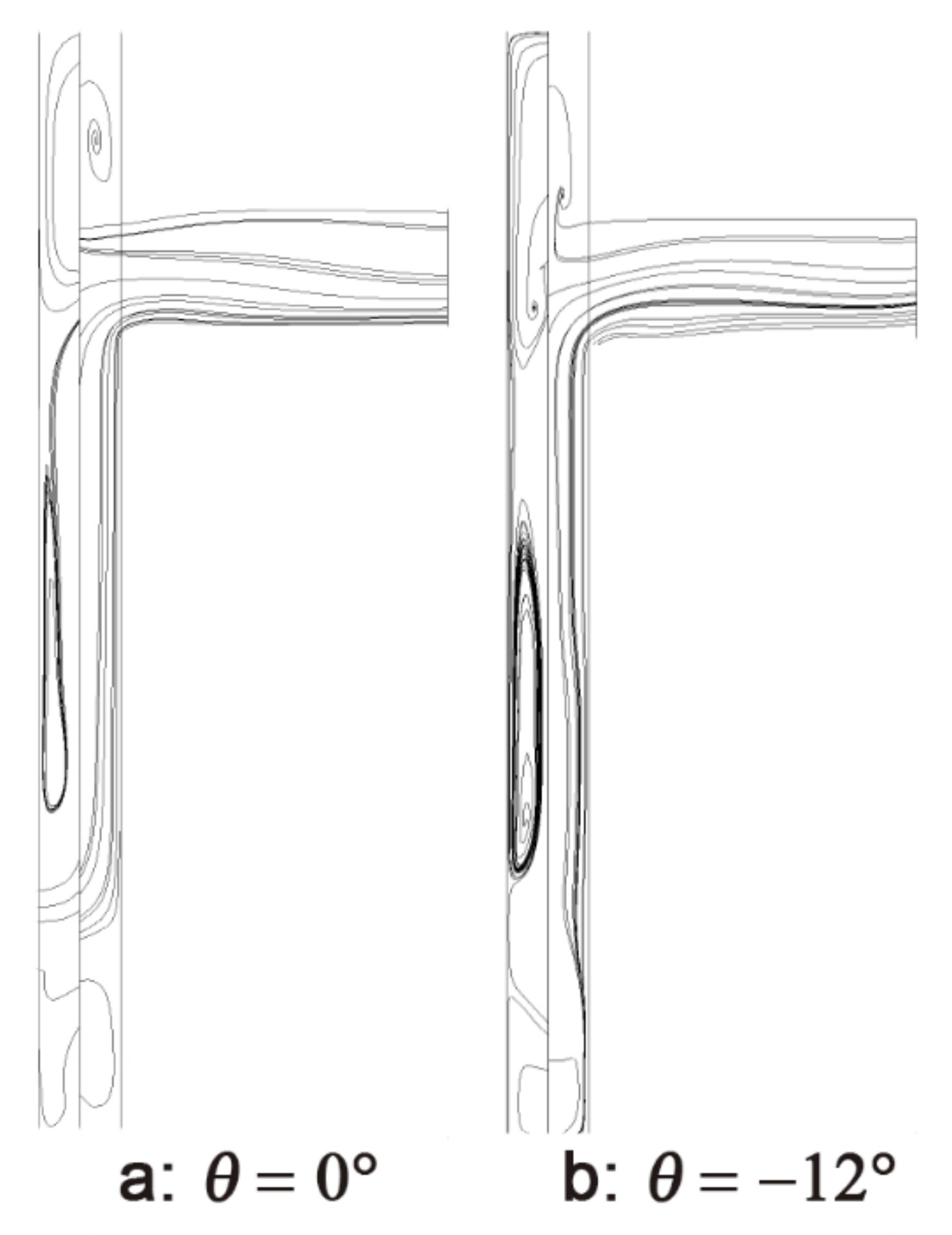
3.1. Influence of Pre-swirl Angle α
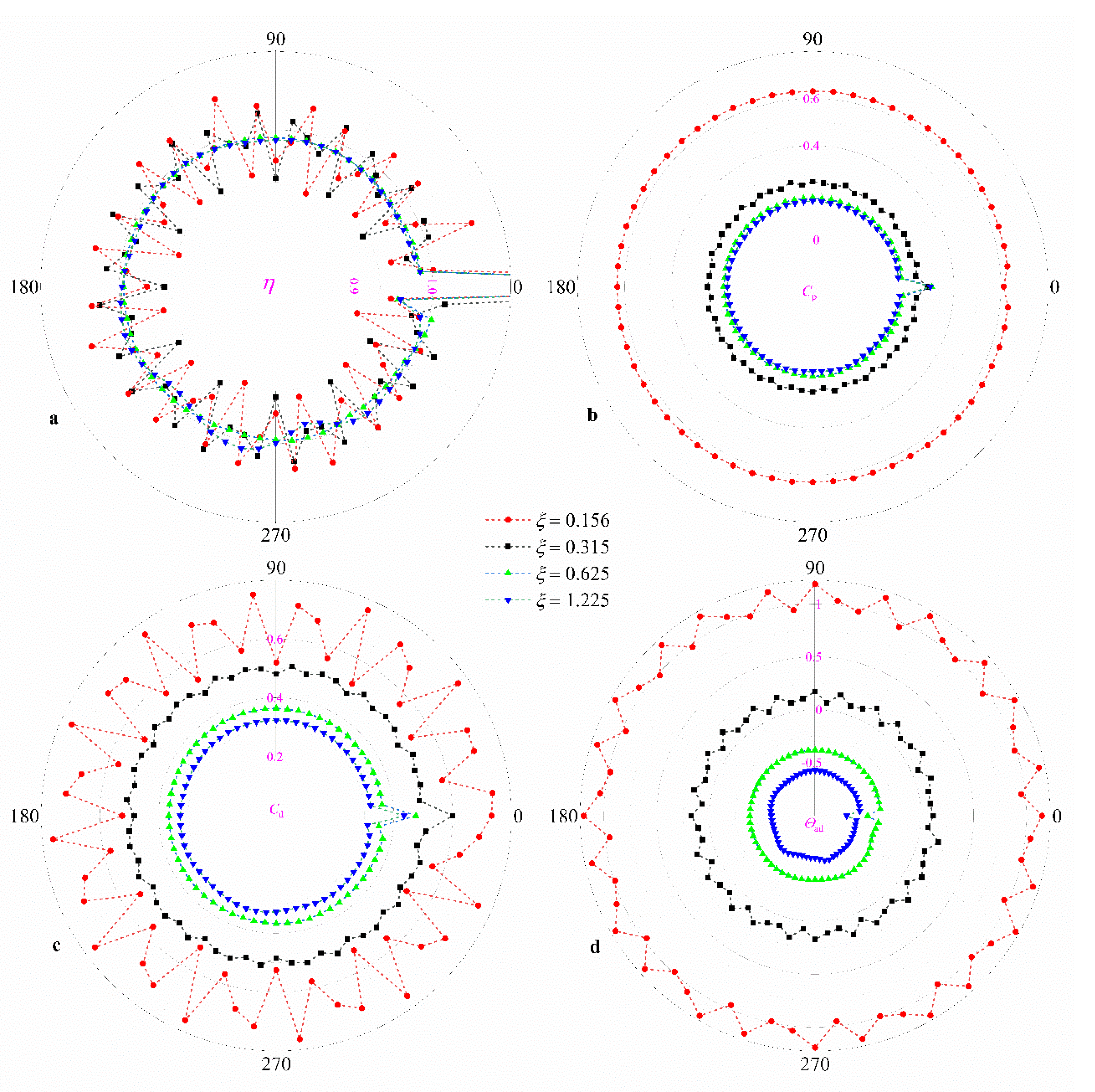
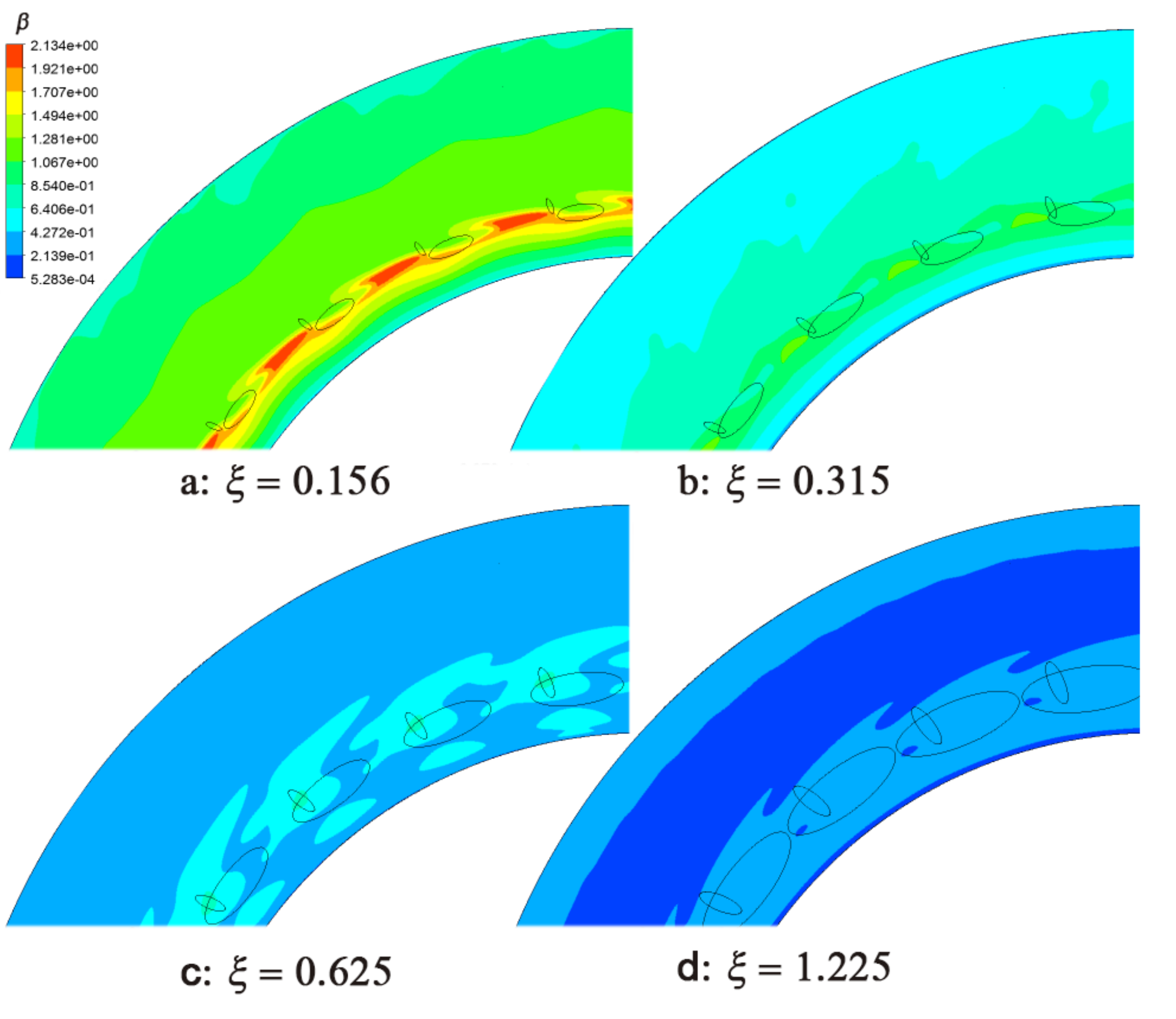
3.2. Influence of Area Ratio of Nozzles to Holes ξ
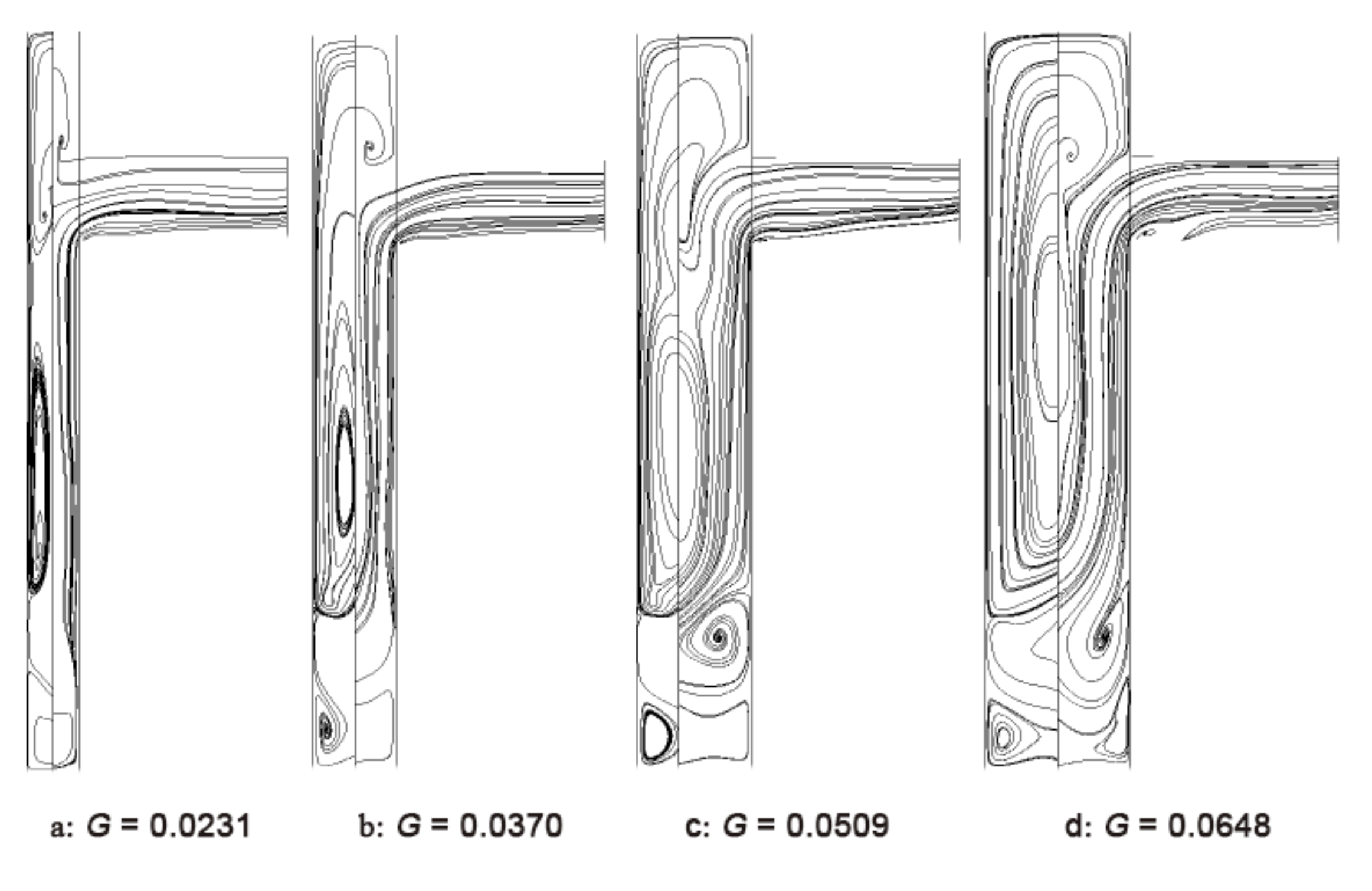
3.3. Influence of Gap Ratio G
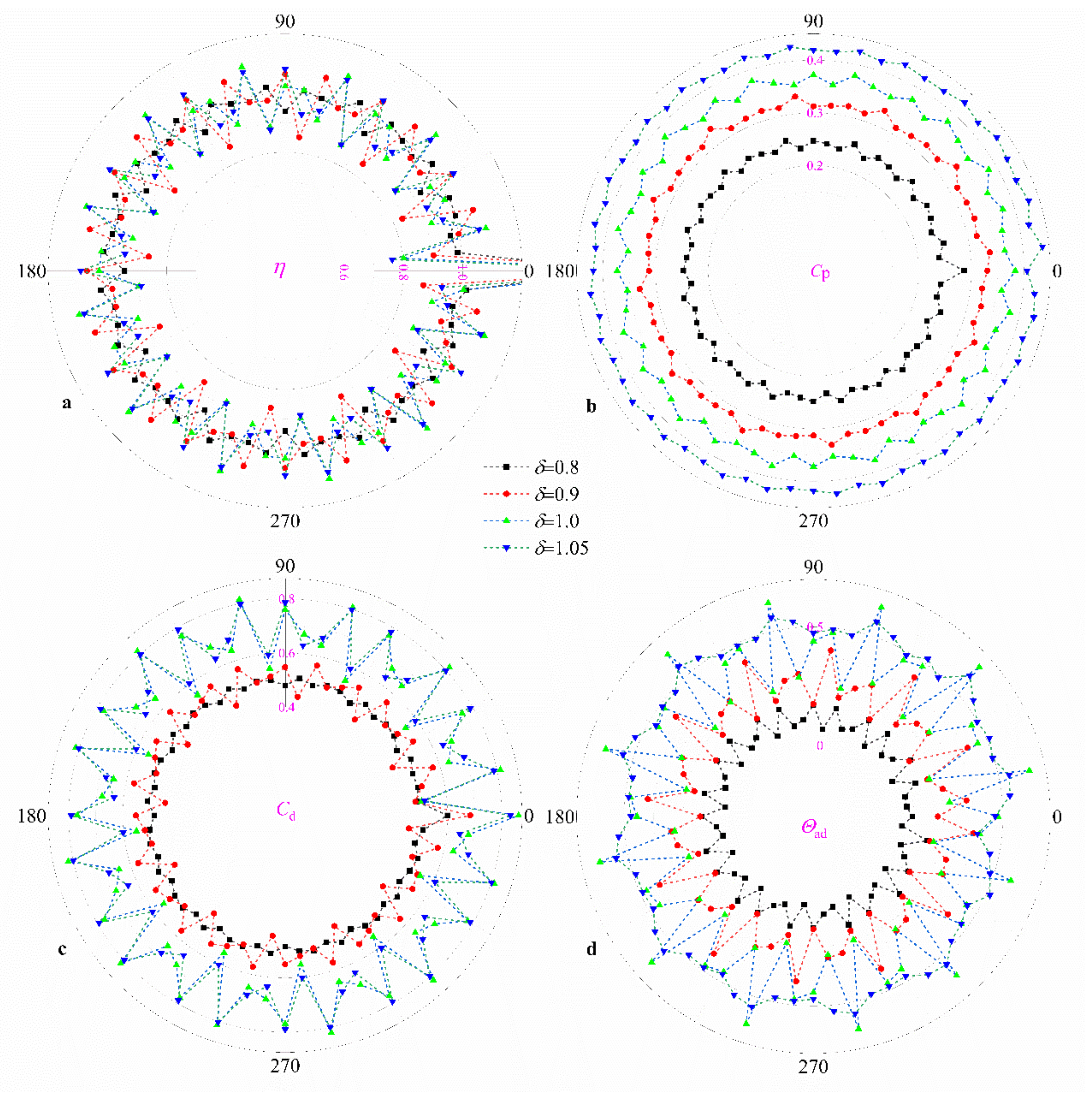
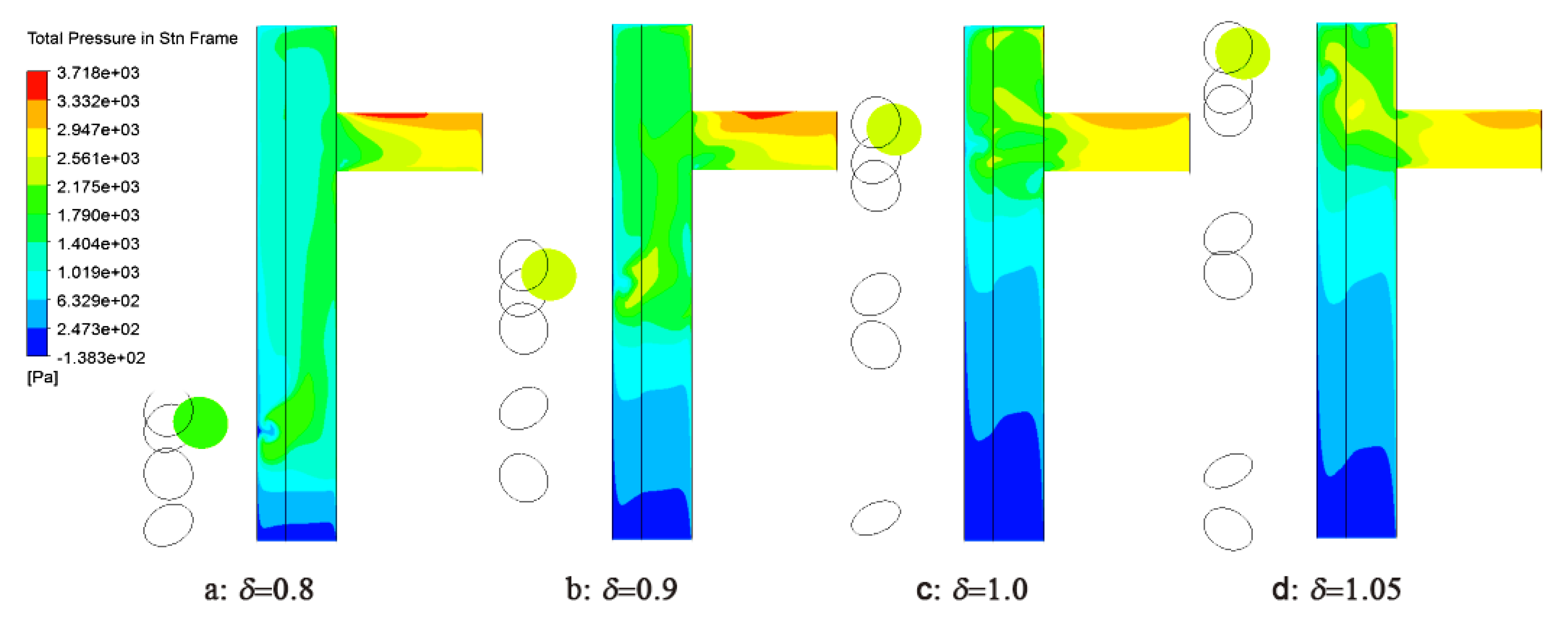
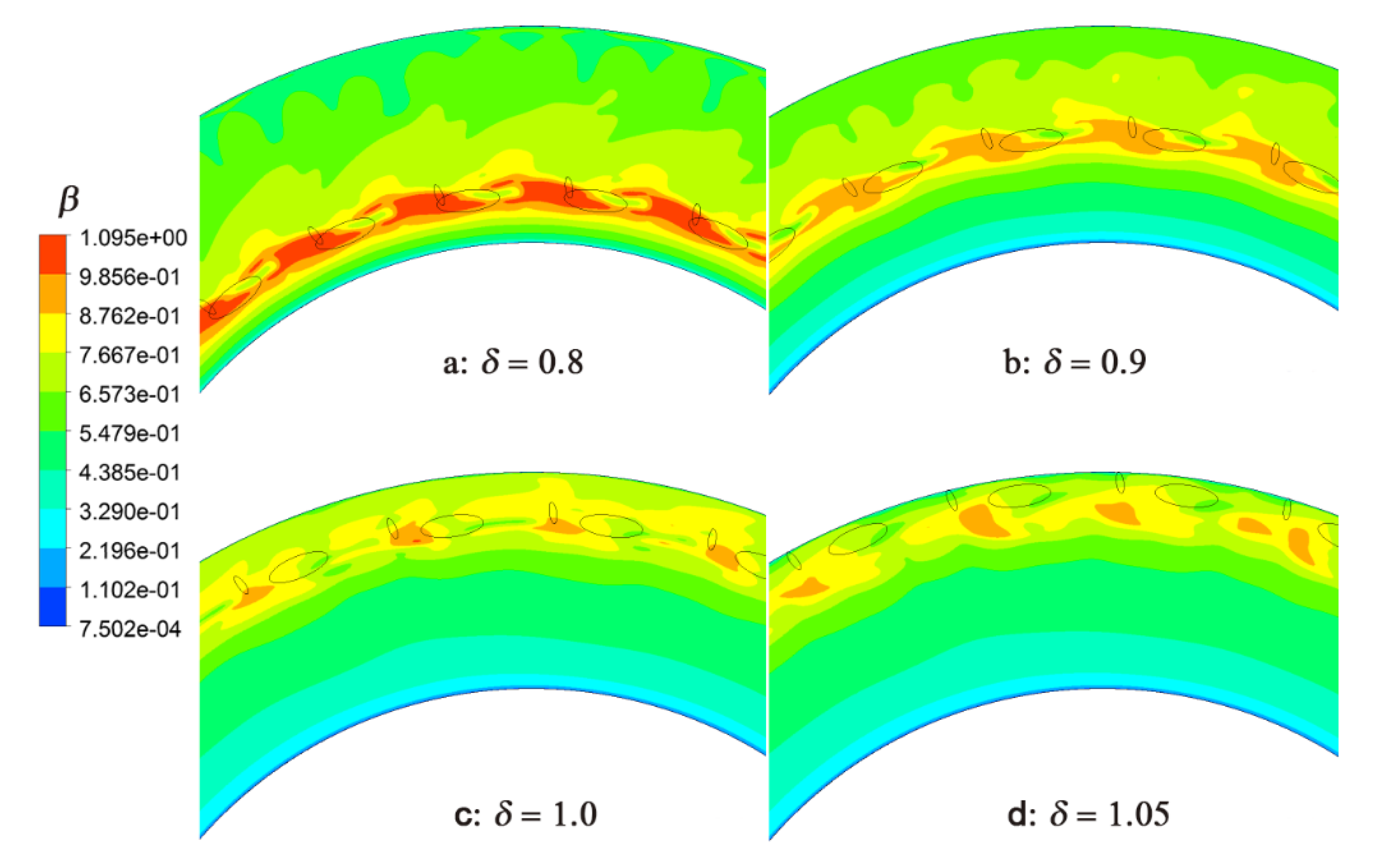
3.4. Influence of Radius Ratio of Nozzles to Holes δ
4. Conclusions
- (1)
- As far as the distribution of η, the η of hole_0 (hole_0 is the receiver hole that corresponds to the fractured blade), ηhole_0, will be larger than that of hole_i (i ≠ 0), ηhole_i. Furthermore, most of the geometric parameter changes do not increase ηhole_0. However, measures to increase the influence of the pre-swirl nozzles can reduce the influence of the blade fracture on mass flow distribution, such as larger α, smaller ξ, and larger δ.
- (2)
- As for Cp, Cd, and Θad, α and ξ have a greater impact on it. For example, the Cd of receiver holes far from hole_0 decreases by over 70% when α increases from 0° to 70°. Of course, similar to η, increasing the influence of the pre-swirl nozzles can reduce the difference of Cp, Cd, and Θad between receiver holes. Moreover, taking α for an example, the Cd,hole_0 is 34.7%, 27.7%, 24.5%, and 20.1% greater than the average of Cd,hole_i (i ≠ 0), when α is 0°, 30°, 50°, and 70°, respectively.
- (3)
- For the pre-swirl system, the structure that minimizes the change in cold-air conditions (it is better to include all four parameters) for different receiver holes when the turbine blades fracture is the best design. From this perspective, increasing the influence of the pre-swirl nozzle seems to be a better design, for example, by increasing α, or decreasing ξ. However, although increasing the effect of the nozzle serves the purpose, it increases the volatility of the flow. From the investigation of other researchers, the pre-swirl nozzle of the leaf grille type should be able to mitigate the fluctuation in the flow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Alphabet | |
| a | inlet radius, m |
| A | area, m2 |
| b | radius of rotor and stator, m |
| Cp | total-pressure-loss coefficient |
| Cd | discharge coefficient |
| Cw | dimensionless mass flow rate, mnozzle/μb |
| s | axial spacing between rotor and stator, m |
| T* | total temperature, K |
| E | Euler number, (P2-P1)/0.5ρΩ2b2 |
| G | gap ratio, s/b |
| m | mass flow rate, kg/s |
| N | number of nozzles or receiver holes |
| P | static pressure, Pa |
| P* | total pressure, Pa |
| r* | dimensionless radius, r/b |
| rh | radius of receiver hole, m |
| rp | radius of pre-swirl nozzle |
| z* | dimensionless axial location, z/a |
| Reφ | rotational Reynolds number, Ωb2/ν |
| Vr, Vφ | radial and tangential velocity, m/s |
| Greeks | |
| α | pre-swirl angle, degree |
| β | swirl ratio, Vφ/Ωr |
| βp | pre-swirl ratio, Vφ,nozzle,out/Ωrp |
| θ | axes of polar coordinates, degree |
| ξ | area ratio of nozzles and receiver holes, Anozzle/Ahole |
| δ | radial location ratio of nozzles and receiver holes, rp/ rh |
| η | mass-flow ratio, mhole_i/(mnozzle/Nhole) |
| Ω | rotating velocity of the rotor, rad/s |
| ν | kinematic viscosity, m2/s |
| ρ | density, kg/m3 |
| λT | turbulent flow parameter, Cw/ Reφ0.8 |
| Θad | adiabatic effectiveness |
| Subscript | |
| r, z, φ | radial, axial, and tangential coordinates |
| nozzle | pre-swirl nozzle |
| hole | receiver hole |
| stn | in the frame of static |
| rel | in the frame of relative |
| hole_i | receiver hole numbered i |
| p | pre-swirl nozzle |
| h | receiver hole |
References
- Lee, J.; Lee, H.; Kim, D.; Cho, J. The effect of rotating receiver hole shape on a gas turbine pre-swirl system. J. Mech. Sci. Technol. 2020, 34, 2179–2187. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.J.; Li, J. Numerical investigation of flow and heat transfer characteristics in radial pre-swirl system with different pre-swirl nozzle angles. Int. J. Heat Mass Tran. 2016, 95, 984–995. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.J.; Li, J. Numerical investigation on the flow and heat transfer characteristics in radial pre-swirl system with different fillet radius at the junction of inlet cavity and nozzle. Appl. Therm. Eng. 2016, 106, 1165–1175. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Liao, G.; Li, J. Computational fluid dynamics analysis for effect of length to diameter ratio of nozzles on performance of pre-swirl systems. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 381–392. [Google Scholar] [CrossRef]
- Zhao, G.; Ding, S.; Qiu, T.; Zhang, S. Numerical Investigation of the Effect of an Axial Pre-Swirl Nozzle With a Radial Angle in a Pre-Swirl Rotor-Stator System. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 7–11 June 2021; p. V05BT14A016. [Google Scholar]
- Lewis, P.; Wilson, M.; Lock, G.D.; Owen, J.M. Effect of radial location of nozzles on performance of preswirl systems: A computational and theoretical study. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 179–190. [Google Scholar] [CrossRef]
- Kakade, V.U.; Lock, G.D.; Wison, M.; Owen, J.M.; Mayhew, J.E. Effect of radial location of nozzles on heat transfer in preswirl cooling systems. J. Turbomach. 2011, 133, 1051–1060. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.; Kim, D.; Cho, J. Optimization of pre-swirl nozzle shape and radial location to increase discharge coefficient and temperature drop. J. Mech. Sci. Technol. 2019, 33, 4855–4866. [Google Scholar] [CrossRef]
- Kong, X.; Huang, T.; Liu, Y.; Chen, H.; Lu, H. Effects of pre-swirl radius on cooling performance of a rotor-stator pre-swirl system in gas turbine engines. Case Stud. Therm. Eng. 2022, 37, 102250. [Google Scholar] [CrossRef]
- Meher-Homji, C.B. Blading vibration and failures in gas turbines: Part A—Blading dynamics and the operating environment. In Proceedings of the ASME 1995 International Gas Turbine and Aeroengine Congress and Exposition, Houston, TX, USA, 5–8 June 1995; pp. 1–11. [Google Scholar]
- Australian Transport Safety Bureau, Power Plant Failures in Turbofan-Powered Aircraft 2008 to 2012; AR-2013-002; Australian Transport Safety Bureau: Canberra, Australia, 19 June 2014; pp. 1–34.
- Australian Transport Safety Bureau, Power Plant Failures in Turbofan-Powered Aircraft 2012 to 2016; Australian Transport Safety Bureau: Canberra, Australia, 2017.
- Federal Aviation Administration, Airworthiness Standards: AIRCRAFT Engines: 33.75 Safety Analysis; Federal Aviation Administration: Washington, DC, USA, 2009; Volume e-CFR 14 part 33.
- Bein, M.; Shavit, A.; Solan, A. Nonaxisymmetric flow in the narrow gap between a rotating and a stationary disk. J. Fluids Eng. 1976, 98, 217–223. [Google Scholar] [CrossRef]
- Bein, M.; Shavit, A. Nonaxisymmetric Flow in the Narrow Gap Between a Rotating and a Stationary Disk with an Eccentric Source. J. Fluid Eng. 1977, 99, 418–421. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Banerjee, S.; Gupta, C. Fully developed hydrodynamic and thermal transport in combined pressure and electrokinetically driven flow in a microchannel with asymmetric boundary conditions. Int. J. Heat Mass Tran. 2009, 52, 2145–2154. [Google Scholar] [CrossRef]
- Chan, Y.; Chen, G.; Tso, C. Effect of asymmetric boundary conditions on Couette–Poiseuille flow of power-law fluid. J. Thermophys. Heat Tr. 2015, 29, 496–503. [Google Scholar] [CrossRef]
- Zhao, G.; Qiu, T.; Liu, P. Influence of blade fracture on the flow of rotor-stator systems with centrifugal superposed flow. Aerospace 2022, 9, 106. [Google Scholar] [CrossRef]
- Owen, J.M.; Rogers, R.H. Flow and Heat Transfer in Rotating Disc Systems: Rotor-Stator Systems, 5th ed.; Research Studies Press Ltd., Ed.; Research Studies Press Ltd.: Somerset, UK, 1989; Volume 90, p. 278. [Google Scholar]
- Lock, G.D.; Yan, Y.Y.; Newton, P.J.; Wilson, M.; Owen, J.M. Heat transfer measurements using liquid crystals in a preswirl rotating-disk system. J. Eng. Gas Turbines. Power-Trans. Asme 2005, 127, 375–382. [Google Scholar] [CrossRef]
- Lock, G.D.; Wilson, M.; Owen, J.M. Influence of fluid dynamics on heat transfer in a preswirl rotating-disk system. J. Eng. Gas Turbines Power-Trans Asme 2005, 127, 791–797. [Google Scholar] [CrossRef]
- Kakade, V.U.; Lock, G.D.; Wilson, M.; Owen, J.M.; Mayhew, J.E. Accurate heat transfer measurements using thermochromic liquid crystal. Part 2: Application to a rotating disc. Int. J. Heat Fluid Flow 2009, 30, 950–959. [Google Scholar] [CrossRef]
- Yan, Y.; Gord, M.F.; Lock, G.D.; Wilson, M.; Owen, J.M. Fluid dynamics of a pre-swirl rotor-stator system. J. Turbomach. 2003, 125, 641–647. [Google Scholar] [CrossRef]
- Karnahl, J.; von Wolfersdorf, J.; Tham, K.M.; Wilson, M.; Lock, G. Computational fluid dynamics simulations of flow and heat transfer in a preswirl system: Influence of rotating-stationary domain interface. J. Eng. Gas Turbines Power-Trans. Asme 2012, 134, 052502. [Google Scholar] [CrossRef]
- Liao, G.; Wang, X.; Li, J. Numerical investigation of the pre-swirl rotor–stator system of the first stage in gas turbine. Appl. Therm. Eng. 2014, 73, 940–952. [Google Scholar] [CrossRef]
- Luo, X.; Han, G.; Wu, H.; Wang, L.; Xu, G. Experimental investigation of pressure loss and heat transfer in a rotor–stator cavity with two outlets. Int. J. Heat Mass Tran. 2014, 78, 311–320. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Wilson, M.; Owen, J.M. Numerical and theoretical study of flow and heat transfer in a pre-swirl rotor-stator system. In Proceedings of the ASME Turbo Expo 2005, Reno, NV, USA, 6–9 June 2005; pp. 943–949. [Google Scholar]

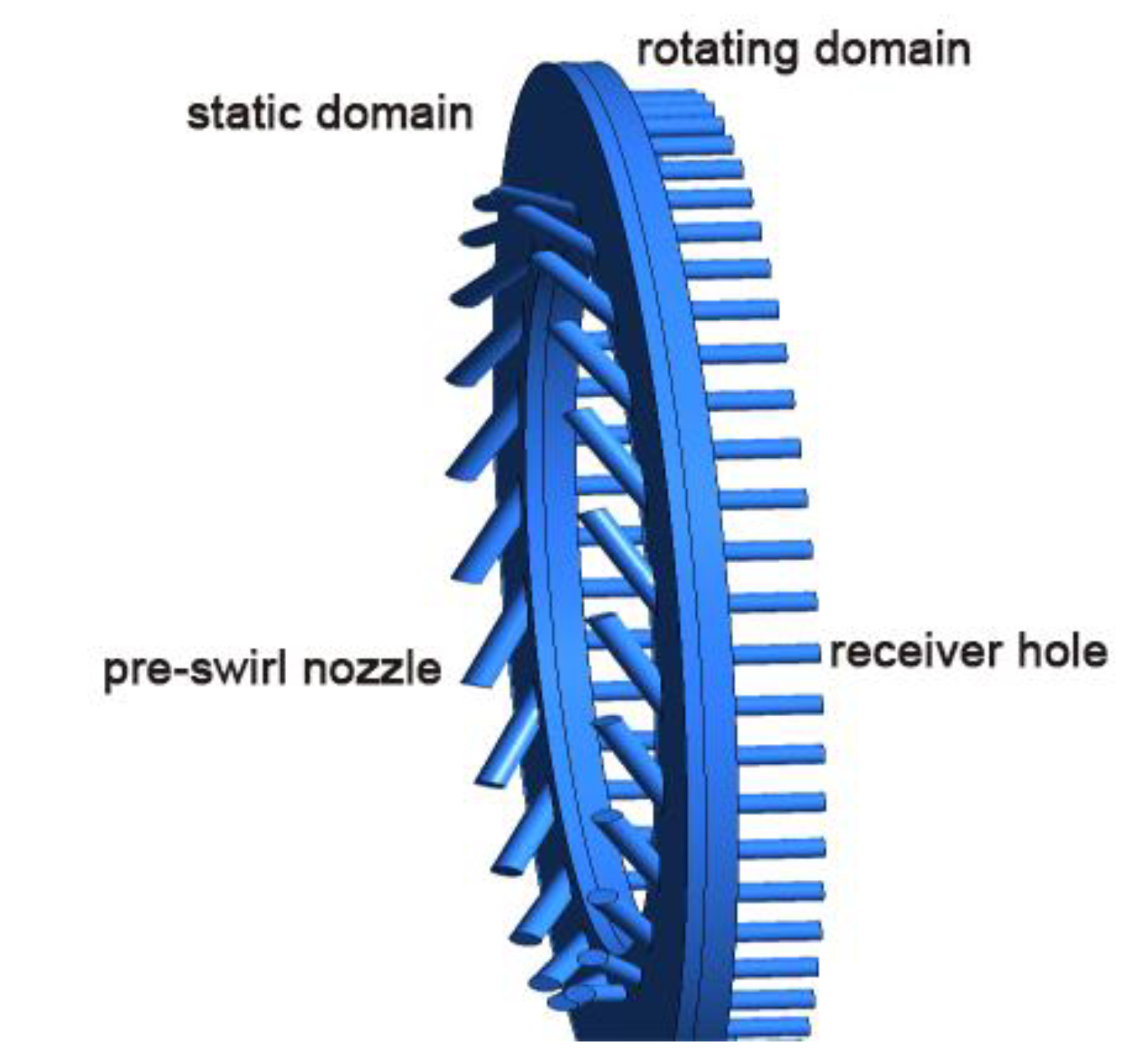


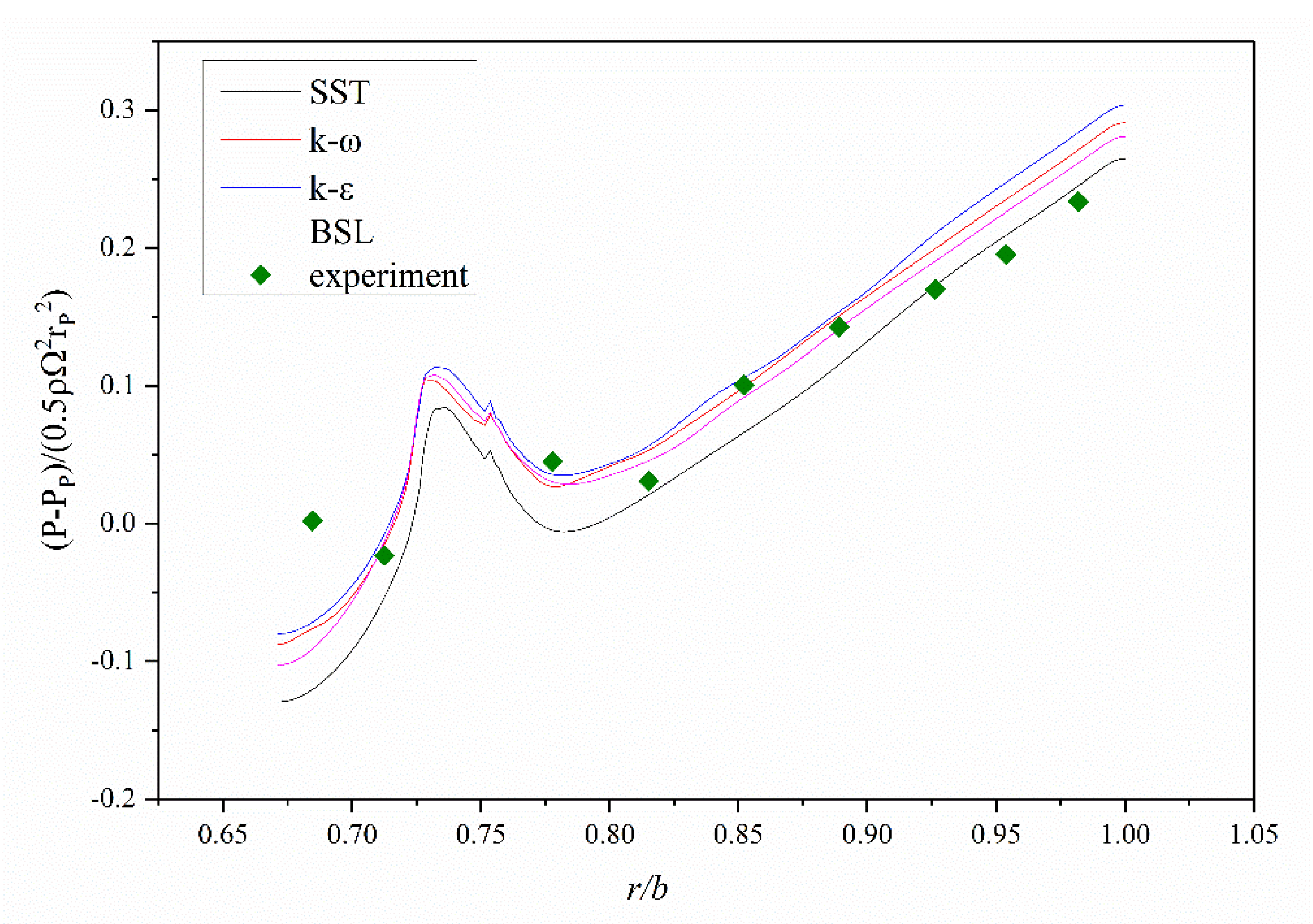
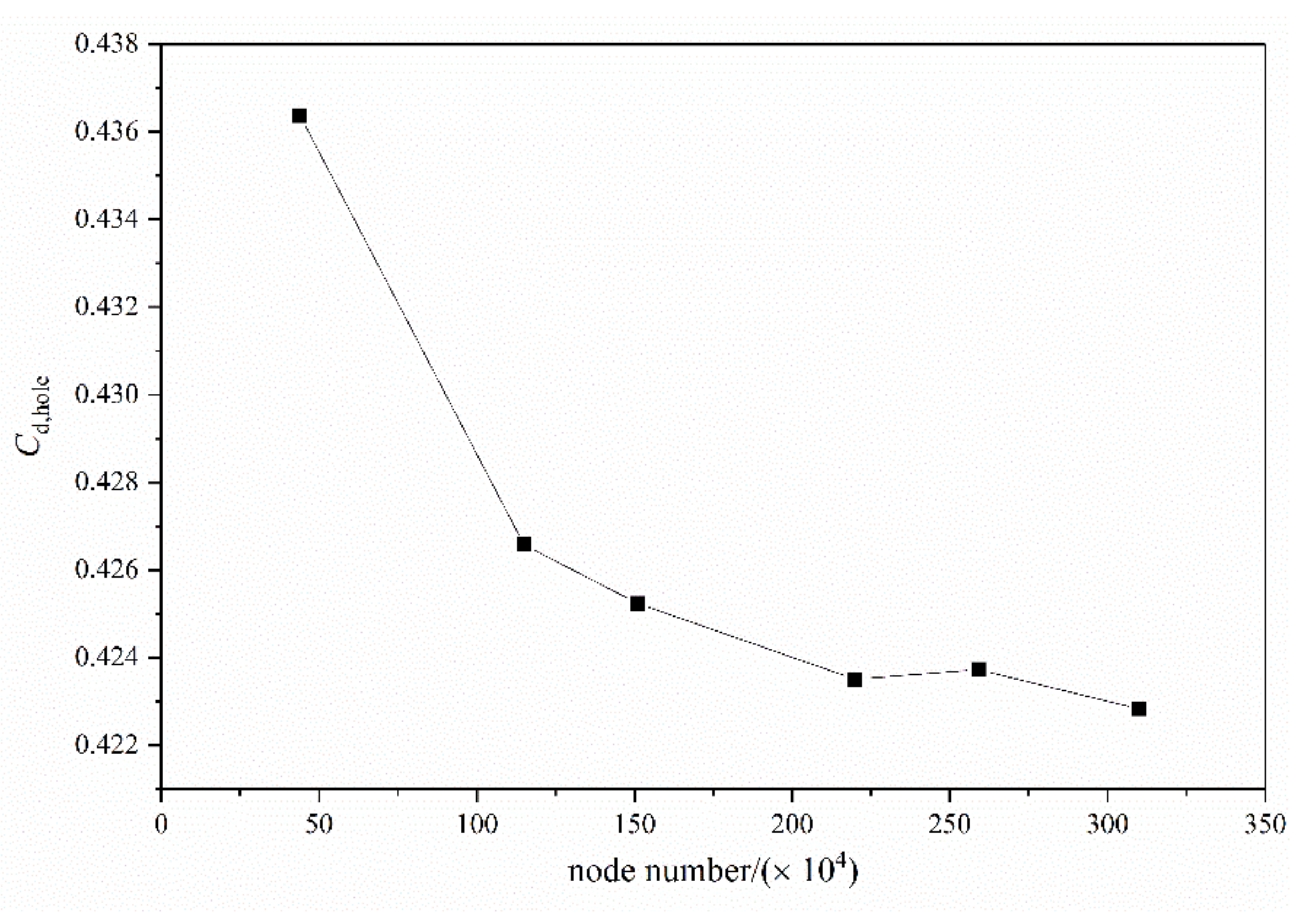
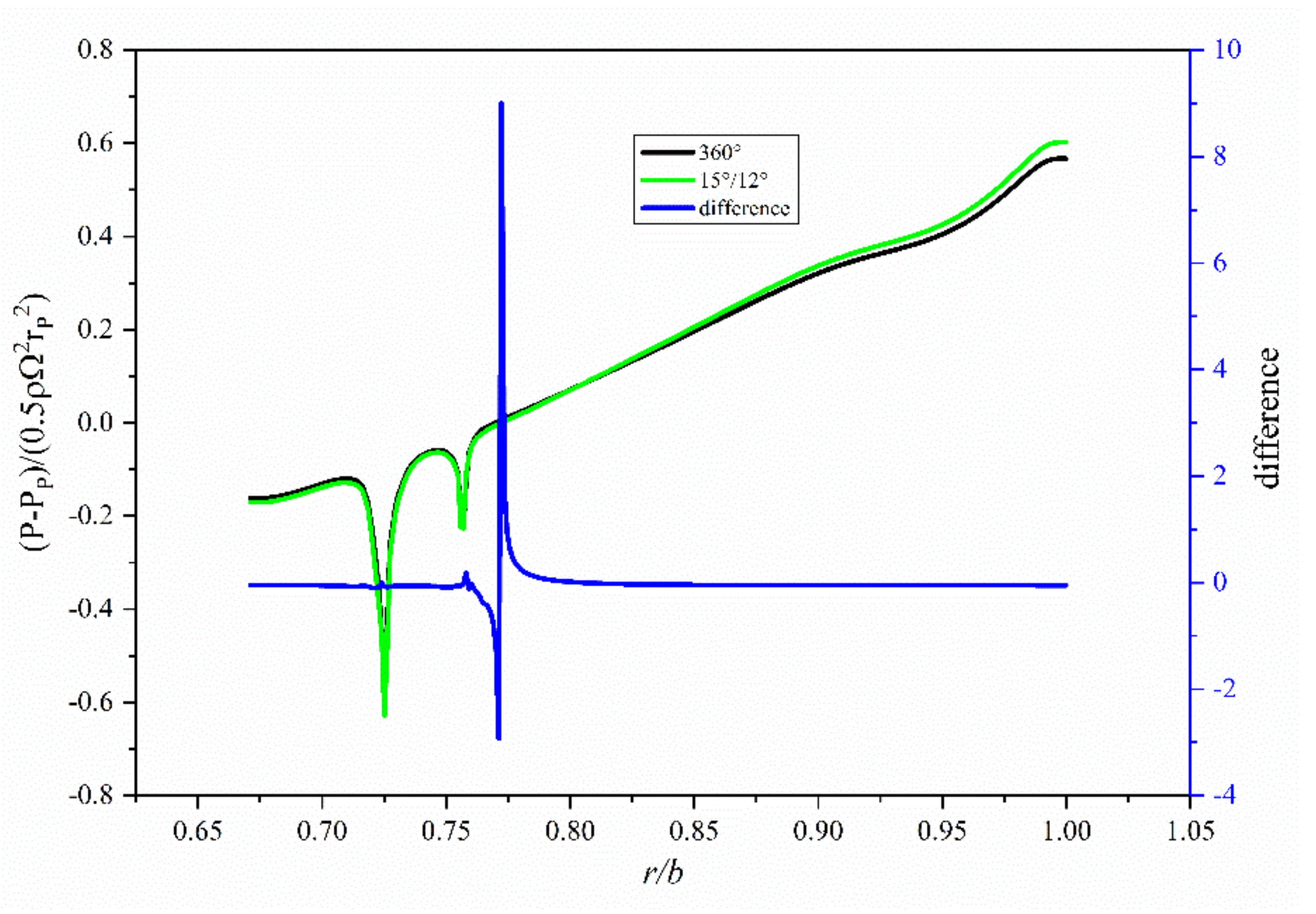






| Parameters | Values |
|---|---|
| Outer disk radius b | 0.216 m |
| Inner radius a | 0.145 m |
| Cavity width s | 0.011 m |
| Pre-swirl-nozzle radius, rp | 0.160 m |
| Sealing-slot width | 0.001 m |
| Receiver-hole radius, rh | 0.200 m |
| Receiver-hole diameter | 0.008 m |
| Nozzle diameter | 0.0071 m |
| Pre-swirl angle, α | 70° |
| Parameters | Values |
|---|---|
| Pre-swirl-nozzle angle, α | 0°~70° |
| The area ratio of nozzles and holes, ξ | 0.156~1.225 |
| Gap ratio, G | 0.0231~0.0648 |
| Radial location ratio of nozzles and holes, δ | 0.8~1.05 |
| Parameters | Values |
|---|---|
| Inlet total temperature, T*nozzle,in,stn | 65.06 °C |
| Inlet mass flow, mnozzle | 0.06 kg/s |
| Outlet static pressure of hole_0, Phole_0,out | −571 Pa |
| Outlet static pressure of hole_i (i ≠ 0), Phole_i,out | 0 Pa |
| Reference pressure | 101,325 Pa |
| Rotation speed, Ω | 350 rad/s |
| Cw | 13164 |
| Reω | 7.7 × 105 |
| λT | 0.26 |
| E [14,18] | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Qiu, T.; Liu, P. Sensitivity Analysis of Geometrical Parameters to the Flow of Pre-swirl System after Turbine Blade Fracture. Aerospace 2022, 9, 783. https://doi.org/10.3390/aerospace9120783
Zhao G, Qiu T, Liu P. Sensitivity Analysis of Geometrical Parameters to the Flow of Pre-swirl System after Turbine Blade Fracture. Aerospace. 2022; 9(12):783. https://doi.org/10.3390/aerospace9120783
Chicago/Turabian StyleZhao, Gang, Tian Qiu, and Peng Liu. 2022. "Sensitivity Analysis of Geometrical Parameters to the Flow of Pre-swirl System after Turbine Blade Fracture" Aerospace 9, no. 12: 783. https://doi.org/10.3390/aerospace9120783
APA StyleZhao, G., Qiu, T., & Liu, P. (2022). Sensitivity Analysis of Geometrical Parameters to the Flow of Pre-swirl System after Turbine Blade Fracture. Aerospace, 9(12), 783. https://doi.org/10.3390/aerospace9120783







