Abstract
The aim of the presented study is to optimize the different classes of high-temperature superconducting (HTS) DC cables for improving their performances in a cryo-electric aircraft considering their weight, peak temperature during faults, and the ratio of current passing through each tape to the critical current of HTS tapes. These terms were interpreted into three objective functions, and a multi-objective optimization algorithm known as non-dominated sorting genetic algorithm II was used to find the optimal solution clusters. The cable optimization was conducted for different former materials by changing the former thickness and radius. Results showed that the DC HTS cables with aluminum former have the lowest weight while cables with copper formers have the best thermal performance against faults.
1. Introduction
The aviation sector is responsible for emitting around 2% to 6% of total greenhouse gases into the Earth’s atmosphere, annually [1]. Although in recent years, outstanding improvements have been attained to increase the efficiency of aircraft engines, due to the large and growing number of flights, the ratio of emitted greenhouse gases by aircraft is still increasing [2]. According to FlightPath 2050, the amount of CO2 and NOx in new aircraft units must be reduced by 75% and 80% by 2050 compared to the 2000 baseline [3]. Among the proposed solutions, electrification seems to be one of the most promising solutions. Electric machines along with electrified drivetrains are capable of increasing the efficiency and power density of propulsion systems with almost zero greenhouse gases depending on the scenario. Although electrification provides multiple benefits, the low power density of conventional electric devices is still a real challenge that must be dealt with [4]. To address it, high-temperature superconducting (HTS) devices could be used in a combination with cryogenic fluids, especially hydrogen [5]. This will lead to the concept of cryo-electric aircraft. HTS devices such as machines [6], cables [7,8], busbars, and superconducting fault current limiters [9] are the main components of aircraft propulsion and power systems while cryogenic fluids are used to dissipate any heat load imposed on superconducting devices [10,11].
As shown in Figure 1, HTS cables can be used to transmit and distribute power to electrical loads such as electrical motors in propulsion systems. Although HTS cables can principally operate both in alternative current (AC) and direct current (DC) regimes, due to some considerations related to higher AC loss and heat loads in the AC regime, DC cables seem to be the better choices for the power system of cryo-electric aircraft. DC HTS cables should be optimized so that they have the lowest possible weight while their performance against fault events is improved. Such a multi-objective optimization problem is complicated and difficult to deal with by using conventional mathematical formulas. Thus, artificial intelligence (AI) techniques could be used to find the optimum solution [12,13,14].
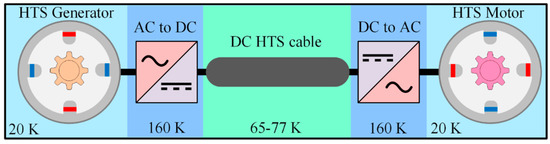
Figure 1.
The structure of HTS devices in a cryo-electric aircraft, cooled down to cryogenic temperatures.
In this paper, a non-dominated sorting genetic algorithm II (NSGA II) is used to optimally design multiple DC HTS cables with respect to weight and fault performance considerations for a cryo-electric aircraft. For this purpose, three objective functions are considered, namely minimization of total cable weight, minimization of peak temperature of the superconducting layer during faults, and optimization of the ratio of current passing through each HTS tape to the critical current of the tape. In addition, four materials were selected to analyze their impact on the structure and the geometrical design of a DC HTS cable with respect to fault conditions, specialized for cryo-electric aircraft.
2. Modelling Procedure
If one considers Figure 2 as the equivalent circuit model of a single-layer DC HTS cable consisting of a former and as the number of yttrium barium copper oxide (YBCO) HTS tapes, the current sharing between these two layers is calculated based on Equations (1) and (2):
where is the current passing through superconducting tapes, is the current passing through the former layer, is the total current entering the DC HTS cable, is the temperature-dependent resistance of the former layer, and is the current-dependent resistance of superconducting tapes.
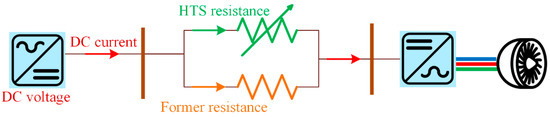
Figure 2.
The equivalent circuit model of a DC HTS cable used in cryo-aircraft to deliver the required power by the propellers.
To calculate the current-dependent resistance of superconducting tapes, Equation (3) is adapted based on [13], and to calculate the temperature-dependent resistance of the former, Equation (4) could be applied:
where is the critical electrical field, is the index value of YBCO HTS tape, is the temperature-dependent critical current, is the cable length, is the operational temperature, and is the coefficient of temperature-dependency of metallic former resistance [15].
By passing the calculated currents through superconducting layers and the former layer, heat is generated as a consequence of Joule heating, which causes a temperature violation of the operational temperature. The generated heat could be calculated by Equation (5) [16]:
where is generated heat under different temperatures and currents, and is critical temperature.
Part of the generated heat is transferred to the cryogenic coolant fluid of the DC HTS cable, in the form of convection, which is calculated in this paper based on Equation (6) [17]:
where is the heat transfer coefficient in , is the total cross-section of the HTS cable in , and is the coolant fluid bulk temperature in [17].
By obtaining the values of Equations (5) and (6), the temperature can be calculated according to Equations (7) and (8) [18]:
where is the density of understudied material (former or HTS tapes) in , is time in , is the specific heat capacity of understudied material in , and stands for time sample interval. It should be mentioned that the term of must be expressed in .
Finally, the critical current variations caused by temperature changes can be calculated by Equation (9) [19]:
where, is the reference critical current at operational temperature and self-field.
3. Multi-Objective: NSGA II
Non-dominated genetic algorithm II is one of the fastest sorting algorithms that have been used to deal with multi-objective optimization problems. This algorithm was firstly introduced in 2000 by K. Deb et al. at the “International Conference on Parallel Problem Solving from Nature” [20].
A multi-objective optimization problem consists of decision variables, fitness functions, and a set of in-equality and equality constraints, as defined in Equations (10) to (13) [21]:
Usually, the solution to this problem is not a single and exclusive solution, so it is presented as a set of possible and efficient solutions, known as the Pareto front or Pareto frontier. NSGA II follows four main principles to offer the optimum Pareto front, as shown in Figure 3, namely non-dominated sorting, elite preserving operator, crowding distance, and selection operator [21].
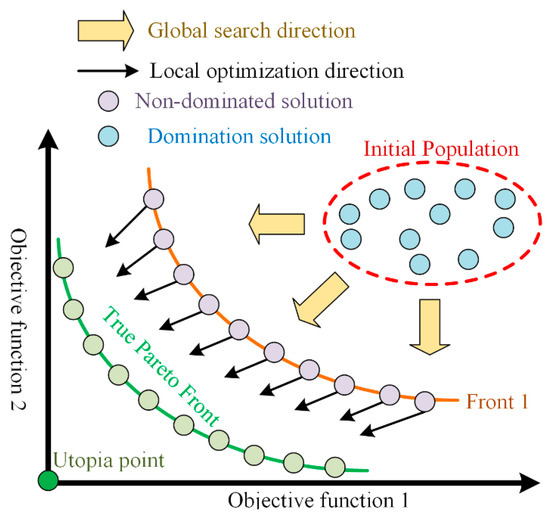
Figure 3.
A schematic of how the Pareto front results in the optimal solution of two objective functions.
Firstly, the NSGA II randomly generates a set of non-dominated population with the desired size and computes the objective functions for each individual. Then, by using the non-dominated sorting method, individuals are sorted into the different non-domination levels, and after that, by application of the crowding distance method, the individuals that have the same level are sorted. Crossover is conducted in this level by means of the arithmetic crossover function that hands us two offspring from two parents, as shown in Equations (14) and (15) [22]:
where, and are parent one and two, and are offspring one and two, is a random number, and is the crossover fraction. Then, to preserve the diversity in the population, a Gaussian mutation is applied to the individual set, as defined in Equation (16) [22]:
where is a random number, is the standard deviation of a random number, is a scalar number that reduces the ratio of mutation, is the current number of individuals, is the maximum allowable number of individuals, and and are the upper bound and lower bound of the main optimization problem.
At the last step, individuals must be selected for next generation, based on a binary tournament selection method that is shown in Equation (17) [22]:
where is the crowding distance of the individual, is the number of fitness functions, and is the fitness function. The program goes on until the stoppage conditions are met to terminate the program.
4. Results and Discussions
4.1. Objective Function for the DC HTS Cable
An optimization procedure is conducted to optimally design the structure and fault performance of a DC HTS cable based on the following fitness function, shown in Equations (18)–(24):
where is the former weight, is the superconducting layer weight, is the former volume, is the former density, is the cable length, is the outer radius of the former, is the inner radius of the former, is the number of HTS tapes, is the density of each layer of HTS tape, is the volume of each sub-layer of HTS tape, is the number of considered sub-layers, is the width of HTS tapes, is the thickness of tape sub-layers, is the peak temperature of YBCO tapes, is the current passing through each tape, and is the temperature-dependent critical current of the HTS tape. To solve this multi-objective function, the parameters of the NSGA II algorithm are considered as tabulated in Table 1.

Table 1.
Values for controlling parameters of NSGA II.
4.2. Cable and Test System Specifications
Three HTS cables were considered in this study, known as cable A, cable B, and cable C. The first cable is designed to carry 560 A current and 2.25 MW power in the drivetrain of electric aircraft. Then, to increase the power density of the cable, its current was increased to 2 kA while using the same HTS tape of cable A. Due to the low critical current of YBCO HTS tapes in cable B, three layers are needed to carry 2 kA/9 MW, which results in a weight increase in the cable and power density reduction. To solve this issue, the HTS tape was changed to another type of YBCO tape that has a higher critical current at 65 K. Table 2 shows the properties of the three DC HTS cables discussed and analyzed in this paper. For these cables, the critical temperature is considered to be 92 K, the heat transfer coefficient () is considered to be 2000 , and the fluid bulk temperature (K) is considered as 65 K. Table 3 lists the specifications of the two different YBCO tapes used in DC cable analysis according to [23,24]. Former material must have a low resistivity, low density, high cryogenic stability, and high specific heat capacity. Based on these requirements, four different candidates were chosen also for our study and are shown in Table 4 based on their different properties.

Table 2.
The specifications of the understudied DC HTS cables.

Table 3.
The specification of YBCO superconducting tapes used in the understudied DC HTS cables.

Table 4.
Properties of metallic materials that are used as former for the understudied DC HTS cables.
To analyze the behavior of understudied DC HTS cables, the test grid shown in Figure 4 was put to work. This figure represents the characteristics of fault current in the DC grid of a cryo-electric aircraft. The current waveform injected into the DC HTS cable by this grid is shown in Figure 5. As can be seen, after 10 ms, the current increases to charge the capacitor Cf and when it is discharged, the current gets back to its operational state.
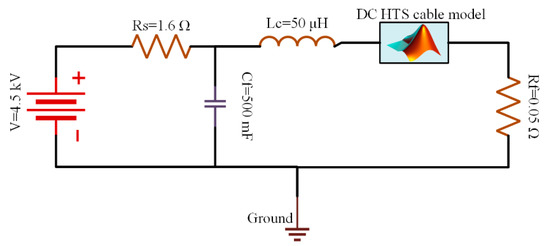
Figure 4.
The test grid used for characterizing the understudied DC HTS cables.
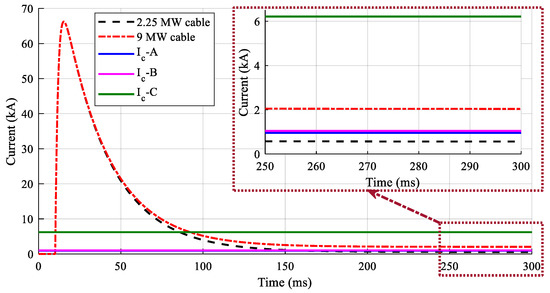
Figure 5.
The fault and operational currents passing through the DC HTS cables.
4.3. Multi-Objective Optimization Results
Figure 6a shows the Pareto front related to cable A with a 0.56 kA nominal current. According to this figure, the weight range of DC cable with copper former is from 110 kg to around 300 kg, the same as brass and stainless steel formers, which is due to the fact that they have a density value very similar to each other. On the other hand, DC cable with aluminum former has a range of 60 kg to 150 kg, which is a result of the low density of aluminum, around 2700 kg/m3. Thus, for cable A, aluminum is selected as the lightest former while copper has a better performance when one considers the peak temperature of the superconducting layer as the objective function. Also, if we consider the third objective function, it can be seen that F3 has values ranging from 0.2 to 0.5 that lie in an acceptable range. Figure 6b illustrates the Pareto front of multi-objective optimization for cable B. This cable consists of three superconducting layers, two dielectric layers, and one former layer. In order to have a sufficient number of SC1 tapes in one HTS layer for carrying 2000 A rated current, the former must have a radius of around 40 mm, which makes just the weight of the former around 220 kg. The weight of HTS tapes and dielectrics must be added to this value, which results in an extremely heavy HTS cable that could not fit into an electric aircraft. Thus, by adding the new layers to cable B, its weight range has increased in comparison to cable A, while the delivered power by cable B has also increased by 300%. The important factor here is the value of the third objective function that in some cases increased to 0.9, which could jeopardize the safe operation of DC HTS cable and cause hot spots and quench. Finally, Figure 6c shows the results of optimization on cable C, which has a 2000 A current, one superconducting layer, one dielectric layer, and one former. The number of superconducting and dielectric layers has been reduced by changing the superconducting tape to SC2. It should be noted that the presented values of weight are related to the summation of the weight of former, HTS tapes, and dielectrics.
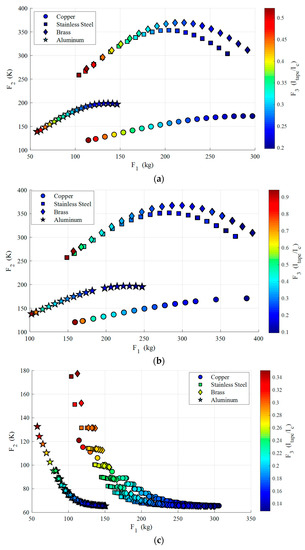
Figure 6.
Pareto front of NSGA II optimization for different former materials of understudied DC HTS cables: (a) cable A, (b) cable B, (c) cable C.
4.4. Thermoelectric Characteristic of Optimized Cable
In this section, after selecting the optimum structure for the understudied DC HTS cables among the results offered by the Pareto front, the electrothermal characteristic of DC HTS cable is evaluated. For this purpose, Table 5 tabulates the selected design for DC HTS cable A with different former materials. It can be seen that the lightest cable is the one with aluminum former, which has 49% lower weight than one with copper former, 44% lower than one with stainless steel former, and 48% lower than cable with brass former. Meanwhile, cable with copper former has a temperature of 14%, 52%, and 54% lower than cable with aluminum, stainless steel, and brass formers, respectively. This shows that copper has the best thermal performance among all former materials, which is due to its lower resistivity, which generates a lower heat load, and also the acceptable heat capacity of copper. So, for further analyses, the cable with copper former is selected as the cable with the best performance against faults while the cable with aluminum former is selected as the lightest DC HTS cable A. Table 5 shares the information on the structure of the selected former for DC cable B resulting from NSGA II optimization. Although the former radius and thickness remained approximately similar to cable A, the weight of the optimized structure has been increased. This increase resulted from adding extra superconducting and dielectric layers to the cable. So, in the optimized structure of cable B, the weight of the cable with copper former has increased by 38% while its temperature has only been reduced by 4%. These changes are also valid for other former materials in cable B, compared to cable A. Finally, by changing the type of superconducting tape into one with a higher critical current, i.e., SC2, both the weight and size of DC cable, i.e., Cable C, have been reduced, as shown in Table 5.

Table 5.
The results of applying multi-objective optimization algorithms for designing a light, fault-tolerable, and reliable DC HTS cable in cryo-electric aircraft—Cable A.
Now the thermal characteristic of all three cables must be evaluated to show how HTS cables would perform against a fault in the drivetrain of electric aircraft. This is conducted by considering two optimum scenarios, one with the lowest weight and the other with the lowest temperature during faults. Figure 7 depicts the temperature characteristic of HTS tapes in each of the understudied cables. Due to the lower critical current of HTS tapes in cable A, the peak temperature in this cable is higher than in the other two cables, with both copper and aluminum formers.
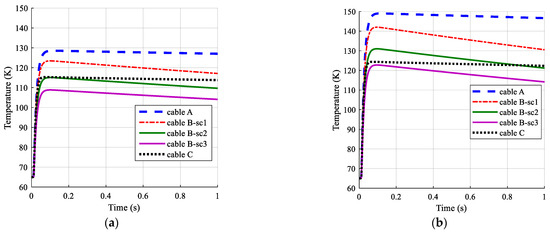
Figure 7.
Temperature of the superconducting layer in each of three HTS cables, (a) copper former, (b) aluminum former.
The temperature of copper and aluminum formers are shown in Figure 8 for all three cables. Due to the higher thermal mass of former layers, the temperature in this layer increases at a slower rate in comparison to HTS tapes. As seen in Figure 8, the peak temperature of former in cable C is lower than the peak temperature of formers in cables A and B. This is due to the fact that in cable C, the critical current is higher than the critical current in the other two cables. As a result of this, HTS tapes transit to a normal state at a later time (which can be considered as a kind of a slower transition) and thus, less fault current passes through the former of cable C. Consequently, the Joule loss generated in the former layer of cable C is lower than Joule losses in cables A and B, and this results in lower peak temperature of the former in cable C.
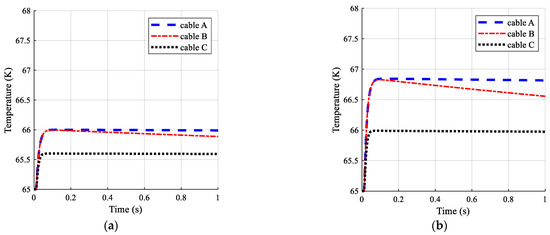
Figure 8.
Temperature of the former layer in each of three HTS cables, (a) copper former, (b) aluminum former.
Finally, the temperature profile of dielectric layers is shown in Figure 9a,b for copper and aluminum former cables, respectively. The different temperature profile in dielectric layers of the second DC HTS cable is a result of a lower heat accumulation ratio in these layers, compared to cable A and cable C.
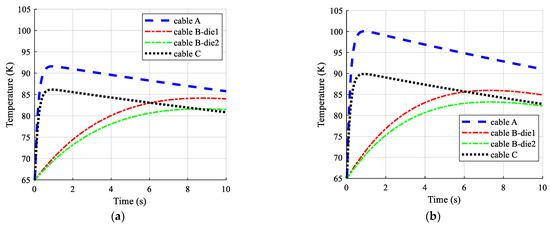
Figure 9.
Temperature of the dielectric layer in each of the three HTS cables, (a) copper former, (b) aluminum former.
By knowing these temperature profiles, one can evaluate the temperature characteristic of different layers in HTS cables during the flight missions of a cryo-electric aircraft. Another important point is that the temperature profile of aluminum-based former HTS cables is not so different from copper-based former cables. This means that with a 50% weight reduction in DC HTS cable, the temperature of HTS tapes increases by just 16%. This means that the peak temperature of HTS tapes is still way lower than 300 K, known as the conservative temperature limit for YBCO tapes [25].
To calculate the specific mass and power density of the DC HTS cable, in addition to the weight of former, HTS tapes, and PPLP-based dielectrics, there is a need for adding the weight of cryostat and coolant fluid to the total weight of the cable. For weight calculation of the dielectrics, according to [26], a 2.5 mm thickness would be sufficient for power cables in a voltage range of 4–6 kV while the PPLP dielectric has a density of 1098 kg/m3 [27]. After that, a cryostat made out of stainless steel with a thickness of 1 mm and outer radius of 37 mm, for cables A and C, and 43 mm for cable B was considered. The difference between the cryostat inner radius and outer radius of the last layer of cable defines the total volume of coolant fluid, LN2, with 811 kg/m3 density [27]. This illustration is shown in Figure 10. By doing this, the total weight of DC HTS cables with respect to different former materials is calculated and tabulated in Table 6. After that, and by dividing the cable weight to the length of the cable (100 m), the specific mass could calculated. Then, the power of each cable in kW is divided to the weight of the cable to calculate the power density of cable. Based on [28], the specific mass for a HTS cable to be fitted into a cryo-electric aircraft system must be lower than 5 kg/m, which is the case for all types of understudied cables except cable B that has specific mass of 7.3 kg/m and 6.7 kg/m for copper and aluminum formers, respectively. On the other hand, the highest power density belongs to cable C with aluminum former, which is 12% higher than cable C with copper former. By comparing the cables with aluminum former, cable C has approximately 35% and around 310% higher power density in comparison to cable B and cable A, respectively. Moreover, cable B with aluminum former has 205% higher power density compared to cable A. In other words, HTS cables would have more benefits if they were used for high current, low voltage (lower deictic weight), and high-power applications, as can be observed in Table 6.
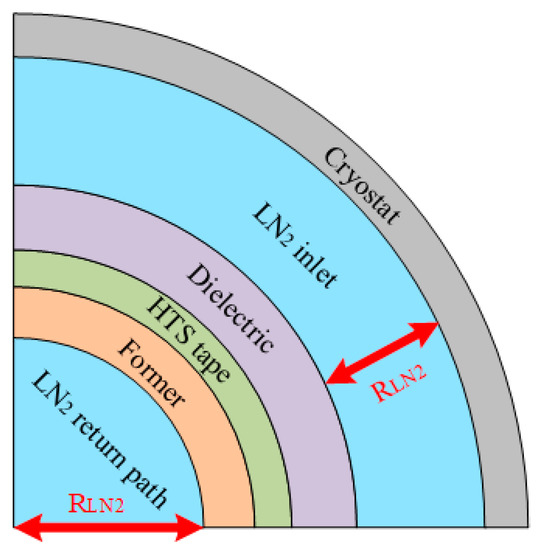
Figure 10.
An illustration of fluid weight calculation in a single-layer DC HTS cable.

Table 6.
Analyzing the specific mass and power density of the optimally designed HTS cables.
5. Conclusions
The application of direct current (DC) high-temperature superconducting (HTS) cables in cryo-electric aircraft units is gaining significant attention. The important parameters for such cables to be fitted into these aircraft fleets are their weight, peak temperature during faults, and the cable critical current. These terms depend on the radius, thickness, and material of the former. Thus, in this study, an investigation is conducted to optimally design 4.5 kV DC HTS cables by considering the weight, temperature, and critical current of cables as separate objective functions solved by a multi-objective optimization algorithm, known as the non-dominated sorting genetic algorithm II (NSGA II). The most important findings of this paper are listed as follows:
- ⮚
- The cables with aluminum former have the lowest weight among all other cables with copper, brass, and stainless steel formers.
- ⮚
- The temperature of cables with copper former is about 10% to 50% lower than cables with other materials in their former.
- ⮚
- The specific mass of all understudied cables lay in the range of 4.9 to 7.3 kg/m, which provides us with a clear index to select the optimum structure and cable type for aviation applications
- ⮚
- The highest power density among all understudied HTS cables belongs to 4.5 kV/2000 A/9 MW DC cable with aluminum former that has 12%–35% higher power density in comparison to other structures and types
- ⮚
- Aluminum former-based cables present an acceptable temperature rise during faults, and the peak temperature of YBCO tapes in such cables is way lower than the burnout limitation of HTS cables.
- ⮚
- The temperature of dielectric and former layers in the understudied cables is lower than the temperature of HTS tapes, which is due to their higher thermal mass.
Author Contributions
Conceptualization, A.S. and M.Y.-A.; methodology, A.S. and M.Y.-A.; formal analysis, A.S. and M.Y.-A.; resources, M.Y.-A.; data curation, A.S. and M.Y.-A.; writing—original draft preparation, A.S. and M.Y.-A.; writing—review and editing, M.Y.-A.; funding acquisition, M.Y.-A.; supervision, M.Y.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available on request due to restrictions, e.g., privacy or ethical reasons.
Acknowledgments
Networking support provided by the European Cooperation in Science and Technology, COST Action CA19108 (Hi-SCALE) is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ciliberti, D.; Vecchia, P.D.; Memmolo, V.; Nicolosi, F.; Wortmann, G.; Ricci, F. The Enabling Technologies for a Quasi-Zero Emissions Commuter Aircraft. Aerospace 2022, 9, 319. [Google Scholar] [CrossRef]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef]
- Darecki, M.; Edelstenne, C.; Enders, T.; Fernandez, E.; Hartman, P.; Herteman, J.P.; Kerkloh, M.; King, I.; Ky, P.; Mathieu, M. Flightpath 2050 Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar]
- Filipenko, M.; Biser, S.; Boll, M.; Corduan, M.; Noe, M.; Rostek, P. Comparative Analysis and Optimization of Technical and Weight Parameters of Turbo-Electric Propulsion Systems. Aerospace 2020, 7, 107. [Google Scholar] [CrossRef]
- Rao, A.G.; Yin, F.; Werij, H.G.C. Energy Transition in Aviation: The Role of Cryogenic Fuels. Aerospace 2020, 7, 181. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Zhang, M.; Yuan, W. Challenges for Developing High Temperature Superconducting Ring Magnets for Rotating Electric Machine Applications in Future Electric Aircrafts. J. Magn. Magn. Mater. 2021, 522, 167543. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Seyyedbarzegar, S.M.; Sadeghi, A.; de Sousa, W.T.B.; Kottonau, D. High Temperature Superconducting Cables and Their Performance against Short Circuit Faults: Current Development, Challenges, Solutions, and Future Trends. Supercond. Sci. Technol. 2022, 35, 083002. [Google Scholar] [CrossRef]
- Sadeghi, A.; Seyyedbarzegar, S.; Yazdani-Asrami, M. Investigation on the Electrothermal Performance of a High-Temperature Superconducting Cable in an Offshore Wind Farm Integrated Power System: Fault and Islanding Conditions. IEEE Trans. Appl. Supercond. 2022, 32, 5401011. [Google Scholar] [CrossRef]
- Xi, J.; Pei, X.; Song, W.; Xiang, B.; Liu, Z.; Zeng, X. Experimental Tests of DC SFCL under Low Impedance and High Impedance Fault Conditions. IEEE Trans. Appl. Supercond. 2021, 31, 5601205. [Google Scholar] [CrossRef]
- Yazdani Asrami, M.; Sadeghi, A.; Atrey, M. Selecting a Cryogenic Cooling System for Superconducting Machines: General Considerations for Electric Machine Designers and Engineers. Int. J. Refrig. 2022, 140, 70–81. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Seyyedbarzegar, S.; Song, W. Role of Insulation Materials and Cryogenic Coolants on Fault Performance of MW-Scale Fault-Tolerant Current-Limiting Superconducting Transformers. IEEE Trans. Appl. Supercond. 2022, 33, 1–15. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Song, W.; Madureira, A.; Pina, J.M.; Morandi, A.; Parizh, M. Artificial Intelligence Methods for Applied Superconductivity: Material, Design, Manufacturing, Testing, Operation, and Condition Monitoring. Supercond. Sci. Technol. 2022, 35, 54. [Google Scholar] [CrossRef]
- Nolan, S.; Jones, C.E.; Norman, P.J.; Burt, G.M. Sizing of Superconducting Cables for Turbo- Electric Distributed Propulsion Aircraft Using a Particle Swarm Optimization Approach. IEEE Trans. Transp. Electrif. 2022, 8, 4789–4798. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Seyyedbarzegar, S.; Song, W. DC Electro-Magneto-Mechanical Characterization of 2G HTS Tapes for Superconducting Cable in Magnet System Using Artificial Neural Networks. IEEE Trans. Appl. Supercond. 2022, 32, 4605810. [Google Scholar] [CrossRef]
- Sadeghi, A.; Seyyedbarzegar, S.M.; Yazdani-Asrami, M. Transient Analysis of a 22.9 KV/2 KA HTS Cable under Short Circuit Using Equivalent Circuit Model Considering Different Fault Parameters. Phys. C Supercond. Appl. 2021, 589, 1353935. [Google Scholar] [CrossRef]
- Hu, N.; Toda, M.; Ozcivan, A.N.; Yagai, T.; Tsuda, M.; Hamajima, T. Fault Current Analysis in a Tri-Axial HTS Cable. IEEE Trans. Appl. Supercond. 2010, 20, 1288–1291. [Google Scholar] [CrossRef]
- Nolan, S.; Jones, C.E.; Alzola, R.P.; Norman, P.J.; Burt, G.; Miller, P.; Husband, M. Voltage Based Current Compensation Converter Control for Power Electronic Interfaced Distribution Networks in Future Aircraft. IEEE Trans. Transp. Electrif. 2020, 6, 1819–1829. [Google Scholar] [CrossRef]
- Morandi, A. HTS Dc Transmission and Distribution: Concepts, Applications and Benefits. Supercond. Sci. Technol. 2015, 28, 123001. [Google Scholar] [CrossRef]
- Duron, J.; Grilli, F.; Antognazza, L.; Decroux, M.; Dutoit, B.; Fischer, Ø. Finite-Element Modelling of YBCO Fault Current Limiter with Temperature Dependent Parameters. Supercond. Sci. Technol. 2007, 20, 338. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Palaparthi, A.; Riede, T.; Titze, I.R. Combining Multiobjective Optimization and Cluster Analysis to Study Vocal Fold Functional Morphology. IEEE Trans. Biomed. Eng. 2014, 61, 2199–2208. [Google Scholar] [CrossRef] [PubMed]
- Barth, C.; Mondonico, G.; Senatore, C. Electro-Mechanical Properties of REBCO Coated Conductors from Various Industrial Manufacturers at 77K, Self-Field and 4.2K, 19T. Supercond. Sci. Technol. 2015, 28, 045011. [Google Scholar] [CrossRef]
- Robinson HTS Wire Critical Current Data Base. Available online: https://htsdb.wimbush.eu/ (accessed on 1 June 2022).
- Yazdani-Asrami, M.; Staines, M.; Sidorov, G.; Davies, M.; Bailey, J.; Allpress, N.; Glasson, N.; Gholamian, S.A. Fault Current Limiting HTS Transformer with Extended Fault Withstand Time. Supercond. Sci. Technol. 2019, 32, 035006. [Google Scholar] [CrossRef]
- Kasman, M.B. 6–36 kV Medium Voltage Underground Power Cables XLPE Insulated Cables; Nexans: Paris, France, 2016. [Google Scholar]
- De Sousa, W.T.B.; Shabagin, E.; Kottonau, D.; Noe, M. An Open-Source 2D Finite Difference Based Transient Electro-Thermal Simulation Model for Three-Phase Concentric Superconducting Power Cables. Supercond. Sci. Technol. 2020, 34, 015014. [Google Scholar] [CrossRef]
- Aigner, B.; Nollmann, M.; Stumpf, E. Design of a Hybrid Electric Propulsion System within a Preliminary Aircraft Design Software Environment; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV: Germany, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).