Experimental Investigation into the Effect of Fin Shapes on Heat Dissipation Performance of Phase Change Heat Sink
Abstract
1. Introduction
2. Model Preparation
2.1. Physical Model
2.2. Theoretical Enthalpy Calculation
3. Experimental
3.1. Materials
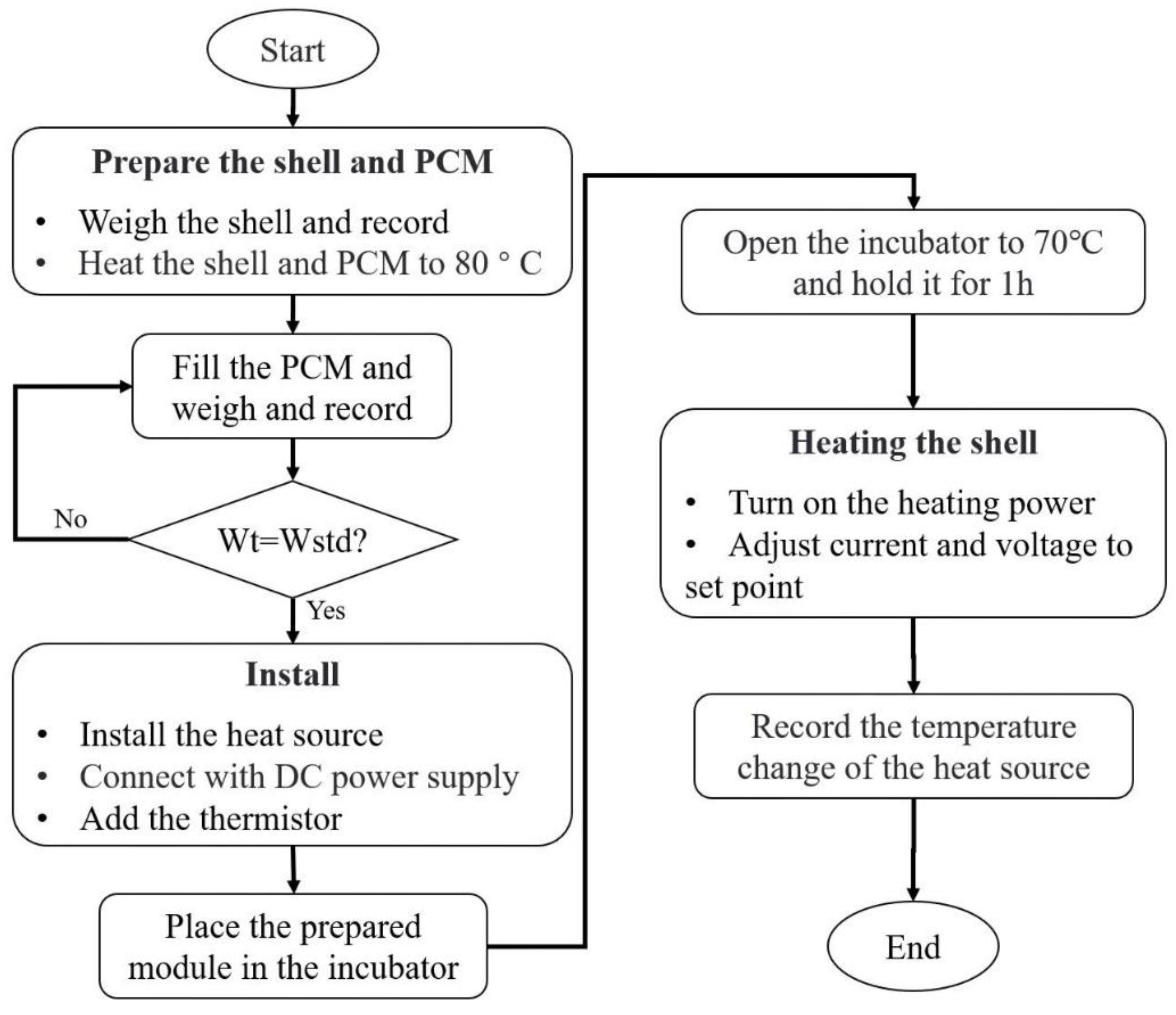
3.2. Experimental Procedure
4. Uncertainty Analysis
4.1. Error of Input Power
4.2. Error of Ambient Temperature
4.3. Error of Processing and Filling
5. Results and Discussions
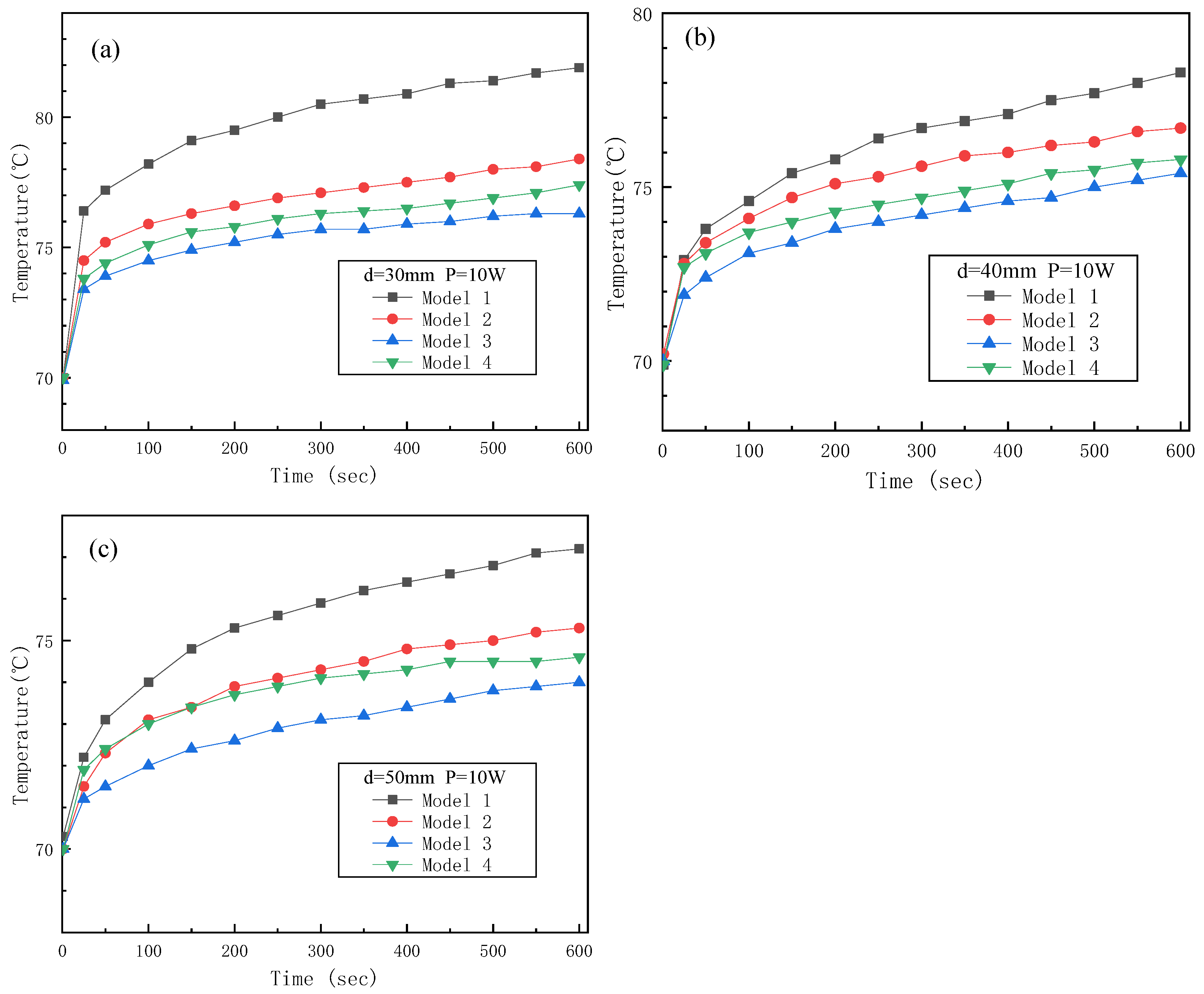
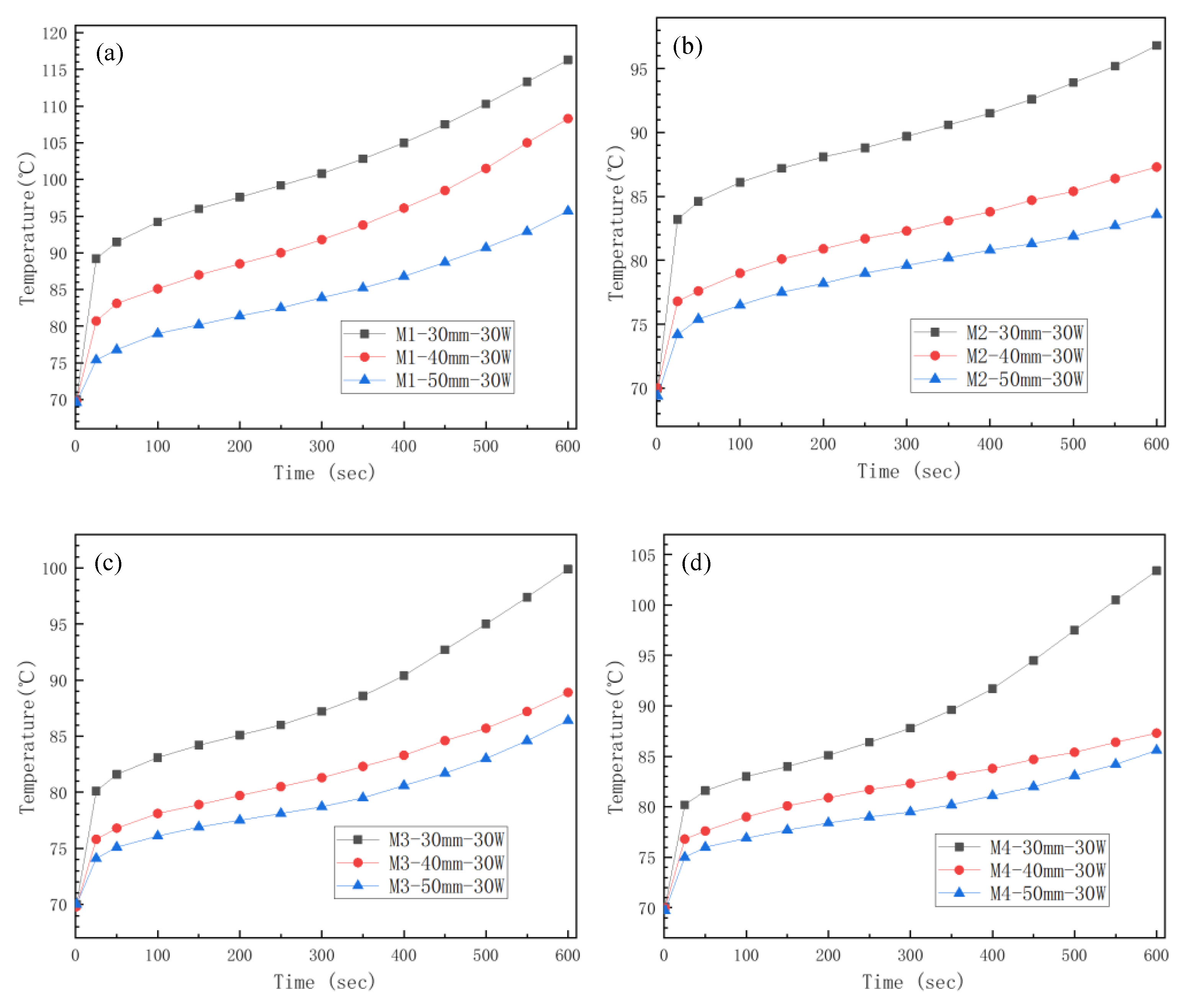
5.1. Temperature Rise of Different Fin Structures
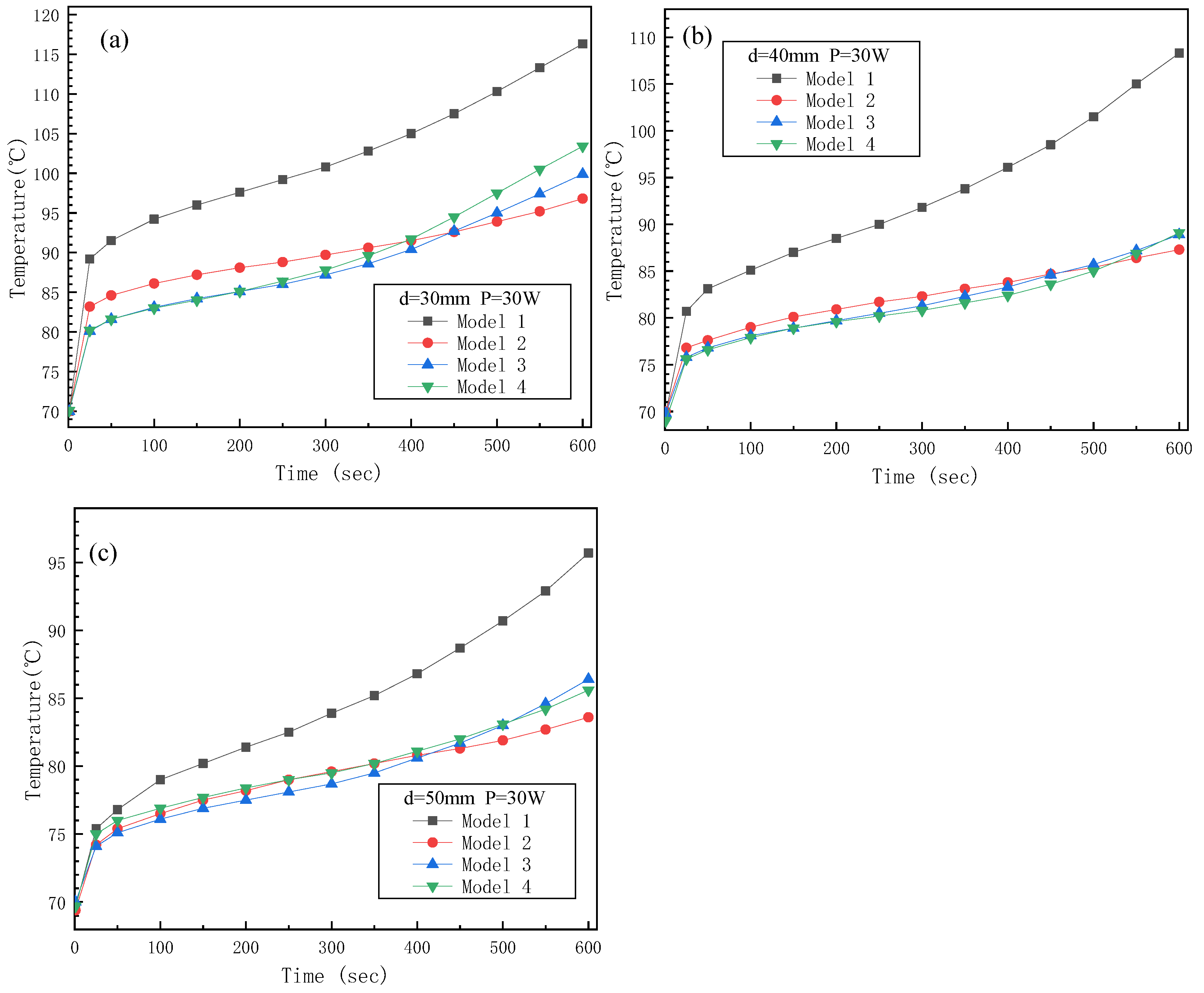
5.2. Thermal Performance under Different Powers and Heater Areas
5.3. Analysis of the Temperature Rise Curve
6. Conclusions
- In the case of low power (10 W), the continuous fin structure in module 3 and module 4 had better performance. Under the power consumption of 10 W, the square-shaped fin structure in module 3 performed the best. Based on the temperature rise of module 1, the temperature rise of module 3 was about 10%~20% lower than that of module 2.
- Under the condition of 30 W power, the early stage in module 3 and module 4 had a better heat transfer effect. However, with the prolongation of heating time, the thickness and spacing of the fins played an important role; the linear fin structure in module 2 showed a more stable and lasting enhanced heat dissipation capability.
- For heat sources that work for a long time, the emphasis is on extending the heat to the surrounding area and extending the time of the second inflection point.
- For heat sources with high power consumption and a short working time, the focus is on strengthening the local thermal conductivity and reducing the temperature of the first inflection point.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, J.G.; Lu, S.; Wang, Y.Z.; Wang, K. Effect analysis on thermal behavior enhancement of lithium-ion battery pack with different cooling structures. J. Energy Storage 2020, 32, 101800. [Google Scholar] [CrossRef]
- Akkaldevi, C.; Chitta, S.D.; Jaidi, J.; Panchal, S.; Fowler, M.; Fraser, R. Coupled Electrochemical-Thermal Simulations and Validation of Minichannel Cold-Plate Water-Cooled Prismatic 20 Ah LiFePO4 Battery. Electrochem 2021, 2, 643–663. [Google Scholar] [CrossRef]
- Sharma, D.K.; Prabhakar, A. A review on air cooled and air centric hybrid thermal management techniques for Li-ion battery packs in electric vehicles. J. Energy Storage 2021, 41, 02885. [Google Scholar] [CrossRef]
- Tousi, M.; Sarchami, A.; Kiani, M.; Najafi, M.; Houshfar, E. Numerical study of novel liquid-cooled thermal management system for cylindrical Li-ion battery packs under high discharge rate based on AgO nanofluid and copper sheath. J. Energy Storage 2021, 41, 102910. [Google Scholar] [CrossRef]
- Pesaran, A.A. Battery Thermal Management in EVs and HEVs: Issues and Solutions," presented at Advanced Automotive Battery Conference. Battery Man 2001, 6, 34–39. [Google Scholar]
- Amine, K.; Liu, J.; Belharouak, I. High-temperature storage and cycling of C-LiFePO4/graphite Li-ion cells. Electrochem. Commun. 2005, 7, 669–673. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures Part I. Cycling performance. J. Power Sources 2002, 112, 606–613. [Google Scholar] [CrossRef]
- Parry, A.J.; Eames, P.C.; Agyenim, F.B. Modeling of Thermal Energy Storage Shell-and-Tube Heat Exchanger. Heat Transf. Eng. 2014, 35, 1–14. [Google Scholar] [CrossRef]
- Elbahjaoui, R.; El Qarnia, H. Numerical Study of a Shell-and-Tube Latent Thermal Energy Storage Unit Heated by Laminar Pulsed Fluid Flow. Heat Transf. Eng. 2017, 38, 1466–1480. [Google Scholar] [CrossRef]
- Lee, Y.T.; Chung, J.D. Performance Estimation of a Latent Heat Thermal Energy Storage System with Different Packing Module Arrangements, Boundary Conditions and Melting Models. Heat Transf. Eng. 2018, 39, 1081–1090. [Google Scholar] [CrossRef]
- Patel, J.R.; Rathod, M.K. Phase change material selection using simulation-oriented optimization to improve the thermal performance of lithium-ion battery. J. Energy Storage 2022, 49, 103974. [Google Scholar] [CrossRef]
- Zhang, P.; Meng, Z.N.; Zhu, H.; Wang, Y.L.; Peng, S.P. Melting heat transfer characteristics of a composite phase change material fabricated by paraffin and metal foam. Appl. Energy 2017, 185, 1971–1983. [Google Scholar] [CrossRef]
- Kumar, P.M.; Anandkumar, R.; Mylsamy, K.; Prakash, K.B. Experimental investigation on thermal conductivity of nanoparticle dispersed paraffin (NDP). Mater. Today 2021, 45, 735–739. [Google Scholar]
- Kumar, R.; Nirwan, A.; Mondal, B.; Kumar, R.; Dixit, A. Study on thermophysical properties of pentadecane and its composites with thermally expanded graphite as shape-stabilized phase change materials. J. Therm. Anal. Calorim. 2022, 147, 8689–8697. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, D.; Fei, H.; Xu, Y.; Zeng, Z.; Ye, W. Preparation and properties of lauric acid-octadecanol/expanded graphite shape-stabilized phase change energy storage material. Mater. Today Commun. 2022, 31, 103325. [Google Scholar] [CrossRef]
- Bianco, N.; Busiello, S.; Iasiello, M.; Mauro, G.M. Finned heat sinks with phase change materials and metal foams: Pareto optimization to address cost and operation time. Appl. Therm. Eng. 2021, 197, 117436. [Google Scholar] [CrossRef]
- Lei, J.; Yang, C.; Huang, X.; Li, Z.; Zhang, Y. Solidification enhancement of phase change materials using nanoparticles and metal foams with nonuniform porosity. J. Energy Storage 2021, 44, 103420. [Google Scholar] [CrossRef]
- Malik, M.; Dincer, I.; Rosen, M.; Fowler, M. Experimental Investigation of a New Passive Thermal Management System for a Li-Ion Battery Pack Using Phase Change Composite Material. Electrochim. Acta 2017, 257, 345–355. [Google Scholar] [CrossRef]
- Wheelock, P.B.; Cook, B.C.; Harringa, J.L.; Russell, A.M. Phase changes induced in hexagonal boron nitride by high energy mechanical milling. J. Mater. Sci. 2004, 39, 343–347. [Google Scholar] [CrossRef]
- Wheelock, P.B.; Cook, B.C.; Harringa, J.L.; Russell, A.M. Anisotropically enhanced heat transfer properties of phase change material reinforced by graphene-wrapped carbon fibers. Sol. Energy Mater. Sol. Cells 2020, 206, 110280. [Google Scholar]
- Samimi, F.; Babapoor, A.; Azizi, M.; Karimi, G. Thermal management analysis of a Li-ion battery cell using phase change material loaded with carbon fibers. Energy 2016, 96, 355–371. [Google Scholar] [CrossRef]
- Ren, Q.; Wang, Z.; Zhu, J.; Qu, Z.G. Pore-scale heat transfer of heat sink filled with stacked 2D metal fiber-PCM composite. Int. J. Therm. Sci. 2021, 161, 106739. [Google Scholar] [CrossRef]
- Haruki, N.; Horibe, A.; Nakashima, K. Anisotropic Effective Thermal Conductivity Measurement of Various Kinds of Metal Fiber Materials. Int. J. Thermophys. 2013, 34, 2385–2399. [Google Scholar] [CrossRef]
- Wu, W.; Yang, X.; Zhang, G.; Ke, X.; Wang, Z.; Situ, W.; Li, X.; Zhang, J. An experimental study of thermal management system using copper mesh-enhanced composite phase change materials for power battery pack. Energy 2016, 113, 909–916. [Google Scholar] [CrossRef]
- Sari, A.; Karaipekli, A. Preparation, thermal properties and thermal reliability of palmitic acid/expanded graphite composite as form-stable PCM for thermal energy storage. Sol. Energy Mater. Sol. Cells 2009, 93, 571–576. [Google Scholar] [CrossRef]
- Du, X.; Xu, J.; Deng, S.; Du, Z.; Cheng, X.; Wang, H. Amino-Functionalized Single-Walled Carbon Nanotubes-Integrated Polyurethane Phase Change Composites with Superior Photothermal Conversion Efficiency and Thermal Conductivity. Acs Sustain. Chem. Eng. 2019, 7, 17682–17690. [Google Scholar] [CrossRef]
- Mitran, R.A.; Ioniţǎ, S.; Lincu, D.; Berger, D.; Matei, C. A Review of Composite Phase Change Materials Based on Porous Silica Nanomaterials for Latent Heat Storage Applications. Molecules 2021, 26, 241. [Google Scholar] [CrossRef]
- Qin, Z.; Low, Z.H.; Ji, C.; Duan, F. Efficacy of angled metallic fins for enhancing phase change material melting. Int. Commun. Heat Mass Transf. 2022, 132, 105921. [Google Scholar] [CrossRef]
- Hussein, A.; Abd-Elhady, M.S.; El-Sheikh, M.N.; El-Metwally, H.T. Improving Heat Transfer Through Paraffin Wax, by Using Fins and Metallic Strips. Arab. J. Sci. Eng. 2018, 43, 4433–4441. [Google Scholar] [CrossRef]
- Shanks, M.; Shoalmire, C.M.; Deckard, M.; Gohil, K.N.; Lewis, H., II; Lin, D.; Shamberger, P.J.; Jain, N. Design of Spatial Variability in Thermal Energy Storage Modules for Enhanced Power Density. Appl. Energy 2022, 314, 118966. [Google Scholar] [CrossRef]
- Woods, J.; Mahvi, A.; Goyal, A.; Kozubal, E.; Odukomaiya, A.; Jackson, R. Rate capability and Ragone plots for phase change thermal energy storage. Nat. Energy 2021, 6, 295–302. [Google Scholar] [CrossRef]
- Marske, F.; Dasler, J.; Haupt, C.; Bacia, K.; Hahn, T.; Enke, D. Influence of surfactants and organic polymers on monolithic shape-stabilized phase change materials synthesized via sol-gel route. J. Energy Storage 2022, 49, 104127. [Google Scholar] [CrossRef]
- Ge, M.; Cheng, X.; Huang, W.; Hu, R.; Cheng, Y. Damage mode and load distribution of countersunk bolted composite joints. J. Compos. Mater. 2021, 55, 1717–1732. [Google Scholar] [CrossRef]
- Ge, M.; cheng, X.; Zhang, Q. Compressive test and numerical simulation of center-notched composite laminates with different crack configurations. Polym. Compos. 2017, 38, 2631–2641. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N.W. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- Mundra, S.S.; Pardeshi, S.S. Analysis of phase change material inside horizontally oriented heat storage unit: A numerical and experimental approach. Case Stud. Therm. Eng. 2022, 31, 101831. [Google Scholar] [CrossRef]
- Venkateshan, S. Mechanical Measurement; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
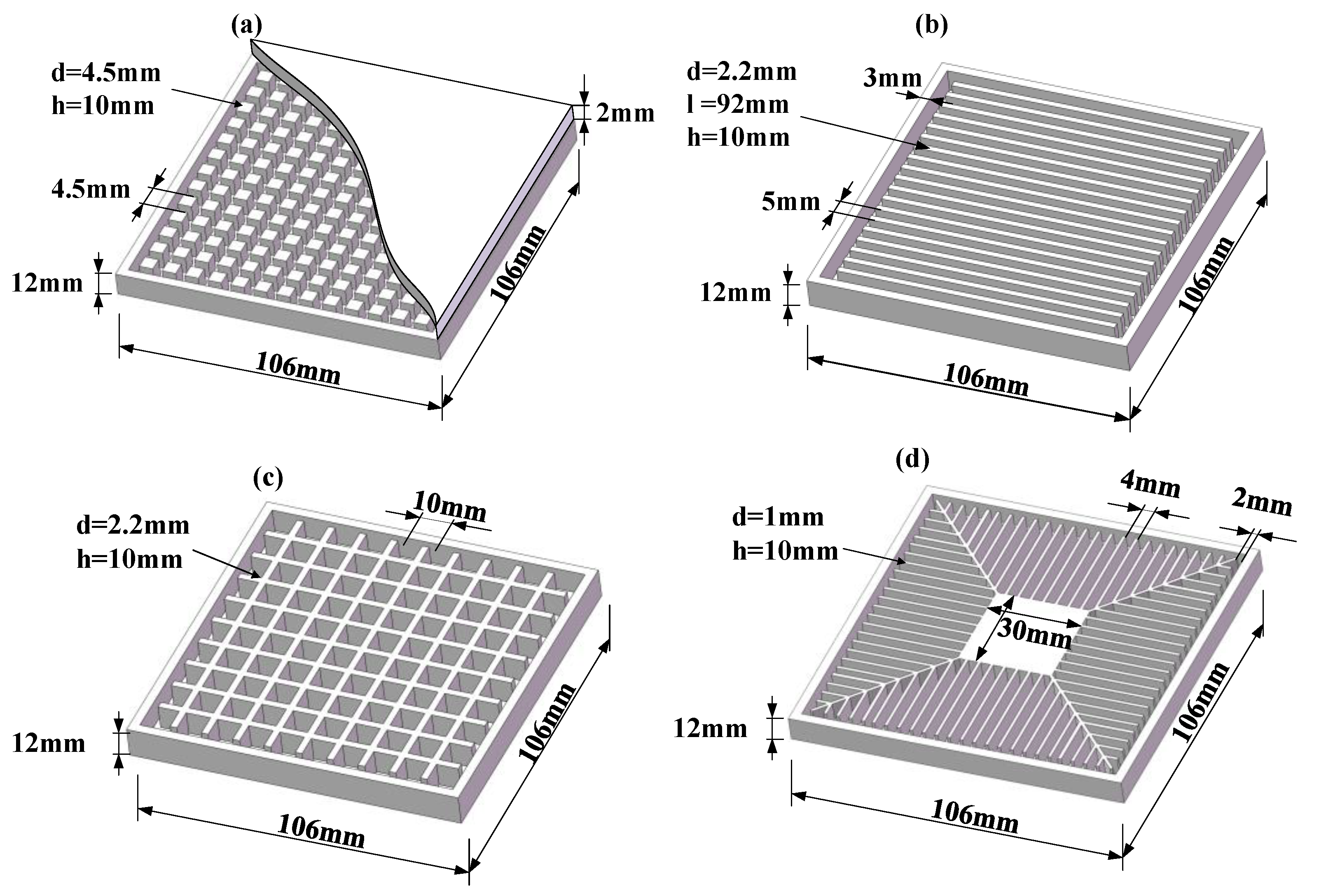




| Model | Shell Weight (g) | PCM Weight (g) | Total Weight (g) | ||||
|---|---|---|---|---|---|---|---|
| Theoretical | Practical | Deviation Ratio | Theoretical | Practical | Deviation Ratio | Practical | |
| M1 | 189.75 | 194.8 | 2.67% | 52 | 52.1 | 0.19% | 246.9 |
| M2 | 189.75 | 194 | 2.23% | 52 | 52 | 0% | 246 |
| M3 | 189.75 | 195 | 2.77% | 52 | 52 | 0% | 247 |
| M4 | 189.75 | 192.9 | 1.67% | 52 | 52.8 | 1.54% | 245.7 |
| Material | k (Wm−1 K−1) | ρ (kg m−3) | Cp (Jkg−1 K−1) |
|---|---|---|---|
| Al (T6-6063) | 202.4 | 2719 | 871 |
| PCM | 0.2 | 867 (l) | 2000 |
| Thermal ester | 6 | 1900 | 1200 |
| Plate heater | 20 | 3600 | 750 |
| Module Number | S (mm) | P (W) | I (A) | V (Volt) | dP | dp/p × 100% |
|---|---|---|---|---|---|---|
| Module 1 | 30 × 30 | 10 W | 1.66 | 5.98 | 0.07 | 0.70% |
| 20 W | 2.33 | 8.72 | −0.32 | −1.60% | ||
| 30 W | 2.81 | 10.68 | −0.01 | −0.03% | ||
| 40 × 40 | 10 W | 1.68 | 5.91 | 0.07 | 0.70% | |
| 20 W | 2.39 | 8.38 | −0.03 | −0.15% | ||
| 30 W | 2.75 | 10.8 | 0.3 | 1.00% | ||
| 50 × 50 | 10 W | 1.46 | 6.90 | −0.07 | −0.70% | |
| 20 W | 2.03 | 9.75 | 0.21 | 1.05% | ||
| 30 W | 2.50 | 12.00 | 0 | 0.00% | ||
| Module 2 | 30 × 30 | 10 W | 1.65 | 5.97 | 0.15 | 1.50% |
| 20 W | 2.34 | 8.72 | −0.4 | −2.00% | ||
| 30 W | 2.74 | 10.79 | 0.44 | 1.47% | ||
| 40 × 40 | 10 W | 1.62 | 6.12 | 0.09 | 0.90% | |
| 20 W | 2.33 | 8.72 | −0.32 | −1.60% | ||
| 30 W | 2.92 | 10.3 | −0.08 | −0.27% | ||
| 50 × 50 | 10 W | 1.51 | 6.64 | −0.03 | −0.30% | |
| 20 W | 2.12 | 9.44 | −0.01 | −0.05% | ||
| 30 W | 2.58 | 11.61 | 0.05 | 0.17% | ||
| Module 3 | 30 × 30 | 10 W | 1.69 | 5.94 | −0.04 | −0.40% |
| 20 W | 2.35 | 8.67 | −0.37 | −1.85% | ||
| 30 W | 2.82 | 10.63 | 0.02 | 0.07% | ||
| 40 × 40 | 10 W | 1.67 | 5.98 | 0.01 | 0.10% | |
| 20 W | 2.40 | 8.34 | −0.02 | −0.10% | ||
| Module Number | S (mm) | P (W) | I (A) | V (Volt) | dP | dp/p × 100% |
| Module 3 | 40 × 40 | 30 W | 2.79 | 10.8 | −0.13 | −0.43% |
| 50 × 50 | 10 W | 1.46 | 6.90 | −0.07 | −0.70% | |
| 20 W | 2.02 | 9.71 | 0.39 | 1.95% | ||
| 30 W | 2.63 | 11.4 | 0.02 | 0.07% | ||
| Module 4 | 30 × 30 | 10 W | 1.63 | 6.14 | −0.01 | −0.10% |
| 20 W | 2.34 | 8.72 | −0.4 | −2.00% | ||
| 30 W | 2.74 | 10.81 | 0.38 | 1.27% | ||
| 40 × 40 | 10 W | 1.59 | 6.24 | 0.08 | 0.80% | |
| 20 W | 2.28 | 8.78 | −0.02 | −0.10% | ||
| 30 W | 2.98 | 10.6 | −0.40 | −1.32% | ||
| 50 × 50 | 10 W | 1.51 | 6.64 | −0.03 | −0.30% | |
| 20 W | 2.14 | 9.41 | −0.14 | −0.70% | ||
| 30 W | 2.47 | 12.12 | 0.06 | 0.20% |
| Power | Size | Module | Initial Temperature | End Temperature | Temperature Rise | Temperature Contrast |
|---|---|---|---|---|---|---|
| 10 W | 30 mm | M1 | 69.9 °C | 81.8 °C | 11.9 °C | 0% |
| M2 | 70 °C | 78.4 °C | 8.4 °C | 29.4% | ||
| M3 | 70 °C | 76.3 °C | 6.3 °C | 47.1% | ||
| M4 | 70.1 °C | 77.9 °C | 7.8 °C | 34.5% | ||
| 40 mm | M1 | 70.1 °C | 80.3 °C | 10.2 °C | 0% | |
| M2 | 70.1 °C | 76.7 °C | 6.6 °C | 34% | ||
| M3 | 70 °C | 75.8 °C | 5.4 °C | 47.1% | ||
| M4 | 70 °C | 75.4 °C | 5.8 °C | 43.1% | ||
| 50 mm | M1 | 70.2 °C | 77.2 °C | 7.0 °C | 0% | |
| M2 | 70 °C | 75.3 °C | 5.3 °C | 24.3% | ||
| M3 | 70.1 °C | 74 °C | 3.9 °C | 44.3% | ||
| M4 | 70 °C | 74.6 °C | 4.6 °C | 34.3% |
| Power | Size | Module | Initial Temperature | End Temperature | Temperature Rise | Temperature Contrast |
|---|---|---|---|---|---|---|
| 30 W | 30 mm | M1 | 70 °C | 116.3 °C | 46.3 °C | 0% |
| M2 | 70 °C | 96.8 °C | 26.8 °C | 42.1% | ||
| M3 | 70.1 °C | 99.9 °C | 28.8 °C | 37.8% | ||
| M4 | 70.1 °C | 103.4 °C | 33.4 °C | 27.9% | ||
| 40 mm | M1 | 70.1 °C | 108.3 °C | 38.2 °C | 0% | |
| M2 | 70 °C | 87.3 °C | 17.3 °C | 54.7% | ||
| M3 | 69.9 °C | 88.9 °C | 19 °C | 50.3% | ||
| M4 | 69.9 °C | 89.1 °C | 19.2 °C | 49.7% | ||
| 50 mm | M1 | 70 °C | 95.7 °C | 25.7 °C | 0% | |
| M2 | 70.1 °C | 83.6 °C | 13.5 °C | 47.5% | ||
| M3 | 70 °C | 86.4 °C | 16.4 °C | 36.2% | ||
| M4 | 69.8 °C | 85.6 °C | 15.8 °C | 38.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhu, K.; Wei, Y.; Chen, Z.; Ge, M.; Huang, Y. Experimental Investigation into the Effect of Fin Shapes on Heat Dissipation Performance of Phase Change Heat Sink. Aerospace 2022, 9, 664. https://doi.org/10.3390/aerospace9110664
Liu X, Zhu K, Wei Y, Chen Z, Ge M, Huang Y. Experimental Investigation into the Effect of Fin Shapes on Heat Dissipation Performance of Phase Change Heat Sink. Aerospace. 2022; 9(11):664. https://doi.org/10.3390/aerospace9110664
Chicago/Turabian StyleLiu, Xu, Keyong Zhu, Yijie Wei, Ziwei Chen, Mingming Ge, and Yong Huang. 2022. "Experimental Investigation into the Effect of Fin Shapes on Heat Dissipation Performance of Phase Change Heat Sink" Aerospace 9, no. 11: 664. https://doi.org/10.3390/aerospace9110664
APA StyleLiu, X., Zhu, K., Wei, Y., Chen, Z., Ge, M., & Huang, Y. (2022). Experimental Investigation into the Effect of Fin Shapes on Heat Dissipation Performance of Phase Change Heat Sink. Aerospace, 9(11), 664. https://doi.org/10.3390/aerospace9110664





