Study of the Mechanical Properties of Near-Space Airship Envelope Material Based on an Optimization Method
Abstract
1. Introduction
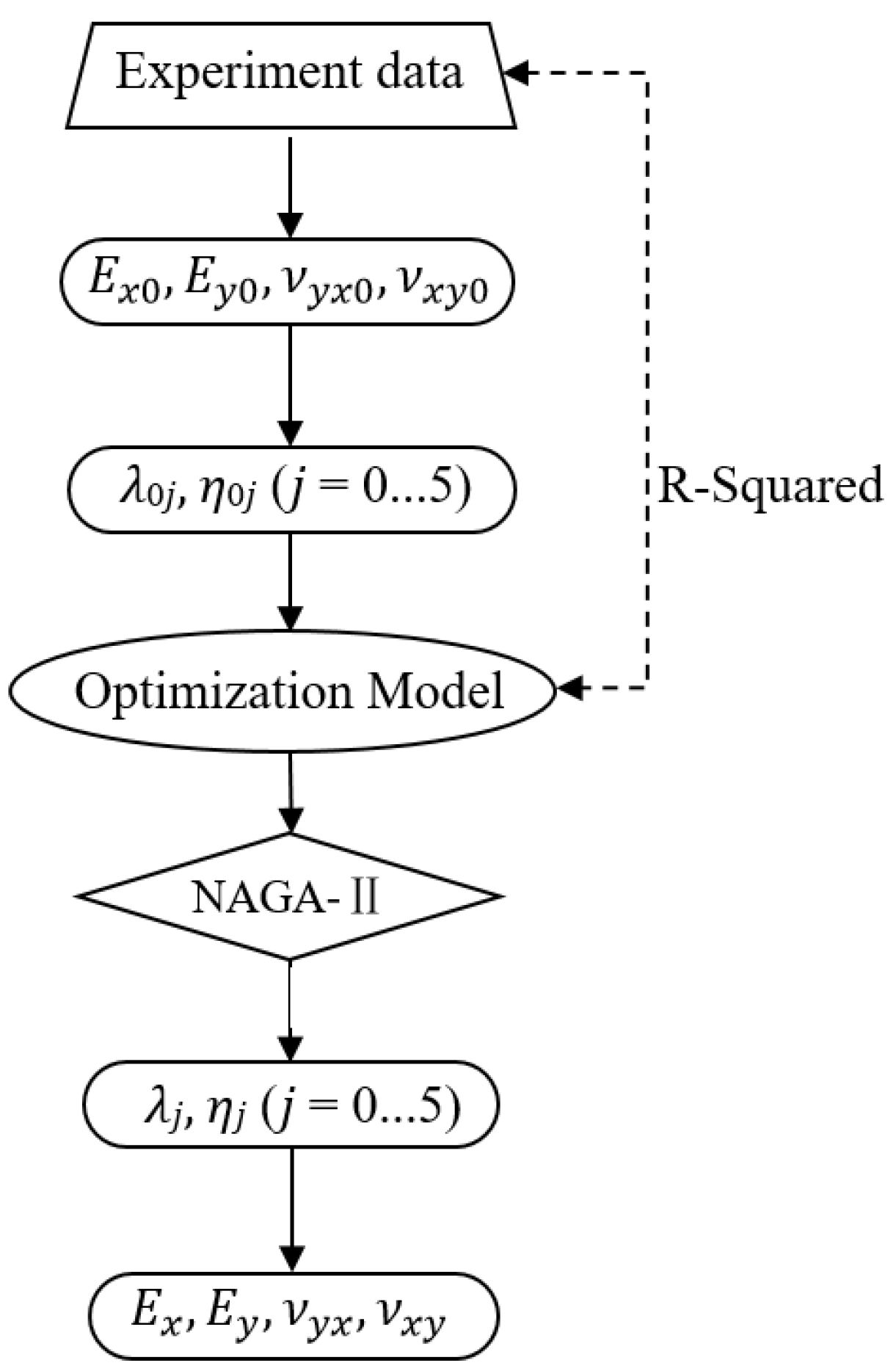
2. Methodology
2.1. Optimization Calculation Model
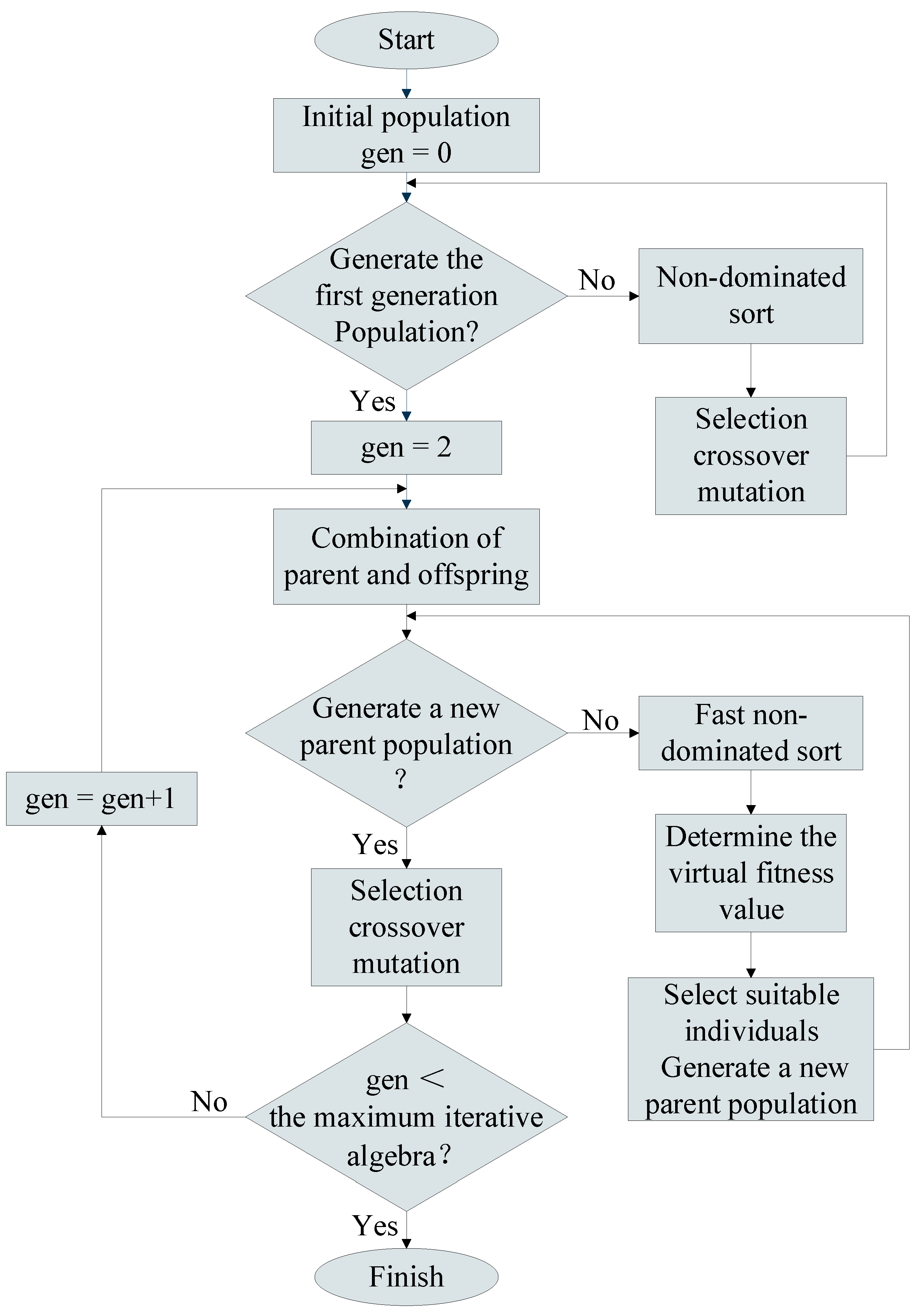
2.2. Optimization Algorithm Method
3. Experiments
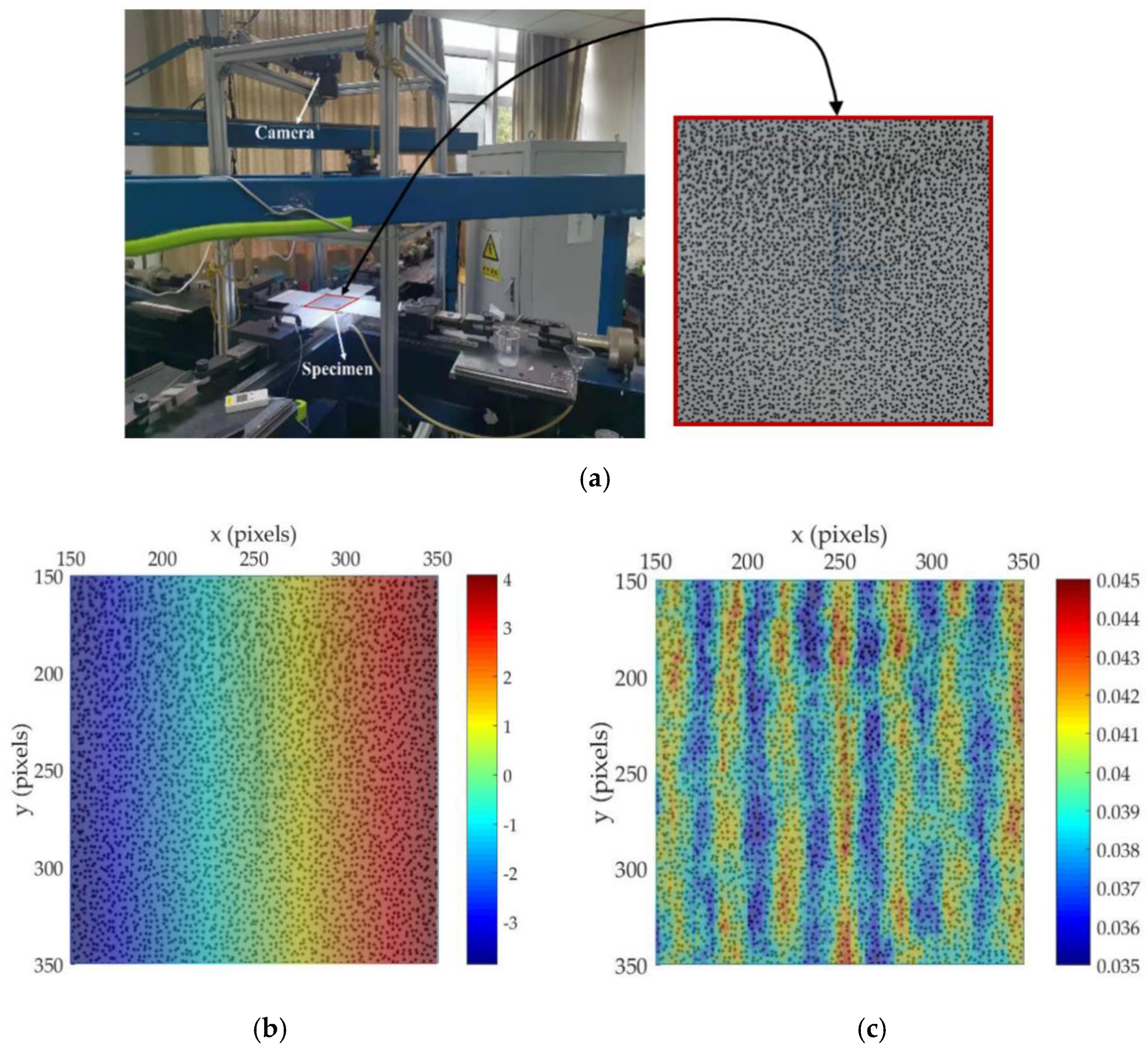
3.1. Experimental Material and Equipment
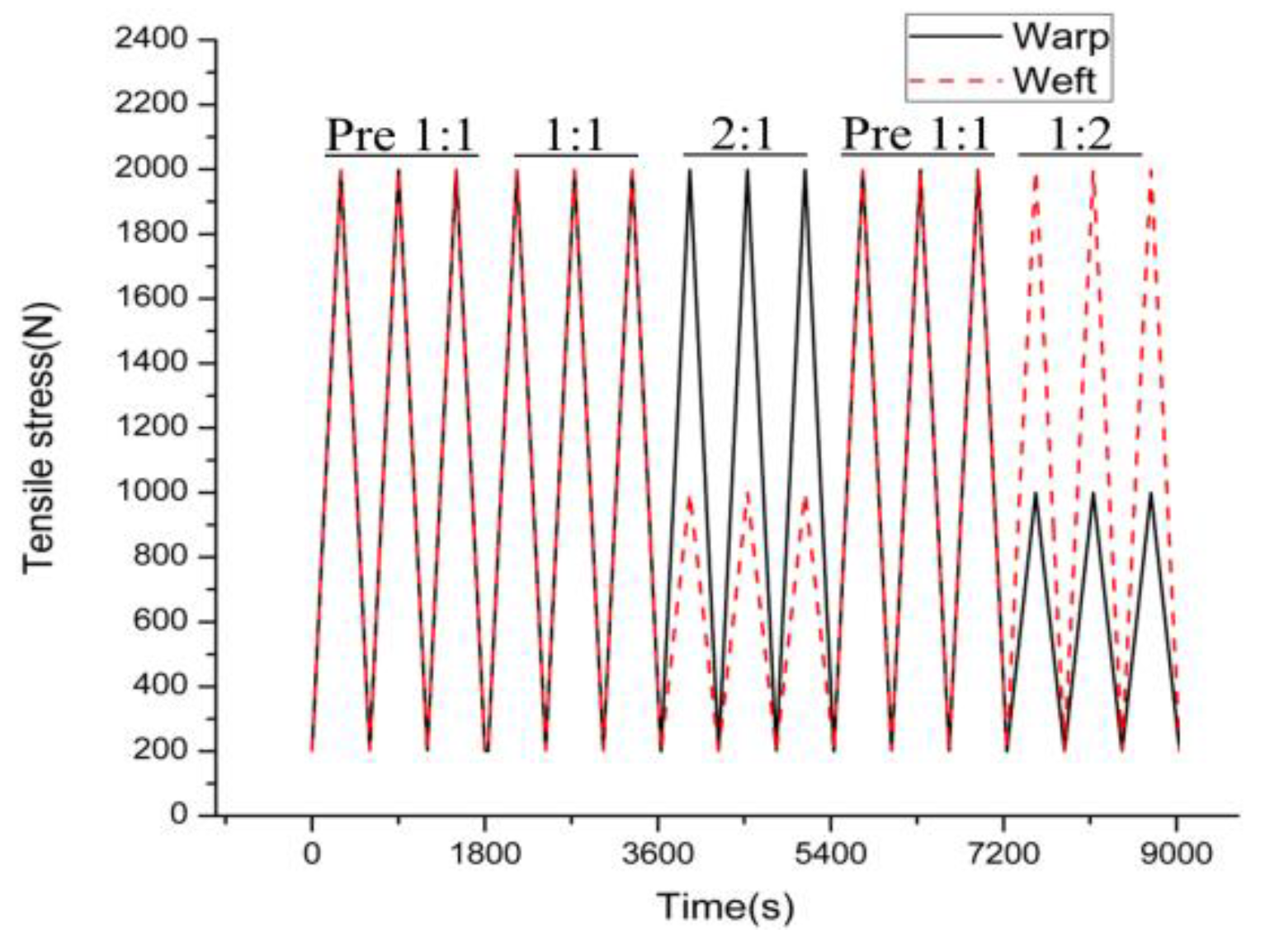
3.2. Test Procedure
4. Results and Discussions
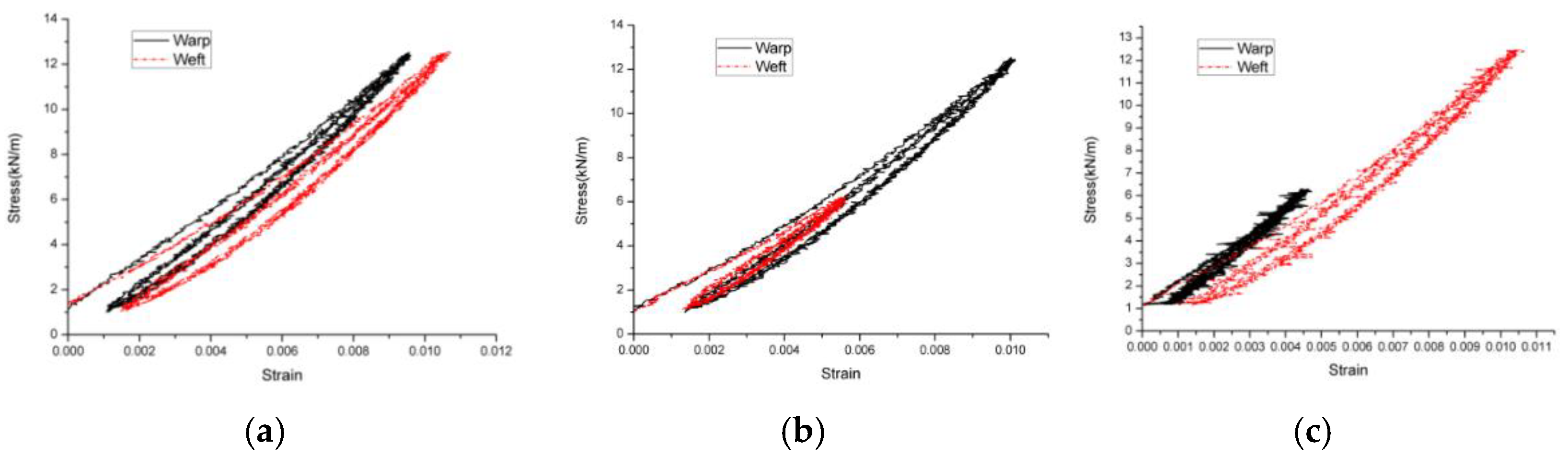
4.1. Analysis of Experimental Data
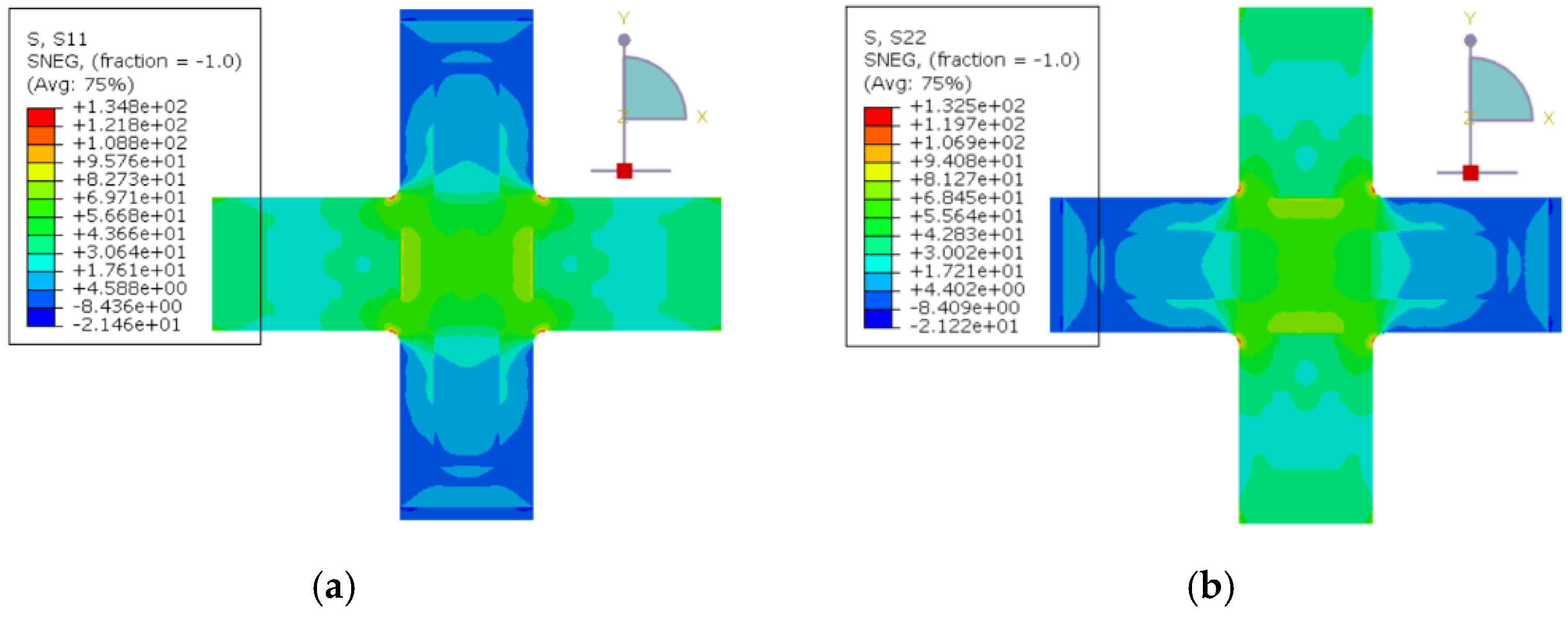
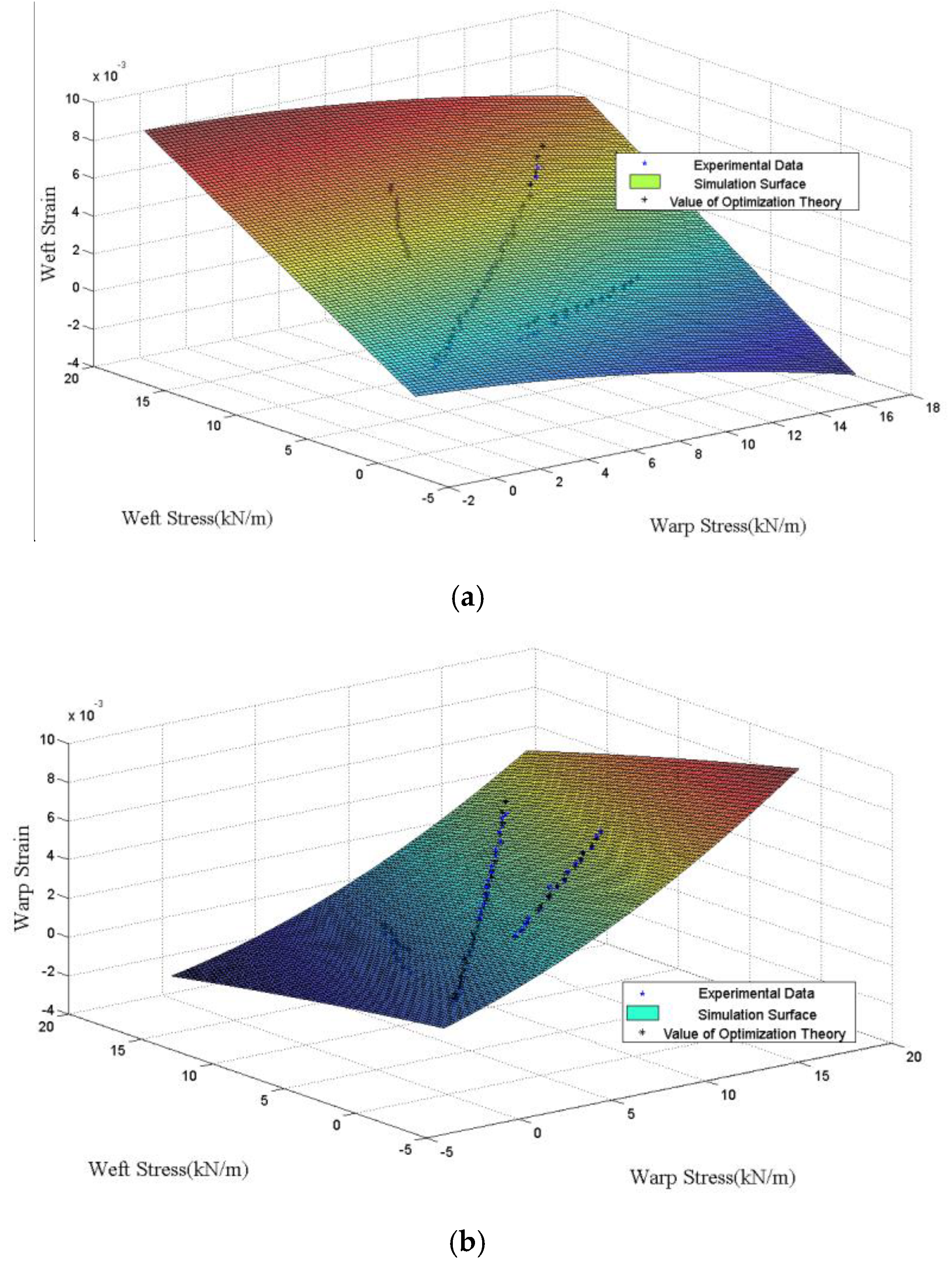
4.2. Analysis of Optimization Results
4.3. Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, J.; Duan, D.; Xie, W. Shape Exploration and Multidisciplinary Optimization Method of Semirigid Nearing Space Airships. J. Aircr. 2021, 59. [Google Scholar] [CrossRef]
- Adak, B.; Joshi, M. Coated or Laminated Textiles for Aerostat and Stratospheric Airship. In Advanced Textile Engineering Materials; Wiley: Hoboken, NJ, USA, 2018; pp. 257–288. [Google Scholar]
- Smith, M.S.; Rainwater, E.L. Applications of Scientific Ballooning Technology to High Altitude Airships. In Proceedings of the AIAA’s 3rd Annual Aviation Technology, Integration, and Operations (ATIO) Forum, Denver, CO, USA, 17–19 November 2003. [Google Scholar]
- Wang, X.-L. Effect of Ballonet Sloshing on the Stability Characteristics of an Airship. AIAA J. 2016, 5, 360–363. [Google Scholar] [CrossRef]
- Tang, J.; Wang, X.; Duan, D.; Xie, W. Optimisation and Analysis of Efficiency for Contra-Rotating Propellers for High-Altitude Airships. Aeronaut. J. 2019, 123, 706–726. [Google Scholar] [CrossRef]
- Stockbridge, C.; Ceruti, A.; Marzocca, P. Airship Research and Development in the Areas of Design, Structures, Dynamics and Energy Systems. Int. J. Aeronaut. Space Sci. 2012, 13, 170–187. [Google Scholar] [CrossRef]
- Tang, J.; Xie, W.; Wang, X.; Chen, C. Simulation and Analysis of Fluid–Solid–Thermal Unidirectional Coupling of Near-Space Airship. Aerospace 2022, 9, 439. [Google Scholar] [CrossRef]
- Tang, J.; Pu, S.; Yu, P.; Xie, W.; Li, Y.; Hu, B. Research on Trajectory Prediction of a High-Altitude Zero-Pressure Balloon System to Assist Rapid Recovery. Aerospace 2022, 9, 622. [Google Scholar] [CrossRef]
- Xie, W.-C.; Wang, X.-L.; Duan, D.-P.; Tang, J.-W. Optimization Analysis of Stratospheric Airship Suspended Curtains. J. Mech. 2020, 36, 763–772. [Google Scholar] [CrossRef]
- Xie, W.-C.; Wang, X.-L.; Duan, D.-P.; Tang, J.-W. Finite Element Simulation of the Microstructure of Stratospheric Airship Envelopes. AIAA J. 2020, 58, 3690–3699. [Google Scholar] [CrossRef]
- Ambroziak, A. Analysis of Non-Linear Elastic Material Properties of PVC-Coated Panama Fabric. Task Q. 2005, 9, 167–178. [Google Scholar]
- Argyris, J.; Doltsinis, I.S.; Silva, V.D.D. Constitutive Modeling and Computation of Non-Linear Viscoelastic Solids. Part I: Rheological Models and Numerical Integration Techniques. Comput. Methods Appl. Mech. Eng. 1991, 88, 135–163. [Google Scholar] [CrossRef]
- Klosowski, P.; Zagubien, A.; Woznica, K. Investigation on Rheological Properties of Technical Fabric “Panama”. Arch. Appl. Mech. 2004, 73, 661–681. [Google Scholar] [CrossRef]
- Nayfeh, A.; Kress, G. Non-Linear Constitutive Model for Plain-Weave Composites. Compos. Part B Eng. 1997, 28, 627–634. [Google Scholar] [CrossRef]
- Nedjar, B. An Anisotropic Viscoelastic Fibrematrix Model at Finite Strains: Continuum Formulation and Computational Aspects. Comput. Methods Appl. Mech. Eng. 2007, 196, 1745–1756. [Google Scholar] [CrossRef]
- Meng, J.; Lv, M. The Constitutive Relation of a Fabric Membrane Composite for a Stratospheric Airship Envelope based on Invariant Theory. Comput. Mater. Contin. 2017, 53, 73–89. [Google Scholar]
- Bridgens, B.; Gosling, P. Interpretation of Results from the MSAJ Testing Method for Elastic Constants of Membrane Materials. In Proceedings of the TensiNet Symposium, Sofia, Bulgaria, 16–18 September 2010; pp. 49–57. [Google Scholar]
- M-02-1995; Testing Method for Elastic Constants of Membrane Materials. Membrane Structures Association of Japan: Tokyo, Japan, 1995.
- ASCE-1852; Tensioned Fabric Structure—A Practical Introduction. ASCE Standards: Reston, VA, USA, 1996.
- Dinh, T.; Rezaei, A.; Laet, L.D.; Mollaert, M.; Hemelrijck, D.V.; Paepegem, W.V. A New Elasto-Plastic Material Model for Coated Fabric. Eng. Struct. 2014, 71, 222–233. [Google Scholar] [CrossRef]
- Bridgens, B.N. Direct StressStrain Representation for Coated Woven Fabrics. Comput. Struct. 2004, 82, 1913–1927. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Wang, M.; Ding, Y.; Zhou, H.; Zhao, B.; Fan, J. Mechanical Behaviors and Elastic Parameters of Laminated Fabric URETEK3216LV Subjected to Uniaxial and Biaxial Loading. Appl. Compos. Mater. 2017, 24, 1107–1136. [Google Scholar] [CrossRef]
- Galliot, C.; Luchsinger, R. A simple model describing the non-linear biaxial tensile behaviour of PVC-coated polyester fabrics for use in finite element analysis. Compos. Struct. 2009, 90, 438–447. [Google Scholar] [CrossRef]
- Bai, X. Research on the Evolution of Mechanical Properties of Airship Envelopes. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2009. [Google Scholar]
- Xie, W.; Wang, X.; Duan, D.; Tang, J.; Wei, Y. Mechanical properties of UN-5100 envelope material for stratospheric airship. Aeronaut. J. 2021, 125, 472–488. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Z.; Fang, Y. Static Load Test and Finite Element Simulation of Vertical Bearing Capacity of Bored Piles. Struct. Eng. 2021, 37. [Google Scholar] [CrossRef]
- Xia, Y. A Discussion on the Value Field of Possions Ratio-v. J. Xian Inst. Highw. 1984, 2, 106–111. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarian, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Belegundu, A.D.; Berke, L.; Patnaik, S.N. An Optimization Algorithm based on the Method of Feasible Directions. Struct. Optim. 1995, 9, 83–88. [Google Scholar] [CrossRef]
- Hager, W.W.; Zhang, H.C. A New Conjugate Gradient Method with Guaranteed Descent and an Efficient Line Search. SIAM J. Optim. 2005, 16, 170–192. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization using Evolutionary Algorithms; Wiley: New York, NY, USA, 2003; pp. 7–21. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison Wesley: New York, NY, USA, 1989; pp. 1–18. [Google Scholar]
- Bai, Q.H. Analysis of Particle Swarm Optimization Algorithm. Comput. Inf. Sci. 2010, 180, 184. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Srinivas, N. Multi-objective Function Optimization Using Nondominated Sorting Genetic Algorithms. Evol. Comput. 1995, 3, 221–248. [Google Scholar]
- Khoury, G.A. Airship Technology; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Zheng, L.; Yi, H.; Wang, J.; Jiao, W.; Wu, J.; Gai, S.; Wu, G. Tearing strength of Vectran Fiber anodic fabric. Shanghai Text. Sci. Technol. 2018, 46, 8–9. [Google Scholar]
- Gao, C. Biaxial Test Methods, Experiments and Mechanical Behavior of Fabric Membranes. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2016. [Google Scholar]




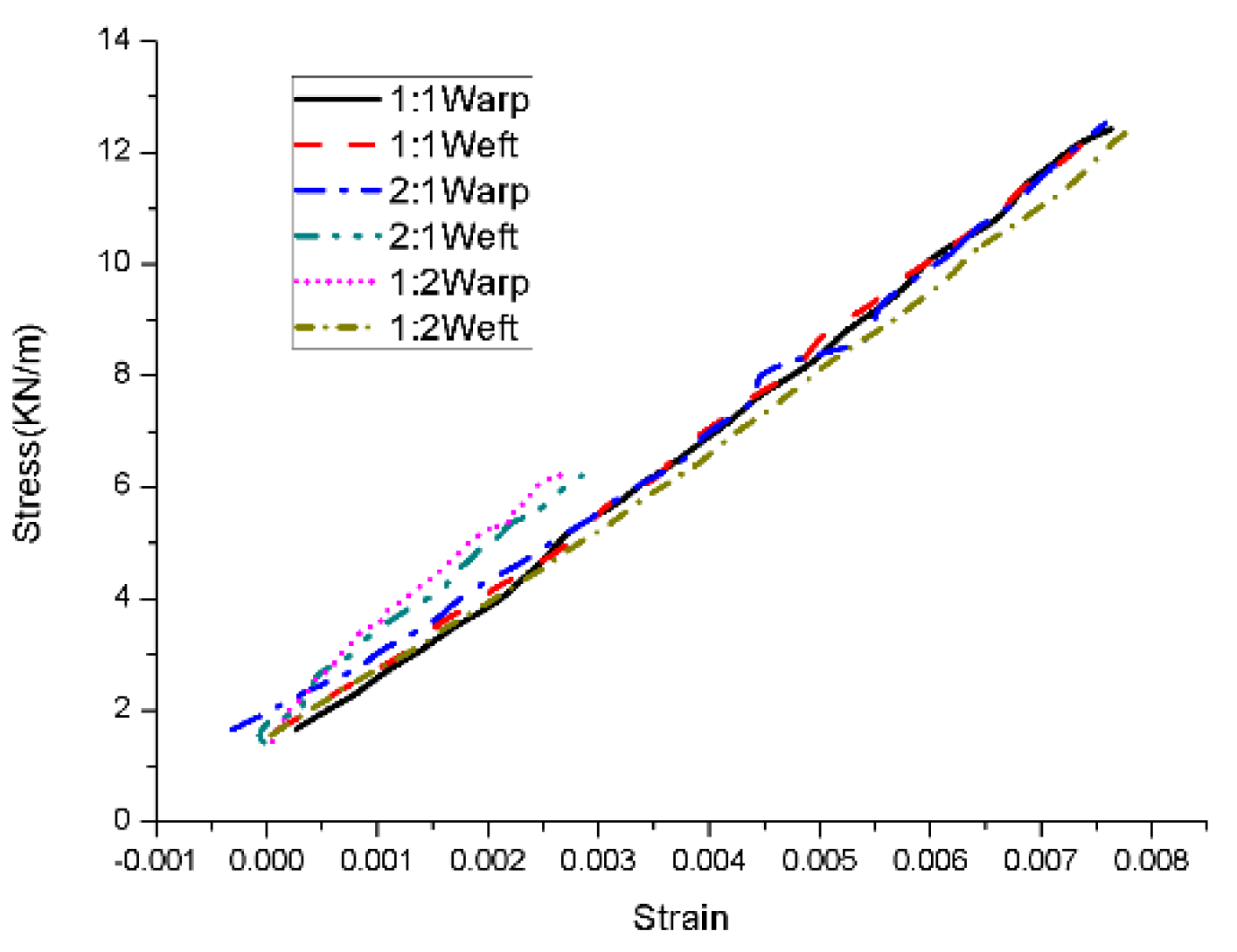

| Stress Ratio (Warp:Weft) | Warp Slope (102 kN/m) | Weft Slope (102 kN/m) |
|---|---|---|
| 1:1 | 13.77∼16.38 | 13.24∼16.64 |
| 2:1 | 11.40∼18.20 | 18.86∼14.03 |
| 1:2 | 24.72∼14.01 | 11.88∼17.06 |
| Poisson’s Ratio | |||
|---|---|---|---|
| EX | |||
| 12.98 | 13.35 | 0.1903 | 0.1957 |
| 𝜆0 | 𝜆1 | 𝜆2 | 𝜆3 | 𝜆4 | 𝜆5 |
|---|---|---|---|---|---|
| 1715.832 | −109.514 | −0.27352 | 5.279409 | 0.536042 | 0.127741 |
| 𝜅0 | 𝜅1 | 𝜅2 | 𝜅3 | 𝜅4 | 𝜅5 |
| 1429.07 | −0.01938 | −43.7049 | 0.142972 | 1.823383 | 0.136431 |
| 𝜂0 | 𝜂1 | 𝜂2 | 𝜂3 | 𝜂4 | 𝜂5 |
| 0.40475 | 0.02569 | −0.02771 | −0.00098 | 0.001955 | −0.00193 |
| Stress Ratio (Warp:Weft) | E (102 kN/m) | 𝜈 | R-Squared | |||
|---|---|---|---|---|---|---|
| Warp | Weft | Warp | Weft | Warp | Weft | |
| 1:1, 1:2, 2:1 | 12.26∼15.81 | 12.41∼14.16 | 0.216∼0.436 | 0.200∼0.458 | 0.975 | 0.970 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Xie, W.; Wang, X.; Chen, Y.; Wu, J. Study of the Mechanical Properties of Near-Space Airship Envelope Material Based on an Optimization Method. Aerospace 2022, 9, 655. https://doi.org/10.3390/aerospace9110655
Tang J, Xie W, Wang X, Chen Y, Wu J. Study of the Mechanical Properties of Near-Space Airship Envelope Material Based on an Optimization Method. Aerospace. 2022; 9(11):655. https://doi.org/10.3390/aerospace9110655
Chicago/Turabian StyleTang, Jiwei, Weicheng Xie, Xiaoliang Wang, Yonglin Chen, and Junjie Wu. 2022. "Study of the Mechanical Properties of Near-Space Airship Envelope Material Based on an Optimization Method" Aerospace 9, no. 11: 655. https://doi.org/10.3390/aerospace9110655
APA StyleTang, J., Xie, W., Wang, X., Chen, Y., & Wu, J. (2022). Study of the Mechanical Properties of Near-Space Airship Envelope Material Based on an Optimization Method. Aerospace, 9(11), 655. https://doi.org/10.3390/aerospace9110655







