Abstract
Automated fiber placement (AFP) systems accommodate complex-shaped structures by pressing fibers against the non-planar surfaces of mandrels, in which compaction mechanisms are of crucial significance. A conventional compaction mechanism utilizes an independent actuator with compacting rollers to conform surfaces. Compared with these mechanisms, underactuated mechanisms can improve self-adjustability and functionality. This research introduces the concept design and the analysis of a planar underactuated compaction mechanism for automated fiber placement heads. Firstly, the requirements and design premise are determined. Then, a novel planar underactuated compaction mechanism with a bistable structure is constructed based on the metamorphic design theory. Secondly, the analytical models are established to give insight into the motion characteristics of the mechanism. Moreover, the example and simulation results are presented to verify the conceptual design. Furthermore, the standard deviation of the contact force of the planar underactuated compaction mechanism is much lower than that of a conventional compaction mechanism under equal conditions. Finally, the potential application of the underactuated mechanisms is discussed. Thus, this research shows that the designed compaction mechanism increases the adjustability, robustness, and high repeatability in positioning and can be used to simplify the motion planning for AFP systems when producing complex structures.
1. Introduction
Advanced composite materials, composed of two or more substances, have been widely used in aerospace, automotive, and infrastructure fields, offering a synergistic performance [1]. Particularly, continuous carbon fiber reinforced composite shows enhanced mechanical properties while remaining lightweight. This type of material provides a great possibility for replacing traditional materials to some extent, such as steel, with advanced performance, which promotes the composite manufacturing techniques for its quality [2]. Currently, AFP is one of major automation technologies for manufacturing composite components [3,4]. An AFP machine includes a computer-controlled moving platform with an AFP head that governs the delivery of each prepreg fiber strap from creels to a mold. Since AFP heads are able to control the movement of each fiber slit, it fits better for structures with high complexity-shaped surfaces which need to be produced consistently and efficiently, such as engine blades and S-shaped inlets (as seen in Figure 1). During this process, straps are dragged from creels and then fed through a delivery system into an AFP head, where straps are arranged side-by-side and compacted onto a mold surface with consistent compaction force and consolidation temperature by a compaction mechanism [5]. The compaction process influences the interlayer and/or intra-layer adhesion and defects, and it has been proven that compaction mechanisms play a significant role in composite material manufacturing [6,7].

Figure 1.
Schematic diagrams of (a) an engine blade and (b) an S-shaped inlet.
The early development of compaction mechanisms [8,9,10] consist of pneumatic cylinders and a compaction roller composed of several separated compact segments. This kind of mechanism has such weaknesses as slow response and low precision. In order to promote the adaptability on a complex-curved mold, a series of compaction mechanisms with an elastic layer [11,12,13] have been developed so that the elastic layer acts as a buffer against unexpected collision. Another alternative attempt was proposed by adding a flexible element. For example, Markus Steeg et al. [14] designed a compaction mechanism to compensate for slight angular misalignment between the mold and roller. Chapman [15] directly used a plurality spring connected with the compaction roller to conform sophisticated profiles passively. An elastomeric bladder [16] was employed by Alliant Techsystems Inc to maintain the contact force of individual compaction segments. Hu [17] also demonstrated that a series elastic actuator (SEA) can be used as a buffer to improve the stability of compression. However, given the insufficient compaction of a single roller [18,19], further investigation of compaction mechanisms utilizes multiple rollers [20,21,22,23,24] to enhance the compression in the upper layer. Ingersoll Machine Tools [20] designed an auxiliary compaction mechanism to realize a post-pressing process and improve tackiness. A separate deposition system composed of two compaction rollers [24] was invented, and it can compact fiber bands in two directions continuously. The main drawback is that multiple rollers are only suitable for laminates instead of complicated structures. Despite the progress having been made to improve the compaction quality, the conventional compaction mechanisms still hardly provide consistent force and performance in a complex environment. Alternatively, underactuated mechanisms removing the degree of freedom (DOF) can improve the robustness and self-adaptability. As a response to the perturbation, the mechanical configuration is passively regulated, and a new stable position will be given. This method is extensively used in the design of grippers/graspers, such as the tendon-driven robogami gripper [25], UACT robotic figure [26], chopstick-type gripper [27], SRI hand [28], and others seen in [29]. This type of underactuated mechanism has the capability to combine the advantages of a single roller and multiple rollers to fulfill all kinds of mold surfaces. However, underactuated mechanisms have advantages for self-adjustability with poor robustness. Many practical control approaches have been considered to maintain its stability in the presence of abrupt changes [30,31]. In this study, we introduce bistable structures so that the mechanism has flexible working states that can adapt to different types of mold surfaces. It is interesting to implement the concept and enlighten our minds about the behavior of the mechanism when it compacts a fiber band on a predetermined mold surface with unexpected waves. In this study, we proposed an underactuated mechanism for compaction devices. Using the metamorphic design theory and bistable structures, stiff and compliant states are made for a horizontal plane and curved surface with only a single actuator. The outline of the paper is organized as follows. In Section 2, the requirement analysis and execution process of the designed mechanism are proposed. The kinematic models and validation are established in Section 3. In Section 4, the simulation and the analytical results are also presented. Following the simulation and results, a thorough discussion of the performance is provided in Section 6.
2. Methods
2.1. Premise and Conceptual Design
2.1.1. Design Premise
The stability of the force is defined as the capability of the system to conform to a mold surface. We use the standard deviation of contact force between a compaction roller and a mold to describe the response to disturbance and the self-adaptivity of the mechanism. Equation (1) is as follows:
where is the contact force between the primary roller and a mold in Newtons, and is the average value of the contact force in Newtons. In order to simplify the design and analytical modelling, the basic premise and assumptions are made; n represents the acquisition times of contact force during the entire compaction process.
- All masses and inertia of the links and parts are negligible;
- The flexible element only deforms in an elastic range along the link;
- The frame of the design is fixed with an AFP head, and the actuation force Fa is applied to the center of the part in the direction aligned to the mechanism frame (shown as link T in Figure 2).
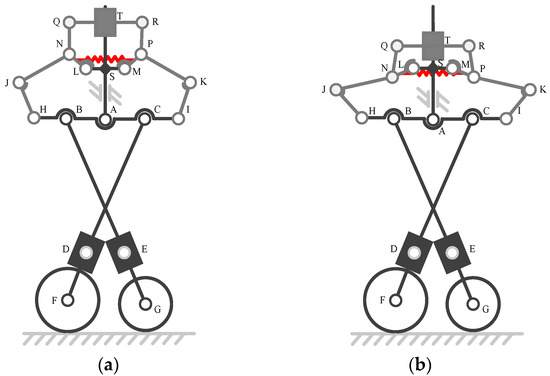 Figure 2. Schematic diagram of the conceptual design in a (a) compliant and (b) stiff state.
Figure 2. Schematic diagram of the conceptual design in a (a) compliant and (b) stiff state.
2.1.2. Requirements
Function analysis of an underactuated compaction mechanism is carried out to clarify the requirements of the device. Firstly, compared with traditional automated tape laying (ATL) systems, AFP heads not only can efficiently place fiber bands onto a flat surface but are more compatible with complex profiles (as shown in Figure 3). The specific function is given as follows: compact for flat surfaces, and passively adjust the posture of a compaction roller for complex surfaces. As a result, there should be greater flexibility for the compaction device of an AFP head concerning complex geometrical profiles. Once a flat surface has been produced, the compliance should reduce and remain unchanged until compacting a curved surface. Herein, the compaction mechanism should be separated into two states, namely the compliant state and the stiff state. The transformation between two states can be obtained by the actuation. Furthermore, it is worth noting that adjusting the posture of a compaction roller should not influence the force acting on the compaction segments. Otherwise, the static force equilibrium and reconfiguration of the mechanism will be changed. Additionally, a single-driven mechanism is considered to implement the motion of surface lamination and stiffness adjustment.
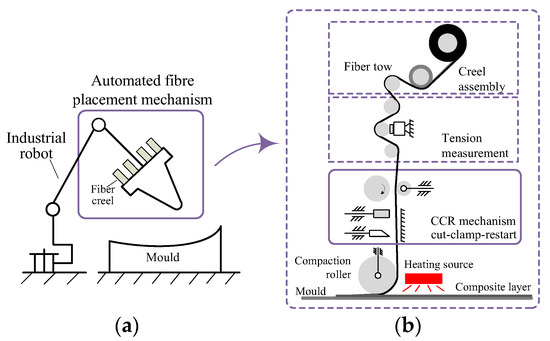
Figure 3.
(a) An automated fiber placement system; (b) a single fiber transmission path.
2.2. Final Concept
With the intention of generating a conceptual design, we investigated underactuated mechanism design to understand the working principle of configuration adaptation. As a means of adjusting stiffness, variable kinematic joints are designed using geometric limits and/or constrained forces [32]. This type of joint is essential to achieving the expected movement for metamorphic mechanisms. Special focus is given to the compaction movement and limited space, so that linear actuation, such as a linear motor and pneumatic cylinder, is selected. The basic schematic solutions are formed by the above findings and then redesigned for an underactuated compaction mechanism with an implemented adjustable posture, as shown in Figure 2.
For the interpretation of Figure 2, the basic framework is a linkage underactuated mechanism, and another metamorphic mechanism is merged to change the compliance of the compaction mechanism. As expected, a single driver is adopted to implement the action of compaction and to change the compliance of the mechanism. This is conducted by allocating the actuation force to part (HAI) through a bistable structure (NLMP).
In Figure 2a, two compaction segments, namely an auxiliary roller and a primary roller, are designed for the compaction mechanism. This concept is similar to the design of the planar-compliant grasper in Ref. [29]. These two segments are connected with part (HAI) at one end, and with the prismatic joint in D and E at the other end. The two stable positions of the bistable structure correspond to the stiff state and compliant state of the compaction mechanism. The compliant state represents that the posture of each compaction segment can adaptively realize fast regulation against any curvature changes in the mold surface. The stiff state implies that the postures of the compaction segments remain, which is suitable for laminate structures with high repeatability. Only when the actuation force exceeds a specific threshold can the stiffness of the mechanism change from compliant to stiff. The principle of conforming curved surfaces of the compaction mechanism is based on the rotation and translation of the linkages of the segments (CF and BG). The linkages rotate corresponding to the exact movement of these two segments and the stiffness of the spring (DF and EG). Both linkages are related to part (HAI), therefore, the conformity of the compaction mechanism will be affected by the spring stiffness.
To achieve the stiffness transformation, the symmetrical bistable structure is designed to be attached to the translational joint S of the compaction mechanism. The bistable structure includes a translational joint T and six rotational joints. In the compliant state, the rotational degree of freedom (DOF) in joints L and M is restricted by a geometric limit and a preloaded spring NP, which is at a stable position, as shown in Figure 1a. The actuation force is at translational joint T following the axis TA. The transformation occurs as the actuation force exceeds a certain threshold and the restraint of joints L and M will be gradually released. Consequently, the type of the variable kinematic joints J and K is changed from a rotational pair to fixed pair. When combined with the force of spring NP, the bistable structure is at a second stable position, as shown in Figure 2b.
Specifically, due to the preloaded spring and geometric limit, the actuation force at translational joint T is transmitted into joint A through the bistable structure (Figure 2a). Thus, part HAI can passively rotate and allocate the actuation force between two compaction segments. This allows the mechanism to compact a mold surface to a certain extent. Furthermore, the connection between the bistable structure and the underactuated mechanism can rotate following the movement of part HAI. In Figure 2b, the angles between parts JH–JN and IK–KP are at a minimum. The applied force at translational joint T is directly delivered to joints H and I. In other words, the freedom of the closed chain IHJNTPK is zero. As a result, symmetrical forces are applied to joints H and I to keep the compaction segments in a stable position, which can be regarded as a stiff state
Following the concept, Figure 4 describes the lamination process of the compaction mechanism. It illustrates how the mechanism places fiber tape onto a surface in its compliant and stiff state. The mechanism is on a compliant surface for curved surfaces (shown in Figure 4a–d). At first, the actuation force is exerted on translation joint T, and the roller segments compact a flat surface (Figure 4a,b). After compacting a curved surface, the contact force of one of the rollers changes and the link BAC rotates around point A to adjust the curved surface passively (Figure 4c,d) rather than by changing the posture of the AFP heads. When the stiffness of the mechanism changes, the actuation force should be larger than the threshold value given by a preload spring and the bistable structure (Figure 4e,f). The position of the primary and auxiliary rollers relative to the AFP head is fixed. In this state, fiber straps can be compressed onto a plane with high efficiency and quality. The mechanism is kept in the stiff state until the actuation force exceeds the spring force and switches to the compliant state. This brings the compaction mechanism return to its initial configuration, as shown in Figure 4a.
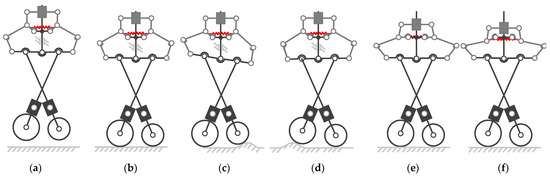
Figure 4.
Conforming movement of the compaction mechanism in which (a–d) describe how the mechanism conforms to an arbitrary surface passively in compliant state, while (e,f) describe the transformation from compliant state to stiff state for sheet manufacturing.
3. Analytical Model
In this section, analytical models are established and simulated in MATLAB. The analytical models give insight into the behavior of the compaction mechanism when the compaction roller compresses fiber straps into a mold surface along a predetermined path. In the compliant state, the part BAC rotates and both compaction segments maintain compression of the mold surface. In the stiff state, the part BAC can no longer rotate and stay in a symmetrical position. In particular, the bistable structure and geometric limits do not allow the part BAC to rotate and, instead, the part BAC translates in the axial direction. As a result, the attitude of compaction segments is fixed.
The modelling and resolving processes are introduced and detailed. The geometric equation of each part is built representing the configuration of the mechanism and the posture. Combined with the force balance equation, the contact forces of the segments can be calculated based on the geometric relationship of molds in both compliant and stiff states. Thus, the geometric relationship and force distribution are determined for a given roller displacement. The stiffness transformation process is also modelled, and the threshold value of actuation force is given. In order to verify the analytical model in MATLAB, we also conducted a similar experiment in ADAMS.
The geometric equations and static force analysis are discussed as follows.
3.1. Compaction Mechanism Geometry Equation
The original point of the coordinate system XOY is coincident with the center of DE. Basically, in the stiff state, these two compaction segments can place fiber tapes on a flat plane, and the geometric relationship of each part’s length and roller radius can be obtained in Equation (2). In the compliant state, the part BAC rotates around A to adjust a curved surface, so that two ways of the compaction rollers making contact with the mold are considered. Figure 5 shows these two ways. In both cases, the relation of angles and positions for the compaction segments (FC and BG) can be described in the following Equation (2), and the exact length of each part can be calculated in Equation (3) through (7):
where is the degree between the part (BC) and (CF) in rads at the initial state of the compaction mechanism and, in this case, ; and represent the radius of the primary roller and the auxiliary roller, respectively; li represents the length of each part i in millimeters (Figure 5).

Figure 5.
Schematic diagram of compaction segments conforming arbitrary surfaces with different longitudinal displacements, illustrating the lifting angles to , link lengths , , , and , longitudinal displacement and and other geometric information; (a) and (b) show the compacting process corresponding to Figure 4d,c, respectively.
The geometric information of the underactuated mechanism and length of each part can be calculated in Equation (3) through (7), as follows:
with the following:
3.2. Contact Force
In the compliant state, the actuation force of the compaction mechanism is applied to the translational joint in point A. Through the parts (BAC, BG, and CF), the actuation force leads to the contact forces and . The contact forces are related to the lifting angle and displacement of part BAC. Figure 6a shows the adjustment of the compaction mechanism and the force distribution. Based on the geometric analysis, the relation of the actuation force Fa and the contact forces can be expressed in Equation (8) through (11), as follows:
with the following:
where and represent the angles between tangent vectors of the contour and horizontal direction.

Figure 6.
Schematic diagram of force distribution for the compaction mechanism conforming a surface in both (a) the compliant state and (b) the stiff state, illustrating the actuation force , contact forces and , and the frame forces and .
The effect of the bistable structure and transformation process are illustrated in Figure 7. It shows the bistable structure will be triggered if the actuation force exceeds the threshold value given by a linear spring. The relationship of the actuation force Fa with respect to the spring force Fs can be expressed in Equations (12) and (13) as follows, so that the threshold value of the actuation force is obtained:
with the following:
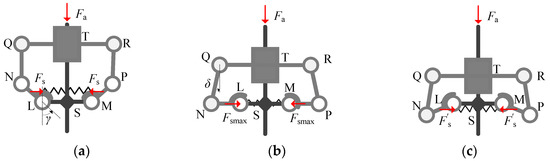
Figure 7.
Schematic diagram of compliant bistable structure in different positions: (a) a static equilibrium position; (b) an unstable position; (c) another static equilibrium position.
In the case of the compaction mechanism in the stiff state, as shown in Figure 6b, it indicates that parts JH and JN, and IK and BK, are bounded by a mechanical stop and the spring force. As a result, the two compaction segments (BG and CF) are distributed symmetrically. Using the expressions and in Equations (8) and (9), the contact force in the stiff state can then be calculated according to Equations (14) and (15). Thus, the motion characteristics and response behavior of the underactuated compaction mechanism are acquired.
3.3. Dimensional Design of the Concept
Based on the above analytical models, the specific dimension of the compaction mechanism is designed as follows. The lengths of the compaction segments and rollers are firstly determined. The dimensions of the bistable structure and spring are then fixed. The threshold value set for actuation force is designed based on the range of contact force. Finally, considering the workspace of the underactuated mechanism, the links’ dimensions between the bistable structure and the underactuated mechanism (BCDE) are determined.
Given a mold curvature with a 10 mm height difference and a minimum radius of 40 mm to be adjusted for two compaction rollers, the total length of the compaction segments and rollers is determined. As for the underactuated mechanism, the specific parameters are determined by minimizing the angle between the direction of contact force and compaction segments with the following conditions. Herein, mm, 300.8 mm,40 mm, = 32 mm, 28 mm, and 60 mm.
The rest values we used for the compaction mechanism are listed in Table 1. Their value was obtained by maximizing the axial pull-out force, under the following conditions.

Table 1.
Optimized dimensions of the compaction mechanism.
- Contact forces must be required to be positive and to apply between the compaction roller and mold surface;
- Unstable compaction behavior and singular configuration are avoided by obtaining a consistent force perpendicular to the contoured surfaces;
- Clashing or overlapping among the components must be avoided.
3.4. Experiments Analysis
A mechanical model of the final design is established and illustrated in Figure 8. These components are connected by using axles with a radius of 5 mm. Bearings and guide rails are used to realize the translational joint T. The ground links are rigidly conjoined with the AFP head. The bi-stable structure is designed to have a maximum contact force of 180 N as an example. By connecting a pneumatic cylinder via the part QR to the translational joints, a constant actuation force can be obtained, which is not shown in Figure 8.
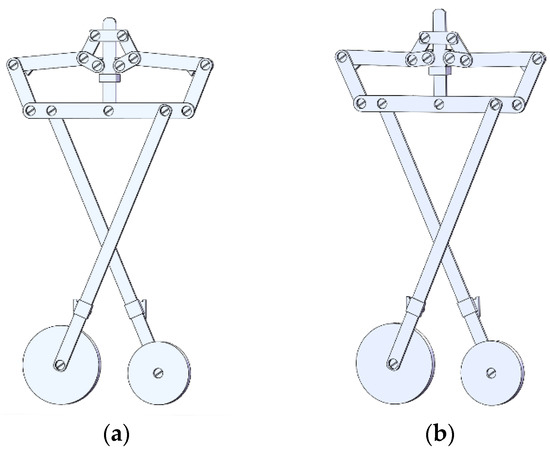
Figure 8.
Prototype of the planar underactuated compaction mechanism with (a) the compliant state and (b) the stiff state.
Figure 9a manifests that experiment A. The compaction mechanism passed through a curved surface with a radius of 40 mm at a constant speed along the x-axis in the compliant state. The actuation force of the pneumatic cylinder was 160 N. The contact forces of both rollers are determined when two rollers contact the mold surface and create the input forces. We also conducted experiment B, where the compaction mechanism passed through a flat surface at a constant speed in the stiff state. The actuation force of the pneumatic cylinder remained constant.


Figure 9.
Results comparison. Here, (a) shows the schematic diagram of the mold’s geometric information for experiment A; (b) shows the MATLAB results in and the ADAMS results in the compliant state; (c) shows the MATLAB results in and the ADAMS results in the stiff state; (d) shows the schematic diagram of the mold’s geometric information for experiment C; (e,f) show the results for the force of experiments for different curved surfaces in ADAMS.
With experiment C, the mold surfaces with different radii and arch heights were established, and the actuation force Fa was applied to compact the link T. After that, the compaction mechanism in the compliant state moved along the x-axis at a constant velocity through curved surfaces (as shown in Figure 9d). In order to demonstrate the advantage of the underactuated compaction mechanism, the conventional compaction mechanism designed in the Ref. [33] experiment was built and compacted on the same curved surface with a radius of 50 mm and 150 mm as experiment D. Experiments A and B are conducted in ADAMS and MATLAB to validate the analytical models. Experiments C and D are conducted in ADAMS to compare the performance between the conventional mechanism and the conceptual design. In both experiments, the mechanism was moved step by step, and the resulting forces for each roller position were measured.
4. Results
The results of the analytical models in MATLAB, the simulation in ADAMS, and the errors for the two methods are illustrated in Figure 9b. It shows the resultant contact force on the primary roller in the compliant state. As shown in the dotted line in Figure 9b, the contact force held steady at 104 N, except for the collision at the beginning and when the curvature changes. As a result, the error for the two methods is less than 12 N, shown as the blue solid line in Figure 9b.
Figure 9c presents the resultant forces on two compaction rollers in MATLAB and ADAMS, as well as errors for the two methods. The graph of the stiff state in ADAMS starts at the origin. Generally, the contact forces on the primary and auxiliary rollers remain at 100 N and 98 N, respectively. Nevertheless, there is a slight fluctuation during the compaction process, which might be influenced by the contact properties of the rollers and molds. A similar tendency also can be found in the analytical model. As a result, the error for these two methods is less than 1.5 N.
Figure 9e shows the contact force between the primary roller and the mold with different radii and arch heights in the ADAMS model. For both curvatures, a fluctuation within 22 N can be observed. Meanwhile, the standard deviations of contact forces are 25.7 when the mechanism compacted the mold with an arch height h of 5 mm, and the rest are 7.8. In the case that the AFP head did not actively change the posture for the surface, the curvature radius is smaller, and then the force fluctuation is more prominent. It could be the fact that the force fluctuation is mostly influenced by the difference between the two rollers’ displacement on the y-axis. This also results in configuration changes.
Figure 9f shows the resulting forces between the compaction roller and the mold in experiment D in which the traditional compaction is composed of a pneumatic cylinder and compact segment. The actuation force was 100 N. A large fluctuation for both cases can be observed once the difference between the two rollers’ displacement in the y-axis changes. This phenomenon is more obvious in the case of that arch height h of 8 mm, as shown in the dotted line, and the standard deviation of the contact force is 384.3. As a result, the standard deviations of contact forces are 25.7 when the mechanism compacted the mold with an arch height h of 5 mm.
5. Discussion
The resultant forces obtained from the simulation and the corresponding errors shown in Figure 9b,c show that the simulation does resemble the behavior of the analytical model well. Herein, this paper declares that the analytical models are verified. The anomalous amplitude of contact force in the results of experiment A shows that the configuration and force distribution is strongly influenced by the collision and vibration. Comparing the standard deviation of contact force in Experiments C and D, the benefits of the underactuated mechanism can be seen. The fluctuation in Figure 9f is more apparent than in Figure 9e. Especially compared with conventional mechanisms, the standard deviation of contact force within the underactuated mechanism is significantly reduced. This concept allows for greater flexibility and better responsiveness to a sophisticated surface. There is still a small collision and vibration present, as indicated by the tendency of the results. It can be expected that the robustness of the compaction mechanism could be improved by optimizing the dimensional design.
The concept of using available DOF, as shown in this article, is capable of changing the posture and configuration in two states separately. This is carried out to ensure the manufacturing stability of laminates and complicated structures rather than adding an actuator. Literally, according to the curvature changes in the mold surface, the compaction mechanism can regulate the configuration and state. It is designed with the help of a bi-stable structure, in such a way that the two stable positions correspond to the two states. When the actuation force is less than the threshold value, it is possible to self-adaptively adjust the posture of compaction segments within the workspace. The preload of the spring can be changed to regulate the threshold value of the bistable structure from a compliant and stiff state.
An advantage of an underactuated compaction mechanism compared to a traditional compaction mechanism would be that AFP manipulation motion planning could be greatly simplified but with accurate force control accuracy, so as to improve productivity. Furthermore, each laminated layer would be compacted twice to avoid defects, such as porosity, cracks, and non-homogeneous hardness. Meanwhile, the exact configuration of the mechanism is unidentified before the compaction segments make contact with the mold surface. The symmetrical structure of the mechanism only has a reference, and two segments have the freedom to be able to adjust the curved surface slightly. The specific arrangement of such a mechanism in which the roller’s movement is effectively limited.
6. Conclusions
This article proposed the first thorough investigation of underactuated compliant compaction mechanisms which are able to adjust complex-shaped surfaces passively. The concept and design procedure, as well as the modelling analysis of the underactuated compaction mechanism, are discussed. Due to the combination of a bi-stable structure, the compliant state and stiff state can be used for different types of mold surface. The mechanism in the compliant state has relatively high compliance and the part BAC is allowed to rotate with respect to a mold surface instead of regulating the mechanism’s posture actively. Additionally, a transformation between two states occurs when the actuation force on the translational joint T exceeds a specific value given by the bi-stable structure. Therefore, the combination retains the advantages of underactuated mechanisms and bi-stable structures while eliminating their defects instead of increasing the number of actuators.
Ideally, this research can be used to simplify motion planning of AFP systems when conforming complicated mold surfaces with fewer defects, such as gaps/overlaps or wrinkles. The analytical results were verified by the experiments in ADAMS. It is also interesting to note that the standard deviations of the underactuated mechanism are 25.5 and 7.8 which is smaller than the standard deviation of the traditional compaction mechanism. The results show that the underactuated compaction mechanism with self-adaptive capabilities has excellent potential to conform to sophisticated profiles. More comprehensive experiments will be conducted, including dimensional optimization and dynamic performance analysis, since these parameters and properties are more sensitive, so that the realization of the underactuated compaction mechanism can be reached.
Author Contributions
Conceptualization, F.L. and W.Z.; methodology, F.L.; software, S.W.; validation, F.L., M.Y. and W.Z.; formal analysis, J.S.; investigation, F.L.; writing—original draft preparation, F.L.; writing—review and editing, F.L.; visualization, S.W.; supervision, X.D.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 52205003, Zhejiang Provincial Natural Science Foundation, grant number LD22E050011, and Ningbo Key Projects of Science and Technology Innovation 2025 Plan, grand number 2022Z070.
Acknowledgments
The authors would like to acknowledge the support from their research team and Sun Zhen.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this paper.
References
- Liu, F.; Ferraris, E.; Ivens, J. Mechanical Investigation and Microstructure Performance of a Two-Matrix Continuous Carbon Fibre Composite Fabricated by 3D Printing. J. Manuf. Process. 2022, 79, 383–393. [Google Scholar] [CrossRef]
- Croft, K.; Lessard, L.; Pasini, D.; Hojjati, M.; Chen, J.; Yousefpour, A. Experimental Study of the Effect of Automated Fiber Placement Induced Defects on Performance of Composite Laminates. Compos. Part A 2011, 42, 484–491. [Google Scholar] [CrossRef]
- Skinner, M.L. Trends, Advances and Innovations in Filament Winding. Reinf. Plast. 2006, 50, 28–33. [Google Scholar] [CrossRef]
- Grant, C. Automated Processes for Composite Aircraft Structure. Ind. Robot Int. J. 2006, 33, 117–121. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, F.; Jiang, T.; Minghui, Y.I.; Chen, W.; Ding, X. Overview of Current Design and Analysis of Potential Theories for Automated Fibre Placement Mechanisms. Chin. J. Aeronaut. 2022, 35, 13. [Google Scholar] [CrossRef]
- Oromiehie, E.; Gain, A.K.; Prusty, B.G. Processing Parameter Optimisation for Automated Fibre Placement (AFP) Manufactured Thermoplastic Composites. Compos. Struct. 2021, 272, 114223. [Google Scholar] [CrossRef]
- Bendemra, H.; Vincent, M.J.; Compston, P. Optimisation of Compaction Force for Automated Fibre Placement. In Proceedings of the 8th Australasian Congress on Applied Mechanics, ACAM 2014, as Part of Engineers Australia Convention 2014, Melbourne, Australia, 25–26 November 2014; pp. 957–965. [Google Scholar]
- Vaniglia, M.M. Fiber Placement Head. U.S. Patent No. 5,110,395, 5 May 1992. [Google Scholar]
- Martin, J.P. Multiple Tape Laying Apparatus and Method. U.S. Patent No. 7,293,590, 13 November 2007. [Google Scholar]
- Yarlagadda, S.; Gillespie, J.W., Jr. Development of an Automated Materials Placement (AMP) System for Composite Processing. In Proceedings of the SAMPE 2012, Baltimore, MD, USA, 21–24 May 2012; pp. 1–14. [Google Scholar]
- Denkena, B.; Schmidt, C.; Weber, P. Automated Fiber Placement Head for Manufacturing of Innovative Aerospace Stiffening Structures. Procedia Manuf. 2016, 6, 96–104. [Google Scholar] [CrossRef]
- Mischler, P.L.; Tingley, M.C.; Hoffmann, K. Compaction Roller for a Fiber Placement Machine. U.S. Patent No. 7,810,539, 12 October 2010. [Google Scholar]
- Johnson, B.A. Conformable Compaction Apparatus for Use with a Fiber Placement Machine. U.S. Patent No. 6,390,169, 21 May 2002. [Google Scholar]
- Steeg, M.; Schledjewski, R.; Schlarb, A.K. Automation Implementation and Process Development of Thermoplastic Tape Placement for 3-Dimensional Parts. SAMPE J. 2006, 42, 18–24. [Google Scholar]
- Chapman, M.R.; Watson, R.M.; Williams, S.H. Compaction Method and Device for Automated Fiber Placement. U.S. Patent No. 9,849,635, 26 December 2017. [Google Scholar]
- Miller, L.G.; Harris, D.G.; Benson, V.M.; Shupe, K.G.; Wade, K.L. Compaction Device for Fiber Placement Using Interdependent Segment Travel. U.S. Patent No. 8,042,594, 25 October 2011. [Google Scholar]
- Hu, X. Design and Research of Fiber Placement Machine. Ph.D. Dissertation, Wuhan University of Technology, Wuhan, China, 1 June 2011. [Google Scholar]
- Van Hoa, S.; Duc Hoang, M.; Simpson, J. Manufacturing Procedure to Make Flat Thermoplastic Composite Laminates by Automated Fibre Placement and Their Mechanical Properties. J. Thermoplast. Compos. Mater. 2017, 30, 1693–1712. [Google Scholar] [CrossRef]
- Khan, M.A.; Mitschang, P.; Schledjewski, R. Identification of Some Optimal Parameters to Achieve Higher Laminate Quality through Tape Placement Process. Adv. Polym. Technol. 2010, 29, 98–111. [Google Scholar] [CrossRef]
- Oldani, L.E. Fiber Placement Head with Secondary Compaction Arrangement. U.S. Patent Application No. 15/639,944, 30 June 2018. [Google Scholar]
- August, Z.; Hauber, H. Additive Manufacturing of High-Performance Composite Structures. 2014. Available online: https://www.semanticscholar.org/paper/ADDITIVE-MANUFACTURING-OF-HIGH-PERFORMANCE-August/a2813fc138d9be4f71976f7ae56a48d12036f874 (accessed on 1 September 2022).
- Tam, A.S. Control of Thermoplastic Tow Placement. U.S. Patent No. 5,447,586, 5 September 1995. [Google Scholar]
- Lamontia, M.A.; Gruber, M.B.; Waibel, B.J.; Cope, R.D.; Hulcher, A.B. Conformable Compaction System Used in Automated Fiber Placement of Large Composite Aerospace Structures. In Proceedings of the 23rd SAMPE EUROPE Conference, Paris, France, 9–11 April 2002; pp. 9–11. [Google Scholar]
- Sorrentino, L.; Carrino, L.; Tersigni, L.; Leone, A. Innovative Tape Placement Robotic Cell: High Flexibility System to Manufacture Composite Structural Parts with Variable Thickness. J. Manuf. Sci. Eng. 2009, 131, 041002. [Google Scholar] [CrossRef]
- Firouzeh, A.; Paik, J. Grasp Mode and Compliance Control of an Underactuated Origami Gripper Using Adjustable Stiffness Joints. IEEE/ASME Trans. Mechatron. 2017, 22, 2165–2173. [Google Scholar] [CrossRef]
- Qiao, S.; Guo, H.; Liu, R.; Deng, Z. Self-Adaptive Grasp Process and Equilibrium Configuration Analysis of a 3-DOF UACT Robotic Finger. Mech. Mach. Theory 2019, 133, 250–266. [Google Scholar] [CrossRef]
- Kim, H.K.; Jeong, H.; Park, J.; Park, J.; Kim, W.-S.; Kim, N.; Park, S.; Paik, N.-J. Development of a Comprehensive Design Guideline to Evaluate the User Experiences of Meal-Assistance Robots Considering Human-Machine Social Interactions. Int. J. Hum. Comput. Interact. 2022, 38, 1687–1700. [Google Scholar] [CrossRef]
- Aukes, D.; Kim, S.; Garcia, P.; Edsinger, A.; Cutkosky, M.R. Selectively Compliant Underactuated Hand for Mobile Manipulation. In Proceedings of the IEEE International Conference on Robotics & Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 2824–2829. [Google Scholar]
- Stavenuiter, R.A.J.; Birglen, L.; Herder, J.L. A Planar Underactuated Grasper with Adjustable Compliance. Mech. Mach. Theory 2017, 112, 295–306. [Google Scholar] [CrossRef]
- Tutsoy, O.; Barkana, D.E. Model Free Adaptive Control of the Under-Actuated Robot Manipulator with the Chaotic Dynamics. ISA Trans. 2021, 118, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Qin, G.; Wu, H.; Cheng, Y.; Pan, H.; Zhao, W.; Shi, S.; Song, Y.; Ji, A. Adaptive Trajectory Control of an Under-Actuated Snake Robot. Appl. Math. Model 2022, 106, 756–769. [Google Scholar] [CrossRef]
- Zhang, W.X.; Ding, X.L.; Dai, J.S. Morphological Synthesis of Metamorphic Mechanisms Based on Constraint Variation. ARCHIVE Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2997–3010. [Google Scholar] [CrossRef]
- Baho, O.; Ausias, G.; Grohens, Y.; Férec, J. Simulation of Laser Heating Distribution for a Thermoplastic Composite: Effects of AFP Head Parameters. Int. J. Adv. Manuf. Technol. 2020, 110, 2105–2117. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).