Spectral Correlation for Signal Presence Detection and Frequency Acquisition of Small Satellites

Abstract

Challenges in interference-limited satellite detection arising from the low-earth orbit (LEO) and the Industrial, Scientific and Medical (ISM) frequency bands are addressed. In particular, a novel signal presence detector based on cyclostationary signal properties is proposed and analyzed for a low signal-to-noise-plus-interference ratio (SINR) regime. The performance of the proposed detector, which is applicable to various small-satellite scenarios, is evaluated on both simulated and real-world measurement data. This measurement data has been collected from the scientific satellite mission “Picosats Realizing Orbital Propagation Calibrations using Beacon Emitters” (PROPCUBE).

1. Introduction

The great potential of small satellites is increasingly recognized. The integration of satellites in both existing and emerging networks allows the development of new services, such as aeronautical ad hoc networking [1] and the Internet of Things (IoT) in Smart Cities [2]. Moreover, low-earth orbit (LEO) small-satellite constellations are a key enabler in 5G and post 5G networks to provide ubiquitous network coverage [3]. Many research institutions as well as companies are investigating the challenges and possibilities imposed by small satellites, sometimes by using their own small-satellite space missions. The Space Systems Academic Group (SSAG) at the Naval Postgraduate School (NPS) in Monterey, CA, has been building and operating small satellites for many years. Especially on the PROPCUBE mission, the need for reliable signal presence detection arose in two use cases: For continuous health monitoring and for frequency correction. Health monitoring is extremely important in the early stages of a satellite’s life to verify its successful deployment, the so-called “bringing into use”. Moreover, when operating the satellite, signal presence detection can be used to provide an accurate Doppler shift estimate at low elevation angles. Hence, the establishment of the actual communication link can be performed earlier in an overflight and successful signal synchronization and demodulation are facilitated. In general, techniques for signal presence detection can be applied in the context of both civil and military applications, such as cognitive-radio concepts, to provide an effective spectrum usage. In 5G and beyond 5G networks, satellites will be integrated into the radio access networks to enable seamless communication over large distances and to provide global coverage. To this end, several work items have been recently started by the 3rd Generation Partnership Project (3GPP) that investigate the seamless transmission of the new radio (NR) waveforms via non-terrestrial relays [4]. In this context it has been reported that the high Doppler shifts introduced by LEO satellites require coarse compensation measures in addition to the carrier frequency synchronization of NR. In [5], Doppler compensation via Global Navigation Satellite System (GNSS) data is proposed, leading to a residual Doppler estimation error on the order of kilohertz due to positioning errors. To implement low sub-carrier spacings and thus to ensure an efficient spectrum usage, spectral correlation can be exploited to compensate for the residual Doppler estimation error.

In contrast to conventional signal detection problems, LEO satellite signal detection is complicated by physics: The small satellite size implies small transmit power. The signal power received at the ground station varies greatly in the course of an overflight due to the change of distance and due to multipath propagation effects leading to a dynamic signal-to-noise ratio (SNR) at the receiver. Moreover, a substantial time-varying Doppler shift is introduced by the high satellite velocities at LEO causing uncertainty in the frequency domain. In many scenarios, no exclusive frequencies are assigned to the communication link resulting in an environment of high interference, which is mostly ground-based and, therefore, tends to have high energy. The effects of terrestrial interference on aeronautical satellite communication have been studied in [6], pointing out substantial impacts despite receiver antenna directivity. In the future, an increase of space-based interference is expected due to new large satellite constellations, exacerbating the detection problem.

Conventional signal detection techniques, such as energy-based detection [7], are prone to raise false alarms under interference. The dynamic range of signal power received at the ground station complicates thresholding approaches in general. Signal detection achieved by pilot insertion or preambles requires at least coarse synchronization of the signal in frequency and time, which is hard to accomplish for low SNRs. New methods that are able to perform reliably in the described environment must be developed.

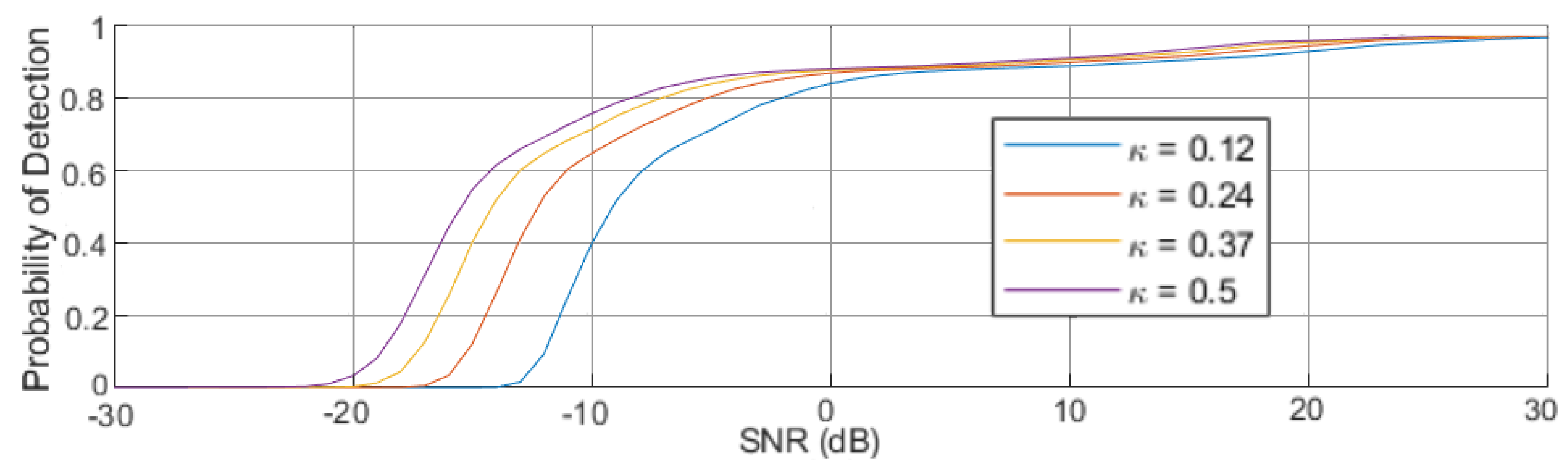
In this paper, we propose a novel detector with an adaptive detection statistic tailored to the LEO small satellite scenario based on the cyclostationary nature of communication signals. Cyclostationary approaches are considered to be tolerant against noise and interference since noise does not exhibit cyclostationarity and different signals can be distinguished by their different cyclic features. Cycle detectors as first proposed in [8] exploit second-order cyclostationarity. For scenarios with non-stationary noise, performance advantages of cycle detectors over energy-based detectors have been shown [9]. However, the time-varying Doppler shift of the LEO satellite channel complicates the estimation of cyclic features. In fact, time-varying frequency offsets tend to destroy the cyclostationarity exhibited in the received signal. In this paper, we demonstrate that knowledge about the orbital mechanics of LEO satellites enables the estimation of cyclic features. Although the concept can be applied to many modulation schemes, in this paper we focus on Gaussian frequency-shift keying (GFSK) modulated signals. GFSK is used in technologies like SigFox, a candidate for the integration of 5G into satellite networks [10]. It combines excellent power efficiency with acceptable bandwidth efficiency [11]. Moreover, GFSK belongs to the more complex class of non-linear modulation schemes with 0 dB peak-to-average power ratio, it can be decoded with very low-complexity linear phase-shift-keying receivers. Hence, an adaptive detection statistic for GFSK modulated signals based on a derivation of the ideal spectral correlation function (SCF) is proposed to cope with the dynamic power range of the received signal. The proposed detector is tested on real-world data, and effects of the LEO satellite channel at 914 MHz, i.e., Doppler shift, dynamic range of received power and interference, are presented.

The remainder of this paper is structured as follows: The PROPCUBE mission is introduced first. In Section 2.1, a brief history is provided, its research goals are explained, the challenges of the communication link are pointed out. An analysis of the given communication link and a channel model is given in Section 2.2. Section 3.1 introduces the SCF, which is then tailored to the special case of GFSK modulated signals. To be able to estimate cyclic features for signals with time-varying Doppler rates, knowledge about the LEO is exploited in Section 3.3. The core of the proposed detector, its adaptive detection statistic, is proposed in Section 3.4. The detector performance is evaluated on both simulated and real-world data in Section 4.

2. Scenario and Communication Link

2.1. The PROPCUBE Mission

The cyclostationary detector developed as part of this research was tested against three identical small satellites in LEO called PROPCUBEs. The PROPCUBEs were a technology demonstration for the Naval Research Laboratory. Each satellite aided in mapping the Earth’s ionosphere by carrying a calibrated radio signal source and radiating over specific ground stations instrumented to analyze these signals as they were distorted by the ionosphere. The satellites were operated by NPS and have been utilized in numerous research projects including the one described in this paper. Given cost limitations, the satellites were launched as secondary payloads. One common form factor for such free-flying payloads is the CubeSat, an international standard by which each satellite measures in multiples of 10 cm${}^3$ and 1 kg “units”, or simply “U”. Common sizes for CubeSats range from 1U to 12U. The PROPCUBE satellites were each 1U and weighing approximately 1 kg. Two of the satellites launched in 2015 aboard the NROL-39 mission, and one launched in 2017 aboard the CRS-8 mission to the International Space Station. Given the size of a 1U CubeSat, there is very little onboard power generation from its solar cells. The limited power generation therefore severely restricts the power system and its ability to operate its other subsystems such as the flight computer and communications systems. These satellites each included two radios; the payload radio used for the ionospheric experiment, and the spacecraft bus radio used for command and control. The payload radio was only used for occasional scientific experiments and did not represent a challenge for signal detection given its continuous wave (CW) signal and repeating low bandwidth modulated signal. However, the command and control downlink presented numerous challenges for detection and demodulation. The factors complicating the downlink included a rotating satellite (the satellites had no active attitude control), only 1.5 Watts of maximum radio transmission power, a 914 MHz center frequency, which was subject to substantial ground-based interference, and low-cost yagi ground antennas tasked with tracking these satellites. The result was a low-performing downlink, which often resulted in dropped packets and lost satellite heath data. The uplink was not an area of concern given that the ground stations were limited to 100 W of power at a center frequency of 450 MHz and could therefore utilize high power amplifiers (HPAs), which closed the link to the LEO satellite with a substantial margin. One of the most valuable lessons learned from the mission was to avoid the 902–928 MHz ISM band for future downlinks due to the limitations in licensed transmission power and competing signals on the ground. The PROPCUBE mission was assigned this band due to ease of licensing; however, in subsequent programs the team has secured licenses in dedicated universal S-band (USB) channels, which experience less terrestrial interference and allow for more bandwidth.

Development of the cyclostationary detection algorithm was motivated by the need to overcome the weak downlink signal to extract mission data that would otherwise be lost. Detecting the presence of signal was important given that mission operations were mostly performed without operators sitting on the console. If an attempted contact was not able to demodulate data, a detection of signal would at least inform the operators that the satellite was functioning and available for future contacts. A lack of detected signal could trigger troubleshooting procedures, which would involve resetting the flight computer and attempting to clear common fault states “in the blind” from the ground until a downlink was re-established. These recovery techniques were used relatively often over the course of the mission. The fault states were due to known software and hardware issues, as well as occasional environmental effects such as radiation-induced single event upsets.

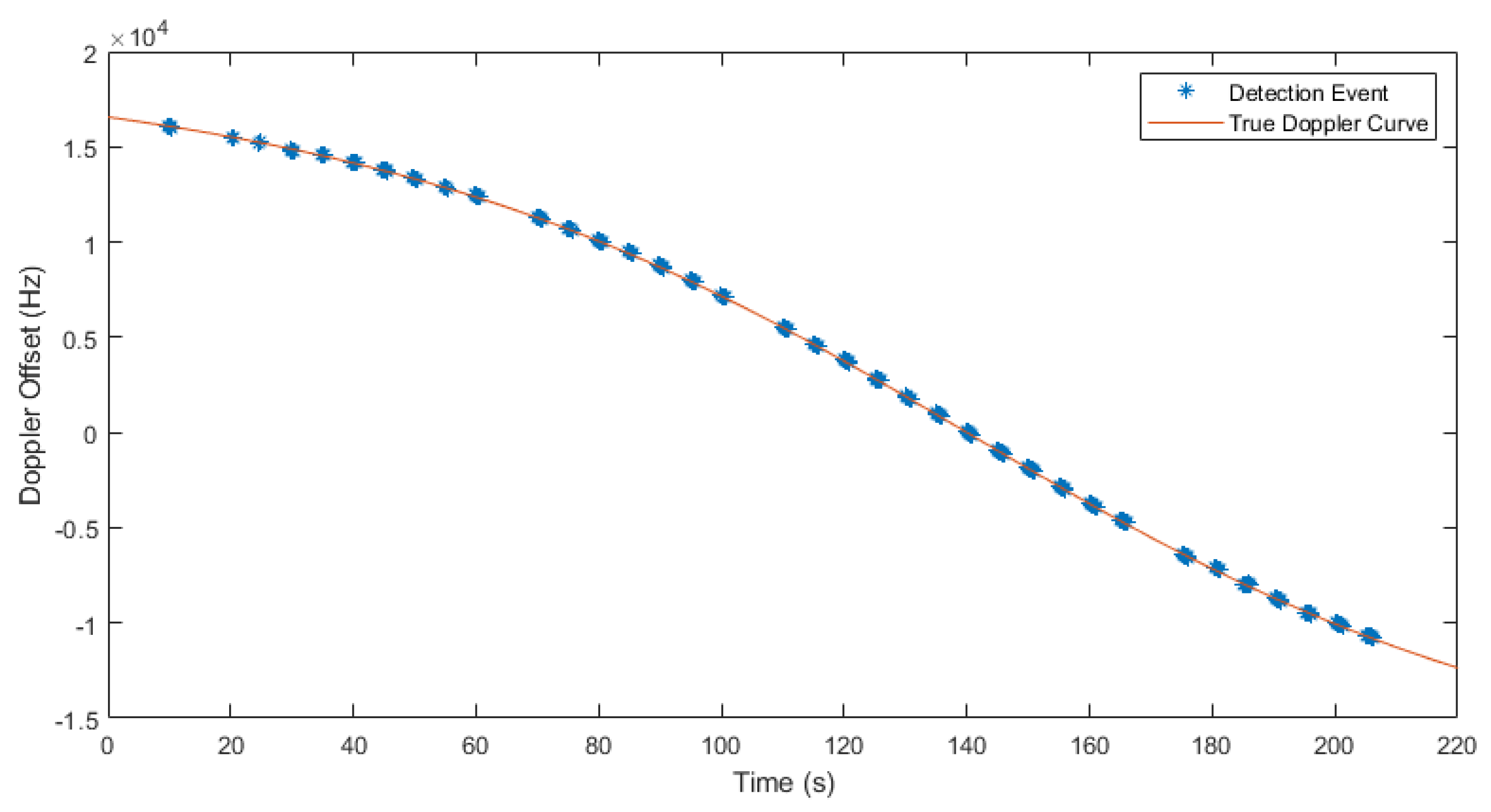
Using a brute-force energy-based signal detection technique was not feasible given the substantial radio frequency interference at each ground station. A signal unique to the satellite had to be found. Additionally, the weak signals were subject to a Doppler shift, as with any satellite, and though predictable, were calculated open-loop using the satellites’ estimated ephemeris, not the real-time shift as observed by the ground station. The difference between the two often ranged from 0.5 to 2 kHz and had the potential to affect the efficacy of the demodulation software. The cyclostationary technique was able to extract the real instantaneous Doppler shift for more precise frequency estimation, resulting in a higher likelihood of demodulation.

2.2. Communication Link

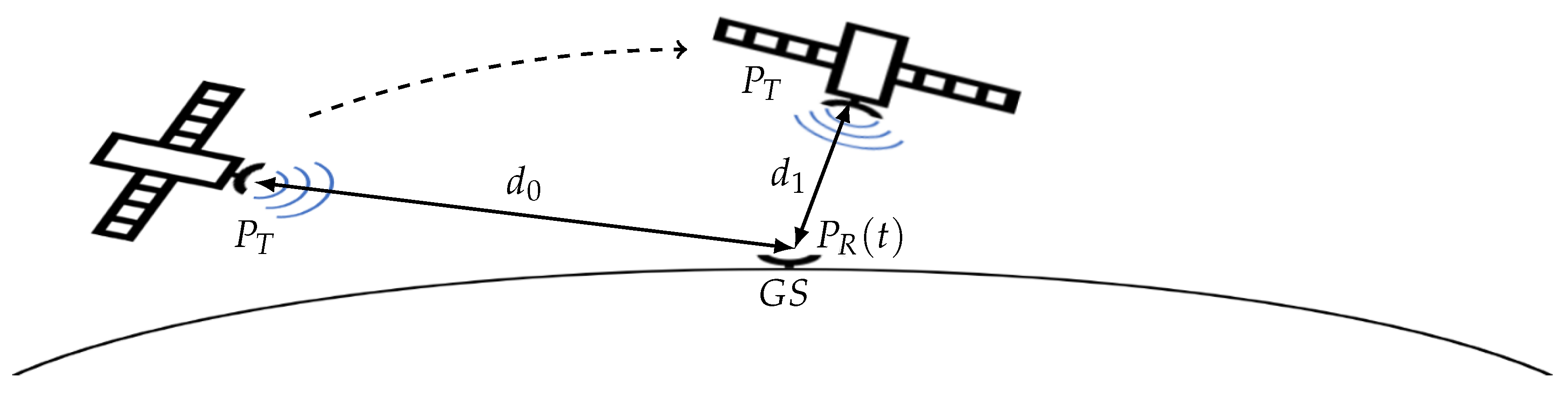
An illustration of the communication link is provided in Figure 1. The channel is considered to be line-of-sight (LoS) and multipath effects are not taken into account due to the directivity of the ground station (GS) antenna, which is following the satellite’s position in the course of an overflight. Ground reflections are neglected since the first contact of a satellite occurs at an elevation angle of 30${}^{\circ }$. The satellite is assumed to have a constant transmit power $P_T$, whereas the power $P_R\left(t\right)$ of the received satellite signal $s\left(t\right)$ changes due to the change of distance d from the satellite to the ground station. Taking stationary white Gaussian noise (WGN) $n\left(t\right)$ of variance ${\sigma }_n^2$ into account leads to a dynamic range of SNR at the GS.

Considering also interference $i\left(t\right)$ of arbitrary characteristics and power I, which is received due to high energy despite the ground-station antenna pattern, yields the received signal $r\left(t\right)$. Therefore, the received signal is composed of three components

$$r\left(t\right)=s\left(t\right)+n\left(t\right)+i\left(t\right)$$

(1)

and the SINR is defined by the ratio of received signal power $P_R\left(t\right)$ divided by the sum of interference power I and noise power ${\sigma }_n^2$.

In the PROPCUBE downlink, a GFSK modulated signal with modulation index $h=1$ and a symbol rate of $f_s=9600\frac{\mathrm{symbols}}{s}$ is used. The signal is transmitted in the ISM-band at 914 MHz via a dipole antenna with a power $P_T=1.76$ dBW. The overall link budget at a distance close to the zenith, corresponding to $d_1$ in Figure 1, yields a received power level of approximately $P_{R1}=-114$ dBm with all gains and losses as stated in

Table 1. Parameters used for the link budget.

Parameter	Value	Description
$P_T$	$1.76$ dBW	transmit power
$G_T$	$2.15$ dBi	gain of transmitting antenna
$Lout$	$-2$ dB	losses on the transmitting side
$G_R$	9 dB	gain of receiving antenna
$L_{FS}$	$-147.93$ dB	free space path loss at slant range $650$ km
$L_{atm}$	$-3$ dB	atmospheric losses
$L_{in}$	$-2$ dB	receiver input losses
$L_{point}$	$-1$ dB	losses due to satellite pointing error
$L_{polar}$	$-1$ dB	polarization losses
$P_{R1}$	$-114.02$ dBm	received signal power

.

To illustrate that this is a typical link budget, the received signal power $P_{R1}$ in captured data was estimated. The noise floor in the signal recording introduced by $n\left(t\right)$ was approximated to be thermal noise amplified only by the noise figure of the low noise amplifier (LNA). This is a valid approximation, since the noise figure of the entire receiver is dominated by the noise figure of the LNA according to the Friis formula [12]. Therefore, the overall noise figure was assumed to be 1.4 dB at 914 MHz corresponding to the LNA model Mini Circuits ZQL-900MLNW+ (13 Neptune Ave Brooklyn, NY 11235, USA). At an estimated SNR of 10.3 dB in a scenario close to the zenith, the received signal power results in $P_{R1}=$$-115.5$ dBm, which matches the above-mentioned forecast.

In Figure 2 and Figure 3, spectrograms of typical PROPCUBE bursts are presented. The GFSK lower and upper tone, as introduced in Section 3.2, can be observed from 0.23 to 1.23 s. The burst in Figure 2 was transmitted early in an overflight at an elevation angle of 35${}^{\circ }$, which corresponds to a Doppler offset of 16.7 kHz. The SNR was estimated to be 0.1 dB when interference seemed to be temporarily absent. In contrast, the SNR for the burst transmitted close to the zenith in Figure 3 was estimated to be 10.3 dB. Since the Gaussian noise component $n\left(t\right)$ is assumed to be stationary and the satellite transmits with constant power $P_T$, the change of received signal power is solely based on the change of distance from the satellite to the GS.

It becomes obvious that conventional thresholding approaches are not suitable in this environment. This corresponds to the experience of prior projects carried out in the SSAG, using variations of energy-based detection or spectral-line pair picking in the described context. The proposed detector must be able to cope with great changes in received signal power at the same time as minimizing the susceptibility to false alarms due to high power interference. Stated as a hypothesis testing problem, the detector must be able to reliably yield hypothesis $H_0$ or $H_1$ defined by:

$$\begin{array}{cc}\hfill & H_0:r\left(t\right)=n\left(t\right)+i\left(t\right),\hfill \\ \hfill & H_1:r\left(t\right)=n\left(t\right)+i\left(t\right)+s\left(t\right).\hfill \end{array}$$

(2)

3. Methods

3.1. Introduction to Cyclostationarity

Communication signals inherently exhibit cyclostationarity. A signal x(t) is said to exhibit cyclostationarity of second order in the wide sense if there exists at least one cycle frequency $\alpha \ne 0$ for which the cyclic autocorrelation function $R_x^{\alpha }\left(\tau \right)\ne 0$, where $R_x^{\alpha }\left(\tau \right)$ is defined by

$$R_x^{\alpha }\left(\tau \right)=\underset{T_b\to \infty }{lim}\frac{1}{T_b}{\int }_{-T_b/2}^{T_b/2}{R}_x(t,\tau )e^{-i2\pi \alpha t}dt$$

(3)

as the block length $T_b$ approaches infinity and $R_x(t,\tau )$ is the conventional autocorrelation function [9]. Via the cyclic Wiener relation, the SCF is defined by

$$S_x^{\alpha }\left(f\right)=\underset{T_b\to \infty }{lim}{\int }_{-\frac{T_b}{2}}^{+\frac{T_b}{2}}{R}_x^{\alpha }\left(\tau \right)e^{-i2\pi f\tau }d\tau ,$$

(4)

where f is the spectral frequency and $\alpha$ the cycle frequency [8]. Using an alternative definition of the SCF,

$$S_x^{\alpha }\left(f\right)=\underset{T_b\to \infty }{lim}\underset{U\to \infty }{lim}\frac{1}{U}{\int }_{-U/2}^{U/2}{I}_{T_b}^{\alpha }(t,f)dt,$$

(5)

where

$$I_{T_b}^{\alpha }(t,f)=\frac{1}{T_b}{X}_{T_b}(t,f+\alpha /2)X_{T_b}^{*}(t,f-\alpha /2)$$

(6)

is the cyclic periodogram and

$$X_{T_b}(t,f)={\int }_{t-T_b/2}^{t+T_b/2}x\left(v\right)e^{-i2\pi fv}dv$$

(7)

is the sliding Fourier transform, it becomes obvious that for a second-order cyclostationary signal there exist correlated frequency components [8]. The resulting characteristics of the SCF are known as cyclic features and vary greatly for different types of modulations, symbol rates, and pulse-shaping filters. Therefore, spectral correlation is a suitable approach not only for signal detection but also for signal classification [8].

3.2. SCF of a GFSK Modulated Signal

Let $s\left(t\right)$ be a GFSK modulated signal defined by

$$s\left(t\right)=exp\left\{j\pi h{\int }_{-\infty }^t\sum _{n=-\infty }^{+\infty }{a}_{n}g(u-n{T}_s)du\right\},$$

(8)

where $a_n\in \{\pm 1\}$ are independent and identically distributed symbols, $T_s$ is the symbol duration, h is the modulation index and $g\left(t\right)$ is a Gaussian pulse defined by

$$g\left(t\right)=\frac{1}{2T_s}\left[erfc\right(\frac{t/T_s-1/2}{\tilde{\delta }\sqrt{2}})-erfc(\frac{t/T_s+1/2}{\tilde{\delta }\sqrt{2}}\left)\right],$$

(9)

where

$$\tilde{\delta }=\frac{\sqrt{ln2}}{2\pi B{T}_s}$$

(10)

and B is the time-bandwidth product.

In [13], approximation methods for cyclic features of continuous-phase modulated signals are provided. The application to the GFSK modulated signal $s\left(t\right)$ with an integer modulation index $h=1$ as used in the PROPCUBE scenario leads to the following expression for the SCF $S_s^{\alpha }\left(f\right)$:

$$S_s^{\alpha }\left(f\right)=\left\{\begin{array}{cc}\delta (f-\frac{1}{2T_s})+\delta (f+\frac{1}{2T_s})+\frac{1}{T_s}{\overline{Q}}_1{\left(f\right)}^2,\hfill & \mathrm{if}\alpha =0\hfill \\ \delta \left(f\right)+\frac{1}{T_s}{\overline{Q}}_1(\frac{1}{2T_s}-f){\overline{Q}}_1(\frac{1}{2T_s}+f),\hfill & \mathrm{if}\alpha =\pm \frac{1}{T_s}\hfill \\ \frac{1}{T_s}{\overline{Q}}_1(\frac{\alpha }{2}-f){\overline{Q}}_1(\frac{\alpha }{2}+f)\hfill & \mathrm{if}\alpha =\frac{k}{T_s};k\in \mathbb{Z}\hfill \\ \hfill & \mathrm{and}\mid k\mid \ne 1\hfill \\ 0\hfill & \mathrm{other},\hfill \end{array}\right.$$

(11)

where $T_s$ is the symbol duration. ${\overline{Q}}_1\left(f\right)$ is derived from the Fourier transform of the real pulse $\overline{q}\left(t\right)$, which is the Laurent approximation for a full-response signal using the Gaussian pulse g(t) as defined above.

Figure 4 illustrates the SCF for the signal parameters corresponding to the PROPCUBE mission. Note that it was smoothed in the frequency domain with a rectangular function of width $\frac{48 \mathrm{kHz}}{500}$ and scaled to unity. For integer modulation indices, GFSK modulated signals contain tones [13], which can be observed clearly in the power spectral density corresponding to $S_s^0\left(f\right)$. Those tones lead to an impulse at $\mid \alpha \mid =f_s$. The lobe-like component is influenced by the Gaussian pulse and can be found at multiples of the symbol rate, i.e., $\mid \alpha \mid =k{f}_s,k\in \mathbb{Z}$.

3.3. Estimation of Cyclic Features under Time-Varying Doppler Shift

In this paper, the time smoothing method (TSM) was used to estimate the SCF. An explanation of the TSM, implementational aspects and a detailed analysis of computational costs are provided in [14]. The algorithm proposed in this paper can be executed on a custom-of-the-shelf computer in real time. Each estimation uses sampling data as defined by the finite block-length $T_b$. In general, the estimation of cyclic features relies on time-invariance of the signal in the frequency domain. While a constant frequency offset results in a shift of cyclic features in the spectral frequency domain, a continuous frequency shift over time, as imposed by time-varying Doppler shift, leads to a smearing of cyclic features. However, finite resolution of the discrete Fourier transform (DFT) used in the TSM can be exploited to limit the amount of possible smearing within one block of length $T_b$. Due to orbital mechanics, the highest Doppler rate ${\delta }_{DR}$ in the course of an overflight can be determined in advance. Then, by introducing a design parameter $ϵ$, which represents the maximum allowed smearing in units of DFT bin width, the maximum block length $T_b$ for a given DFT length N and sampling frequency $f_{samp}$ can be calculated by evaluation of

$$T_b=ϵ\frac{f_{samp}}{N}\frac{1}{{\delta }_{DR}}.$$

(12)

For the determination of all design parameters, a trade off must be found in a manner that the SCF estimation can be considered as statistically reliable, i.e., the time-resolution product must fulfill the following condition [8]:

$$T_{b}F\gg 1,$$

(13)

where F is the spectral resolution of the DFT used in the TSM. In the previously described scenario of a PROPCUBE satellite, a choice of $ϵ=0.5$ and $T_{b}F=15$ was found to perform well.

3.4. Adaptive Detection Statistic

Cycle detectors use the ideal SCF as a weighting function multiplying the estimated SCF of a received signal [8]. If the resulting integrated product is above a defined threshold, a detection is declared. However, the application to LEO satellites is complicated by the fact that the signal power is changing greatly in the course of an overflight. Moreover, in the case of a GFSK modulated signal with integer modulation index, the weighting operation relies mainly on the presence of impulses in the estimated SCF. If an interfering signal containing the same cycle frequencies but broader cyclic features of sufficient strength is applied, the detector is prone to yield a false positive. Therefore, another detection statistic is proposed in the sequel.

As shown in Section 3.2, the most significant cyclic feature for a GFSK modulated signal with modulation index $h=1$ can be found at its symbol rate $f_s$, i.e., $\mid \alpha \mid =f_s$. Due to symmetry properties of the SCF, only $\alpha =+f_s$ is considered in the following analysis. To cope with the variability in power, the detection statistic is proposed in an adaptive manner: First, the magnitude of the SCF slice $\mid {\widehat{S}}_{r_{T_b}}^{f_s}\left(f\right)\mid$ is estimated from the received signal $r\left(t\right)$ of block length $T_b$ and its maximum $H_{max}$ is determined. A detection is made if the following condition is fulfilled:

$$\mid {\widehat{S}}_{r_{T_b}}^{f_s}\left(f\right)\mid <H_{max}(1+\kappa )\mid S_s^{f_s}\left(f\right)\mid \forall f,$$

(14)

where $S_s^{f_s}\left(f\right)$ is the ideal SCF and $H_{max}$ is used to scale it according to the power of the received signal. The ideal SCF is smoothed in the frequency domain with a rectangular function of width $\frac{48 \mathrm{kHz}}{500}$ corresponding to the final detector’s resolution as defined in Section 4 and scaled to unity, as presented in Figure 4.

This can be interpreted as an adaptive threshold with a tolerance region defined by the design parameter $\kappa$. Unlike cycle detectors, this upper-bound condition puts hard constraints on the shape of the estimated SCF, i.e., there must be one significant peak in $\mid {\widehat{S}}_{r_{T_b}}^{f_s}\left(f\right)\mid$. However, erraticism in the estimation and interference that cause contributions at the same cycle frequency are accepted within the tolerance region.

The detection condition as defined in (14) represents a frequency-centered case, which can simply be modified for signals corrupted by Doppler shift $f_0$ by frequency shifting either the estimated SCF, i.e., ${\widehat{S}}_{r_{T_b}}^{f_s}(f-f_0)$, or the ideal SCF, i.e., $S_s^{f_s}(f+f_0)$. For GFSK modulated signals with modulation index $h=1$, the estimated Doppler shift $f_0$ is revealed by the location of the peak in $\mid {\widehat{S}}_{x_{T_b}}^{f_s}\left(f\right)\mid$.

4. Results

4.1. Implementation and Parameter Settings

To apply the proposed detector to a small satellite GFSK modulated signal with modulation index $h=1$, a priori knowledge is only required about its maximum Doppler rate (derived from its orbit), its symbol rate, and its carrier frequency, assuming that frequency offsets do not exceed the bandwidth of the receiving system. In this paper, a sampling frequency of $f_{samp}=48$ kHz was used for a symbol rate of $f_s=9600\frac{\mathrm{symbols}}{\mathrm{second}}$. The length of the DFT was set to $N=500$. The fact that a power of two might be computationally slightly more efficient is outweighed by desirable properties in the TSM. The application of (12) and $ϵ=0.5$ yields a block length of $T_b=7433$ samples or approximately $T_b=0.155$ s, which was used in the following.

Figure 5 illustrates the application of the detection statistic to a satellite burst of length $1.1$ s. On the abscissa, each point marks a detection event in the time-domain, whereas its position on the ordinate corresponds to the estimated Doppler offset $f_0$. While an application of the detection algorithm to each of a number of successive $T_b$-blocks provided by sliding along time by a single sample would provide the best results in terms of time resolution, its realization is computationally expensive. Subsequent applications with a slide of $0.02$ s were found to perform well with a block length of $T_b=0.155$ s. The discrete levels of estimated Doppler offset $f_0$ are introduced by the frequency resolution of the estimation method. For the parameter settings as introduced above, the spectral frequency bin width is $\frac{48 \mathrm{KHz}}{500}=96$ Hz. Hence, once the Doppler shift changes sufficiently, the detection events are estimated to be at a Doppler offset corresponding to the adjacent spectral frequency bin. Interpolating all detection events linearly, as illustrated by the red line, yields an approximation of the Doppler rate for short observation times and can be used for frequency correction in the subsequent processing.

4.2. WGN Environment

First, a WGN background was simulated and the detection statistic was applied to gain information on the false-alarm rate. Despite exhaustive simulations, no false alarms could be achieved for reasonable values of $k\le 0.5$ in (14), which implies that the false-alarm rate is very close to zero. This can be explained by (13): For statistically reliable estimations, it is highly unlikely that frequency components of WGN are estimated to be correlated, especially in a manner such that (14) is satisfied. The noise power does not influence this matter due to the adaptiveness of the detection statistic. Hence, the receiver operating characteristics would appear close to perfect, regardless of the true positive rate. A more meaningful plot can be found in Figure 6, providing the detection rates for a range of SNR values. For each SNR value, simulated GFSK modulated bursts were added to the WGN background and the detection rate was determined by the ratio of declared detections to the number of all detections.

4.3. ISM Spectrum

The ISM band is a highly non-stationary environment, which is hard to model. Therefore, a more practical approach was taken: The ISM band at 914 MHz was recorded when it was known that the PROPCUBE satellite signal was absent. Then, the number of detections was measured and the ratio of detections to the number of total applications yields the false-alarm rate. Hence, the false-alarm rate does not depend on the signal power.

Table 2. False positive rate in an Industrial, Scientific and Medical (ISM) environment.

$\mathit{\kappa }$-Value	False-Positive Rate
0.12	0
0.24	$3.7·{10}^{-4}$
0.37	$3.3·{10}^{-3}$
0.5	$4.7·{10}^{-2}$

presents the results for the given values of $\kappa$.

To determine the true positive rate, analogous to Section 4.2, GFSK modulated bursts were added to the ISM recording and the detection statistic was applied. The results are presented in Figure 7.

The probability of detection is calculated not for the SINR but for the SNR, which was estimated when interference seemed to be temporarily negligible. When an entire block length consists mainly of interference exceeding the signal power by orders of magnitudes, it might happen that erraticism in the estimation of $\mid {\widehat{S}}_{r_{T_b}}^{f_s}\left(f\right)\mid$ causes a missed detection. Therefore, a degradation of performance compared to the WGN environment can be observed. Since the detection of a satellite burst is based on many subsequent applications of the detection statistic as shown in Figure 5, a few missed detections are an acceptable trade off for false-alarm rates as low as presented in Table 2.

4.4. Real World Performance

Figure 8 illustrates the results for a real-world PROPCUBE overflight. Again, on the abscissa, each point marks a detection event in the time-domain, whereas its position on the ordinate corresponds to the estimated Doppler offset $f_0$. The blurriness in the markers is caused by the fact that each burst is detected by multiple applications of the detection statistic, as shown in Figure 5.

The shape of the detection events over time correspond to the S-curve of Doppler shift over time for PROPCUBE satellites and therefore verify the detection results in the frequency domain [15]. It is important to notice that PROPCUBE satellites transmit in a burst mode behavior, which can be observed in spectrograms similar to Figure 2 and Figure 3. Each burst lasts around 1 s and is followed by a 3–10 s break. The duty cycle depends on various factors, such internal processes of a PROPCUBE, the current availability of energy and uplink commands. Hence, it is difficult to provide a reference in terms of known signal-present/signal-absent information for a given point of time during an overflight. A verification that no burst was missed was performed by hand. Consequently, every burst of approximately 1 s was detected multiple times with an average of 37.1 out of 43 possible detections. No outliers are present, which leads to the conclusion that no false alarms occurred. The tolerance parameter was set to $\kappa =0.12$.

5. Conclusions

In this paper, we tackled the problem of detecting the presence of a small satellite signal under high interference. We demonstrated that cyclostationarity can be exploited in the challenging communication link despite substantial time-varying Doppler shift. Moreover, the efficiency of our proposed detection statistic is evaluated on both simulations and real-world data. The results show a solid detection rate while maintaining a very low rate of false alarms. Hence, for scientific or academic small satellite missions the consideration of advantageous cyclostationary signal features in the design and selection process of the transmission scheme can offer a robust and cost-efficient approach for signal presence detection in the densely occupied ISM frequency band.