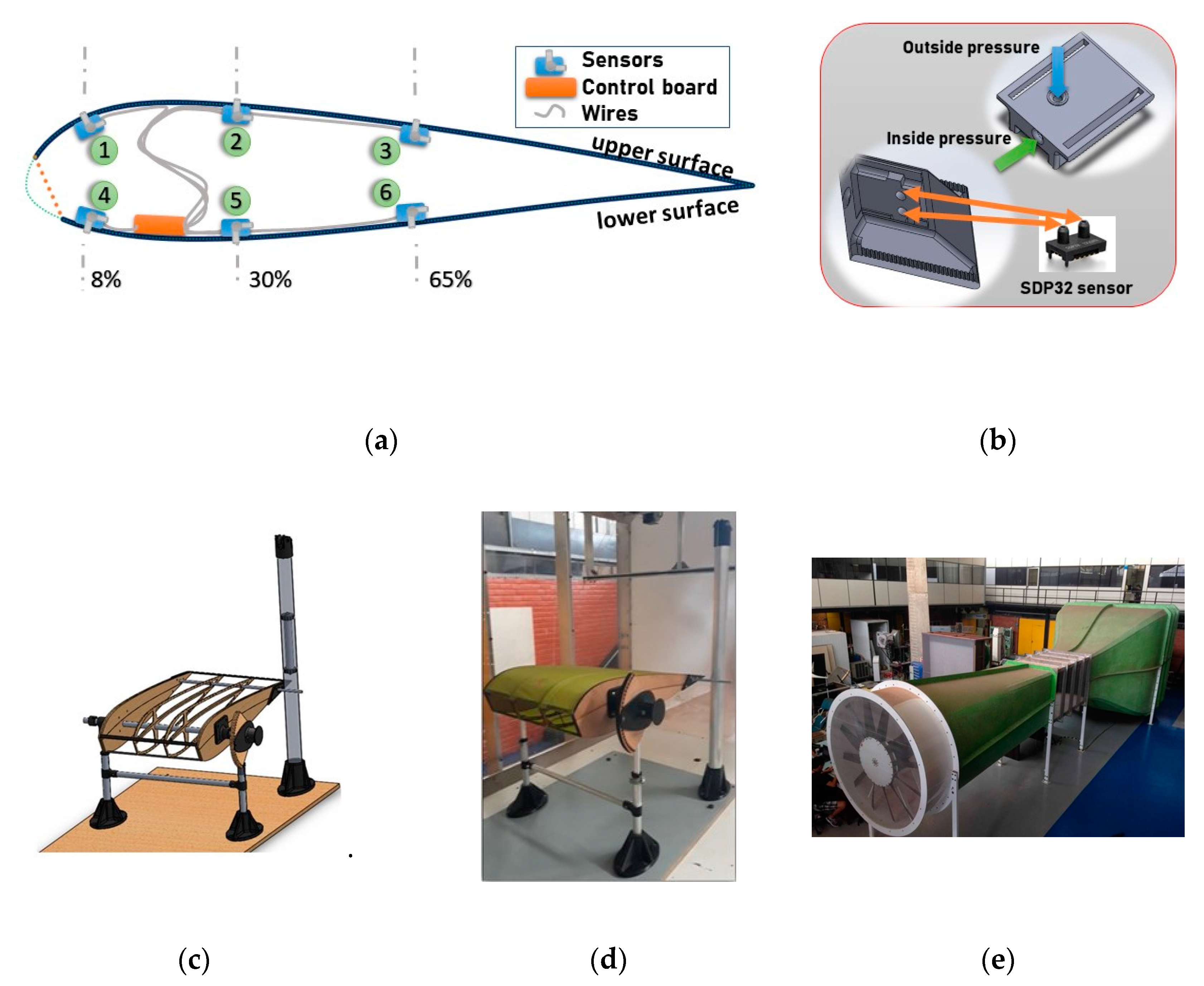
3.1. Differential Pressure Readings
The wind-tunnel tests covered normal flight conditions (operational range) and out-of-envelope conditions (exploratory range), which included pre-inflation speeds, negative incidence, and post-stall angles of attack. Data shows that, at the operational range (0° < AOA < 15°), the aerodynamic behavior follows the principles observed in rigid airfoils, whereas, in the exploratory range, the inflatable nature of the wing overcomes typical characteristics.
An initial measurement with no flow speed was conducted to evaluate sensors setting at zero speed. The sensors presented stable readings under 1.0 Pa. Another measurement at 12 m/s, representing the maximum speed, was executed and the range limit of the sensors was reached as expected (125 Pa). No adverse measurement behavior was identified in any condition. Static measurements were evaluated in 10 s of stabilization intervals.
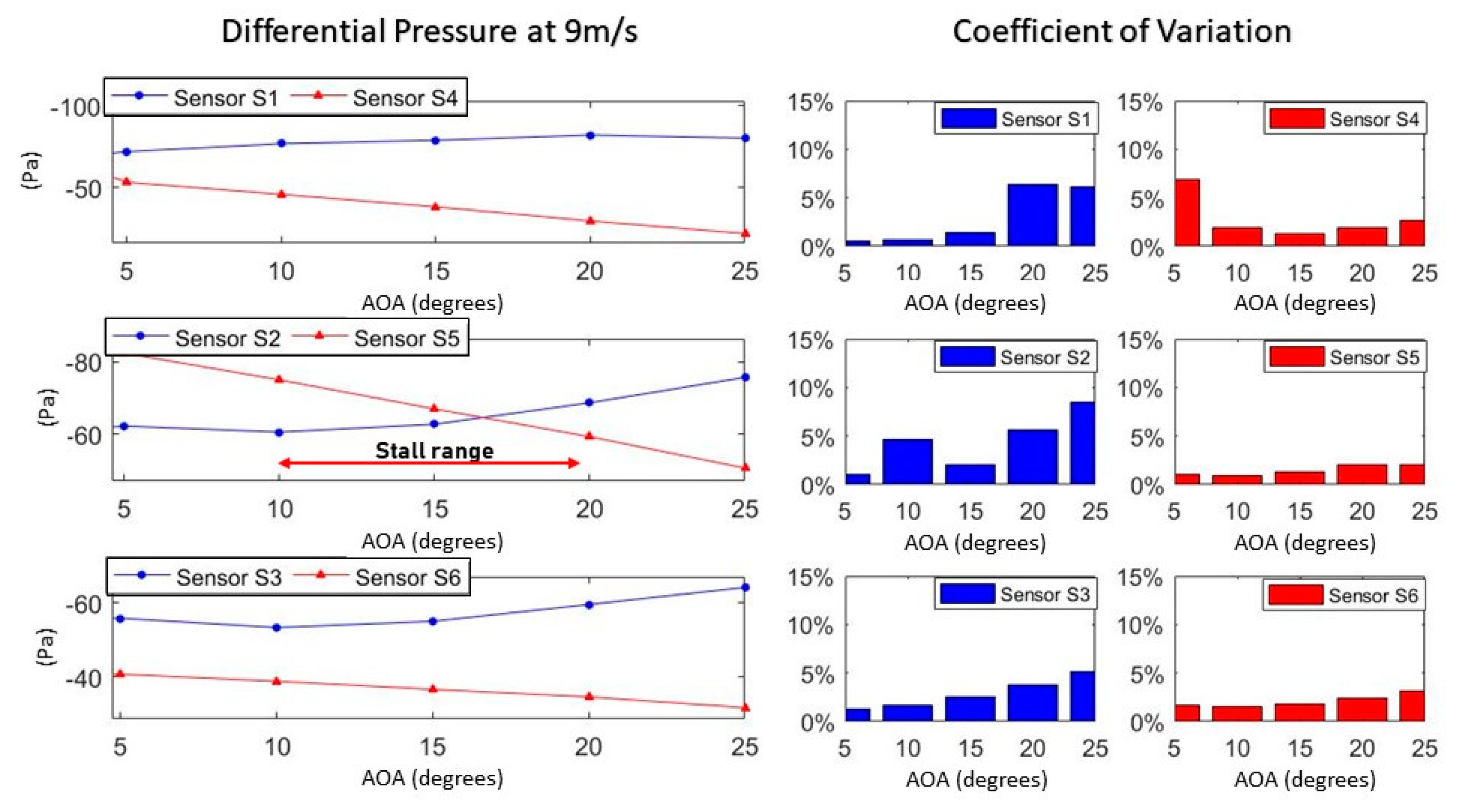
Figure 3 shows differential pressure readings for an airspeed of 9 m/s as a function of the wing’s angle of attack, along with the calculated coefficient of variation.
Figure 3 present the data obtained at 9 m/s grouped by airfoil regions. As can be seen, differential pressures varied from less than −10 Pa to about −100 Pa. The upper-front (S1) and the bottom-front (S4) sensors present a wider range, as expected, since lift is concentrated at the initial portion of the airfoil. For the same reason, the upper-rear (S3) and the bottom-rear (S6) sensors present a more stable pattern. The upper-middle (S2) and bottom-middle (S5) sensors present the intermediate conditions linking the leading and trailing edges, which reveals a distinctive behavior at the bottom surface, which is strongly affected by the air intake. It is worth reaffirming the intention of working with pressure differentials and not with traditional external pressure coefficients, since the direct measurement of pressure differentials reveals the combined effect of external and internal flow dynamics, which are crucial for inflatable wings.
The coefficient of variation (CV) consistently shows increased data scattering outside the operational flight envelope (0° < AOA < 15°). At negative incidences or at angles above stall CV up to five times higher. It demonstrates the system’s capability of indicating detachment vortex formation. For angles of attack inside the operational envelope, the coefficients of variation were very close to the sensor’s resolution (3%), as informed by the manufacturer, except for the bottom-front sensor at low angles of attack, which have reached about 7%. This higher deviation corroborates Fogell’s observation [
6] about the occurrence of a recirculation bubble at the bottom leading edge of the wing due to the air intake. The significant data scattering from sensor S4 materializes the effect of a vortex linked to the recirculation bubble acting on that region. It becomes even more noticeable by inspecting the change on sensor S4 measure pattern after entering the operational envelope. This effect is linked to both the low Reynolds number regime and the existence of an air-intake at the leading edge.
Another didactic way of looking into the data is taking the pressure differentials at the rear sensors (S3 and S6) as a baseline. These readings are supposed to be more stable in respect to AOA and to reflect the pressure-differential potential provided by the flow speed.
Table 2 represents data extracted from
Figure 3 for the operational flight envelope measured as a percentage of the baseline pressure differentials:
At 9 m/s, the average pressure measured by S3 and S6 are, respectively, 55 Pa and 39 Pa at 65% of the chord, revealing enough of a pressure differential to sustain inflation and a difference of 16 Pa between pressure differentials at the upper and lower surfaces, indicating lift at that region. These measures are almost unaffected by AOA variation inside the operational flight envelope, presenting standard variations of ± 1.7 Pa and ± 1.1 Pa, respectively. However, the frontal and middle sensors’ readings vary considerably with AOA. In the same way, it is made clear how perceptible is the pressure-differential variation throughout the chord at both upper and lower surfaces for each flight condition. These observations are extremely important because it shows that the measurement of local pressure-differentials at the selected regions of the cell can provide an effective way of characterizing flight condition. For instance, increases in the pressure gradient at the upper surface, together with the decreasing in pressure gradient at the lower surface, between the second and third lines in
Table 2, clearly indicates a pitching up from 5° to 10° AOA.
The pressure-differential distribution profile defines a standard in-flight signature for a particular wing model. Measuring the differential pressure profile at the steady glide condition provides a baseline, which can be used to identify in-flight dynamic reactions through pressure profile variation. As the inflatable wing will be dynamically deformed by aerodynamic loads originating from maneuvering or atmospheric disturbances, local variations on the pressure differential readings will be perceived, revealing reactions that can be linked to wing motion. Therefore, the wing can be characterized by correlating its motion, using standard accelerometers and inertial sensors, to the aerodynamic loads captured as pressure differential variation.
Considering the exploratory range,
Figure 3 also shows that the coefficient of variation follows a path driven by the position of the vorticities. It moves from the bottom surface (at negative AOA) to the upper surface (at post-stall AOA) causing data scattering. Such a phenomenon can be better visualized in
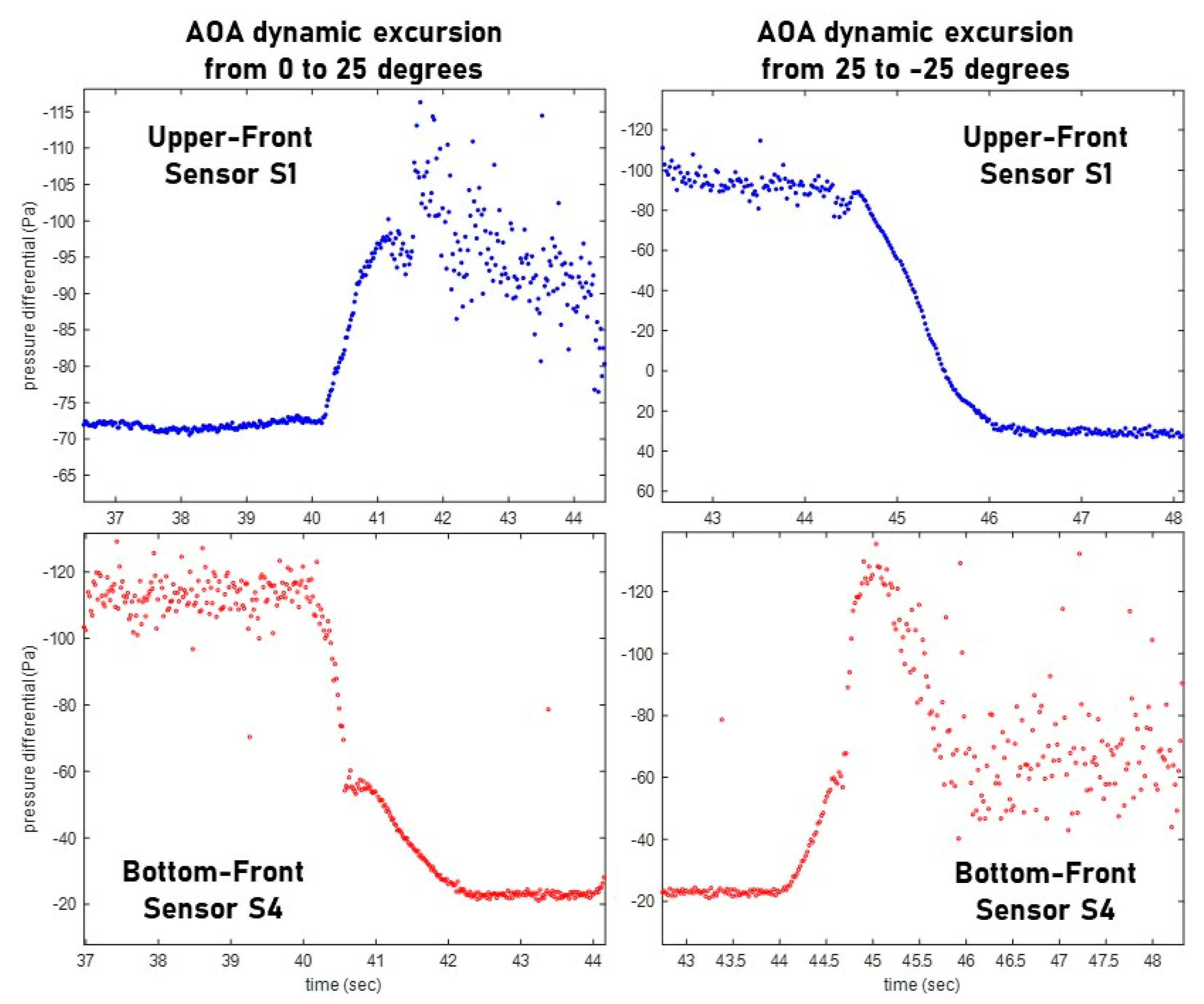
Figure 4, which presents two dynamic AOA excursions, from −25° to 25°, at an airspeed of 10 m/s.
Data corroborates the consistency of readings under dynamic variation. When the wing is pitched down, the differential pressure over the upper surface is inverted and becomes positive. The appearance of a vortex at the bottom surface is detected by the scattering of data from sensor S4. When the wing is pitched up, there is a clear manifestation of a post-stall vortex at the upper surface, however some air still enters the airfoil providing residual internal pressure, which sustains a low negative differential at the bottom surface.
The observed values remain fully consistent with those obtained for the stabilized conditions. It is interesting to point out that the bottom-front recirculation bubble disappears when the wing if fully pitched-up. It ascertains the source of deviations systematically observed for sensors S4 and S5, corroborating the existence of strong flow disturbances at the wing’s bottom leading edge at operational conditions.
Figure 4 is important for demonstrating instrumentation capability of continuously capturing relevant pressure differential variation caused by in-flight motion, and the ability to distinctly identify change in the flow regime. It must be considered that such capabilities make the system, as it is, a tool for shape stability monitoring.
3.2. The Inflation Phenomenon
The inflation phenomenon is characterized by the provision of minimum conditions, in terms of speed and AOA, for the wing to inflate. The limits associated to AOA are related to aerodynamic stability, whereas the limits related to speed are related to minimum dynamic pressure, thus providing wing stiffness.
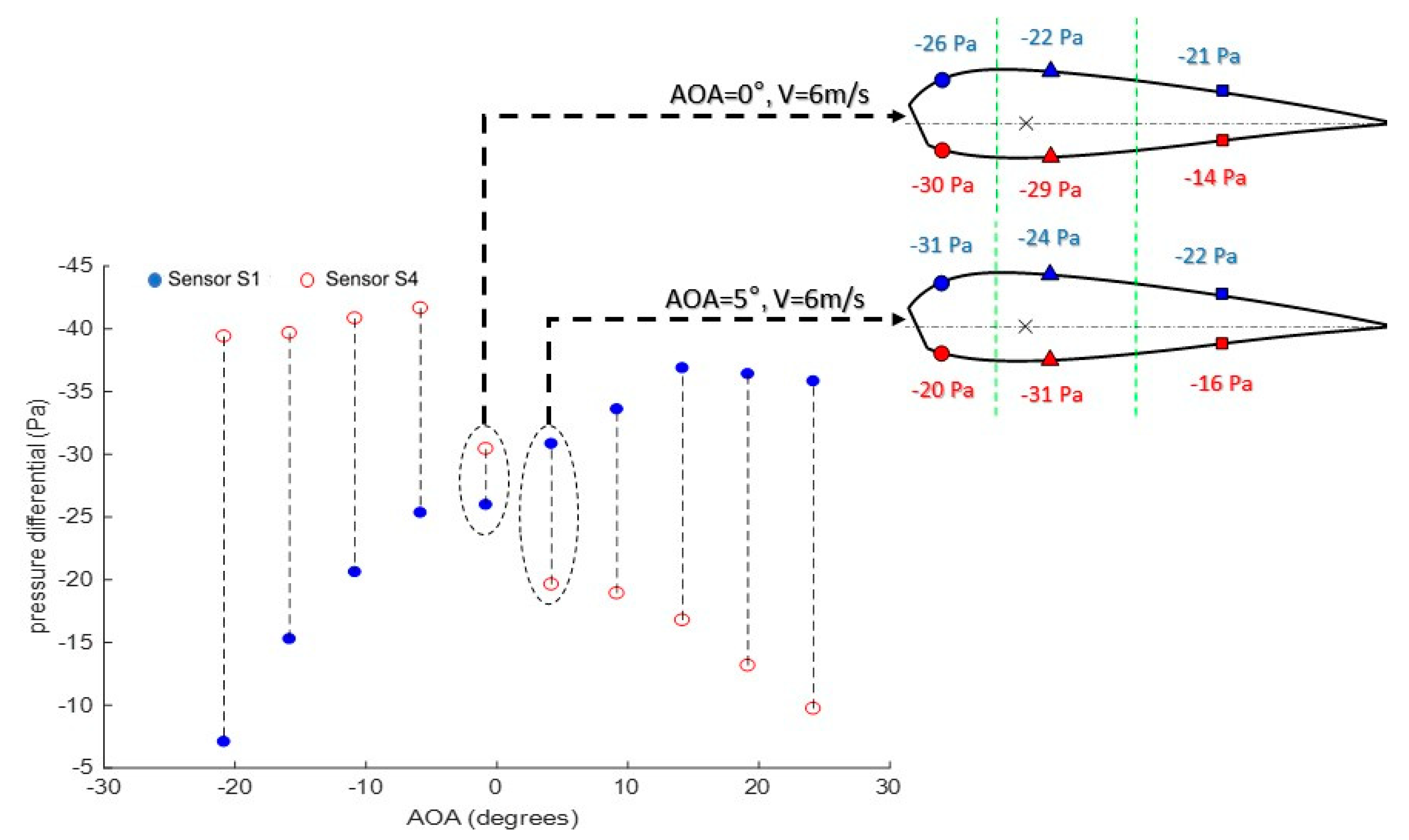
Figure 5 presents the readings for sensors S1 and S4 at airspeeds of 6 m/s and highlights differential pressure distribution for two angles of attack, before and after inflation. It makes clear that, for negative angles, or even for a very small AOA depending on the air intake’s geometry, the airfoil condition is unstable because the moment generated by higher-pressure differentials at the bottom leading edge and at the upper trailing edge tends to rotate the cell downwards, leading to a frontal collapse. After the incidence angle is further increased, the internal pressure augments, and the difference between the upper and bottom pressure-differentials at the leading edge is inverted. The expressive frontal lift tends to rotate the airfoil clockwise, providing stability conditions. In-flight, the pendulum mechanism would automatically adjust the speed and AOA, reaching the stable glide condition. In a wind-tunnel, the supports or actuators balance the resultant pitching moment.
As is known from the classic airfoil theory, the frontal part of the airfoil is responsible for most of the lift, meaning that this region drives airfoil behavior depending on the local ratio of the upper-lower pressure. Data plots from sensors S1 and S4, as depicted in
Figure 5, reveal a substantial change in differential pressure distribution as the angle of attack goes from zero to five degrees. The sharp alteration of the differential pressure from sensor S4 characterizes the inflation of the cell, as observed by Mashud and Umemura [
5,
7]. This takes place when the stagnation point coincides with the air intake, which rapidly increases the wing internal pressure, thus making the cell potentially stable.
Prior to inflation, when the wing is pitched down, causing high levels of differential pressure at the bottom leading edge, the air accelerates through the upper surface, absorbing most of the dynamic pressure imposed by the flow. In such a case, the wing is sustained by the test-bench ribs but would collapse in an actual flight. When AOA increases, the inner pressure is sufficient to provide structural stiffness, and the flow over the airfoil becomes stable as in the rigid wing. Both internal and external pressure at the bottom leading edge is entirely reconfigured.
Table 3 present data for 6 m/s between −10° and 10° AOA, illustrating the abrupt change in the pressure gradient at the leading edge of the airfoil:
For the tested airfoil, a linear interpolation based on the frontal differential pressures indicates that inflation occurs near 1.43°, which is compatible with those reported by other researchers [
5,
7]. It is possible that the presence of a rigid structure has slightly dislocated the point of inflation, favoring cell’s stiffening at a lower AOA. These characteristics can be used to design collapse prevention automatic systems, which can monitor the difference between pressure at the upper and lower leading edge, avoiding further reductions in AOA when this value decreases.
Finally, it is important to mention that speed itself plays an important part in inflation, as better explained in
Section 3.4. Tests at 3 m/s proved that, even at favorable AOA, speeds lower than 6 m/s do not provide sufficient airfoil stiffness, resulting in shape instability, visual fabric deflections, vibration, and consequently, unrepresentative data.
3.3. The Stall Approximation
The stall condition is reached as the AOA is increased and the airflow can no longer contours the airfoil. Different wings present different stall characteristics, which may be progressive, starting from the trailing edge region, or abrupt, depending on the geometric proprieties and flight conditions as rotation rate or air density. However, a full stall is characterized by complete flow detachment at the upper surface. It is essential to highlight that, for inflatable wings, the stall itself may not result in an immediate collapse but has major effects on it.
Figure 6 shows the stall approximation at 9 m/s represented by a consistent decrease in the bottom surface differential pressures (S4, S5, and S6) combined with an increase in the upper surface differentials (S1–S3), resulting in a substantial increase in data scattering at the upper surface when detachment is complete.
This shows that, as AOA increases, the global pressure differential increases, and then there is lift and drag. This combined effect leads to a progressive decrease in speed to a point where inflation is jeopardized, and collapse is imminent. As represented in
Figure 3 and
Figure 4, when a full-stall condition is reached, the low-pressure vortex formed at the upper surface can sustain inflation, even if the flow is detached. The aerodynamic stall does not directly cause collapse. However, such a situation will abruptly increase drag, decelerating the wing down to a point where dynamic pressure is too low to sustain inflation. This observed time lag between stall and collapse can be explored to build collapse prevention systems.
Figure 6 show that throughout the operational range (0–15°), the upper-middle differential pressure (S2) shows an inflection point between 10° and 15° AOA, revealing a perceptible change on the pattern of pressure-differential variation with AOA. At the same time, pressure-differentials at the lower surface diminish consistently as the wing pitches up. The rapid decay in the upper-middle readings (S2) from 5° to 25° confirms previous findings [
22,
23,
27], indicating that, for paragliders and parafoils, stall effects are triggered above nine degrees and are fully characterized above 13°. The full stall configuration can be identified by the jump on data scattering at 20° indicated by the coefficient of variation, however the relations between sensors S2 and S5 are useful parameters to identify stall approximation before it reaches dangerous levels of flow detachment.
The rate of variation of the upper-middle pressure and the difference between up and bottom middle readings are relevant aspects for the central portion of the cell. The first one reveals lift evolution and the second one reveals the pressure gradient at the middle of the profile. Setting a reference at the steady glide condition (V = 9m/s and AOA = 5°), it is possible to judge stall eminence by monitoring the climbing in upper-middle readings (S2/S2
std) and the difference between upper-middle and bottom-middle readings. The first parameter reveals whether the characteristic of the flow has changed perceptibly, and the second parameter reveals how far from the inflation condition the system might be.
Table 4 illustrates the use of these parameters.
Finally, the sharp variation of values on
Table 4 demonstrates that stall approximation can be efficiently identified using these parameters, which opens the path to a stall alert and prevention system based on local pressure-differential monitoring.
3.4. Collapse Triggers and Shape Stability
Collapses are phenomena particularly important for inflatable wings. Naturally, there are several levels of wing collapse, starting from the perceptible loss of internal pressure, which might evolve into partial transient deflations, and then into a complete loss of the wing’s shape and stiffness. Three primary triggers might lead to collapse situations. One is a negative incidence resulting in an angle of attack below inflation. A second one is an excessive incidence resulting in a full stall. The third refers to the relative speed drops, which may be caused by maneuvering and atmospheric disturbances.
The effects directly linked to AOA limits were already explored in previous sections. However, there may be conditions where, even at an operational AOA, a general reduction on internal-external differential pressure results in a noticeable loss of wing’s stiffness. For instance, when a tailwind gust hits the wing, the relative speed is suddenly reduced with a perceived pressure loss. The lift reduction will cause the wing to accelerate regaining equilibrium. Notwithstanding, the reactions are not instantaneous and result in a period in which the low inner-outer differential pressure causes perceptible shape instability. The disturbance may be transient, but a high-speed drop may lead to stall or to an intense pendulum reaction that leads to an negative incidence. Then, it is interesting to evaluate the level of differential pressures captured by the sensors at different levels of flow speed tested.
Table 5 presents the mean value obtained with the readings from the six sensors at 5° AOA for an unsustainably low speed (3 m/s), an inflation speed (6 m/s), and an operational speed (9 m/s):
Table 5 reveals that the level of pressure-differentials change perceptibly with speed, and the mean value can be used to characterize the level of available dynamic pressure. It should also be noticed that the general level of pressure-differential measured is directly related to the wing load, a factor traditionally used as a design parameter. None of these values correspond to the final wing load, which requires integration throughout the surface, but they are a fair indicative based on local evaluations. Considering that common paragliders and parafoils present wing-loads around 40 Pa [
8], the collected data show that the average reading at operational speed (9 m/s) is substantially above this value, whereas, at inflation speed (6 m/s), the average differential pressure is much lower. Consequently, a calibrated system can dynamically monitor wing stiffness using the average differential pressure, and its time derivative sign, to provide an alert preventing further reductions in speed.
3.5. Pressure Coefficient (Cp) Distribution and Lift Estimation
One of the main objectives of the present work is to sustain the use of local pressure differential measurements to characterize inflatable wings instead of using classic approaches based on external pressure coefficients or global lift and drag coefficients. The use of geometry-based aerodynamic coefficients for wing design encounters relevant limitations even in cases where the wing is fully closed. For example, dealing with inflatable-wing drones for planetary exploration, as discussed in the work by Hassanalian et al. [
44], the same issues originating from elastic deformation can be anticipated. For these situations the use of local differential pressure monitoring can, as well, represent a more suitable approach, since it provides information about the external pressure field and the wing stiffness simultaneously. However,
Cp assessments can still be useful with the only purpose of comparing data obtained from previous experiments and numerical simulations, demonstrating that the pressure differential approach generates consistent results and, at the same time, provides important information about the internal flow, which is a major player for inflatable wings.
Previous studies show conflicting conclusions regarding the confined flow structure due to the method through which data was obtained. Some researchers claim that relevant flow occurs inside the cell [
22,
27], leading to significant effects on global lift and drag, whereas others [
5,
7] affirm that the encapsulated air is mostly stationary in the cell cavity, being slightly affected at low angles of attack. Data obtained from differential pressure readings indicated that the inner flow is a relevant phenomenon and proves that methods using absolute pressure are not the best option for characterizing dynamically inflatable wings.
From basic aerodynamic theory, it is expected that the pressure at the upper surface should be consistently lower than the pressure at the bottom surface for positive AOA. If the inner pressure was constant and near the stagnation level, upper differential pressures should be considerably higher than the bottom differential pressures in the same region. However, as illustrated in
Figure 3, the bottom-middle differential pressure was consistently higher for a considerable range of operational AOAs. Further, at a low AOA, the difference between the upper and bottom differential pressures at the middle diminished as AOA increased, which is a singular response. The logical explanation for such behavior comes from the internal pressure gradients. This means that the cell’s internal flow increases the pressure at the inner bottom surface more than it does at the inner upper surface, around the initial portions of the wing. The internal flow is highly dependent on the airfoil thickness, the air intake geometry and the airflow condition. Therefore, further experiments exploring these variables are needed to fully model the phenomenon. However, for the purpose of establishing the suitability of differential-pressure based analysis, a simplified approach is enough.
When the air intake is perfectly aligned with the incoming air, the inflation process is more productive through the ram effect. It is also important to realize that the recirculation bubble observed at the bottom leading edge is linked to the internal flow, thus affecting its extension and magnitude. At the virtual origin of the reference chord, the internal flow factor is almost null, since there is no airfoil surface and the incoming flow is nearly undisturbed. At the end of the cell, on the other hand, where the air was already contained, and the internal pressure gradients were dumped, the pressure approaches its stagnation value. As the flow passes the air intake, at positive AOA, the bottom flow is supposed to decelerate much faster than the upper flow, which may be even in acceleration when filling up the airfoil internal space. The expected result is a complementary behavior between upper and bottom inner pressure coefficients, which rise from zero to one following a different pattern. The bottom pressure rapidly increases, whereas the upper flow only starts a definitive pressure rise after passing the maximum thickness of the airfoil. Therefore, as a theoretical model, the following correlations are proposed for the internal flow factor, at the upper and bottom surfaces, respectively:
An accurate characterization of the internal flow can be achieved by designing additional experiments combining differential and absolute pressure readings. Such an approach is scientifically relevant but moves away from the objective of minimizing instrumentation to deliver a suitable on-board system. An alternative way of separating the effects of internal flow using only differential pressure is to rely on computational simulations, setting averaged parameters (a, b) for Equations (13) and (14). Considering airflow speed of 10 m/s and AOA varying from 5° to 15°, simulation data revealed that, where the thickness is maximum (x = 0.21), the inner bottom pressure coefficient should be near 80 ± 5%, and the upper-pressure coefficient should be around 10 ± 5%. It allowed for the defining of the theoretical curve for the internal flow factor (a = 0.35, b = 6.25), associated to the ASCENDER airfoil at 10 m/s and 5° < AOA < 15°.
For the external pressure coefficient, considering the baseline airfoil, a wide number of traditional methods are available providing the Cp distribution curve, which can also be averaged for a defined AOA range. Equations (15) and (16) present the mathematical modeling reflecting the Cp distribution observed on the same computational simulations:
While Equations (15) and (16) define the type of curve representing the Cp distribution based on the characteristics observed computationally, the specific parameters were numerically adjusted to fit the model to the experimental data based on Equation (3). The results applying the suggested model are illustrated in
Figure 7, and the specific values were obtained by adjusting the parameters to the experimental data, as presented in
Table 6.
The distribution calculated using the proposed model to fit experimental data reveals an upper-surface
Cp distribution pattern fully compatible with
Cp distribution obtained theoretically for the same baseline airfoil. It also presents levels of
Cp that are fully coherent with previous experimental results [
5,
7], as obtained by completely different methods.
The most distinct observation brought up by
Figure 7 is the singularity present at the bottom surface resulting from the recirculation bubble at the bottom leading edge. This phenomenon, which was already observed following a completely independent rationale, presents itself as a major player that helps explain the significant reduction in lift and the increase in drag informed by several researches.
Combining the external Cp estimation and the airfoil geometry, it is possible to integrate lift coefficients for different AOA. Drag was not calculated, since the pressure coefficients would provide only a small component of the total drag, which is highly affected by parasites and induce drag. These two components require force measurement methods, which are out of scope of the present experiments. Nonetheless, the estimated CL is useful to characterize the wing and to corroborate the methodological adequacy.
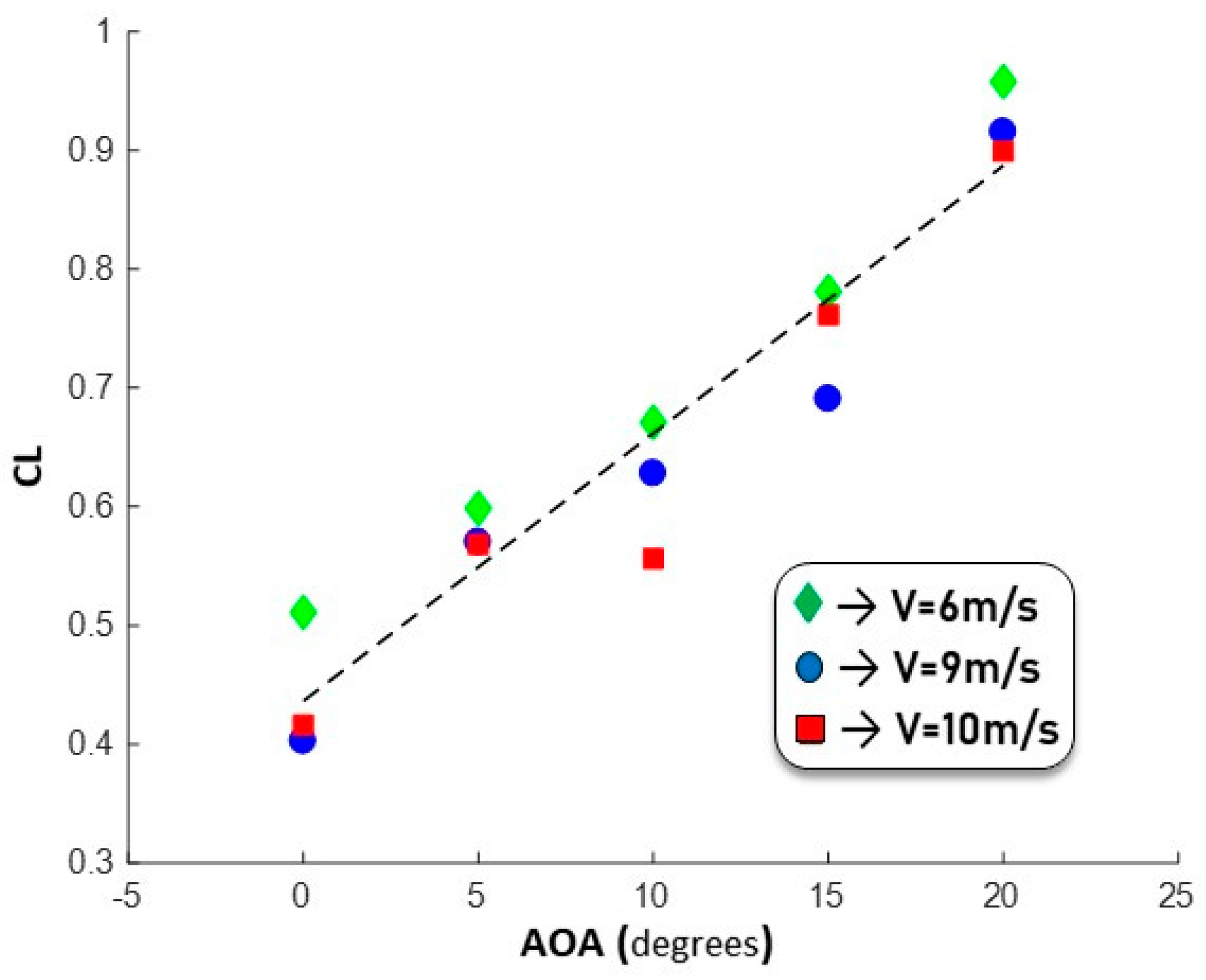
The CL-Alpha curve plotted in
Figure 8, presenting an average lift slope of 0.024 per degree, is fully compatible with the results obtained by previous researchers [
27]. Further, the resulting wing load range from 30 Pa to 50 Pa corresponds precisely to the expected range previously calculated [
8]. Therefore, parallel observations seem to lead to consistent results, reinforcing the usefulness of the differential pressure measurement approach, and the relevance of the inner flow.
It is never enough to emphasize that the external pressure coefficient, the internal flow factor, and the lift coefficient were derived in
Section 3.5 to provide a classic representation of the observed characteristics, allowing useful reflections about the collected data. However, no theoretical model was used for analyzing the main characteristics in
Section 3.1,
Section 3.2,
Section 3.3 and
Section 3.4, but only the differential pressure data directly measured. Therefore, the potential uncertainties related to modeling pressure coefficients distribution profiles do not impair the main objective, which is demonstrating that a pressure-differential approach is more suitable for inflatable wing analysis and can be used to characterize the wing and to prevent undesirable in-flight conditions.