Abstract
Traditional swash plates generally have numerous parts, which may result in the abrasion of key parts. In this paper, to avoid the problems of traditional swash plates, a low-cost and high-reliability rotor micro-aerial vehicle integrated attitude-adjustment mechanism (IAAM) is designed based on compliant mechanism theory. The mechanism is composed of a series of curved plates and connecting convex plates. In this context, the relationship of the loads and deformations of a cantilever curved plate is analytically determined. Meanwhile, the geometrical parameters of the IAAM are optimized to the minimum mass by a genetic algorithm. The performance of the optimized IAAM is verified by finite element analysis. Modal and static analyses are performed to ensure that the mechanism meets the requirements of the flight process of the aircraft. The designed attitude adjustment mechanism reduces the complexity of the structure and installation and improves the structural reliability. Furthermore, this mechanism can be 3D printed, thus reducing production costs and improving production efficiency.
1. Introduction
Micro-aerial vehicles (MAVs), particularly rotorcrafts, are becoming popular due to their ability to hover and move arbitrarily in 3D space. These capabilities support a wide range of applications, including hazardous environment inspection and package delivery. Making aerial vehicles smaller, simpler, and cheaper is the goal of MAV design. Reducing the number of components can promote these goals as long as complicated mechanisms are not added in their place [1].
The basic swash plate (SP) control concept was invented in the 1930s and is a successful design. Nevertheless, the weight, drag, cost, and probability of failure of the mechanical components of the SP control system provide an impetus to search for alternative forms of main rotor pitch control. Meanwhile, these SPs generally have numerous exposed linkages, bearings, push rods, and hinges. These components are maintenance intensive and costly. Therefore, a series of SP-less MAV modes have been studied [2,3,4,5,6]. However, SP-less helicopters usually need complex control algorithms to introduce a difference in the blade pitch angles of the upper blades versus the lower blades.
For the above reasons, we plan to design an integrated attitude adjustment mechanism (IAAM) by considering the advantages of compliant mechanisms. Compliant mechanisms have several advantages [7,8]: 1. Different functions can be integrated into a few parts, and costs can be significantly reduced by adopting a compliant mechanism due to the need for less assembly (or even no assembly), fewer parts, and a simplified manufacturing process; 2. Compliant mechanisms are more accurate than normal mechanisms due to the reduction in wear between parts; 3. Compliant mechanisms have a small mass, are easy to miniaturize, and are more suitable for designing the key parts of micro aircraft.
The pitching moment and rolling moment of a signal rotor/coaxial aircraft are produced through the angle between the tip path plane (TPP) and the aircraft. Attitude control will be attained through the pitching moment and rolling moment. The micro-rotor aircraft scheme presented in this paper adopts a coaxial reverse layout. The gyroscopic precession moment caused by the deflection of the motor shaft can be offset by a pair of contrarotating motors and rotors. The rotor of the micro-rotor aircraft is rigidly connected with the hub. In addition, due to the small diameter and light weight of the rotor, the swing amplitude of the rotor is very small. Therefore, we can assume that the TTP is perpendicular to the motor shaft and take the rotors and the motor as a whole structure, which is denoted as WB. From the above analysis, a micro coaxial reverse aircraft can tilt the TPP by tilting the WB structure directly with the proposed IAAM instead of a traditional SP. The IAAM can greatly reduce the complexity of the attitude adjustment mechanism and production costs. IAAM can also improve reliability. The installation method of the IAAM is shown in Figure 1. The servos will be connected to the bottom of the IAAM, and the rotor motors will be connected to the top of the IAAM. The installation plane of the servos will be connected with the installation plane of the motor through wire ropes. The angle of the installation of the motor changes with deformations of the IAAM by pulling the ropes by the servos. In the process of changing the flying direction, the rotor angle changes by changing the angle of the installation plane of the motor.
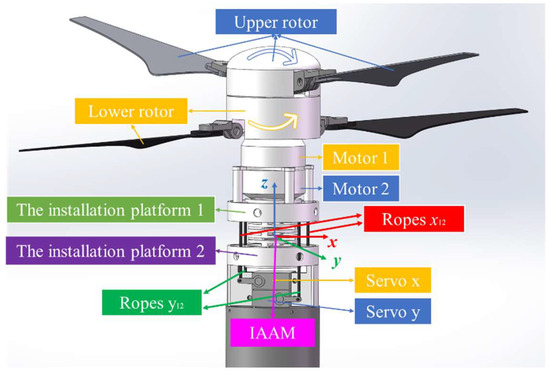
Figure 1.
Installation method of the IAAM. (The upper rotor will be spinning with a clockwise rotation derived from motor 1, while the lower rotor will be spinning with a counter-clockwise rotation derived from motor 2. The rotors are installed on the installation platform 1. There are two servos which are used to adjust the attitude of platform 1 in the x-direction and y- direction by IAAM and four ropes. Servos are installed on platform 2).
Based on the above point of view, a low-cost and high-reliability attitude adjustment mechanism of a rotor MAV based on compliant mechanisms is designed and analyzed in this paper. In addition, the designed IAAM is applicable to the thrust-vector control of microfixed wing aerial vehicles. It avoids the shortcomings of classical SPs of structural complexity and installation. The IAAM also avoids the shortcomings of the complex control algorithms of classical SP-less structures. This provides theoretical support for its application in MAVs and provides technical support for the goal of being lightweight and improving the flight efficiency of MAVs.
2. Mechanism Design
An IAAM is a special device for changing the direction of a helicopter rotor. The servo can control the flight state of the helicopter by changing the angle of the IAAM.
2.1. Preliminary Design of the IAAM
In our daily life, we find that the spine of the human body is an active compliant mechanism; we only consider the bending characteristic of the spine. Its working process is similar to the IAAM’s working mechanism: with changes in body movement loads, the intervertebral spaces shift, resulting in bending and other movements that change the direction of body movement. However, the length of the intermediate axis of the spine hardly changes during this process. Therefore, based on the principle of bionics and taking the bending characteristic of the human spine as the research object, we designed an integrated multigap IAAM to satisfy the requirements of micro-rotor aircraft. As the designed IAAM is an integrated and short structure, it can avoid the phenomenon of rotation around its own axis.
An integrated multigap IAAM is preliminarily designed (shown in Figure 2) based on the human spine. The compliant mechanism is a cylinder with a through-hole in the middle. The through-hole mainly meets the requirements of the line arrangement in the process of driving the IAAM and reduces the IAAM’s weight. Unwanted materials in the x- and y-directions are removed, and a five-layer IAAM element is generated. The first layer is the setting surface and is assumed to be a rigid and full constraint. The third and fifth layers are core flexures of the mechanism. The most important purpose of the IAAM is realized through flexible deformations of this part. The second and fourth layers are the connecting convex plates of the compliant core areas. The convex plates are designed as a cross distribution of adjacent layers, which are also assumed to be rigid.
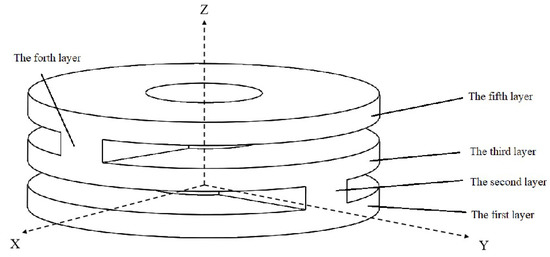
Figure 2.
Schematic drawing of the proposed IAAM.
The design objects are determined as follows, according to the requirements of these aircraft:
- For applicability to micro-rotor aircraft, the helicopter blade diameter is less than 300 mm, and the mass is less than 500 g.
- The deflection angle of the x-, y-, and z-axes (the x, y, and z coordinates are shown in Figure 2) is ± 15°;
- The stiffness in the Z-axis direction is large; thus, the vertical deformation of the IAAM is small when it is subjected to a 500 g lift during hovering. The shape variable is less than 2% of the height of the intermediate axis.
- To satisfy the requirements of a lightweight micro-helicopter, the weight of the IAAM should be less than 15 g.
- The factor of safety (FOS) of the IAAM is greater than 1.5.
2.2. Theoretical Analysis
To simplify the theoretical analysis process of designing the geometric parameters of the IAAM, the following hypotheses are established:
- Deformation occurs mostly in the flexible part of the core flexure, and deformation outside this part is ignored;
- The interferences between different gaps are neglected;
- The applied loads can be transferred 100%.
According to an empirical formula of helicopter design [9], the required rotor unit power can be calculated.
Therefore, when the micro unmanned helicopter is subjected to a 500 g lift, the motor power required is approximately 90 W. The outer diameter of the DC motor designed according to the power demand is approximately 24 mm. Based on the design requirements and assumptions, the deflection angle of the x-, y-, and z-axes is . According to the working schematic diagram of the IAAM shown in Figure 3, the outer edge of the motor installation platform should be tilted by :
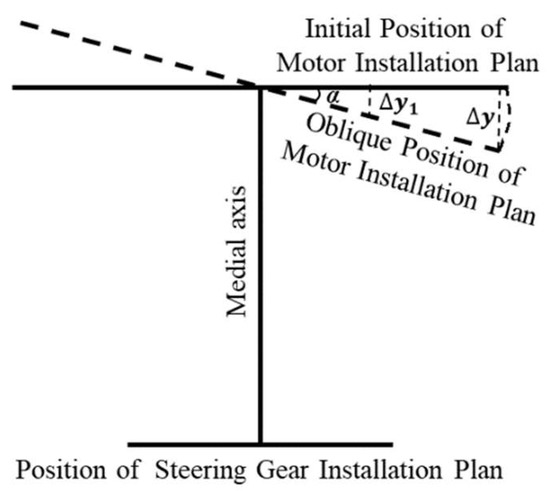
Figure 3.
Working schematic diagram of the IAAM.
To reduce the weight of the structure, the diameter of the designed IAAM can be less than the outer diameter of the motor. It is assumed that the diameter of the IAAM is d. The outer diameter of the IAAM needs to be tilted by :
To determine the parameters of the IAAM and meet the design objectives, the parameters of the IAAM are designed and analyzed.
Materials have an important impact on the performance of flexible mechanisms. Excessive flexibility of materials affects the overall stiffness and the dynamic performance and accuracy of the mechanism, while excessive stiffness affects the working stroke or size of the working space of the mechanism [7]. According to the basic principles of material selection for flexible mechanisms given by Yu et al. [10], PA6 was selected as the main material of the IAAM. The material properties of this material, such as density, elasticity modulus, yield stress, and Poisson ratio, are shown in Table 1.

Table 1.
The material properties of PA6.
According to hypothesis 1, IAAM deformations mainly occur in the third and fifth flexure layers, as shown in Figure 2. As the flexure layers are axisymmetric, to simplify the calculation process, we take a quarter cantilever curved plate with a uniform cross-section as the analysis target and analyze the relationship of the loads and deformations. Fortunately, Jafari and Mahjoob [11] have derived the exact stiffness matrix of curved beams with a nonuniform cross-section by using a direct method, featuring an arc of a circle as a centroidal axis and a rectangular cross-section. The plate features one fixed end (on the left, s = 0) and is generically loaded at the opposite free end (on the right). For the plate, we refer to this curve “s” passing through the center of the area of the plate cross-section. We define a coordinate system S0 shown in Figure 4, with its origin in point O and orthogonal axes i, j, and k, where i lies along the intersection between the right end plane and centroidal axis plane, k is perpendicular to the centroidal axis plane and points downward, and j follows the right-hand rule. In addition, we define a local coordinate system Sl located on the centroid of a generic plate cross-section and with axes l, m, and n lying along the tangent, normal, and binormal to the plate centroidal axis (that is, l, m, and n are the cross-section tangent and principal unit vectors, with n being parallel to k). The geometrical parameters and axes of the plate’s cross-section are shown in Figure 5. The radius and subtended angle of the centroidal axis are represented by r and t.
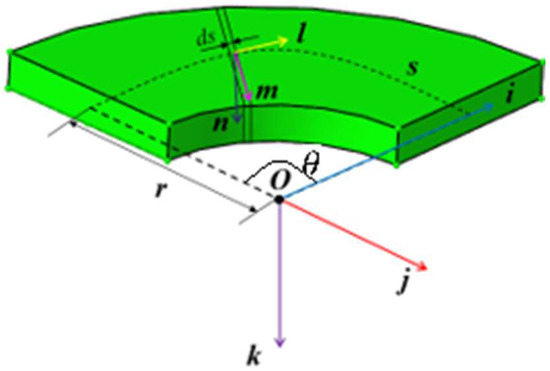
Figure 4.
Quarter cantilever curved plate with uniform cross-section.
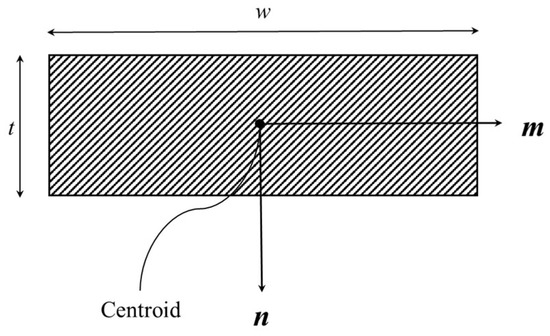
Figure 5.
Cross-section of the curved plate.
The relation between local and global coordinates can be written as follows:
where B is the rotation matrix that relates global and local coordinate frames and is defined as Equation (5). The range of values of is [0,π/2].
As a result of load application, the plate deforms and produces a change in the position and orientation of the free end. The loads on the free node and its displacements are represented by two column matrices p and q, where
A load p’ is developed at element ds on curve s due to load p applied at the free node. The element ds undergoes deformation in unit length, , due to this load. The matrices p’, and their relations are as follows:
The matrix K below is the rigidity matrix of the element ds.
The deformation of element ds, called dq’, is defined as
where E, G, A, J, , , and are Young’s modulus, the shear modulus of the employed material, the cross-sectional area, the torsional constant, shear coefficients, and moments of interstitial constant of the beam’s cross-section, respectively. In case the flexure can be reasonably approximated as a slender beam (i.e., when the length-to-thickness ratio is ≥ 10, as suggested in [12]), shear-induced deformations become negligible, and the shear coefficients and in Equation (10) can be set to infinity.
The matrix p’ can be computed from matrix p via a transfer matrix C.
where matrix C is determined from the curve of centroids, the shear center curve, and the local coordinate equations. Therefore,
where , which is a vector from the shear center of the section to the node. Hence,
Displacement dq’ of element ds causes a displacement dq at the free node, that is,
We combine Equations (14) and (15):
Finally, the relation between p and q can be expressed by Equation (17).
To verify Equation (17), three cases were computed by NASTRAN, and the results are shown in Table 2.

Table 2.
FEA verification.
Table 2 shows the effectiveness of Equation (17), regardless of the radius of the curved plate and whether the length of the cross-section is large or small.
Meanwhile, to satisfy the requirements of the IAAM, the geometrical parameters of the IAAM have been designed by the above theory and nominal stress approach. According to the design philosophy, the ropes on the IAAM produce loads only in the vertical direction. Therefore, the loads in p shown in Equation (6) are equal to zero besides fz. According to the FEA analysis, the maximum normal stress is found at the location of the fixed cross-section. The maximum normal stress of a cantilever plate is [13].
Combining Equation (18) and the nominal stress approach, the parameters of the IAAM are optimized and designed by using the minimal mass as the objective function and combining Equations (3), (17), and (18) and the nominal stress approach as the constraint. In addition, the diameter of the through hole of the IAAM should be greater than 8 mm to meet the requirements of the line arrangement in the process of driving the IAAM. In addition, to meet the third requirement, we should perform the force analysis shown in Figure 6. The bottom of the IAAM element is assumed to be a fixed constraint, and a 500 g uniform lift force is excited on the top of the IAAM element.
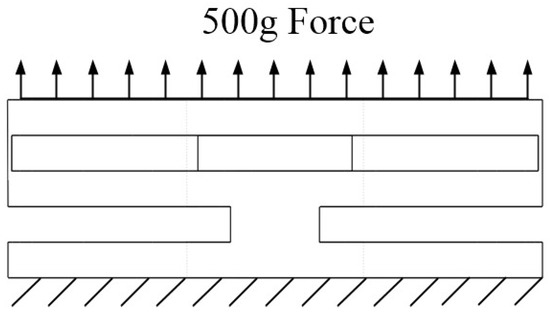
Figure 6.
A 500 g uniform lift-force analysis.
We assume that the force can be transferred 100% uniformly and that the connecting convex plates are simplified as rectangular plates, as shown in Figure 7. The length of plate L1 equals w. The height h1 equals the maximum deflection of the compliant flexure. Meanwhile, the width of the convex plate is unknown and can be obtained by optimization.
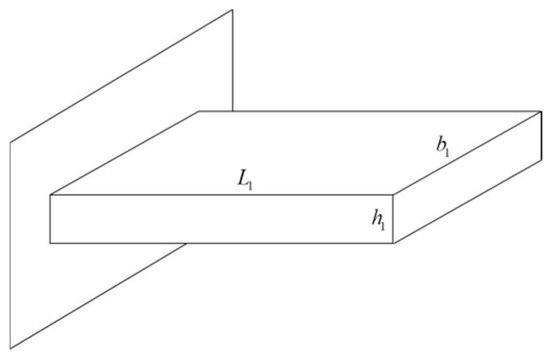
Figure 7.
Simplified connecting convex plates.
The parameter “w” is the width of the cantilever curved plate’s cross-section, and the parameter “r” is the radius of the centroidal axis shown in Figure 4. The parameter “n” is the number of core flexures in the IAAM.
According to the theory of elastic-plastic deformation, the deformations of the connecting convex plates are [13]:
The total height of the IAAM is:
According to Equations (17) and (19)–(21), the total deformations of compliant flexures in the vertical direction with a 500 g lift are:
Therefore, the third constraint is:
3. Numerical Analysis
According to the optimization model, we optimized the parameters of w, t, r, n, and b1 by using a genetic algorithm (GA). The optimized parameters are as follows: w = 6.5 mm, t = 1.7 mm, r = 14.1 mm, n = 2, and b1 = 4.7 mm.
3.1. Static Analysis
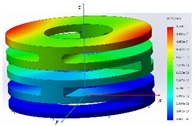
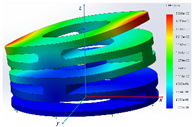
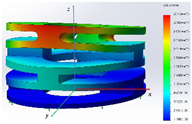
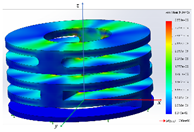
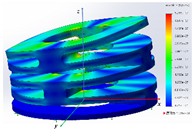
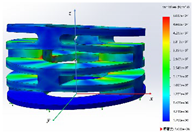
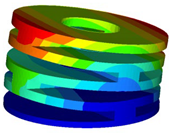
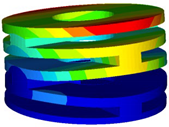
A static analysis model was carried out for the structure, which is shown in Figure 8. A tetrahedral mesh was used in the finite element model, and the total number of finite elements was 57,779. A linear-elastic material model was used in the FEA. To analyze whether the designed IAAM meets the requirements of the flying process of a rotor MAV, three cases were calculated:
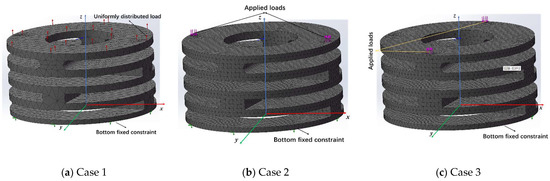
Figure 8.
Finite element analysis model of the IAAM.
- The stress-distribution characteristics of the lift on the IAAM were analyzed by applying uniform tension on the upper surface of the finite element model. The boundary conditions and applied loads are shown in Figure 8a.
- An upward tension was applied to one end of the finite element model in the x-direction, and a downward pressure was applied to the symmetrical position to analyze the characteristics of tilting state 1 of the IAAM. The boundary conditions and applied loads are shown in Figure 8b.
- An upward tension was applied to one end of the finite element model in the y-direction, and a downward pressure was applied to the symmetrical position to analyze the characteristics of tilting state 1. The boundary conditions and applied loads are shown in Figure 8c.
The factor of safety (FOS) is defined by the maximum normal stress and yield stress:
The results are shown in Table 3.

Table 3.
The results of the numerical analysis.
The results shown in Table 3 show that the maximum stress of the material under all three cases is far less than the yield stress of PA6. Cases 2 and 3 indicate that the mechanism meets design requirement 2. In addition, the total height of the structure is 14.41 mm. When the structure is subjected to a 500 g lift, the maximum deformation is only 0.038 mm, which is less than 2% of the total height of the structure. Hence, this configuration meets design requirement 3. In addition, the total weight of the structure is 5.63 g, which meets design requirement 4. Therefore, the structure of the IAAM designed in this paper completely meets the requirements for the flight process of a rotor MAV.
3.2. Modal Analysis
The first three orders of the free state modal analysis are carried out for the above design structure, and the analysis results are shown in Table 4.

Table 4.
The first three orders of modal analysis of the IAAM.
As shown in Table 4, the first-order mode of the IAAM is the bending of the intermediate axis of the IAAM towards the x-axis. The second-order mode is the bending of the intermediate axial y-axis. The third mode is the vertical vibration along the z-axis of the intermediate axis of the IAAM. The first two modes are close in frequency and similar in mode shape, but there is a phase difference caused by different connections between the gaps of the designed tilting device in the direction of .
The purpose of calculating and analyzing the natural frequency and mode of the model is to avoid the mechanical resonance of the IAAM caused by the vibration signal generated at the selected motor speed. The following relationship exists between the motor speed n and the IAAM frequency f.
n = 60f
The results are shown in Table 5.

Table 5.
The natural frequency of the IAAM corresponds to the motor speed.
As the motor speed in common use is approximately 3000–8000 RPM and the motor speed corresponding to the first three natural frequencies of the IAAM is much higher than that in common use, the designed mechanism satisfies the design requirements.
4. Conclusions
A new IAAM mechanism for adjusting a rotor MAV’s attitude is introduced and analyzed in this paper. The relation between the load and displacement on the free end of a quarter cantilever curved plate with a uniform cross-section is derived in this paper. The optimization model of the IAAM was built based on the derived theory, max normal stress approach, and izotropic linear elastic constitutive model. The mass of the optimized IAAM is 4.17 g, which is much lower than the fourth requirement. FEA was carried out on the optimized IAAM to ensure that the mechanism met the requirements of the flight process of a micro-rotor aircraft. The results show that the maximum normal stress of the IAAM is much lower than the yield stress of the used material. In addition, the first three modal frequencies are high enough to prevent resonance.
The IAAM reduces structural and installation complexity and improves structural reliability. Furthermore, the mechanism can be produced through 3D printing, which reduces production costs and improves production efficiency.
Author Contributions
Conceptualization, J.Z. and J.L.; methodology, J.Z. and J.L.; software, J.Z.; validation, J.Z.; formal analysis, J.Z.; investigation, J.Z.; resources, J.Z.; data curation, J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, J.L.; visualization, J.Z.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52005106.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.; Zhou, Y. Micro Air Vehicle Visual Navigation Based on Principal Component Analysis. J. Acta Aeronaut. Astronaut. Sin. 2008, 5, S220–S223. [Google Scholar]
- Shen, J.; Chopra, I. A Parametric Design Study for a Swashplateless Helicopter Rotor with Trailing-Edge Flaps. J. Am. Helicopter Soc. 2004, 49, 43–53. [Google Scholar] [CrossRef]
- Paulos, J.; Yim, M. Flight Performance of A Swashplateless Micro Air Vehicle; IEEE International Conference on Robotics & Automation: Washington, DC, USA, 2015; pp. 5284–5289. [Google Scholar]
- Ganguli, R.; Jehnert, B.; Wolfram, J. Optimal location of centre of gravity for swashplateless helicopter UAV and MAV. J. Aircr. Eng. Aerosp. Technol. 2007, 79, 335–345. [Google Scholar] [CrossRef]
- Saxena, A.; Chopra, I. Design, Development, and Hover Testing of a Mach-Scale Swashplateless Rotor Using Brushless DC Motor-Actuated Trailing Edge Flaps for Rotor Primary Control. J. Am. Helicopter Soc. 2017, 62, 1–12. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Wu, C. Development of swashplateless helicopter blade pitch control system using the limited angle direct-drive motor (LADDM). Chin. J. Aeronaut. 2015, 28, 1416–1425. [Google Scholar] [CrossRef][Green Version]
- Howell, L.L. Compliant Mechanisms; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Howell, L.L.; Magleby, S.; Olsen, B. Handbook of Compliant Mechanisms; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Seddon, J.; Newman, S. Basic Helicopter Aerodynamics; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Yu, J.; Bi, S.; Pei, X. Flexure Design: Analysis and Synthesis of Compliant Mechanism; Higher Education Press: Beijing, China, 2018. [Google Scholar]
- Mahjoob, M.J. An Exact Three-Dimensional Beam Element with Nonuniform Cross Section. J. Appl. Mech. 2010, 77, 3214–3220. [Google Scholar]
- Blake, A.; Epstein, H.I. Handbook of Mechanics, Materials, and Structures; Wiley Series in Mechanical Engineering Practice: Hoboken, NJ, USA, 1985. [Google Scholar]
- Yang, J.M.; Zeng, L.Z.; Xiong, C.H. Bending of cantilever beams of variable cross section under arbitrary loads. J. Nanchang Inst. Aeronaut. Technol. 1999, 13, 31–36. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).