Pareto Optimal PID Tuning for Px4-Based Unmanned Aerial Vehicles by Using a Multi-Objective Particle Swarm Optimization Algorithm
Abstract
1. Introduction
1.1. Historical Perspective of UAVs
1.2. Classification of UAVs
- Platform: (a) Fixed-wing. (b) Rotary wing: multirotor (quadrotor, hexarotor, octotor, etc.) or helirotor.
- Application: (a) recreational; (b) professional; (c) research.
- Weight, the altitude of flight and endurance: There are multiple articles and consensuses on how to classify UAVs according to these characteristics. One of these classifications is based on the combination of research and military literature: micro air vehicle (MAV), mini, tactical, medium-altitude and long-endurance (MALE) and high-altitude and long-endurance (HALE).
1.3. Control of UAVs
- Swarm control: centralized; decentralized; distributed [26].
1.4. Motivation and Innovation
1.5. Paper Organization
2. Problem Statement
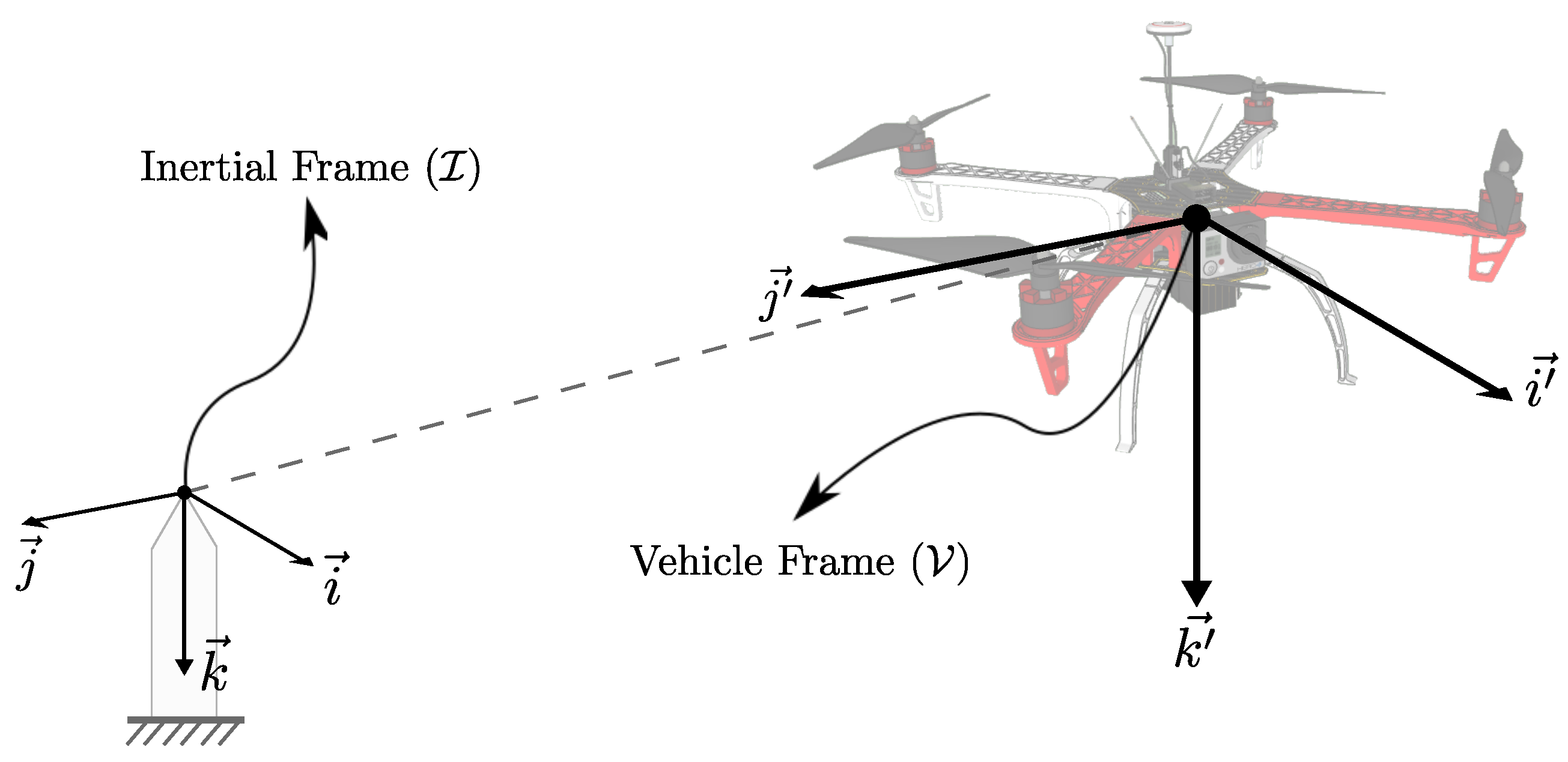
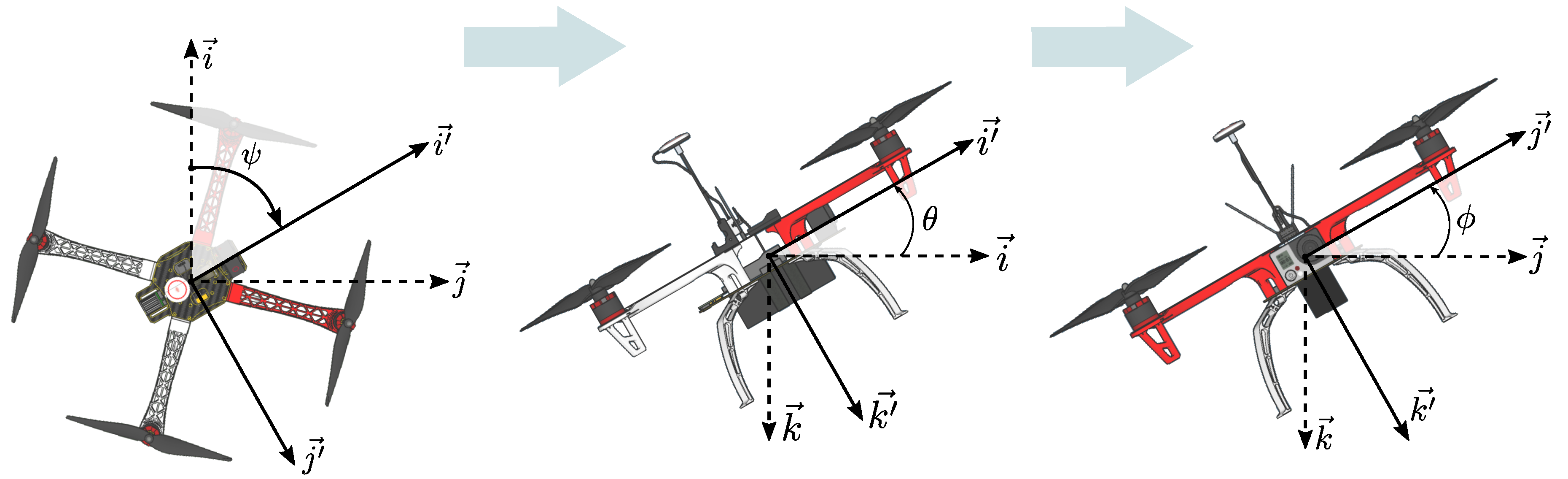
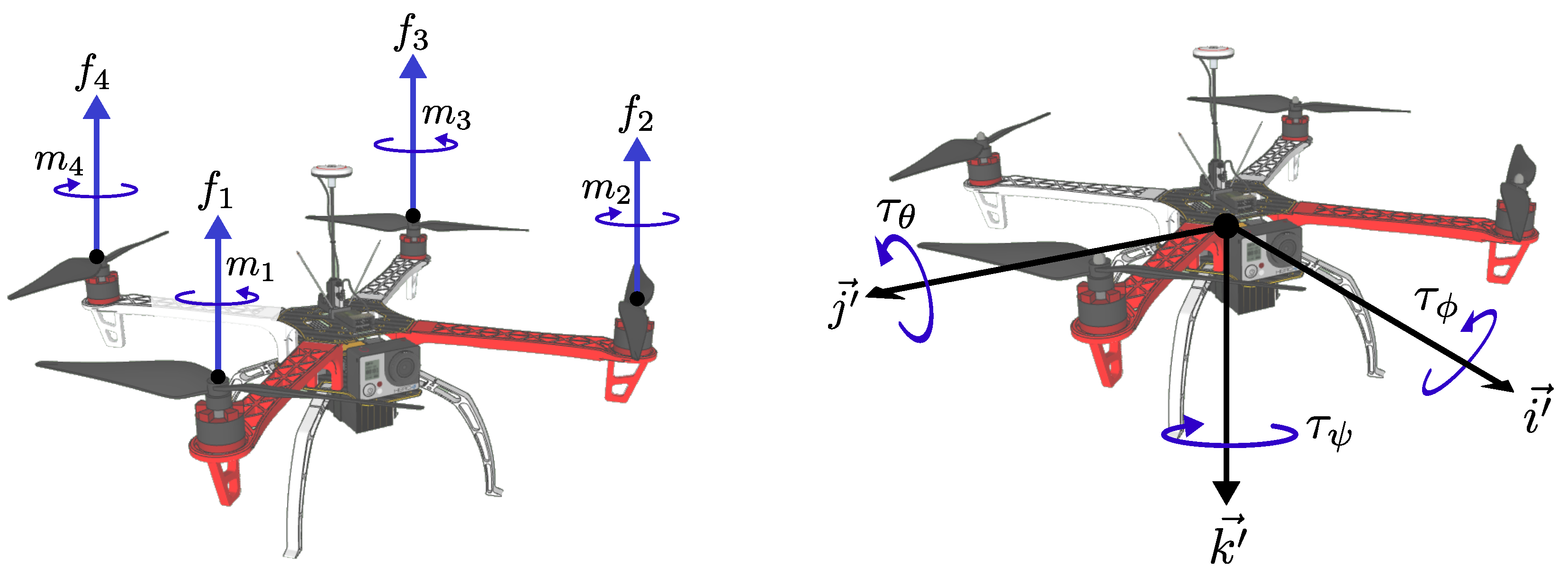
2.1. Mathematical Model of the Quadrotor
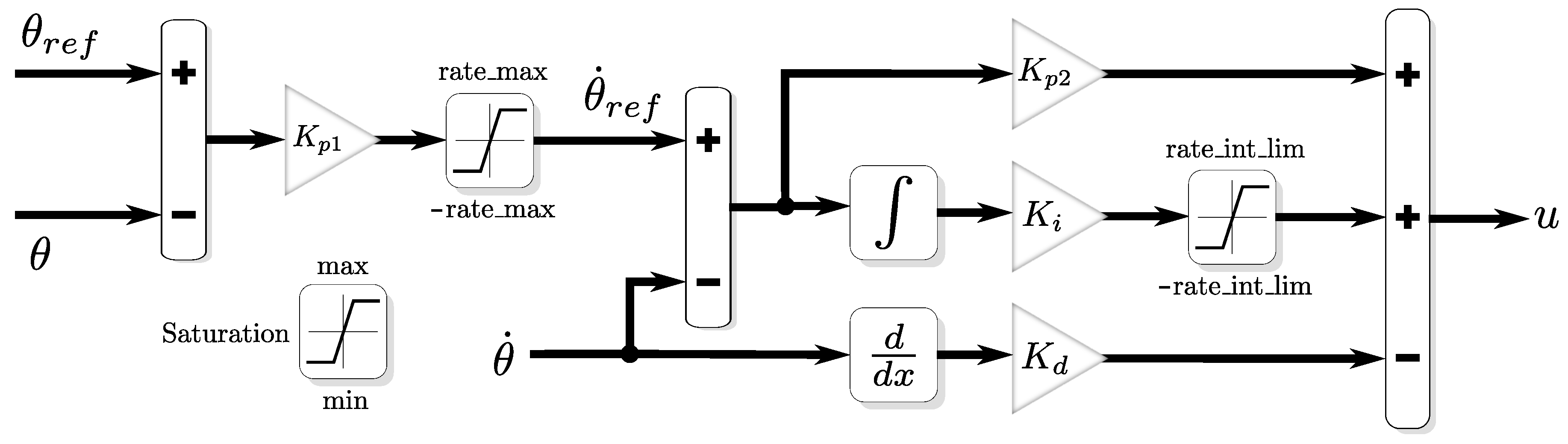
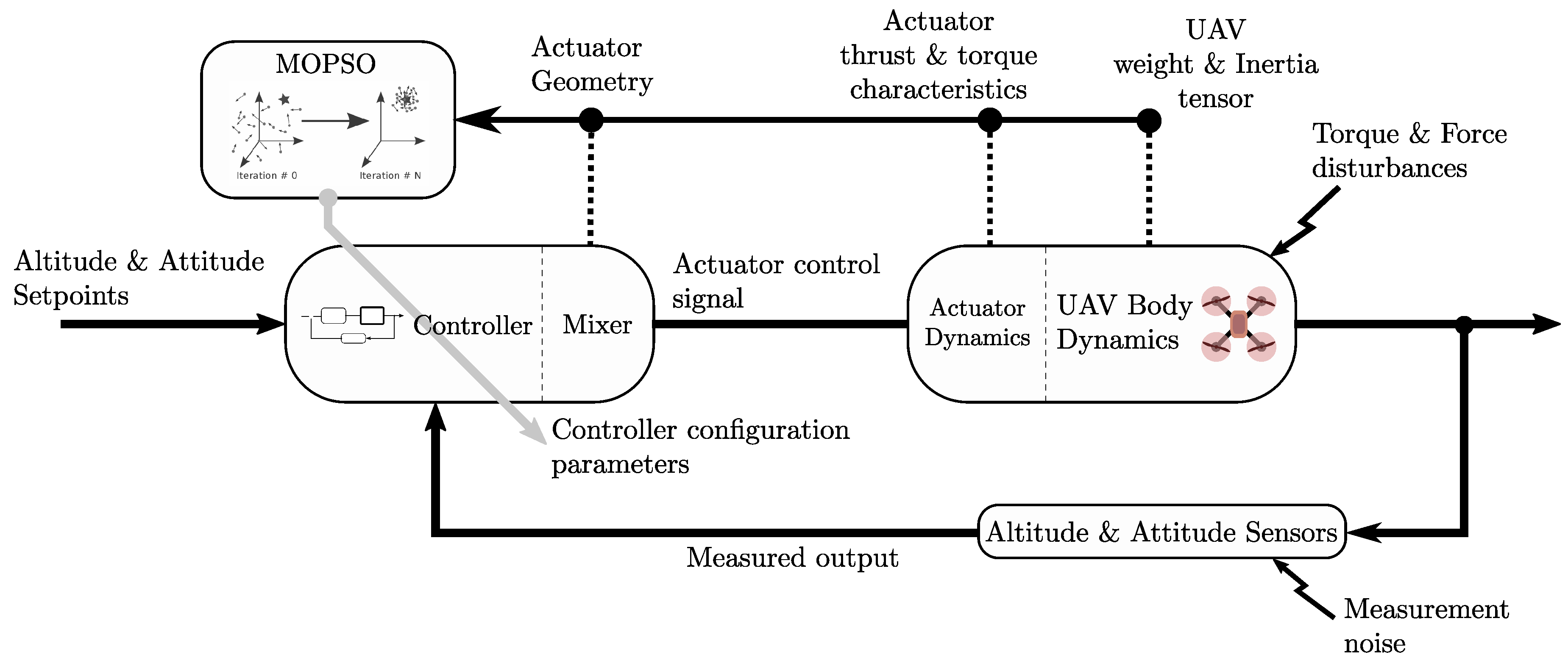
2.2. Control Architecture
3. Proposed Tuning Procedure for the Gains of the PID Controller Based on MOPSO
3.1. Particle Swarm Optimization (PSO) Algorithm
3.2. Multi-Objective Particle Swarm Optimization (MOPSO) Algorithm
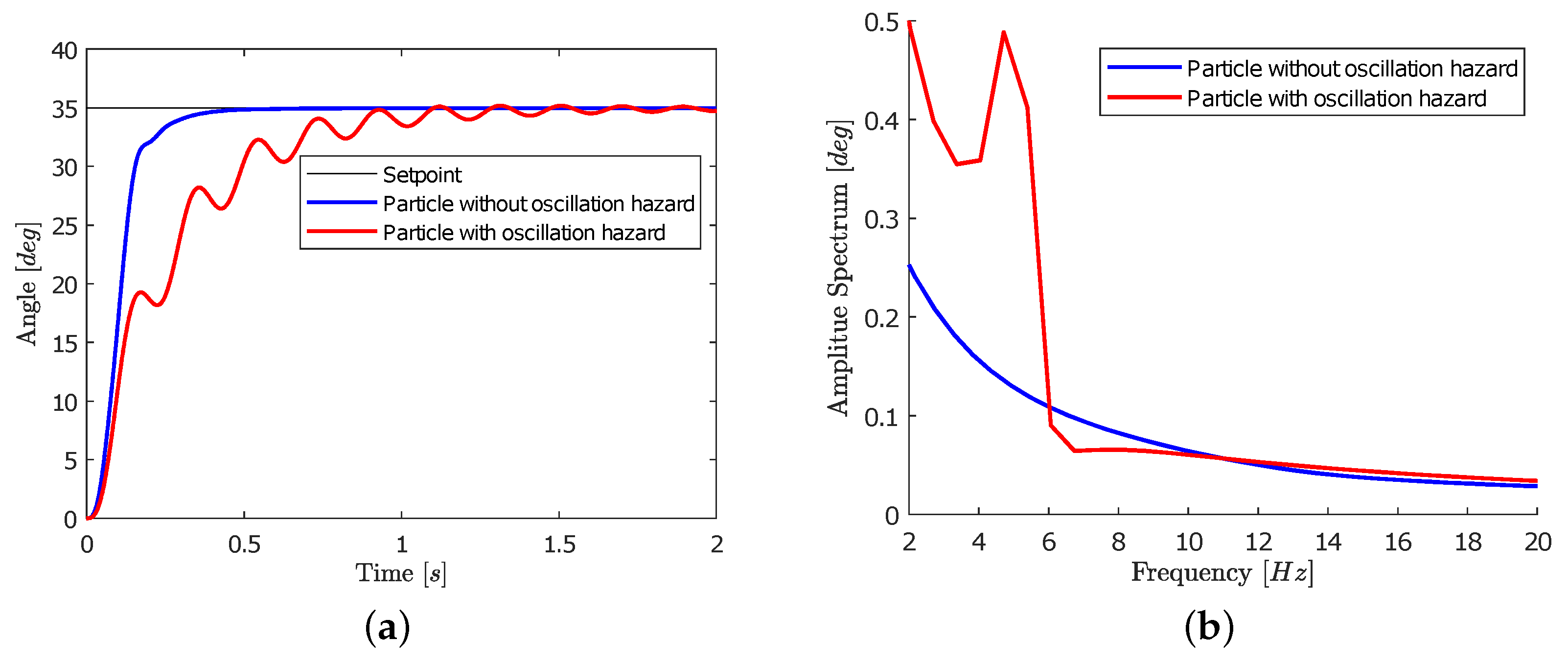
3.3. Proposed Tuning Procedure
- The mass of the UAV. This can be computed by measuring it directly on a scale or by using an estimation method such as that proposed in [38].
- The moment of inertia of the UAV. This input consists of the moment of inertia in the three-axes, . These values can be obtained by using the pendulum method [39]. However, CAD Software such as Solidworks can be used to compute the moments of inertia as well.
- The torque and thrust responses of the propellers. A method to find these values is shown in Section 4.1. This method allows one to define a relationship between the responses and the pulse-width modulation (PWM) signals issued by the controller. However, an alternative could be to just use maximum thrust and torque that will be loaded.
| Algorithm 1 Proposed tuning procedure based on the MOPSO algorithm. |
| {Assign values to the control factors.} {Randomly initialize particles and their velocities} {Initially empty archive} while do while do {Update the random vector.} Update with (12). Update with (11). if exceeds a boundary then Enforce constraints with (16) and (17) end if {Use the position of the particle as the parameters for a new PID controller.} Simulate UAV with its new controller’s gains. {Overshoot (O), root-mean-square error (RMSE) and rise-time (RT) are used as objectives, these are obtained from the UAV simulation} if then {Remove particles dominated by from A} {Add to A} end if if then {Update personal guide} end if {Update global guide for the next particle. Here, j is an index from A chosen randomly using PROB (see Section 3.2).} end while end while Select one of the particles from A as the final tuning. |
4. Simulation and Experimental Results
4.1. Quadrotor Parameters
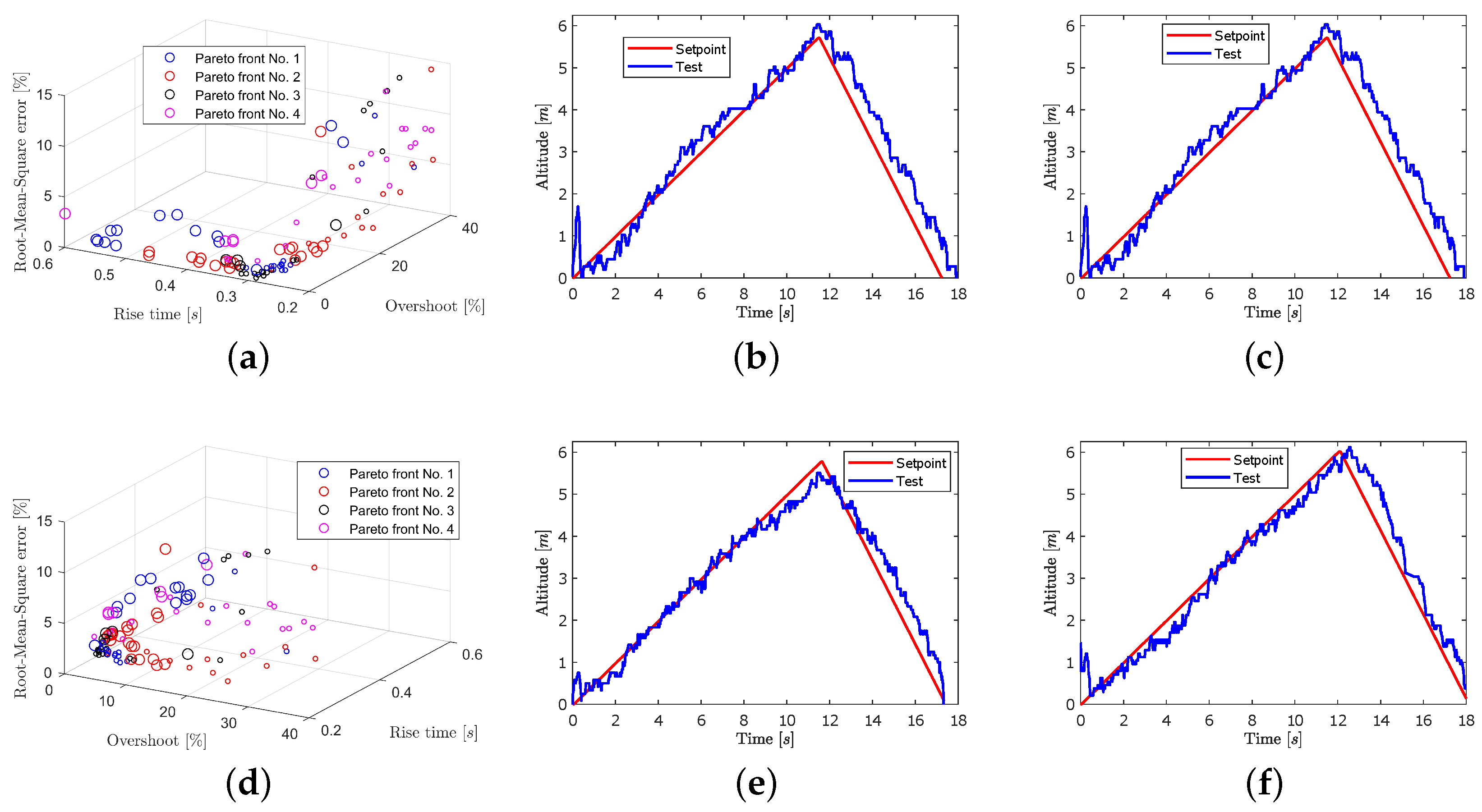
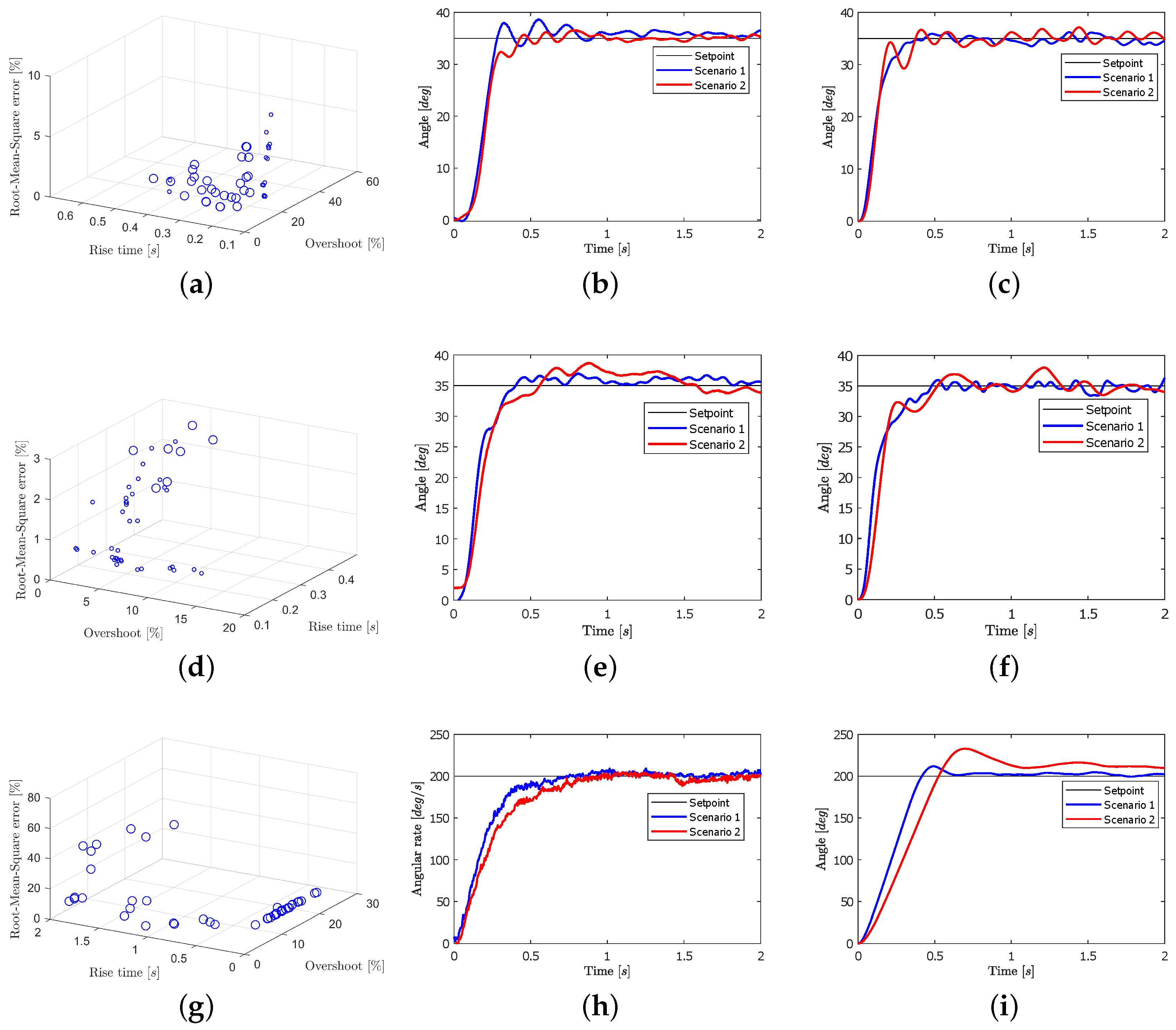
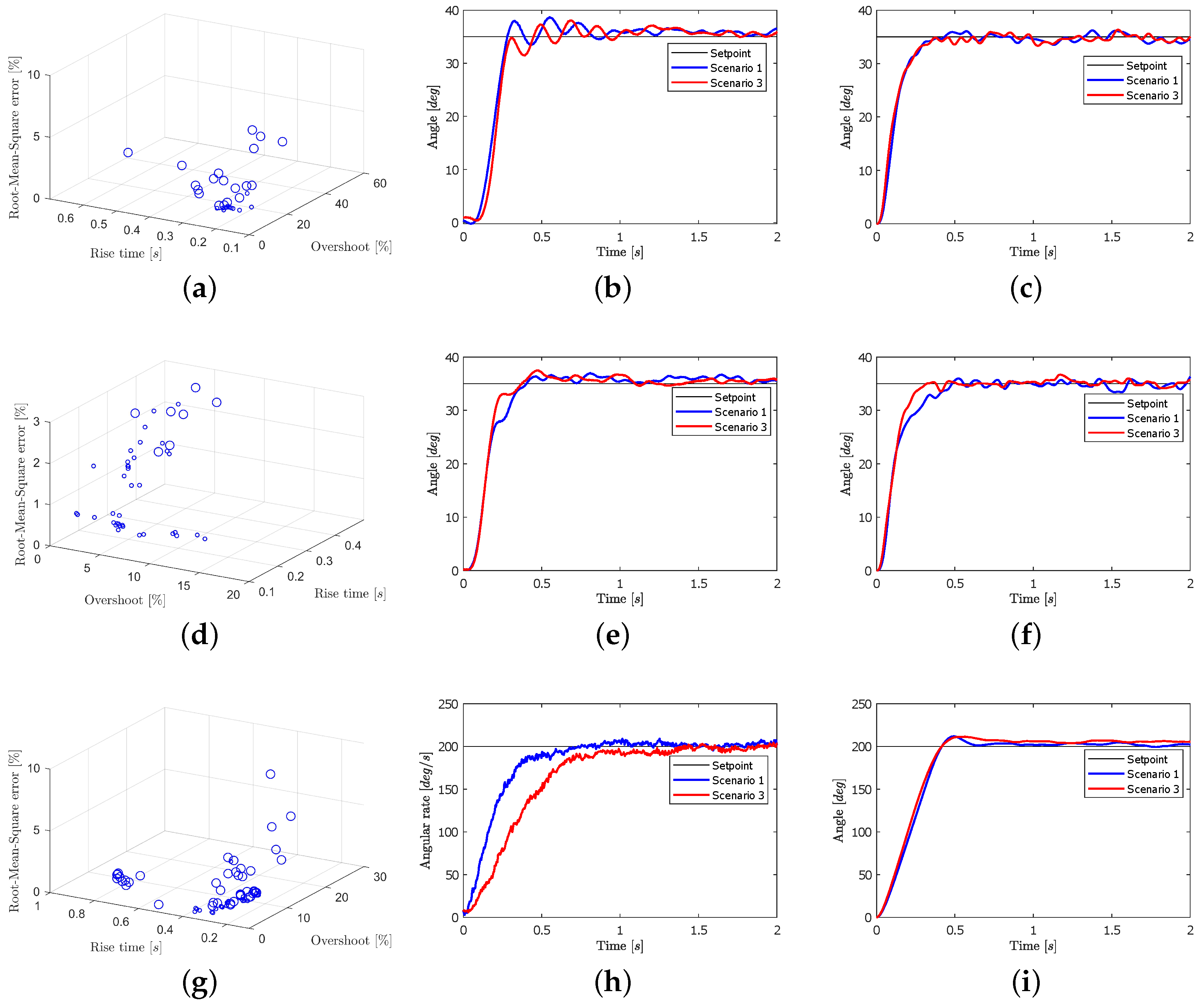
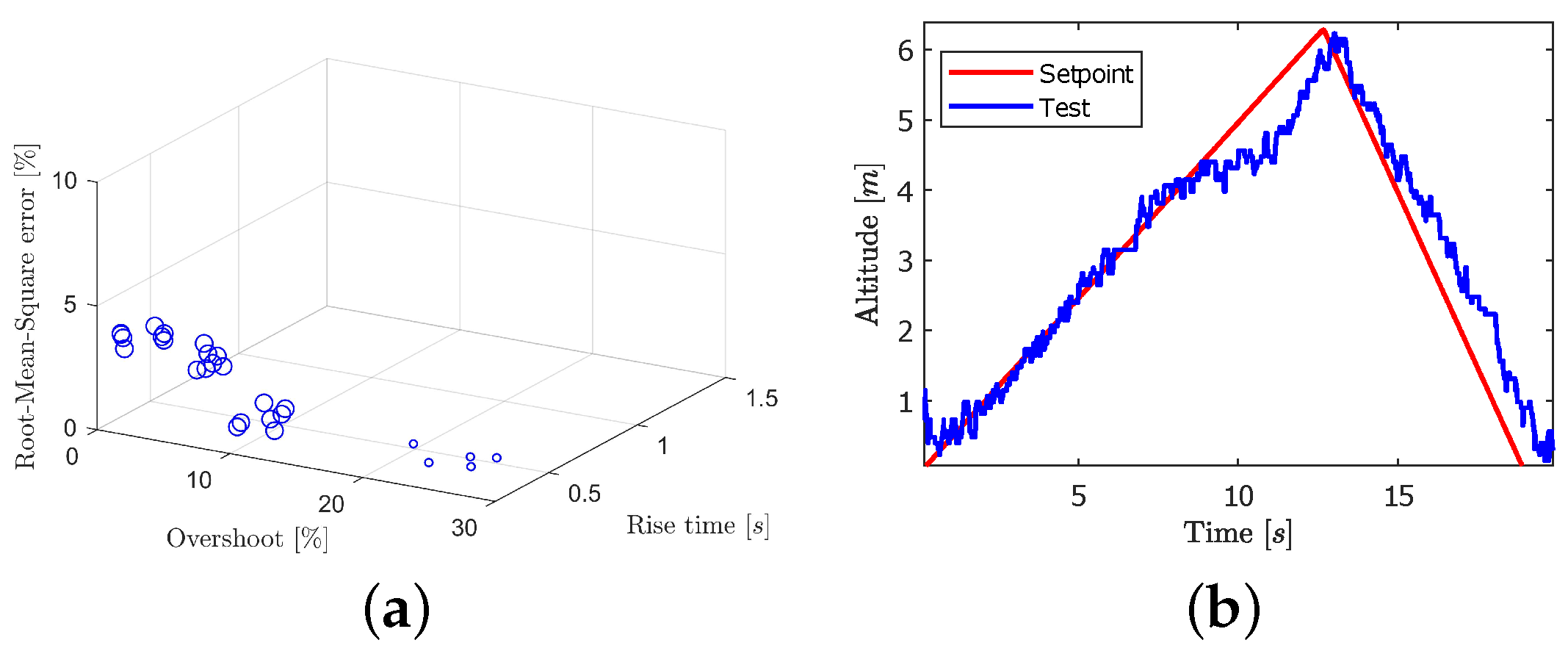
4.2. Simulation and Experimental Validation the Proposed MOPSO Algorithm
- Scenario 1: The model uses the nominal UAV parameters.
- Scenario 2: The UAV mass and inertia matrix values are changed by +15% relative to their nominal values. Moreover, the values of the diameter of the UAV, the and the are also modified by −15% from their nominal values.
- Scenario 3: The UAV mass and inertia matrix values are changed by −15% relative to their nominal values. Moreover, the values of the diameter of the UAV, the and the are also modified by +15% from their nominal values.
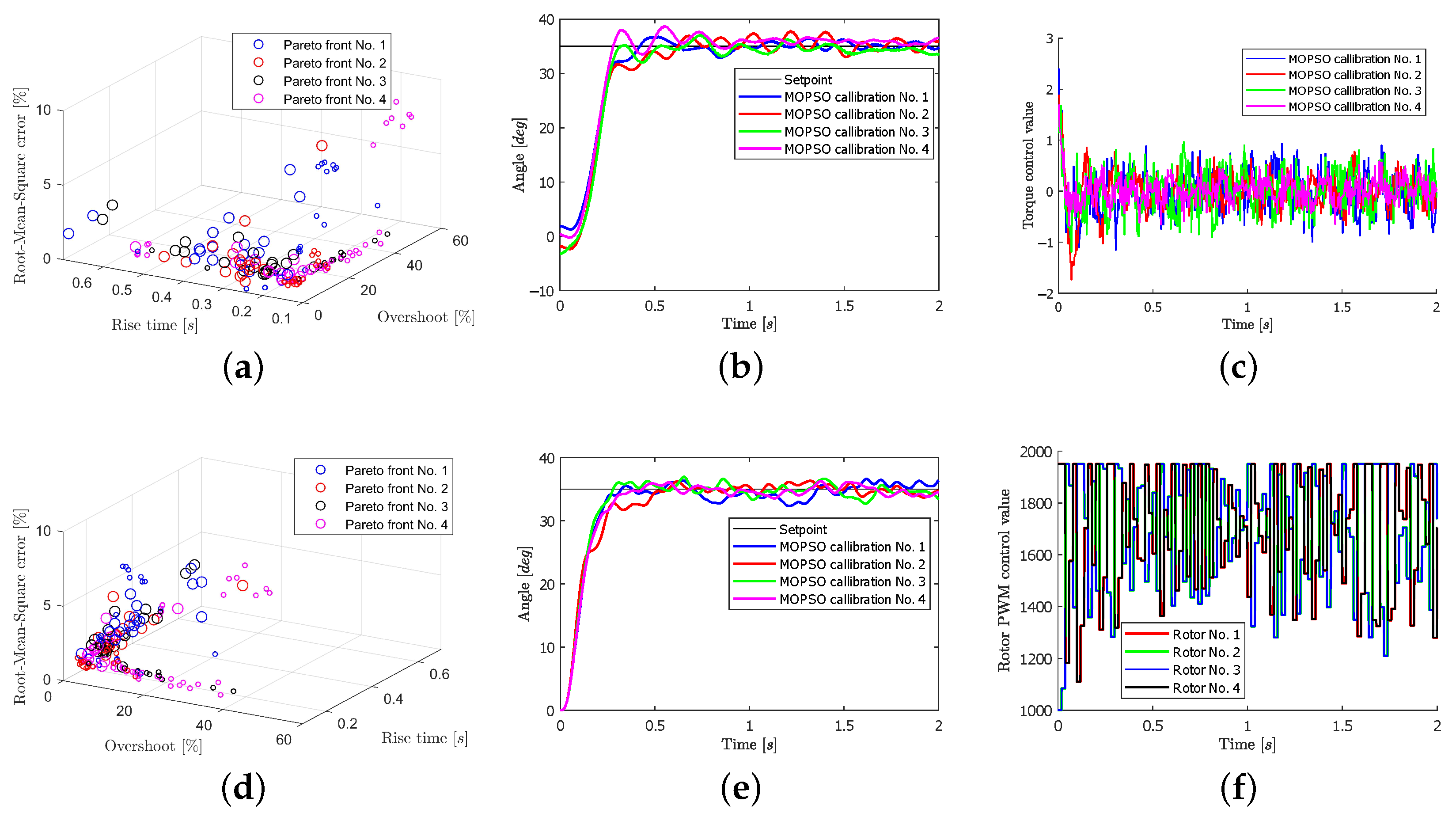
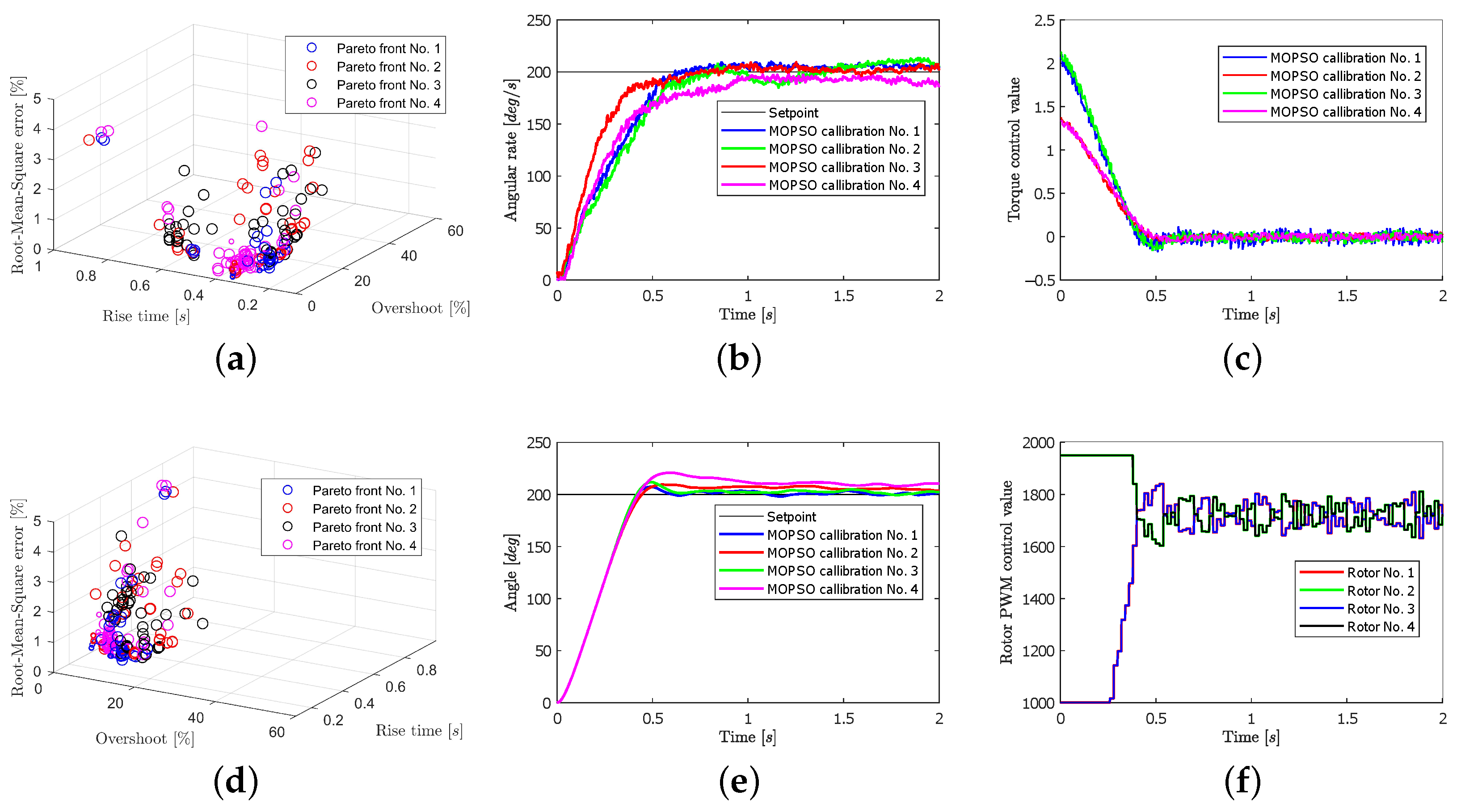
4.2.1. Scenario 1 Analysis
4.2.2. Scenario 2 Analysis
4.2.3. Scenario 3 Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Acronyms
| FFT | Fast Fourier transform. |
| GPS | Global positioning system. |
| HALE | High-altitude and long-endurance. |
| MALE | Medium-altitude and long-endurance. |
| MAV | Micro air vehicle. |
| PID | Proportional-integral-derivative. |
| PSO | Particle swarm optimization. |
| PWM | Pulse-width modulation. |
| UAV | Unmanned aerial vehicles. |
| MOPSO | Multi-objective particle swarm optimization. |
Symbols Used to Describe the UAV and Its PID Controller
| Distance between the axes of opposite motors in the UAV (m). | |
| Attitude and altitude rate error used in the PID controllers(rad/s or m/s). | |
| Thrust generated by each propeller (N). | |
| Gravity constant (m/s). | |
| Inertia tensor (k m). | |
| Proportional gain for the attitude and altitude position states controllers (s). | |
| Proportional gain for the attitude and altitude rate states controllers. | |
| Integral gain for the attitude and altitude rate states controllers. | |
| Derivative gain for the attitude and altitude rate states controllers. | |
| Mass of the UAV (kg). | |
| Torque generated by each propeller (N m). | |
| p, q, r | Angular velocity states (rad/s). |
| Control actions for the various degrees of freedom. | |
| U, V, W | Linear velocity states (m/s). |
| X, Y, Z | Linear position states (m). |
| , , | Angular position states for roll, pitch, and yaw (rad). |
| , , | Input torque for the angular position states (N m). |
| Input thrust for the altitude position state (N). |
Symbols Used to Describe the PSO and MOPSO Algorithms
| A | Repository of non-dominated particles. |
| B | Boundary of a search space. |
| , | Control factors of the Personal and Global bests influence on the particles. |
| D | Total number of objectives to be optimized. |
| f(x) | Fitness function. |
| G | Total number of iterations. |
| Gb | Global guide (or Global best) of a swarm. Best solution found so far by the whole swarm. |
| K | Size of the search-space or number of decision variables. |
| N | Total population of a swarm. |
| Pb | Personal guide (or Personal best) of a particle. Best solution found so far by the particle. |
| , | Random numbers used to update the velocity of a particle. |
| v | Velocity of a particle. |
| x | Location of a particle in the search-space. |
| y | Vector containing the responses of a particle to all the fitness functions. |
| Each of the objectives to be optimized. | |
| Generic vectors used to describe the Pareto dominance. | |
| Random vector for the velocity. | |
| Constraint value for the velocity. | |
| w | Inertia factor of the particles. |
References
- Prisacariu, V. The history and the evolution of UAVs from the beginning till the 70s. J. Def. Resour. Manag. (JoDRM) 2017, 8, 181–189. [Google Scholar]
- Black, J. Air Power: A Global History; Rowman & Littlefield: Lanham, MD, USA, 2016; pp. 26–28. [Google Scholar]
- Newcome, L.R. Unmanned Aviation: A Brief History of Unmanned Aerial Vehicles; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2004. [Google Scholar]
- Marshall, D.M.; Barnhart, R.K.; Hottman, S.B.; Shappee, E.; Most, M.T. Introduction to Unmanned Aircraft Systems; CRC Press: Boca Raton, FL, USA, 2016; pp. 6–7. [Google Scholar]
- Custers, B. Future of Drone Use; Springer: New York, NY, USA, 2016; p. 9. [Google Scholar]
- Hundley, R.O.; Gritton, E.C. Future technology-driven revolutions in military operations; RAND Corporation: Santa Monica, CA, USA, 1994; Document No. DB-110-ARPA. [Google Scholar]
- Miller, M. The Internet of Things: How Smart TVs, Smart Cars, Smart Homes, and Smart Cities are Changing the World; Pearson Education: London, UK, 2015. [Google Scholar]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Brooke-Holland, L. Unmanned Aerial Vehicles (Drones): An Introduction; House of Commons Library: London, UK, 2012. [Google Scholar]
- Arjomandi, M.; Agostino, S.; Mammone, M.; Nelson, M.; Zhou, T. Classification of Unmanned Aerial Vehicles; Report for Mechanical Engineering Class; University of Adelaide: Adelaide, Australia, 2006. [Google Scholar]
- Weibel, R.E. Safety Considerations for Operation of Different Classes of Unmanned Aerial Vehicles in the National Airspace System. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned aerial vehicles in agriculture: A review of perspective of platform, control, and applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Kim, J.; Gadsden, S.A.; Wilkerson, S.A. A Comprehensive Survey of Control Strategies for Autonomous Quadrotors. Can. J. Electr. Comput. Eng. 2019, 43, 3–16. [Google Scholar]
- Salih, A.L.; Moghavvemi, M.; Mohamed, H.A.; Gaeid, K.S. Modelling and PID controller design for a quadrotor unmanned air vehicle. In Proceedings of the 2010 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 28–30 May 2010; IEEE: Piscataway, NJ, USA, 2010; Volume 1, pp. 1–5. [Google Scholar]
- Reyes-Valeria, E.; Enriquez-Caldera, R.; Camacho-Lara, S.; Guichard, J. LQR control for a quadrotor using unit quaternions: Modeling and simulation. In Proceedings of the CONIELECOMP 2013, 23rd International Conference on Electronics, Communications and Computing, Cholula, Puebla, Mexico, 11–13 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 172–178. [Google Scholar]
- Masuda, K.; Uchiyama, K. Robust control design for quad tilt-wing UAV. Aerospace 2018, 5, 17. [Google Scholar] [CrossRef]
- Ataka, A.; Tnunay, H.; Inovan, R.; Abdurrohman, M.; Preastianto, H.; Cahyadi, A.I.; Yamamoto, Y. Controllability and observability analysis of the gain scheduling based linearization for uav quadrotor. In Proceedings of the 2013 International Conference on Robotics, Biomimetics, Intelligent Computational Systems, Yogyakarta, Indonesia, 25–27 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 212–218. [Google Scholar]
- Voos, H. Nonlinear control of a quadrotor micro-UAV using feedback-linearization. In Proceedings of the 2009 IEEE International Conference on Mechatronics, Málaga, Spain, 14–17 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Lee, D.; Ha, C.; Zuo, Z. Backstepping control of quadrotor-type UAVs and its application to teleoperation over the internet. In Intelligent Autonomous Systems 12; Springer: New York, NY, USA, 2013; pp. 217–225. [Google Scholar]
- Paiva, E.; Gomez-Redondo, M.; Rodas, J.; Kali, Y.; Saad, M.; Gregor, R.; Fretes, H. Cascade First and Second Order Sliding Mode Controller of a QuadRotor UAV based on Exponential Reaching Law and Modified Super-Twisting Algorithm. In Proceedings of the 2019 Workshop on Research, Education and Development of Unmanned Aerial Systems (RED UAS), Cranfield, UK, 25–27 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 100–105. [Google Scholar]
- Kali, Y.; Rodas, J.; Saad, M.; Gregor, R.; Alqaisi, W.; Benjelloun, K. Robust Finite-time Position and Attitude Tracking of a Quadrotor UAV using Super-Twisting Control Algorithm with Linear Correction Terms. In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics—Volume 2: ICINCO, Prague, Czech Republic, 29–31 July 2019; INSTICC, SciTePress: Setubal, Portugal, 2019; pp. 221–228. [Google Scholar] [CrossRef]
- Paiva, E.; Rodas, J.; Kali, Y.; Gregor, R.; Saad, M. Robust flight control of a tri-rotor UAV based on modified super-twisting algorithm. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 551–556. [Google Scholar]
- Kang, Y.; Hedrick, J.K. Linear Tracking for a Fixed-Wing UAV Using Nonlinear Model Predictive Control. IEEE Trans. Control. Syst. Technol. 2009, 17, 1202–1210. [Google Scholar] [CrossRef]
- Nafia, N.; El Kari, A.; Ayad, H.; Mjahed, M. Robust full tracking control design of disturbed quadrotor UAVs with unknown dynamics. Aerospace 2018, 5, 115. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Output feedback control of a quadrotor UAV using neural networks. IEEE Trans. Neural Netw. 2009, 21, 50–66. [Google Scholar] [CrossRef]
- Liu, L.; Liang, X.; Zhu, C.; He, L. Distributed cooperative control for UAV swarm formation reconfiguration based on consensus theory. In Proceedings of the 2017 2nd International Conference on Robotics and Automation Engineering (ICRAE), Shanghai, China, 29–31 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 264–268. [Google Scholar]
- Px4 Tuning Guide. Available online: https://docs.px4.io/v1.9.0/en/config_mc/pid_tuning_guide_multicopter.html (accessed on 16 April 2020).
- Mac, T.T.; Copot, C.; Duc, T.T.; De Keyser, R. AR.Drone UAV control parameters tuning based on particle swarm optimization algorithm. In Proceedings of the 2016 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Jaafar, H.I.; Mohd Ali, N.; Mohamed, Z.; Selamat, N.; Zainal Abidin, A.F.; Jamian, J.J.; Kassim, A. Optimal Performance of a Nonlinear Gantry Crane System via Priority-based Fitness Scheme in Binary PSO Algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2013, 53, 1–6. [Google Scholar] [CrossRef]
- Alvarez-Benitez, J.E.; Everson, R.M.; Fieldsend, J.E. A MOPSO algorithm based exclusively on pareto dominance concepts. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; Springer: New York, NY, USA, 2005; pp. 459–473. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Musa, S. Techniques for quadcopter modeling and design: A review. J. Unmanned Syst. Technol. 2018, 5, 66–75. [Google Scholar]
- Ortiz, N.A.S.; Laroche, E.; Kiefer, R.; Durand, S. Controller tuning strategy for quadrotor MAV carrying a cable-suspended load. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV), Beijing, China, 17–21 October 2016. [Google Scholar]
- Px4 Parameter Reference. Available online: https://docs.px4.io/v1.9.0/en/advanced_config/parameter_reference.html (accessed on 16 April 2020).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Azabi, Y.; Savvaris, A.; Kipouros, T. The Interactive Design Approach for Aerodynamic Shape Design Optimisation of the Aegis UAV. Aerospace 2019, 6, 42. [Google Scholar] [CrossRef]
- Coello, C.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No. 02TH8600), Chiang Mai, Thailand, 26–30 July 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Ho, D.; Linder, J.; Hendeby, G.; Enqvist, M. Mass estimation of a quadcopter using IMU data. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1260–1266. [Google Scholar]
- Krznar, M.; Kotarski, D.; Piljek, P.; Pavković, D. On-line Inertia Measurement of Unmanned Aerial Vehicles using on board Sensors and Bifilar Pendulum. Interdiscip. Descr. Complex Syst. INDECS 2018, 16, 149–161. [Google Scholar] [CrossRef]
- Px4 Manual Mode. Available online: https://docs.px4.io/v1.9.0/en/flight_modes/manual_stabilized_mc.html (accessed on 16 April 2020).
- Px4 Altitude Mode. Available online: https://docs.px4.io/v1.9.0/en/flight_modes/altitude_mc.html (accessed on 16 April 2020).
- Px4 Mission Mode. Available online: https://docs.px4.io/v1.9.0/en/flight_modes/mission.html (accessed on 16 April 2020).



| Axis | min | max | min | max | min | max | min | max |
|---|---|---|---|---|---|---|---|---|
| Roll | 0 | 12 | 0 | 0.5 | 0 | 0.2 | 0 | 0.01 |
| Pitch | 0 | 12 | 0 | 0.6 | 0 | 0.2 | 0 | 0.01 |
| Yaw | 0 | 5 | 0 | 0.6 | 0 | 0.2 | 0 | 0.1 |
| Altitude | 0 | 1.5 | 0.1 | 0.4 | 0.01 | 0.1 | 0 | 0.1 |
| Parameter | Value | |
|---|---|---|
| a = b | m | (X, Y, Z axes) |
| h | m | (X axis) |
| h | m | (Y axis) |
| h | m | (Z axis) |
| m/s | ||
| kg |
| Moment of Inertia | Value |
|---|---|
| kgm | |
| kgm | |
| kgm |
| Axis | Overshoot | Rise Time | Root-Mean-Square Error | ||||
|---|---|---|---|---|---|---|---|
| Roll | % | s | % | ||||
| Pitch | % | s | % | ||||
| Yaw | % | s | % | ||||
| Altitude | m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, V.; Gomez, N.; Rodas, J.; Paiva, E.; Saad, M.; Gregor, R. Pareto Optimal PID Tuning for Px4-Based Unmanned Aerial Vehicles by Using a Multi-Objective Particle Swarm Optimization Algorithm. Aerospace 2020, 7, 71. https://doi.org/10.3390/aerospace7060071
Gomez V, Gomez N, Rodas J, Paiva E, Saad M, Gregor R. Pareto Optimal PID Tuning for Px4-Based Unmanned Aerial Vehicles by Using a Multi-Objective Particle Swarm Optimization Algorithm. Aerospace. 2020; 7(6):71. https://doi.org/10.3390/aerospace7060071
Chicago/Turabian StyleGomez, Victor, Nicolas Gomez, Jorge Rodas, Enrique Paiva, Maarouf Saad, and Raul Gregor. 2020. "Pareto Optimal PID Tuning for Px4-Based Unmanned Aerial Vehicles by Using a Multi-Objective Particle Swarm Optimization Algorithm" Aerospace 7, no. 6: 71. https://doi.org/10.3390/aerospace7060071
APA StyleGomez, V., Gomez, N., Rodas, J., Paiva, E., Saad, M., & Gregor, R. (2020). Pareto Optimal PID Tuning for Px4-Based Unmanned Aerial Vehicles by Using a Multi-Objective Particle Swarm Optimization Algorithm. Aerospace, 7(6), 71. https://doi.org/10.3390/aerospace7060071








