Abstract
At present, most small satellites are delivered as hosted payloads on large launch vehicles. Considering the current technological development, constellations of small satellites can provide a broad range of services operating at designated orbits. To achieve that, small satellite customers are seeking cost-effective launch services for dedicated missions. This paper deals with performance and cost assessments of a set of launch vehicle concepts based on a solid propellant rocket engine (S-50) under development by the Institute of Aeronautics and Space (Brazil) with support from the Brazilian Space Agency. Cost estimation analysis, based on the TRANSCOST model, was carried out taking into account the costs of launch system development, vehicle fabrication, direct and indirect operation cost. A cost-competitive expendable launch system was identified by using three S-50 solid rocket motors for the first stage, one S-50 engine for the second stage and a flight-proven cluster of pressure-fed liquid engines for the third stage. This launch system, operating from the Alcantara Launch Center, located at 220’ S, would deliver satellites from the 500 kg class in typical polar missions with a specific transportation cost of about US$39,000 per kilogram of payload at a rate of 12 launches per year, in dedicated missions. At a low inclined orbit, vehicle payload capacity increased, decreasing the specific transportation cost to about 32,000 US$/kg. Cost analysis also showed that vehicle development effort would claim 781 work year, or less than 80 million dollars. Vehicle fabrication accounted for 174 work year representing less than 23 million dollars per unit. The launch system based on the best concept would, therefore, deploy small satellite constellations in cost-effective dedicated launches, 224 work year per flight, from the Alcantara Launch Center in Brazil.
1. Introduction
At present, most small satellites are launched as secondary payloads on large launch vehicles. A remarkable example of piggybacking payloads took place on 19 June 2014, when the Dnepr launch vehicle, in a single mission, placed 33 spacecrafts in orbit, including the Brazilian nanosatellite NanoSatC-Br1. On 14 February 2017, the PSLV, from India, deployed a record of 104 satellites in a single mission, of which 101 spacecraft were cubesats. On 3 December 2018, Falcon-9 from SpaceX delivered 64 satellites in a sun-synchronous orbit from Vandenberg Air Force Base SLC-4. The dedicated rideshare launch was contracted by Spaceflight Industries for the SSO-A smallsat express mission.
A major breakthrough in the small satellite launch service took place on 21 January 2018, as the Electron launcher placed three nanosatellites in the programmed orbit [1]. As for June 2019, the Electron launch vehicle had already delivered 28 satellites distributed in six different missions. The micro-launcher is capable of placing up to 150 kg of payload in a 500 km circular sun-synchronous orbit. At 45, elliptical orbit, with 180 km perigee and 500 km apogee, the payload capacity increases to about 220 kg. The launch system, operating from Rocket Lab Launch Complex 1 (Mahia, New Zealand), can deliver satellites in orbit inclinations limited to 39 to 98, and customers may choose dedicated or rideshare launch.
Small satellites have become a trend in the space segment. The benefit-cost ratio of such systems is now attractive to traditional and newcomer stakeholders that are populating the market with a variety of solutions and applications with growing levels of quality at competitive prices. Developers want to provide standalone services relying on small satellite constellations, such as remote sensing, communication, Internet of Things, and so on. As a result, there has been an increase in demand for space transportation of such small devices. More than a dozen launch vehicles, with LEO launch capacity ranging from a few kilograms up to a few hundred kilograms, are under development worldwide, mostly by private investors.
Cubesats are a good case in point exemplifying this boom in the sector of small satellites, which will drive the launch services market. In less than a decade, the number of cubesat launches has grown from very few to more than a hundred per year, as displayed in Figure 1. The chart was produced using information from 1058 spacecraft available at the Cubesat Database Saint Louis University [2]. The market is observing the small satellite trend with great attention. When we examine the log data from the last decade of cubesats launched, from 2008 until the end of 2019, we see a scenario clearly dominated by American (USA), Indian, and Russian launch vehicles. If we sort these vehicles as a function of the number of cubesats inserted into orbit, we verify that PSLV, Atlas, Antares, Soyuz, Dnepr, and Falcon are leading this trend, as shown in Figure 2, but, except for the Electron launcher (Rocket Lab), none of these rockets was specifically designed to launch small satellites [2].

Figure 1.
Distribution of cubesats launched yearly with data from launch vehicle by country [2].

Figure 2.
Percentage of cubesats inserted in orbit as a function of launch vehicle [2].
Rocket Lab started the commercial exploitation of the Electron launch vehicle in November 2018, after two qualification launches on May 2017 and January 2018. Since 2018, the company has conducted six missions, giving an average launch rate of three per year. The company was granted a license to perform a launch every 72 h, meaning more than 100 launches per year [3].
The Brazilian system for the development of space activities is composed of three public entities, the Brazilian Space Agency, as the central organization, the National Institute for Space Research (INPE) and the Institute of Aeronautics and Space (IAE). INPE is responsible for the development, integration, and test of spacecrafts while IAE is concerned with the development of sounding rockets and launch vehicles. The industrial sector and academia complete the system.
For decades, the Brazilian Space Agency (AEB) and the German Aerospace Center (DLR) have been cooperating in many space-related activities. DLR-Moraba, for instance, is investigating hypersonic flight techniques through re-entry vehicles launched from sounding rockets developed in Brazil. The program has already conducted two experiments, SHEFEX-1 and SHEFEX-2 [4], based on different launching platforms. The launch system for SHEFEX-2 was a two-stage sounding rocket, comprised of an S-40 and an S-44 solid rocket engines designed by IAE-Brazil.
For a potential SHEFEX-3 experiment, Moraba partnered with IAE-Brazil to support the development of a novel three-stage vehicle with increased payload capacity. It has been decided that Brazil would develop a new solid rocket engine, named S-50, to perform as the first and second stages of the improved launch system. The new launch vehicle would also rely on an S-44 engine for the upper-stage, the same used in the SHEFEX-2 experiment. In this configuration, the launch system would be capable of placing small payloads into low Earth near-equatorial orbits. The launch system was then named VLM-1 (Microsatellite Launch Vehicle).
The ongoing National Program of Space Activities points IAE-Brazil as the prime contractor to develop the VLM-1 launcher. Figure 3 shows the micro-satellite launcher for orbital missions (A) and its sub-orbital version (B) as claimed by the SHEFEX-3 experiment. In the basic configuration, the launch vehicle has, approximately, 18 m of length, 1.4 m in diameter and 26 tons of total weight. The S-50 rocket motor was designed to have about 11,100 kg of propellant, 440 kN of average thrust, 266 s of sea level specific impulse. The S-44 solid rocket motor has about 800 kg of propellant, 38 kN of average thrust, 277 s of vacuum specific impulse. The S-50 motor is scheduled to have qualification tests within 2019–2021 period, whereas the S-44 motor is already qualified. In this configuration, the launch vehicle has a payload mass capacity of about 50 kg, for a 500 km altitude polar mission. For low-inclined orbits, the payload capacity increases to about 150 kg.

Figure 3.
The VLM-1 launch system in orbital (A) and sub-orbital (B) configurations.
Based on these mass figures, the specific transportation cost of VLM-1 would be over US$100,000.00 per kilogram of payload inserted in high inclined orbits. From a commercial point of view, this high specific transportation cost resulted in serious concerns about the vehicle’s market penetration. Therefore, the Brazilian Space Agency and the MORABA team from DLR (Germany) conducted independent studies to enhance the performance of the VLM-1 launch system. Besides increasing vehicle performance, the Brazilian team also investigated the costs of development and operation of selected launch vehicle configurations based on the VLM-1 platform.
A survey of the literature showed that very few journal articles pay attention to cost analysis in the creation of future launch systems for the satellite market [5]. Duret and Fabrini [6], who addressed key aspects of the Vega launch system development plan, estimated the launch price of 18.5 M€(as in 1999) for one metric ton of payload mass, inserted in a circular polar orbit at 700 km of altitude. No detailed information, though, was given on cost assessment for the proposed launch system. The launch price for the Vega rocket weeks before the maiden flight was estimated at about 32 million euros [7]. Corrected for inflation, the estimated launch price of 1999 would be approximately 24.5 M€ in 2012 and 26 M€ in 2019. These figures are clearly much higher than the reported estimates of Duret and Fabrini [6]. Vega payload lift capability is 1430 kg for 700 km polar circular orbit insertion. The launch system can, therefore, place small to medium sized payload mass with a specific transportation cost of about 19,000 US$/kg of payload.
More recently, Drenthe et al. [8] presented a hybrid novel tool for space system cost analysis. The proposed model is based on subsystem level development costs estimates, proposed by the authors, in combination with operation cost correlations from the TRANSCOST model. Manufacturing cost predictions were compared to three launch system, a sounding rocket (Maxus 9), Falcon-1 and Pegasus XL. Price per flight estimations were conducted for Falcon 1 and Pegasus XL. Overall, the accuracy of the proposed hybrid model was within 20% for both manufacturing and operation costs.
In a recent review, Wekerle and colleagues [9] listed a series of launch vehicles designed for the small satellite market. The reported specific transportation cost for those vehicles ranged from about 20 to 67 thousand US dollars per kilogram of payload. The authors inferred specific transportation cost after dividing the reported cost of the vehicle by its payload capacity delivered at some reference orbit.
In another publication Nightingale and collaborators [10] listed a set of launch vehicles (operational and under development) with payload capacity varying from 1.33 to 584 kg, from which, specific transportation costs were in the range of 20 to 120 thousand US dollars per kilogram of payload. This large dispersion estimate on specific transportation cost would suggest a strong scaling effect considering limitations in vehicle performance, which depend on the type of technology adopted for the stages as well as how the vehicle is fabricated and the launch system operated. Heavier expendable launchers have ratios of payload mass to launch mass as high as 4% compared to less than 1% for the smaller launchers. In comparison to heavy launchers, one should expect much higher specific transportation costs for those small vehicles [11]. Most of the heavier launchers (the US and European) operate in the range of, roughly, 13 to 34 thousand dollars per kilogram of payload. Small satellites, however, are launched as hosted payloads from these heavy platforms.
For the last couple of years, a great number of launch vehicle developers have unveiled their systems with a target launch price for small payloads (<500 kg) that seems too low for that class of vehicle. It is clear, therefore, whether comprehensive cost analysis is a key element in the development of future commercial launch systems. In this paper, we present a cost analysis of three launch vehicle systems that could offer competitive prices to deliver small satellites at dedicated orbits. We combined a detailed cost valuation for development, fabrication and operation (direct and indirect costs) along with vehicle performance to infer launch system specific transportation costs.
A straightforward vehicle configuration was obtained by simply adding two S-50 motors to the first stage of VLM-1 launcher. Therefore, the proposed vehicle would rely on three S-50 motors for the first stage, one S-50 motor for the second stage and one S-44 for the upper-stage.
The next two concepts follow the preliminary version of the Ariane-6 family in which the first stage would comprise a bundle of three identical solid-rocket motors, operating as a single unit, and the same solid motor would be employed in the second stage. A LOx/LH engine was considered for the upper stage. The final concept of Ariane-6, however, changed to a modular three-stage launcher (solid–cryogenic–cryogenic). Similarly, we targeted increased commonalities among lower rocket stages and very low development effort for the upper stage, taking advantage of COTS (commercial off-the-shelf) propulsion hardware from the satellite industry. Therefore, in the other two proposed configurations, the launch vehicle combines three S-50 solid motors for the first stage, an S-50 motor for the second stage and a more conventional upper stage based on a pressure fed liquid rocket engine relying on hypergolic storable propellants. In this case, the main differences between the upper stages are related to the total engine thrust and propellant mass.
The launch system would operate from the Alcantara Launch Center in Brazil. The launch site is located 220’ S, making it the closest to the Equator, as compared to any other permanent launch centre worldwide. By virtue of its geographic position, launch operations allow rocket expendable stages and payload fairing to fall in the Atlantic Ocean reducing, accordingly, insurance coverage regarding third party and government property damage.
2. Methodology and Launch Vehicle Configuration
2.1. Vehicle Performance
For vehicle performance predictions, we used the DBallistic model developed by the Dnepropetrovsk National University (DNU) from Ukraine. The algorithm is based on a simple two-dimensional trajectory analysis. The accuracy of the model is in the range of 0.5 to 3.0%, considered adequate for the conceptual design phase carried out in this work. Essentially, the DBallistic model solves the reverse orbital mechanic’s problem with payload mass as the main criteria for trajectory optimization [12,13]. The task is solved from numerical analysis of the launch vehicle equations of motion. The system of equation is based on the hypothesis of a non-rotating Earth. Figure 3 shows the reference coordinate system and parameters for the trajectory analysis.
Within the active phase of the trajectory of the i-th stage of the rocket, the system of equations is integrated with respect to the following dimensionless variable
For a Cartesian earth-fixed coordinate frame, as shown in Figure 4, the planar rocket trajectory can be calculated by a set of differential equations with as the independent variable [14]. Acceleration and velocity along the orthogonal - plane (Figure 3) are given by
terms , , and in Equations (2)–(5) are estimated from
where,
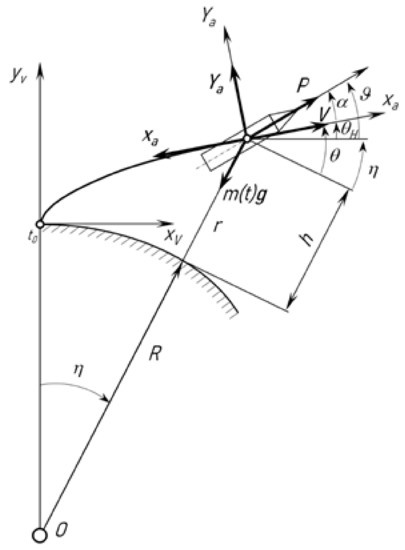
Figure 4.
Schematics of the rocket flight on the active flight regime with respect to the Earth’s coordinate system.
- M—Mach number;
- —sea-level specific impulse of i-th stage;
- —change in specific impulse due to the ambient pressure;
- —ratio of local atmospheric pressure to sea-level pressure as a function of altitude
- —pitch angle;
- —angle of attack.
The increase in engine-specific impulse due to altitude gain, on the active propulsion stage, is calculated with the help of the coefficient which varies progressively for the first stage and is null for the second and upper stages. The variation in rocket specific impulse is then given by
Rocket angle of attack and the programmed pitch angle variation are given by
Rocket total velocity and altitude are given by
Aerodynamic coefficients dependency on the velocity (Mach number) are given by the following relations [13,14]:
The system of equations of the rocket flight trajectory is solved with the assumptions of: (i) gravitational acceleration on the active flight regime is constant; (ii) angles of attack are small, thus, and ; (iii) rocket flight on the active trajectory is defined by the function . The gravitational model of the Earth and the characteristics of the standard atmosphere are also employed over the calculations. In addition, for each specific launch vehicle, initial input data includes the number of stages, the distribution of the initial dry mass and propellants over the stages, the law of change in propellant consumption for the main and attitude control engines, as well as some other characteristics (specific impulse of engines, aerodynamic coefficients, change of the center of mass during the flight, center of pressure, points of application of control forces, control system model and its coefficients). The launch trajectory provides the lowest possible energy losses, which is an indispensable condition for the operation thriftiness when satisfying several constraints on structural strength of a rocket, stability of flight, and so on. Minimization of energy costs is achieved by reducing the irreversible energy losses on the active flight regime, particularly, losses due to the gravity of the Earth and its atmosphere. These can be expressed as velocity difference when compared with the ideal or characteristic speed the launcher could obtain during a straight flight in the absence of the Earth’s gravity field and atmosphere. Choice of a launch best trajectory is based on determining the optimal control law under previously stated limitations, where payload mass is the parameter to be optimized by the differential equations. This trajectory is defined with known basic characteristics of the launch vehicle and given kinematic parameters. Based on above dependencies, it can be noted that maximization of a given payload mass is provided by choosing a law for the angle of attack at which aerodynamic and gravitational losses are reduced and vehicle’s is maximized.
2.2. Cost Analysis
Recently, Drenthe and colleagues [15] proposed a new methodology in which the development and manufacturing costs are inferred for each equipment element individually of the proposed launcher configuration (sub-system level) as opposed to the system-level approach which forms the basis of the TRANSCOST model [16]. Cost assessment, applied to launch vehicle concepts, should help to rank the cost-effective solutions proposed in this study. Considering we rely on system level data, we chose the TRANSCOST model for the space launch system cost analysis. TRANSCOST’s launch systems cost database is rather comprehensive and had been updated from 1960 to 2009.
In the TRANSCOST model, cost unit is based on Work-Year (WYr), therefore, not linked to a specific currency, independent from inflation and fluctuation of the exchange rate for a given country. Work-Year cost is defined as the total company annual budget, subcontracts excluded, divided by the number of productive full-time employees. The cost of one Work-Year, as suggested by the reference, is a measurement of direct cost labour, fees, and many other related parameters. As for Brazil, the space industry is comprised of very few small enterprises, but the aeronautic industry is well established, considering that Brazil has the third largest airplane producer in the world (EMBRAER). Based on the country’s aeronautic sector, we estimated a reference value of 378,000 BRL, or about 102,000 USD (as for January 2019) for the cost of one Work-Year in Brazil.
The TRANSCOST model is organized in three cost areas, i.e., launch system development cost, vehicle fabrication cost, and ground and flight operation costs. These costs were derived based, mostly, on the mass of a given system or subsystem. The reference data base was collected from 1960 to 2009, from US, European and Japanese space systems.
Cost estimation relationships (CER), for development and fabrication, are based on:
- mass of engine or stage, ;
- system-specific cost-to-mass sensitivity factor b;
- technical development status factor, ;
- technical quality factor, ;
- team experience factor, ;
- cost reduction factor for series production, .
The degression factors, , , and were introduced into the TRANSCOST model to bring cost predictions, which are mass-based, to the reference data of engine and stage development costs from actual projects within to 20% accuracy. Technical development status factor is related to the necessary effort to develop a given space system. Higher factor values, 1.3 to 1.4, are used for first generation system development. If just minor modifications to the existing system are needed, should be within 0.4 to 0.6. Factor values within 0.7 to 1.2, should be used, accordingly for moderate levels of system development effort, as proposed by the model [16]. Technical quality factor () is directed related to the level of reliability required for the liquid rocket engine, varying from 0.6 to about 1.8 depending on the number of qualification firings. If the system is space qualified, the reference value is one. Team experience factor () varies from 0.7 to 1.4. The lower limit refers to a team with superior experience in similar projects, while higher values are used when the team has little experience in similar projects. For a given level of experience, between these limits, the factor has to be set accordingly [16]. Parameter is used to refine vehicle fabrication cost estimations based on learning factors from system series production. For most systems, learning factor varies from 0.25 to 1.0. Lower mass systems and high annual production rates decrease the value of the learning factor. Reference [16] has a chart to help infer the value of this parameter.
2.2.1. Launch System Development Costs
For the system development cost, we considered cost estimate relationships restricted to the launch vehicle and its engines, disregarding the application of boosters. The vehicle should be composed of at least two stages, each comprised of a liquid or solid rocket propellant engine or cluster of them. Stages or engines previously developed are not included in this cost assessment. The total development cost is, therefore, the cost addition to develop stages and engines, multiplied by some correcting factors, as detailed in Equation (18). More specifically, the sub-model takes into consideration cost growth for deviation from optimum time schedule (), cost growth for development by parallel contractors () and a correction for productivity (). refers to the number of organizations contracted to develop the launch vehicle. The cost growth by deviation from the optimum schedule varies almost linearly from 1.0 (no deviation) to 1.5, with the latter value referring to a 70% increase in the relative development schedule. In the model, productivity refers the local industry working hours, level of education and dedication to work. The reference value is 1.0 (USA), spanning from 0.7 (Japan) to 2.11 (Russia). Higher values of () increase the cost of development or fabrication of a given space system. System engineering integration factor () is directly related to the number of vehicle stages (). All the costs are estimated in WYr. Launch system development cost is given by
where,
—system engineering integration factor;
—vehicle stage development cost;
—engine development cost;
—number of stages to be developed;
—number of engines to be developed;
—programmatic cost impact factors.
Engine development is restricted to the S-50 solid rocket motor. In Equation (19), the engine development cost for a solid propellant rocket engine, based on its mass (), in kilogram, is calculated by
For a liquid propellant propulsion system, stage development based on its dry mass (), can be estimated using the following equation
Stage development cost based on solid propellant rocket engines is not predicted by the TRANSCOST model. We proposed that stage development cost should be a fraction of the engine development cost. Therefore, the effort is estimated by the following relationship
Stage development effort is, therefore, estimated as 5% of the cost to develop the related engine since very little extra hardware is needed for the proper integration of that stage, multiplied by the number of engines employed ().
2.2.2. Vehicle Fabrication Cost
Launch vehicle production cost is based on the costs of material, processing and manufacturing, assembly and verification, engineering support and quality assurance costs [16]. These costs are applied to the fabrication of the vehicle and its engines. Total fabrication cost is further influenced by the system engineering integration factor powered to the number of stages and the productivity correction factor as shown in Equation (22).
where,
—stage fabrication cost;
—engine fabrication cost.
In Equation (22), unit engine fabrication cost of solid and storable (liquid) propellant rockets (), based on their inert mass (), in kilogram, is calculated respectively by
Also, in Equation (22), stage fabrication cost based on solid () and storable (liquid) propellant (), from their inert mass () without engine, in kilogram, is calculated respectively by
The fabrication cost of a solid propulsion stage, Equation (25), was also proposed by our group. It follows the same rationale of the solid stage development cost.
2.2.3. Ground and Flight Operations Costs
This sub-model is divided into direct () and indirect () operations costs. Direct operation costs apply to ground preparation of a vehicle, launch, and mission operation activities, including the cost of propellants. While, indirect operation costs are comprised of administration and management costs of the launch service provider, costs related to technical support along with general launch site and range costs, insurance fees, launch provider profit, and so on [16]. Ground operation cost is given by Equation (27). Essentially, this cost model considers the main activities related to the preparation of the range facilities, payload encapsulation, vehicle transportation, and erection to the launchpad, propellant loading, and other supporting direct activities relevant to the launch mission.
where,
—total dry mass of the vehicle;
L—launch rate (number of launches per year);
—impact of vehicle type;
—impact on assembling integration mode;
—learning cost reduction factor.
Flight operation cost is comprised of mission planning and preparation, launch and ascent flight control up to payload separation as well as flight safety control and tracking, given by the following equation
where,
Q—stage complexity factor.
This parameter accounts for the number and type of stages of the proposed launch vehicle. The suggested value for small solid rocket stages is 0.15 and 0.4 for an expendable liquid propellant stage.Vehicle propellant cost is estimated by
where,
—cost per kilogram of a given propellant,
—total mass of a given propellant.
Indirect operation costs are related to administration and management, launch service provider, general launch site and range costs. For simplicity, we considered these costs a fraction (10–15%) of the total cost per flight, as suggested by the TRANSCOST model [16]. Additional costs, such as insurance fees, nominal profit, and vehicle development amortization charges, or royalties, are also a fraction of the cost per flight. Combining vehicle performance and system cost analysis, launch system specific transportation cost, for a given reference orbit can be estimated from
where,
—vehicle development cost amortization;
—cost for nominal profit;
—additional costs;
—mass of payload @ given orbit;
—correction factor for vehicle performance estimates accuracy;
—number of flights.
2.3. Vehicle Configurations
Concerning orbital stages, solid rocket motors have limited applications when multiple burns are necessary. Consequently, some configurations have a liquid propellant upper stage with re-ignition capability for multiple payload orbit insertion and de-orbiting operation. To speed up the development of the launch system, as well as to reduce overall costs, the upper stage was designed to rely on off-the-shelf components, mostly from the satellite industry. Therefore, we selected for the liquid upper stage the RD-843 motor from Yuzhnoye SDO, Ukraine. This engine is employed in the fourth stage (AVUM) of the VEGA launch vehicle. Table 1 presents the main characteristics of the RD-843 liquid engine [17].

Table 1.
RD-843 main characteristics [17].
We conducted a preliminary performance analysis considering six configurations for the small satellite launch system based on combinations of the S50 motor for lower stages and the S44 and RD-843 for the upper stages. From this set of candidates, we selected the best three configurations for further cost assessment analysis, namely:
- Concept 1 (C-1)—this expendable launch system relies on adding two S-50 engines to the first stage of the basic VLM-1 configuration, We kept the S-50 and S-44 motor in the second and upper stages, respectively;
- Concept 2 (C-2)—is a three-stage (all serial) expendable launcher, in which three S-50 motors are combined into the first stage, one S-50 motor is used for the second stage and one RD-843 engine (2.5 kN) is employed for the upper stage;
- Concept 3 (C-3)—this expendable launch vehicle has three S-50 motors for the first stage, one S-50 motor for the second stage and a liquid upper stage comprised of four RD-843 engines.
Figure 5 shows the vehicle concept number 3, in which the first stage is comprised of a cluster of three S-50 motors, another S-50 motor is employed in the second stage and a cluster of four RD-843 liquid rocket engines is used for the upper stage.

Figure 5.
Launch vehicle concept with four RD-843 engines in the upper stage.
Table 2 presents relevant properties for each stage, as claimed by the DBallistic model for performance predictions. The propellant mass and specific impulse necessary to model the S-50 and S-44 motors were taken from system requirement data documentation from the Brazilian Space Agency. On the C-1 configuration, the S-44 is used as the circularization motor and that stage is comprised of the motor and payload adapter masses. In Table 3, PM, PMF, and area refer to the total stage propellant mass, propellant mass fraction, and aerodynamic area, respectively. The propellant mass for the liquid upper stage (C-2 and C-3) was calculated based on the maximization of vehicle’s . The liquid stage dry mass was inferred based on commercial components from geostationary satellites propulsion systems with a composite tube structure similar to a satellite’s central tube, thus ensuring a short design to operation time. The mass of the fairing was also included to the dry mass of the third stage. The mass of the interstage linking the second and upper stage was included into the dry mass of the second stage.

Table 2.
Relevant parameters for different vehicle stages.

Table 3.
Adopted correction factors for system costs.
The first stage derived from the combination of three S-50 motors was modelled considering a dry mass equivalent to three S-50 motors plus and addition of 550 kg to account for the interstage, structural linkage and reinforcements. This modelling seems conservative for performance and cost estimation. Propellant mass fraction estimations were based on the adopted technology for the engines. The S-50 solid-fuel motor, for instance, is manufactured based on composite casing technology. From Table 2 it is possible to infer the gross lift-off weight (GLOW) of each configuration, without payload mass. For concepts 1, 2 and 3, the gross lift-off weight (without payload) is about 50.68, 50.46 and 50.73 metric tons, respectively.
3. Results and Discussion
Figure 6 presents vehicle performance curves (DBallistic model) for a range of orbital altitudes (300 to 900 km) in sun synchronous missions. For the calculated altitude range, the vehicle concepts could launch payload masses stretching from about 350 to 650 kg, thereby covering the entire spectrum of the small satellites class. We considered, throughout our analysis, 500 km altitude, circular polar mission, as a reference orbit. As it can be seen, concept 1 would deliver a payload mass up to about 436 kg, to the reference orbit, while concepts 2 and 3 would deliver a total mass of about 467 and 593 kg, respectively. Concept 3 is the only one capable of sending a satellite relying on the Brazilian Multi Mission Platform-MMP ( 500 kg) on polar-orbiting missions in the range of 300 to nearly 900 km. The Brazilian Space Program [18], in its 10 year long program, lists a certain number of remote sensing and scientific missions based on the multi mission platform. The qualification flight of the platform is schedule to take place in 2020, carrying a wild field image sensor for optical remote sensing application. When operational, concept 3 would, therefore, give access to space to the majority of the Brazilian satellite missions for LEO.

Figure 6.
Launch vehicle concept performance in polar missions for different altitudes.
The performance plots show a modest gain in payload capacity by changing the upper stage solid motor (S-44) of concept 1 by a pressure fed liquid engine of 2.50 kN thrust. Thrust modulation and re-ignition capabilities would make concept 2 preferable over concept 1, from a purely operational point of view. The choice between these two concepts would depend on a cost analysis prior to the definition of a business plan for the space launch system. It can also be seen, in Figure 5, that the use of four RD-843 engines (concept 3), performing up to 10 kN of thrust, greatly increases the capacity of the launch system. The definition of which transportation system could be implemented must rely on performance and cost assessment for various scenarios and vehicle configurations.
As far as performance is concerned, concept 3 would be a potential launch system for the small satellite market, operating from the Alcantara Launch Center. At lower altitudes, about 500 km (circular polar orbit), concept 3 would deliver a payload as heavy as 593 kg. For lower orbit inclination (near equatorial), the capacity of the concept 3 launch system increases to about 725 kg, at 500 km altitude mission from the Alcantara Launch Center. With regards to concepts 1 and 2 the launch systems would deliver payloads up to 550 and 565 kg, respectively, in LEO equatorial missions.
The launch capacity of the three concepts are higher than most of the vehicles (micro launchers) under development, reported in a recent compilation [9]. Concept 3, thus, would fill a gap for the mini-satellite launch market (500 kg) considering dedicated missions for low Earth orbit, in any requested inclination, from the Alcantara Launch Center.
In addition to vehicle performance, we also conducted a cost estimation analysis for the selected vehicle configurations. Cost analysis was based on the specific set of Equations (18)–(30) and correction factors. Table 3 summarizes the value of each correction factor for system development, fabrication and ground and flight operations costs analysis.
System engineering integration factor () was taking into account for the launch system development cost by simply setting the number of stages equal to three. Development standard factor ( = 1.1) was taken as a first generation system, which require new techniques and new technologies along with the development. IAE-Brazil is internationally recognized as a preeminent organization in solid rocket propulsion development based on metal casing technology, and is rapidly acquiring knowledge in composite casing structures. The first S-50 motor engineering model had been subjected to structural analysis. The composite motor casing was approved to initiate the static fire test campaign. Technical quality factor () relates to the minimum number of engine qualification tests necessary for a given reliability. It has to be applied in the development of liquid rocket engines, whose qualification campaign claims hundreds of test firings. The RD-843 engine is already qualified. For solid rocket engines, fewer tests are necessary; therefore, we consider a unit value for the quality factor. Team experience factor () was taken as 0.75 by virtue of the technical staff long expertise in the development of similar projects. We assumed a lower value for these factors considering the qualification of our technical staff (IAE-Brazil), the associated infrastructure and the level of maturity of the Brazilian space industry in solid rocket production, notably AVIBRAS. The learning factor () adopted in the present work considered the large number of motors expected to run the launch system based on the adopt commonalities. At a launch rate of 12 missions per year, 48 S-50 motors would be necessary to assemble the first and second stages. The production rate of S-44 would be 12 per year. Liquid engine development cost (RD-843) is null considering it is an off-the-shelf component, and, therefore, the learning factor was subjected only to stage integration. The correction factor for vehicle performance estimates accuracy () was set to the highest expected error (3%) from the DBallistic model, i.e., 1.03. We assumed a margin of 10% of deviation of the development time schedule, thus setting a value of 1.1 for this programmatic factor (). The programmatic factor referring to the number of organizations contracted () for vehicle development was set to unity, considering that IAE-Brazil is the sole prime-contractor responsible for the project development. The productivity correction factor, which is a relative measure of annual working hours, education and dedication to work of a country (US as the reference, = 1), was set as 1.1, or, a 10% increase in the WYr compared to the US counterpart. The impact on the launch vehicle type () was taken as 0.3 which is suggested for solid propellant vehicles. The impact of the launch vehicle assembly and integration mode () was set to 0.5, corresponding to horizontal assembling and transport to pad for erection. Stage complexity factor () was taken as 0.15 for stage comprised of small solid rocket engines and 0.4 for a stage relying on liquid rocket engines.
Business plans for the small satellite launch providers are often based on a very high number of launches per year (≈100). For such figures there should be more than one launch site with dedicated operation teams. For indirect operation costs () we assumed that the Alcantara Launch Center can sustain, in its commercial phase, up to 12 launch campaigns per year. This pace, however, can only be achieved after performing a certain number of missions during two to three years following the maiden flight. The number of total flights were set to 100, over a decade of system operation. Nominal profit and additional costs were set to 5% and 1% of the cost per flight (CPF), respectively.
Table 4 presents the estimated cost parameters for the three launch vehicle concepts. Cost per flight, in dollars, was estimated after multiplying the correspondent cost in work years by the cost, in dollars, of one WYr. Specific transportation cost (Equation (30)) was inferred diving the sum of the related costs by the payload mass capacity, for a given reference orbit (@ 500 km, polar). A correction factor was employed to consider the vehicle performance estimates from the DBallistic model. Monetary data was rounded up to million.

Table 4.
Launch vehicle (LV) related costs in WYr for the three concepts, C-1, C-2, and C-3.
For concepts 1, 2 and 3, the maximum payload mass insertion capability for the reference orbit, calculated by the DBallistic model, was 436, 467 and 593 kg, respectively. Vehicle development effort for the configurations 1, 2 and 3 was 755, 754 and 782 WYr, respectively. We can see that development efforts for concepts 1 and 2 are quite similar and concept 3 claims about 4% more work and investment than the previous ones. Considering a WYr equivalent to 102,000.00 USD (Brazilian figures), the development cost in US dollars for concepts 1 and 2 would approach 77 million, while for concept 3, near 80 million. The replacement of the S-44 solid motor by a cluster of RD-843 liquid engine proved adequate by taking into consideration a 36% increase in launch mass capacity for less than three million dollars added to develop the launch system as compared to concept 1.
Vehicle fabrication costs are in the range of 141 to 175 WYr, with the lowest value for the all-solid stages concept and the highest for the vehicle concept based on a cluster of RD-843 engines as the upper stage. In US dollars the effort would represent nearly 14, 16, and 18 million, for vehicle concepts 1, 2 and 3, respectively.
The share of direct operation cost from the associated values of fabrication and operations (direct and indirect) is about 4.5% for concept 1, decreasing to 3.87% for concept 3. The share of propellants cost in the cost per flight is less than 2% for all the concepts. Amortization of development, nominal profit and additional costs amounted 18.6, 19.6 and 21.2 WYr, respectively for concepts 1, 2 and 3, representing about 10% of the respective cost per flight.
As it can be seen from Table 4, the cost per flight, in dollars, varied from 19 to 23 million. In terms of specific transportation costs, the proposed vehicle configurations would charge about 43, 44 and 39 thousands of US dollars per kilogram of payload inserted into the reference orbit. For comparison, the Scout small launch vehicle, a four stage all-solid launcher that operated from 1961 to 1994, totalling 99 missions, had a specific transportation cost of 0.4 WYr per kg of payload inserted into LEO [16]. Thor Delta-E was another small launch vehicle (540 kg @ LEO) which operated in the 1960s with estimated specific transportation cost of 0.6 WYr/kg [16]. The calculated specific transportation cost for concepts 1, 2 and 3 would be 0.42, 0.43 and 0.38 WY/kg, respectively. Therefore, the proposed launch systems have estimated costs similar to retired launch vehicles of the same class. These figures also confirm the higher cost per kilogram for smaller launchers compared to heavy-lifters, for which the reported specific transportation cost is in the range of 0.04–0.1 WYr/kg [16].
Figure 7 shows a plot of satellite payload masses versus specific transportation costs for launch systems under development as well as in commercial operation [9] along with those proposed by this work, with a 20% error bar. Additionally, the figure shows plots of the specific charges for a broad range of satellite masses taken from an US company currently offering rideshare launch opportunities [19].

Figure 7.
Market trends in specific transportation cost versus payload mass. Black crosses refers to rideshare charges [19]; red crosses [9]; blue triangles C-1/2/3 (@ 500 km/polar); green bullets C-1/2/3 (@ 500/equatorial).
For payloads weighting 300 kg or less, there is a large variation in specific transportation costs ranging from 22 to 65 thousand dollars per kilogram, for both rideshare and the estimated figures of new projects and some already in commercial phase. Above 400 kg vehicle capacity, the price per kilogram is in the range of 25 to 50 thousands of US dollars, except for the Epsilon launch vehicle from Jaxa which charges 67,000 US$/kg for LEO missions [9].
As it can be seen, the proposed configurations (concepts 1, 2 and 3) present larger average payload capacity along with lower specific transportation costs compared to most of the small launchers currently under development (black crosses) and in commercial operation. Also, the price per kilogram of the payload of concept 3 is at the same level of those charged by a launch service provider selling rideshare opportunities [19]. Concept 3, however, would offer the service, for a 500 kg class satellite, in a dedicated flight for an equivalent price per kilogram thus opening the opportunity for satellite providers to establish their planned constellations [20,21].
4. Conclusions
Considering the current development of the S-50 solid rocket motor for the Brazilian space program, we investigated a set of three expendable launch vehicle concepts to deliver small satellites to low-Earth orbit from the Alcantara Launch Center, Brazil. We combined launch vehicle performance and cost analysis to help judge the most cost-effective solution for small satellite costumers. Performance analysis showed that the three concepts would be capable of sending payloads in the range of 350 to 750 kg for LEO missions, in a variety of orbit inclinations. Concept 3 can deliver a satellite up to 725 kg in low inclination orbit (500 km altitude). This launch system, based on the S-50 motor and a liquid upper stage would offer dedicated launch services for the minisatellite class at affordable prices, from 32,000 to 39,000 US$/kg). Cost analysis showed that vehicle development effort claimed 781 WYr, or less than 80 million dollars and vehicle fabrication accounts for 174 WYr representing less than 23 million dollars per unit. The implementation of the cost model along with the vehicle performance model will facilitate future investigation on new types of launch systems; in particular, those relying on clusters of small liquid rocket engines, similar to the Electron (Rocket Lab). The large amount of data generated in the current development of the enhanced VLM should be used to refine the TRANSCOST model for improved cost predictions of small launchers.
Author Contributions
Conceptualization, P.L.K.d.C. and C.A.G.V.; cubesat data analysis, R.L.; DBallistic model validation, O.S.; writing original draft, P.L.K.d.C., C.A.G.V., O.S., and R.L.; writing review and editing, C.A.G.V.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript
| ALC | Alcantara Launch Center |
| CER | Cost estimating relationship |
| C-1 | Launch vehicle configuration number 1 |
| C-2 | Launch vehicle configuration number 2 |
| C-3 | Launch vehicle configuration number 3 |
| IAE | Institute of Aeronautic and Space |
| INPE | National Institute for Space Research |
| LEO | Low Earth orbit |
| LRE | Liquid rocket engine |
| LV | Launch vehicle |
| PM | Propellant mass |
| PMF | Propellant mass fraction |
| SRE | Solid rocket engine |
| STC | Specific transportation cost |
| WYr | Work Year |
Nomenclature
| Gravitational acceleration | |
| h | Altitude |
| M | Mach number |
| m | Mass |
| Launch vehicle total dry mass | |
| Propellant mass flow | |
| Initial mass of vehicle stage | |
| R | Radius of the Earth |
| x | Coordinate |
| y | Coordinate |
| Aerodynamic coefficient | |
| Aerodynamic coefficient | |
| r | Radial distance |
| t | Time |
| Specific impulse | |
| V | Velocity |
| Ratio of atmospheric pressure to sea-level pressure | |
| Pitch angle | |
| Angle of attack | |
| Independent variable (dimensionless) | |
| System engineering integration factor | |
| H | Development cost |
| Parameter | |
| Index for fabrication | |
| Number of vehicle stages | |
| Number of engines in vehicle stage | |
| Programmatic cost impact factor for deviation of optimum time schedule | |
| Programmatic cost impact factor for development by parallel contractors | |
| Programmatic cost impact factor for productivity | |
| Thrust to weight ratio | |
| Technical development status factor | |
| Technical quality factor | |
| Team experience factor | |
| Cost reduction factor for series production | |
| Impact factor for vehicle type | |
| Impact factor for assembling integration mode | |
| L | Launch rate (number of launches per year) |
| Index for development | |
| S | Index for stage |
| E | Index for engine |
| Index for solid engine | |
| Index for liquid engine | |
| Index for solid stage | |
| Index for liquid stage | |
| Index for amortization | |
| Index for profit | |
| Index for propellant | |
| Index for payload | |
| Index for additional | |
| F | Fabrication cost |
| Index for ground operation costs | |
| Index for flight operation costs | |
| C | Cost |
References
- Rocket Lab. Available online: https://www.rocketlabusa.com/electron (accessed on 18 June 2019).
- Cubesat Database. Available online: https://sites.google.com/a/slu.edu/swartwout/home/cubesat-database (accessed on 2 June 2019).
- Messier, D. Rocket Lab Plans for Electron Commercial Flight. Available online: http://www.parabolicarc.com/2018/03/14/rocket-lab-plans-electron-commercial-flight/ (accessed on 2 June 2019).
- Turner, J.; Ettl, J.; Hörschgen-Eggers, M.; Turner, P.; Jung, W. Shefex II vehicle and subsystem design, flight performance and their application to future hypersonic missions. In Proceedings of the ESA-PAC 21st Symposium, Thun, Switzerland, 9–13 June 2013. [Google Scholar]
- Keith, E.L. The Science of Cost Models. In The New Rocket Science, 1st ed.; Jiffy Astro: Lexington, KY, USA, 2010; pp. 9–18. ISBN 978-0557421336. [Google Scholar]
- Duret, F.; Fabrizi, A. VEGA, a small launch vehicle. Acta Astronaut. 1999, 44, 507–514. [Google Scholar] [CrossRef]
- Selding, P.B. Vega Expected to be Price-Competitive With Russian Rockets. Available online: https://spacenews.com/vega-expected-be-price-competitive-russian-rockets/ (accessed on 1 July 2019).
- Drenthe, N.T.; Zandbergen, B.T.C.; Curran, R.; van Pelt, M.O. Cost estimating of commercial smallsat launch vehicles. Acta Astronaut. 2019, 7, 160–169. [Google Scholar] [CrossRef]
- Wekerle, T.; Pessoa Filho, J.B.; Costa, L.E.V.L.; Trabasso, L.G. Status and trends of smallsats and their launch vehicles—An up to date review. J. Aerosp. Technol. Manag. 2017, 7, 269–286. [Google Scholar] [CrossRef]
- Nightingale, E.S.; Pratt, L.M.; Balakrishnan, A. The Cubesat Ecosystem: Examining the Launch Niche. Available online: https://www.ida.org/-/media/feature/publications/t/th/the-cubesat-ecosystem-examining-the-launch-niche-paper-and-presentation/d-5678.ashx (accessed on 25 March 2019).
- Lele, A.; Shrivastava, T. Rocket Launchers for Small Satellites. Available online: https://www.files.ethz.ch/isn/195949/ib_rocket-launchers-for-small-satellites_alele.tshrivastav.pdf) (accessed on 26 March 2019).
- Appazov, R.F.; Lavrov, S.S.; Mishin, V.P. Ballistics of the Controlled Long Range Rockets; Nauka: Moscow, Russia, 1966. [Google Scholar]
- Varfolomeev, V.I.; Kopitov, M.I. Ballistic Missile Design and Testing; Voenizdat: Moscow, Russia, 1970. [Google Scholar]
- Lysenko, L.N. Targeting and Navigation of Ballistic Missiles; MGTU: Moscow, Russia, 2007. [Google Scholar]
- Drenthe, N.T.; Zandbergen, B.T.C.; van Pelt, M.O. Cost estimating of commercial smallsat launch vehicles. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017. [Google Scholar] [CrossRef]
- Koelle, D.E. TRANSCOST 7.3 Statistical-Analytical Model for Cost Estimation and Economical Otimization of Launch Vehicles. In Handbook of Cost Engineering for Space Transportation Systems; rev. 3; TCS—TransCostSystems: Ottobrunn, Germany, 2010. [Google Scholar]
- Liquid Rocket Engines, RD-843. Available online: https://www.yuzhnoye.com/en/technique/rocket-engines/marching/rd-843/ (accessed on 5 February 2019).
- PNAE. Available online: http://www.aeb.gov.br/central-de-conteudos/publicacoes/pnae/ (accessed on 4 March 2019).
- Spaceflight, Pricing Information. Available online: http://spaceflight.com/schedule-pricing/#pricing (accessed on 23 June 2019).
- Spacenews, Small Satellites Are at the Center of a Space Industry Transformation. Available online: https://spacenews.com/small-satellites-are-at-the-center-of-a-space-industry-transformation/ (accessed on 27 June 2019).
- Crisp, N.H.; Smith, K.; Hollingsworth, P. Launch and deployment of distributed small satellite systems. Acta Astronaut. 2015, 114, 65–78. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).