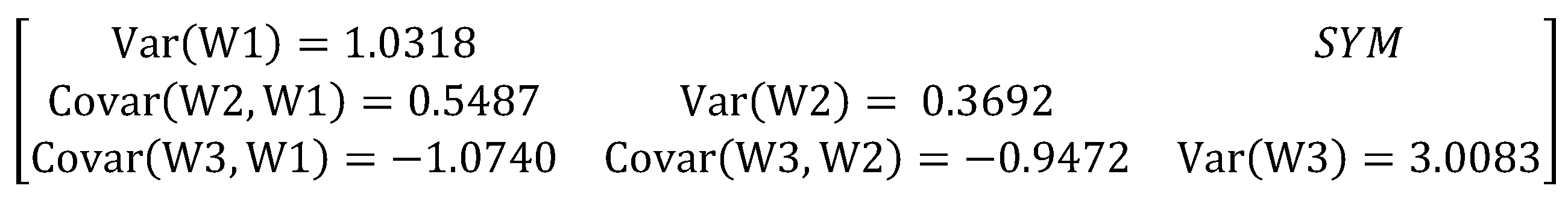1. Introduction
Most spacecraft have at least one pressurized vessel on board; for robotic spacecraft, it is usually a liquid propellant tank. In some satellite or spacecraft designs, the fuel tank or some other pressurized vessel is necessarily exposed to the hazards of space, including the micro-meteoroid and orbital debris (MMOD) environment. Because of the potential of serious mission-threatening damage that might result following an on-orbit MMOD impact, one of the primary design considerations of such spacecraft is the anticipation and mitigation of the possible damage that might occur in the event of such an impact.
Considerable energy and effort have been expended in the study of the response of non-pressurized spacecraft components under room temperature conditions to MMOD-like impacts. However, fuel tanks are pressurized internally and so their main walls will develop bi-axial stress fields because of that internal pressurization. Technical and safety challenges have limited the number of high-speed tests that have been conducted on the pressurized elements of such spacecraft, especially under cryogenic conditions.
In addition to a hole, it is possible that for certain tank designs, impact parameters, and operating conditions, a pressurized tank may experience catastrophic failure (i.e., a rupture) as a result of a hypervelocity impact. While a puncture and the resulting leak could result in the destabilization of the spacecraft’s orbit, a tank rupture following an on-orbit MMOD impact could lead to loss of the spacecraft and quite possibly, for human missions, the loss of life. To perform risk assessments during the design phase of a spacecraft that consider and weigh the likelihoods and consequences of the various failures that might occur following an on-orbit MMOD impact, equations are required that can discriminate between combinations of impact parameters and operating conditions that may or may not lead to a catastrophic failure event.
This paper presents the results of an effort directed at addressing one aspect of this problem, namely, the development of a general, data-driven equation for highly pressurized elements, such as fuel tanks, that would differentiate between the combinations of impact parameters and operating conditions that would result in only a small hole or crack from those that would cause catastrophic tank failure following a perforating high-speed impact event. This equation is an improvement over a previous version [
1] in that the current version is comprised of unitless or non-dimensional terms, whereas the previous version was not. As a result, the equation developed herein is more amenable to incorporating additional, new impact test data and results for similar test conditions as they become available.
The developed equation is referred to as a rupture limit equation, or RLE, as it is constructed to distinguish between conditions resulting in either tank rupture or non-rupture. This is an important consideration in the design of a pressurized tank—if possible, design parameters and operating conditions should be chosen such that in the event of an on-orbit MMOD particle impact both spacecraft failure and the creation of additional sizable debris pieces (such as those that would be created in the event of tank rupture or catastrophic failure) are avoided.
The RLE presented herein is developed by applying multi-linear regression techniques to data obtained in earlier studies involving cryogenic composite overwrapped pressure vessels (COPVs) under high-speed impact loading conditions. This, then, is another improvement of the RLE presented herein over the previous version, which was, in effect, merely a hand-drawn or faired curve between two sets of data points. Since the equation is this paper is statistics based, it (and the statistics associated with it) can easily be included in a risk assessment analysis, whereas the previous version could not.
2. Data Overview
There have been many high-speed impact test studies performed using tanks or pressure vessels over the past 50 years. These tests have been performed with varying amounts of internal pressure (including none); with internal fluids, air, or at a vacuum; using metallic tanks and composite material tanks; with spherical tanks as well as cylindrical tanks; using internal fluids at temperatures ranging from room temperature to cryogenic temperatures; and, with and without MMOD shielding. Reference [
2] provides a breakdown of the high-speed impact testing that has been performed using pressurized tanks over the past 50 years.
In this particular study, we focus on the high-speed impact tests performed on unshielded composite material overwrapped pressure vessels (COPVs) with internal cryogenic fluids. Data from these tests have been used to develop a rupture limit equation (or RLE) for these kinds of pressure vessels under these operating conditions. The purpose of this equation is to distinguish between impact parameters and operating conditions that would result in either only a small hole or crack (i.e., a non-rupture) from those that would cause catastrophic failure (i.e., a rupture).
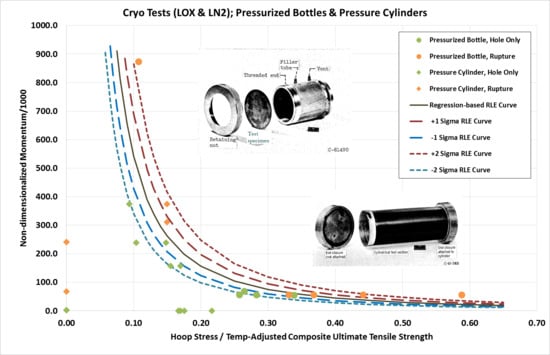
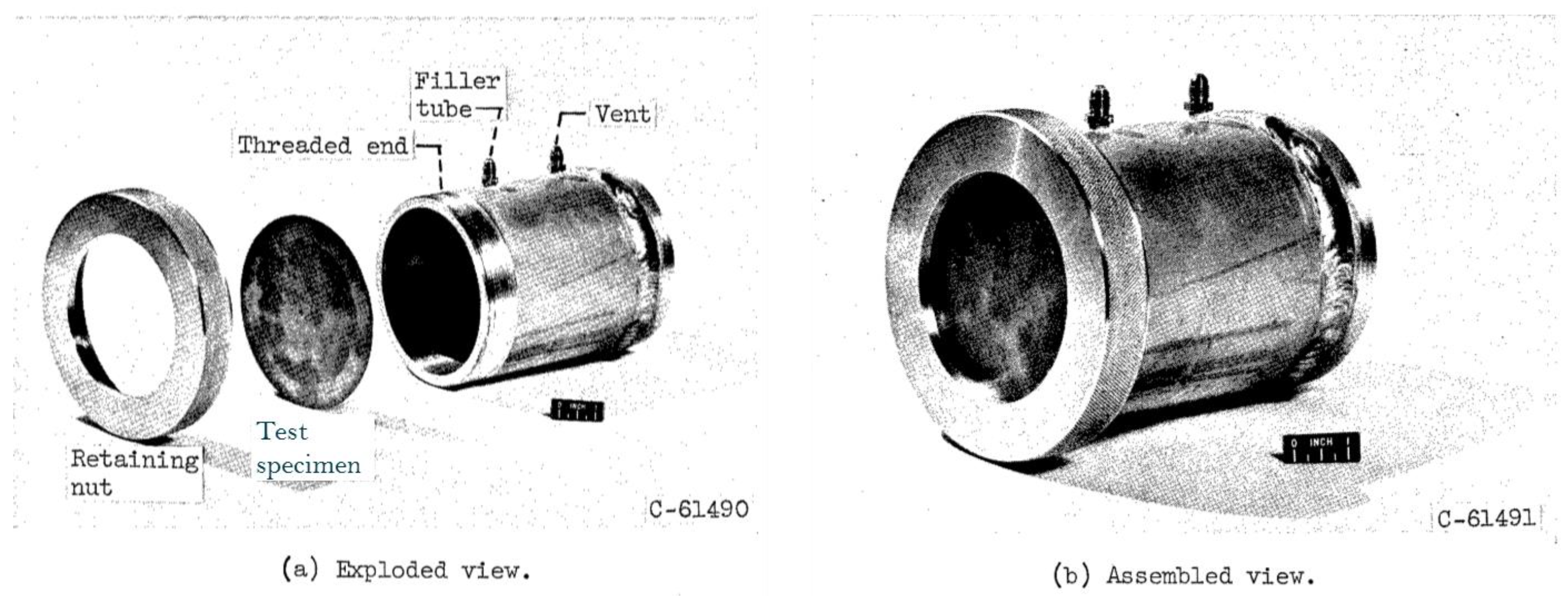
The RLE is constructed using data from 24 impact tests—fifteen (15) were performed using so-called “pressure cylinders” (see
Figure 1) while nine (9) of the tests were performed using “pressurized bottles” (see
Figure 2). The pressure cylinders consisted of one flexible endcap plate made of the material of interest attached to a thick metal cylinder; impacts occurred along a line normal to the flexible endcap test specimen plate. The pressurized bottles consisted of a cylindrical test section to which heavy aluminum end closures were attached to form a closed tank; impacts occurred along a radial line normal to the cylindrical test section.
Table 1,
Table 2 and
Table 3 present a summary of the impact test conditions and the geometric parameters/material properties of the COPVs used in the development of the RLE, respectively.
The tests performed as reported in references [
3,
4] were motivated by a desire to understand the high-speed impact response of COPVs that were in use at the time when those studies were performed. The cryogenic strength values for the composite overwrap and liner materials used in those studies were not typically reported by the investigators of those studies, and so had to be estimated from corresponding room temperature strength values. In some cases, the required room temperature strength values could be found in the literature for composite materials similar in construction to those used in these studies. However, in others, room temperature strength values could not be found and had to be estimated using simple mixture theory and strength values for the component materials involved. The cryogenic strength values were then calculated using published information regarding changes in the strength values of the component materials as the ambient temperature was decreased to cryogenic conditions.
3. Rupture Limit Equation Development
The empirically-based rupture limit equation (RLE) was developed using the rupture/non-rupture data from references [
3,
4]. To render the equation as broadly applicable as possible, the operating conditions (
x-axis) were parameterized as the hoop stress in the tank (non-dimensionalized by the temperature-adjusted uni-axial ultimate tensile stress of the composite overwrap material), and the impact conditions (
y-axis) were parameterized as the impact momentum (non-dimensionalized by a number of appropriate tank wall material properties). This approach was used successfully to model the rupture/non-rupture response of cylindrical and spherical metallic tanks [
2], as well as air-filled COPVs at room temperature [
5] and flat composite plates [
6] under high-speed impact loading conditions.
Following on the successful application of this approach in these previous studies, a simple power law form was chosen for the cryogenic COPV RLE to be developed herein. Specifically, the power law for the curve that is intended to separate the regions of rupture and non-rupture was chosen as follows:
where
σhoop and
are the COPV hoop stress and uni-directional ultimate stress of the COPV composite material, respectively. In the case of the pressure cylinder tests, the COPV hoop stresses were taken as the stress values in the composite plate endcaps as given in references [
3,
4]. However, in the case of the pressurized bottle tests, the COPV hoop stresses were calculated using the equation:
where
ttot = tcomp + tliner is the total nominal thickness of the COPV and is given by the sum of the thicknesses of the composite overwrap and liner (if any),
pint is the internal pressure in the COPV, and
rOD is the COPV outer radius.
In addition, the non-dimensional form of projectile momentum was taken to be as follows:
The first term in the denominator in Equation (3) has units of mass while the second has units of velocity, thereby rendering the right-hand side of Equation (3) unitless, or non-dimensional, so long as there is consistency in the units of mass and velocity used in its numerator and denominator.
To include the effects of other material parameters and the differences between the shapes of the cryogenic test articles, Equation (3) was modified through the addition of a number of other unitless terms, with the following result:
where
T is the temperature of the cryogenic fluid (in °F), and the ultimate and yield stresses of the liner material,
and
, respectively, if there is a liner present (in MPa). The yield and ultimate stress values are divided by 100 so the terms involving these quantities can have a meaningful effect without being excessively large compared to the values of the other terms in the equation. Combining Equations (1) and (4) yields the final form of the RLE as follows:
The coefficient
P and the exponents
Q, R, S, and
T in Equation (4) were selected so as to allow, as much as possible, a natural separation between the rupture and non-rupture data points. This would, in turn, facilitate the development of an RLE that would, again, as much as possible, lie between those two regions. The attractiveness and benefit of this approach are that if additional test results were to become available, the values of
P, Q, R, S, and
T in Equation (3) could again be adjusted to allow the incorporation of the new rupture/non-rupture data and the subsequent development of a new RLE. To this end,
Table 4 presents the values of the coefficient
P and exponents
Q, R, S, and
T used in the non-dimensionalization scheme defined in Equation (4):
The constants
A and
B in Equation (1) are determined through a linear regression of the rupture/non-rupture data using the Levenberg–Marquardt algorithm [
7]. This is a common algorithm for minimizing a function over the space of parameters of the function (i.e., in this particular case, the coefficients in a user-defined function). In addition to solving for the coefficients, this algorithm also provides statistical information that can be used to assess the “goodness of fit” of the regression results, as well as standard deviation curves for the regression model.
The actual regression exercise was performed by first creating a function
Z that would take on values of +1 or −1 depending on whether a particular test resulted in either a rupture or a non-rupture. This function is derived from the linearized form of Equation (5) and written as follows:
where
Y is a non-dimensionalized projectile momentum and
X is the non-dimensionalized hoop stress, respectively. It is actually, then, the constants
W1,
W2, and
W3 that are obtained through a regression of the test parameters given by
X and
Y against test results given by
Z and represented by a + 1 or a − 1. Once
W1,
W2, and
W3 are obtained, setting
Z = 0 yields the desired RLE. Furthermore, when we set
Z = 0, solving for
Y gives the following expression for
A and
B in terms of the regression parameters
W1,
W2, and
W3:
Table 5 and
Figure 3 contain the results of this exercise, namely, the coefficients
W1,
W2, and
W3, the correlation coefficient
R2, the standard deviations of
W1,
W2, and
W3, and the covariance matrix for
W1,
W2, and
W3.
From the information in
Table 5 and Equations (7) and (8), we find that
A = 8.5636 and
B = −1.8019. This completes the development of the RLE for the test data considered in this study. In the next section, we compare the predictions of the RLE against test data and offer comments on the utility and limitations of this RLE.
4. Comparison with Empirical Results
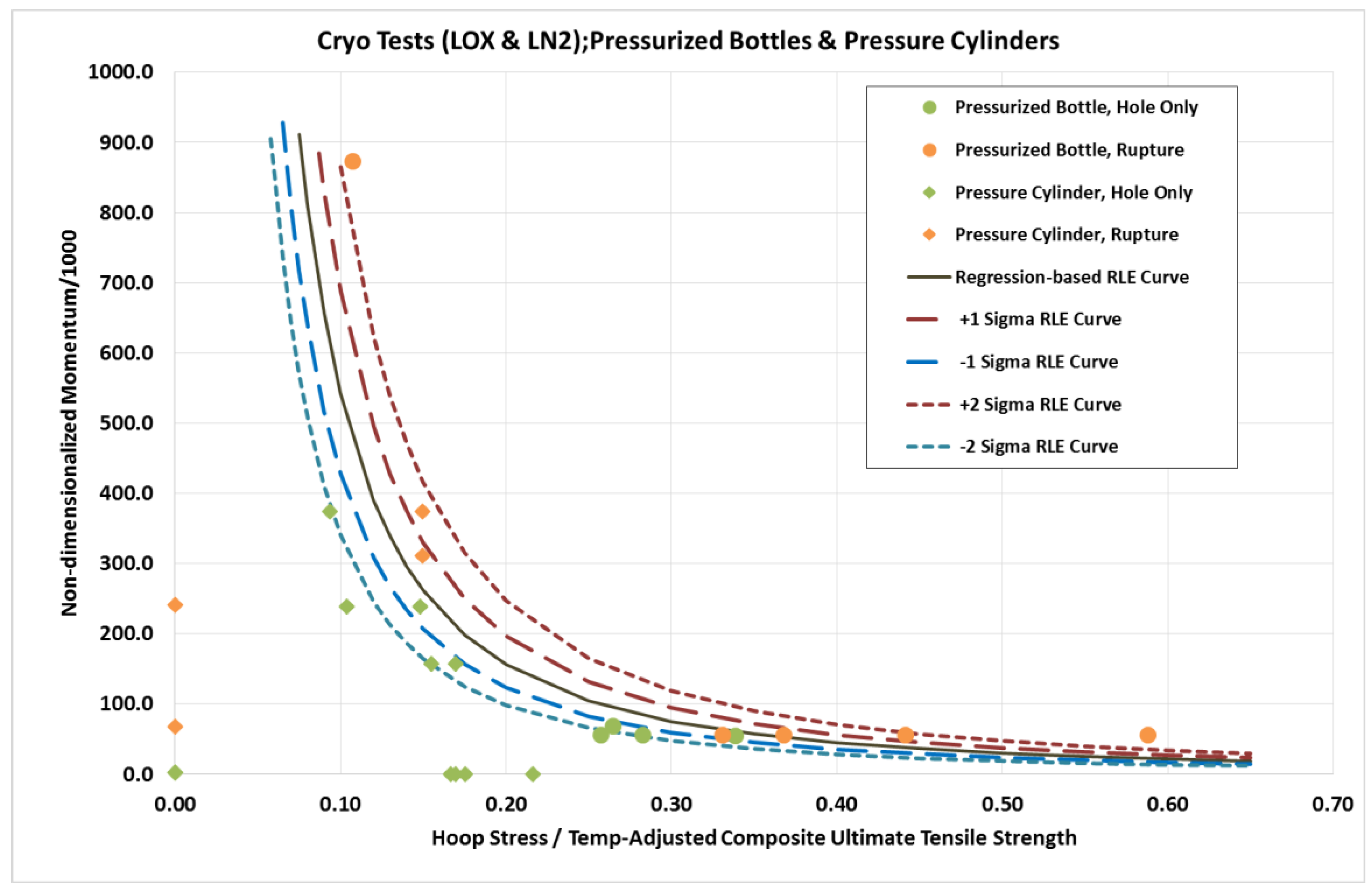
Figure 4 shows plots of the RLE developed herein compared to experimental rupture/non-rupture results. This figure also shows plots of ±one standard deviation curves and ±two standard deviation curves about the RLE curve. The orange data points represent those tests that resulted in tank rupture, while the green data points show those that did not for both types of test specimen configurations.
As can be seen in
Figure 4, with the exception of the two ruptured unpressurized pressure cylinder tests, the RLE developed herein appears to predict fairly well the rupture/non-rupture response of COPVs at cryogenic temperatures. This is supported by the “tightness” of the confidence-bound curves about the RLE—another indication of the goodness of fit of the RLE to the rupture/non-rupture data. A possible explanation for the rupture of the two unpressurized cylinders is offered in reference [
3]—namely, that the resins in these two tests had high percentages of organic polymeric matter. In the presence of liquid oxygen, this possibly made them highly susceptible to a catastrophic response, even without any internal pressure.
Of further note are the non-rupture points for several pressure cylinder tests that appear to lie on the x-axis (i.e., they appear to have a non-dimensional momentum value of zero, which would correspond to a zero impact velocity). These points are actually not on the x-axis, just exceedingly close to allow comparison with the other non-rupture points.
Another means for assessing the ability of the RLE to discriminate between the region of impact parameters and operating conditions that would result in rupture from those that would not is through the use of specificity and sensitivity ratios. In the medical world, these values are frequently used to distinguish between false positives and false negatives. For example, if we designate a rupture event as the event we are testing for, then an actual rupture might be considered as a “positive reading,” while a non-rupture might be considered as a “negative reading.” As such, the following definitions could be applied to the demarcation line derived from the RLE developed herein:
These ratios yield a quantitative assessment of whether or not the RLE developed herein could be considered as conservative or non-conservative in the following manner:
a low specificity value (i.e., many non-ruptures predicted as ruptures) and a high sensitivity value (i.e., fewer ruptures predicted as non-ruptures) → a conservative RLE
a high specificity value (i.e., fewer non-ruptures predicted as ruptures) and a low sensitivity value (i.e., many ruptures predicted as non-ruptures) → a non-conservative RLE
Furthermore, if both values were found to be high, the RLE could be considered as fairly accurate, whereas if both values were low, that would indicate either a problem with the testing method or with test repeatability.
For the data considered herein and the RLE developed based on that data, we find that, even including the two ruptures that lie below the RLE curve, we have a sensitivity value of 0.78 and a specificity value of 0.93 (if the two “odd” rupture data points were removed, the sensitivity value would be exactly 1.0). Based on these results, we can again conclude that the RLE performs rather well in separating the test results where a rupture occurred from those that resulted in non-rupture.
It is important to note, of course, that there are a number of other parameters that can affect whether or not a COPV ruptures or merely sustains a hole following a high-speed impact event. This includes the filament winding pattern, the particular composite layup configuration, and the actual COPV contents (e.g., gas, liquid, or both), and others. These parameters were not considered in this investigation because the desire was to develop as simple an RLE as possible so that a user, for example, would not need to be concerned about knowing the particular layup configuration. As additional tests are performed and additional data made available, it is entirely possible that the RLE developed herein might need to be modified to take into account these and other parameters.