Wake-Model Effects on Induced Drag Prediction of Staggered Boxwings
Abstract
:1. Introduction
1.1. Problem Definition
1.2. Contribution of Present Work
2. Relevant Theory
3. Computational Models
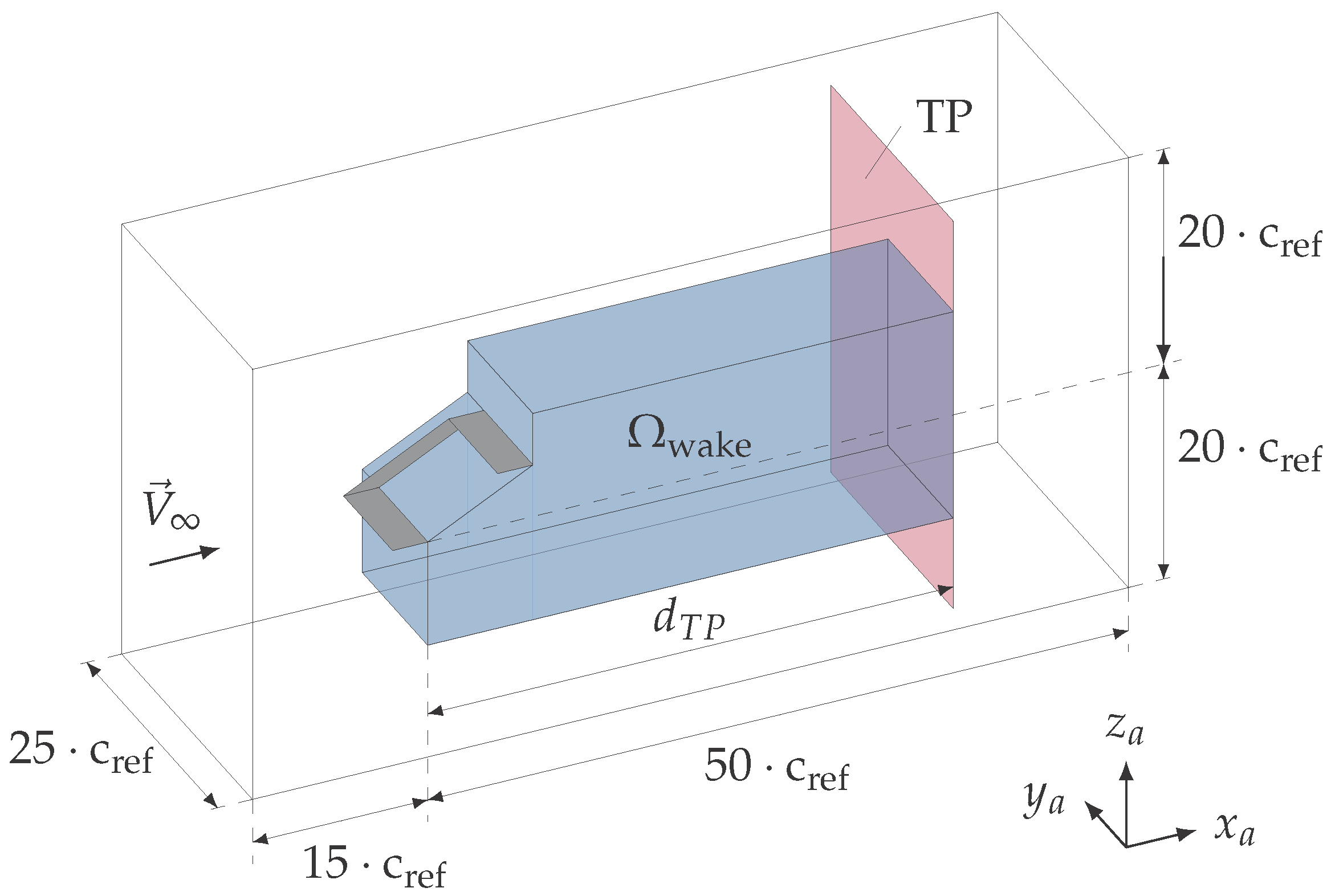
3.1. Test Cases
3.2. Higher-Order Potential-Flow Model
3.3. Euler-Flow Model
4. Results and Discussion
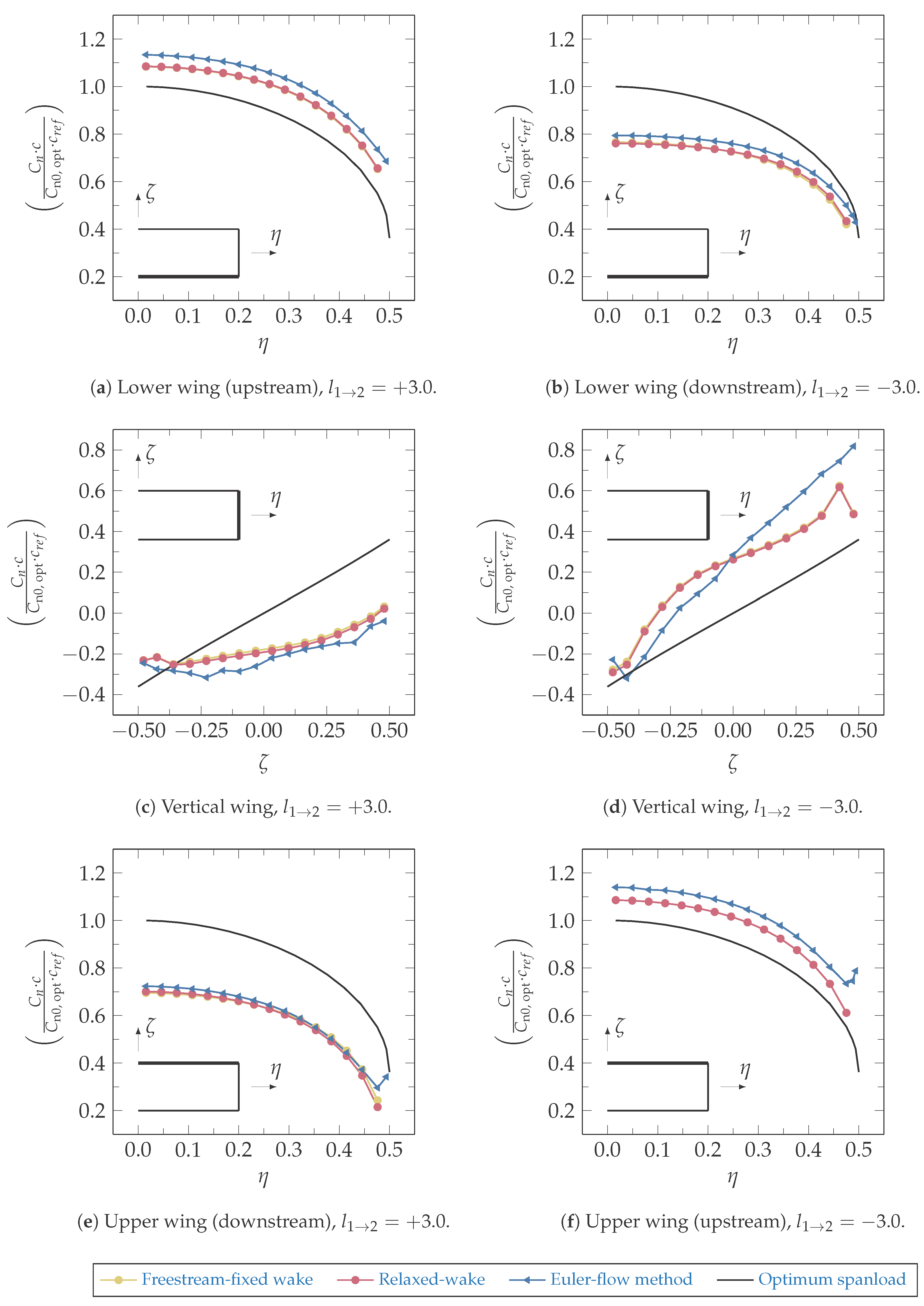
4.1. Spanwise Load Distribution
4.2. Computed Span Efficiency Factor
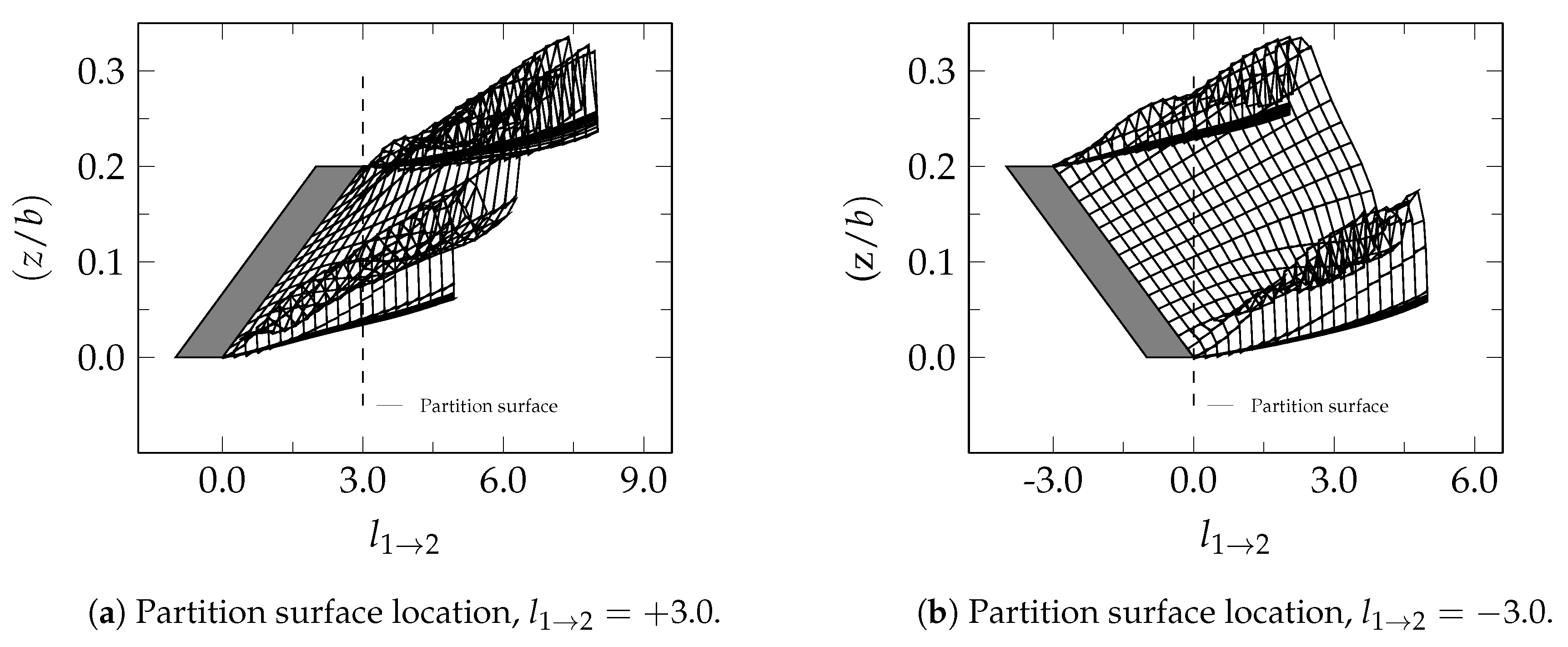
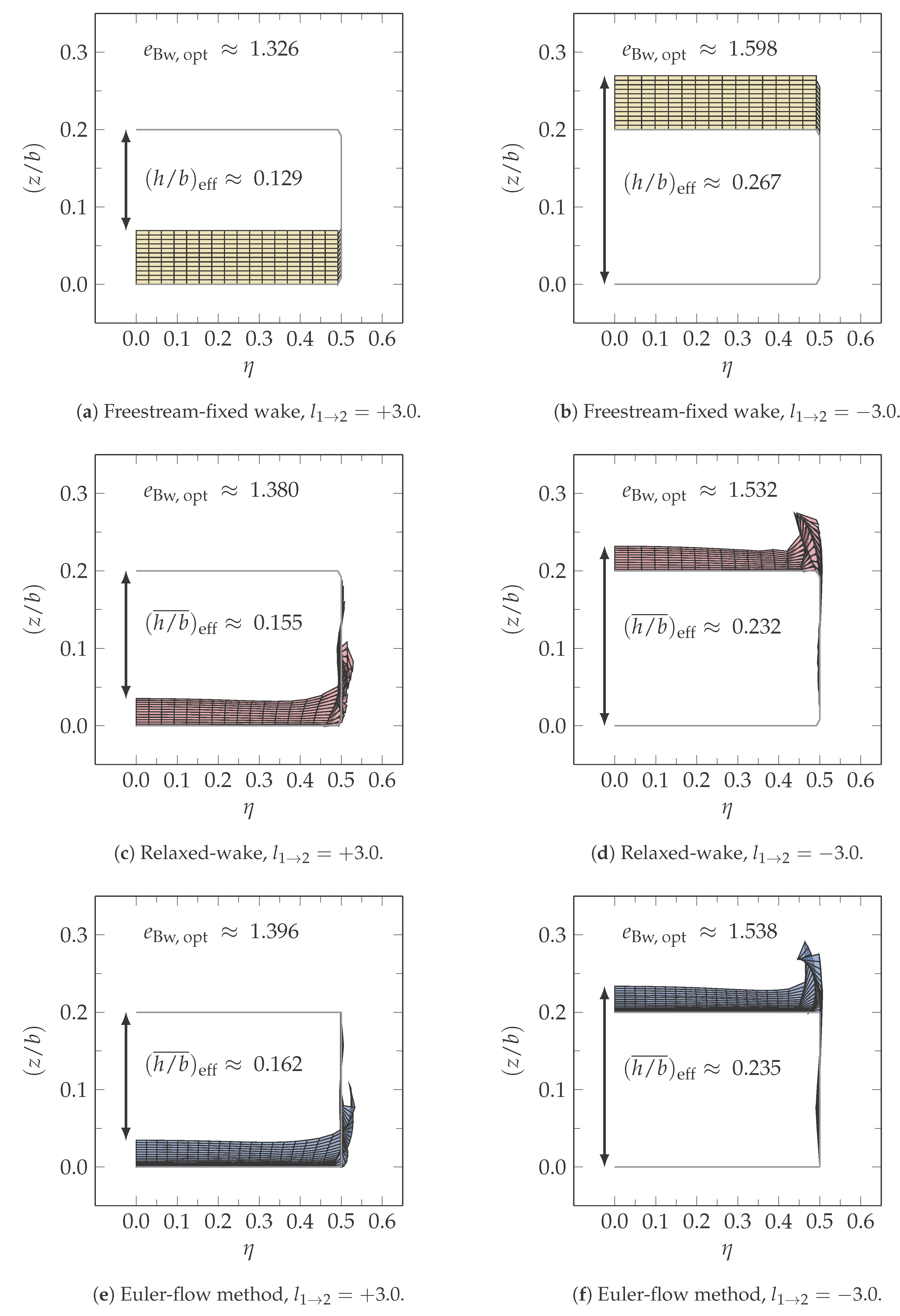
4.3. Wake Traces on Partition Surface
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| b | Wing span |
| Sectional normal force coefficient | |
| Optimum sectional normal force coefficient | |
| c | Chord length |
| Reference chord length | |
| Longitudinal trailing edge separation | |
| Induced drag | |
| Span efficiency factor | |
| Height-to-span ratio | |
| L | Lift |
| Stagger factor | |
| Freestream stagnation pressure | |
| Freestream velocity | |
| x, y, z | Cartesian coordinates |
| Freestream angle of attack | |
| Circulation | |
| Non-dimensional wing span | |
| Single wing aspect ratio | |
| Freestream air density | |
| Non-dimensional height |
References
- Kroo, I.M. Drag due to Lift: Concepts for Prediction and Reduction. Annu. Rev. Fluid Mech. 2000, 587–617. [Google Scholar] [CrossRef]
- Darecki, M.; Edelstenne, C.; Enders, T.; Fernandez, E.; Hartman, P.; Herteman, J.P.; Kerkloh, M.; King, I.; Ky, P.; Mathieu, M.; et al. Europe’s Vision for Aviation: Maintaining Global Leadership and Serving Society’s Needs; European Commission: Luxembourg, 2011. [Google Scholar]
- Cummings, R.M.; Morton, S.A.; Mason, W.H.; McDaniel, D.R. Applied Computational Aerodynamics: A Modern Engineering Approach; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Thokala, P.; Scanlan, J.; Chipperfield, A. Framework for Aircraft Cost Optimization Using Multidisciplinary Analysis. J. Aircr. 2012, 49, 367–374. [Google Scholar] [CrossRef]
- Schmidt-Göller, S. Zur Genauen Berechnung des Induzierten Widerstandes von Tragflügeln. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 1992. [Google Scholar]
- Smith, S.C. A Computational and Experimental Study of Nonlinear Aspects of Induced Drag. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1995. [Google Scholar]
- Frediani, A. The Prandtl Wing. In VKI Lecture Series: Innovative Configurations and Advanced Concepts for Future Civil Aircraft; von Karman Institute: Rhode Saint Genese, Belgium, 2005. [Google Scholar]
- Seywald, K.; Hellmundt, F.; Wildschek, A.; Holzapfel, F. Airworthiness Investigation of a Highly Nonplanar Flexible Wing Concept. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 7–12 September 2014. ICAS Paper 2014-0088. [Google Scholar]
- Salam, I.R.; Bil, C. A Methodology for Multi-Disciplinary Analysis of the Box Wing Concept. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015. AIAA Paper 2015-3003. [Google Scholar]
- Andrews, S.A.; Perez, R.E. Parametric Study of Box-Wing Aerodynamics for Minimum Drag Under Stability and Maneuverability Constraints. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015. AIAA Paper 2015-3291. [Google Scholar]
- Gagnon, H.; Zingg, D.W. Aerodynamic Optimization Trade Study of a Box-Wing Aircraft Configuration. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015. AIAA Paper 2015-0695. [Google Scholar]
- Skinner, S.N.; Zare-Behtash, H. Aerodynamic Optimisation of Non-Planar Lifting Surfaces. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-0164. [Google Scholar]
- Prandtl, L. Induced Drag of Multiplanes. Technische Berichte; National Advisory Committee for Aeronautics: Washington, DC, USA, 1924; Volume 3.
- Rizzo, E. Optimization Methods Applied to the Preliminary Design of Innovative, Non Conventional Aircraft Configurations. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2007. [Google Scholar]
- Demasi, L. Investigation on the Conditions of Minimum Induced Drag of Closed Wing Systems and C-Wings. J. Aircr. 2007, 44, 81–99. [Google Scholar] [CrossRef]
- DeYoung, J. Induced Drag Ideal Efficiency Factor of Arbitrary Lateral-Vertical Wing Forms; NASA Contractor Report 3357; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1980.
- Demasi, L.; Monegato, G.; Dipace, A.; Cavallaro, R. Minimum Induced Drag Theorems for Joined Wings, Closed systems, and Generic Biwings: Theory. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015. AIAA Paper 2015-0697. [Google Scholar]
- Demasi, L.; Monegato, G.; Rizzo, E.; Cavallaro, R.; Dipace, A. Minimum Induced Drag Theorems for Joined Wings, Closed Systems, and Generic Biwings: Results. In Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Kissimmee, FL, USA, 5–9 January 2015. AIAA Paper 2015-0698. [Google Scholar]
- Jansen, P.W.; Perez, R.E.; Martins, J.R.R.A. Aerostructural Optimization of Nonplanar Lifting Surfaces. J. Aircr. 2010, 47, 1490–1503. [Google Scholar] [CrossRef]
- Kroo, I.M.; Smith, S.C. The Computation of Induced Drag with Nonplanar and Deformed Wakes. In Proceedings of the Aerospace Technology Conference and Exposition, Long Beach, CA, USA, 1–4 October 1990. SAE Paper 901933. [Google Scholar]
- Prandtl, L. Applications of Modern Hydrodynamics to Aeronautics; NACA Technical Report 116; National Advisory Committee for Aeronautics: Washington, DC, USA, 1923.
- Pistolesi, E. Aerodinamica. In Biblioteca Dell’Ingegnere Scienze Propedeutiche; Torinese: Torino, Italy, 1932; Volume 1. [Google Scholar]
- Cone, C.D. The Theory of Induced Lift and Minimum Induced Drag of Nonplanar Lifting Systems; NASA Technical Report R-139; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1962.
- Frediani, A.; Montanari, G. Best Wing System: An Exact Solution of the Prandtl’s Problem. In Variational Analysis and Aerospace Engineering; Buttazzo, G., Frediani, A., Eds.; Springer: New York, NY, USA, 2009; Volume 33, pp. 183–211. [Google Scholar]
- Demasi, L.; Dipace, A.; Monegato, G.; Cavallaro, R. An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems. J. Aircr. 2014, 52, 2223–2240. [Google Scholar]
- Von Karman, T.; Burgers, J. Aerodynamic Theory: A General Review of Progress Under a Grant of the Guggenheim Fund for the Promotion of Aeronautics; Springer: Berlin, Germany, 1935; pp. 165–280. [Google Scholar]
- Munk, M.M. The Minimum Induced Drag of Aerofoils; NACA Technical Report 121; National Advisory Committee for Aeronautics: Washington, DC, USA, 1923.
- Lowson, M.V. Minimum Induced Drag for Wings with Spanwise Camber. J. Aircr. 1990, 27, 627–631. [Google Scholar] [CrossRef]
- Munk, M.M. General Biplane Theory; NACA Technical Report 151; National Advisory Committee for Aeronautics: Washington, DC, USA, 1923.
- Gall, P.D.; Smith, H.C. Aerodynamic Characteristics of Biplanes with Winglets. J. Aircr. 1987, 24, 518–522. [Google Scholar] [CrossRef]
- Kang, H.; Genco, N.; Altman, A. Gap and Stagger Effects on Biplanes with End Plates: Part I. In Proceedings of the 47th AIAA Aerospace Sciences Meeting and the New Horizons Forum and Aerospace Exhibit, Orlando, FL, USA, 5–8 January 2009. AIAA Paper 2009-1085. [Google Scholar]
- Kang, H.; Genco, N.; Altman, A. Gap and Stagger Effects on Biplanes with End Plates: Part II. In Proceedings of the 47th AIAA Aerospace Sciences Meeting and the New Horizons Forum and Aerospace Exhibit, Orlando, FL, USA, 5–8 January 2009. AIAA Paper 2009-1086. [Google Scholar]
- Addoms, R.; Spaid, F.W. Aerodynamic Design of High-Performance Biplane Wings. J. Aircr. 1975, 12, 629–630. [Google Scholar] [CrossRef]
- Gall, P.D. An Experimental and Theoretical Analysis of the Aerodynamic Characteristics of a Biplane-Winglet Configuration; NASA Technical Memorandum 85815; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1984.
- Lange, R.H.; Cahill, J.F.; Bradley, E.S.; Eudaily, R.R.; Jenness, C.M.; MacWiikinson, D.G. Feasibility Study of the Transonic Biplane Concept for Transonic Aircraft Application; NASA Contractor Report 132462; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1974.
- Eppler, R.; Schmidt-Göller, S. A Method to Calculate the Influence of Vortex Roll-up on the Induced Drag of Wings: Finite Approximations in Fluid Mechanics II. In Notes on Numerical Fluid Mechanics; Springer: Berlin, Germany, 1990; Volume 25. [Google Scholar]
- Bramesfeld, G. A Higher Order Vortex-Lattice Method with a Force-Free Wake. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2006. [Google Scholar]
- Bramesfeld, G.; Maughmer, M.D. Relaxed-Wake Vortex-Lattice Method Using Distributed Vorticity Elements. J. Aircr. 2008, 45, 560–568. [Google Scholar] [CrossRef]
- CD-Adapco. STAR-CCM+, Version 8.04.010, 2013. Available online: www.cd-adapco.com (accessed on 1 April 2016).
- Destarac, D.; van der Vooren, J. Drag/Thrust analysis of Jet-Propelled Transonic Transport Aircraft; Definition of Physical Drag Components. Aerosp. Sci. Technol. 2004, 8, 545–556. [Google Scholar] [CrossRef]
- van Dam, C.P.; Nikfetrat, K. Accurate Prediction of Drag Using Euler Methods. J. Aircr. 1992, 29, 516–519. [Google Scholar] [CrossRef]
- Gariépy, M.; Malouin, B.; Trépanier, J.Y.; Laurendeau, É. Far-Field Drag Decomposition Applied to the Drag Prediction Workshop 5 Cases. J. Aircr. 2013, 50, 1822–1831. [Google Scholar] [CrossRef]
- Vos, J.B.; Sanchi, S.; Gehri, A. DPW4 Results Using Different Grids Including Near-Field/Far-Field Drag Analysis. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. AIAA Paper 2010-4552. [Google Scholar]
- Roache, P.J. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Schirra, J.C. Accurate Induced Drag Prediction for Highly Non-Planar Lifting Systems. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2016. [Google Scholar]
- Selberg, B.P. Aerodynamic Investigation of Closely Coupled Lifting Surfaces with Positive and Negative Stagger for General Aviation Applications. In Proceedings of the 21st AIAA Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983. AIAA Paper 1983-57. [Google Scholar]
- Selberg, B.P.; Cronin, D.L. Aerodynamic - Structural Optimization of Positive/Negative Stagger Joined Wing Configurations. In Proceedings of the AIAA Aircraft Systems Design and Technology Meeting, Dayton, OH, USA, 20–22 October 1986. AIAA Paper 1986-2626. [Google Scholar]
- Mamla, P.; Galinski, C. Basic Induced Drag Study of the Joined-Wing Aircraft. J. Aircr. 2009, 46, 1438–1440. [Google Scholar] [CrossRef]
- Eppler, R. Induced Drag and Winglets. Aerosp. Sci. Technol. 1997, 1, 3–15. [Google Scholar] [CrossRef]
- Verstraeten, J.G.; Slingerland, R. Drag Characteristics for Optimally Span-Loaded Planar, Wingletted, and C Wings. J. Aircr. 2009, 46, 962–971. [Google Scholar] [CrossRef]
- Maughmer, M.D. Design of Winglets for High-Performance Sailplanes. J. Aircr. 2003, 40, 1099–1106. [Google Scholar] [CrossRef]
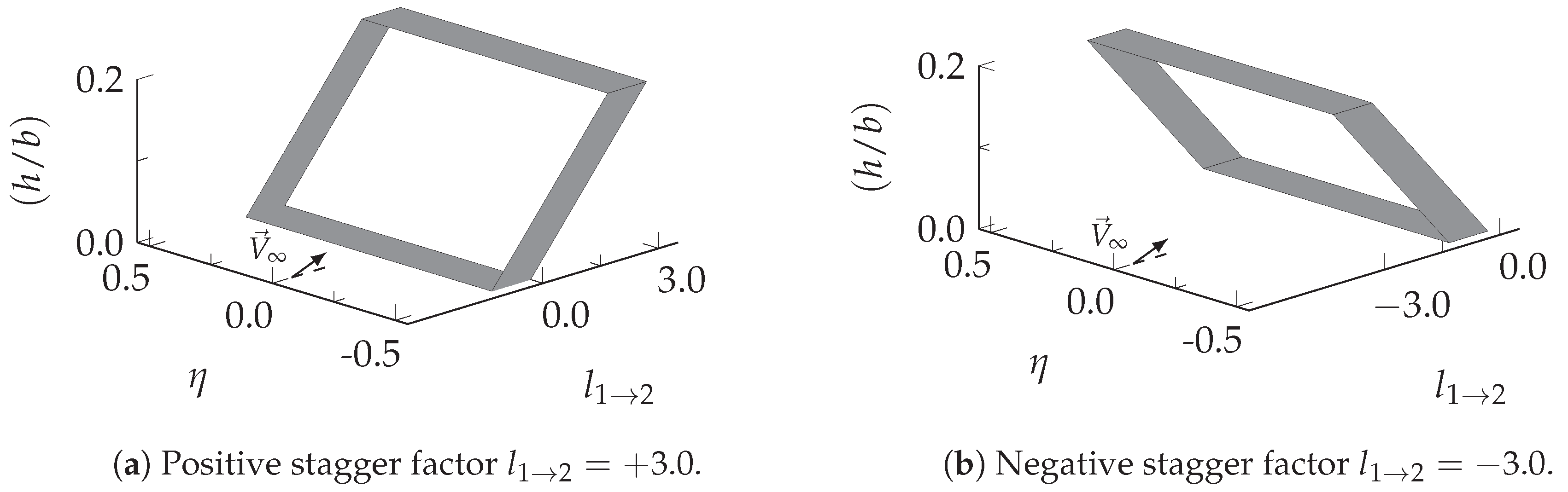

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schirra, J.; Bissonnette, W.; Bramesfeld, G. Wake-Model Effects on Induced Drag Prediction of Staggered Boxwings. Aerospace 2018, 5, 14. https://doi.org/10.3390/aerospace5010014
Schirra J, Bissonnette W, Bramesfeld G. Wake-Model Effects on Induced Drag Prediction of Staggered Boxwings. Aerospace. 2018; 5(1):14. https://doi.org/10.3390/aerospace5010014
Chicago/Turabian StyleSchirra, Julian, William Bissonnette, and Götz Bramesfeld. 2018. "Wake-Model Effects on Induced Drag Prediction of Staggered Boxwings" Aerospace 5, no. 1: 14. https://doi.org/10.3390/aerospace5010014
APA StyleSchirra, J., Bissonnette, W., & Bramesfeld, G. (2018). Wake-Model Effects on Induced Drag Prediction of Staggered Boxwings. Aerospace, 5(1), 14. https://doi.org/10.3390/aerospace5010014



