Hydrodynamic Performance of Aquatic Flapping: Efficiency of Underwater Flight in the Manta
Abstract
:1. Introduction
2. Materials and Methods
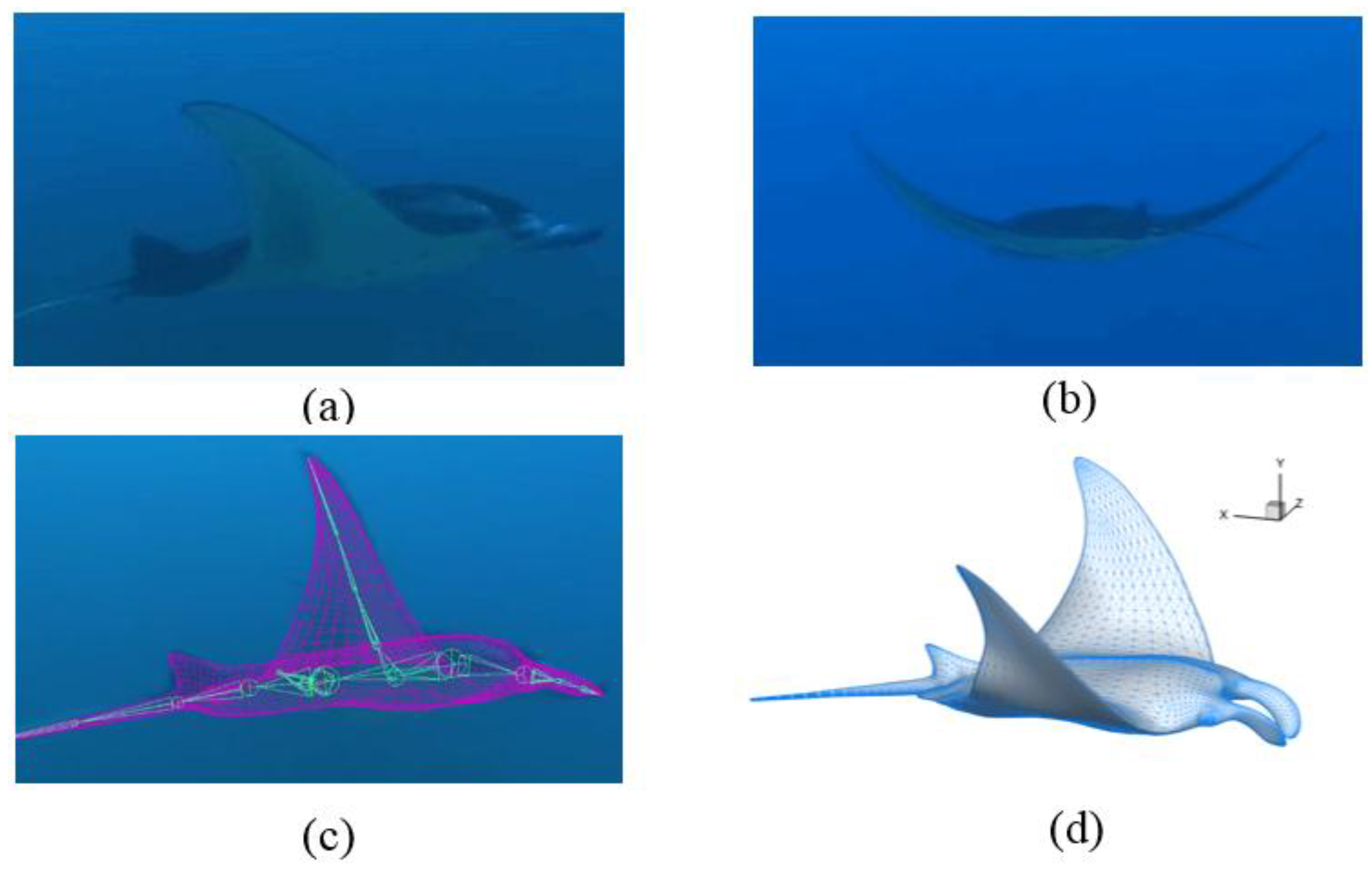
2.1. Manta Kinematics
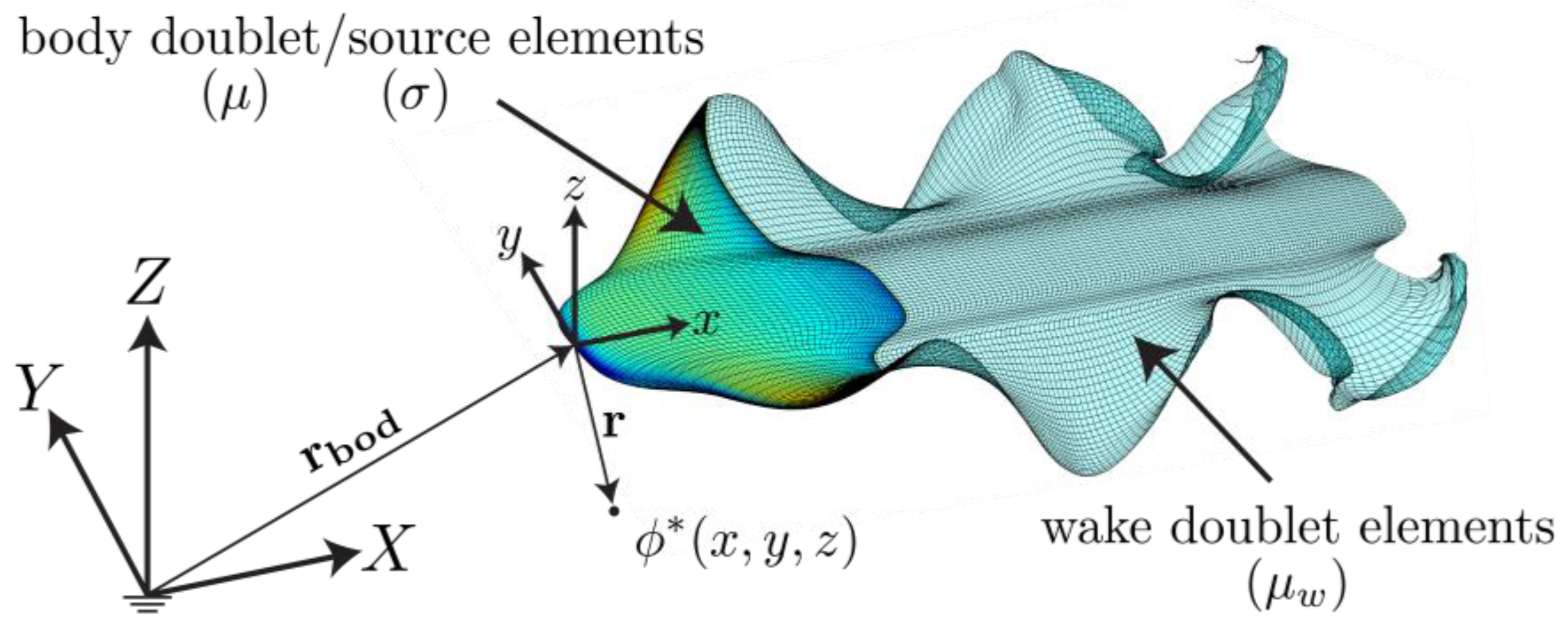
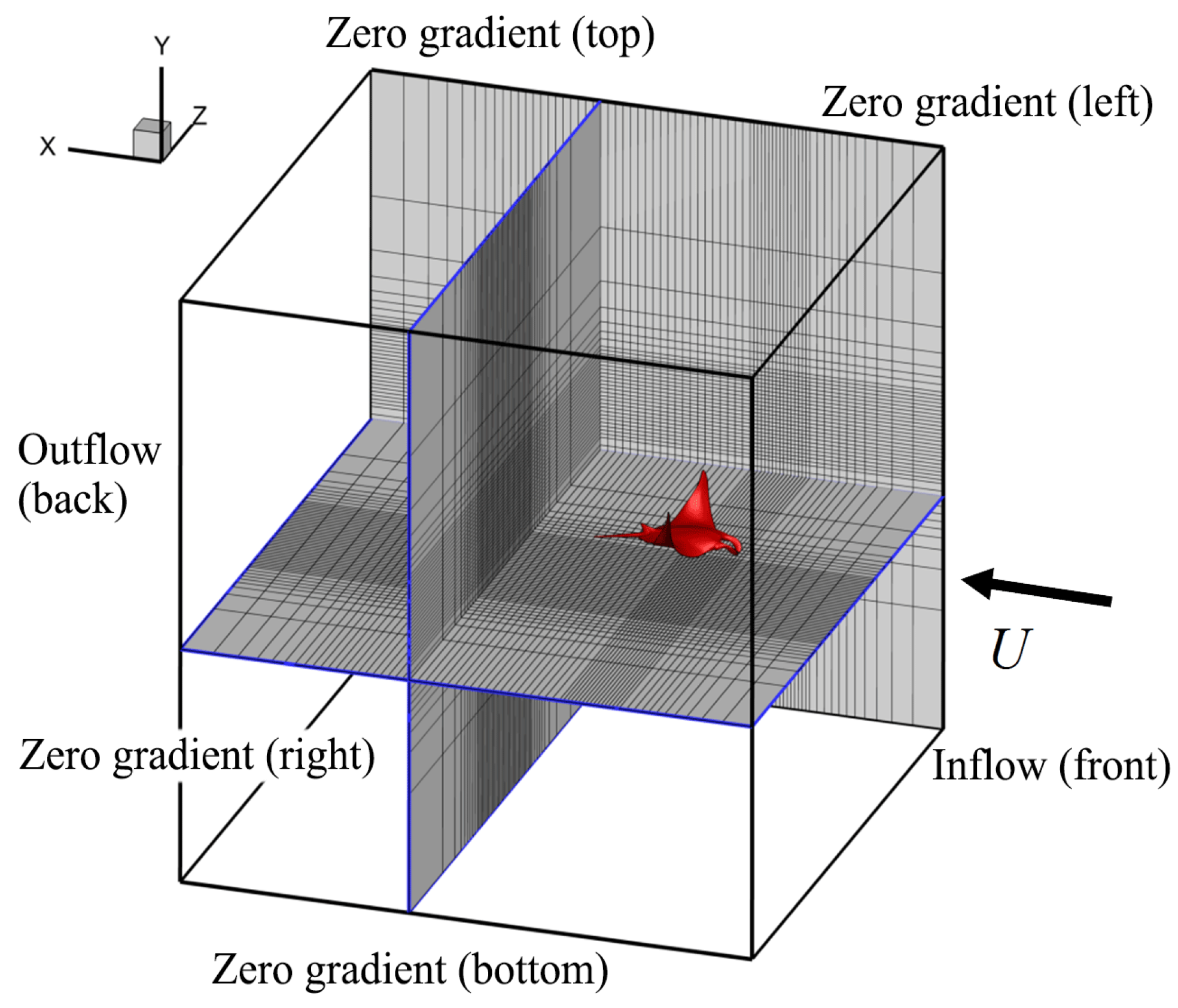
2.2. Potential Flow Model
2.3. Viscous Model
3. Results
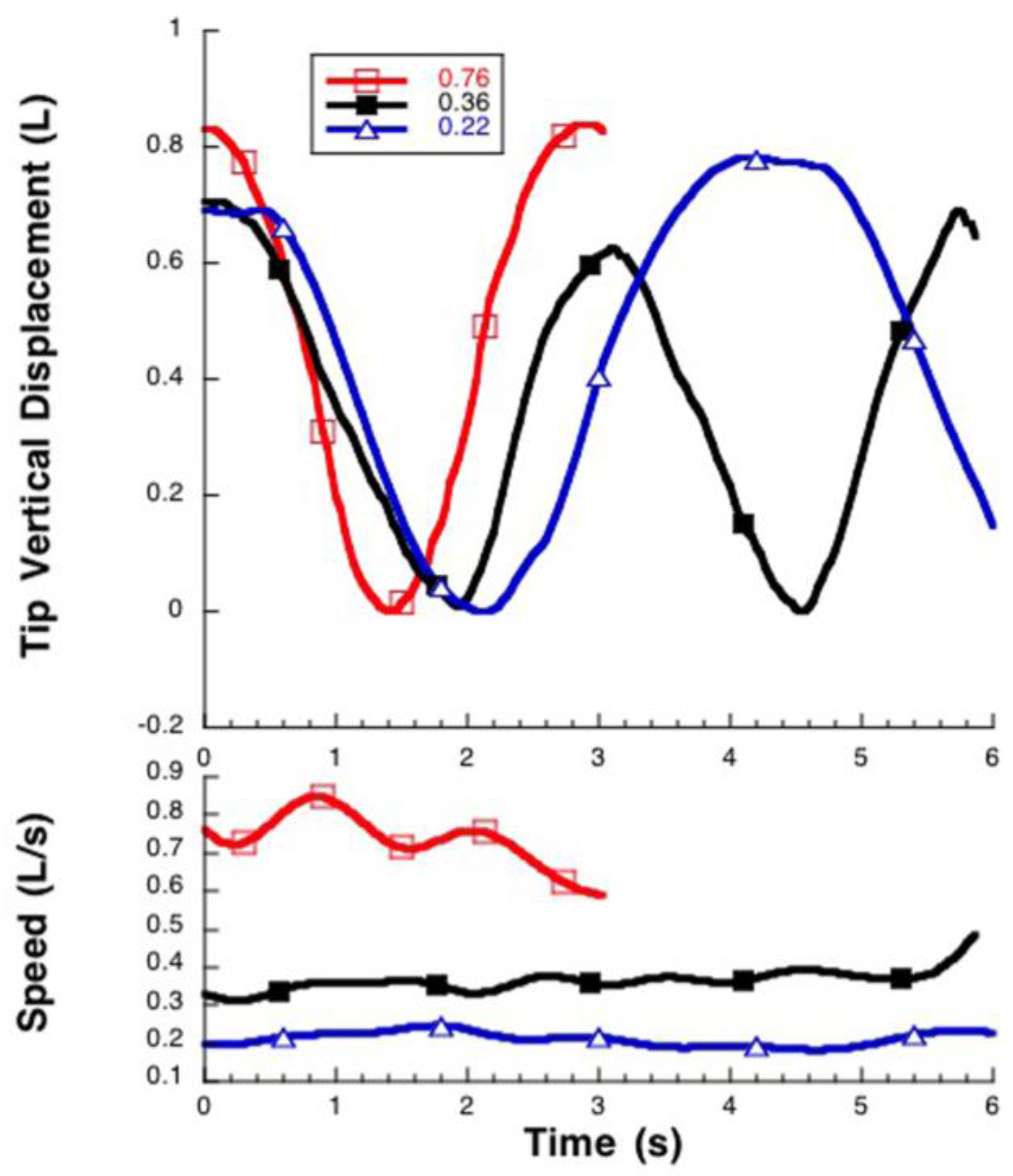
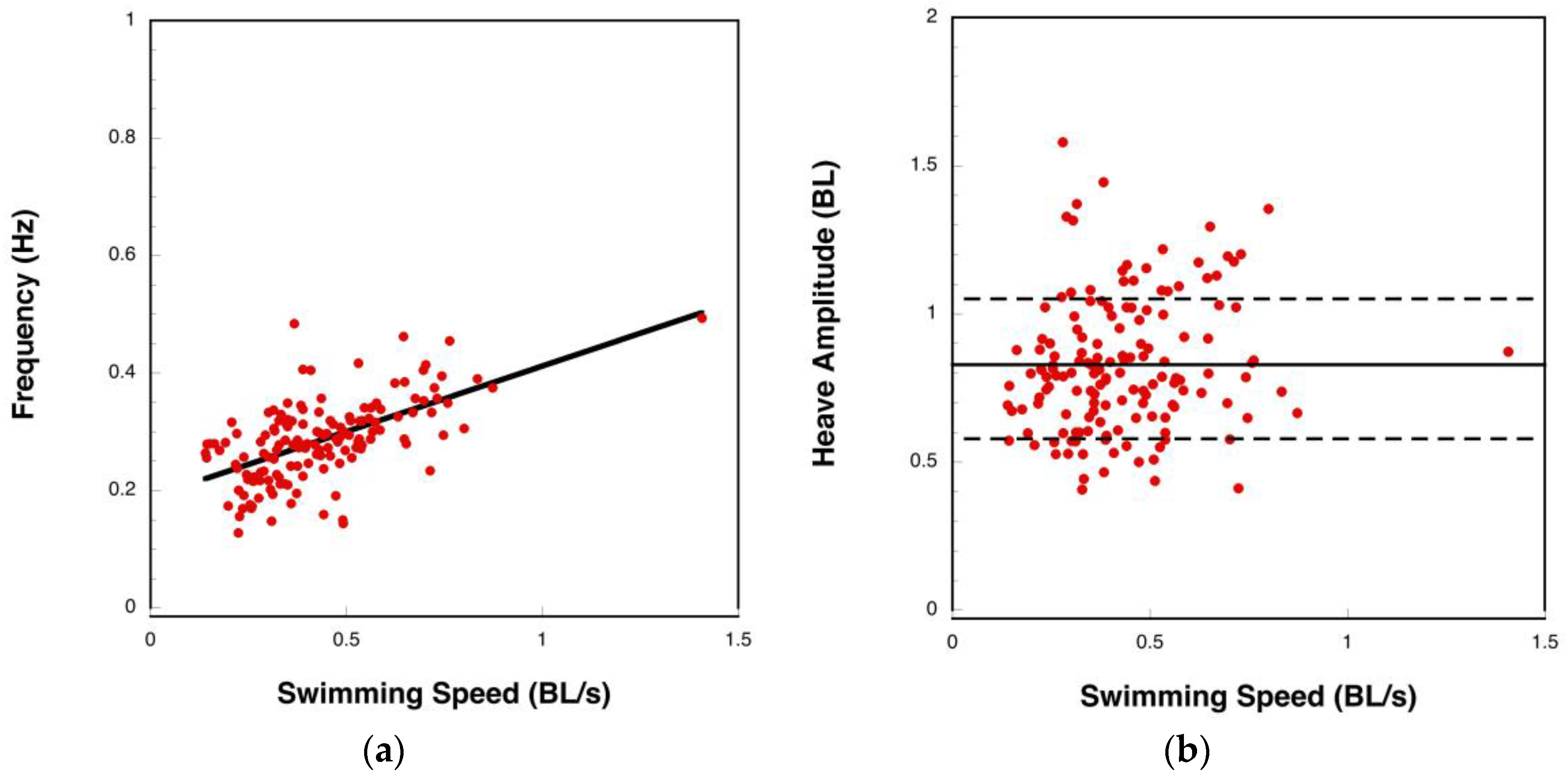
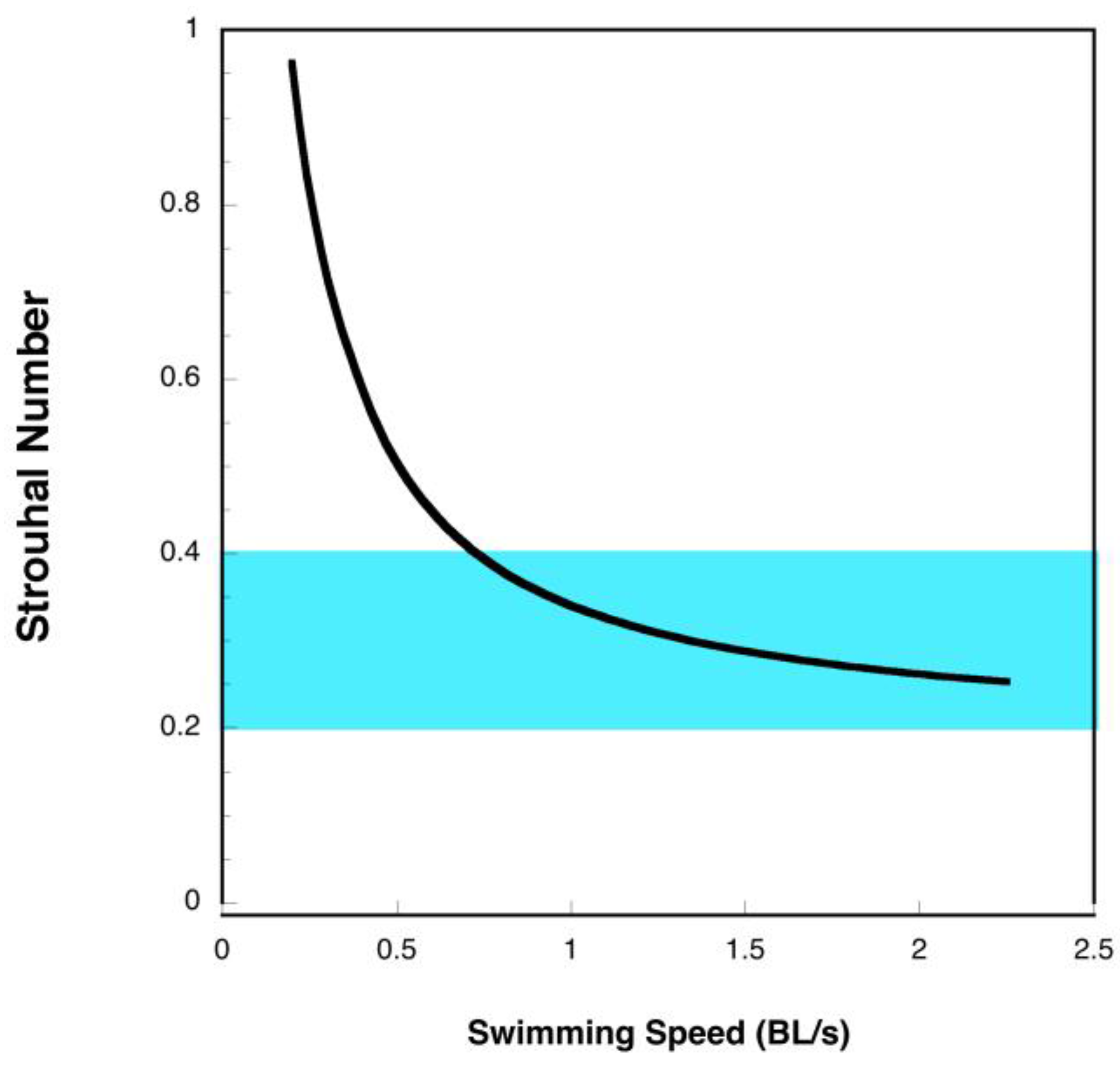
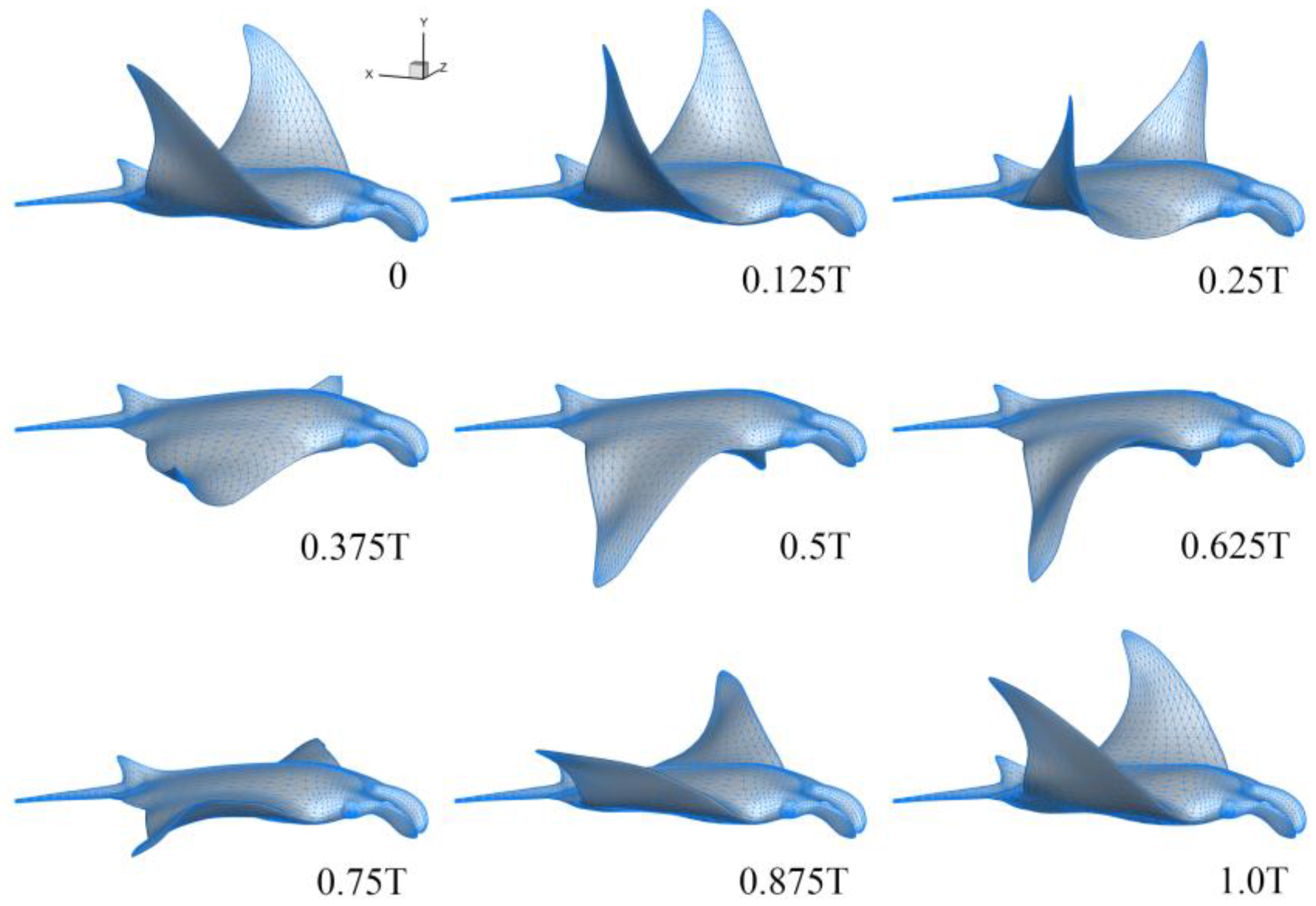
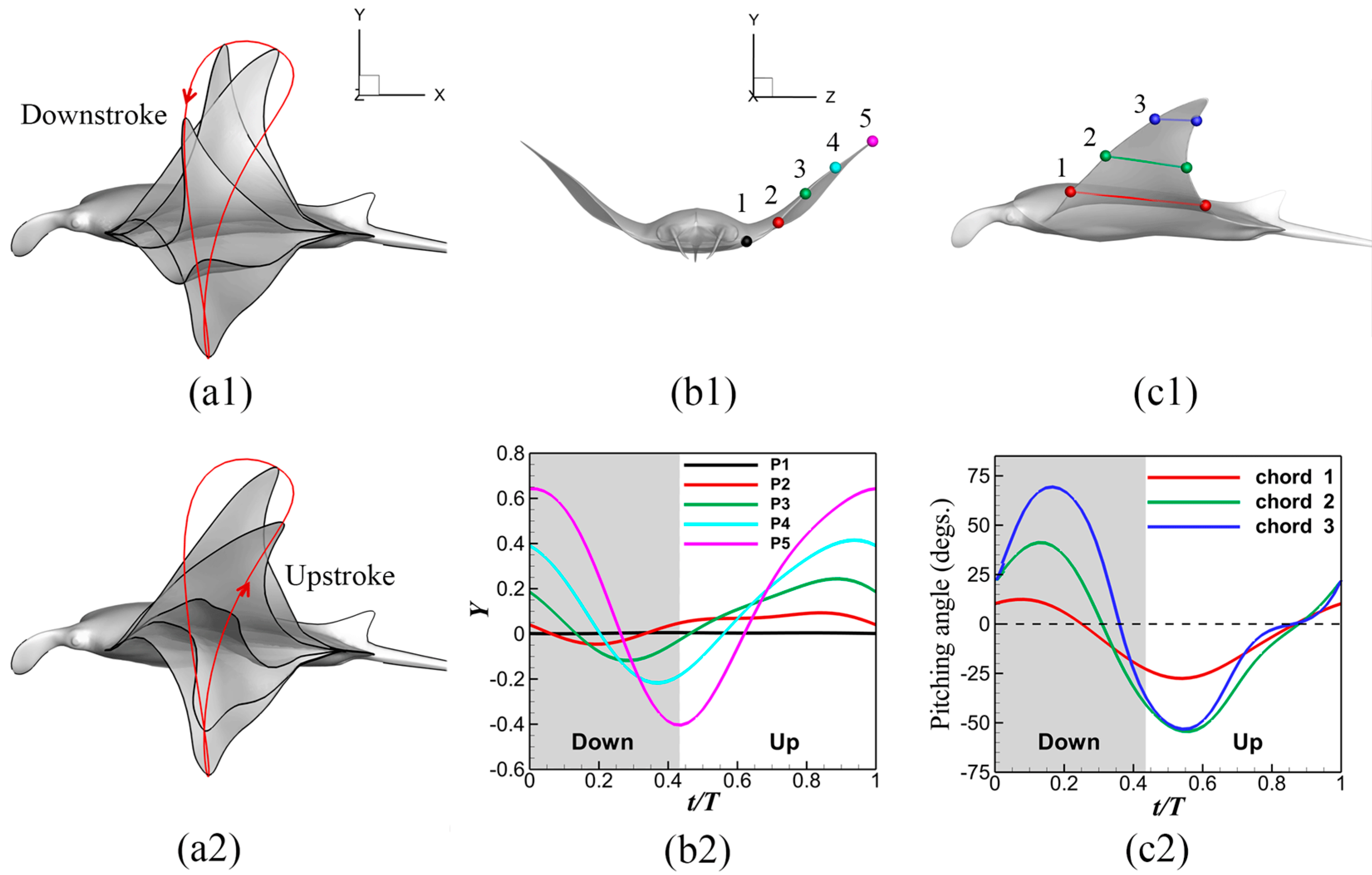
3.1. Manta Kinematics
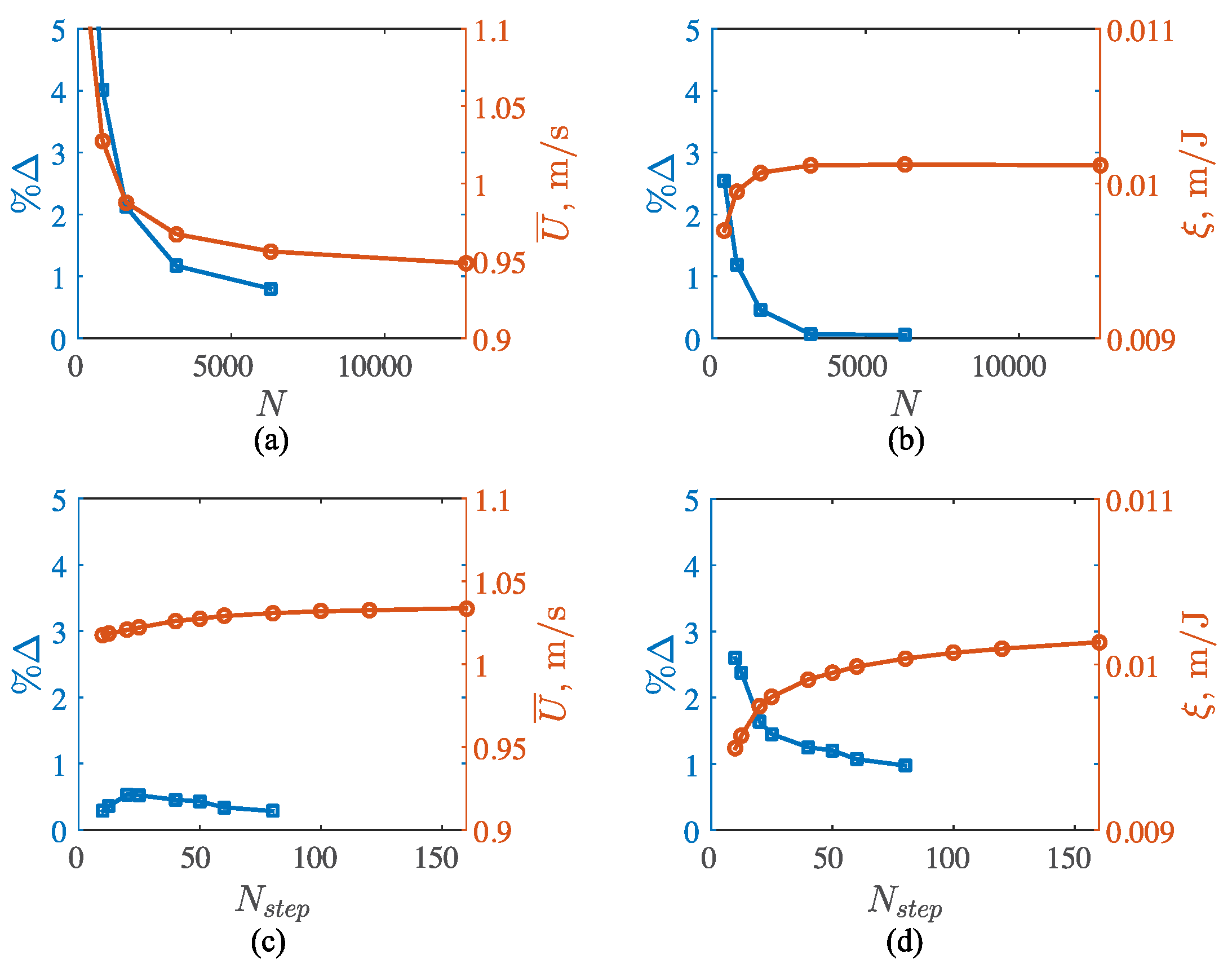
3.2. Potential Flow Model
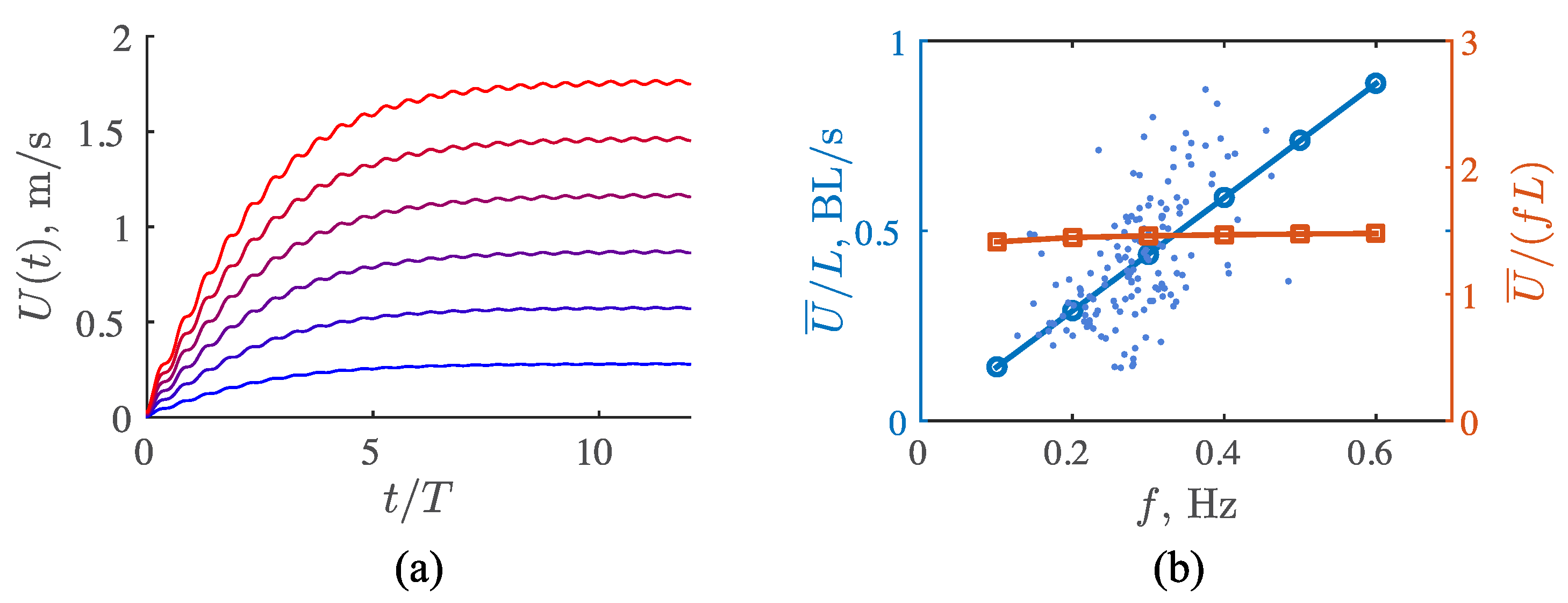
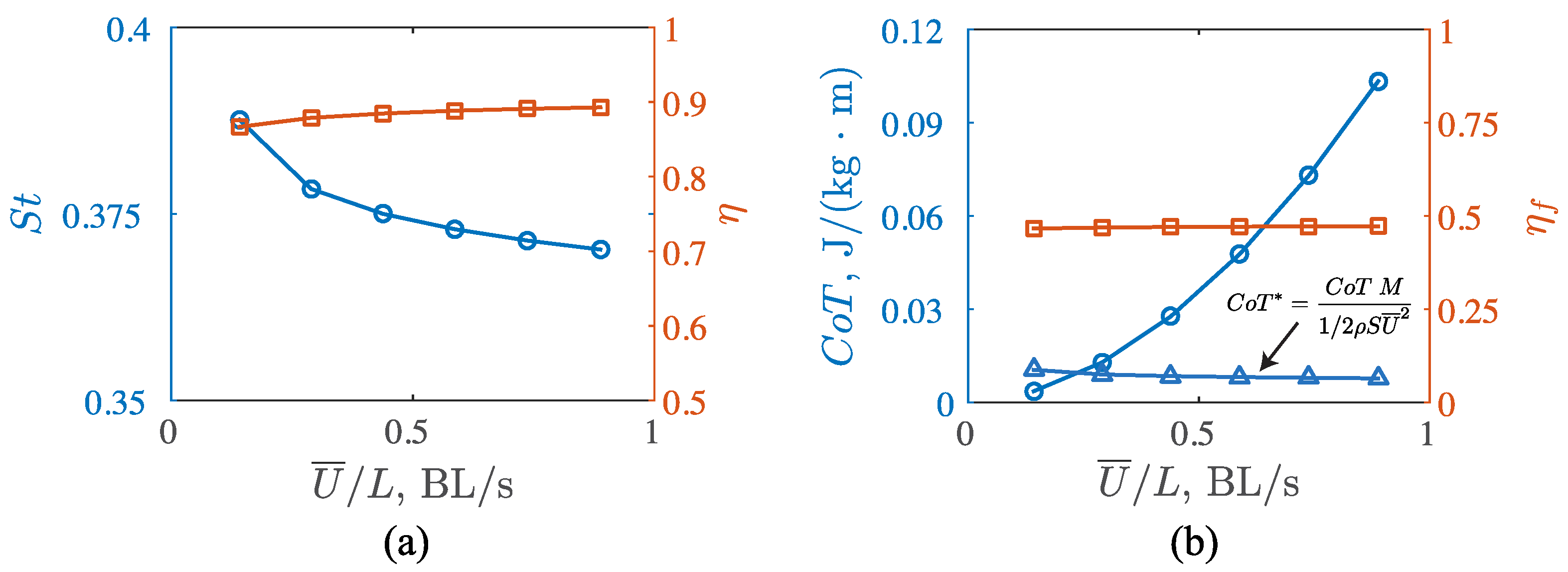
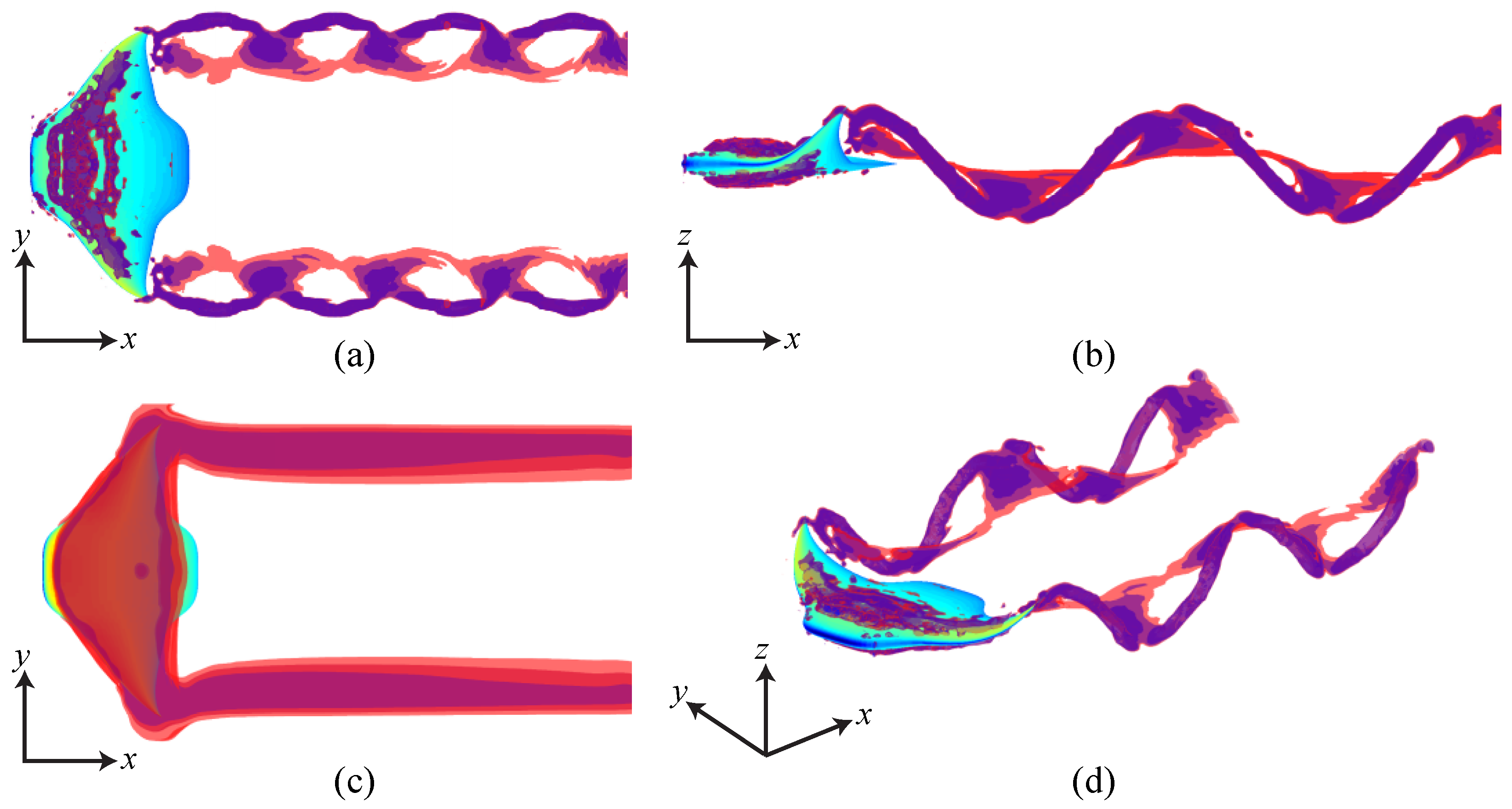
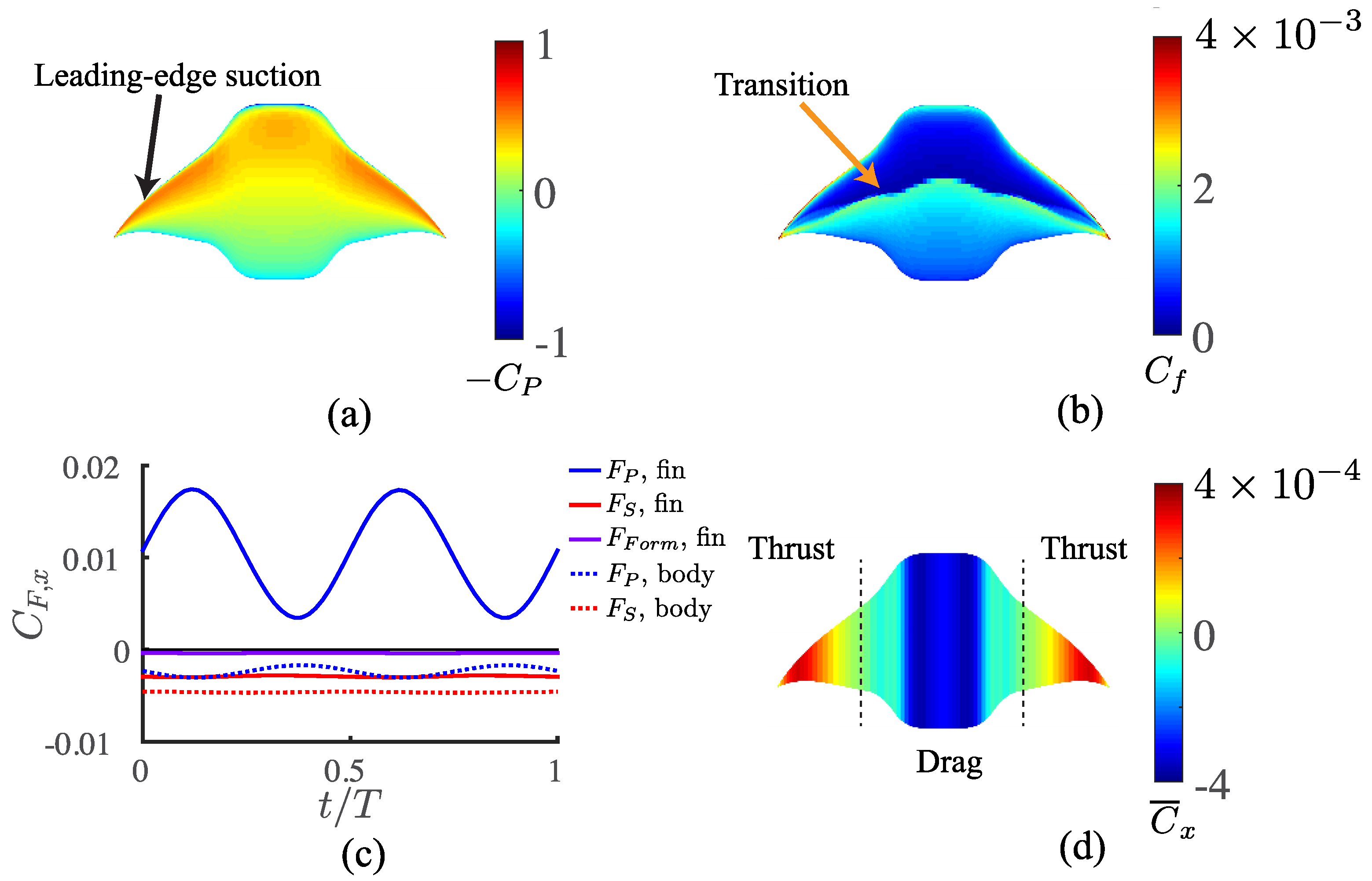
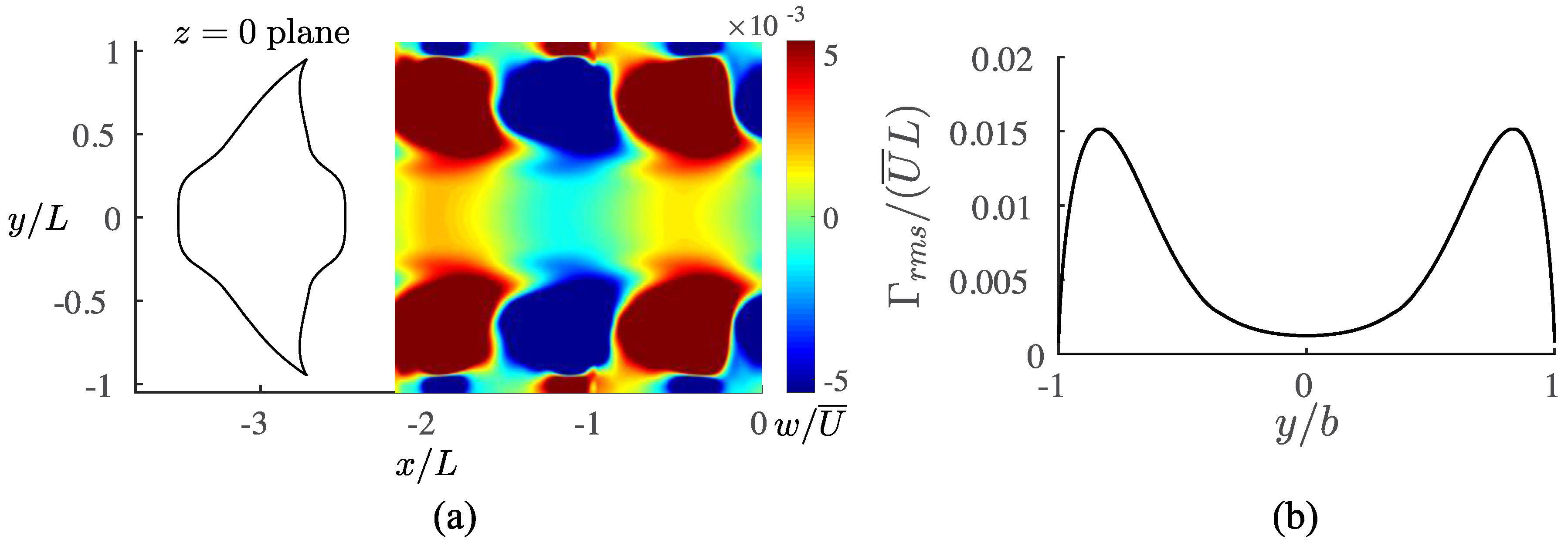
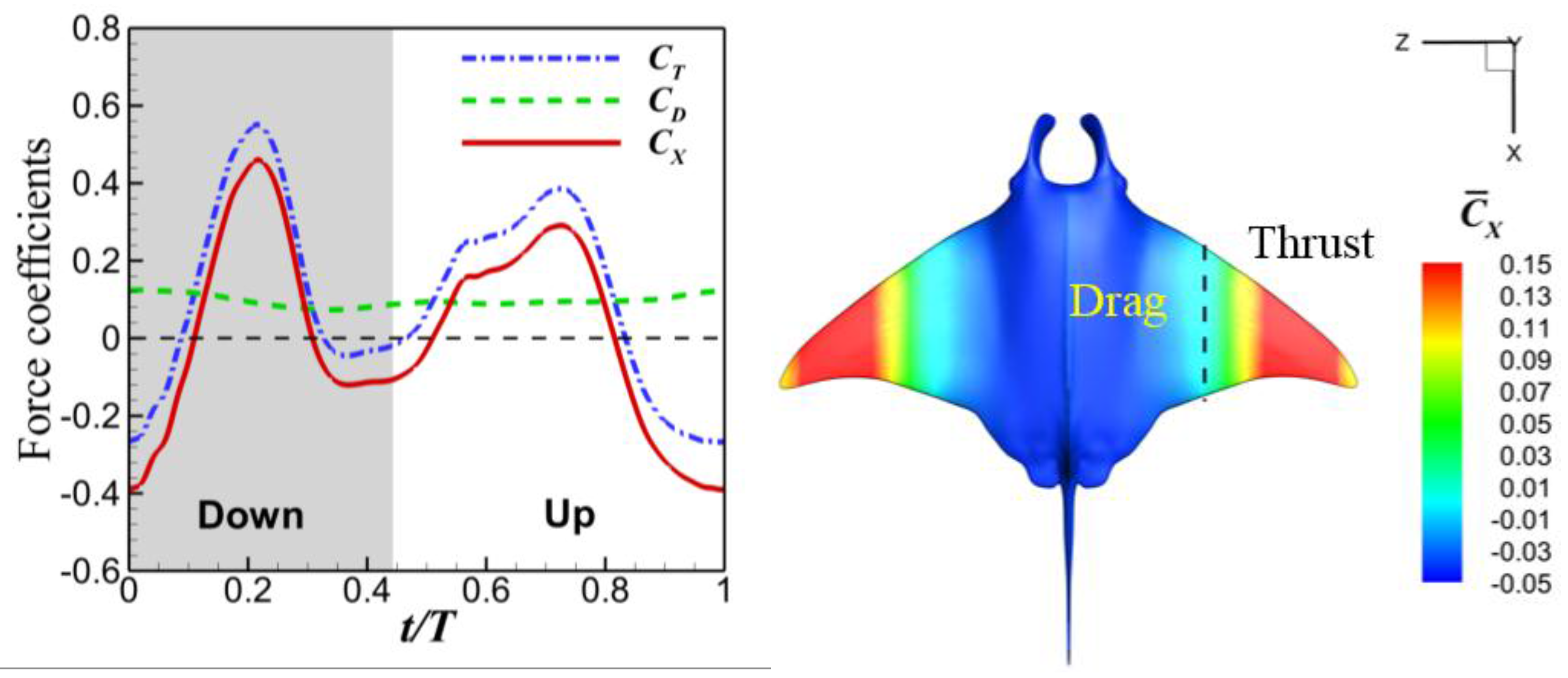
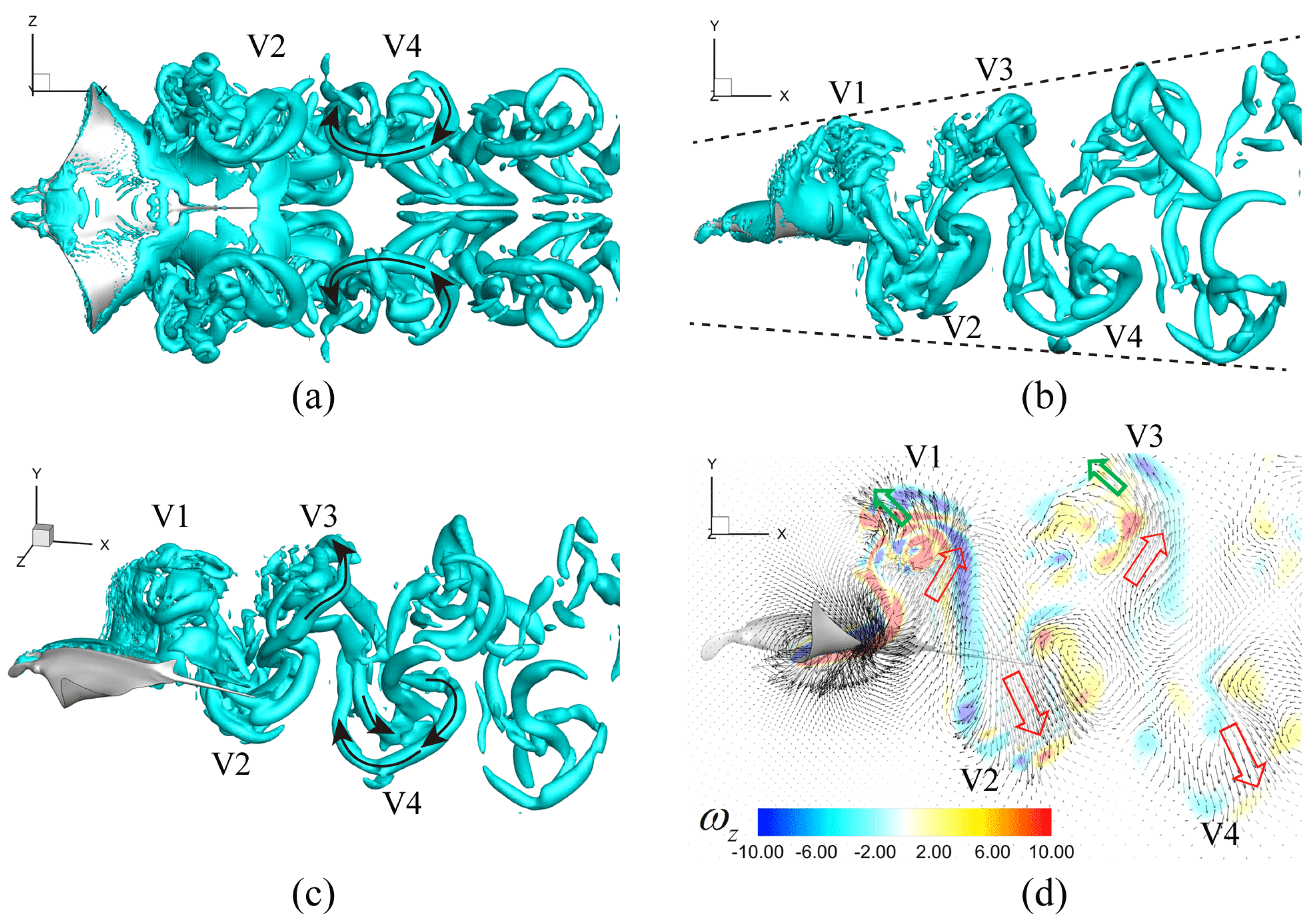
3.3. Viscous Model
4. Discussion
4.1. Comparisons among the Biological Data, Potential Flow, and Viscous Models
4.2. Manta Efficiency
4.3. Applications of Research (MantaBot)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dewar, H.; Mous, P.; Domeier, M.; Muljadi, A.; Pet, J.; Whitty, J. Movements and site fidelity of the giant manta ray, Manta birostris, in the Komodo Mari Park, Indonesia. Mar. Biol. 2008, 155, 121–133. [Google Scholar] [CrossRef]
- Rosenberger, L.J. Pectoral fin locomotion in batoid fishes: Undulation versus oscillation. J. Exp. Biol. 2001, 204, 397–394. [Google Scholar]
- Marshall, A.D.; Compagno, L.J.V.; Bennett, M.B. Redescription of the genus Manta with resurrection of Manta alfredi (Krefft, 1868) (Chondrichthyes; Myliobatoidei; Mobulidae). Zootaxa 2009, 2301, 1–28. [Google Scholar]
- Deacon, K.; Last, P.; McCosker, J.E.; Taylor, L.; Tricas, T.C.; Walker, T.I. Sharks and Rays; Fog City Press: San Francisco, CA, USA, 1997. [Google Scholar]
- Last, P.R.; Stevens, J.D. Sharks and Rays of Australia; Harvard University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Fontanella, J.E.; Fish, F.E.; Barchi, E.I.; Campbell-Malone, R.; Nichols, R.H.; DiNenno, N.K.; Beneski, J.T. Two- and three-dimensional geometries of batoids in relation to locomotor mode. J. Exp. Mar. Biol. Ecol. 2013, 446, 273–281. [Google Scholar] [CrossRef]
- Graham, R.T.; Witt, M.J.; Castellanos, D.W.; Remolina, F.; Maxwell, S.; Godley, B.J.; Hawkes, L.A. Satellite tracking of manta rays highlights challenges to their conservation. PLoS ONE 2012, 7, e36834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klausewitz, W. Der Lokomotionsmodus der Flügelrochen (Myliobtoidei). Zool. Anz. 1964, 173, 110–120. [Google Scholar]
- Heine, C. Mechanics of Flapping Fin Locomotion in the Cownose Ray, Rhinoptera bonasus (Elasmobranchii: Myliobatidae). Ph.D. Dissertation, Duke University, Durham, NC, USA, 1992. [Google Scholar]
- Webb, P.W. Hydrodynamics and energetics of fish propulsion. Bull. Fish. Res. Board Can. 1975, 190, 1–158. [Google Scholar]
- Lighthill, J. Mathematical Biofluiddynamics; Society Industry and Applied Mathematics: Philadelphia, PA, USA, 1975. [Google Scholar]
- Russo, R.S.; Blemker, S.S.; Fish, F.E.; Bart-Smith, H. Biomechanical model of batoid skeletal structure and kinematics: Implications of bio-inspired design. Bioinspir. Biomim. 2015, 10, 46002. [Google Scholar] [CrossRef] [PubMed]
- Bose, N.; Lien, J.; Ahia, J. Measurements of the bodies and flukes of several cetacean species. Proc. R. Soc. Lond. B 1990, 242, 163–173. [Google Scholar] [CrossRef]
- Katz, J.; Weihs, D. Hydrodynamic propulsion by large amplitude oscillation of an airfoil with chordwise flexibility. J. Fluid Mech. 1978, 88, 485–497. [Google Scholar] [CrossRef]
- Bose, N. Performance of chordwise flexible oscillating propulsors using a time-domain panel method. Int. Shipbuild. Progr. 1995, 42, 281–294. [Google Scholar]
- Triantafyllou, G.S.; Triantafyllou, M.S.; Grosenbaugh, M.A. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Triantafyllou, G.S.; Triantafyllou, M.S. An efficient swimming machine. Sci. Am. 1995, 272, 40–48. [Google Scholar] [CrossRef]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Rohr, J.J.; Fish, F.E. Strouhal numbers and optimization of swimming by odontocete cetaceans. J. Exp. Biol. 2004, 207, 1633–1642. [Google Scholar] [CrossRef] [PubMed]
- Eloy, C. Optimal Strouhal number for swimming animals. J. Fluids Struct. 2012, 30, 205–218. [Google Scholar] [CrossRef]
- Triantafyllou, M.S.; Triantafyllou, G.S.; Yue, D.K. Hydrodynamics of fishlike swimming. Ann. Rev. Fluid Mech. 2000, 32, 33–53. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics, 13th ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Willis, D.J.; Peraire, J.; White, J.K. A combined pFFT-multipole tree code, unsteady panel method with vortex particle wakes. Int. J. Numer. Meth. Fluids 2006, 53, 1399–1422. [Google Scholar] [CrossRef]
- Zhu, Q. Numerical simulation of a flapping foil with chordwise or spanwise flexibility. AIAA J. 2007, 45, 2448–2457. [Google Scholar] [CrossRef]
- Krasny, R. Desingularization of periodic vortex sheet roll-up. J. Comp. Phys. 1986, 65, 292–313. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Cebeci, T.; Smith, A.M. Analysis of Turbulent Boundary Layers; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Koehler, C.; Liang, Z.; Gaston, Z.; Wan, H.; Dong, H. 3D reconstruction and analysis of wing deformation in free-flying dragonflies. J. Exp. Biol. 2012, 215, 3018–3027. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.M.; Vargas, A.; von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comp. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Mittal, R.; Najjar, F.M. Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 2006, 566, 309–343. [Google Scholar] [CrossRef]
- Liu, G.; Ren, Y.; Zhu, J.; Bart-Smith, H.; Dong, H. Thrust producing mechanisms in ray-inspired underwater vehicle propulsion. Theor. Appl. Mech. Lett. 2015, 5, 54–57. [Google Scholar] [CrossRef]
- Wan, H.; Dong, H.; Gai, K. Computational investigation of cicada aerodynamics in forward flight. J. R. Soc. Interface 2015, 12, 20141116. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Dong, H.; Li, C. Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 2016, 795, 634–651. [Google Scholar] [CrossRef]
- Li, C.; Dong, H.; Liu, G. Effects of a dynamic trailing-edge flap on the aerodynamic performance and flow structures in hovering flight. J. Fluids Struct. 2015, 58, 49–65. [Google Scholar] [CrossRef]
- Bozkurttas, M.; Mittal, R.; Dong, H.; Lauder, G.V.; Madden, P. Low-dimensional models and performance scaling of a highly deformable fish pectoral fin. J. Fluid Mech. 2009, 631, 311–342. [Google Scholar] [CrossRef]
- Buchholz, J.H.; Smits, A.J. The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 2008, 603, 331–365. [Google Scholar] [CrossRef] [PubMed]
- Gabrielli, G.; von Kármán, T. What price speed? Specific power required for propulsion vehicles. Mech. Eng. 1950, 72, 775–781. [Google Scholar]
- Videler, J.J. Fish Swimming; Chapman & Hall: London, UK, 1993; pp. 185–205. [Google Scholar]
- Dabiri, J.O. On the estimation of swimming and flying forces from wake measurements. J. Exp. Biol. 2005, 208, 3519–3532. [Google Scholar] [CrossRef] [PubMed]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming. J. Exp. Biol. 2004, 11, 1825–1841. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Ghias, R.; Mittal, R.; Dong, H. A sharp interface immersed boundary method for compressible viscous flows. J. Comput. Phys. 2007, 225, 528–553. [Google Scholar] [CrossRef]
- Liu, G.; Dong, H.; Ren, Y.; Li, C.; Bart-Smith, H.; Fish, F.E. Understanding the role of fin flexion in rays’ forward swimming. In Proceedings of the 2015 Annual Meeting of Society for Integrative and Comparative Biology, West Palm Beach, FL, USA, 3–7 January 2015.
- Mittal, R.; Balachandar, S. Generation of streamwise vortical structures in bluff body wakes. Phys. Rev. Lett. 1995, 75, 1300–1304. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, G.; Dong, H. Effect of surface morphing on the wake structure and performance of pitching-rolling plates. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, AIAA-2015-1490, Kissimmee, FL, USA, 5–9 January 2015.
- Munson, B.; Young, D.; Okiishi, T. Fundamentals of Fluid Mechanics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Fish, F.E.; Lauder, G.V. Passive and active flow control by swimming fishes and mammals. Ann. Rev. Fluid Mech. 2006, 38, 193–224. [Google Scholar] [CrossRef]
- Boraziani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008, 211, 1541–1558. [Google Scholar] [CrossRef] [PubMed]
- Boraziani, I.; Sotiropoulos, F. Numerical investigation of the hydrodynamics of anguilliform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2009, 212, 576–592. [Google Scholar] [CrossRef] [PubMed]
- Bottom, R.G.; Borazjani, I.; Blevins, E.L.; Lauder, G.V. Hydrodynamics of swimming in stingrays: Numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 2016, 788, 407–443. [Google Scholar] [CrossRef]
- Fish, F.E. Comparative kinematics and hydrodynamics of odontocete cetaceans: Morphological and ecological correlates with swimming performance. J. Exp. Biol. 1998, 201, 2867–2877. [Google Scholar] [PubMed]
- Webb, P.W.; de Buffrénil, V. Locomotion in the biology of large aquatic vertebrates. Trans. Am. Fish. Soc. 1990, 119, 629–641. [Google Scholar] [CrossRef]
- Clark, R.P.; Smits, A.J. Thrust production and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 2006, 562, 415–429. [Google Scholar] [CrossRef] [PubMed]
- Moored, K.W.; Fish, F.E.; Kemp, T.H.; Bart-Smith, H. Batoid fishes: Inspiration for the next generation of underwater robots. Mar. Tech. Soc. J. 2011, 45, 99–109. [Google Scholar] [CrossRef]
- Wang, Z.J. Vortex shedding and frequency selection in flapping flight. J. Fluid Mech. 2000, 410, 323–341. [Google Scholar] [CrossRef]
- Moored, K.W.; Dewey, P.A.; Smits, A.J.; Haj-Hariri, H. Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J. Fluid Mech. 2012, 708, 329–348. [Google Scholar] [CrossRef]
- Moored, K.W.; Dewey, P.A.; Smits, A.J.; Haj-Hariri, H. Linear instability mechanisms leading to optimally efficient locomotion with flexible propulsors. Phys. Fluids 2014, 26, 1–15. [Google Scholar] [CrossRef]
- Fish, F.E.; Haj-Hariri, H.; Smits, A.J.; Bart-Smith, H.; Iwasaki, T. Biomimetic swimmer inspired by the manta ray. In Biomimetics: Nature-Based Innovation; Bar-Cohen, Y., Ed.; CRC Press: Boca Rotan, FL, USA, 2012; pp. 495–523. [Google Scholar]
- Wen, L.; Wang, T.M.; Wu, G.H.; Liang, J.H. Hydrodynamic investigation of a self-propelled robotic fish based on a force-feedback control method. Bioinspir. Biomim. 2012, 7, 036012. [Google Scholar] [CrossRef] [PubMed]
- Moored, K.W.; Kemp, T.H.; Houle, N.E.; Bart-Smith, H. Analytical predictions, optimization, and design of a tensegrity-based artificial pectoral fin. Int. J. Solids Struct. 2011, 48, 3142–3159. [Google Scholar] [CrossRef]
- Fish, F.E. Limits of nature and advances of technology: What does biomimetics have to offer to aquatic robots? Appl. Bionics Biomech. 2006, 3, 49–60. [Google Scholar] [CrossRef]




| 0.111 | 0.097 | 0.014 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fish, F.E.; Schreiber, C.M.; Moored, K.W.; Liu, G.; Dong, H.; Bart-Smith, H. Hydrodynamic Performance of Aquatic Flapping: Efficiency of Underwater Flight in the Manta. Aerospace 2016, 3, 20. https://doi.org/10.3390/aerospace3030020
Fish FE, Schreiber CM, Moored KW, Liu G, Dong H, Bart-Smith H. Hydrodynamic Performance of Aquatic Flapping: Efficiency of Underwater Flight in the Manta. Aerospace. 2016; 3(3):20. https://doi.org/10.3390/aerospace3030020
Chicago/Turabian StyleFish, Frank E., Christian M. Schreiber, Keith W. Moored, Geng Liu, Haibo Dong, and Hilary Bart-Smith. 2016. "Hydrodynamic Performance of Aquatic Flapping: Efficiency of Underwater Flight in the Manta" Aerospace 3, no. 3: 20. https://doi.org/10.3390/aerospace3030020
APA StyleFish, F. E., Schreiber, C. M., Moored, K. W., Liu, G., Dong, H., & Bart-Smith, H. (2016). Hydrodynamic Performance of Aquatic Flapping: Efficiency of Underwater Flight in the Manta. Aerospace, 3(3), 20. https://doi.org/10.3390/aerospace3030020






